Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 7 సమతలం Exercise 7(a) will help students to clear their doubts quickly.
AP Inter 1st Year Maths 1B Solutions Chapter 7 సమతలం Exercise 7(a)
అభ్యాసం – 7 (ఎ)
I.
ప్రశ్న 1.
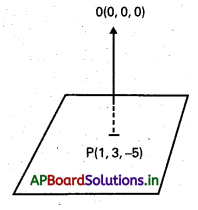
మూలబిందువు నుంచి తలానికి గీసిన లంబపాదం (1, 3, -5) అయితే, ఆ తలం సమీకరణం రాయండి.
సాధన:
OP రేఖ గమన తలానికి లంబంగా ఉంది. OP యొక్క
D.R లు 1, 3, -5
సమతలము P(1, 3, 5) గుండా పోతుంది. సమతల సమీకరణము
– 1 (x – 1) + 3(y -3) – 5(z + 5) = 0
x – 1 + 3y – 9 – 5z – 25 = 0
x + 3y – 5z – 35 = 0
ప్రశ్న 2.
తలం సమీకరణం x + 2y – 3z – 6 = 0 ని అభిలంబ రూపానికి కుదించండి. [Mar. ’14]
సాధన:
సమతల సమీకరణము x + 2y – 3z-6=0
i.e., x + 2y – 3z = 6
\(\sqrt{1^2+2^2+(-3)^2}\) = \(\sqrt{1+4+9}\)
= \(\sqrt{14}\) తో భాగించగా
అభిలంబ రూపంలో సమతల సమీకరణము
x+y+ z=
\(\left(\frac{1}{\sqrt{14}}\right)\) x + \(\left(\frac{2}{\sqrt{14}}\right) \) y + \(\left(\frac{-3}{\sqrt{14}}\right)\) z = \(\frac{6}{\sqrt{14}}\)
![]()
ప్రశ్న 3.
X, Y, Z – అంతర ఖండాలు 1, 2, 4 గా కలిగిన సమతలం సమీకరణం రాయండి.
సాధన:
అంతరఖండ రూపంలో సమతల సమీకరణము
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1
దత్తాంశం a = 1, b = 2, c = 4.
అంతరఖండ రూపంలో సమతల సమీకరణము
\(\frac{x}{1}+\frac{y}{2}+\frac{z}{4}\) = 1
4తో గుణించగా, 4x + 2 y + z = 4
ప్రశ్న 4.
నిరూపకాక్షాలపై 4x + 3y + 2z + 2 = 0 తలం చేసే అంతర ఖండాలను కనుక్కోండి.
సాధన:
సమతల నిరూపకము 4x + 3y – 2z + 2 = 0
– 4x – 3y + 2z = 2
\(-\frac{4 x}{2}-\frac{3 y}{2}+\frac{2 z}{2}\) = 1
\(\frac{x}{\left(-\frac{1}{2}\right)}+\frac{y}{\left(-\frac{2}{3}\right)}+\frac{z}{1}\) = 1
x – అంతరఖండము = \(\frac{-1}{2}\)
y – అంతరఖండము = \(\frac{-2}{3}\)
z – అంతరఖండము = 1.
ప్రశ్న 5.
x + 2y + 2z – 4 = 0 తలానికి అభిలంబ రేఖ దిక్ కొసైన్లు కనుక్కోండి. [Mar ’13; May ’12]
సాధన:
సమతల సమీకరణం x + 2y + 2z– 4 = 0
అభిలంబరేఖకు DR లు (1, 2, 2)
\(\sqrt{1+4+4}\) = 3 తో, భాగించగా,
అభిలంబరేఖ D.c. లు \(\left(\frac{1}{3}, \frac{2}{3}, \frac{2}{3}\right)\)
![]()
ప్రశ్న 6.
(−2, 1, 3) గుండాపోతూ, (3, -5, 4) అభిలంబ రేఖ దిక్ సంఖ్యలుగా గలిగిన తలం సమీకరణం కనుక్కోండి.
సాధన:
అభిలంబరేఖ D.r. లు (3, -5, 4) మరియు
తలము (-2, 1, 3) గుండా పోతుంది. ‘
సమతల సమీకరణము
3(x + 2) – 5(y – 1) + 4(z – 3) = 0
3x + 6 – 5y + 5 + 4z – 12 = 0.
3x – 5y + 4z – 1 = 0
ప్రశ్న 7.
4x – 4y + 2z + 5 = 0 సమీకరణాన్ని అంతర ఖండ రూపంలోకి మార్చండి. [May ’12]
సాధన:
సమతల సమీకరణము 4x – 4y + 2z + 5 = 0
– 4x + 4y – 22 = 5
–\(\frac{4x}{5}\) + \(\frac{4y}{5}\) – \(\frac{2z}{5}\) = 1
అంతరఖండ రూపము \(\frac{x}{\left(\frac{-5}{4}\right)}+\frac{y}{\left(\frac{5}{4}\right)}+\frac{z}{\left(-\frac{5}{2}\right)}\) = 1
x – అంతర ఖండము = –\(\frac{5}{4}\)
y – అంతర ఖండము = \(\frac{5}{4}\)
z – అంతర ఖండము = –\(\frac{5}{2}\)
![]()
ప్రశ్న 8.
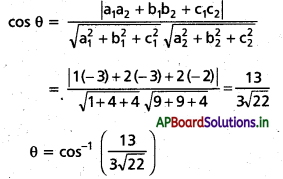
x + 2y + 2z – 5 = 0, 3x + 3y + 2z – 8 = 0 తలాల మధ్యకోణం కనుక్కోండి. [T.S Mar. ’15]
సాధన:
సమతలాల సమీకరణాలు x + y + 2z – 5 = 0
3x + 3y + 2z – 8 = 0
II.
ప్రశ్న 1.
(1, 1,1 ) గుండాపోతూ, x + 2y + 3z – 7=0 తలానికి సమాంతరంగా ఉండే తలం సమీకరణం రాయండి. [May ’11]
సాధన:
దత్త సమతల సమీకరణము x + y + 3z – 7 = 0.
సమాంతర తలం సమీకరణము x + 2 + 3z = k.
ఈ తలం P (1, 1, 1) గుండా పోతూ,
1 + 2 + 3 = k ⇒ k = 6
కావలసిన సమతల సమీకరణము x + 2 y + 3z = 6
ప్రశ్న 2.
(2, 3, 4) బిందువు గుండా పోతూ, X- అక్షానికి లంబంగా ఉండే తలం సమీకరణం కనుక్కోండి.
సాధన:
సమతలం X అక్షానికి లంబంగా ఉంటుంది.
∴ X – అక్షం సమతలానికి అభిలంబరేఖ
X – అక్షం d.c. లు 1, 0, 0
కావలసిన సమతల సమీకరణము x = k
ఈ తలము P(2, 3, 4) గుండా పోతుంది.
∴ 22 = k
కావలసిన సమతల సమీకరణము x = 2.
![]()
ప్రశ్న 3.
2x + 3y + 7 = 0, XY – తలానికి లంబంగా ఉండే + + 7 తలాన్ని సూచిస్తుందని చూపండి.
సాధన:
దత్త సమతల సమీకరణము 2x + 3y + 7 = 0
xy తలం సమీకరణము z = 0
a1a2 + b1b2 + c1c2 = 2.0 + 3.0 + 0.1
= 0 + 0 + 0 = 0
2x + 3y + 7 = 0 తలము XY-తలానికి లంబంగా ఉంది.
ప్రశ్న 4.
x – 2y + kz = 0, 2x + 5y – z = 0 తలాలు పరస్పరం లంబంగా ఉండేటట్లు k విలువ కనుక్కోండి. ఈ తలాలకు లంబంగా ఉంటూ, (1, -1, -1) బిందువు గుండా పోయే తలాన్ని కనుక్కోండి.
సాధన:
దత్త తలాల సమీకరణాలు x – 2 y + kz = 0
మరియు 2x + 5y – z = 0
ఈ తలాలు లంబంగా ఉన్నాయి.
1.2 – 2.5 + k (-1) = 0
2 – 10 = k ⇒ k = -8
సమతల సమీకరణాలు x – 2y – 8z = 0 ……………. (1)
2x + 5y – z. = 0 ………………… (2)
ఈ తలం (1, −1, −1) గుండాపోతూ సమతల సమీకరణాన్ని
a(x + 1) + b(y + 1) + c(z + 1) = 0 ……………… (3) గా వ్రాయగలము.
ఈ తలం (1), (2) తలాలకు లంబం
a – 2b – 8c = 0
2a + 5b – c = 0
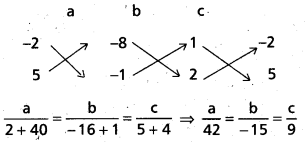
(3) లో ప్రతిక్షేపించగా, కావలసిన సమతల సమీకరణము
42(x – 1) – 15(y + 1) + 9(z + 1) = 0
42x – 42 – 15y – 15 + 9z + 9 = 0
42x – 15y + 92 – 48 = 0.
![]()
ప్రశ్న 5.
(-1, 6, 2) గుండాపోతూ (1, 2, 3), (−2, 3, 4) బిందువులను కలిపే రేఖకు లంబంగా ఉండే తలం సమీకరణం రాయండి.
సాధన:
A(1, 2, 3), B(-2, 3, 4) బిందువులను కలిపే రేఖాఖండానికి లంబంగా ఉంది.
AB యొక్క d.r. లు 1 + 2, 2 – 3, 3 – 4
i.e., 3, -1, – 1
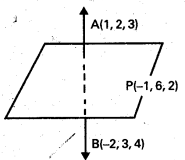
AB రేఖ అభిలంబరేఖ సమతలము P(-1, 6, 2) గుండా పోతుంది.
కావలసిన సమతల సమీకరణము
3(x + 1) – 1(y – 6) – 1 (z – 2) = 0
3x + 3 y + 6 – z + 2 = 0
3x = y – z + 11 = 0
ప్రశ్న 6.
(2, 0, 6), (–6, 2, 4) బిందువులను కలిపే రేఖకు లంబంగా ఉంటూ, దానిని సమద్విఖండన చేసే తలం సమీకరణం రాయండి.
సాధన:
A (2, 0, 6), B(-6, 2, 4) లు దత్త బిందువులు.
AB కి మధ్యబిందువు ‘0’
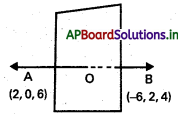
0 నిరూపకాలు \(\left(\frac{2-6}{2}, \frac{0+2}{2}, \frac{6+4}{2}\right)\) = (-2, 1, 5)
సమతలము AB కి లంబంగా ఉంది.
సమతల అభిలంబరేఖ d.r.లు
2 + 6, 0 – 2, 6 – 4.
8, -2, 2
సమతల సమీకరణము
+8 (x + 2) – 2(y – 1) + 2 (2 – 5) = 0
8x + 16 – 2y + 2 + 2z – 10 = 0
8x – 2y + 2z + 8 = 0
![]()
ప్రశ్న 7.
(0, 0, – 4) బిందువు గుండా పోతూ (1, −2, 2); (-3, 1, -2) బిందువులను కలిపే రేఖకు లంబంగా ఉండే ‘తలం సమీకరణం రాయండి.
సాధన:
A(1, -2, 2), B (-3, 1, -2) లు దత్తబిందువులు.
AB యొక్క d.r.లు 1 + 3, -2 – 1, 2 + 2 i. e., 4, -3, 4
AB సమతలానికి లంబంగా ఉంటే P(0, 0, -4) సమతల సమీకరణము
4(x – 0) – 3 (y – 0) + 4(z + 4) = 0
4x – 3y + 4z + 16 = 0
ప్రశ్న 8.
(4, 4, 0) గుండా పోతూ, 2x + y + 2x + 3 = 0, 3x + 3y + 2z – 8 = 0 తలాలకు లంబంగా ఉండే తలం సమీకరణం కనుక్కోండి.
సాధన:
(4; 4, 0) గుండా పోయే సమతల సమీకరణం
a(x – 4) + b(y – 4) + c(z – 0) = 0 ……………. (1)
ఈ తలం 2x + y + 2z – 3 = 0
3x + 3y + 2z – 8 = 0 లకు లంబంగా ఉంది.
∴ 2a + b + c = 0 ………………….(2)
3a + 3b + 2c = 0 …………………. (3)
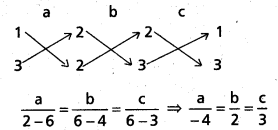
(1) లో ప్రతిక్షేపిస్తే, సమతల సమీకరణము
-4 (x – 4) + 2(y – 4) + 3(z – 0) = 0
-4x + 16 + 2y – 8 + 3z = 0
-4x + 2y + 3z + 8 = 0
![]()
III.
ప్రశ్న 1.
(2, 2, -1), (3, 4, 2), (7, 0, 6) బిందువుల గుండా పోయే తలం సమీకరణం కనుక్కోండి.
సాధన:
A(2, 2, -1), B (3, 4, 2), C(7, 0, 6) లు దత్త బిందువులు.
A(2, 2, -1) గుండాపోవు సమతల సమీకరణము
a(x – 2) + b(y – 2) + c(z + 1) = 0 ……….. (1)
ఈ సమతలం B(3, 4, 2) మరియు C(7, 0, 6) ల గుండా పోతుంది.
a(3 – 2) + b(4 – 2) + c(2 + 1) = 0
a + 2b + 3c = 0 ……………. (2)
a(7 – 2) + b(0 – 2) + c(6 + 1) = 0
5a – 2b + 7c = 0 ……………. (3)
(2) మరియు (3) ల నుండి
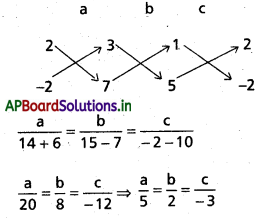
(1) లో ప్రతిక్షేపించగా, సమతల సమీకరణము
5(x – 2) + 2(y – 2) – 3(z + 1) = 0
5x – 10 + 2y – 4 – 3z – 3 = 0
5x + 2y – 3z – 17 = 0
5x + 2y – 3z = 17
ప్రశ్న 2.
బిందువులు (0, 1, 0), (2, 1, -1), (1, 1, 1), (3, 3, 0) సతలీయాలని చూపండి. (మూడు బిందువుల గుండా పోయే తలం సమీకరణం కనుక్కొని నాలుగో బిందువు ఆ తలంపై ఉంటుందని చూపండి.
సాధన:
A(0, -1, 0) గుండా పోవు సమతల సమీకరణము
ax + b(y + 1) + cz = 0 ………………… (1)
ఈ తలము B(2, 1, – 1), C(1, 1, 1) ల గుండా పోతుంది.
2a + 2b c = 0 ……………….. (2)
a + 2b + c = 0 ……………… (3)
(2) – (3) ⇒ a – 2c = 0 ⇒ a = 2c ⇒ \(\frac{a}{2}=\frac{c}{1}\)
(2) + (3) ⇒ 3a + 4b = 0 ⇒ 3a = -4b
⇒ \(\frac{a}{4}=\frac{b}{-3}\)
∴ \(\frac{a}{4}=\frac{b}{-3}=\frac{c}{2}\)
(1) లో ప్రతిక్షేపించగా, ABC తల సమీకరణము
4x – 3(y + 1) + 2 (z – 0) = 0
4x – 3y + 2z – 3 = 0
4x – 3y + 2z – 3 = 4.3 – 3.3.+0.3
= 12 – 9 – 3 = 0
సతలీయాలు A, B, C, D బిందువులు.
![]()
ప్రశ్న 3.
(6, – 4, 3), (0, 4, -3) బిందువుల గుండాపోతూ నిరూపకాక్షాలపై అంతర ఖండాల మొత్తం సున్నా అయ్యే తలాల సమీకరణాలను కనుక్కోండి.
సాధన:
a, b, c లు అంతర ఖండాలు అనుకొనుము.
సమతల సమీకరణము \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1
a + b + c = 0
c = – (a + b)
ఈ తలం P (6, – 4, 3), Q(0, 4, – 3)ల గుండా పోతుంది.
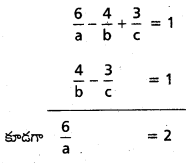
a = \(\frac{6}{2}\) = 3
\(\frac{4}{b}-\frac{3}{c}\) = 1 ⇒ 4c – 3b= bc
c = -a – b = -3 – b
4(-3 – b) – 3b = b(-3 – b)
-12 – 4b – 3b = -3b – b2
b2 – 4b – 12 = 0
(b – 6) (b + 2) = 0 ⇒ b = 6, -2
సందర్భం i) : b = 6
c = -3 – b = -3 – 6 = -9
సమతల సమీకరణము
\(\frac{x}{3}+\frac{y}{6}-\frac{z}{9}\) = 1
6x + 3y – 2z = 18
సందర్భం ii): b = -2
c = -3 – b = -3 + 2 = − 1
సమతల సమీకరణము
\(\frac{x}{3}+\frac{y}{-2}+\frac{z}{-1}\) = 1
![]()
ప్రశ్న 4.
ఒక తలం నిరూపకాక్షాలను A, B, C బిందువులలో ఖండిస్తుంది. ∆ABC కేంద్రాభాసం (a, b, c) అయితే, తలం సమీకరణం \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 3 అని చూపండి.
సాధన:
α, β, γ లు ABC ల సమతలం నిరూపకాక్షాలను చేసే, అంతరఖండాలు అనుకుందాం. అంతరఖండ సమతల సమీకరణము
\(\frac{x}{\alpha}+\frac{y}{\beta}+\frac{z}{\gamma}\) = 1 …………… (1)
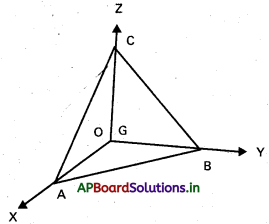
A, B, C ల నిరూపకాలు
A(α, 0, 0), B(0, β, 0), C (0, 0, γ)
∆ABC యొక్క కేంద్రాభాసము G
G నిరూపకలు \(\left(\frac{\alpha}{3}, \frac{\beta}{3}, \frac{\gamma}{3}\right)\) = (a, b, c)
\(\frac{\alpha}{3}\) = a, \(\frac{\beta}{3}\) = b, \(\frac{\gamma}{3}\) = c
α = 3a, β = 3b, γ = 3c
(1) లో ప్రతిక్షేపిస్తే, ABC తల సమీకరణము
\(\frac{x}{3 a}+\frac{y}{3 b}+\frac{z}{3 c}\) = 1
⇒ \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 3
ప్రశ్న 5.
(1, 1, 1), (1, -1, 1), (- 7, -3, -5) బిందువుల గుండాపోయే తలం Y-అక్షానికి సమాంతరంగా ఉంటుందని చూపండి.
సాధన:
A(1, 1, 1) గుండా పోయే సమతల సమీకరణము
a(x – 1) + b(y − 1 ) + c(z – 1) = 0 ……………… (1)
ఈ తలం B(1, – 1, 1), C (- 7, – 3, – 5) ల గుండా పోతుంది.
0 – 2b + 0 = 0 = b = 0
zx-తలం సమీకరణము y = 0
0.x + 1. y + 0. z = 0
a. 0 + 0. 1 + c.0 = 0
కావలసిన తలం zx – తలానికి లంబంగా ఉంది.
కనుక Y – అక్షానికి లంబంగా ఉంది.
![]()
ప్రశ్న 6.
ax + by + r = 0, by + cz + p = 0, cz + ax + q = 0 సమీకరణాలు వరుసగా XY, YZ, ZX – తలాలకు లంబంగా ఉండే తలాలను సూచిస్తాయని చూపండి.
సాధన:
దత్త సమతల సమీకరణము
ax + by + c = 0
అభిలంబరేఖ d.r.లు (a, b, c)
XYZ తలం సమీకరణము z = 0
అభిలంబరేఖ d.r.లు (0, 0, 1)
a.0 + b.0 + 0.1 = 0
∴ ax + by + r = 0 తలం xy- తలానికి లంబంగా ఉంది.
ఇదేవిధంగా by + cz + p = 0
yz – తలానికి మరియు cz + ax + q = 0
zx – తలానికి లంబంగా ఉన్నాయని చూపవచ్చును.