AP Inter 1st Year Maths 1B Solutions Chapter 9 అవకలనం Ex 9(c)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 9 అవకలనం Exercise 9(c) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 9 అవకలనం Exercise 9(c)

అభ్యాసం – 9 (సి)

I.

ప్రశ్న 1.
క్రింది ప్రమేయాలకు అవకలజాలను కనుక్కోండి.

i) sin^-1 (3x – 4x³) (May ’11)
సాధన:
x = sin θ ప్రతిక్షేపించగా,
y = sin^-1 (3 sin θ – 4 sin³ θ)
= sin^-1 (sin 3θ)
= 3θ = 3 sin^-1 x.
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{3}{\sqrt{1-x^2}}\)

ii) cos^-1 (4x³ – 3x) (Mar. ’14)
సాధన:
x = cos θ ప్రతిక్షేపించగా,
y = cos^-1 (4 cos³ θ – 3 cos θ)
= cos^-1 (cos 3θ) = 3θ = 3 cos^-1x
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(-\frac{3}{\sqrt{1-x^2}}\)

iii) sin^-1 \(\left(\frac{2 x}{1+x^2}\right)\) (T.S Mar. ’15)
సాధన:
x = tan θ ⇒ y
= sin^-1 \(\left(\frac{2 \tan \theta}{1+\tan ^2 \theta}\right)\) = sin^-1 (sin 2θ)
= 2θ = 2 tan^-1 x; \(\frac{d y}{d x}\) = \(\frac{2}{1+x^2}\)

iv) tan^-1 \(\left(\frac{a-x}{1+a x}\right)\)
సాధన:
a = tan α, x = tan θ
y = tan^-1 \(\left(\frac{\tan \alpha-\tan \theta}{1+\tan \alpha \tan \theta}\right)\)
= tan^-1(tan (α – θ)) = α – θ
= tan^-1 a – tan^-1 x;
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 0 – \(\frac{1}{1+x^2}\) = –\(\frac{1}{1+x^2}\)

v) tan^-1 \(\sqrt{\frac{1-\cos x}{1+\cos x}}\)
సాధన:

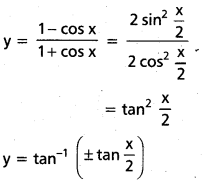
సందర్భము :1.
y = tan^-1\(\left(\tan \frac{x}{2}\right)\) 0 < x < π
x దృష్ట్యా అవకలనం చేయగా
\(\frac{d y}{d x}\) = \(\frac{1}{2}\)

సందర్భము : 2.
y = tan^-1 \(\left(-\tan \frac{x}{2}\right)\)0 – π < x < 0
= \(-\frac{x}{2}\)
x దృష్ట్యా అవకలనం చేయగా
\(\frac{d y}{d x}\) = \(-\frac{1}{2}\)
= \(\frac{d y}{d x}\) = \(-\frac{1}{2}\), 0 < x < π అయితే
= –\(\frac{1}{2}\), -π < x < 0 అయితే

vi) sin[cos (x²)]
సాధన:
\(\frac{d y}{d x}\) = cos [cos (x²)] + \(\frac{d}{d x}\)[cos (x²)]
= cos [cos (x²)]. [- sin (x²)] \(\frac{d}{d x}\left(x^2\right)\)
= cos [cos (x²)] [- sin (x²)]. 2x
= -2x. sin (x²). cos [cos (x²)]

vii) sec^-1 \(\left(\frac{1}{2 x^2-1}\right)\) \(\left(0<x<\frac{1}{\sqrt{2}}\right)\) (Mar. 13)
సాధన:
x = cos θ అనుకొందాం
2x² – 1 = 2 cos² θ – 1 = cos 2θ
y = sec^-1\(\left(\frac{1}{\cos 2 \theta}\right)\) = sec^-1 (sec 2θ) = 2θ
= 2 cos^-1 x
\(\frac{d y}{d x}\) = 2\(\left(\frac{-1}{\sqrt{1-x^2}}\right)\) = \(\frac{-2}{\sqrt{1-x^2}}\)

viii) sin [tan^-1 (e^-x)]
సాధన:
\(\frac{d y}{d x}\) = cos [tan^-1 (e^-x)]. [tan^-1 (e^-x)]¹
= cos (tan^-1 (e^-x)] – \(\frac{1}{1+\left(e^{-x}\right)^2}\)(e^-x)¹
= \(\frac{-e^{-x}}{1+e^{-2 x}}\) . cos [tan^-1 (e^-x)]

ప్రశ్న 2.
క్రింది వాటికి g(x) దృష్ట్యా f(x) ను అవకలనం చేయండి.

i) f(x) = e^x, g(x) = \(\sqrt{x}\)
సాధన:
y = e^x, z = \(\sqrt{x}\) అనుకుందాం.

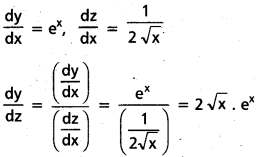
ii) f(x) = e^{sin x}, g(x) = sin x
సాధన:
y = e^{sin x}, g(x) = sin x
\(\frac{d y}{d x}\) = e^{sin x} . cos x, \(\frac{d z}{d x}\) = cos x
\(\frac{\mathrm{dy}}{\mathrm{dz}}\) = \(\frac{\left(\frac{d y}{d x}\right)}{\left(\frac{d z}{d x}\right)}\) = \(\frac{e^{\sin x} \cdot \cos x}{\cos x}\) = e^{sin x}

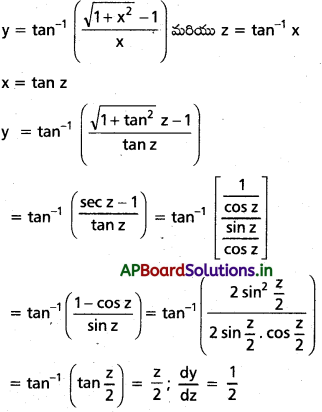
iii) f(x) = tan^-1 \(\left(\frac{2 x}{1-x^2}\right)\), g(x) = sin^-1 \(\left[\frac{2 x}{1+x^2}\right]\)
సాధన:
y = tan^-1 \(\left(\frac{2 x}{1-x^2}\right)\) మరియు z = sin^-1 అనుకుందాం.
x = tan θ ప్రతిక్షేపించగా,

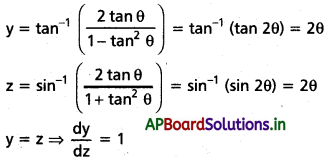
ప్రశ్న 3.
y = e^{a sin-1x} అయితే \(\frac{d y}{d x}\) = \(\frac{\text { ay }}{\sqrt{1-x^2}}\) అని నిరూపించండి.
సాధన:
y = e^{a sin-1 x}
\(\frac{d y}{d x}\) = e^{a sin-1x} x(a sin^-1 x)¹
= e^{a sin-1x}. a \(\frac{1}{\sqrt{1-x^2}}\) = \(\frac{\text { ay }}{\sqrt{1-x^2}}\)

II.

ప్రశ్న 1.
క్రింది ప్రమేయాల అవకలజాలను కనుక్కోండి.

i) tan^-1 \(\left(\frac{3 a^2 x-x^3}{a\left(a^2-3 x^2\right)}\right)\)
సాధన:
x = a tan θ ప్రతిక్షేపించగా,

ii) tan^-1 (sec x + tan x)
సాధన:
y = sec x + tan x

iii)
tan^-1 \(\left(\frac{\sqrt{1+x^2}-1}{x}\right)\)
సాధన:
x = tan θ ప్రతిక్షేపించగా,

iv) (log x)^{tan x}
సాధన:
log y = log (log x)^{tan x}
= (tan x). log (log x)
x దృష్ట్యా అవకలనం చేయగా,

v) (x^x)^x
సాధన:
f(x) = x^x
log y = log x^x = x. log x
\(\frac{1}{y} \cdot \frac{d y}{d x}\) = \(x^2 \cdot\left(\frac{\log }{x} x\right)\) + (log x) \(\frac{d}{d x}\)(x²)
= x². \(\frac{1}{x}\) + 2x. log x
= x + 2x log x = x (1 + 2 log x)
= x (log e + log x²)
= x. log (e)x²
\(\frac{d y}{d x}\) = y. x. log (ex²)
= \(x^{x^2}\) .x. log (ex²)
= \(x^{x^2+1}\) + 1 log (ex²)

vi) 20^{log (tan x)}
సాధన:
f(x) = 20^{log (tan x)}
log y = log (20)^{log (tan x)}
= log (tan x) log 20
x దృష్ట్యా అవకలనం చేయగా,

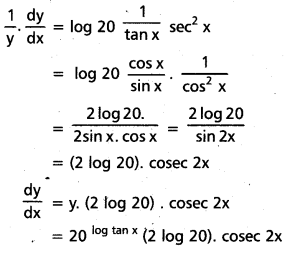
vii) x^x + \(e^{e^x}\)
సాధన:

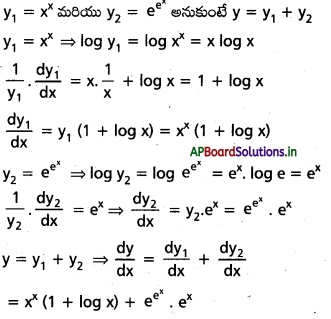
viii) x. log x. log (log x)
సాధన:
f(x) = x. log x. \(\frac{\mathrm{d}}{\mathrm{dx}}\)(log. (log x)) + log (log x) log x. 1 + x. log (log x)\(\frac{1}{x}\)
= x log x. \(\frac{1}{\log x}\) . \(\frac{1}{x}\) + log x. log (log x) + log (log x)
= 1 + log (log x) (1 + log x) = 1 + log (log x) + log x log (log x)
= log e + log (log x) + log x. log (log x)
= log (e log x) + log x. log (log x)

ix) \(e^{-a x^2}\) sin (x log x)
సాధన:
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(e^{-a x^2}\) sin (x log x)
\(\frac{d y}{d x}\) = \(\mathrm{e}^{-a x^2}\) . \(\frac{\mathrm{d}}{\mathrm{dx}}\) (sin (x log x)) + sin (x log x) \(\frac{d}{d x}\left(e^{-a x^2}\right)\)
= \(e^{-a x^2}\) cos (x log x). (x.\(\frac{1}{x}\) + log x) + sin (x log x) \(\mathrm{e}^{-a x^2}\) (-2ax)
= \(e^{-a x^2}\) (cos (x log x) (1 + log x) -2 ax.sin (x log x))
= \(e^{-a x^2}\) (cos (x log x) (log ex)-2 ax. sin (x log x))

x) sin^-1 \(\left(\frac{2^{x+1}}{1+4^x}\right)\) (2^x = tan θ ప్రతిక్షేపించండి)
సాధన:

2^x. log 2. \(\frac{d x}{d \theta}\) = sec² θ
= 1 + tan² θ = 1 + (2^x)²
= 1 + 4^x
\(\frac{\mathrm{d} \theta}{\mathrm{dx}}\) = 2^x – log 2(1 + 4^x)
\(\frac{d y}{d x}\) = \(\frac{d y}{d \theta}\) . \(\frac{d \theta}{d x}\) = 2 . 2^x . log 2/(1 + 4^x)
= 2^{x + 1} . log 2/(1 + 4^x)

ప్రశ్న 2.
క్రింది ప్రమేయాలకు \(\frac{d y}{d x}\) ను కనుక్కోండి.
i) x = 3 cos t – 2 cos³ t,
y = 3 sin t – 2 sin³t
సాధన:
\(\frac{d x}{d t}\) = – 3 sin t – 2(3 cos² t) (- sin t)
= -3 sin t + 6 cos²t – sin t
= 3 sin t (2 cos² t – 1)
= 3 sin t. cos 2t
y = 3 sin t – 2 sin³ t
\(\frac{d y}{d t}\) = 3 cost – 2 (3 sin² t) – cos t
= 3 cost (1 – 2 sin² t) = 3 cost. cos 2t

ii) x = \(\frac{3 a t}{1+t^3}\), y = \(\frac{3 a t^2}{1+t^3}\)
సాధన:

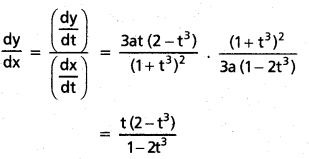
iii) x = a (cos t + t sin t), y = a (sin t− t cost)
సాధన:
\(\frac{d x}{d t}\) = a(- sin t + t cos t + sin t) = at cos t
y = a (sin t – t cos t)
\(\frac{d y}{d t}\) = a (cos t – cos t + t sin t)

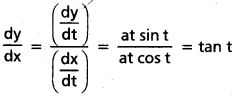
iv) x = a\(\left[\frac{1-t^2}{1+t^2}\right]\), y = \(\frac{2 b t}{1+t^2}\)
సాధన:

ప్రశ్న 3.
క్రింది వాటిని g(x) దృష్ట్యా f(x) ను అవకలనం చేయండి.

i) f(x) = log_a x, g(x) = a^x
సాధన:
y = f(x) = \(\log _a^x\) = \(\frac{\log x}{\log _e^a}\)
y = \(\log _a x\) = \(\frac{\log x}{\log _{\mathrm{e}}^{\mathrm{a}}}\)
\(\frac{d y}{d x}\) = \(\frac{1}{x \log _e^a}\)

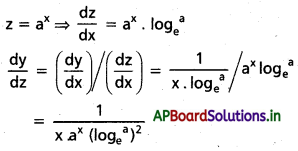
ii) f(x) = sec^-1 \(\left(\frac{1}{2 x^2-1}\right)\), g(x) = \(\sqrt{1-x^2}\)
సాధన:

iii) f(x) = tan^-1 \(\left(\frac{\sqrt{1+x^2}-1}{x}\right)\), g(x) = tan^-1 x
సాధన:

ప్రశ్న 4.
క్రింది సమీకరణాల ద్వారా నిర్వచితమైన అంతర్లీన ప్రమేయాలు y ల అవకలజాలను కనుక్కోండి.

i) x⁴ + y⁴ – a² xy = 0
సాధన:
x దృష్ట్యా అవకలనం చేయగా,
4x³ + 4y³. \(\frac{d y}{d x}\) – (x . \(\frac{d y}{d x}\) + y . 1) = 0
4x³ + 4y³ . \(\frac{d y}{d x}\) – a² x \(\frac{d y}{d x}\) – a² y = 0
(4y³ – a²x)\(\frac{d y}{d x}\) = a²y – 4x³ \(\frac{d y}{d x}\) = \([\frac{a^2 y-4 x^3}{4 y^3-a^2 x}/latex]

ii) y = xy May ’04
సాధన:
log y = log x^y = y log x
x దృష్ట్యా అవకలనం చేయగా,

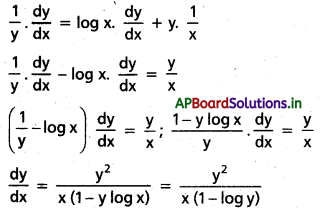
iii) y^x = x^{sin y}
సాధన:
ఇరువైపులా సంవర్గమానాలు తీసుకొంటే,
log y^x = log x^{sin y} ⇒ x. log y = (sin y) log x
x దృష్ట్యా అవకలనము చేయగా,

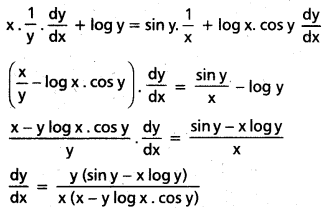
ప్రశ్న 5.
క్రింది వాటిని నిరూపించండి.

i) = a (x – y) అయితే
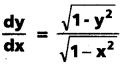(May ’11; Mar. ’05)
సాధన:

ii)

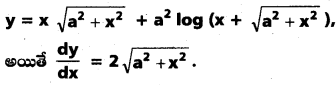
(A.P. Mar. 15)
సాధన:

iii) x^{log y} = log x, అయితే

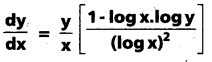
సాధన:
x^{log y} = log x, log x^{log y} = log log x
(log y) (log x) = log (log x).
x దృష్ట్యా అవకలనం చేయగా,

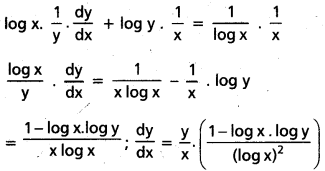
iv)

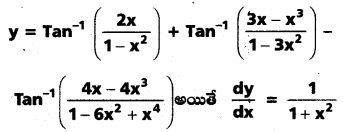
సాధన:
y = x tan θ

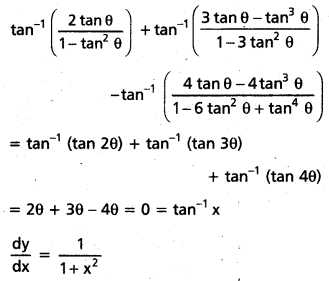
v)

సాధన:
x^y = y^x ⇒ log x^y = log y^x
y log x = x log y
x దృష్ట్యా అవకలనం చేయగా,
y. [latex]\frac{1}{x}\) log x. \(\frac{d y}{d x}\) = x. \(\frac{1}{y}\) . \(\frac{d y}{d x}\) + log y

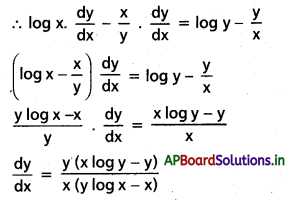
vi) x^2/3 + y^2/3 = a^2/3 అయితే \(\frac{d y}{d x}\) = \(-\sqrt[3]{y / x}\)
సాధన:
x^2/3 + y^2/3 = a^2/3
x దృష్ట్యా అవకలనం చేయగా

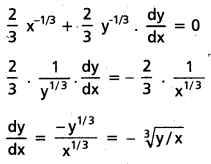
ప్రశ్న 6.
క్రింద పేర్కొన్న ప్రమేయాలకు \(\frac{d y}{d x}\) లను కనుక్కోండి.

i) y = \(\frac{(1-2 x)^{2 / 3}(1+3 x)^{-3 / 4}}{(1-6 x)^{5 / 6}(1+7 x)^{-6 / 7}}\)
సాధన:

ii) y = \(\frac{x^4 \cdot \sqrt[3]{x^2+4}}{\sqrt{4 x^2-7}}\)
సాధన:

iii) y = \(\frac{(a-x)^2(b-x)^3}{(c-2 x)^3}\)
సాధన:
log y = log \(\frac{(a-x)^2(b-x)^3}{(c-2 x)^3}\)
= log (a – x)² + log (b – x)³ – log (c – 2x)³
= 2 log (a – x) + 3 log (b – x) – 3 log (c – 2x)
x దృష్ట్యా అవకలనం చేయగా,

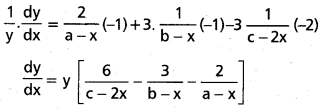
iv) y = \(\frac{x^3 \cdot \sqrt{2+3 x}}{(2+x)(1-x)}\)
సాధన:
log y = log \(\frac{x^3(2+3 x)^{1 / 2}}{(2+x)(1-x)}\)
= log x³ + log (2 + 3x)^1/2 – log (2 + x) – log (1 – x)
= 3 log x + \(\frac{1}{2}\) log (2 + 3x) – log (2 + x) – log (1 – x)
x దృష్ట్యా అవకలనం చేయగా,

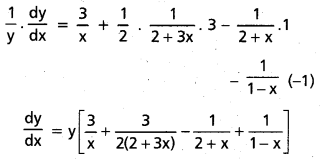
v) y = \(\sqrt{\frac{(x-3)\left(x^2+4\right)}{3 x^2+4 x+5}}\)
సాధన:

III

1. కింది ప్రమేయాలకు అవకలజాలను కనుక్కోండి.

i) (sin x)^{log x} + x^{sin x} (T.S Mar. ’15, ’13)
సాధన:
y₁ = (sin x)^{log x}, y₂ = x^{sin x} y = y₁ + y₂
y₁ = (sin x)^{log x}
log y₁ = log {(sin x)^{log x}} = log x. log (sin x)
x దృష్ట్యా అవకలనము చేయగా,

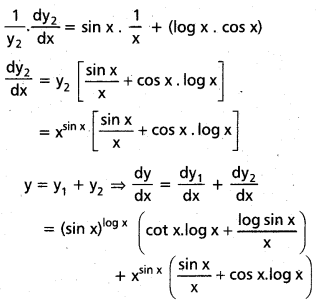
ii) (x^x)^x
సాధన:

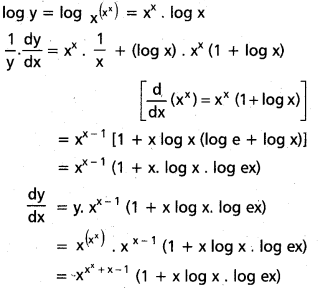
iii) (sin x)^x + x^{sin x}
సాధన:
y₁ = (sin x)^x, y₂ = x^{sin x} అనుకుంటే
y = y₁ + y₂ అవుతుంది
log y₁ = log (sin x)^x = x. log sin x
\(\frac{1}{y_1} \cdot \frac{d y_1}{d x}\) = x. \(\frac{1}{\sin x}\). cos x + log (sin x)
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = y₁ (x cot x + log sin x)
= (sin x)^x (x cot x + log (sin x))
y₂ = x^{sin x} ⇒ log y₂ = log. x^{sin x} = (sin x) log x
\(\frac{1}{y_2} \cdot \frac{d y_2}{d x}\) = sin x. \(\frac{1}{x}\) + (log x) cos x
\(\frac{\mathrm{dy}_2}{\mathrm{dx}}\) = y₂ (\(\frac{\sin x}{x}\) + cos x. (log x))
y = y₁ + y₂
\(\frac{d y}{d x}\) = \(\frac{\mathrm{dy}_1}{\mathrm{dx}}\) + \(\frac{\mathrm{dy}_2}{\mathrm{dx}}\)
= (sin x)^x (x cot x + log (sin x)) + x^{sin x}(\(\frac{\sin x}{x}\) + cos x. (log x))

iv) x^x + (cot x)^x
సాధన:
y₁ = x_x మరియు y₂ = (cot x)^x అనుకుందాం.
log y₁ = log x^x = x – log x

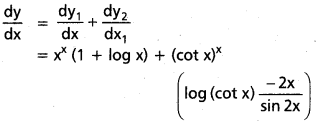
ప్రశ్న 2.
క్రిందివాటిని నిరూపించండి.

i) x^y + y^x = a^b, అయితే
\(\frac{d y}{d x}\) = \(-\left(\frac{y x^{y-1}+y^x \log y}{x^y \log x+x y^{x-1}}\right)\)
సాధన:
y₁ = x^y మరియు y₂ = y^x ⇒ y₁ + y₂ = a^b
log y₁ = log x^y = y log x

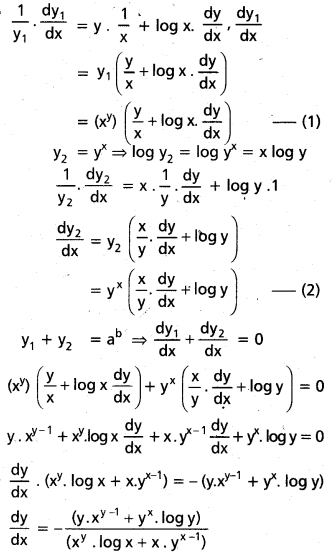
ii) f(x) = sin ^-1 \(\sqrt{\frac{x-\beta}{\alpha-\beta}}\), g(x) = tan^-1 \(\sqrt{\frac{x-\beta}{\alpha-x}}\), అయితే f'(x) = g'(x) (β< x < α) (Mar. ’06)
సాధన:

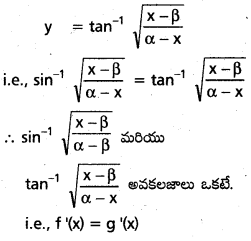
iii) f(x) = (a² – b²)^-1/2. cos^-1 \(\left(\frac{a \cos x+b}{a+b \cos x}\right)\), a > b > 0 మరియు 0 < x < π ; అయితే f'(x) = (a + b cos x)^-1
సాధన:

ప్రశ్న 3.
(x² – 5x + 8) (x³ + 7x + 9) ను క్రింద చూపిన రెండు పద్ధతులలో అవకలనం చేయండి.
i) లబ్ధ సూత్రం ప్రకారం
ii) బహుపదిని సూక్ష్మీకరించి తర్వాత
iii) సంవర్గమాన అవకలనాన్ని అనుసరించి పై అన్ని పద్ధతులు ఒకే జవాబును ఇస్తున్నాయా ?
సాధన:
లబ్ధ సూత్రం ప్రకారం :
y = (x² – 5x + 8) (x³ + 7x + 9)
\(\frac{d y}{d x}\) = (x² – 5x + 8) \(\frac{d}{d x}\)(x³ + 7x + 9) + (x³ + 7x + 9)\(\frac{d}{d x}\) (x² – 5x + 8)
= (x² – 5x + 8) (3x² + 7) + (x³ + 7x + 9)(2x – 5)
= 3x⁴ – 15x³ + 24x² + 7x² – 35x + 56 + 2x⁴ + 14x² + 18x – 5x³ – 35x – 45
= 5x⁴ – 20x³ + 45x² – 52x + 11 —- (1)

ii) బహుపదిని సూక్ష్మీకరించి :
సాధన:
y = (x² – 5x + 8) (x³ + 7x + 9)
= x⁵ +7x³ + 9x² – 5x⁴ – 35x² – 45x + 8x³ + 56x + 72
= x⁵ – 5x⁴ + 15x³ – 26 x² + 11x + 72
\(\frac{d y}{d x}\) = 5x⁴ – 20x³ + 45x² – 52 x + 11 ——— (2)

iii) సంవర్గమాన అవకలనమును అనుసరించి : y = (x² – 5x + 8) (x³ + 7x + 9)
సాధన:
log y = log (x² – 5x + 8) (x³ + 7x + 9)
= log (x² – 5x + 8) + log (x³ + 7x + 9)

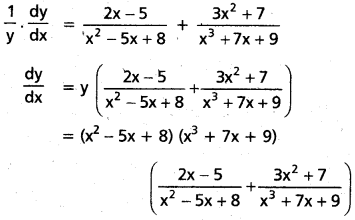
= (2x – 5) (x³ + 7x + 9) + (x² – 5x + 8) (3x² + 7)
= 2x⁴ + 14x² + 18x – 5x³ – 35x – 45 + 3x⁴ – 15x³ + 24x² + 7x² – 35x + 56
= 5x⁴ – 20x³ + 45x² – 52x + 11 —— (3)
(1), (2), (3) ల నుండి అవి ఒకే జవాబును ఇస్తున్నాయి అని గ్రహించగలము.