AP Inter 2nd Year Maths 2A Important Questions Chapter 5 ప్రస్తారాలు-సంయోగాలు

Students get through AP Inter 2nd Year Maths 2A Important Questions Chapter 5 ప్రస్తారాలు-సంయోగాలు which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2A Important Questions Chapter 5 ప్రస్తారాలు-సంయోగాలు

ప్రశ్న 1.
ⁿP₄  = 1680 అయిన n విలువ ఎంత ?
సాధన:
ⁿp₄  = 1680
= n(n – 1) (n – 2) (n – 3) = 8 x 7 x 6 x 5
∴ n = 8

ప్రశ్న 2.
¹²P_r  = 1320 అయితే r విలువ కనుక్కోండి.
సాధన:
¹²P_r  = 1320
= 10 x 132 = 10 x 11 x 12
= 12 x 11 x 10 = ¹²P₃
∴ r = 3.

ప్రశ్న 3.
⁽ⁿ⁺¹⁾P₅ : ⁿP₅ = 3:2 అయితే n విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 4.
⁵⁶P_(r+6) : ⁵⁴P_(r+3) = 30800 : 1 అయితే r విలువ కనుక్కోండి.
సాధన:

ప్రశ్న 5.
9 గణితశాస్త్ర పరీక్షాపత్రాలను, వాటిలో (శేష్ఠమయినది (the best), హీనమైనది (the worst)
(i) కలిసి ఉండేట్లుగా
(ii) వేరు వేరుగా ఉండేట్లు ఎన్ని విధాలుగా అమర్చవచ్చు.
సాధన:
(i) ఈ రెండు రకాలైన పేపర్లను ఒక యూనిట్గా భావిస్తే మనకి మొత్తం 9-2+1=7+1=8 పేపర్లు ఉన్నాయి. వీటిని 8! విధాలుగా అమర్చవచ్చు, ఆ రెండు పేపర్లను 2! విధాలుగా వాటిలో వాటిని అమర్చవచ్చు. కనుక కావలసిన అమరికల సంఖ్య (ఆ రెండు పేపర్లు కలిసి ఉండేట్లుగా) 8! 2!.

ii) మొత్తం 9 పేపర్లను అమర్చే విధానాలు 9!.వీటిలో శేేష్రమైనది, హీనమైనది కలిసి ఉండేట్లుగా అమర్చే విధానాలు 8! 2!. కనుక, రెండు గణితశాస్త్ర పేపర్లు వేరు వేరుగా ఉండేట్లుగా అమర్చే విధానాలు
9! – 8! 2! (9-2)=8 ! × 7

ప్రశ్న 6.
ఆరుగురు బాలురు, ఆరుగురు బాలికలను ఒక వరసలో అమర్చగలిగే విధానాలెన్ని ? వాటిలో ఎన్నిటిలో
(i) బాలికలందరూ కలిసి ఉంటారు.
(ii) ఏ ఇద్దరు బాలికలు పక్క పక్కన రాకుండా ఉంటారు.
(iii) బాలారం, బాలికలా ఒకరిశరువాత ఒకరంగా ఉంటారా.
సాధన:
ఆరుగురు బాలురు, ఆరుగురు బాలికలు కలిపి మొత్తం 12 మంది వ్యక్తులున్నారు. కనుక వీరిని ఒక వరసలో అమర్చ గలిగే విధానాలు 12 !

(i) ఆరుగురు బాలికలను ఒక యూనిట్గా భావిస్తే, అప్పుడు ఆరుగురు బాలురు + ఒక బాలికల యూనిట్ ఉంటాయి. వాటిని ఒక వరసలో 7! విధాలుగా అమర్చవచ్చు. ఇప్పుడు, ఆరుగురు బాలికలను వారిలో వారిని 6! విధాలుగా అమర్చవచ్చు. కనుక ఆరుగురు బాలికలు కలిసి ఉండేలా అమర్చగలిగే విధానాలు.
=7 ! × 6 !

(ii) ముందుగా ఆరుగురు బాలురను ఒక వరసలో 6 ! విధాలుగా అమర్చవచ్చు. అప్పుడు బాలుర మధ్యలో మొదట, చివర మొత్తం.

7 ఖాళీలుంటాయి (పైన ఖాళీలను x తో సూచించాం).
ఈ 7 ఖాళీలలో ఆరుగురు బాలికలను అమర్చే విధానాలు ⁷P₆ కనుక ఏ ఇద్దరు బాలికలు పక్క పక్కన రాకుండా అమర్చే విధానాలు. 6! ×⁷P₆ =7.6 !. 6 !

(iii) వరస బాలుడు లేదా బాలికతో మొదలు కావచ్చు అంటే అవి 2 విధాలు ఉదాహరణకు బాలుడితో మొదలయిందను కొందాం. అప్పుడు బాలురు, బాలికలు ఏకాంతంగా రావాలంటే బాలురను బేసిసంఖ్య గల స్థానాల్లో బాలికలను సరిసంఖ్య గల స్థానాల్లో అమర్చాలి. కనుక ఆరుగురు బాలురను సరి సంఖ్యగల 6 స్థానాలలో అమర్చే విధానాలు = 6!
ఆరుగురు బాలికలను బేసి సంఖ్య గల 6 స్థానాలలో అమర్చే విధానాలు =6 !
కనుక కావలసిన ప్రస్తారాల సంఖ్య =2 ×6! × 6!

ప్రశ్న 7.
MIRACLE పదంలోని అక్షరాలను ఉపయోగించి 4 ఆక్షరాల పదాలు ఎన్ని తయారు చేయవచ్చు? వాటిలో ఎన్ని పదాలు
(i) అచ్చుతో మొదలవుతాయి ?
(ii) అచ్చుతో మొదలయి, అచ్చులో అంతమవుతాయి ?
(iii) హల్లుతో అంతమవుతాయి.
సాధన:
MIRACLE పదంలో 7 అక్షరాలున్నాయి. కనుక వీటిని ఉపయోగించి ఏర్పరిచే 4 అక్షరాల పదాల సంఖ్ర
⁷P₄ = 7 × 6 × 5 × 4 = 840
ఇప్పుడు నాలుగు ఖాళీ స్థానాలు తీసుకుందాం.

(i) మొదటి స్థానాన్ని ఇచ్చిన పదంలోని 3 అచ్చులలో {I, A,E} ఏదో ఒకదానితో 3 విధాలుగా నింపవచ్చు మిగిలిన 3 స్థానాలను మిగిలిన 6 అక్షరాలతో నింపే విధానాల సంఖ్య
=⁶P₃  =6 × 5 × 4 = 120
కనుక అచ్చుతో మొదలయ్యే 4 అక్షరాల పదాల సంఖ్య
=3 × 120 = 360

(ii) ముందుగా మొదటి, చివరి స్థానాలను అచ్చులతో { I, A,E) నింపే విధానాల సంఖ్య ³P₂ 2= 3 × 2 = 6
మిగిలిన 2 స్థానాలను మిగిలిన 5 అక్షరాలలో నింపే విదానాల సంఖ్య ⁵P₂ = 5 × 4 = 20 కనుక అచ్చుతో మొదలయ్యి అచ్చుతో అంతమయ్యే 4 అక్షరాల పదాలు = 6 × 20=120

(iii) చివరి స్థానాన్ని 4 హల్లులలో ఒక దానితో నింపే విధానాలు = ⁴P₁ =4
మిగిలిన 3 స్థానాలు విగిలిన 6 అక్షరాలతో నింపే విధానాల సంఖ్య =  ⁶P₃=6 × 5 × 4=120
కనుక హల్లుతో అంతమయ్యే 4 అక్షరాల పదాల సంఖ్య
= 4 × 120 = 480

ప్రశ్న 8.
PICTURE అనే పదంలోని అక్షాలన్నింటినీ ఉపహాగించి ఏర్పరిచే ప్రస్తారాలలో ఎన్నిటిలో
(i) అచ్చులన్నీ కలిసి ఉంటాయి
(ii) ఏ రండు అచ్చులు పక్క పక్కన లేకుండా ఉంటాయి?
(iii) అచ్చులు, హల్లులు సాపేక్ష స్థానాలు మారకుండా ఉంటాయి.
సాధన:
పదంలో 3 అచ్చులు (I, U, E), 4 హల్లులు (P, C, T, R) ఉన్నాయి.

(i) 3 అచ్చును ఒక యూనిట్గా భావిస్తే, 4 హల్లులు + 1 యూనిట్ అచ్చులు మొత్తం 5 అవుతాయి. ఈ ఐదింటిని 5 ! విధాలుగా అమర్చవచ్చు. ఇప్పుడు 3 అచ్చులను వాటిలో వాటిని 3! విధాలుగా అమర్చవచ్చు. కనుక ప్రాథమిక సూత్రం ప్రకారం, ఈ రెండు పనులను 5 ! × 3 ! విధాలుగా చేయవచ్చు. కనుక మూడు అచ్చులు కอిసి వుండే ప్రస్తారాల సంఖ్య
= 5! × 3 ! = 120 × 6 = 720

(ii) ముందుగా 4 హల్లులను.ఒక వరసలో 4 ! విధాలుగా అమర్చవచ్చు. ఇప్పుడు హల్లుల మధ్యలో మూడు, మొదట, చివర మొత్తం 5 ఖాళీ స్థానాలు ఉంటాయి వీటిని x తో సూచిందాం

ఈ 5 ఖాళీలలో 3 అచ్చులను ⁵P₃ విధాలుగా అమర్చవచ్చు
కనుక ఏ రెండు అచ్చులు పక్క పక్కన రాకుండా అమర్చే
విధానాలు
= 4! × ⁵P₃
=24 × 5 × 4 × 3 = 1440

(iii) మూడు హల్లలను వాటి సాపేక్ష స్థానాలలో 3 ! విధాలుగా అమర్చవచ్చు. అదే విధంగా 4 అచ్చులను వాటి సాపేక్ష స్థానాలలో 4! విధాలుగా అమర్చవచ్చు.

కనుక కావలసిన ప్రస్తారాలు సంఖ్య 3!  4! = 144

ప్రశ్న 9.
PRISON పదంలోని అక్షరాలతో ఏర్పడే 6 అక్షరాల పదాలన్నింటినీ నిఘంటువులోని క్రమంలో అమరిస్తే, (పునరావృతం లేకండా) ఆ (క్రమంలో దాని మొక్క కోటిని కనుక్కోండి.
సాధన:
దత్త పదంలోని అక్షరాల నిఘంటువు క్రమం
I  N  O P R S
నిఘంటువులో ముందుగా I తో మొదలయ్యే పదాలన్నీ వస్తాయి. ఆతరువాత N తో మొదలయ్యేవి, O తో మొదలయ్యే పదాలు వస్తాయి. వీటి తరువాత P తో మొదలయ్యే పదాలు వస్తాయి. వీటిలోనే మనకు కాలసిన పదం PRISON ఉంది. కనుక వీటి నిఘంటువు క్రమాన్ని గమనిస్తే వీటిలో ముందుగా PI తో మొదలయ్యే, పదాలు తదుపరి PN తో, ఆ తరువాత PR తో మొదలయ్యేవి వస్తాయి. ఈ విధంగా PRISON అనే పదం వచ్చేంత వరకు లెక్కించాలి.

ముందుగా I తో మొదలయ్యే పదాల సంఖ్యను గణించ డానికి I ని మొదటి స్థానంలో ఉంచి మిగిలిన 5 అక్షరాలను రకరకాలుగా అమర్చాలి. ఈ రకమైన అమరికలు 5! ఉంటాయి. అంటే I మొదటి అక్షరంగా గల పదాల సంఖ్య 5! అన్నమాట, ఈ విధంగా PRISON అనే పదం వచ్చే వరకు కింది విధంగా గణిస్తాం.

కనుక PRISON అనే పదం కోటి
= 3 x 5! +3 x 4 + 2 x 2! +1+1
= 360 + 72 + 4 + 1 + 1 = 438

ప్రశ్న 10.
2,3,5,6,8 అంకెలనుపయోగించి పునరావృతం లేకుండా ఎన్ని 4 అంకెల సంఖ్లలు తయారు చేయవచ్చు? వాటిలో ఎన్ని
(i) 2
(ii) 3
(iii) 4
(iv) 5
(v) 25
సాధన:
2, 3, 5, 6, 8 అనే.5 అంకెలనుపయోగించి తయారు చేయగల 4 అంకెల సంఖ్లలు ⁵P₄ = 120.

(i) 2తో భాగించబడేవి : ఒక సంఖ్య 2తో భాగించబడటానికి దాని చివర (ఒకట్ల) స్థానంలో సరిసంఖ్య ఉండాలి. అంటే ఈ స్థానాన్ని 2 లేదా 6 లేదా 8 తో నింపవచ్చు. ఇప్పుడు మిగిలిన 3 స్థానాలను.

మిగిలిన 4 అంకెలతో ⁴P₃ విధాలుగా నింపవచ్చు. కనుక =3 x ⁴P₃ = 3 x 24=72

(ii) 3 తో భాగించబడేవి : ఒక సంఖ్య 3 తో భాగించబడటానికి ఆ సంఖ్యలోని అంకెల మొత్తం 3 తో భాగించబడాలి. మనకు ఇచ్చిన 5 అంకెల మొత్తం 24 కనుక వీటి నుంచి 4 అంకెలను ఆ అంకెల మొత్తం 3 తో భాగించబడే విధంగా 2 రకాలుగా ఎంచుకోవచ్చు,
(i) 2,5,6,8
(ii) 2,3,5,8

పైన చెప్పిన రెండు సందర్భాలలో ప్రతిసారి 4 అంకెలతో తయారు చేయగల 4 అంకెల సంఖ్యల సంఖ్య 4 ! (ఇవి అన్నీ 3 తో భాగించబడతాయి). కనుక 3 తో భాగించబడే 4 అంకెల సంఖ్యల సంఖ్య
2 × (4!)=2 × 24 = 48

(iii) 4 తో భాగించణడేవి : ఒక సంఖ్య 4 తో భాగించ బడాలంటే చివరి రెండు స్థానాల్లో అంటే పదులు, ఒకట్ల స్థానాల్లో ఉన్న రెండంకెల సంఖ్య 4తో భాగించబడాలి.
కనుక ఈ రెండు స్థానాలను 28,32,36,52,56 అనే సంఖ్యలతో నింపాలి.

అంటీ 5 విధాలుగా ఈ రెండు స్థానాలు నింపవచ్చు. ఇప్పుడు మిగిలిన రెండు స్థానాలను 3 అంకెలతో ³P₂ విధాలుగా సంఖ్.
= 5 × ³P₂=30.

(iv) 5 తో భాగించణడేవి : ఒక సంఖ్య 5 తో భాగించ బడాలంటే చివరి (ఒకట్ల) స్థానంలో 5 ఉండాలి. (‘0’ కూడా ఉండవచ్చు కాని దత్త అంకెలలో ‘0’ లేదు). కనుక ఒకట్ల స్థానంలో5ఉంచితే మిగిలిన 3 స్థానాలను మిగిలిన 4 అంకెలతో ⁴P₃ విధాలుగా నింపవచ్చు. కనుక 5 తో భాగించబడే 4 అంకెల సంఖ్యల సంఖ్ల ⁴P₃ =24.

(v) 25 తో భాగించణడేవి : ఒక సంఖ్య 25 తో భాగించ బడాలంటే చివరి రెండు స్థానాలను 25 మాత్రమే నింపాలి (50 లేదా 00తో కూడా నింపవచ్చు కాని .దత్త అంకెలలో ‘ 0 ‘ లేదు) అంటే ఈ స్థానాలు ఒక విధంగా మాత్రమే నింపవచ్చు. ఇప్పుడు మిగిలిన 2 స్థానాలను మిగిలిన 3 అంకెలతో ³P₂ విధాలుగా నింపవచ్చు.

ప్రశ్న 11.
1, 3,5,7,9 అంకెలను ఉపయోగించి ఏర్పరచగల 4 అంకెల సంఖ్యల మొత్తం కనుక్కోండి.
సాధన:
1,3,5,7,9 అనే 5 అంకెలతో ఏర్పరచగల 4 అంకెల సంఖ్ల సంఖ్  ⁵P₄ = 120.
ఇప్పుడు ఈ 120 సంఖ్యల మొత్తం కనుక్కోవాలి. ముందుగా మనం ఈ 120 సంఖ్యల ఒకట్ల స్థానంలోని అంకెల మొత్తం కనుక్కొందాం. ఒకట్ల స్థానంలో 1 ఉంచితే మిగిలిన 3 స్థానాలను మిగిలిన 4 అంకెలతో  ⁴P₃  విధాలుగా నింపవచ్చు.

అంటే పైన చెప్పివ 120 నాలుగంకెల సంఖ్యలలో ⁴P₃ సంఖ్య ఒకట్ల స్థానంలో 1 వస్తుంది. ఇదేవిధంగా 3, 5, 7, 9 అంకెలు ఒక్కొక్కటి ⁴P₃ సార్లు ఒకట్ల స్థానంలో వస్తాయి. ఈ అంకెలన్నీ కలిపితే మనకు 120 సంఖ్య ఒకట్ల స్థానంలోని మొత్తం.
= ⁴P₃ x 1 + ⁴P₃ x 3 + ⁴P₃  x 5
= ⁴P₃ x 7 + ⁴P₃ x 9
= ⁴P₃ (1+3+5+7+9)
= ⁴P₃  (25)
ఇదే విధంగా ఈ 120 సంఖ్యల పదుల స్థానంలో కూడా పైన చెప్పిన అంకెలు మాత్రమే వస్తాయి. కనుక పదుల స్థానంలోని అంకెలు మొత్తం కూడా ⁴P₃ x 25 కాని ఇది పదుల స్థానంలోని మొత్తం కనుక దాని విలువ ⁴P₃ x 25 x 10. ఇలాగే వందల స్థానంలోని అంకెల మొత్తం విలువ ⁴P₃ x 25 x 100  కనుక 1,3,5,7,9 అంకెలనుపయోగించి ఏర్పరిస్తే వచ్చే 4 అంకెల సంఖ్ల మొత్తం.

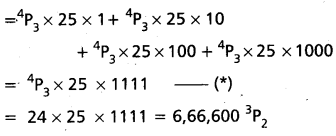
ప్రశ్న 12.
1,2,5,7,8,9 అంకెలలో ఎన్ని 4 అంకెల సంఖ్యలా సంఖ్యలు ఎన్ని?
సాధన:
1, 2, 5, 7, 8,9 అంకెలతో ఏర్పడే నాలుగు అంకెల సంఖ్యలు ⁴P₂ = 360 ఇప్వుడు మొదటి స్థినాన్ని 9తో, చివరిస్థానాన్ని 2 తో నింపే విధానాల సంఖ్య 1.⁴P₂ = 12.

ప్రశ్న 13.
5 మూలకాలున్న సమితి A నుంచి 7 మూలకాలున్న సమితి B క గల అన్వేక ప్రమేయాల సంఖ్య కనుక్కొండి.
సాధన:
A లోని మొదటి మూలకానికి ప్రతిబింబాన్ని B లోని 7 మూలకాలలో ఏదో ఒక మూలకంగా అంటే 7 విధాలుగా నిర్వచించవచ్చు.A లోని రెండవ మూలకానికి, (ప్రతిబింభాన్ని B లోని మిగిలిన 6 మూలకాలలో ఏదో ఒక మూల కంగా అంటే 6 విధాలుగా మాత్రమే నిర్వచించ గలం.
ఇలా చేసుకుంటూ పోతే A నుంచి B కి గల అన్వేక ప్రమేయాల సంఖ్ల = ⁷P₅
= 7 × 6 × 5 × 4 × 3 = 2,520
గమనిక : సమితి A లోని m మూలకాలు, సమితి B లోని n మూలకాలుంటే A నుంచి B కి నిర్వచించగల అన్వేక (ప్రమేయాల సంఖ్య
= ⁿP_m m ≤ n అయితే
0, m ≤ n అయితే

ప్రశ్న 14.
ఉత్తరాలను వాటికి సంబంధించిన చిరునామాలు ఉన్న 4 కవర్లలో ఏ ఉత్తరమా దానికి సంబంధించిన కవరులోకి ఏోకుండా ఉండేలా, ఒక్కొక్క కవరులో ఒక్కొక్క ఉత్తరం ఉండేలా ఎన్ని విధాలుగా ఆమర్చవచ్చు.
సాధన:
కావలసిన అమరికల సంఖ్య \( = 4 !\left(\frac{1}{2 !}-\frac{1}{3 !}+\frac{1}{4 !}\right)\)
= 12 – 4 + 1 = 9

ప్రశ్న 15.
MIXTURE పదంలోని అక్షరాలతో, పునరావృతాన్ని అనుమతించినపడు, ఏర్పరచగల 5 ఆక్షరాల పదాలలో అచ్చుతో మొదలయ్యే పదాలెన్ని?
సాధన:
MIXTURE పదంలో 7 అక్షరాలున్నవి. అందు 3 అచ్చులు (I, U, E), 4హల్లలలు (M, X,T, R)

కనుక మొదటి స్థానాన్ని ఒక అచ్చుతో 3 విధాలుగా నింపవచ్చు. మిగిలిన 4 స్థానాలలో ఒక్కొస్థానాన్ని 7 విధాలుగా నింపవచ్చు. (పునరావృతాన్ని అనుమతించాం కనుక)
∴  అచ్చుతో మొదలయ్యే 5 అక్షరాల పదాలు
= 3 × 7 × 7 × 7 × 7=3 × 7⁴

ప్రశ్న 16.
(a) m మూలకాలాన్న ఒక సమితి A నుండి n మాలకాలున్న సమితి B అన్ని (ప్రమేయాలు నిర్వచించవచ్చు ?
సాధన:
A = {a_1,a_2,………….. a_m}
B = {b_1,b_2,………….. b_m}
గా తీసుకొందాం. ముందుగా a₁ ప్రతిబింబానికి B లో ఒక మూలకం ఎంచుకోవాలి. దీనిని మనం n విధాలుగా ఎంచుకోవాలి. ఈ విధంగా A లో ఉన్న m మూలకాలలో ప్రతి మూలకం యొక్క (పతిబింబాన్ని n విధాలుగా నిర్వబించ వచ్చు. ఒక ప్రమేయాన్ని నిర్వచించినపుడు ఒకటి కన్నా ఎక్కువ మూలకాలకు ఒకే (పతిబింబం ఉండవచ్చు. కనుక A లోని m మూలకాల ప్రతిబింబాలను
n × n × …………….. x n (m సార్లు) = n^m
విధాలుగా నిర్వచించవచ్చు. కనుక A నుండి B కి గల ప్రమేయాల సంఖ్య n^m

(b) n మూలకాలున్న ఒక సమితి A నుంచి 2 మాలకాలున్న సమితి B కు ఎన్ని సంగ్రస్త ప్రమేయాలు నిర్వచించ వచ్చు ?
సాధన:
A = {a_1,a_2,………….. a_n} గా తీసుకొందాం. పై సమస్య ప్రకారం A నుండి B కి గల [ప్రమేయాల సంఖ్య 2ⁿ ఒక ప్రమేయం సంగ్రస్తం కావాలంటే B లోని రెండు మాలకాల x, y లు ప్రమేయం వ్యాప్తిలో ఉండాలి.కనుక (ప్రమేయం సంగ్రస్తం కాకుండా ఉండాలంటే హ్యాప్తిలో x (లేదా y) మాత్రమే ఉండేలా A లోని అన్ని మూలకాల (ప్రతిబింబాలు x (లేదా y) అ ్లేటటట్లు నిర్వచించాలి. ఈ విధమైన ప్రమేయాలు రెండు మాత్రమే ఉంటాయి. కనుక A నుండి B కి నిర్వచించగల 2ⁿ (ప్రేయాల్లో 2 ప్రమేయాలు సంగ్రస్తం కావు. అంటే A సుంచి B కి గల సంగ్రస్త ప్రమేయాల సంఖ్య 2ⁿ– 2.

ప్రశ్న 17.
ప్రావృతాన్ని అనుమతించినప్పుడు 1, 2, 3, 4, 5, 6 అంకెలలో ఏర్పరచగలిగే 4 అంకెల సంఖ్లల సంఖ్యను కనుక్రోండి.
సాధన:
పునరావృతాన్ని అనుమతించినప్పుడు 4 స్థానాలను ఇచ్చిన 6 అంకెలతో నింపే విధానాలు
= 6 × 6 × 6 × 6=6⁴=1,296

ప్రశ్న 18.
పునరావృతాన్ని అనుమతించినప్పుడు 1,2,3,4,5,6 అంకెలతో ఏర్పరిచే 4 అంకెల సంఖ్యలలో ఎన్ని
(i) 2 (ii) 3 తో ఖాగించబడతాయి?
సాధన:
(i) 2 తో భాగించణడే సంఖ్లలు 4 ఖాళీస్థానాలు తీసుకొందాం. ఒక సంఖ్య 2 తో భాగించ బడాలంటే

ఒకట్ల స్థానంలో సరిసంఖ్య ఉండాలి. కనుక ముందుగా ఒకట్ల స్థానాన్ని ఒక సరిసంఖ్య (2 లేదా 4 లేదా 6) తో ‘3’ విధాలుగా నింపవచ్చు. మిగిలిన 3 స్థానాలలో ఒక్కో స్థానాన్ని ఇచ్చిన 6 అంకెలలో దేనితోనైనా 6 విధాలుగా నింపవచ్చు. కనుక 2 తో భాగించబడే 4 అంకెల సంఖ్యల సంఖ్య
= 3 × 6³=3 × 216 = 648

(ii) 3తో భాగించణడే సంఖ్యలు
మొదటి 3 స్థానాలలో ఒక్కో స్థానాన్ని 6 విధాలుగా, అంటే మొత్తం 6³ విధాలుగా నింపవచ్చు.

ఈ విధంగా మొదటి. మూడు స్థానాలు నింపాక ఒకట్ల స్థానం నింపడానికి 6 వరుస పూర్ణాంకాలున్నాయి. వీటితో ఒకట్ల స్థానాన్ని నింపితే 6 వరుస ధన సంఖ్యలు వస్తాయి. ప్రతి 3 వరుస ధనపూర్ణాంకాల్లో ఖచ్చితంగా ఒక సంఖ్య 3తో భాగింపబడుతుందని మనకు తెలుసు. కనుక పైన చెప్పిన 6 వరుస ధన పూర్ణాంకాల్లో ఖచ్చితంగా 2 మాత్రమే 3 తో భాగించబడతాయి. అంటే ఒకట్ల స్ధానాన్ని 2 విధాలుగా మాత్రమే నింపవచ్చు కనుక 3 తో భాగించబడే 4 అంకెల సంఖ్యల సంఖ్య.
= 6³ × 2 = 216 × 2 = 432

ప్రశ్న 19.
ఫునరావృతాన్ని అనుమతించినపుడు EXPLAIN పదం లోని అక్షరాలతో మొదట, చివర అచ్చులు ఉండేటట్లు 5 అక్షరాల పదాలు ఎన్ని ఏర్చరచవచ్చు ?
సాధన:
EXPLAIN పదములో 7 అక్షరాలున్నవి అందులో 3 అచ్చులు (A,E,I) లు ఉన్నాయి. కనుక మొదటి, చివరి స్థానాలలోను అచ్చులతో ఒక్కోదాన్ని 3 విధాలుగా నింపవచ్చు. మిగిలిన మూడు స్థానాలలో ఒక్కోదాన్ని ఇచ్చిన పదంలోని 7 అక్షరాలలో ఏదో ఒక అక్షరంతో 7 విధాలుగా నింపవచ్చు.
కనుక మొదటి, చివిరి అచ్చులు ఉండే 5 అక్షరాల పదాల సంఖ్య.
=3 × 7 ×7 ×7 × 3
=9 × 343=3,087

ప్రశ్న 20.
SINGING పదంలోని అక్షరాలను
(i) Iతో మొదలయి, Iతో అంతమయ్యేలా
(ii) రెండు Gలుకలిసి ఉండేలా ఎన్ని విధాలుగా అమర్చవచ్చు ?
(iii) అచ్చులు, హల్లులు సాపేక్ష స్థానాలు మారకుండా ఎన్ని విధాలుగా అమర్చవచ్చు ?
సాధన.
SINGING పదంలో 2I లు, 2G లు, 2Nలు, ఒక S మొత్తం 7 అక్షాాలున్నవి.

(i) ముందుగా మొదటి,చివరి స్థానాలను రెండు Iలతో

నింపితే ఇంకా 5 స్థానాలు, 5 అక్షరాలు ఉంటాయి. కనుక వీటిని అమర్చే విధానాలు \(\frac{5 !}{2 ! 2 !}\) (రెండు N లు)
రెండు G లు ఉన్నాయి. కనుక I లు రెండూ ఒకే రకంగా ఉన్నందువల్ల వాటిలో వాటిని ఒక రకంగా మాత్రమే మార్చగలం.
కనుక కావలసిన ప్రస్తారాల సంఖ్య \(\frac{5 !}{2 ! ~ 2 !}\) = 30

(ii) రెండు ‘G’ లను.ఒక యూనిట్ గా భావిస్తే, విగిలిన 5 అక్షరాలు + 1 యూనిట్= 6 వీటిలో 2I లు, 2N లు ఉన్నాయి. కనుక
ఈ 6 అక్షరాలను అమర్చే విధానాలు \(\frac{6 !}{2 ! 2 !}=\frac{720}{2 \times 2}=180\)
ఇప్పుడు ఒక యూనిట్ లో ఉన్న G లను వాటిలో
కనుక రెండు G లు కలసి ఉండే పదాల సంఖ్ల = 180

(iii) SINGING పదంలో రెండు అచ్చులు (1,1). 5 హల్లులు (రెండు nలు, రెండు Gలు ఒక S) ఉన్నాయి. రెండు అచ్చులను వాటిలో వాటిని అమర్జే విధానాలు \(=\frac{2 !}{2 !}\) 1.5 హల్లులను వాటిలో వాటిని అమర్చే విధానాలు \(\frac{5 !}{2 ! 2 !}\) = 30
C V C C V C C (ఇక్కడ V ఒక అచ్చుని, C ఒక హల్లుని
∴ కావలసిన ప్రస్తారాల సంఖ్య = 130 x 30=30

ప్రశ్న 21.
a⁴, b³, c⁵ పదంలోని అక్షరాలను విస్తరించి రాసి వాటిని అమర్చడం ద్వారా వచ్చే (ప్రస్తారాల సంఖ్లను కనుక్రోండి.
సాధన:
a⁴, b³, c⁵ విస్తరించి రాస్తే
aaaa bbb ccccc
దీనిలో 12 అక్షరాలున్నాయి. వాటిలో 4 ‘a’ లు, 3 ‘b’ లు, 5 ‘c’ లు. కనుక వాటిని అమర్చడం ద్వారా వచ్చే (ప్రస్తారాల సంఖ్య
\(\frac{12 !}{4 ! 3 ! 5 !}\)

ప్రశ్న 22.
1,1,2,2,3 అనే అంకెలతో ఏర్పర్గగ 5 అంకెల సంఖ్లెన్ని ? వీటిలో సరిసంఖ్యలన్ని ?
సాధన:
1, 1, 2, 2, 3 అనే 5 అంకెలలో రెండు ‘1’ లు, రెండు ‘2’ లు ఉన్నాయి. కనుక వీటి నుంచి ఏర్పరచగల 5 అంకెల
సంఖ్య = \(\frac{5 !}{2 ! 2 !}\) = 30
ఇప్పుడు సరి సంఖ్యలు కనుక్కోవడానికి ఒకట్ల స్థానాన్ని 2 తో నింపుదాం.
మిగిలిన 4 స్థానాలను మిగిలిన 4 అంకెలతో (1,1,2,3) నింపే విధానాలు \(\frac{4 !}{2 !}=12\)
కనుక దత్త అంకెలతో ఏర్పరచగల 5 అంకెల సరి సంఖ్యల సంఖ్య =12

ప్రశ్న 23.
మూడు వేర్వేరు పుస్తకాలకు ఒక్రోదానికి నాలుగు ప్రతులున్నాయి. ఈ 12 పస్తకాలను ఒక అరలో ఎన్ని రకాలుగా అమర్చవచ్చు ?
సాధన:
దత్తాంశం (ప్రకారం, ఇచ్చిన 12 పుస్తకాలలో 4 పుస్తకాలు ఒక రకంగా, 4 పుస్తకాలు రెండో రకంగా, 4 పుస్తకాలు మూడో రకంగా ఉన్నాయి. కనుక సిద్ధాంతం 5.5 .2 (ప్రకారం ఈ 12 పుస్తకాలను ఒక అరలో అమర్చే విధానాలు.
\(\frac{12 !}{4 ! 4 ! 4 !}\)

ప్రశ్న 24.
EAMCET పదంలోని అక్షరాలతో ఏర్పడే 6 అక్షరాల పదాలన్నింటినీ నిఘంటువులోని క్రమంలో అమరిస్తే, ఆ క్రమంలో EAMCET పదం యొక్క కోటిని కనుక్కోండి.
సాధన:
దత్తపదం EAMCET లోని అక్షరాల నిఘంటువు క్రడుం ACEEMT నిఘంటువులో ముందుగా A తో మొదలజ్యే పదాలన్నీ వస్తాయి. కనుక మొదటిి స్థానాన్ని A తో నింపితే మిగిలిన 5 అక్షరాలను \(\frac{5 !}{2 !}\) విధాలుగా (2E’ లు ఉన్నవి కనుక) అమర్చవచ్చు. ఈ విధంగా చేసుకొంటూ EAMCET పదం వచ్చే వరకూ కింది విధంగా గణిస్తాం.

ప్రశ్న 25.
ఎనిమిదిమంది పురుషును, నలుగురు స్త్రీలను ఒక వృత్తాకార బల్ల చుట్టూ ఎన్ని రకాలుగా అమర్చవచ్చు ? వీటిలో ఎన్ని (ప్తస్తారాలలో
(i) స్త్రీలంతా ఒకేచోట ఉంటారు.
(ii) ఏ ఇద్దరు స్త్రీలు పక్క పక్కన రాకుండా ఉంటారు.
సాధన:
మొత్తం వ్యక్తుల సంఖ్య = 12 (ఎనిమిదిమంది పురుషులు + నలుగురు స్త్రీలు
కనుక వీరిని వృత్లాకార బల్ల చుట్టూ అమర్చే విధానాలా = (11)!

(i) నలుగురు స్త్రీలను ఒక యూనిట్గా భావిస్తే, ఎనిమిది మంది పురుషులు ఎనిమిది యూనిట్లు అనుకుంటే ఈ తామ్మిది యూనిట్లను వృత్తాకార బల్ల చుట్టూ అమర్చే విధానాలు= 8!
ఇప్పుడు నలుగురు స్త్రీలను వారిలో వారిని 4! విధాలుగా అమర్చవచ్చు.
∴ స్త్రీలంతా ఒకచోట ఉండేలా అమర్చగల విధానాల సoఖ్య = 8! × 4!

(ii) ముందుగా ఎనిమిది మంది పురుషులను ఒక వృత్తాకార బల్ల చుట్టూ అమర్చే విధానాలు =(8-1)! = 7! వీరిలో ప్రతి ఇద్దరు పురుషుల మధ్య

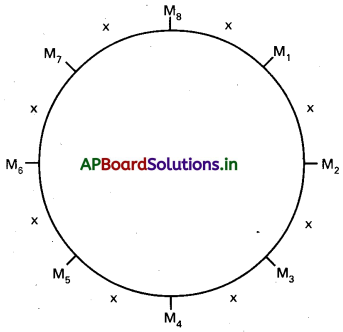
ఒక్కో ఖాళీ చొప్పున మొత్తం 8 ఖాళీలు ఉంటాయి. (ఈ ఖాళీలను పైన పటంలో x అనే గుర్తుతో సూచించాం) ఇప్పుడు ఈ 8 ఖాళీలలో నలుగురు స్త్రీలను అమర్చే విధానాలు= ⁸P₄ కనుక ఏ ఇద్దరు స్త్రీలు పక్క పక్కన లేని వృత్తాకార ప్రస్తారాల సoఖ్య 7! × ⁸P₄.

ప్రశ్న 26.
అయిదురుగురు భారతీయులను, నలుగురు అమెరికా దేశస్థులను, ముగ్గురు రష్యా దేశస్థులను ఒక వృత్తాకార ఐల్ల చుట్టా
(i) భారతీయులంతా ఒకే చోట కలిసి ఉండేలా
(ii) ఏ ఇద్దరు రష్యా దేశస్థులు పక్క పక్కన లేకుండా
(iii) ఒక దేతానికి చెందిన వారందరూ ఒకేచోట ఉండేలా ఎన్నిరకాలుగా అమర్చవచ్చు) ?
సాధన:
(i) అయిదుగురు భారీీయలను ఒక యూనిట్గా భావిస్తే, నలుగురు అమెరికా దేశస్థులు, ముగ్గరు రష్యా దేశస్థులు. 1 యూనిట్ భారతీయులు అంటే 8 మంది వ్యక్తులుంటారు. వీరిని ఒక వృత్తారార బల్లచుట్టూ అమర్చే విధానాలు
= (8-1)! = 7 !
ఇప్పుడు అయిదుగురు భారతీయులను వారిలో వారిని 5! విధాలుగా అమర్చవచ్చు. కనుక కావలసిన వృత్తాకార [ప్రస్తారాల సంఖ్య =7! × 5 !

(ii) ముందుగా ముగ్గరు రష్యా దేశస్థులను ఒక పక్కుగా ఉంచి, మిగిలిన 9 మంది వ్యక్తులను (అయిదుగురు భారతీయులు + నలుగురు అమెరికా దేశస్థులు) ఒక వృత్తాకార బల్ల చుట్టూ అమర్చే విధానాలు =(9-1)!=8 ! ఇప్పుడు, ఈ 9 మంది వ్యక్తుల మధ్యలో ఖాళీలు 9 ఉంటాయి.
ఈ 9 ఖాళీలలో ముగ్నురు రష్లా దేశస్థులను అమర్చే విధానాలు ⁹P₃
కనుక కావలసిన వృత్తాకార (ప్రస్తారాల సంఖ్య 8! × ⁹P₃

(iii) అయిదుగురు భారతీయులను ఒక యూనిట్, నలుగురు అమెరికా దేశస్థులను రెండ్ర యూనిట్గానూ ముగ్గురు రష్యా దేశస్థులను మూడో యూనిట్గాను భావిస్తే 3 యూనిట్లు అవుతాయి. ఈ మూడు యూనిట్లతో వచ్చే వృత్తాకార ప్రస్తారాల సంఖ్ =(3-1) !=2 !
ఇప్పుడు అయిదుగురు భారతీయులను వారిలో వారిని అమర్చే విధానాలు 5!. ఇదే విధంగా నలుగురు అమెరికా దేశస్కులను 4! విధాలుగానూ, ముగ్గురు రష్యా దేశస్థులను 3! విధాలుగానూ అమర్చవచ్చు, కనుక కావలసిన విధానాలు
=2! × 5! × 4! × 3!

ప్రశ్న 27.
విభిన్నమైన రంగుల హూసలతో ఏర్పరచగల పూసల గొలుసుల సంఖ్యను కనుక్రోండి.
సాధన:
n అసరూప వస్తువులతో ఏర్పరచగల వేలాడే రకం వృత్తాకార ప్రస్తారాల సంఖ్య \(\frac{1}{2}(n-1)\) ! అని మనకు తెలుసు.
కనుక ఇచ్చిన 7 పూసలతో ఏర్పరచగల దండల సంఖ్య
\(\frac{1}{2}(n-7) !=\frac{1}{2}(6 !)=360\)

ప్రశ్న 28.
7 విభిన్నమైన ఎర్ర గులాబీలు, 4 విభిన్నమైన పసుపు రంగు గులాబీలతో 3 రెండు పసుపు రంగు గులాబీలు పక్క పక్కన రాకుండా ఎన్ని రకాలుగా దండలు తయారు చేయవచ్చు?
సాధన:
ముందుగా 7 విభిన్నమైన ఎర్రగులాబీలతో ఏర్పరచగల వృత్తాకార (ప్తస్తారాల సంఖ్య =(7-1)!=6!
ఈ 7 ఎర్రగులాబీల మధ్యలో ఉన్న 7 ఖాళీలలో 4 పసుఫు రంగుగులాబీలను ⁷P₄ విధాలుగా అమర్చవచ్చు. కనుక మొత్తం వృత్తాకార (ప్రస్తారాల సంఖ్య = 6 ! × ⁷P₄
కాని పువ్వుల దండలు వేలాడే వృత్తాకార ప్రస్తారాల కోవలోకి వస్తాయి. కనుక కావలసిన (ప్రస్తారాల సంఖ్య
\(=\frac{1}{2}\left(6 ! \times{ }^7 P_4\right)\)

ప్రశ్న 29.
ఒక వృత్తాకార బల్ల చుట్టూ 14మంది వ్యక్తులు కూర్చొని ఉన్నారు. వారిలో ఇద్దరు వ్యక్తలను (ప్కక్క పక్కన లేకుండా ఎన్ని రకాలుగా ఎంచుకోవచ్చు ?
సాధన. మనకు ఇచ్చిన 14 మంది వ్యక్తులు వృత్తాకార బల్ల చుట్టూ a₁  a₂ …………………… a₁₄ క్రమంలో పటంలోలాగా కూర్చొని ఉన్నారనుకొందాం.
ఈ 14 మంది వ్యక్తుల నుంచి ఇద్దరిని ఎంచుకొనే విధానాలు = ¹⁴C₂ =91.

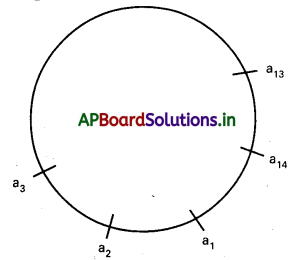
ఈ విధానాలలో ఎంచుకొన్న ఇద్దరు వ్యక్తులు పక్క పక్కనే ఉండే విధానాలు a_1, a₂, a₂, a₃, ……………….. a_13,a₁₄, a₁₄, a₁₅ అంటే 14 విధానాలు కనుక ఎంచుకొన్న ఇద్దరు వ్యక్తులు పక్కపక్కన లేని విధానాలు =91-14 = 77

ప్రశ్న 30.
ఎనిమిది మంది బాలురు, అయిదుగురు బాలికల నుంచి నలుగురు బాలురు, ముగ్నురు బాలికలు ఉండేలా ఎన్ని కమిటీలా ఎంచుకోవచ్చు ?
సాధన:
ఇచ్చిన ఎనిమిది మంది బాలుర నుంచి నలుగురు బాలురను ఎంచుకొనే విధానాల సంఖ్య = ⁸C₄
ఇంకా అయిదుగురు బాలికల నుంచి ముగ్గురు బాలికలను ఎంచుకొనే విధానాలు = ⁵C₃
కనుక, ప్రాఠామిక సూత్రం ప్రకారం నలుగురు బాలురు, ముగ్గురు బాలికలను ఎంచుకొనే విధానాలు.
= ⁸C₄ × ⁵C₃ = 70 × 10 = 700

ప్రశ్న 31.
విభిన్నమైన 7 ఇంగ్లీష, 6 తెలుగు, 5 హిందీ పుస్తకాల నుంచి 4 ఇంగ్లీష, 3 తెలుగు, 2 హిందీ పుస్తకాలను ఎంచుకొనే విధానాలు ఎన్ని?
సాధన:
ముందుగా 7 ఇంగ్లీషు పుస్తకాల నుంచి 4 పుస్తకాలను ఎంచుకొనే విధానాలు = ⁷C₄
6 తెలుగు పుస్తకాల నుంచి 3 తెలుగు పుస్తకాలను ఎంచుకొనే విధానాలు = ⁶C₃
5 హిందీ పుస్తకాల నుంచి 2 హిందీ పుస్తకాలను ఎంచుకొనే విధానాలు = ⁵C₂
కనుక, కావలసిన విధానాలు
= ⁷C₄ x ⁶C₃ x ⁵C₂

ప్రశ్న 32.
ఆరుగురు బాలురు, నలుగురు బాలికలనుంచి కనీసం ఒక బాలిక ఉండేలా నలుగురు సభ్యలున్న కమిటీలు ఎన్ని ఏర్పరచవచ్బు ?
సాధన:
ఏ నిబంధనా లేకుండా మొత్తం 10 మంది వ్యక్తుల (ఆరుగురు బాలురు + నలుగురు బాలికలు) నుంచి నలుగురు సభ్యులున్న కమిటీని ఎంచుకొనే విధాలు ¹⁰C₄ వీటిలో అసలు బాలికలు లేకుండా బాలురు మాత్రమే ఉండేటట్లు కమిటీ ఎంచుకొనే విధాలు ⁶C₄ కనుక కనీసం ఒక బాలికైనా ఉండే కమిటీల సంఖ్య
= ¹⁰C₄  – ⁶C₄= 210 – 15 = 195.

ప్రశ్న 33.
ఏడుగురు బాట్స్మెన్, అరుగురు బౌలర్లు, ఇద్దరు వికెట్ కీపర్లు నుంచి కనీసం నలుగురు బౌలర్లు, ఒక వికెట్ కీపరు ఉండేలా 11 మంది ఆటగాళ్ళతో క్రికట్ టీమును ఎన్ని రకాలుగా ఎంచుకోవచ్చు ?
సాధన:
కనీసం నలుగురు బౌలర్లు, ఉండాలంటే టీమును కింద చూపిన విధాలుగా ఎంచుకోవచ్చు.

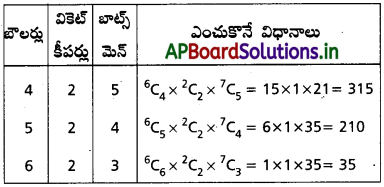
కనుక కోరిన విధంగా క్రికెట్ టిముని ఎంచుకొనె విధానాలు =315+210+35=560.

ప్రశ్న 34.
‘m’ సమాంతర రేఖలా మరాక ‘n’ సమాంతరరేఖలను (మొదటి రేఖలకు సమాంతరంగా లేని) ఖండిస్తే ఎన్ని సమాంతర చతుర్భుజాలేర్పడతాయి ?
సాధన:
ఒక సమాంతర చతుర్భుజం ఏర్పడాలంటే మొదటి m సరళరీఖల నుంచి 2 సరళరేఖలు ఎంచుకోవాలి. ఈ విధానాలు ^mC₂ రెండో సమితిలోని n సరళ రేఖల నుంచి 2 సరళరేఖలు ఎంచుకోవాలి. ఈ విధానాల సంఖ్య ⁿC₂ కనుక, దత్త సరళరేఖలు ఖండించుకోవడం వల్ల ఏర్పడే సమాంతర చతుర్భుజాల సంఖ్య = ^mC₂ x ⁿC₂

ప్రశ్న 35.
ఒక తలంలో m బిందువులున్నాయి. వాటిలో p బిందువులు సరేఖీయాలు,మిగిలిన బిందువులలో 3 మూడు బిందువులు సరేఖీయాలు కాకపోతే, ఈ బిందువులను రేఖాఖండాల ద్వారా కలిపితే వచ్చే విఖిన్న
(i) రేఖా ఖండాలెన్ని?
(ii) త్రిభజాలెన్ని ?
సాధన.
(i) ఇచ్చిన m బిందువుల నుంచి రెండు బిందువులను ఎంచుకొని కలిపితే ఒక రేఖాఖండం వస్తుంది. కనుక ^mC₂ రేఖాఖండాలు రావాలి. కాని m బిందువులలో p బిందువులు సరేఖీలయాలు కనుక ఈ బిందువులను వాటిలో వాటిని రెండు బిందువుల చాప్పున కలిపితే ^pC₂ రేఖాఖండాలు రావడానికి బదులుగా 1 రేఖాఖండం మాత్రమే వస్తుంది. కనుక దత్త m బిందువులను కలపడం ద్వారా వచ్చే విభిన్న రేఖాఖండాల సంఖ్య = ^mC₂ – ^pC₂ +1

(ii) ఇచ్చిన m బిందువులను 3 బిందువుల చొప్పున కలిపితే తిిభుజాలు ఏర్పడతాయి. కనుక ^mC₃ తిిభుజాలు రావాలి.కాని ఈ m బిందువులలో P బిందువులు సరేఖీయాలు కనుక ఈ p బిందువుల నుంచి 3 బిందువుల చాప్పున ఎంచుకొని కలిపితే ^pC₃ (తిభుజాలు దావడానికి బదులుగా ఒక రేఖాఖండం వస్తుంది. (అంటే ఒక్క (యిభుజం కూడా రాదు.) కనుక ఇచ్చిన m బిందువులను కలపడం ద్వారా ఏర్పడే తి่భుజాల సంఖ్య = ^mC₃ – ^pC₃ 

ప్రశ్న 36.
ఒక ఉపాధ్యాయుడు పదిమంది విద్యార్థులను పార్కుకు తీసుకువెళ్ళాలి. ఒక్కొక్కసారి ముగ్నురు విద్యార్థుల చొప్పున తీసుకు వెళ్ళగలరు. కాని ఏ ముగ్గురు విద్యార్థుల బృందాన్నైనా ఒక్కసారి మాత్రమే తీసుకాని వెళ్ళాలి ?
(i) ప్రతీ విద్యార్థికి ఎన్ని సార్లు పార్కుకు వెళ్ళే అవకాశం ఉoది?
(ii) ఉపాధ్యాయుడు ఎన్నిసార్లు పార్కుకు వెళ్ళే అవకాశం ఉoది ?
సాధన:
(i) పదిమంది విద్యార్థులలో x ఒకరు అనుకొందాం. పార్కుకు x వెళ్ళే (పతిసారి ఇంకా ఇరువురు విద్యార్థులను మిగిలిన తొమ్మిది మంది విద్యార్థుల నుంచి ఎంచుకోవాలి. ఈ పనిని ⁹C₂ విధాలుగా చేయవచ్చు.అంటే
x పార్కుకు ⁹C₂ = 36 సార్లు వెళతాడు.

(ii) పదిమంది విద్యార్థుల నుంచి ముగ్గురు విద్యార్థును ఎంపిక చేసిన ప్రతిసారి ఉపాధ్లాయుడు పార్కుకు వెళ్తాడు. కనుక ఉపాధ్యాయుడు ¹⁰C₃ =120 సార్లు పార్కుకు వెళతాడు.

ప్రశ్న 37.
ఒక రెండంతస్తుల బస్సుకు కింది అంతస్తులో 8 సీట్లు, పై అంతస్తులో 10 సీట్లు ఉన్నాయి. ఈ బస్సులో (ప్రయాణించవలసిన 18 ప్రయాకులల్లో ముగ్గురు పిల్లలు పై అంతస్తులో మాత్రమే వెళ్ళాలి. ఇంకా నలుగురు వృద్దులు పైఅంతస్తుకు వెళ్ళలేరు అని ఇస్తే వారిని ఎన్ని విధాలుగా అమర్చవచ్చు ?
సాధన:
ముగ్గురు పల్లలు పై అంతస్థులోనూ, నలుగురు వృద్ధులు కింది అంతస్తులోనూ ప్రయాణిస్తారనుకాంటే మిగిలిన ప్రయాణీకులు 11 మంది ప్రయాణీకులలో 7 కింది అంతస్తులో, 7 మంది పై అంతస్తులో ప్రయాణించాలి. కనుక 11 మంది 7 ఎంచుకొనే విదానాలు
¹¹C₇ కింది అంతస్తులోని 8 సీట్లలో 8! విధాలు గానూ, పై అంతస్థులోని 10 సీట్లలో (10)! విధాలుగానూ అమర్చవచ్చు. కనుక
మొత్తం విధానాల సంఖ్య = ¹¹C₇ × 10! × 8!

ప్రశ్న 38.
(i) \({ }^{10} C_3+{ }^{10} C_6={ }^{11} C_4\)
(ii) \({ }^{25} C_4+\sum_{r=0}^4{ }^{(29-r)} C_3={ }^{30} C_4\) అని నిరూపించండి.
సాధన:

ప్రశ్న 39.
(i) \({ }^{12} \mathrm{C}_{s+1}={ }^{12} \mathrm{C}_{2 \mathrm{~s}-5^{\prime}}\) అయితే s కనుక్కోండి.
(ii)\({ }^n C_{21}={ }^n C_{27} \text {, అయితే }{ }^{50} C_n\) విలువ కనుక్కోండి
సాధన:

ప్రశ్న 40.
ఒకే రకమైన 5 కలాలు, ఒకేరకమైన 6 పెన్సిళ్ళు, ఒకే రకమైన 7 రబ్బర్లు ఉన్నాయి. వాటి నుంచి ఎన్ని వస్తువులనైనా (కనీసం ఒకటి) ఎంచుకొనే విధానాలు సంఖ్యను కనుక్కోండి.
సాధన:
ఎంచుకొనే విధానాల సంఖ్య
= (5+1) (6+1) (7+1) -1 = 335

ప్రశ్న 41.
1080 సంఖ్యకు (1 సంఖ్యతో సహా) ధన భాజకాల సంఖ్యను కనుక్కోండి.
సాధన.
1080=2³ × 3³ × 5¹ (ప్రధాన అంకెల లబ్దం)
= (3+1) (3+1) (1+1)
= 4 × 4 × 2 = 32