AP Inter 2nd Year Maths 2B Solutions Chapter 2 వృత్త సరణులు Ex 2(b)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 2 వృత్త సరణులు Exercise 2(b) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 2 వృత్త సరణులు Exercise 2(b)

అభ్యాసం – 2(బి)

I.

ప్రశ్న 1.
క్రింది వృత్తాల మూలాక్షాల సమీకరణాలను కనుక్కోండి.
i) x² + y² – 3x − 4y + 5 = 0; 3(x² + y²) – 7x + 8y + 11 = 0
సాధన:
S ≡ x² + y² – 3x – 4y + 5 = 0
S ≡ 3x² + 3y² – 7x + 8y + 11 = 0
S – S’ = 0 మూలాక్షము
(x² + y² – 3x – 4y + 5) – (x² + y² – \(\frac{7}{3}\) x + \(\frac{8}{3}\) y + \(\frac{11}{3}\)) = 0
\(\frac{-2}{3}\)x – \(\frac{20}{3}\) y + \(\frac{4}{3}\) = 0
⇒ x + 10y – 2 = 0

ii) x² + y² + 2x + 4y + 1 = 0; x² + y² + 4x + y = 0.
సాధన:
S – S’ = 0 మూలాక్షము
(x² + y² + 2x + 4y + 1)
-(x² + y² + 4x + y) = 0
– 2x + 3y+1=0
లేదా 2x – 3y – 1 = 0 కావలసిన మూలాక్షము.

iii) x² + y² + 4x + 6y – 7 = 0; 4(x² + y²) + 8x + 12y – 9 = 0.
సాధన:
S-S’ = 0 మూలాక్షము
(x² + y² + 4x + 6y – 7) – (x²+ y²+ 2x + 3y – \(\frac{9}{4}\)) = 0
2x + 3y – \(\frac{-19}{4}\) = 0
⇒ 8x + 12y – 19 = 0

iv) x²+ y² – 2x – 4y – 1 = 0; x² + y² – 4x – 6y + 5 = 0.
సాధన:
S – S’ = 0 మూలాక్షము
(x² + y² – 2x – 4y – 1) -(x²+ y² – 4x – 6y + 5) = 0
2x + 2y – 6 = 0 లేదా
x + y – 3 = 0

ప్రశ్న 2.
క్రింది వృత్తాల ఉమ్మడి జ్యాల సమీకరణాలను కనుక్కోండి.
i) x²+ y² – 4x – 4y + 3 = 0; x² + y² – 5x – 6y + 4 = 0.
సాధన:
(x² + y² – 4x – 4y + 3) – (x² + y² – 5x – 6y + 4) = 0
ఉమ్మడి జ్యా సమీకరణము x + 2y – 1 = 0

ii) x² + y² + 2x + 3y + 1 = 0; x² + y² + 4x + 3y + 2 = 0.
సాధన:
(x² + y² + 2x + 3y + 1) – (x² + y² + 4x + 3y + 2) = 0
-2x – 1 = 0
ఉమ్మడి జ్యా సమీకరణము
-2x – 1 = 0
(i.e.,) 2x + 1 = 0

iii) (x – a)² + (y – b)² = c²; (x – b)² + (y – a)² = c² (a ≠ b)
సాధన:
ఉమ్మడి జ్యా సమీకరణము (x² + y² – 2xa – 2yb – c²) – (x² + y² – 2xb – 2ya – c²) = 0
-2x (a – b) – 2y(b – a) = 0
లేదా x – y = 0

II.

ప్రశ్న 1.
ఒకదానికొకటి స్పృశించుకొనే బిందువు వద్ద క్రింది వృత్తాల ఉమ్మడి స్పర్శ రేఖల సమీకరణాలు కనుక్కోండి.
i) x² + y² + 10x – 2y + 22 = 0, x² + y² + 2x – 8y + 8 = 0.
సాధన:
x² + y² + 10x – 2y + 22 = 0
x² + y² + 2x – 8y + 8 = 0
రెండు వృత్తాలు స్పృశించుకుంటే S – S’ = 0 ఉమ్మడి స్పర్శరేఖా సమీకరణము అవుతుంది.
∴ (x² + y² + 10x – 2y + 22) – (x² + y² + 2x – 8y + 8) = 0
8x + 6y + 14 = 0 లేదా
4x + 3y + 7 = 0

ii) x² + y² – 8y – 4 = 0; x² + y² – 2x – 4y = 0.
సాధన:
రెండు వృత్తాలు స్పృశించుకుంటే S – S’ = 0 ఉమ్మడి స్పర్శరేఖా సమీకరణము.
(x² + y² – 8y – 4) – (x² + y² – 2x – 4y) = 0
2x – 4y – 4 = 0
లేదా x – 2y – 2 = 0

ప్రశ్న 2.
x² + y² – 8x – 2y + 8 = 0, x² + y² – 2x + 6y + 6 = 0 వృత్తాలు స్పృశించు కుంటాయని చూపి, వాటి స్పర్శ బిందువును కనుక్కోండి.
సాధన:
C₁ = (4, 1);
C₂ = (1,-3)
r₁ = \(\sqrt{16+1-8}\) = 3
r₂ = \(\sqrt{1+9-6}\) = 2
C₁C₂ = \(\sqrt{(4-1)^2+(1+3)^2}\) = 5
r₁ + r₂ = C₁ + C₂ వృత్తాలు బాహ్యంగా స్పృశించు కుంటాయి.

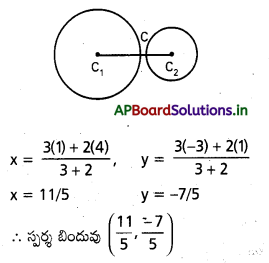
ప్రశ్న 3.
x²+ y² + 2gx + 2fy = 0, x² + y² + 2g’x + 2f’y = 0 వృత్తాలు ఒకదానికొకటి స్పృశించుకొంటే f’g = fg’ అని చూపండి. [T.S. Mar. ’16]
సాధన:
C₁ = (-g, -f)
C₂ = (-g’, -f’)
r₁ = \(\sqrt{g^2+f^2}\)
r₂ = \(\sqrt{g^{\prime^2}+f^{\prime^2}}\)
C₁C₂ = r₁ + r₂
(C₁C₂)² = (r₁ + r₂)²
(g’ – g)² + (f’ – f)² = g² + f² + g’² + f’² + 2\(\sqrt{g^2+f^2} \sqrt{g^{\prime^2}+f^{\prime^2}\) – 2(gg’ + ff’) = 2{g²g’² + f²f’² + g²f’² + f²g’²}^1/2
మరల వర్గీకరించగా
(gg’ + ff’)² = g²g’² + f²f’² + g²f’² + g’²f²
g²g’² + f²f’² + 2gg’ff’ = g²g’² + f²f’² + g²f’² + g’²f’²
2gg’ff’ = g²f’² + f²g’²
⇒ g²f’² + g’²f² – 2gg’ff’ = 0
లేదా (gf – fg’)² = 0
లేదా gf’ = fg’

ప్రశ్న 4.
క్రింది వృత్తాల మూల కేంద్రం కనుక్కోండి.
i) x² + y² – 4x – 6y + 5 = 0
x² + y² – 2x – 4y – 1 = 0
x² + y² – 6x – 2y = 0
సాధన:
x² + y² – 4x – 6y + 5 = 0 ……………. (i)
x² + y² – 2x – 4y – 1 = 0 ………………. (ii)
x² + y² – 6x – 2y = 0 …………………. (iii)
(i) – (ii) చేయగా
-2x – 2y + 6 = 0
x + y – 3 = 0 ……………. (1)
(ii) – (iii) చేయగా
4x – 2y – 1 = 0 ……………….. (2)
2x + 2y – 6 = 0 – (1) × 2
4x – 2y – 1 = 0 …………….. (3)
కూడగా 6x – 7 = 0
x = \(\frac{7}{6}\)
(1) నుండి \(\frac{7}{6}\) + y – 3 = 0
y = 3 – \(\frac{7}{6}\) = \(\frac{11}{6}\)
(1), (2) ల ఖండన బిందువు మూల కేంద్రం అవుతుంది.
∴ (1), (2) లను సాధించగా మూల కేంద్రం = (\(\frac{7}{6}\), \(\frac{11}{6}\))

ii) x² + y² + 4x – 7 = 0, 2x² + 2y² + 3x + 5y – 9 = 0, x² + y²+ y = 0.
సాధన:
S = x² + y² + 4x – 7 = 0 …………….. (i)
S₁ = 2x² + 2y² + 3x + 5y – 9 = 0
S₁ = x² + y² + \(\frac{3}{2}\)x + \(\frac{5}{2}\)y – \(\frac{9}{2}\) = 0 ……………… (ii)
S₁₁ = x² + y² + y = 0 ………….. (iii)
S = 0, S₁; = 0 ల మూలాక్షము S – S₁ = 0
(4x – 7) – (\(\frac{3}{2}\)x + \(\frac{5}{2}\)y – \(\frac{9}{2}\)) = 0
4x – 7 – \(\frac{3}{2}\)x – \(\frac{5}{2}\)y + \(\frac{9}{2}\) = 0
\(\frac{5}{2}\)x – \(\frac{5}{2}\)y – \(\frac{5}{2}\) = 0
5x – 5y – 5 = 0
x – y – 1 = 0 ………………. (iv)
S = 0, S₁₁ = 0 ల మూలాక్షము S – S₁₁ = 0
4x – y – 7 = 0 ……………. (v)
x – y – 1 = 0 ……………… (iv)
తీసివేయగా 3x – 6 = 0 ⇒ 3x = 6
x = \(\frac{6}{3}\) = 2
(iv) లో ప్రతిక్షేపించగా 2 – y – 1 = 0
y = 1
మూలకేంద్రం P(2, 1)

III.

ప్రశ్న 1.
x² + y²-6x-4y+ 9 = 0, x² + y² – 8x – 6y + 23 = 0 వృత్తాల ఉమ్మడి జ్యా రెండో వృత్తపు వ్యాసం అవుతుందని చూపండి. ఇంకా దీని పొడవును కనుక్కోండి.
సాధన:
ఉమ్మడి జ్యా సమీకరణము
(x² + y² – 6x – 4y + 9) – (x² + y² – 8x – 6y + 23) = 0
2x + 2y – 14 = 0
x + y – 7 = 0 …………….. (i)
వృత్త కేంద్రం (−4, -3)
(-4, -3) బిందువు x + y – 7 రేఖపై ఉంది
వ్యాసార్ధం {4² + 3² – 23}^1/2 = \(\sqrt{2}\)
వ్యాసం = 2\(\sqrt{2}\)

ప్రశ్న 2.
క్రింది వృత్తాల ఉమ్మడి జ్యా సమీకరణాన్ని, దాని పొడవును కనుక్కోండి.
i) x² + y² + 2x + 2y + 1 = 0, x² + y² + 4x + 3y + 2 = 0.
సాధన:
x² + y² + 2x + 2y + 1 = 0
x² + y²+ 4x + 3y + 2 = 0
ఉమ్మడి జ్యా సమీకరణము S – S’ = 0
(x² + y² + 2x + 2y + 1) – (x² + y² + 4x + 3y + 2) = 0
-2x – y – 1 = 0
2x + y + 1 = 0
నృత్త కేంద్రం (−1, −1)
వ్యాసార్ధము = \(\sqrt{1+1-1}\) = 1
(-1, -1) నుండి జ్యాకు లంబదూరము

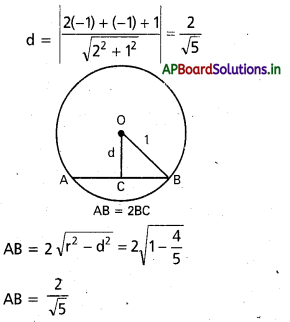
ii) x² + y² – 5x – 6y + 4 = 0 ; x²+ y² – 2x – 2 = 0
సాధన:
ఉమ్మడి జ్యా సమీకరణము
(x² + y² – 5x – 6y + 4) – (x² + y² – 2x – 2) = 0
-3x – 6y + 6 = 0
x + 2y -2 = 0
C₁ = (5/2, 3); .
r₁ = \(\sqrt{\frac{25}{4}+9-4}\)
= \(\frac{3 \sqrt{5}}{2}\)
d = \(\left|\frac{\frac{5^2}{2}+2(3)-2}{\sqrt{1+2^2}}\right|\)
d = \(\frac{13}{2 \sqrt{5}}\)
జ్యా పొడవు = 2\(\sqrt{r^2-d^2}\)
= 2\(\sqrt{\frac{45}{4}-\frac{169}{20}}\)
= \(\frac{2 \sqrt{56}}{\sqrt{20}}\) = 2\(\sqrt{\frac{14}{5}}\)

ప్రశ్న 3.
2g'(g – g’) + 2f'(f – f’) = c – c’ అయితే x² + y² + 2gx + 2fy + c = 0, x² + y²+ 2g’x + 2f’y + c’ = 0
వృత్తాల మూలాక్షం రెండో వృత్త వ్యాసమని (లేదా మొదటి వృత్తం రెండో వృత్త పరిధిని సమద్విఖండన చేస్తుందని) నిరూపించండి.
సాధన:
మూలాక్షము
(x² + y² + 2gx + 2fy + c) – (x² + y² + 2g’x + 2f’y + c’) = 0
2(g – g’) x + 2(f – f’) y + c – c’ = 0 ………………… (i)
రెండో వృత్త కేంద్రం (-g’, -f)
వ్యాసార్ధం = \(\sqrt{g^{\prime^2}+f^{\prime^2}-c^{\prime}}\)
(-g’, -f) బిందువు (i) మీద ఉంది
∴ -2g’ (g – g’) – 2f’ (f – f’) + c – c’ = 0
లేదా 2g’ (g – g’) + 2f’ (f – f’) = c – c’

ప్రశ్న 4.
\(\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{c}\) అయితే x²+ y² + 2ax + c = 0, x² + y² + 2by + c = 0 వృత్తాల ఒకదానికొకటి స్పృశించుకుంటాయని చూపండి.
సాధన:
వృత్తాల కేంద్రాలు C₁ (-a, 0) మరియు C₂ (0, -b)
1వ వృత్త వ్యాసార్ధము \(\sqrt{a^2-c}\) = r₁
2వ వృత్త వ్యాసార్ధము \(\sqrt{b^2-c}\) = r₂
C₁C₂ = r₁ + r₂
(C₁C₂)² = (r₁ + r₂)²
(a² + b²) = a² – c + b² – c + 2 \(\sqrt{a^2-c} \sqrt{b^2-c}\)
c = \(\sqrt{a^2-c} \sqrt{b^2-c}\)
c² = (a² – c) (b² – c)
c² = -c (a² + b²) + a²b² + c²
లేదా c(a² + b²) = a²b² లేదా \(\frac{1}{c}=\frac{1}{a^2}+\frac{1}{b^2}\)

ప్రశ్న 5.
x² + y² – 2x = 0, x² + y² + 6x – 6y + 2 = 0 వృత్తాలు ఒకదానికొకటి స్పృశించుకుంటాయని చూపండి. స్పర్శ బిందువును కనుక్కోండి. ఈ వృత్తాలు బాహ్యంగా స్పృశించుకున్నాయో లేదా అంతరంగా స్పృశించు కున్నాయో తెలపండి.
సాధన:
S = x² + y² – 2x = 0 వృత్తానికి
కేంద్రం C₁ = (1, 0) వ్యాసార్థం r₁ = \(\sqrt{1+0}\) = 1
S’ = x² + y² + 6x – 6y + 2 = 0 వృత్తానికి
కేంద్రం C₂ = (-3, 3)
వ్యాసార్థము r₂ = \(\sqrt{9+9-2}\) = \(\sqrt{16}\) = 4
C₁C₂ = \(\sqrt{(1+3)^2+(0-3)^2}\)
= \(\sqrt{16+9}\) = \(\sqrt{25}\) = 5
r₁ + r₂ = 1 + 4 = 5
C₁C₂ = r₁ + r₂ కనుక దత్త వృత్తాలు బాహ్యంగా స్పృశించు కుంటాయి. స్పర్శ బిందువు P కేంద్ర రేఖను అంతరంగా r₁ : r₂ = = 1 : 4 నిష్పత్తిలో విభజిస్తుంది.
స్పర్శబిందువు P = \(\left(\frac{1(-3)+4(1)}{1+4}, \frac{1(3)+4(0)}{1+4}\right)\)
= \(\left(\frac{1}{5}, \frac{3}{5}\right)\)
వృత్తాలు బాహ్యంగా స్పృశించుకుంటాయి.

ప్రశ్న 6.
క్రింది ఇచ్చిన మూడు వృత్తాలను లంబంగా ఖండించే వృత్త సమీకరణాన్ని కనుక్కోండి.
i) x² + y² + 4x – 7 = 0
2x² + 2y² + 3x + 5y – 9 = 0
x² + y² + y = 0
సాధన:
S ≡ x² + y² + 4x – 7 = 0
S₁ = 2x² + 2y² + 3x + 5y – 9 = 0
S₁₁ = x² + y² + y = 0
4(ii) నుండి మూలకేంద్రం P(2, 1)
PT = P నుండి S = 0 స్పర్శరేఖ పొడవు
= \(\sqrt{4+1+8-7}\) = \(\sqrt{6}\)
P(2, 1) కేంద్రంగా PT వ్యాసార్థంగా గల వృత్తం దత్త వృత్తాలను లంబంగా ఖండిస్తుంది.
దత్త వృత్తాలను లంబంగా ఖండించే వృత్త సమీకరణము
(x – 2)² + (y – 1)² = 6
x² – 4x + 4 + y² – 2y + 1 – 6 = 0
i.e., x² + y² – 4x – 2y – 1 = 0

ii) x² + y² + 2x + 4y + 1 = 0 ; 2x² + 2y² + 6x + 8y – 3 = 0 ; x² + y² – 2x + 6y – 3 = 0
సాధన:
దత్త వృత్తాల సమీకరణాలు
S ≡ x² + y² + 2x + 4y + 1 = 0
S₁ = x² + y² + 3x + 4y – \(\frac{3}{2}\) = 0
S₁₁ = x² + y² – 2x + 6y – 3 = 0
S = 0, S₁ = 0 ల మూలాక్షము S – S₁ = 0
-x + \(\frac{5}{2}\) = 0 ⇒ x = \(\frac{5}{2}\)
S = 0, S₁₁ = 0 ల మూలాక్షము S – S₁₁ = 0
4x – 2y + 4 = 0
⇒ 2x – y + 2 = 0
x = \(\frac{5}{2}\) ⇒ 5 – y + 2 = 0
⇒ y = 7
మూల కేంద్రము P (\(\frac{5}{2}\), 7)
PT P నుండి S = 0 కు స్పర్శరేఖ పొడవు
= \(\sqrt{\frac{25}{4}+49+5+28+1}\)
= \(\sqrt{\frac{25}{4}+83}=\sqrt{\frac{25+332}{4}}=\frac{\sqrt{357}}{2}\)
దత్త వృత్తాలను లంబంగా ఖండించే వృత్త సమీకరణము
(x – \(\frac{5}{2}\))² + (y – 7)² = \(\frac{357}{4}\)
x² – 5x + \(\frac{25}{4}\) + y² – 14y + 49 = \(\frac{357}{4}\)
x² + y² – 5x – 14y + \(\frac{25}{4}\) + 49 – \(\frac{357}{4}\) = 0
x² + y² – 5x – 14y + \(\frac{25+196-357}{4}\) = 0
x² + y² – 5x – 14y – \(\frac{136}{4}\) = 0
x² + y² – 5x – 14y – 34 = 0

iii) x² + y²+ 2x + 17y + 4 = 0 ; x² + y² + 7x + 6y + 11 = 0 ; x² + y² – x + 22y + 3 = 0
సాధన:
దత్త వృత్తాల సమీకరణాలు
S ≡ x² + y² + 2x + 17y + 4 = 0 ………….. (i)
S₁ ≡ x² + y² + 7x + 6y + 11 = 0 ……………… (ii)
S₁₁ ≡ x² + y² – x + 22y + 3 = 0 ……………….. (iii)
S = 0, S₁ = 0 ల మూలాక్షము S – S₁ = 0
-5x + 11y – 7 = 0
5x – 11y + 7 = 0 ……………….. (iv)
S = 0, S₁₁ = 0 ల మూలాక్షము S – S₁₁ = 0
3x – 5y + 1 = 0 ……………….. (v)
(iv), (v) లను సాధించగా

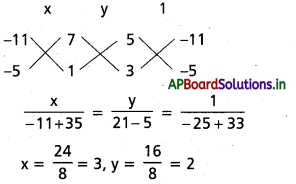
మూల కేంద్రము P(3, 2)
PT P నుండి S = 0 కు స్పర్శరేఖ పొడవు
= \(\sqrt{9+4+6+34+4}\) = \(\sqrt{57}\)
దత్త వృత్తాలను లంబంగా ఖండించే వృత్త సమీకరణము
(x – 3)² + (y – 2)² = 57
x² – 6x + 9 + y² – 4y + 4 – 57 = 0
x² + y² – 6x – 4y – 44 = 0

iv) x² + y² + 4x + 2y + 1 = 0
2(x² + y²) + 8x + 6y – 3 = 0
x² + y²+6x – 2y – 3 = 0
సాధన:
దత్త వృత్తాల సమీకరణాలు
S ≡ x² + y²+ 4x + 2y + 1 = 0 …………….. (i)
S₁ ≡ x² + y² + 4x + 3y – \(\frac{3}{2}\) = 0 ………….. (ii)
S₁₁ ≡ x² + y² + 6x – 2y – 3 = 0 ……….. (iii)
(i) – (ii) చేయగా S = 0, S₁ = 0 ల మూలాక్షము
S – S₁ = 0 ⇒ -y + \(\frac{5}{2}\) = 0 ⇒ y = \(\frac{5}{2}\)
S = 0, S₁₁ = 0 ల మూలాక్షము S – S₁₁ = 0
– 2x + 4y + 4 = 0
x – 2y – 2 = 0
y = \(\frac{5}{2}\) ⇒ x – 5 – 2 = 0
x = 5 + 2 = 7
మూల కేంద్రం P (7, \(\frac{5}{2}\))
PT = P నుండి S = 0 కు స్పర్శరేఖ పొడవు
= \(\sqrt{49+\frac{25}{4}+28+5+1}=\sqrt{83+\frac{25}{4}}\)
= \(\sqrt{\frac{332+25}{4}}=\frac{\sqrt{357}}{2}\)
కావలసిన వృత్త సమీకరణము
(x – 7)² + ( y – \(\frac{5}{2}\))² = \(\frac{357}{4}\)
x² – 14x + 49 + y² – 5y + \(\frac{25}{4}\) – \(\frac{357}{4}\) = 0
x² + y² – 8x – 5y + \(\frac{196+25-357}{4}\) = 0
x² + y² – 14x – 5y – \(\frac{136}{4}\) = 0
లేదా 3x² + y² – 14x – 5y – 34 = 0