AP Inter 2nd Year Maths 2B Solutions Chapter 8 అవకలన సమీకరణాలు Ex 8(c)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 8 అవకలన సమీకరణాలు Exercise 8(c) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 8 అవకలన సమీకరణాలు Exercise 8(c)

అభ్యాసం – 8(సి)

I.

ప్రశ్న 1.
x dy – ydx = \(\sqrt{x^2+y^2} d x\) ను \(\frac{d y}{d x}\) = F\(\left(\frac{y}{x}\right)\) రూపంలో రాయండి.
సాధన:

ప్రశ్న 2.
(x – y Tan^-1\(\frac{y}{x}\))dx + x Tan^-1\(\frac{y}{x}\)dy = 0 ని \(\frac{\mathbf{d y}}{\mathbf{d x}}\) = F\(\left(\frac{y}{x}\right)\) రూపంలో రాయండి.
సాధన:

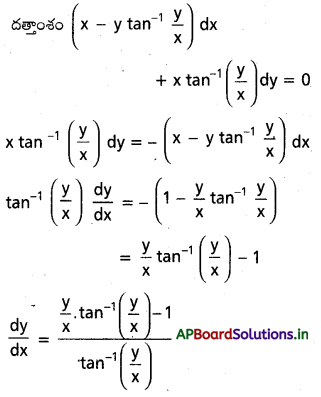
ప్రశ్న 3.
x\(\frac{d y}{d x}\) = y (log y -log x + 1) ను \(\frac{d y}{d x}\) = F\(\left(\frac{y}{x}\right)\) రూపములో వ్రాయండి
సాధన:
x . \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = y (log y – log x + 1)
\(\frac{d y}{d x}\) = \(\frac{y}{x}\left(\log \frac{y}{x}+1\right)\)

II. కింది అవకలన సమీకరణాలను సాధించండి.

ప్రశ్న 1.
\(\frac{d y}{d x}\) = \(\frac{x-y}{x+y}\)
సాధన:

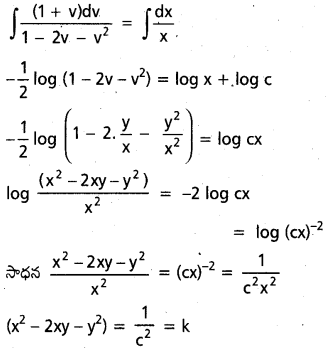
ప్రశ్న 2.
(x² + y²) dy = 2xy dx
సాధన:
(x² + y²) dy = 2xy dx
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{2 x y}{x^2+y^2}\)
Put y = vx

1 + v² = A(1 – v²) + BV(1 – V) + CV(1 + v)
v = 0 ⇒ 1 = A
v = 1 ⇒ 1 + 1 = C(2) ⇒ c = 1
y = -1 ⇒ 1 + 1 = B(-1) (2) ⇒ 2 = – 2B
B = -1
\(\int \frac{1+v^2}{v\left(1-v^2\right)} d v\) = \(\int \frac{d v}{v}\) – \(\int \frac{d v}{1+y}\) + \(\int \frac{d v}{1-v}\)
= log v – log (1 + v) – log (1 – v)
= log \(\frac{v}{1-v^2}\)
∴ log \(\frac{v}{1-v^2}\) = log x + log c = log cx
\(\frac{v}{1-v^2}\) = cx
v = cx(1 – v²)
v = cx\(\left(1-\frac{y^2}{x^2}\right)\)
\(\frac{y}{x}\) = cx\(c x \frac{\left(x^2-y^2\right)}{x^2}\) ⇒ సాధన y = c(x² – y²)

ప్రశ్న 3.
\(\frac{d y}{d x}\) = \(\frac{-\left(x^2+3 y^2\right)}{3 x^2+y^2}\)
సాధన:
\(\frac{d y}{d x}\) = \(\frac{-\left(x^2+3 y^2\right)}{3 x^2+y^2}\)
put y = vx

(v + 1)³ గుణించగా
3 + v² = A(v + 1)² + B(v + 1) + C
v = -1 ⇒ 3 + 1 = C ⇒ C = 4
v² గుణకాలను సమానం చేయగా
A = 1
v గుణకాలను సమానం చేయగా
0 = 2A + B
B = -2A = -2

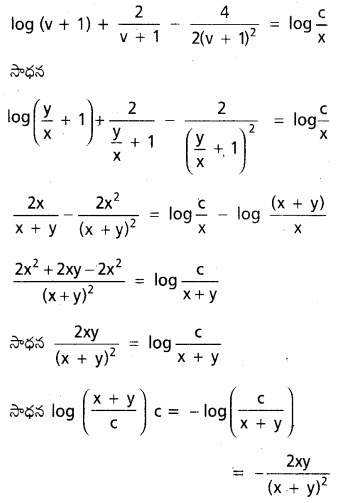
ప్రశ్న 4.
y² dx + (x² – xy) dy = 0
సాధన:
y² dx = -(x² – xy) dy
= (xy – x²) dy

v – log y = log x + log k
v = log v + log x + log k
= log k (vx)
\(\frac{y}{x}\) = log ky
సాధన ky = e^y/x

ప్రశ్న 5.
\(\frac{d y}{d x}\) = \(\frac{(x+y)^2}{2 x^2}\)
సాధన:

ప్రశ్న 6.
(x² – y²) dx – xy dy = 0 (May 06)
సాధన:
(x² – y²) dx – xy dy = 0
(x² – y²) dx = xy . dy

\(-\frac{1}{4}\)log \(\left(\frac{x^2-2 y^2}{x^2}\right)\) = log x + log c
\(-\frac{1}{4}\)[log (x² – 2y²) – log x²] = log x + log c
\(-\frac{1}{4}\)[log (x² – 2y²) + \(\frac{1}{4}\). 2 log x = log x + log
\(-\frac{1}{4}\)(x² – 2y²) = \(\frac{1}{2}\)logx + logc
– log (x² – 2y²) = -2 log x – 4 log c
-log(x² – 2y²) = -2 log x – 4 log c
log (x² – 2y²) = – 2 log x + log k
ఇక్కడ k = \(\frac{1}{c^4}\) = log \(\frac{k}{x^2}\)
x² – 2y² = \(\frac{k}{x^2}\)
సాధన x² (x² – 2y²) = k

ప్రశ్న 7.
(x²y – 2xy²) dx = (x³ – 3x²y dy)
సాధన:
(x²y – 2xy²) dx = (x³ – 3x²y) dy
y = vx అనుకొంటే \(\frac{d y}{d x}\) = v + x . \(\frac{d v}{d x}\)

1 – 3v = A (1 + v) + Bv
v = 0 ⇒ 1 = A
v = -1 ⇒ 4 = -B ⇒ B = -4
\(\int\left(\frac{1}{v}-\frac{4}{1+v}\right) d\) = \(\int \frac{d x}{x}\)
log v – 4 log(1 + y) = log x + log c
log \(\frac{v}{(1+v)^4}\) = log cx
\(\frac{v}{(1+v)^4}\) = cx
v = cx (1 + v)⁴
\(\frac{y}{x}\) = cx\(\left(1+\frac{y}{x}\right)^4\)
\(\frac{y}{x}\) = cx \(\frac{(x+y)^4}{x^4}\)
x²y = e(x + y)⁴

ప్రశ్న 8.
y²dx + (x² – xy + y²) dy = 0
సాధన:
y²dx = – (x² – xy + y²) dy
\(\frac{d y}{d x}\) = \(\frac{-y^2}{x^2-x y+y^2}\)

1 – v² + v² = A(1 + v²) + (Bv + C)v
v = 0 ⇒ 1 = A
v² గుణకాలను సమానం చేయగా
1 = A + B ⇒ B = 0
v గుణకాలను సమానం చేయగా
-1 = C
⇒ \(\frac{1-v+v^2}{v\left(1+v^2\right)}\) = \(\frac{1}{v}\) – \(\frac{1}{1+v^2}\)
\(\int \frac{1-v+v^2}{v\left(1+v^2\right)} d v\) = \(\int \frac{d v}{v}\) – \(\int \frac{d v}{1+v^2}\)
= log v – tan^-1 v
(1) నుండి
log v – tan^-1 v = – log x + log c
tan^-1 v = log v + log x – log c
= log \(\frac{v x}{c}\)
= log \(\frac{y}{c}\)
\(\frac{y}{c}\) = \(\mathrm{e}^{\tan ^{-1} v}\) = \(e^{\tan ^{-1}(y / x)}\)
సాధన y = c. \(e^{\tan ^{-1}(y / x)}\)

ప్రశ్న 9.
(y² – 2xy) dx + (2xy – x²) dy = 0
సాధన:
(y² – 2xy)dx + (2xy – x²) dy = 0
(2xy – x²)dy = -(y² – 2xy) dx

\(\int \frac{2 v-1}{v(1-v)} d v\) = \(3 \int \frac{d x}{x}\) —– (1)
\(\frac{2 v-1}{v(1-v)}\) = \(\frac{A}{v}\) + \(\frac{B}{1-v}\) అనుకుందాం
2v – 1 = A(1 – v) + Bv
v = 0 ⇒ -1 = A ⇒ A = -1
v = 1 ⇒ 1 = B ⇒ B = 1
\(\int\left(-\frac{1}{v}+\frac{1}{1-v}\right) d v\) = \(3 \int \frac{d x}{x}\)
-log v – log (1 – y) = 3 log x + log c
log \(\frac{1}{v(1-v)}\) = log cx³
\(\frac{1}{v(1-v)}\) = cx³
v(1 – v) = \(\frac{1}{c x^3}\)
\(\frac{y}{x}\left(1-\frac{y}{x}\right)\) = \(\frac{1}{c x^3}\)
\(\frac{y}{x}\left(\frac{x-y}{x}\right)\) = \(\frac{1}{\mathrm{cx}^3}\)
xy(x – y) = \(\frac{1}{c}\) = k
xy(y – x) = \(-\frac{1}{c}\) = k’

ప్రశ్న 10.
\(\frac{d y}{d x}\) + \(\frac{y}{x}\) = \(\frac{y^2}{x^2}\)
సాధన:
\(\frac{d y}{d x}\) + \(\frac{y}{x}\) = \(\frac{y^2}{x^2}\)
y = vx ⇒ \(\frac{d y}{d x}\) = v + x. \(\frac{d v}{d x}\)
v + x. \(\frac{d v}{d x}\) + v = \(\frac{v^2 x^2}{x^2}\)
x.\(\frac{d v}{d x}\) = v² – 2v
\(\frac{d v}{v^2-2 v}\) = \(\frac{\mathrm{dy}}{\mathrm{x}}\)
\(\frac{1}{v^2-2 v}\) = \(\frac{A}{v}\) + \(\frac{B}{v-2}\) అనుకుందాం
1 = A(v – 2) + Bv
v = 0 ⇒ 1 = A(-2) ⇒ A = \(-\frac{1}{2}\)
v = 2 ⇒ 1 = 2B ⇒ B = \(\frac{1}{2}\)

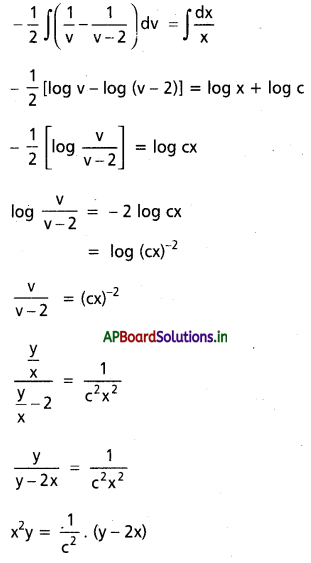
సాధన
y – 2x = c²x²y
= kx²y, k = c² అనుకుందాం

ప్రశ్న 11.
x dy – y dx = \(\sqrt{x^2+y^2}\) dx
సాధన:
x dy – y dx = \(\sqrt{x^2+y^2}\) dx
x \(\frac{\mathrm{dy}}{\mathrm{dx}}\) – y = \(\sqrt{x^2+y^2}\)
\(\frac{d y}{d x}\) – \(\frac{y}{x}\) = \(\frac{\sqrt{x^2+y^2}}{x}\)
y = vx ⇒ \(\frac{d y}{d x}\) = v + x . \(\frac{d v}{d x}\)

ప్రశ్న 12.
(2x – y)dy = (2y – x) dx.
సాధన:

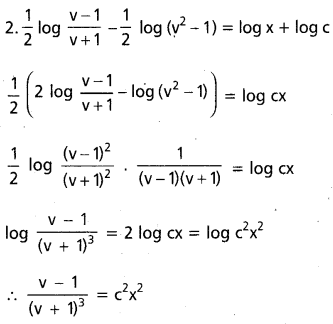
ప్రశ్న 13.
(x² – y²) \(\frac{d y}{d x}\) = xy (May ’11)
సాధన:

= log y + c
\(\frac{-x^2}{2 y^2}\) = (log y + c)
– x² = 2y² (c + log y)
⇒ సాధన x² + 2y² (c + log y) = 0

ప్రశ్న 14.
2\(\frac{d y}{d x}\) = \(\frac{y}{x}\) + \(\frac{y^2}{x^2}\)
సాధన:
y = vx అనుకొందాం
\(\frac{d y}{d x}\) = v + x. \(\frac{d v}{d x}\)
2v + 2x. \(\frac{d v}{d x}\) = v + v²
2x. \(\frac{d v}{d x}\) = v² – v
\(\frac{d v}{v(v-1)}\) = 2.\(\frac{d x}{x}\)
\(\int\left(\frac{1}{v-1}-\frac{1}{v}\right) d v\) = \(2 \int \frac{d x}{x}\)
log (v – 1) – log v = 2 log x + log c

సాధన (y – x) = cx²y

III.

ప్రశ్న 1.
(1 + \(e^{\frac{x}{y}}\))dx + \(e^{\frac{x}{y}}\)(1 – \(\frac{x}{y}\))dy = 0 ను సాధించండి.
సాధన:
x = vy అనుకొందాం

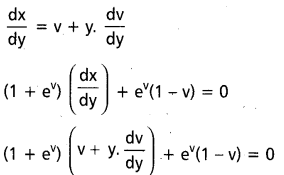
v + v.e^v + y(1 + e^v) + e^v – v.e^v = 0
y(1 + e^v). dv = -(v + e^v) dy
\(\int \frac{1+e^v}{v+e^v}\) = –\(\int \frac{d y}{y}\)
log (v + e^v) = – log y + log c
v + e^y = \(\frac{e}{y}\)
\(\frac{x}{y}\) + e^x/y = \(\frac{e}{y}\) ⇒ x + y. e<sup.x/y = c

ప్రశ్న 2.
x sin \(\frac{y}{x}\). \(\frac{d y}{d x}\) = y sin \(\frac{y}{x}\) – x ను సాధించండి.
సాధన:
x తో భాగించగా

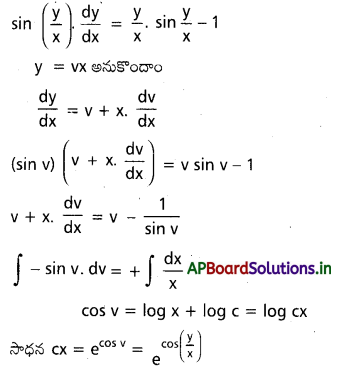
ప్రశ్న 3.
x dy = (y + x cos² \(\frac{y}{x}\)) dx ను సాధించండి.
సాధన:
x. \(\frac{d y}{d x}\) = y + x. cos² \(\frac{y}{x}\)
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{y}{x}\) + cos²\(\frac{y}{x}\)
put y = vx
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = v + x. \(\frac{\mathrm{dv}}{\mathrm{dx}}\)
v + x. \(\frac{\mathrm{dv}}{\mathrm{dx}}\) = v + cos² v
\(\frac{d v}{\cos ^2 v}\) = \(\frac{\mathrm{dx}}{\mathrm{x}}\)
\(\int \sec ^2 v \cdot d v\) = \(\int \frac{d x}{x}\)
tan v = log x + c
i.e., సాధన tan \(\left(\frac{y}{\dot{x}}\right)\) = log x + c.

ప్రశ్న 4.
(x – y log y + y log x)dx + x(log y – log x)dy = 0 ను సాధించండి
సాధన:
x. dx తో భాగించగా

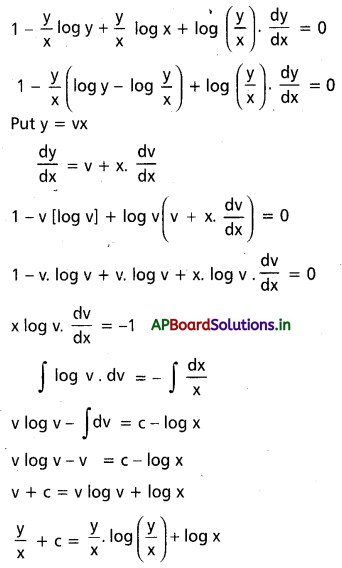
y + cx = ylog\(\left(\frac{y}{x}\right)\) + x log x
= y log y – y log x + x log x
= (x – y) log x + y log y

ప్రశ్న 5.
(y dx + x dy) x cos \(\frac{y}{x}\) = (x dy – y dx) y sin \(\frac{y}{x}\) ను సాధించండి.
సాధన:
ఇచ్చిన సమీకరణమును క్రింది విధంగా వ్రాయగలరు.


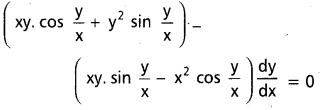
∴ ఇది సమఘాత సమీకరణము

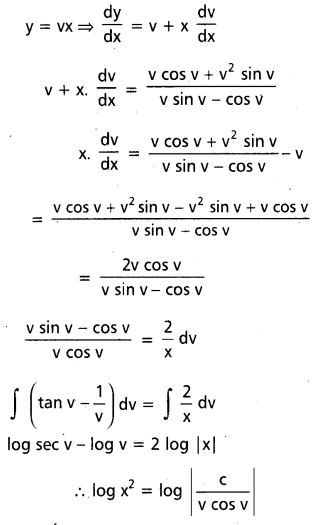
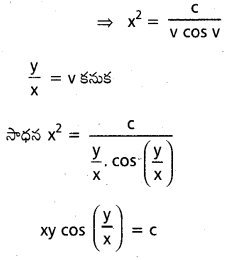
ప్రశ్న 6.
వాలు \(\frac{d y}{d x}\) = \(\frac{y}{x}\) – cos² \(\frac{y}{x}\), (x > 0, y > 0) అవుతూ(1, \(\frac{\pi}{4}\)) బిందువు గుండా పోయే వక్రం సమీకరణం కనుక్కోండి.
సాధన:
\(\frac{d y}{d x}\) = \(\frac{y}{x}\) – cos² \(\frac{y}{x}\)
ప్రతిక్షేపించగా y = vx

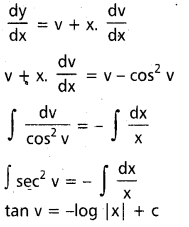
వక్రం (1, \(\frac{\pi}{4}\)) నుంచి పోతాయి
tan (\(\frac{\pi}{4}\)) = x – log 1
c = 1
∴ వక్రం సమీకరణ
tan v = 1 – log |x|
tan (\(\frac{y}{x}\)) = 1 – log |x|