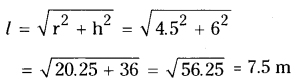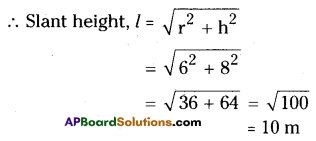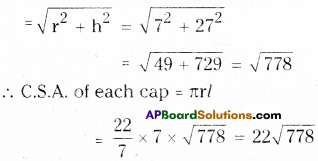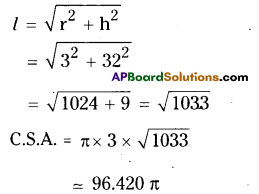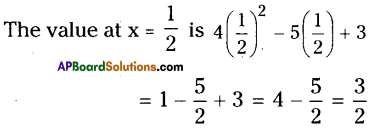Srinivas

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 4 Lines and Angles Ex 4.3 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 4th Lesson Lines and Angles Exercise 4.3

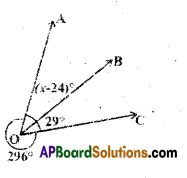
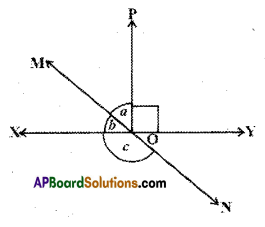
Question 1.
It is given that l // m; to prove ∠1 is supplement to ∠8. Write reasons for the Statements.

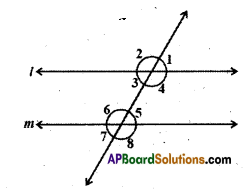
Solution:

Question 2.
In the given figure AB || CD; CD || EF and y: z = 3:7 find x.

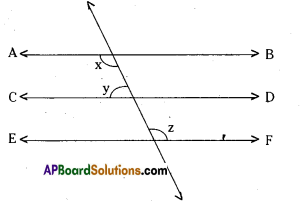
Solution:
Given that AB//CD; CD//EF.
⇒ AB // EF
Also y : z = 3 : 7
From the figure x + y = 180 …………. (1)
[∵ interior angles on the same side of the transversal]
Also y + z = 180 ………….. (2)
Sum of the terms of the ratio y : z
= 3 + 7 = 10
∴ y = \(\frac{3}{10}\) x 180° = 54°
y = \(\frac{7}{10}\) x 180° = 126°
From (1) and (2)
x + y = y + z
⇒ x = z = 126°

Question 3.
In the given figure AB//CD; EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.

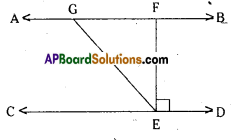
Solution:
Given that EF ⊥ CD; ∠GED = 126°
i. e., ∠FED = 90° and
∠GEF = ∠GED – ∠FED
∠GEF = 126° – 90° = 36°
In ∆GFE
∠GEF + ∠FGE + ∠EFG = 180°
36 + ∠FGE + 90° = 180°
∠FGE = 180° – 126° = 54°
∠AGE = ∠GFE + ∠GEF
(exterior angle in ∆GFE)
= 90°+ 36°= 126°

Question 4.
In the given figure PQ//ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS. [Hint : Draw a line parallel to ST through point R.]

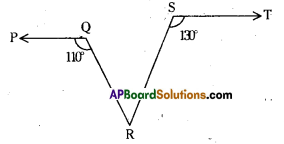
Solution:

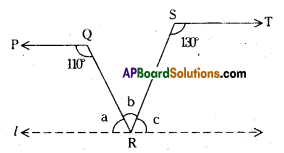
Given PQ // ST
Draw a lipe ‘l’ parallel to ST through R.
From the figure
a + 110° = 180° and c + 130 = 180°
[ ∵ Interior angles on the same side of the transversal]
∴ a = 180° -110° = 70°
c = 180° – 130° = 50°
Also a + b + c = 180° (angles at a point on a line)
70° + b + 50° = 180°
b = 180° – 120° = 60°
∴ ∠QRS = 60°

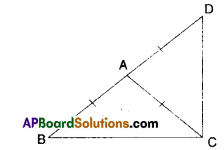
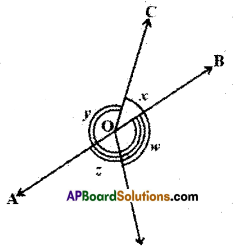
Question 5.
In the given figure m // n. A, B are any two points on in and n respectively. Let C be an interior point between the lines m and n. Find ∠ACB.

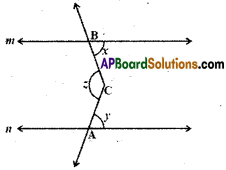
Solution:

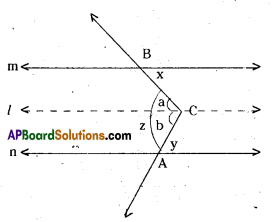
Draw a line ‘l’ parallel to m and n through C.
From the figure
x = a [ ∵ alternate interior angles for l, m]
y = b [ ∵ alternate interior angles for l, n]
∴ z = a + b = x + y

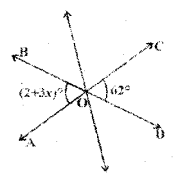
Question 6.
Find the values of a and b, given that p // q and r // s.

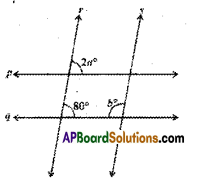
Solution:
Given that p // q and r // s.
∴ From the figure
2a = 80° (∵ corresponding angles)
a = \(\frac { 80° }{ 2 }\) = 40°
Also 80° + b = 180° ( ∵ interior angles on the same side of the transversal)
∴ b = 180° – 80° = 100°

Question 7.
If in the figure a // b and c // d, then name the angles that are congruent to (i) ∠1 and (ii) ∠2.

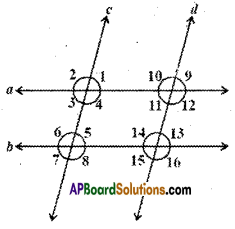
Solution:
Given that a // b and c // d.
∠1 = ∠3 (∵ vertically opposite angles)
∠1 = ∠5 (∵ corresponding angles)
∠1 = ∠9 (∵ corresponding angles)
Also ∠1 = ∠3 = ∠5 = ∠7 ;
∠1 = ∠11 = ∠9 = ∠13 = ∠15
Similarly ∠2 = ∠4 = ∠6 = ∠8
Also ∠2 = ∠10 = ∠12 = ∠14 = ∠16

Question 8.
In the figure the arrow head segments are parallel, find the values of x and y.

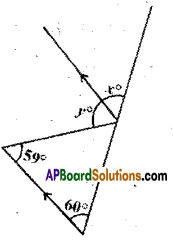
Solution:
From the figure
y = 59° ( ∵ alternate interior angles)
x = 60° ( ∵ corresponding angles)

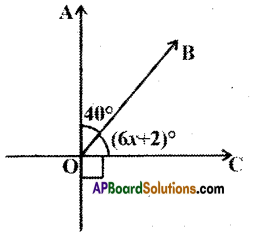
Question 9.
In the figure the arrow head segments are parallel then find the values of x and y.

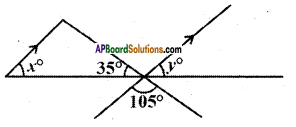
Solution:
From the figure 35° + 105° + y = 180°
∴ y = 180° – 140°
= 40°
∴ x = 40° (∵ x, y are corresponding angles)

Question 10.
Find the values of x and y from the figure.

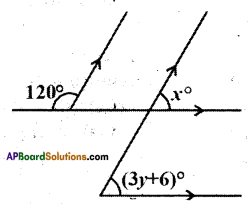
Solution:
From the figure 120° + x = 180°
(∵ exterior angles on the same side of the transversal)
∴ x = 180° – 120°
x = 60°
Also x = (3y + 6)
(∵ corresponding angles)
3y + 6 = 60°
3y = 60° – 6° = 54°
y = \(\frac { 54 }{ 3 }\) = 18°
∴ x = 60°; y = 18°

Question 11.
From the figure find x and y.

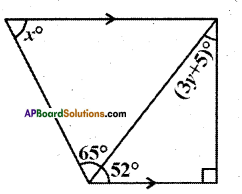
Solution:
From the figure
52° + 90° + (3y + 5)° = 180°
(∵ interior angles of a triangle)
∴ 3y + 147 = 180°
⇒ 3y = 33°
⇒ y = \(\frac { 33 }{ 3 }\) = 11°
Also x + 65° + 52° = 180°
(∵ interior angles on the same side of the transversal)
∴ x = 180° -117° = 63°

Question 12.
Draw figures for the following statement.
“If the two arms of one angle are respectively perpendicular to the two arms of another angle then the two angles are either equal or supplementary
Solution:

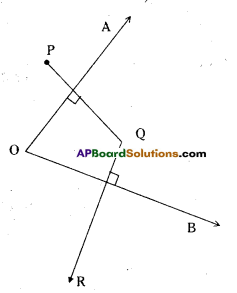
AO ⊥ PQ, OB ⊥ QR
Angles are supplementary.

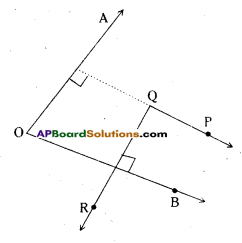
AO ⊥ PQ, OB ⊥ QR
Angles are equal.

Question 13.
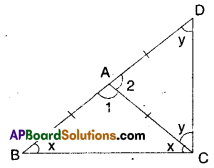
In the given figure, if AB // CD; ∠APQ = 50° and ∠PRD = 127°, find x and y.

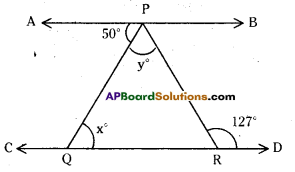
Solution:
Given that AB // CD.
∠PRD = 127°
From the figure x = 50°
(∵ alternate interior angles)
Also y + 50 = 127°
(∵ alternate interior angles)
∴ y = 127-50 = 77°

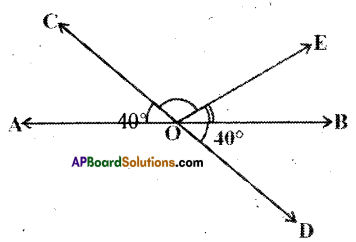
Question 14.
In the given figure PQ and RS are two mirrors placed parallel to each other.
An incident ray \(\overline{\mathrm{AB}}\) strikes the mirror PQ at B, the reflected ray moves along the path \(\overline{\mathrm{BC}}\) and strikes the mirror RS at C and again reflected back along CD. Prove that AB // CD. [Hint : Perpendiculars drawn to parallel lines are also parallel]

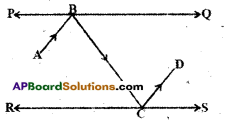
Solution:

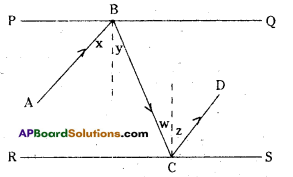
Draw the normals at B and C.
then ∠x = ∠y (angle of incidence angle of reflection are equal)
∠y = ∠w (alternate interior angles)
∠w = ∠z (angles of reflection and incidence)
∴ x + y = y + z (these are alternate interior angles to \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{CD}}\))
Hence AB // CD.

Question 15.
In the figures given below AB // CD. EF is the transversal intersecting AB and CD at G and H respectively. Find the values of x and y. Give reasons.

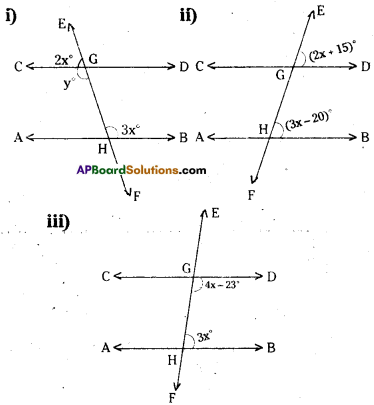
Solution:
For fig(i)
3x = y (∵ alternate interior angles)
2x + y = 180° (∵ linear pair of angles)
∴ 2x + 3x = 180°
5x= 180°
x = \(\frac { 180 }{ 5 }\) = 36°
and y = 3x = 3 x 36 = 108°

For fig (ii)
2x + 15 = 3x- 20°
(∵ corresponding angles)
2x-3x = -20-15
– x = – 35
x = 35°

For fig (iii)
(4x – 23) + 3x = 180° ,
( ∵ interior angles on the same side of the transversal)
7x- 23 = 180°
7x = 203
x = \(\frac { 203 }{ 7 }\) = 29°

Question 16.
In the given figure AB // CD, ‘t’ is a transversal intersecting E and F re-spectively. If ∠2 : ∠1 = 5 : 4, find the measure of each marked angles.

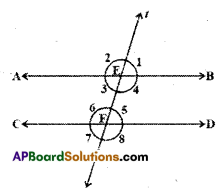
Solution:
Given that AB // CD and ∠2 : ∠1 = 5 : 4 ∠1 + ∠2 = 180° (-. linear pair of angles) Sum of the terms of the ratio ∠2 :∠1 = 5 + 4 = 9
∴ ∠1 = \(\frac { 4 }{ 9 }\) x 180° = 80°
∠2= \(\frac { 5 }{9 }\) x 180° = 100°
Also ∠1, ∠3, ∠5, ∠7 are all equal to 80°. Similarly ∠2, ∠4, ∠6, ∠8 are all equal to 100°.

Question 17.
In the given figure AB//CD. Find the values of x, y and z.

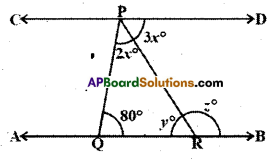
Solution:
Given that AB // CD.
From the figure (2x + 3x) + 80° = 180°
(∵ interior angles on the same side of the transversal)
∴ 5x = 180° – 80°
x = \(\frac{100}{5}\) = 20°
Now 3x = y (∵ alternate interior angles)
y = 3 x 20° = 60° .
And y + z = 180°
(∵ linear pair of angles)
∴ z = 180°-60° = lg0°

Question 18.
In the given figure AB // CD. Find the values of x, y and z.

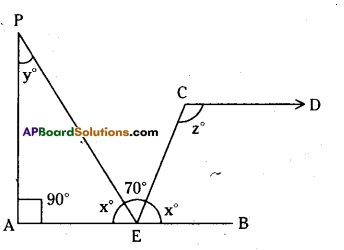
Solution:
Given that AB // CD.
From the figure x° + 70° + x° = 180°
(∵ The angles at a point on the line)
∴ 2x = 180° – 70°
x = \(\frac { 110° }{ 2 }\) = 55-
Also 90° + x° + y° = 180°
[∵ interior angles of a triangle]
90° + 55° + y = 180°
y = 180° – 145° = 35°
And x° + z° = 180°
[∵ interior angles on the same side of a transversal]
55° + z = 180°
z = 180°-55° = 125°

Question 19.
In each of the following figures AB // CD. Find the values of x in each case.

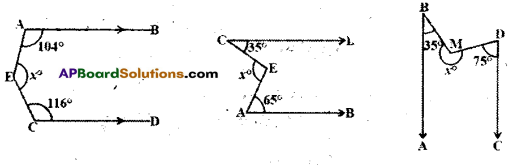
Solution:

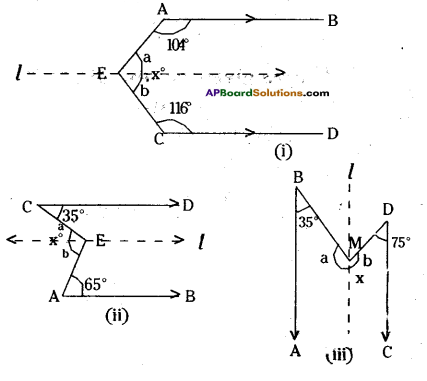
In each case draw a line ‘l’ parallel to AB and CD through F.
fig (i)
a + 104° = 180° ⇒ a = 180° – 104° = 76°
b+ 116° = 180° ⇒ -b = 180°- 116° = 64°
[∵ interior angles on the same side]
∴ a + b = x = 76° + 64° = 140°

fig-(ii)
a = 35°, b = 65° [∵ alt. int. angles]
x = a + b = 35° + 65° = 100°

fig- (iii)
a + 35° = 180° ⇒ a = 145°
b + 75° = 180° ⇒ b = 105°
[ ∵ interior angles on the same side]
∴ x = a + b = 145° + 105° = 250°

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 10 Surface Areas and Volumes Ex 10.3 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 10th Lesson Surface Areas and Volumes Exercise 10.3

Question 1.
The base area of a cone is 38.5 cm Its volume is 77 cm³. Find its height.
Solution:
Base area of the cone, πr² = 38.5 cm²
Volume of the cone, V = \(\frac{1}{3}\) πr² h = 77
πr² = 38.5
\(\frac{22}{7}\) r² = 38.5
r² = 38.5 x \(\frac{7}{22}\)
r² = 12.25
r = \(\sqrt{12.25}\) = 3.5
V= \(\frac{1}{22}\) x \(\frac{22}{7}\) x 3.5 x 3.5 x h = 77
∴ h = \(\frac{77 \times 3 \times 7}{22 \times 12.25}\) = 6
∴ Height of the cone = 6 cm

Question 2.
The volume of a cone is 462 m³. Its base radius is 7 m. Find its height.
Solution:
The volume of a cone”V’= \(\frac{1}{3}\) πr² h = 462
Radius ‘r’ = 7 m
Height = h (say)
\(\frac{1}{3}\) x \(\frac{22}{7}\) x 7 x h = 462
h = \(\frac{462 \times 3}{22 \times 7}\) = 9
∴ Height = 9m

Question 3.
Curved surface area of a cone is 308 cm² and its slant height is 14 cm. Find (1) radius of the base (ii) total surface area of the cone.
Solution:
C.S.A. of the cone, πrl = 308
Slant height, l = 14 cm
i) πrl = 308; l = 14 cm
\(\frac{22}{7}\) x r x 14 = 308
r = \(\frac{308}{44}\) = 7cm

ii) T.S.A. = πrl + πr²
= πr (r + l) = \(\frac{22}{7}\) x 7 x (7 + 14)
= 22 x 21 = 462 cm³

Question 4.
The cost of painting the total surface area of a cone at 25 paise per cm2 is ₹176. Find the volume of the cone, if its slant height is 25 cm.
Solution:
Slant height of the cone, l = 25 cm
Total cost at the rate of 25 p/cm²
= ₹176
∴ Total surface area of the cone
= \(\frac{176}{25}\) x 100 = 176 x 4 = 704cm²
But T.S.A. of the cone = πr (r + l) = 704
Thus \(\frac{22}{7}\)r(r + 25) = 704
r(r + 25) = \(\frac{704 \times 7}{22}\) = 224
r² + 25r = 224
⇒ r² + 32r – 7r – 224 = 0
⇒ r (r + 32) – 7 (r + 32) = 0
⇒ (r + 32) (r – 7) = 0
⇒ r = 7 (∵ ’r’ can’t be negative)

∴ Volume of the cone = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) x \(\frac{22}{7}\) x 7 x 7 24
= 22 x 7 x 8 = 1232cm³

Question 5.
From a circle of radius 15 cm, a sector with angle 216° is cut out and its bounding radii are bent so as to form a cone. Find its volume.
Solution:
Radius of the sector, ‘r’ = 15 cm
Angle of the sector, ‘x’ = 216°
∴ Length of the arc, l = \(\frac{x}{360}\) x 2πr
\(=\frac{216}{360} 2 \pi r=\frac{3}{5}(2 \pi r)\)
Perimeter of the base of the cone = Length of the arc
2πr of cone = \(=\frac{6}{5}\) πr of the circle
Radius of the cone ‘r’ = \(\frac{3}{5}\) x 15 = 9
Radius ‘r’ of the circle = slant height l of the cone = 9 cm

= 1018.3 cm³

Question 6.
The height of a tent is 9 m. Its base diameter is 24 m. What is its slant height ? Find the cost of canvas cloth required if it costs ₹14 per sq.m.
Solution:
Height of a conical tent ‘h’ = 9 m
Base diameter = 24 m
Thus base radius ’r’= \(\frac{d}{2}=\frac{24}{2}\) = 12m
Cost of canvas = ₹ 14 per sq.m.
C.S.A. of the cone = πrl

Question 7.
The curved surface area of a cone is 1159\(\frac { 5 }{ 7 }\) cm². Area of its base is 254 \(\frac { 4 }{ 7 }\) cm². Find its volume.
Solution:
C.S.A. of the cone = πrl

Question 8.
A tent is cylindrical to a height of 4.8 m and conical above it. The ra¬dius of the base is 4.5 m and total height of the tent is 10.8 m. Find the canvas required for the tent in square
meters.
Solution:

Radius of cylinder, l = 4.5 m
Height of the cylinder = h = 4.8 m
∴ C.S.A. of the cylinder = 2πrh
= 2 x \(\frac{22}{7}\) x 4.5 x 4.8
= 135.771 m²
Radius of the cone ‘r’ =
Radius of the cylinder = 4.5 m
Height of the cone ’h’ = 10.8 – 4.8 = 6 m
∴ Slant height of the cone

∴ C.S.A. of the cone = πrl
= \(\frac{22}{7}\) x 4.5 x 7.5
= \(\frac{742.5}{7}\) = 106.071m²
∴ Total canvas required
= C.S.A of cylinder + C.S.A. of cone
= 135.771 + 106.071
= 241.842 m²

Question 9.
What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6m? Assume that extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm (use π = 3.14) [Note : Take 20 cm as 0.6 m²]
Solution:
Radius of the cone, r = 6 m
Height of the cone, h = 8 m

∴ C.S.A. = πrl = 3.14 x 6 x 10 = 188.4 m²
Let the length of the tarpaulin = l
∴ Area of the tarpaulin, lb = 188.4 + 0.6
= 189 m²
⇒ 3l = 189
⇒ l = \(\frac{189}{3}\) = 63m

Question 10.
A joker’s cap is in the form of a right circular cone of base radius 7 cm and height 27 cm. Find the area of the sheet required to make 10 such caps.
Solution:
Radius of the cone, r = 7 cm
Height of the cone, h = 27 cm
Slant height of the cone (l)

∴ Total area of the sheet required for
10 caps = 10 x 22 \(\sqrt{778}\)
= 6136.383 cm²

Question 11.
Water is pouring into a conical vessel (as shown in the given figure), at the rate of 1.8 m³ per minute. How long will it take to fill the vessel?

Solution:
From the figure, diameter of the cone 5.2 m
Thus its radius ’r’ = \(\frac{5.2}{2}\) = 2.6 m
∴ Height of the cone = h = 6.8 m
Volume of the cone = \(\frac{1}{3}\) πr² h
= \(\frac{1}{3} \times \frac{22}{7}\) x 2.6 x 2.6 x 6.8
= \(\frac{1011.296}{21}\)
= 48.156 m³
Quantity of water that flows per minute
= 1.8 m³
∴ Total time required = \(\frac{\text { Total volume }}{1.8}\)
= \(\frac{48.156}{1.8}\) = 26.753
27 minutes.

Question 12.
Two similar cones have volumes 12π CU. units and 96π CU. units. If the curved surface area of smaller cone is 15π sq.units, what is the curved surface area of the larger one?
Solution:

πrl = 15 π
\(r \sqrt{\left(r^{2}+h^{2}\right)}=15\)
Squaring on both sides
r² (r² + h²) = 15 x 15
= 3 x 5 x 3 x 5
= 3 x 3 x 25
r²(r² + h²) = 3²(3² + 4²)
∴ r = 3 cm, h = 4 cm
C.S.A. = π x 3 x \(\left(\sqrt{3^{2}+4^{2}}\right)\) = 15π
\(\frac{1}{3}\)πr²H = 96π
\(\frac{3 \times 3 \times \mathrm{H}}{3}\) = 96
∴ H = \(\frac{96}{3}\) = 32 units

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 7 Frequency Distribution Tables and Graphs Ex 7.1 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 7th Lesson Frequency Distribution Tables and Graphs Exercise 7.1

Question 1.
Find the arithmetic mean of the sales per day in a fair price shop in a week.
₹ 10000, ₹ 10250, ₹ 10790, ₹ 9865, ₹ 15350, ₹ 10110
Solution:

Question 2.
Find the mean ofthe data; 10.25, 9, 4.75, 8, 2.65, 12, 2.35
Solution:

Question 3.
Mean of eight observations is 25. If one observation 11 is excluded, find the mean of the remaining.
Solution:
Given that
The mean of 8 observations = 25
The sum of 8 observations = 8 × 25
= 200
If the observation 11 is subtracted from the sum
⇒ 200 – 11 = 189
∴ The mean of remaining 7 observations = \(\frac { 189 }{ 7 }\) = 27

Question 4.
Arithmetic mean of nine observations is calculated as 38. But in doing so, an observation 27 is mistaken for 72. Find the actual mean of the data.
Solution:
The mean of 9 observations = 38
The sum of 9 observations = 38 × 9
= 342
If the observation 27 is mistaken for 72
then correct observation = 72 – 27
= 45
Sum of correct observations = 342 + 45
= 387
∴ Correct Mean = \(\frac { 387 }{ 9 }\) = 43

Question 5.
Five years ago mean age of a family was 25 years. What is the present mean age of the family ?
Solution:
When all the observations of the data are increased or decreased by a certain number, the mean also increases or decreases by the same number.
Five years ago mean age of a family = 25 years
Present mean age of the family = 25 + 5 = 30 y

Question 6.
Two years ago the mean age of 40 people was 11 years. Now a person left the group and the mean age is changed to 12 years. Find the age of the person who left the group.
Solution:
The present mean age of 40 people = 11 + 2 = 13 years
∴ The total age of 40 people = 40 × 13
= 520 years
If 1 person is left from the group of 40 people then remaining will be = 40 – 1 = 39.
The mean age of 39 people = 12 years
The total age of 39 people = 39 × 12
= 468 years
Age of the person who left from the group = 520 – 468 = 52 years

Question 7.
Find the sum of deviations of all observations of the data 5,8, 10, 15,22 from their mean.
Solution:
A.M. of the observations 5,8,10,15,22 is


∴ Sum of deviations = 0

Question 8.
If sum of the 20 deviations from the mean is 100, then find the mean deviation.
Solution:

Question 9.
Marks of 12 students inaunittestare givenas4,21, 13, 17,5,9, 10,20, 19, 12,20, 14.
Assume a mean and calculate the arithmetic mean of the data. Assume another number as
mean and calculate the arithmetic mean again. Do you get the same result? Comment.
Solution:
Given observations are 4, 21, 13, 17, 5, 9, 10, 20, 19, 12, 20, 14
Estimated mean = 10 say
A.M. Estimated Mean + Average of deviations

= 10 + \(\frac { 44 }{ 12 }\) = 10 + 3.67 = 13.67
∴ A.M = \(\bar{x}\) = 13.67
Another Estimated Mean = 12 then
\(\bar{x}\) = A.M. = Estimated Mean + Average of deviations

= 12 + \(\frac { 20 }{ 12 }\) = 12 + 1.67 = 13.67
\(\bar{x}\) = 13.67
∴ In all cases \(\bar{x}\) = 13.67

Question 10.
Arithmetic mean of marks (out of 25) scored by 10 students was 15. One of the student, named Karishma enquired the other 9 students and find the deviations from her marks are noted as – 8, – 6, – 3, – 1, 0, 2, 3,4, 6. Find Karishma’s marks.
Solution:
Average marks of 10 students = 15
Total marks of 10 students = 10 × 15
= 150
Marks obtained by Karishma = x say
Deviations of 9 students =
-8, -6-3,-1,0, 2, 3,4,6
∴ x-8 + x-6 + x-3 + x-l + x + x + 2 + x + 3 + x + 4 + x + 6 + x = 150
⇒ 10x- 3 = 150
⇒ 10x = 150 + 3 = 153
x = \(\frac { 153 }{ 10 }\) = 15.3

(Or)

The given observations are
-8,-6,-3,-1,0, 2, 3, 4,6
Let the number of marks of Karisima =
Her deviation from x’ are – 8 + x, – 6 + x, – 3 + x, – 1 + x, x + 0, 2 + x, 3 + x, 4 + x, 6 + x

[ ∵ Mean = 15 is given]
10x – 3 = 15 × 10
10x =150 + 3
10x= 153
x = \(\frac{153}{10}\)
x = 15.3
∴ Number of marks obtained by Karishma = 15.3

Question 11.
The sum of deviations of ‘n’ observations from 25 is 25 and sum of deviations of the same ‘n’ observations from 35 is – 25. Find the mean of the observations.
Solution:
From the value ’25’ the sum of deviations of a data = Σx₁ = 25
∴ Mean of the observation = 25 + \(\frac{\Sigma \mathrm{x}_{1}}{\mathrm{n}}\)
= \(25+\frac{25}{n}=\frac{25 n+25}{n}\)
From the value ’35’ the sum of deviations of a data = Σx₁ = -25
∴ Mean of the observation = 35 + \(\frac{\Sigma \mathrm{x}_{1}}{\mathrm{n}}\)
= \(35+\frac{-25}{n}=\frac{35 n+25}{n}\)
Mean of the given data

(Or)

Let x₁, x₂, x₃,…… x_n are the number of
deviations from 25
∴ Number of observations are
x₁ – 25, x₂ – 25, …………. x_n – 25
∴ Sum of the observations = 25
∴ x₁ – 25 + x₂ – 25 +…………. + x_n – 25 = 25
⇒ x₁+ x₂ + + x_n = 25 + 25n …………(1)
= 25 (n + 1)
Deviations from 35 are
x₁ – 35, x₂ – 35y …………., x_n – 35
∴ Sum of the deviations = – 25
∴ (x₁ – 35) + (x₂ – 35) + … (x_n – 35) = – 25
⇒x₁ + x₁ +………………….. + x_n = – 25 + 35 x n …………….(2)
From (1) and (2),
– 25 + 35n = 25 + 25n
⇒ 10n = 50
n = 5
∴ Mean of the observations

Question 12.
Find the median of the data ; 3.3, 3.5, 3.1, 3.7, 3.2, 3.8
Solution:
The ascending order of 3.3, 3.5, 3.1, 3.7, 3.2, 3.8 is 3.1, 3.2, 3.3, 3.5, 3.7, 3.8
∴ n = 6 (is an even)
Median = Mean of \(\frac{n}{2},\left(\frac{n}{2}+1\right)\) terms
= \(\frac{6}{2}, ([latex]\frac{6}{2}\) + 1)[/latex]
= Mean of 3, 4 terms
= \(\frac{3.3+3.5}{2}\)
= \(\frac{6.8}{2}\) = 3.4

Question 13.
The median of the following observations, arranged in ascending order is 15. 10, 12, 14, x – 3, x, x + 2, 25.Then find x.
Solution:
Given observations are
10, 12, 14, x – 3,x ; x + 2, 25
⇒ n = 7 (is an odd)
∴ Median = \(\frac{n+1}{2}=\frac{7+1}{2}\) = 4th term
= x – 3
⇒ x-3 = 15
⇒ x = 15 + 3
∴ x = 18

Question 14.
Find the mode of 10, 12, 11, 10, 15, 20, 19, 21, 11, 9, 10
Solution:
The given observations are
10, 12, 11, 10, 15, 20, 19,21,11,9, 10
∴ The most frequently occurring observation is 10.
∴ Mode = 10

Question 15.
Mode of certain scores is x. 1f each score is decreased by 3, then find the mode of the new series.
Solution:
The mode of some observations is ‘x’. If ‘3’ is subtracted from every observa¬tion then the mode = x – 3

Question 16.
Find the mode of all digits used in Titing the natural numbers from 1 to 100.
Solution:
Natural numbers from 1 to 100 are 1,2,3, …………….99, 100
∴ It has no mode.
[ ∵ Every number appears only once]

Question 17.
Observations of a raw data are 5, 28, 15, 10, 15, 8, 24. Add four more numbers so that mean and median of the data remain the same, but mode increases by 1.
Solution:
The given observations are 5, 28, 15, 10, 15, 8, 24

Ascending order of the observations 5, 8, 10, 15, 15, 24, 28
Median = \(\frac{n+1}{2}=\frac{7+1}{2}\) = 4 th term
= 15 [n = 7 is an odd]
∴ Mode = 15
If 4 observations are inserted for the given data then mode increases by 1.
Let x₁ = x₂ = x₃ = x say .
∴ The mean
= \(\frac{x+x+x+x_{4}+10}{11}\) = 15
⇒ 3x + x₄ = 165 – 105 = 60
∴ 3x + x₄ = 60
If mode will increases by 1 then
x= 15 +1 = 16
∴ 3x + x₄ = 60
⇒ 3 x 16 + x₄ =60
⇒ x₄ = 60 – 48 = 12
∴ The required 4 observations are 12, 16, 16, 16

Question 18.
If the mean of a set of observations x₁, x₁ , x₁₀ is 20. Find the mean of x₁ + 4, x₂ + 8, x₃ + 12 , x₁₀ + 40.
Solution:
Mean of observations x₁, x₂……………….. ,x₁₀ is

= 20 + 2 × 11 = 20 + 22 = 42

Question 19.
Six numbers from a list of nine integers are 7,8,3, 5,9 and 5. Find the largest possible value of the median of all nine numbers in this list.
Solution:
The given 6 integers are 7, 8, 3, 5, 9, 5
Ascending order = 3, 5, 5, 7, 8, 9
Let the remaining 3 observations be x₁, x₂, x₃ say
Median of 3, 5, 5, 7, 8, 9, x₁, x₂, x₃ is
= \(\frac{n+1}{2}\) [ ∵ n is an odd (9)]
= \(\frac{9+1}{2}\) = 5th term = 8
∴ The largest possible median will be 8

Question 20.
The median of a set of 9 distinct observations is 20. If each of the largest 4 observations of the set is increased by 2, find the median of the resulting set.
Solution:
Let the 9 observations be x₁, x₂………..x₉ say
Median = \(\frac{n+1}{2}\) [∵ n = 9 is an odd]
= \(\frac{n+1}{2}\) = 5th term = x₅ = 20
∴ x₅ = 20
If 2 is added to the last 4 largest numbers then x₁, x₂, x₃, x₄, x₅, x₆ + 2 x₇ + 2, x₈ + 2, x₉ +2
∴ Median = \(\frac{n+1}{2}=\frac{9+1}{2}\) = 5th term
∴ x₅ = 20

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 7 Triangles Ex 7.3 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 7th Lesson Triangles Exercise 7.3

Question 1.
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
Solution:

Given that in ΔABC, AB = AC
and AD ⊥ BC
i) Now in ΔABD and ΔACD
AB = AC (given)
∠ADB = ADC (given AD ⊥ BC)
AD = AD (common)
∴ ΔABD ≅ ΔACD (∵ RHS congruence)
⇒ BD = CD (CPCT)
⇒ AD, bisects BC.

ii) Also ∠BAD = ∠CAD
(CPCT of ΔABD ≅ ΔACD )
∴ AD bisects ∠A.

Question 2.
Two sides AB, BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see figure). Show that:
(i) ΔABM ≅ ΔPQN
ii) ΔABC ≅ ΔPQR

Solution:
Given that
AB = PQ
AM = PN
i) Now in ΔABM and ΔPQN
AB = PQ (given)
AM = PN (given)
BM = QN (∵ BC = QR ⇒ \(\frac { 1 }{ 2 }\)BC = \(\frac { 1 }{ 2 }\)QR ⇒ BM = QN)
∴ ΔABM ≅ ΔPQN
(∵ SSS congruence)

ii) In ΔABC and ΔPQR
AB = PQ (given)
BC = QR (given)
∠ABC = ∠PQN [∵ CPCT of ΔABM and ΔPQN from (i)]
∴ ΔABC ≅ ΔPQR
(∵ SAS congruence)

Question 3.
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Solution:

In ΔABC altitude BE and CF are equal.
Now in ΔBCE and ΔCBF
∠BEC = ∠CFB (∵ given 90°)
BC = BC (common; hypotenuse)
CF = BE (given)
∴ ΔBEC ≅ ΔCBF
⇒ ∠EBC = ∠FCB (∵ CPCT)
But these are also the interior angles opposite to sides AC and AB of ΔABC.
⇒ AC = AB
Hence proved.

Question 4.
ΔABC is an isosceles triangle in which AB = AC. Show that ∠B = ∠C.
(Hint : Draw AP ⊥ BQ (Using RHS congruence rule)
Solution:

Given the ΔABC is an isosceles triangle and AB = AC
Let D be the mid point of BC; Join A, D.
Now in ΔABD and ΔACD
AB = AC (given)
BD = DC (construction)
AD = AD (common)
∴ ΔABD ≅ ΔACD (∵ SSS congruence)
⇒ ∠B = ∠C [∵ CPCT]

Question 5.
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see figure). Show that ∠BCD is a right angle.

Solution:

Given that in ΔDBC; AB = AC; AD = AB
In ΔABC
∠ABC + ∠ACB = ∠DAC …………… (1)
[∵ exterior angle]
In ΔACD
∠ADC + ∠ACD = ∠BAC ………………(2)
Adding (1) & (2)
∠DAC + ∠BAC = 2 ∠ACB + 2∠ACD
[∵ ∠ABC = ∠ACB
∠ADC = ∠ACD]
180° = 2 [∠ACB + ∠ACD]
180° = 2[∠BCD]
∴ ∠BCD = \(\frac{180^{\circ}}{2}\) = 90°
(or)
From the figure
∠2 = x + x = 2x
∠1 = y + y = 2y
∠1 + ∠2 = 2x + 2y
180° = 2 = (x + y)
∴ x + y  = \(\frac{180^{\circ}}{2}\) = 90°
Hence proved.

Question 6.
ABC is a right angled triangle in which ∠A = 90° and AB = AC, Show that ∠B = ∠C.
Solution:

Given ΔABC; AB – AC
Join the mid point D of BC to A.
Now in ΔADC and ΔADB
AD = AD (common)
AC = AB (giyen)
DC = DB (construction)
⇒ ΔADC ≅ ΔADB
⇒ ∠C = ∠B (CPCT)

Question 7.
Show that the angles of an equilateral triangle are 60° each.
Solution:

Given ΔABC is an equilateral triangle
AB = BC = CA
∠A = ∠B (∵ angles opposite to equal sides)
∠B = ∠C (∵ angles opposite to equal sides)
⇒ ∠A = ∠B = ∠C = x say
Also ∠A+∠B + ∠C =180°
⇒ x + x + x = 180°
3x = 180°
⇒ x = \(\frac{180}{3}\) = 60°
Hence proved.

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation Ex 2.2 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 2nd Lesson Polynomials and Factorisation Exercise 2.2

Question 1.
Find the value of the polynomial 4x² – 5x + 3, when
(i) x = 0
Solution:
The value at x = 0 is
4(0)² – 5(0) + 3
= 3

(ii) x = – 1
Solution:
The value at x = – 1 is
4 (- 1)² – 5 (- 1) + 3
= 4 + 5 + 3
= 12

iii) x = 2
Solution:
The value at x = 2 is
4(2)² – 5(2) + 3
= 16 -10 + 3
= 9

iv) x = \(\frac{1}{2}\)
Solution:

Question 2.
Find p(0), p(1) and p(2) for each of the following polynomials.
i) p(x) = x² – x + 1
Solution:
p(0) = 0² – 0 + 1 = 1
p(1) = 1² – 1 + 1 = 1
p(2) = 2² – 2 + 1 = 3

ii) P(y) = 2 + y + 2y² – y³
Solution:
p(0) = 2 + 0 + 2(0)² – 0³ = 2
p(1) = 2+ 1 + 2(1)² – 1³ = 4
p(2) = 2 + 2 + 2(2)² -2³ = 4 + 8- 8 = 4

iii) P(z) = z³
Solution:
p(0) = 0³ = 0
p(1) = 1³ = 1
p(2) = 2³ = 8

iv) p(t) = (t – 1)(t + 1) = t² – 1
Solution:
p(0) = (0 – 1) (0 + 1) = – 1
p(1) = t² – 1 = 1² – 1 = 0
p(2) = 2² – 1 = 4 – 1 = 3

v) p(x) = x² – 3x + 2
Solution:
p(0) = 0² – 3(0) + 2 = 2
p(1) = 1² – 3(1) + 2 = 1 – 3 + 2 = 0
p(2) = 2² – 3(2) + 2 = 4- 6 + 2 = 0

Question 3.
Verify whether the values of x given in each case are the zeroes of the polynomial or not ?
i) p(x) = 2x + 1; x = \(\frac{-1}{2}\)
Solution:
The value of p(x) at x = \(\frac{-1}{2}\) is
\(\mathrm{p}\left(\frac{-1}{2}\right)=2\left(\frac{-1}{2}\right)+1\)
= -1 + 1 = 0
∴ x = \(\frac{-1}{2}\) is a zero of p(x).

(ii) p(x) = 5x – π ; x = \(\frac{-3}{2}\)
Solution:
The value of p(x) at x = \(\frac{-3}{2}\) is
\(\mathrm{p}\left(\frac{-3}{2}\right)=5\left(\frac{-3}{2}\right)-\pi=\frac{-15}{2}-\pi \neq 0\)
∴ x = \(\frac{-3}{2}\) is not a zero of p(x).

iii) p(x) = x² – 1; x = ±1
Solution:
The value of p(x) at x = 1 and – 1 is
p(1) = 1² – 1 = 0
p(-1) = (-1)² -1 = 0
∴ x = ±1 is a zero of p(x).

iv) p(x) = (x – 1) (x + 2); x = – 1, – 2
Solution:
The value of p(x) at x = – 1 is
p(-1) = (-1 – 1) (-1 + 2)
=-2 x 1 =-2 ≠ 0
Hence x = – 1 is not a zero of p(x).
And the value of p(x) at x = – 2 is
p (- 2) = (- 2 – 1) (- 2 + 2) = – 3 x 0 = 0
Hence, x = – 2 is a zero of p(x).

v) p(y) = y²; y = o
Solution:
The value of p(y) at y = 0 is p(0) = 0² = 0
Hence y = 0 is a zero of p(y).

vi) p(x) = ax + b ; x = \(\frac{-\mathbf{b}}{\mathbf{a}}\)
Solution:
The value of p(x) at x = \(\frac{-\mathbf{b}}{\mathbf{a}}\) is
\(\mathrm{p}\left(\frac{-\mathrm{b}}{\mathrm{a}}\right)=\mathrm{a}\left(\frac{-\mathrm{b}}{\mathrm{a}}\right)+\mathrm{b}\)
= -b + b = 0
∴ x = \(\frac{-\mathbf{b}}{\mathbf{a}}\) is a zero of p(x).

vii) f(x) = 3x² – 1; x = \(\frac{-1}{\sqrt{3}}, \frac{2}{\sqrt{3}}\)
Solution:

viii) f(x) = 2x – 1; x = \(\frac{1}{2} ;-\frac{1}{2}\)
Solution:

Question 4.
Find the zero of the polynomial in each of the following cases.
i) f(x) = x + 2
Solution:
x + 2 = 0
x = – 2

ii) f(x) = x – 2
Solution:
x – 2 = 0
x = 2

iii) f(x) = 2x + 3
Solution:
2x + 3 = 0
2x = – 3
x = \(\frac{-3}{2}\)

iv) f(x) = 2x – 3
Solution:
2x – 3 = 0
2x = 3
x = \(\frac{3}{2}\)

v) f(x) = x²
Solution:
x² = 0
x = 0

vi) f(x) = px, p ≠ 0
Solutin:
px = 0
x = 0

vii) f(x) = px + q; p ≠ 0; p, q are real numbers.
Solution:
px + q = 0
px = -q
x = \(\frac{-\mathrm{q}}{\mathrm{p}}\)

Question 5.
If 2 is a zero of the polynomial p(x) = 2x² – 3x + 7a, find the value of
a.
Solution:
Given that 2 is a zero of p(x) = 2x² – 3x + 7a
(i.e.) p(2) = 0
⇒ 2(2)² – 3(2) + 7a = 0
⇒ 8 – 6 + 7a = 0
⇒ 2 + 7a = 0
⇒ 7a = – 2
⇒ a = \(\frac{-2}{7}\)

Question 6.
If 0 and 1 are the zeroes of the polynomial f(x) = 2x³ – 3x² + ax + b, find the values of a and b.
Solution:
Given that f(0) = 0; f(1) = 0 and
f(x) = 2x³ – 3x² + ax + b
∴ f(0) = 2(0)³ – 3(0)² + a(0) + b
⇒ 0 = b
Also f(1) = 0
⇒ 2(1)³ – 3(1)² + a(1) + 0 = 0
⇒ 2 – 3 + a = 0 .
⇒ a = 1
Hence a = 1; b = 0

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 4 Lines and Angles Ex 4.2 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 4th Lesson Lines and Angles Exercise 4.2

Question 1.
In the given figure three lines \(\overline{\mathrm{AB}}\) , \(\overline{\mathrm{CD}}\) and \(\overline{\mathrm{EF}}\) intersecting at ‘O’. Find the values of x, y and z, it is being given that x : y : z = 2 : 3 : 5

Solution:
From the figure
2x + 2y + 2z = 360°
⇒ x + y + z = 180°
x : y : z = 2 : 3 : 5
Sum of the terms of the ratio
= 2 + 3 + 5 = 10

Question 2.
Find the value of x in the following figures.
i)

Solution:
From the figure
3x + 18= 180° – 93° (∵ linear pair )
3x + 18 = 87
3x = 87- 18 = 69
∴ x = \(\frac{69}{3}\) = 23

ii)

Solution:
From the figure
(x – 24)° + 29° + 296° = 360“
(∵ complete angle)
x + 301° = 360°
∴ x = 360° – 301° = 59°

iii)

Solution:
From the figure
2 + 3x = 62
(∵ vertically opposite angles)
3x = 62 – 2
∴ 3x = 60° ⇒ x = \(\frac{60}{3}\)
∴ x = 20°

iv)

Solution:
From the figure
40 + (6x + 2) = 90°
(∵ complementary angles)
6x = 90° – 42°
6x = 48
x = \(\frac{48}{6}\) = 8°

Question 3.
In the given figure lines \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\) intersect at ’O’. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.

Solution:
Given that ∠AOC +∠BOE = 70°
∠BOD = 40°
∠AOC = 40°
(∵ ∠AOC, ∠BOD are vertically opposite angles)
∴ 40° + ∠BOE = 70°
⇒ ∠BOE = 70° – 40° = 30°
Also ∠AOC + ∠COE +∠BOE = 180°
( ∵ AB is a line)
⇒ 40° + ∠COE + 30° = 180°
⇒ ∠COE = 180° -70° = 110°
∴ Reflex ∠COE = 110°

Question 4.
In the given figure lines \(\overline{\mathrm{XY}}\) and \(\overline{\mathrm{MN}}\) . intersect at O. If ∠POY = 90° and a : b = 2:3, find c.

Solution:
Given that XY and MN are lines.
∠POY = 90°
a : b = 2 : 3
From the figure a + b = 90°
Sum of the terms of the ratio a : b
= 2 + 3 = 5
∴ b = \(\frac{3}{5}\) x 90° = 54°
From the figure b + c = 180°
(∵ linear pair of angles)
54° + c = 180°
c = 180°-54° = 126°

Question 5.
In the given figure ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.

Solution:
Given that ∠PQR = ∠PRQ
From the figure
∠PQR + ∠PQS = 180° ………….. (1)
∠PRQ + ∠PRT = 180° …………..(2)
From (1) and (2)
∠PQR + ∠PQS = ∠PRQ + ∠PRT
But ∠PQR = ∠PRQ
So ∠PQS = ∠PRT
Hence proved.

Question 6.
In the given figure, if x + y = w + z, then prove that AOB is a line.

Solution:
Given that x + y = w + z = k say
From the figure
x + y + z + w = 360°
(∵ Angle around a point)
Also x + y = z + w
∴ x + y = z + w = \(\frac{360^{\circ}}{2}\)
∴ x + y = z + w = 180°

OR

k + k = 360°
2k = 360°
k = \(\frac{360^{\circ}}{2}\)

(i.e.) (x,y) and (z, w) are pairs of adjacent angles whose sum is 180°.
In other words (x, y) and (z, w) are linear pair of angles ⇒ AOB is a line.

Question 7.
In the given figure \(\overline{\mathrm{PQ}}\) is a line. Ray \(\overline{\mathrm{OR}}\) is perpendicular to line \(\overline{\mathrm{PQ}}\).\(\overline{\mathrm{OS}}\) os is another ray lying between rays \(\overline{\mathrm{OP}}\) and \(\overline{\mathrm{OR}}\) Prove that

Solution:
Given : OR ⊥ PQ ⇒ ∠ROQ = 90°
To prove: ∠ROS = \(\frac{1}{2}\) (∠QOS – ∠POS)
Solution:
Proof: From the figure
∠ROS = ∠QOS – ∠QOR ……………(1)
∠ROS = ∠ROP – ∠POS ……………..(2)
Adding (1) and (2)
∠ROS + ∠ROS = ∠QOS – ∠QOR +∠ROP – ∠POS [ ∵ ∠QOR = ∠ROP = 90° given]
⇒ 2∠ROS = ∠QOS – ∠POS
⇒ ∠ROS = \(\frac{1}{2}\) [∠QOS – ∠POS]
Hence proved.

Question 8.
It is given that ∠XYZ = 64° and XY is produced to point P. A ray \(\overline{\mathrm{YQ}}\) bisects ∠ZYP. Dräw a figure from the given Information. Find ∠XYQ and reflex ∠QYP.
Solution:

∠XYQ = 32°
∠QYP = 32°

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 10 Surface Areas and Volumes Ex 10.2 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 10th Lesson Surface Areas and Volumes Exercise 10.2

Question 1.
A closed cylindrical tank of height 1.4 m and radius of the base is 56 cm is made up of a thick metal sheet. How much metal sheet is required ?
(Express in square metres).
Solution:
Radius of the tank r’ = 56 cm
= \(\frac { 56 }{ 100 }\) m = 0.56m
Height of the tank h = 1.4 m
T.S.A. of a cylinder = 2πr (r + h)
∴ Area of the metal sheet required = 2πr (r + h)
A = 2 × \(\frac { 22 }{ 7 }\) × 0.56 × (0.56 + 1.4)
= 2 × 22 × 0.08 × 1.96
= 6.8992 m²
= 6.90 m²

Question 2.
The volume of a cylinder is 308 cm³ . Its height is 8 cm. Find its lateral surface area and total surface area.
Solution:
Volume of the cylinder V = πr²h
= 308 cm³
Height of the cylinder h = 8 cm
∴ 308 = \(\frac { 22 }{ 7 }\) . r² × 8
r² = 308 × \(\frac { 7 }{ 22 }\) x \(\frac { 1 }{ 8 }\)
r² = 12.25
∴ r = \(\sqrt{12.25}\) = 3.5cm
L.S.A. = 2πrh
= 2 × \(\frac { 22 }{ 7 }\) × 3.5 × 8 = 176cm²
T.S.A. = 2πr (r + h)
2 × \(\frac { 22 }{ 7 }\) × 3.5 (3.5 + 8)
= 2 × 22 × 0.5 × 11.5 = 253 cm²

Question 3.
A metal cuboid of dimensions 22 cm × 15 cm × 7.5 cm was melted and cast into a cylinder of height 14 cm. What is its radius ?
Solution:
Dimensions of the metal cuboid
= 22 cm × 15 cm × 7.5 cm
Height of the cylinder, h = 14 cm
Cuboid made as cylinder
∴ Volume of cuboid = Volume of cylinder
lbh = 2πr²h
⇒ 22 × 15 × 7.5 = \(\frac { 22 }{ 7 }\) × r² × 14
⇒ r² = \(\frac{22 \times 15 \times 7.5 \times 7}{14 \times 22}\)
⇒ r² = 7.5 × 7.5
r = 7.5 cm

Question 4.
An overhead water tanker is in the shape of a cylinder has capacity of 616 litres. The diameter of the tank is 5.6 m. Find the height of the tank.
cagp)
Solution:
Volume of the cylinder, V = πr²h = 616
Diameter of the tank = 5.6 m
Thus its radius, r = \(\frac{d}{2}=\frac{5.6}{2}\) = 2.8 m
Height = h (say)
∴ πr² h = 616
\(\frac{22}{7}\) × 2.8 × 2.8 × h = 616
h = \(\frac{616 \times 7}{22 \times 2.8 \times 2.8}\) = 25
∴ Height = 25 m

Question 5.
A metal pipe is 77 cm long. The inner diametre of a cross section is 4 cm; the outer diameter being 4.4 cm (see figure). Find its

i) Inner curved surface area
ii) Outer curved surface area
iii) Total surface area
i) Inner curved surface area
Solution:
Height of the pipe = 77 cm
Inner diameter = 4 cm
Inner radius = \(\frac{d}{2}=\frac{4}{2}\) = 2 cm
∴ Inner C.S.A. = 2πrh
= 2 × \(\frac{22}{7}\) × 2 × 77
= 88 × 11 = 968cm²

ii) Outer curved surface area
Solution:
Outer diameter = 4.4 cm
∴ Outer radius, r = \(\frac{d}{2}=\frac{4.4}{2}\) = 2.2 cm
Height of the pipe, h = 77 cm
∴ Outer C.S.A. = 2πrh
= 2 × \(\frac{22}{7}\) × 2.2 × 77
= 96.8 × 11
= 1064.8 cm²

iii) Total surface area Sol. Total surface area .
= Inner C.S.A + Outer C.S.A
= 968 + 1064.8
= 2032.8 cm²

Question 6.
A cylindrical pillar has a diameter of 56 cm and is of 35 m high. There are 16 pillars around the building. Find the cost of painting the curved surface area of all the pillars at the rate of ₹ 5.50 per 1 m².
Solution:
Diametre of the cylindrical pillar = 56 cm
Thus its radius, r = \(\frac{d}{2}\)
= \(\frac{56}{2}\) = 28cm = \(\frac{28}{100}\)m = 0.28m
Height of the pillar, h = 35 m
Total number of pillars =16
Cost of painting = ₹ 5.50 per sq. m.
C.S.A. of each pillar = 2πrh
= 2 × \(\frac{22}{7}\) × 0.28 × 35
= 2 × 22 × 0.04 × 35 = 61.6 m²
∴ C.S.A. of 16 pillars = 16 × 61.6 = 985.6 m²
Cost of painting 16 pillars at the rate of ₹ 5.5 per sq.m. = 985.6 × 5.5
= ₹ 5420.8

Question 7.
The diameter of a roller is 84 cm and its length is 120 cm. It takes 500 complete revolutions to roll once over the play ground to level. Find the area of the play ground in m²
Soi. Diameter of the roller = 84 cm
Thus radius = \(\frac{84}{2}\) = 42 cm
= \(\frac{42}{100}\)m = 0.42m
Length of the roller =120 cm
= \(\frac{120}{100}\) = 1.2m
It takes 500 complete revolutions to roll over the play ground.
Thus 500 × L.S.A. of the roller
= Area of the play ground
∴ Area of the play ground = 500 × 2πrh
= 500 × 2 × \(\frac{22}{7}\) × 0.42 × 1.2 = 1584 m²

Question 8.
The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find (i) its inner curved surface area (ii) the cost of plastering this curved surface at the rate of Rs. 40 per m².
Solution:
Inner diameter of the circular well, d = 3.5 m
Thus its radius, r = \(\frac{d}{2}=\frac{3.5}{2}\) = 1. 75 m
Depth of the well (height) = 10 m
i) Inner C.S.A. = 2πrh
= 2 × \(\frac{22}{7}\) × 1.75 × 10
= 110 m²
ii) Cost of plastering at the rate of
₹ 40 / m² = 110 × 40 = ₹ 4400

Question 9.
Find (i) the total surface area of a closed cylindrical petrol storage tank whose diameter 4.2 m and height 4.5 m.
Solution:
Diameter of the cylindrical tank ‘d’ = 4.2m
Thus its radius, r = \(\frac{\mathrm{d}}{2}=\frac{4.2}{2}\) = 2.1 m
Height of the tank, h = 4.5 m
T.S.A. of the tank = 2πr (r + h)
= 2 × \(\frac{22}{7}\) × 2.1 (2.1 + 4.5)
= 2 × 22 × 0.3 × 6.6 = 87.12m²

ii) How much steel sheet was actually used, if \(\frac{1}{12}\) of the steel was wasted in making the tank ?
Solution:
\(\frac{1}{12}\) of the sheet was wasted.
=> 1 – \(\frac{1}{12}\) = \(\frac{11}{12}\) of the sheet was used
in making the tank.
Let the metal sheet originally brought was = x m²
\(\frac{11}{12}\) x = 87.12m²
∴ x = 87.12 x \(\frac{12}{11}\) = 95.04m²

Question 10.
A one side open cylindrical drum has inner radius 28 cm and height 2.1 m. How much water you can store in the drum? Express in litres.
(1 litre = 1000 c.c)
Solution:
Inner radius of the cylindrical drum ‘r’ = 28 cm
. Its height, h = 2.1 m = 2.1 × 100 = 210 cm
Volume of the drum = πr²h
= \(\frac{22}{7}\) × 28 × 28 × 210
= 22 × 4 × 28 × 210
= 517440 cc
= \(\frac{517440}{1000}\)
= 517.44 lit.

Question 11.
The curved surface area of the cylinder is 1760 cm² and its volume is 12320 cm³. Find its height.
Solution:
C.S.A of the cylinder = 2πrh = 1760 cm²
Volume of the cylinder = πr²h
= 12320 cm³
Height = h (say)
\(\frac{\text { Volume }}{\text { C.S.A. }}=\frac{\pi r^{2} h}{2 \pi r h}=\frac{12320}{1760}\)
⇒ \(\frac{r}{2}\) = 7
∴ r = 7 × 2 = 14cm
Now 2πrh = 1760cm²
2 × \(\frac{22}{7}\) × 14h = 1760
h = \(\frac{1760 \times 7}{2 \times 22 \times 14}\) = 20cm
∴Height of the cylinder = 20cm

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation Ex 2.1 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 2nd Lesson Polynomials and Factorisation Exercise 2.1

Question 1.
Find the degree of each of the polynomials given below,
i) x⁵ – x⁴ + 3
Solution:
Degree is 5.

ii) x² + x – 5
Solution:
Degree is 2.

iii) 5
Solution:
Degree is 0.

iv) 3x⁶ + 6y³ – 7
Solution:
Degree is 6.

v) 4 – y²
Solution:
Degree is 2.

vi) 5t – √3
Solution:
Degree is 1.

Question 2.
Which of the following expressions are polynomials in one variable and which are not ? Give reasons for your answer.
i) 3x² – 2x + 5
Solution:
Given expression is a polynomial in one variable.

ii) x² + √2
Solution:
Given expression is a polynomial in one variable.

iii) p² – 3p + q
Solution:
Given expression is not a polynomial in one variable. It involves two variables p and q.

iv) y + \(\frac{2}{\mathbf{y}}\)
Solution:
Given expression is not a polynomial. Since the second term contains the variable in its denominator.

v) \(5 \sqrt{x}+x \sqrt{5}\)
Solution:
Given expression is not a polynomial. Since the first term’s exponent is not an integer.

vi) x¹⁰⁰ + y¹⁰⁰
Solution:
Given expression has two variables. So it is not a polynomial in one variable.

Question 3.
Write the coefficient of x³ in each of the following.
i) x³ + x + 1
ii) 2 – x³+ x²
iii) \(\sqrt{2} x^{3}+5\)
iv) 2x³ + 5
v) \(\frac{\pi}{2} x^{3}+x\)
vi) \(-\frac{2}{3} x^{3}\)
vii) 2x² + 5
viii) 4
Solution:
i) x³ + x + 1 : co-efficient of x³ is 1.
ii) 2 – x³+ x² : co-efficient of x³ is – 1.
iii) \(\sqrt{2} x^{3}+5\) co-efficient of x³ is √2
iv) 2x³ + 5 : co-efficient of x³ is 2.
v) \(\frac{\pi}{2} x^{3}+x\) co-efficient of x³ is \(\frac{\pi}{2}\)
vi) \(-\frac{2}{3} x^{3}\) co-efficient of x³ is \(-\frac{2}{3}\)
vii) 2x² + 5 : co-efficient of x³ is ‘0’.
viii) 4 : co-efficient of x³ is ‘0’.

Question 4.
Classify the following as linear, quadratic and cubic polynomials.
i) 5x²+ x – 7 : degree 2 hence quadratic polynomial.
ii) x – x³ , : degree 3 hence cubic polynomial.
iii) x² + x + 4 : degree 2 hence quadratic polynomial.
iv) x – 1 : degree 1 hence linear polynomial.
v) 3p : degree 1 hence linear polynomial.
vi) πr² : degree 2 hence quadratic polynomial.

Question 5.
Write whether the following statements are True or False. Justify your answer.
i) A binomial can have at the most two terms
ii) Every polynomial is a binomial
iii) A binomial may have degree 3
iv) Degree of zero polynomial is zero
v) The degree of x² + 2xy + y² is 2
vi) πr² is monomial
Solution :
i) A binomial can have at the most two terms -True
ii) Every polynomial is a binomial – False
[∵ A polynomial can have more than two terms]
iii) A binomial may have degree 3 – True
iv) Degree of zero polynomial is zero – False
v) The degree of x² + 2xy + y² is 2 – True
vi) πr² is monomial – True

Question 6.
Give one example each of a monomial and trinomial of degree 10.
Solution :
– 7x¹⁰ is a monomial of degree 10.
3x²y⁸ + 7xy – 8 is a trinomial of degree 10.

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 6 Linear Equation in Two Variables Ex 6.2 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 6th Lesson Linear Equation in Two Variables Exercise 6.2

Question 1.
Find three different solutions of the each of the following equations.
i) 3x + 4y = 7
Solution:
Given equation is 3x + 4y = 7

Choice of x or y Simplification for y or x
Solution

ii) y = 6x
Solution: Given equation is y = 6x ⇒ 6x – y = 0

iii) 2x – y = 7
Solution:
Given equation is 2x – y = 7

iv) 13x – 12y = 25
Solution:
Given equation is 13x – 12y = 25

v) 10x + 11y = 21
Solution:
Given equation is 10x + 11y = 21

vi) x + y = 0
Solution:
Given equation is x + y = 0

Question 2.
If (0, a) and (b, 0) are the solutions of the following linear equations. Find a and b.
8x – y = 34
Solution:
Given that (0, a) and (b, 0) are the solutions of 8x – y = 34
∴ 8(0) – a = 34 and 8(b) – 0 = 34
⇒ a = -34 and b = \(\frac{34}{8}=\frac{17}{4}\)

ii) 3x = 7y – 21
Solution:
Given that (0, a) and (b, 0) are the solutions of 3x = 7y – 21
⇒ 3x – 7y = – 21
∴ 3(0) – 7(a) = -21 and 3(b) – 7(0) = -21
⇒ a = \(\frac{-21}{-7}\) and b = \(\frac{-21}{3}\)
⇒ a = 3 and b = -7

iii) 5x – 2y + 3 = 0
Given that (0, a) and (b, 0) are the solutions of 5x – 2y = – 3
i. e., 5(0) – 2a = – 3 and 5 (b) – 2(0) = – 3
⇒ -2a = -3 and 5b = -3
⇒ a = \(\frac{3}{2}\) and b = \(\frac{-3}{5}\)

Question 3.
Check which of the following is solution of the equation 2x – 5y = 10.
(i) (0, 2) (ii) (0,-2) (iii)(5, 0) (iv) (2√3, -√3) (v) (\(\frac{1}{2}\) , 2)
Solution:
i) (0, 2)
The given equation is 2x – 5y = 10
On substituting (0, 2), the L.H.S becomes
2(0)-5(2) = 0-10 = -10
R.H.S = 10
L.H.S ≠ R.H.S
∴ (0, 2) is not a solution.

ii) (0. – 2)
Substituting (0, – 2) in the L.H.S of 2x – 5y = 10, we get
2(0) – 5 (- 2) = 0 + 10 = 10 = R.H.S
∴ (0, – 2) is a solution.

iii) (5, 0)
Substituting (5, 0) in the L.H.S of 2x – 5y = 10, we get
2(5)-5(0) = 10-0 = 10 = R.H.S
∴ (5, 0) is a solution.

iv) 2√3, -√3
On substituting (2√3, -√3 ), the L.H.S becomes
2(2√3) – 5(-√3) = 4√3 + 5√3 = 9√3 ≠ R.H.S
∴ (2√3, -√3) is not a solution.

v) (\(\frac{1}{2}\), 2)
Given equation is 2x – 5y = 10
Put x = \(\frac{1}{2}\) and y = 2 in the given equation.
Then 2(\(\frac{1}{2}\)) – 5(2) =10
1-10 = 10
-9 = 10 false
∴ (\(\frac{1}{2}\) , 2) is not a solution.

Question 4.
Find the value of k, if x = 2; y = 1 is a solution of the equation 2x + 3y = k. Find two more solutions of the resultant equation. £3 Each
Solution:
Given that x = 2 and y = 1 is a solution of 2x + 3y = k .
∴ 2(2) + 3(1) = k ⇒ 4 + 3 = k ⇒ k = .7 ’
∴ The equation becomes 2x + 3y = 7

Two more solutions are (0, \(\frac{7}{3}\)) and (1, \(\frac{5}{3}\))

Question 5.
If x = 2 – α and y = 2 + α is a solution of the equation 3x – 2y + 6 = 0, find the value of ‘α’. Find three more solutions of the resultant equation.
Solution:
Given that x = 2 – α and y = 2 + α is a solution of 3x – 2y + 6 = 0
Thus 3 (2 – α) – 2 (2 + α) + 6 = 0
⇒ 6 – 3α – 4 – 2α + 6 = 0
⇒ -5α + 8 = 0
⇒ -5α = -8
∴ α = \(\frac{8}{5}\)
Three more solutions are

Question 6.
If x = 1;y = 1 is a solution of the equation 3x + ay = 6, find the value of ‘a’.
Solution:
Given that x = 1; y = 1 is a solution of 3x + ay = 6.
Thus 3(1) + a(1) = 6
⇒ 3 + a = 6 ⇒ a = 6 – 3 = 3

Question 7.
Write five different linear equations in two variables and find three solutions for
each of them.
Solution:
i) Let the equations are 2x – 4y = 10

ii) 5x + 6y = 15

iii) 3x-4y = 12

iv) 2x – 7y = 9

v) 7x- 5y = 3

Andhra Pradesh AP Board 3rd Class English Solutions 5th Lesson The Good Samaritan Textbook Exercise Questions and Answers.

AP State Syllabus 3rd Class English Solutions Chapter 5 The Good Samaritan

Textbook Page No. 53

Look at the picture.

Activity-1

Answer the following questions orally.

Question 1.
How many children are there ?
Answer:
There are ten children.

Question 2.
What are the girls doing ?
Answer:
The girls are playing.

Question 3.
What happened to the boy ?
Answer:
The boy was injured.

Question 4.
What is the other boy doing ?
Answer:
The other boy is helping him to get up.

Question 5.
Have you ever helped anyone
Answer:
Yes, I did.

Textbook Page No. 57

Comprehension

Activity-2

Answer the following questions.

Question 1.
Where did the Jewish man live ?
Answer:
The Jewish man lived in Jerusalem.

Question 2.
Who started the journey to Jericho ?
Answer:
The Jewish man started journey to Jericho.

Question 3.
Where was the Jewish man left by the robbers ?
Answer:
He was left on the road.

Question 4.
Who helped the Jewish man ?
Answer:
The Samaritan helped the Jewish man.

Question 5.
Why was the Samaritan called ’The Good Samaritan’ ?
Answer:
It is because he helped the Jewish man with goodness.

Vocabulary

Read the following opposite words.

open × close
after × before
near × far
stop × start
kind × cruel

Textbook Page No. 58

Activity – 3

Observe the above two pictures. Identify the differences in them and fill in the blanks with the words given in the box.

many tall small closed white fat start

1. A ____ house × A big house.
Answer:
A small house × A big house.

2. A black boat × A _____ boat.
Answer:
A black boat × A white boat.

3. A _____ coconut tree × A short coconut tree.
Answer:
A tall coconut tree × A short coconut tree.

4. A ___ girl. × A thin girl.
Answer:
A fat girl. × A thin girl.

5. A stop board × A ____ board.
Answer:
A stop board × A start board.

6. Few birds × ____ birds.
Answer:
Few birds × many birds.

7. ____ gate × opened gate.
Answer:
closed gate × opened gate.

Textbook Page No. 63

Activity – 4

Your teacher will read out the following words / phrases. Write them in your note book.

1. honest…..
2. money…….
3. coat……..
4. journey…….
5. a gang of robbers…….
6. wound ……..
7. footsteps…….
8. innkeeper……
9. hometown…….
10. gesture……..

Grammar

Read the following statements. Observe the underlined words.

1. Jewish man lived in jerusalem.
2. He started his journey One morning.
3. He opened his eyes with great difficulty.
4. He stopped his donkey.

The underlined words are action words. They are called verbs. They denote completed actions. They are used here in simple past tense.
The root forms of the above verbs are live, start, open and stop. The past tense form of the above verbs are formed by adding -ed or -d.
Such verbs are called regular verbs.

Textbook Page No. 60

Activity-5

Frame meaningful sentences from the following table.

e.g. I painted a picture.
Answer:
1) I played cricket.
2) He painted a picture.
3) They closed the door.
4) We ordered coffee.
5) She asked a question.

Activity-6

Read the following passage. Find the regular past form of verbs.

Once there lived an old man named Suranna. One day, he invited his friends to his home. He called his wife and asked her to prepare dinner. She prepared a delicious dinner. All of them enjoyed the dinner. They thanked the couple.
Answer:

Circle the regular past tense form of the verbs in the passage and write them down in the blanks.

1. lived
2. invited
3. called
4. prepared
5. enjoyed
6. thanked

Writing

Activity-7

Rewrite the following with correct punctuation. (Full stop, Capitalization)

the jewish man saw a man coming towards him he was riding a donkey the man was a Samaritan
Answer:
The Jewish man saw a man coming towards him. He was riding a donkey.
The man was a Samaritan.

Textbook Page No. 61

Activity – 8

Write 4 or 5 sentences about your visit to a place (a temple / a church / mosque). Use the following clues.

visited – with parents – last month – enjoyed – bought toys

1. I visited a temple nearby.
2. I went along with my parents.
3. All of us enjoyed together.
4. We visited this temple the last month.
5. We bought toys and had fun.

Activity – 9

You are going to school. On the way, you have seen a puppy limping and crying.
What do you do ?
You have helpoed the puppy. You are late to school. How do you feel ?
Enact the above scene as a skit.

Activity – 10

Your teacher will read the following words. Repeat after your teacher.

owl
cow
howl
bow
loud
doubt
down
round
around
vowel
devour

Textbook Page No. 62

Activity-11

Read the following poster.

Prepare your own poster.
Answer:

Activity-12

Look at the picture. A girl is tying a bandage to her brother’s finger. Colour the picture.

Student activity.

The Good Samaritan

Summary :

Once, there lived a Jewish man in Jerusalem. One day, he started his journey to Jericho. Suddenly, a gang of robbers beat him and took away all money from him. the man was injured. After sometime he saw a priest nearby. He thought he would help him but he went on. Later, a Levite came and went away. Then a Samaritan there.

Jews didn’t like Samaritans. So, he expected that the man wouldn’t help him. But the Samaritan stopped his donkey and came to him with compassion. Jewish man was almost fainting. The Samaritan gave him water and bandaged the wounds. Then he took him to an inn on his donkey. He paid the inn-keeper enough money and left the Jewish man there. Soon, he recovered and went home. He always remembered Samaritan’s kindness.

సారాంశము

అనగనగా జెరూసలెం అనే ప్రదేశంలో ఒక యూదు దేశస్థుడు నివసించేవాడు. ఒక రోజు అతను జెరికో అనే ఊరికి బయలు దేరాడు. హఠాత్తుగా ఒక దొంగల గుంపు తనను బాగా కొట్టి, అతని డబ్బు అంతా తీసుకువెళ్ళారు. ఆ దెబ్బలకి ఆ యూదు దేశస్థుడు గాయపడ్డాడు. కొంత సేపటికి అక్కడ ఒక పురోహితుడు అటుగా రావడం చూసి తనను ఆదుకుంటాడని భావిస్తాడు. కాని అతను తన దారిన వెళ్ళిపోతాడు. ఆ తర్వాత ఆ దారిన ఒక సమరిటన్ వస్తాడు. తాను కూడా వచ్చిన దారిన వెళ్తాడు. అప్పుడు ఒక దయాళువు అటుగా వస్తాడు.

కాని యూదులకు, వారికి మంచి సంబంధాలు లేకపోవడంతో తను సహాయం చేయడని భావిస్తాడు. కాని ఆ దయాళువు తన దగ్గరకు వచ్చి మంచి నీళ్ళు తాగించి, గాయాలకు మందు రాస్తాడు. ఆ తర్వాత దగ్గర్లో ఉన్న సత్రములో యజమానికి డబ్బు ఇచ్చి, యూదుడిని బాగా చూసుకోమని చెప్పి వెళ్తాడు. కొన్ని రోజులకు యూదుడు కోలుకొని తన ఇంటికి తిరిగి వెళ్తాడు. ఎప్పుడు ఆ దయాళువును తలచుకొనేవాడు.

Glossary

Jewish man = a man belonging to Judaism; (యూదు)
compassion = pity (కరుణ)
robber = a thief who steals by violence; (దొంగ)
priest = a person who performs religious duties; (పురోహితుడు)
Levite = a member of the tribe of Levi;
Samaritaninn = a member of people inhabiting Samaria; దయాళువు
a hotel providing lodging for travelers. సత్రము
wound = injury గాయం
have in mind (గుర్తుపెట్టుకొనుట)

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 4 Lines and Angles Ex 4.1 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 4th Lesson Lines and Angles Exercise 4.1

Question 1.
In the given figure, name:

i) Any six points
Solution:
A, B, C, D, P, Q, M, N etc.

ii) Any five line segments
Solution:
\(\overline{\mathrm{AX}}, \overline{\mathrm{XM}}, \overline{\mathrm{MP}}, \overline{\mathrm{PB}}, \overline{\mathrm{MN}}, \overline{\mathrm{PQ}}, \overline{\mathrm{AB}} \ldots \ldots\) etc.

iii) Any four rays
Solution:
\(\overline{\mathrm{MA}}, \overline{\mathrm{PA}}, \overline{\mathrm{PB}}, \overline{\mathrm{NC}}, \overline{\mathrm{QD}} \ldots \ldots\) etc.

iv) Any four lines
Solution:
\(\overline{\mathrm{MA}}, \overline{\mathrm{PA}}, \overline{\mathrm{PB}}, \overline{\mathrm{NC}}, \overline{\mathrm{QD}} \ldots \ldots\)

v) Any four collinear points
Solution:
A, X, M, P and B are collinear points on the line \(\overline{\mathrm{AB}}\).

Question 2.
Observe the following figures and identify the type of angles in them.

Solution:
∠A – reflex angle
∠B – right angle
∠C – acute angle

Question 3.
State whether the following state¬ments are true or false
i) A ray has no end point.
ii) Line \(\overline{\mathrm{AB}}\) is the same as line \(\overline{\mathrm{BA}}\)
iii) A ray \(\overline{\mathrm{AB}}\) is same as the ray \(\overline{\mathrm{BA}}\)
iv) A line has a definite length.
v) A plane, has length and breadth but no thickness.
vii) Two lines may intersect in two points.
viii) Two intersecting lines cannot both be parallel to the same line.
Solution:
i) A ray has no end point. – False
ii) Line \(\overline{\mathrm{AB}}\) is the same as line \(\overline{\mathrm{BA}}\) – True
iii) A ray \(\overline{\mathrm{AB}}\) is same as the ray \(\overline{\mathrm{BA}}\) – False
iv) A line has a definite length. – False
v) A plane, has length and breadth but no thickness. – True
vi) Two distinct points always determine a unique line. – True
vii) Two lines may intersect in two points. – False
viii) Two intersecting lines cannot both be parallel to the same line. – True

Question 4.
What is the angle between two hands of a clock when the lime in the clock
is
a) 9 ‘o clock
b) 6 ‘o clock
c) 7 ; 00 p.m.
Solution:

a) 12 hours = = 360°
1 hour = \(\frac{360^{\circ}}{12}\) = 30°
∴Angle between hands when the time is 9 o clock = 3 x 30 = 90

b)

Angle between hands = 6 x 30° = 180°

c)

Angle between hands = 7 x 30° = 210°

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 10 Surface Areas and Volumes Ex 10.1 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 10th Lesson Surface Areas and Volumes Exercise 10.1

Question 1.
Find the lateral surface area and total surface area of the following right prisms.
i)
L.S.A. = 4l²
= 4 × 4²
= 64cm²
T.S.A = 6l²
= 6 × 4² = 96cm²

ii) L.S.A. =2h(l + b)
= 2 × 5 (8 + 6)
= 10 × 14 = 140 cm²
T.S.A. = 2 (lb + bh + lh)
= 2(8 × 6 + 6 × 5 + 8 × 5)
= 2 (48 + 30 + 40)
= 236 cm²

Question 2.
The total surface area of a cube is 1350 sq.m. Find its volume.
Solution:
Given T.S.A. of a cube 6l² = 1350
l² = \(\frac{1350}{6}\)
l² = 225
∴ l = \(\sqrt{225}\) = 15m
∴ Volume of the cube = l³
= 15 × 15 × 15
= 3375 m³

Question 3.
Find the area of four walls of a room (Assume that there are no doors or windows) if its length 12 m; breadth 10 m and height 7.5 m.
Solution:
Length of the room = 12 m
Breadth of the room = 10 m
Height of the room = 7.5 m
Area of four walls of the room
A = 2h (l + b)
A = 2 × 7.5 (12 + 10)
= 15 × 22
= 330 m²

Question 4.
The volume of a cuboid is 1200 cm³. The length is 15 cm and breadth is 10 cm. Find its height.
Solution:
Length of a cuboid, ‘l’ = 15 cm
Breadth of the cuboid, b = 10 cm
Volume of the cuboid, V = lbh = 1200.cm³
Let the height = h
∴ 15 × 10 × h = 1200
∴ h = \(\frac{1200}{15 \times 10}\)
= 8 cm

Question 5.
How does the total surface area of a box change if
i) Each dimension is doubled ?
Solution:
Let the original dimensions be Length – l units
Breadth – b units
Height – h units
Then T.S.A = 2 (lb + bh + lh)
If the dimensions are doubled then
Length = 2l
Breadth = 2b
Height = 2h
T.S.A. = 2 (2l. 2b + 2b . 2h + 2l . 2h)
= 2 (4lb + 4bh + 4lh)
= 4 × [2 (lb + bh + lh]
= 4 × original T.S.A.
i.e., T.S.A. increases by 4 times.

ii) Each dimension is tripled ?
Solution:
Let the original and changed dimensions are l, b, h and 31, 3b, 3h
Original T.S.A. = 2 (lb + bh + lh)
Changed T.S.A
= 2 (3l . 3b + 3b . 3h + 3l. 3h)
Changed T S.A. = 2 (9lb + 9bh + 9lh)
= 9 × [2 (lb + bh + lh)]
= 9 [original T.S.A.]
Thus original T.S.A. increased by 9 times if each dimension is tripled.

Question 6.
The base of a prism is triangular in shape with sides 3 cm, 4 cm and 5 cm. Find the volume of the prism if its height is 10 cm.
Solution:
Volume of triangular prism = Area of the base × height
Sides of the triangle are 3 cm, 4 cm and 5 cm.
Area = s (s – a) (s – b) (s – c)

∴ Volume of the prism = 6 × 10 = 60 cm³
(OR)
3 cm, 4 cm and 5 cm are the sides of right triangle.
∴ Area of the triangle
= \(\frac { 1 }{ 2 }\) bh = \(\frac { 1 }{ 2 }\) × 3 × 4 = 6 cm²
Volume of prism = base area × height
= 6 × 10 = 60cm³

Question 7.
A regular square pyramid is 3 m height and the perimeter of its base is16 m Find the volume of the pyramid.
Solution:
Perimeter of the base = 16 m
Height of the pyramid 3 m
Volume of the pyramid
= \(\frac { 1 }{ 3 }\) × volume of prism
= \(\frac { 1 }{ 3 }\) × (base area x height)
= \(\frac { 1 }{ 3 }\) × 4 × 4 × 3= 16m [4 × side=16 ∴ side = 4 m Area = s² = 4 × 4]

Question 8.
An Olympic swimming pool is in the shape of a cuboid of dimensions 50 m long and 25 m wide. If it is 3 m deep throughout, how many litres of water does it hold ?
Solution:
Dimensions of the swimming pool are
Length = 50 m
Breadth = 25 m
Deep = 3 m
∴ Volume of the swimming pool
V = lbh
V = 50 × 25 × 3 = 3750 m³
∴ It can hold 37,50,000 litres of water.
[∵ 1 m³ = 1000 lit.]