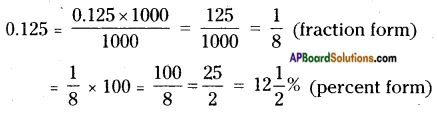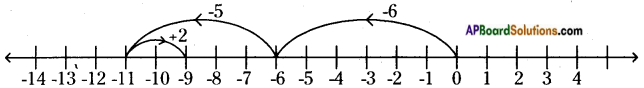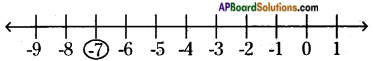Class 6

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 4 Integers InText Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 4th Lesson Integers InText Questions

Check Your Progress?(Page No. 47)

Question 1.
Write any five positive integers.
Solution:
1, 2, 3, 4, 5, 6, 7,

Question 2.
Write any five negative integers.
Solution:
-1, -2, -3, -4, -5, -6,

Question 3.
Which number is neither positive nor negative?
Solution:
0 (zero)

Question 4.
Represent the following situations with integers,
(i) A gain of ₹ 500 ( )
(ii) Temperature is below 5°C ( )
Solution:
i) + 7 500
ii) – 5° C

Question 5.
Represent the following using either positive or negative numbers.
a) A bird is flying at a height of 25 meters above the sea level and a fish at a depth of 2 meters.
b) A helicopter is flying at a height of 60m above the sea level and a submarine is at 400m below sea level.
Solution:
a) Height of the flying bird 25 meters from th$ sea level = + 25 meters
Depth of the fish 2 meters from the sea level = – 2 meters
b) Height of the flying helicopter 60 meters from the sea level = + 60 m
Depth of the submarine 400 m from the sea level = – 400 m

Check Your Progress (Page No. 49)

Question 1.
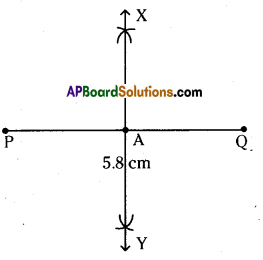
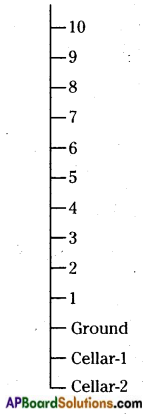
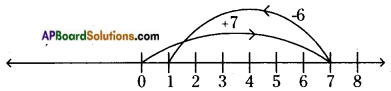
Draw a vertical number line and represent -5,4,0,-6, 2 and 1 on it.
Solution:

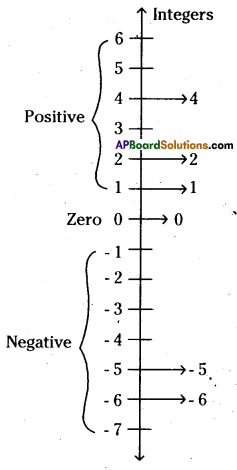
Question 2.
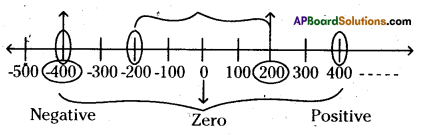
Represent opposite integers of – 200 and + 400 on integer number line.
Solution:
Opposite integers means, additive inverse.
∴ Opposite integer (additive inverse) of – 200 is 200.
Opposite integer (additive inverse) of +400 is – 400.

Let’s Think (Page No. 50)

Question 1.
For any two integers, say 3 and 4, we know that 3 < 4.
Is it true to say -3 < -4? Give reason.
Solution:
On the number line, the value of a number increases as we move to right and decreases as we move to the left. As -3 lies right to -4 on the number line.
So, -3 < -4 is not true.

(Pg. No. 52)

Question 1.
What is additive inverse of 7 ?
Solution:
Additive inverse of 7 is -7.

Question 2.
What is additive inverse of -8 ?
Solution:
Additive inverse of -8 is 8.

Let’s Explore (Page.No. 52)

Question 1.
Find the value of the following using a number line.
i) (-3) + 5 ii) (-5) + 3
Make two questions on your own and solve them using the number line.
Solution:
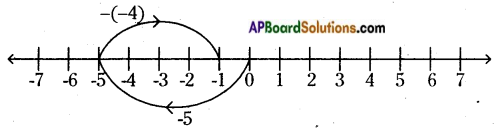
i) (-3) + 5

On the number line, we first move 3 steps to the left of 0 to reach -3.
Then, we move 5 steps to the right of -3 and reach +2. So, (-3) + 5 = 2

ii) (-5) + 3

On the number line, we first move 5 steps to the left of 0 to reach -5. Then, we move 3 steps to the right of -5 and reach -2. So, (-5) + 3 = – 2

iii)(+6) + (-3)

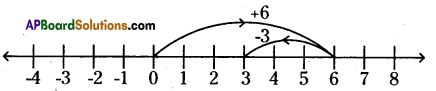
On the number line, we first move 6 steps to the right of 0 to reach +6.
Then, we move 3 steps to the left of 6 and reach +3. So, (+6) + (-3) = 3

iv) (-4) + (-3)

On the number line, we first move 4 steps to the left of 0 to reach -4. Then, we move 3 steps to the left of -4 and reach -7.
So (-4) + (-3) = -7.

Question 2.
Find the solution of the following:
i) (+5) + (-5) (ii) (+6) + (-7) (iii) (-8) + (+2)
Ask your friend five such questions and solve them.
Solution:
i) (+5) + (-5) = 0

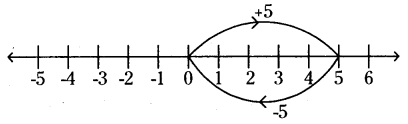
On the number line, we first move 5 steps to the right of 0 to reach +5.
Then, we move 5 steps to the left of +5 and reach 0.

ii) (+6) + (-7) = -1

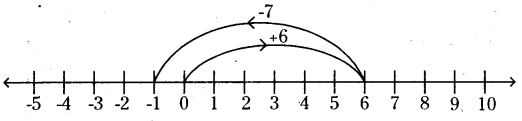
On the number line, we first move 6 steps to the right of 0 to reach +6.
Then, we move 7 steps to the left of +6 and reach -1.

(iii) (-8) + (+2)

On the number line, we first move 8 steps to the left of 0 to reach -8. Then, we move 2 steps to the right of -8 and reach -6.

iv)(-4) + (+8) = +4

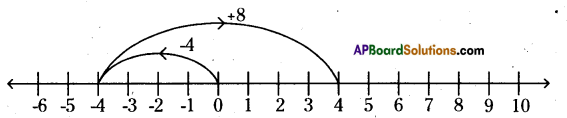
On the number line, we first move 4 steps to the left of 0 to reach -4. Then, we move 8 steps to the right of -4 and reach +4.

v) (+3) + (-4) = -1

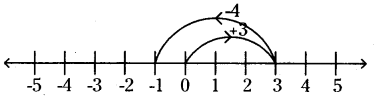
On the number line, we first move 3 steps to the right of 0 to reach +3. Then, we move 4 steps to the left of +3 and reach -1.

vi) (+5) + (-6) = -1

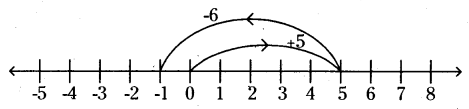
On the number line, we first move 5 steps to the right of 0 to reach +5. Then, we move 6 steps to the left of +5 and reach -1.

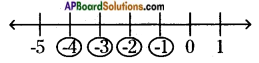
vii) (+4) + (-4) = 0

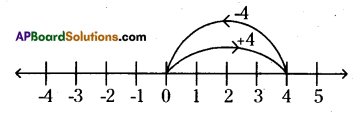
On the number line, we first move 4 steps to the right of 0 to reach +4. Then, we move 4 steps to the left of +4 and reach 0.

viii) (-6) +(+4) =-2

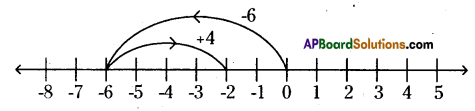
On the number line, we first move 6 steps to the left of 0 to reach -6. Then, we move 4 steps to the right of -6 and reach -2.
So, (-6) + (+4) = -2

Let’s Explore (Page No. 55)

Question 1.
Take any two integers a and b. Check whether a+b is also an integer.
Case (i) : Consider two integers 3 and -2 (Positive and negative)
Sum = 3 + (-2) = +1 + 2 – 2 = +1 + 0 = +1 is also an integer.
Case (ii) : Consider two ihtegers 5 and 6 (Both are positive)
Sum = 5 +6 = + 11 is also an integer
Case (iii) : Consider two integers -4 and -6 (Both are negative)
Sum = -4 + (-6) = -4 -6 = -10 is also an integer
Case (iv) : Consider two integers -5 and 4 (Negative and positive)
Sum = -5 + 4 = -1 -4 + 4 = -1 + 0 = -1 is also an integer.
So, if a and b are integers, then their sum a + b is also an integer. Integers are closed under addition.

Question 2.
Check the following Properties on integers, a, b, c are any integers.
i) Closure Property under subtraction ‘
ii) Commutative Property under addition and subtraction (a + b = b + a ?, a – b = b – a?)
iii) Associative Property under addition and subtractioji.
(a + b) + c = a + (b + c) ? (a – b).- c = a – (b – c)?
Solution:
i) Closure Property under subtraction :
Case (i) : Consider two integers 4, -5 (positive and negative)
Then, difference a – b = 4 – (-5) = 4 + 5 = + 9is also an integer.
Case (ii) : Consider two integers 3, 8 (Both are positive)
Then, difference a – b = 3 – (+8) = 3-8
= +3 – 3 – 5 = 0 – 5 = -5is also an integer.
Case (iii) : Consider two integers -2, -6 (Both are negative) .
Then, difference a – b = -2 – (-6) = -2 + 6
= -2 + 2 + 4 = 0 + 4 = +4 is also an integer.

Case (iv) : Consider two integers -3, 2 (Negative and positive)
Then, difference a – b = -3 – (+2) = -3 -2 = -5 is also an integer.
So, if a and b are any two integers, then their difference a – b is also an integer. Integers are closed under subtraction.

ii) Commutative Property under addition and subtraction :
(a + b = b + a, a-b = b-a)
(A) Case (Q : Consider two integers-3 and 5 (Negative and positive)
Then, a + b = -3 + (+5)
= -3 + 5 = – 3 + 3 + 2 = 0 + 2 = + 2
b + a = +5 + (-3) = +2 + 3- 3 = +2 + 0 = + 2
∴ a + b = b + a

Case (ii) : Consider two integers +4 and +2 (Both are positive)
Then, a + b = +4 + (+2) = +4 + 2 = + 6 ‘b + a = +2 + (+4) = +2 + 4 = + 6
∴ a + b = b + a

Case (iii) Consider two integers -5 and -3 (Both are negative) Then, a + b = -5 + (-3) = -5 – 3 = -8 b + a = -3 + (-5) = – 3 – 5 = -8
∴ a + b = b + a

Case (iv) : Consider two integers +4 and -1 (Positive and negative)
Then, a + b = +4 + (*1) = +4 -1 = +3 + 1 -1 = +3 + 0 = +3 b + a = -1 + (+4) =-l + 4 = -l + l+ 3 = 0 + 3 = + 3
∴ a + b = b + a
So, integers are commutative under addition.

(B) Consider two integers -4 and +6 (Negative and positive)
Then, a – b = -4 – (+6) = -4 – 6 = -10 b-a = + 6-(-4) = +6 +4 = +10 -10*10
a – b ≠ b – a
So, integers are not commutative under subtraction.

iiO Associative property under addition and subtraction :
(a + b) + c = a + (b + c) ; (a – b) – c = a – (b – c)
(A) Case (i) : Consider any three integers 2, 4, -5
(a + b) + c = (2 + 4) + (-5) = 6 – 5 = +1 + 5- 5 = +1 + 0 = +1
a + (b + c) = 2 + (4 + (-5)) = 2 + (4 – 5) = 2 + (4 – 4 -1)
= 2 + (0-1) = + 2 – 1 = + 1 + 1 – 1 = +1 + 0 = +1
∴ (a + b) + c = a + (b + c)

Case (ii) : Consider any three integers +2, -5, +3
Then, (a + b) + c = [2 + (-5)] + 3 = [+2 -5] + 3 = +2 -2 -3 + 3 = 0 + 0 = 0
a + (b + c) = +2 + [( – 5)+3] = +2 + [-2 – 3 + 3] = +2 + (-2 + 0) = +2 -2 = 0
∴ (a + b) + c = a + (b + c)

Case (iii) : Consider any three integers 3, 4, 6
Then, (a + b) + c = [2 + (-5)] + 3 [+2-5] + 3
a + (b + c) = 3 + (4 + 6) = 3 + 10 = + 13
∴ (a + b) + c = a + (b + c)

Case (iv) : Consider any three integers -4, -2, +5
Then, (a + b) + c = [-4 + (-2)] + 5 = [-4 -2] + 5 = -6 + 5
= -1-5 + 5 = – 1 + 0 = – 1
a + (b + c) = -4 + [(-2) + 5] = -4 + [-2 + 5]
= _4 + [_2 + 2 +3] = -4 + 0 + 3 =-1-3+ 3
= -1 + 0 = -1
∴ (a + b) + c = a + (b + c)

Case (v) : Consider any three integers-3, 4, 1
Then, (a + b) + c = (-3 + 4) + 1 = (-3 + 3 + 1) + 1 = 0 + 1 + 1 = + 2
a + (b + c) = -3 + (4 + 1) = -3 + 5 = -3 + 3 + 2 = 0 + 2 = +2
∴ (a + b) + c = a + (b + c)

Case (vi) : Consider any three integers -2, 6, -7
Then, (a + b) + c = (-2 + 6) + (-7) = (-2 + 2 + 4) + (-7) = 0 + 4 – 7
= + 4 – 4 – 3 = 0 – 3 = -3
a + (b + c) = -2 + [6 + (-7)] = -2 + (6 – 7) = -2 + [+6 – 6 -1]
= -2 + (-1) = -2 -1 = -3
∴ (a + b) + c = a + (b + c)

Case (vii) : Consider any three integers +6, -3, -1
Then, (a + b) +c = [+6 + (-3)] + (-1) = (6 – 3) – 1 = (+3 +3 -3) -1
=+3-1 =+2 + 1 – 1 =+2 + 0 = + 2
a + (b + c) = +6 + [-3 + (-1)] = 6 + [-3 – 1] = 6 + (-4) .
= +2 + 4 – 4 = 2 + 0 = + 2
∴ (a + b) + c = a + (b + c)

Case(viii)
Consider any three integers -4, -1, -7
Then, (a + b) + c = [-4 + (-1)] + (-7) = (-4 -1) – 7 = -5 -7 = -12
a + (b + c) = -4 + [(-1) + (-7)] = -4 + [-1 -7] = -4 + (-8)
= -4 – 8 = -12
∴ (a + b) + c = a + (b + c)
From all the above cases we conclude that, integers are associative under addition.

(B) Consider any three integers +5, -4, 1
Then, (a – b) – c = (+5 – (-4)) – (+1) = (5 + 4) – 1 .
= + 9 – 1 = + 8 + 1 – 1 = + 8 + 0 = + 8
a – (b – c) = +5 – [- 4 – (+1)] = + 5 – [-4 – 1]
= + 5 – [ -5] =+ 5 + 5 = + 10
+ 8 ≠ +10
∴ (a – b) – c ≠ a – (b – c)
So, integers are not associative under subtraction.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 12 Data Handling InText Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 11th Lesson Data Handling InText Questions

Let’s Do (Page No. 159)

Question 1.
Take a die. Throw it and record the number. Repeat the activity 40 times and record the numbers. Represent the data in a frequency distribution table using tally marks.
Solution:

(Page No. 159)

Question 1.
In what way is the bar graph better than the pictograph ?
Solution:
Bar graphs are better indicative as they show exact numerical value. Also, to indicate negative values and positive values, it looks easier in a bar graph.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 3 HCF and LCM InText Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 3rd Lesson HCF and LCM InText Questions

(Page No. 35)

Question 1.
How does the Sieve of Eratosthenes work ?
Solution:
The following example illustrates how the Sieve of Eratosthenes, can be used to find all the prime numbers that are less than 100. .
Step 1: Write the numbers from 1. to 100 in ten rows as shown below.
Step 2: Cross out 1 as 1 is neither a prime nor a composite number.
Step 3: Circle 2 and cross out all the multiples of 2. (2, 4, 6, 8, 10, 12, ………… )
Step 4: Circle 3 and cross out all the multiples of 3. (3, 6, 9, 12, 15, 18,………….)
Step 5: Circle 5 and cross out all the multiples of 5. (5, 10. 15, 20, 25……………… )
Step 6: Circle 7 and cross out all multiples of 7. (7, 14, 21. 28, 35, ………………….. )

Circle all the numbers that are not crossed out and they are the required prime numbers less than 100.

First arrange the numbers ffom 1 to 100 in a table as shown above.
Enter 6 numbers in each row until the last number 100 is reached.
First we select a number and we strike off all the multiples of it.
Start with 2 which is greater than 1.
Round off number 2 and strike off entire column until the end.
Similarly strike off 4th column and 6th column as they are divisible by 2.
Now round off next number 3 and strike off entire column until end.
The number 4 is already gone.

Now round off next number 5 and strike off numbers in inclined fashion as shown in the figure (they are all divisible by 5). When striking off ends in some row, start again striking off with number in another end which is divisible by 5. New striking off line should be parallel to previous strike off line as. shown in the figure.
The number 6 is already gone.
Now round off number 7 and strike off numbers as we did in case of number 5.
8,9,10 are also gone. .
Stop at this point.
Count all remaining numbers. Answer will be 25.

Prime numbers :
There are 25 prime numbers less than 100.
These are:

What if we go above 100 ? Around 400 BC the Greek mathematician. Euclid, proved that there are infinitely many prime numbers.

Co-primes: Two numbers are said to be co-prime if they have no factors in common. Example: (2, 9), (25, 28)
Any two consecutive numbers always form a pair of co-prime numbers.

Example:
Co-prime numbers are also called relatively prime number to one another.
Example: 3, 5, 8, 47 are relatively prime to one another/co-prime to each other.

Twin primes: Two prime numbers are said to be twin primes, if they differ by 2.
Example: (3, 5), (5, 7), (11, 13), …etc.

Prime factorization: The process of expressing the given number as the product of prime numbers is called prime factorization.
Example: Prime factorization of 24 is
24 = 2 x 12
= 2 x 2 x 6
= 2 x 2 x 2 x 3, this way is unique.

Every number can be expressed as product of primes in a unique manner. We can factorize a given number in to product of primes in two methods. They are
a) Division method
b) Factor tree method

Common factors: The set of all factors which divides all the given numbers are called their common factors.
Example: Common factors to 24, 36 & 48 are 1, 2, 3, 4, 6 & 12
Factors of 24 = 1, 2, 3, 4, 6, 8, 12 & 24
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18 & 36
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24 & 48
Common factors to 24, 36 & 48 are 1, 2, 3, 4, 6 & 12
We can see that among their common factors 12 is the highest common factor. It is called H.C.F. of the given numbers. So H.C.F. of 24, 36 & 48 is 12.

H.C.F./G.C.D : The highest common factor or the greatest common divisor of given numbers is the greatest of their common factors.
H.C.F. of given two or more numbers can be found in two ways.
a) By prime factorization
b) By continued division
H.C.F. of any two consecutive numbers is always 1.
H.C.F. of relatively prime/co-prime numbers is always 1.
H.C.F. of any two consecutive even numbers is always 2.
H.C.F. of any two consecutive odd numbers is always 1.

Common multiples:
Multiples of 8: 8, 16, 24, 32, 40, 48,
Multiples of 12: 12, 24, 36, 48, … .
Multiples.common to 8 & 12: 24, 48; 72, 96, …
Least among the common multiple is 24. This is called L.C.M. of 8 & 12. The number of common multiples of given two or more numbers is infinite, as such greatest common multiple cannot be determined.

L.C.M.: The least common multiple of two or more numbers is the smallest natural number among their common multiples.
L.C.M. of given numbers can be found by the
a) Method of prime factorization.
b) Division method.
L.C.M. of any two consecutive numbers is always equal to their product.
L.C.M. of 8 &9 is 8 x 9 = 72
L.C.M. of co-prime numbers is always equal to their product.
L.C.M. of 8 & 15 is 8 x 15 = 120

Relation between the L.C.M. & H.C.F:
For a given two numbers Nj & N2 , the product of the numbers is equal to the product of their L.C.M.(L) & H.C.F.(H)
N₁ x N₂ = L x H

Check Your Progress (Page No. 29)

Question 1.
Are the numbers 900, 452, 9534, 788 divisible by 2? Why?
Solution:
Yes. Because these numbers have 0, 2, 4 and 8 in their ones place. The numbers having 0, 2, 4, 6 and 8 in their ones place are divisible by 2.

Question 2.
Are the numbers 953, 457, 781, 325, 269 divisible by 2? Why?
Solution:
No. Because, these numbers have 3, 7, 1, 5 and 9 in their ones place. The numbers having 0, 2,
4, 6 and 8 in their ones place are only divisible by 2. So, these are not divisible by 2.

Question 3.
Are the numbers 452, 673, 259, 356 divisible by 2? Verify.
Solution:
452 and 356 have 2 and 6 in their ones place respectively.
So, they are divisible by 2.
673 and 259 have 3 and 9 in their ones place respectively.
So, they are not divisible by 2.

Question 4.
Check whether the following numbers are divisible by 3 (using rule). Verify by actual division.
(i) 12345 (ii) 61392 (iii)8747
Solution:
i)12345
1 + 2 + 3 + 4 + 5=15 is a multiple of 3.
If the sum of the digits of a number is the multiple of 3, then the number is divisible by 3.
So, 12345 is divisible by 3.

ii) 61392
6 + 1 + 3 + 9 + 2 = 21is a multiple,of 3.
If the sum of the digits of a number is a multiple of 3, then the number is divisible
by 3.

So, 61392 is divisible by 3.

iii) 8747
8 + 7 + 4 + 7 = 26is not a multiple of 3.
If the sum of the digits of a number is a multiple of 3, then the numbei is divisible by 3. So, 8747 is not divisible by 3.

So, 8747 is not divisible by 3.

Let’s Explore (Page No. 29)

Question 1.
Is 8430 divisible by 6? Why?
Given number is 8430.
The given number has zero in the ones place.
So, 8430 is divisible by 2. –
And the unit sum is8 + 4 + 3 + 0 = 15 is a multiple of 3.
So, 8430 is divisible by 3.
If a number is divisible by both 2 and 3, then only it is divisible by 6.
8430 is divisible by both 2 and 3.
Therefore 8430 is divisible by 6.

Question 2.
Take any three 4 digit numbers and check whether they are divisible by 6.
Solution:
Consider: i) 5632, ii) 6855, iii) 9600 are three 4 digit numbers.
i) 5632 has 2 in its ones place. So, 5632 is divisible by 2.
The unit sum is
5 + 6 + 3 + 2 = 16 is not a multiple of 3. So, 5632 is not divisible by 3.
If a number is divisible by both 2 and 3, then only it is divisible by 6.
5632 is qnly divisible by 2, but not divisible by 3.
So, 5632 is not divisible by 6.

ii) 6855 has 5 in the ones place. So, 6855 is not divisible by 2.
6 + 8 + 5 + 5 = 24 is a multiple of 3.
So, 6855 is divisible by 3.
If a number is divisible by both 2 and 3, then only it is divisible by 6.
6855 is not divisible by 2, but it is divisible by 3.
So, 6855 is not divisible by 6.

iii) 9600 has ‘0’ in the ones place. So, 9600 is divisible by 2.
9 + 6 + 0 + 0 = 15 is a multiple of 3.
So, 9600 is divisible by 3. .
If a number is divisible by both 2 and 3, then only it is divisible by 6, 9600 is divisible by 1 both 2 and 3.
So, 9600 is divisible by 6.

Question 3.
Can you give an example of a number which is divisible by 6 but not by 2 and 3? Why?
Solution:
No. We can’t give any example, because if any number is divisible by both 2 and 3, then only it is divisible by 6. Otherwise it is not possible.

Check Your Progress (Page No. 30 & 31))

Question 1.
Test whether 6669 is divisible by 9. ,
Solution:
Given number is 6669.
Sum of the digits = 6 + 6 + 6 + 9 = 27 is divisible by 9
If the sum of the digits of a number is divisible by 9 then, it is divisible by 9. ” 27 is divisible by 9. So, 6669 is divisible by 9.

Question 2.
Without actual division, find whether 8989794 is divisible by 9.
Solution:
Given number is 8989794.
Sum of the digits =8+9+8+9+7+9+4=54 – 1
If the sum of the digits of a number is divisible by 9.
Then, it is divisible by 9.
54 is divisible by 9. So, 8989794 is divisible by 9.

Question 3.
Are the numbers 28570, 90875 divisible by 5? Verify by actual division also.
Solution:
a) Given number be 28570.
The numbers with zero or five at ones place are divisible by 5
28570 has zero in its ones place. So, 28570 is divisible by 5.
Actual division :

So, 28570 is completely divisible by 5.

b) Given number is 90875
In 90875, ones place digit is 5. So, 90875 is divisible by 5.
Actual division :

In the given number 90875 the digit in the units place is 5,
‘ So, it is divisible by 5.
So, 90875 is divisible by 5.

Question 4.
Check whether the number 598, 864, 4782 and 8976 are divisible by 4. Use divisibility rule and verify by actual division.
Solution:
a) Given number is 598.
The number formed by the digits in tens and ones places of 598 is 98.
If the number formed by last two digits (Ones and Tens) of the number is divisible
by 4, then the number is divisible by 4.
98 is not divisible by 4. So, 598 is not divisible by 4.

b) Given number is 864.
The number formed by tens and ones places of 864 is 64.
If the number formed by last two digits (ones and tens)
of the number is divisible by 4, then the number is divisible by 4.
64 is divisible by 4. So, 864 is divisible by 4.

c) Given number is 4782.
The number formed by ones and tens places of 4782 is 82.
If the number formed by last two digits (ones and tens) of the number is divisible by 4, then the number is divisible by 4. 82 is not divisible by 4.

d) Given number is 8976.
The number formed by the digits in tens and ones places of 8976 is 76.
If the number formed by last two digits
(Tens and ones) of the number is divisible by 4. Then the number is divisible by 4.
76 is divisible by 4. So, 8976 is divisible by 4.

Question 1.
Fill the blanks and complete the table. (Page No. 32)
Solution:

Lets Explore (Page No.33)

Question 1.
1221 is a polindrome number, which on reversing its digits gives the same number. Thus, every polindrome number with even number of digits is always divisible by 11. Write polindrome number of 6 – digits.
Solution:

There are some polindrome number of 6 – difits.

Check Your Progress (Page No.34)

Question 1.
Find the factors of 60.
Solution:
60 = 1 x 60
60 = 2 x 30
60 = 3 x 20
60 = 4 x 15
60 = 5 x 12
60 = 6 x 10
∴ The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.

Question 2.
Do all the factors of a given number divide the number exactly? Find the factors of 30 and verify by division.
30 = 1 x 30
30 = 3 x 10
30 = 2 x 15
30 = 5 x 6
The factors of 30 are 1, 2, 3, 5, 6,10, 15 and 30.

Yes, the factors of a given numbers are divide the number exactly.

Question 3.
3 is a factor of 15 and 24. Is 3 a factor of their difference also?
Solution:
Difference = 24 – 15 = 9 is the multiple of 3.
Yes, 3 is a factor of difference of 15 and 24.

Let’s Explore (Page No. 35)

Question 1.
What is the smallest prime number?
Solution:
2

Question 2.
What is the smallest composite number?
Solution:
4

Question 3.
What is the smallest odd prime number?
Solution:
3

Question 4.
What is the smallest odd composite number?
Solution:
9

Question 5.
Write 10 odd and 10 even composite numbers.
Solution:
Odd composite numbers are 9, 15, 21, 25, 27, 33, 35, 39, 45, 49.
Even composite numbers are 4, 6, 8, 10, 12, 14, 16, 18, 20, 22.
Except 2, every even number is a composite number.

Let’s Explore (Page No. 36)

Question 1.
Can you guess a prime number which when on reversing its digits, gives another prime number? (Hint a 2 digit prime number)
Solution:
13 and 31; 17 and 71, 37 and 73 79 and 97.

Question 2.
311 is a prime number. Can you find the other two prime numbers just by rearrang-ing the digits?
Solution:
113, 131

Check Your Progress (Page No. 36)

Question 1.
From the following numbers identify different pairs of co-primes. 2, 3,4, 5,6,7, 8, 9 and 10.
Solution:
The numbers which have only 1 as the common factor are called co-primes, (or) Numbers having no common factors, other than 1 are called co-primes.
2,3; 2, 5; 2, 7; 2, 9; 3,4; 3, 5; 3, 7; 3, 8; 3,10; 4,5; 4, 7; 4, 9; 5, 6; 5, 7; 5,8; 5, 9; 6, 7; 8, 9 and 9,10. These are the different pairs of co-primes with 2, 3, 4, 5, 6, 7, 8, 9 and 10.
1) Any two primes always forms a pair of co-primes.
2) Any two consecutive numbers always form a pair of co-primes.
3) Any two primes cilways form a pair of co-primes. .

Question 2.
Write the pairs of twin primes less than 50.
Solution:
Two prime numbers are said to be twin primes, if they differ each other by 2.
Twin primes less than 50 are (3, 5); (5, 7); (11,13); (17, 19); (29, 31) and (41, 43).

(Page No. 36)

Question 1.
Find the HCF of 12, 16 and 28
Solution:

Thus 12 = 2 x 2 x 3
16 = 2 x 2 x 2 x 2
28 = 2 x 2 x 7
The common factor of 12, 16 and 28 ¡s 2 x 2 = 4.
Hence, H.C.F of 12, 16 and 28 is 4.

Let’s Explore (Page No. 40)

What is the HCF of any two
i) Consecutive numbers ?
ii) Consecutive even numbers ?
iii) Consecutive odd numbers? What do you observe? Discuss with your Mends.
Solution:
Consider the two consecutive number are 5, 6 and 9, 10.

We observed that HCF of any two consecutive numbers is always 1.

ii) Consider two consecutive even numbers are 8, 10 and 20, 22.

We observed that HCF of any two consecutive even numbers is always 2.

iii)Consider the consecutive odd numbers are 7, 9 and 13, 15.

We observed that HCF of any two consecutive odd numbers is always 1.

(Page No. 42)

Question 1.
Find LCM of (i) 3, 4 (ii) 10, 11 (iii) 10, 30 (iv) 12, 24 (v) 3, 12 by prime factorization method.
Solution:
i) Given numbers are 3, 4
Factors of 3 = 1 x 3
Factors of 4 = 2 x 2
LCM of 3, 4 = 1 x 3 x 2 x 2 = 12

ii) Given numbers are 10, 11
Factors of 10 = 2 x 5
Factors of 11 = 1 x 11
LCM of 10, 11 = 2 x 5 x 11 = 110

iii) Given numbers are 10, 30
Factors of 10 = 2×5
Factors of 30 = 2x3x5
LCM of 10, 30 = 2 x 3 x 5 = 30

iv) Given numbers are 12, 24
Factors of 12 = 2x2x3 ,
Factors of 24 =. 2 x 2 x 2 x 3
LCM of 12, 24 = 2 x 2 x 2 x 3 = 24

v) Given numbers are 3,12 Factors of 3 = 1×3
Factors of 12 =2 x 2 x 3,
LCM of 3, 12 = 3 x 2 x 2 = 12

(Page No. 43)

Question 1.
What is the LCM and HCF of twin prime numbers ?
Solution:
LCM = Product of the taken twin primes and HCF = 1

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 10 Practical Geometry Ex 10.2 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 10th Lesson Practical Geometry Ex 10.2

Question 1.
Draw a line segment PQ = 5.8 cm and construct its perpendicular bisector using ruler and compasses.
Solution:

Steps of construction :

1. Draw a line segment \(\overline{\mathrm{PQ}}\) = 5.8 cm.
2. Set the compasses as radius with more than half of the length of \(\overline{\mathrm{PQ}}\).
3. With P as centre, draw arcs below and above the line segment.
4. With the same radius and Q as centre draw two arcs above and below the line segment to cut the previous arcs. Name the intersecting points of arcs as X and Y.
5. Join the points X and Y. So, the line I is the perpendicular bisector of PQ.
   Hence l is required perpendicular bisector of PQ which meets at A.

Question 2.
Ravi made a line segment of length 8.6 cm. He constructed a bisector of AB on C. Find the length of AC and BC.

Solution:

As it is a bisector, it divides the line segment into two equal parts.
Each equal part is half of AB (8.6 cm) = \(\frac{\mathrm{AB}}{2}=\frac{8.6}{2}\) = 4.3 cm
∴ AC = BC = 4.3 cm

Question 3.
Using ruler and compasses, draw AB = 6.4 cm. Locate its mid point by geometric construction.
Solution:

1. Draw a line segment \(\overline{\mathrm{PQ}}\) = 6.4 cm
2. Set the compasses as radius with more than half of the length of \(\overline{\mathrm{PQ}}\).
3. With A as centre, draw arcs below and above the line segment.
4. With the same radius and B as centre draw two arcs above and below the line segment to cut the previous arcs. Name the intersecting points of arcs as X and Y.
5. Join the points X and Y. So, the line l is the perpendicular bisector of AB.
   Hence l is the required perpendicular bisector of AB which meets at M.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 10 Practical Geometry Ex 10.1 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 10th Lesson Practical Geometry Ex 10.1

Question 1.
Construct a line segment of length 6.9 cms using ruler and compass.

Solution:
Steps of construction:

1. Draw a line l. Mark a point A on the line l.
2. Place the metal pointer of the compass on the zero mark of the ruler. Open the compass, so that pencil point touches the 6.9 cm mark on the ruler.
3. Place the pointer at A on the line l and draw an arc to cut the line. Mark the point where the arc cuts the line as B
4. On the line l, we got the line segment AB of required length.
   

Question 2.
Construct a line segment of length 4.3 cms using ruler.
Solution:

Steps of construction:

1. Place the ruler on paper and hold it firmly.
2. Mark a point with a sharp edged pencil against 0 cm mark on the ruler. Name the point as P.
3. Mark another point against 3 small divisions just after the 4 cm mark. Name this point as Q.
4. Join points P and Q along the edge of the ruler.
   Therefore, PQ is the required line segment of length 4.3 cm.

Question 3.
Construct a circle with centre M and radius 4 cm.
Solution:

Steps of construction:

1. Mark a point M on the paper.
2. By using compasses take 4 cm as the radius on with the scale.
3. Place the metal point on M and draw a circle from M.
   Hence required circle is constructed with center M and radius 4 cm.

Question 4.
Draw any circle and mark three points A, B and C such that
(i) A is on the circle
(ii) B is in the interior of the circle
(iii) C is in
Solution:

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 4 Integers Unit Exercise Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 4th Lesson Integers Unit Exercise

Question 1.
Write the integers for the following situations.
i) A kite is flying at a height of 225 m in the sky. ( )
ii) A whale is at a depth of 1250 m in the ocean. ( )
iii) The temperature in Sahara desert is 12°C below freezing temperature. ( )
iv) Ravi withdrawn Rs. 3800 from ATM using his debit card. ( )
Answer:
i) 225 m
ii) – 1250 m
iii) – 12°C
iv) -3800

Question 2.
Justify the following statements with an example.
i) A positive integer is always greater than a negative integer.
ii) All positive integers are natural numbers.
iii) Zero is greater than a negative integer.
iv) There exist infinite integers in the number system.
v) All whole numbers are integers.
Answer:
i) A positive integer is always greater than a negative integer:
Consider
a) 3, -5 are two integers
3 > -5
b) – 10, 1 are two integers
1 > -10
∴ A positive integer is always greater than a negative integer.

ii) All positive integers are natural numbers:
Positive integers = 1, 2, 3, …..
Natural numbers = 1, 2, 3, …..
So, all positive integers are natural numbers.

iii) Zero is greater than a negative integer:
On a number line, for a given pair of numbers the number on R.H.S is always greater than the number on L.H.S.
All negative integers lie on the L.H.S. of zero, on a number line.
As such all negative numbers are less than zero or zero is greater than all negative integers.

iv) There exist infinite integers in the number system:
If we write integer on a number line, as the line extends on both sides endlessly so as the integers.
(Or)
For every integer there exists another integer which is 1 more than the given integer. Hence the integers are infinite.

v) All whole numbers are integers:
Whole numbers : 0, 1, 2, 3,……
Integers: ……, -3, -2, -1, 0, 1, 2, 3,…..
So, whole number are part of integers.
∴ All whole numbers are integers.

Question 3.
Represent
i) 3+4
ii) 8+(-3)
iii) -7-2
iv) 6-(5)
v)-5-(-4)
on number line.
Answer:
i) 3 + 4 = +7.

On the number line we first move 3 steps to the right of 0 to reach +3.
Then, we move 4 steps to the right of +3 and reach + 7.

ii) 8 + (-3) = +5.

On the number line we first move 8 steps to the right of 0 to reach +8.
Then, we move 3 steps to the left of +8 and reach +5.

iii) -7 -2 = -9

On the number line we first move 7 steps to the left of 0 to reach -7.
Then we move 2 steps to the left of -7 and reach -9.

iv) 6 – (5) = + 1

On the number line we first move 6 steps to the right of 0 to reach +6.
Then, we move 5 steps to the left of +6 and reach +1.

v) -5 – (-4) = -1

-5 – (-4) = -5 + 4 = -1 (∵ -(-a) = a)
On the number line, we first move 5 steps to the left of 0 to reach -5.
Then, we move 4 steps to the right of -5 and reach -1.

Question 4.
Write all the integers lying between the given numbers.
i) 7 and 12
ii) -5 and -1
iii) -3 and 3
iv) -6 and 0
Answer:
i) 7 and 12
Integers lying between 7 and 12 are 8, 9, 10, ll.

ii) -5 and -1
Integers lying between -5 and -1 are -2, -3 and -4.

iii) -3 and 3
Integers lying between -3 and 3 are -2, -1, 0, 1, 2.

iv) -6 and 0
Integers lying between -6 and 0 are -5, -4, -3, -2, -1.

Question 5.
Arrange the following integers in ascending order and descending order.
-1000, 10, -1, -100, 0, 1000, 1, -10
Answer:
Given numbers -1000, 10, -1, -100, 0, 1000, 1, -10
Ascending order: – 1000, -100, -10, -1, 0, 1, 10, 1000
Descending order: 1000, 10, 1, 0, -1, -10, -100, -1000

Question 6.
Write a real life situation for each of the following integers.
i) -200 m
ii) +42°C
iii) -4800(cr)
iv) -3.0 kg
Answer:
i) -200 m
In the Singareni coal mines workers will go 200 m below the ground level.
ii) +42°C
In summer average temperature of May month is 42°C.
iii) Rs. 4800 (crores)
Central Government sanctioned Rs. 4800(crores) for education in the Annual Budget.
iv) – 3.0 kg
In a Primary School the ground balance of rice = -3 kg

Question 7.
Find:
i) (-603) + (603)
ii) (-5281) +(1825)
iii) (-32) + (-2) + (-20) + (-6)
Answer:
i) (-603) + (603)
Sum of a number and its additive number is 0.
Additive inverse of – 603 is 603.
So, -603 + 603 = 0

ii) (-5281) + (1825)
= – 5281 + 1825 = – 3456

iii) (-32) + (-2) + (-20) + (-6)
= -32 – 2 – 20 – 6 = -60

Question 8.
Find:
i)(-2) – (+1)
ii) (-270) – (-270)
iii) (1000) – (-1000)
Answer:
i) -2 – (+1)
= -2 -1 = -3

ii) – 270 – (-270)
= -270 + 270 [∵ -(-a) = a]
= 0 [-a + a = 0]

iii) 1000 – (-1000)
= 1000 + 1000 [∵ -(-a) = a]
= 2000

Question 9.
In a quiz competition, where negative score for wrong answer is taken,Team A scored +10, -10, 0, -10, 10, -10 and Team B scored 10,10, -10,0,0,10 in 6 rounds successively .Which team wins the competition? How?
Answer:
Score of Team A = (+10), (-10), 0, (-10), 10, (-10)
Total score of Team A = (+10) + (-10) + (0) + (-10) + (10) + (-10)
= +10 – 10 + 0 – 10 + 10 – 10
= +20 – 30 = -10
Score of Team B = 10, 10, -10, 0, 0, 10
Total Score of Team B = (+10) + (+10) + (-10) + 0 + 0 + (+10)
= +10 + 10 – 10 + 10
= + 30 – 10
= + 20
-10 < + 20
Team A < Team B
So, Team B is the winner. Because, Team B got more score than Team A.

Question 10.
An apartment has 10 floors and two cellars for car parking under the basement. A lift is now, at the ground floor. Ravi goes 5 floors up and then 3 floors up, 2 floors down and then 6 floors down and come to lower cellar for taking his car. Count how many floors does Ravi travel all together? Represent the result on a vertical number line.
Answer:

First move:
Ground to 5th floor up = 5
(Can reach 5th floor)
Second move:
5th floor to 3 floors up = 3
(Can reach 8)
Third move:
8th floor to 2 floors down = 2
(Can reach 6th floor)
Fourth move:
6th floor to 6 floors down = 6
(Can reach ground floor)
Final move:
Ground to lower cellar = 2
(Can reach cellar -2)
No. of floors Ravi travelled = 18

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 6 Basic Arithmetic Ex 6.4 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 6th Lesson Basic Arithmetic Ex 6.4

Question 1.
Express each of the following percents as fractions in the simplest form,
a) 15%
b) 35%
c) 50%
d) 75%
Answer:
a) Given percent is 15%
= \(\frac{15}{100}\) = \(\frac{3}{20}\) (fraction form) [∵ To express a percentage as a fraction first drop the symbol % and then divide it by 100.]

b) Given percent is 35%
= \(\frac{35}{100}\) = \(\frac{7}{20}\) (fraction form)

c) Given percent is 50%
= \(\frac{50}{100}\) = \(\frac{1}{2}\) (fraction form)

d) Given percent is 75%
= \(\frac{75}{100}\) = \(\frac{3}{4}\) (fraction form)

Question 2.
Express each of the following fractions as percents.
a) \(\frac{15}{2}\)
b) 8\(\frac{1}{4}\)
c) 5\(\frac{3}{4}\)
d) 3\(\frac{1}{3}\)
Answer:
a) Given number \(\frac{15}{2}\) is in fraction form.
To convert the fraction into percent we have to multiply the fraction by 100%
\(\frac{15}{2}\) = \(\frac{15}{2}\) × 100 = 15 × 50 = 750% (percent form)

b) Given number 8\(\frac{1}{4}\) is in fraction form.
To convert the fraction into percent we have to multiply the fraction by 100%
8\(\frac{1}{4}\) = \(\frac{33}{4}\) = \(\frac{33}{4}\) × 100 = 33 × 25 = 825%,(percent form).

c) Given number 5\(\frac{3}{4}\) is in fraction form.
To convert the fraction into percent we have to multiply the fraction by 100 and assign the percentage symbol %
5\(\frac{3}{4}\) = \(\frac{23}{4}\) × 100 = 23 × 25 = 575% (percent form)

d) Given number is 3\(\frac{1}{3}\) in fraction form.
To convert the fraction into percent we have to multiply the fraction by 100%
3\(\frac{1}{3}\) = \(\frac{10}{3}\) × 100 = \(\frac{1000}{3}\) = 333\(\frac{1}{3}\) % (percent form)

Question 3.
Express each of the following ratios as percents.
(a) 3 : 5 (b) 5 : 8 (c) 2.5 : 55 (d) 4 : 36
Answer:
a) 3 : 5
Given ratio is 3 : 5.
3 : 5 = \(\frac{3}{5}\) (fraction form)
To convert the fraction into percent we have to multiply the fraction by 100%
\(\frac{3}{5}\) = \(\frac{3}{5}\) × 100 = 60% (percent form)

b) 5 : 8
Given ratio is 5 : 8
5 : 8 = \(\frac{5}{8}\) (fraction form)
To convert the fraction into percent we have to multiply the fraction by 100%
\(\frac{3}{5}\) = \(\frac{3}{5}\) × 100 = 62 \(\frac{1}{2}\) % (percent form)

c) 2.5 : 55
Given ratio is 2.5 : 55
2.5 : 55 = \(\frac{2.5}{55}\)
To convert the fraction into percent we have to multiply the fraction by 100%

d) 4 : 3 6
Given ratio is 4 : 36
4 : 36 = \(\frac{4}{36}\) (fraction form)
To convert the fraction into percent we have to multiply the fraction by 100%
\(\frac{4}{36}\) = \(\frac{4}{36}\) × 100 = \(\frac{100}{9}\) = 11 \(\frac{1}{9}\) % (percent form)

Question 4.
Express each of the following percents as ratios in the simplest form.
(a) 12% (b) 25% (c) 45% (d) 84%
Answer:
a) Given percent is 12%
= \(\frac{12}{100}\) = \(\frac{3}{25}\) (fraction form)
= 3 : 25 (ratio form)

b) Given percent is 25%
= \(\frac{25}{100}\) = \(\frac{1}{4}\) (fraction form)
= 1 : 4 (ratio form)

c) Given percent is 45%
= \(\frac{45}{100}\) = \(\frac{9}{20}\) (fraction form)
= 9 : 20 (ratio form)

d) Given percent is 84%
= \(\frac{84}{100}\) = \(\frac{21}{25}\) (fraction form)
= 21 : 25 (ratio form)

Question 5.
Express each of the following percents as decimals,
(a) 1% (b) 6% (c) 19% (d) 67%
Answer:
a) Given percent is 1%
= 1% = \(\frac{1}{100}\) (fraction form)
= 0.01 (decimal form)

b) Given percent is 6%
= 6% = \(\frac{6}{100}\) = \(\frac{3}{50}\) (fraction form)
= 0.06 (decimal form)

c) Given percent is 19%
= 19% = \(\frac{19}{100}\) (fraction form)
= 0.19 (decimal form)

d) Given percent is 67%
= 67% = \(\frac{67}{100}\)
= 0.67 (decimal form)

Question 6.
Express each of the following decimals as percent.
(a) 0.04 (b) 0.52 (c) 0.125 (d) 0.0006
Answer:
a) Given decimal number is 0.04.
Convert this into fraction

b) Given decimal number is 0.52.
Convert this into fraction

c) Given decimal number is 0.125.
Convert this into fraction

d) Given decimal number is 0.0006.
Convert this into fraction

Question 7.
Find the number, which is 12\(\frac{1}{2}\)% of 75.
Answer:
Given 12\(\frac{1}{2}\)% of 75
We know that x% of y = \(\frac{x}{100}\) × y

(OR)

Question 8.
Pavani secured 85% marks in mathematics paper. If maximum marks in the paper are 80, find the marks secured by her in that paper.
Answer:
Given maximum marks of the paper = 80
Percentage of marks secured by Pavani = 85%
Marks secured by Pavani

∴ Marks secured by Pavani = 68

Question 9.
Siva spends 78% of his monthly income. If he saves Rs. 7,700/- per month, what is his monthly income?
Answer:
Let Siva’s monthly income = Rs. x
Percentage of income spent = 78%
Percentage of income saved = 100% – percentage of spent income
= 100% – 78% = 22%
Saved income = 22% of monthly income = 7700
= 22% of x = 7700
⇒ \(\frac{1}{2}\) × x = 7700
⇒ x = \(\frac{7700×100}{2}\)
⇒ x = Rs. 35000
∴ Siva’s monthly income = Rs. 35000

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 2 Whole Numbers InText Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 2nd Lesson Whole Numbers InText Questions

Question 1.
Fill the following table with the successor and predecessor of the numbers provided. (Page No. 15)

Solution:

Discuss

Question 1.
Which number has no successor ? (Page No. 15)
Answer:
Each and every number has a successor.

Question 2.
Which number has no predecessor? (Page No. 15)
Answer:
Zero (0) has no predecessor in the set of whole numbers.

Check Your Progress (Page No. 16)

Question 1.
Which is the smallest whole number?
Answer:
Zero(0) is the smallest whole number.

Let’s Think (Page No. 16)

Question 1.
Are all natural numbers whole numbers? .
Solution:
Yes. All the natural numbers are whole numbers.

Question 2.
Are all whole numbers natural numbers?
Solution:
No. All the whole numbers are not natural numbers.

Let’s Do (Page No. 17)

Show these on number line:

i) 5 + 3
Solution:

Draw the number line starting with ‘O’.
Start from 5, make 3 jumps to the right of 5 on the number line. We reach 8.
So, 5 + 3 = 8

ii) 5 – 3
Solution:

Draw the number line starting with zero (0).
Start from 5, make 3 jumps to the left of 5 on the number line, we reach 2.
So, 5 – 3 = 2

iii) 3 + 5
Solution:

Draw the number line starting with zero (0).
Start from 3, we make 5 jumps to the right of 3 on the number line. We reach 8. So, 3 + 5 = 8

iv) 10 + 1
Solution:

Draw the number line which starts with zero (0).
Start from 10, make 1 jump to the right of 10 on the number line. We reach’ll. So, 10 + 1 = 11

v) 8 – 5
Solution:

Draw the number line which starts with zero (0).
Start from 8, we make 5 jumps to the left of 8 on the number line. We reach 3. So, 8-5 = 3

Let’s Explore (Page No. 17)

Find the following by using number line:

Question 1.
Which number should be deducted from 8 to get 5?
Solution:

Draw the number line, which starts with zero (0).
To get 5 from 8. We have to start from 8. We make 3 jumps to the left of 8 on the number line, we reach 5. As we are moving on left side we have minus sign.
So, 8 – 3 = 5
Therefore to get 5 we deduct 3 from 8.

Question 2.
Which number should be deducted from 6 to get 1?
Solution:

Draw the number line starting with zero (0).
To get 1 from 6 we have to start from 6.
We make 5 jumps to the left of 6 on the number line. We reach 1. As we have moved to left side, we have 6-5 = 1 Threfore to get 1 we deduct 5 from 6.

Question 3.
Which number should be added to 6 to get 8?
Solution:

Draw the number line starts with zero (0).
To get 8 from 6, we have to start from 6.
We make 2 jumps to the right of 6 on the number line to reach 8; So, 6 + 2 = 8 ‘
Therefore to get 8 we add 2 to 6.

Question 4.
How many 6 are needed to get 30?
Solution:

Draw the number line starts with zero (0).
Start from 0 and make 6 jumps to the right of the zero as the number line. Now, treat 6 jumps as one step. So, to reach 30, we make 5 steps.
So, 5 × 6 = 30

Question
Raju and Gayatri together made a number line and played a game on it.

Raju asked “Gayatri, where will you reach if you jump thrice, taking leaps of 3, 8 and 5”? Gayatri said the first leap will take me to 3 and then from there I will reach 11 in the second step and another five steps from there to 16′.
Draw Gayatri’s steps and verify her answers.
Play this game using addition and subtraction on this number line with your friend.
Solution:

Lets Think (Page No. 19)

Question 1.
Are the whole numbers closed under subtraction?
Solution:
8 – 5 = 3, a whole number
5 – 8 = -3 is not a whole number
Therefore whole numbers are not closed under subtraction.

Question 2.
Are the whole numbers closed under division?
Solution:
6 ÷ 3 = 2, a whole number
3 ÷ 6 = \(\frac{3}{6}\), not a whole number 6
Therefore, whole numbers are not closed under division.

Check Your Progress (Page No. 19)

Question 1.
Find out 12 ÷ 3 and 4 ÷ 7.
Solution:
12 ÷ 3
12 is divided by 3 means, we subtract 3 from 12 repeatedly till, we get zero i.e., we subtract 3 from 12 again and again till, we get zero.
12 – 3 = 9 once
9-3 = 6 twice
6-3 = 3 thrice
3-3 = 0 four times
So, 12-3 = 4

42 ÷ 7
42 is divided by 7 means, we subtract 7 from 42 repeatedly, i.e., we subtract 7 from 42 again and again till, we get zero a number less than 7.
42 – 7 = 35 once
35 – 7 = 28 twice
28 – 7 = 21 thrice
21-7 = 14 four times
14-7 = 7 five times
7 – 7 = 0 six times
i.e., we can subtract 7 from 42 for 6 times successively. ,
So, 42 ÷ 7 = 6.

Question 2.
What would 6 4-0 and 9 4- 0 be equal to?
Solution:
6 ÷ 0
6 is divided by 0 means, we subtract 0 from 6 repeatedly i.e., we subtract 0 from 6 again and agian from 6.
6 – 0 = 6 once
6 – 0 = 6 twice
6 – 0 = 6 thrice and ……………….
If we subtract zero from 6 successively we can’t get zero at any end.
So, 6 ÷ 0 is not a number that we can reach.
So, division of a whole number by 0 does not give a known number as answer, so it is not defined.
Similarly 9 ÷ 0 is not defined.
So, we can’t say whether they are equal or not.

Let’s Explore (Page No. 20)

Take few examples and check whether

a) Subtraction is commutative over whole numbers or not?
Solution:
Let’s take two whole numbers 4 and 6
6 – 4 = 2 and (4 – 6) = – 2 is not a whole number.
So, 6 – 4 ≠ 4 – 6.
Therefore we say that subtraction is not commutative over the whole numbers.

b) Division is commutative over whole numbers or not ?
Solution:
Let’s take two whole numbers 8 and 2
8 ÷ 2 = 4 and (2 ÷ 8) = \(\frac{1}{4}\) is not a whole number.
So, 8 ÷ 2 ≠ 2 ÷ 8
Therefore, we say that division is not commutative over the whole numbers.

Check Your Progress (Page No. 22)

Verify the following:
i) (5 × 6) × 2 = 5 × (6 × 2)
Solution:
L.H.S : (5 × 6) × 2 = 30 × 2 = 60
R.H.S : 5 × (6 × 2) = 5 × 12 = 60
∴ L.H.S = R.H.S
So (5 × 6) × 2 = 5 × (6 × 2)
∴ Multiplication of whole numbers is associative.

ii) (3 × 7) × 5 = 3 × ( 7 × 5 )
Solution:
L.H.S : (3 × 7) × 5 = 21 × 5 = 105
R.H.S : 3 × (7 × 5) = 3 × 35 = 105
∴ (3 × 7) × 5 = 3 × (7 × 5)
∴ Multiplication of whole numbers is associative.

Check Your Progress (Page No. 22)

Use the commutative and associative properties to simplify the following:

i) 319 + 69 + 81
Solution:
319 + 69 + 81 = 319 +(81 + 69) (Commutative property)
= (319 + 81) + 69 (Associative property)
= 400 + 69 = 469

ii) 431 + 37 + 69 + 63
Solution:
431 + 37 + 69 + 63
= 431 + (37 + 69) + 63
= 431 + (69 + 37) + 63 (Commutative property)
= (431 + 69) + (37 + 63) (Associative property)
=(431 + 69) + 100
= 500+ 100 = 600

iii) 2 × (71 × 5)
Solution:
2 × (71 × 5) = 2 × (5 × 71) (Commutative property)
= (2 × 5) × 71 (Associative property)
= 10 × 71
= 710

iv) 50 × 17 × 2
Solution:
50 × (17 × 2) = 50 × (2 × 17) (Commutative property)
= (50 × 2) × 17 (Associative property)
= 100 × 17 = 1700

Let’s Think (Page No. 22)

a) Is(8 ÷ 2) ÷ 4 = 8 ÷ (2 ÷ 4)?
Is there any associative property for division ?
Check if this property holds for subtraction of whole numbers too.
Solution:
a) (8 ÷ 2) ÷ 4 = (8 ÷ 2) ÷ 4
= 4 ÷ 4 = 1
8 ÷ (2 ÷4) = 8 ÷ \(\left(\frac{2}{4}\right)\)
= 8 – \(\frac{4}{2}\) = 8 × 2 = 16
So, (8 ÷ 2) ÷ 4 ≠ 8 ÷ (2 ÷ 4) .
Therefore, associative property does not holds in division.

b) Is (8 – 2) – 4 = 8 – (2 – 4) ?
Solution:
(8 – 2) – 4 = 6 – 4 .
= 2
8 – ( 2 – 4 ) = 8 – ( – 2)
= 8 + 2 = 10
So, (8 – 2) – 4 ≠ 8 – (2 – 4)
Therefore, associative property does not holds in subtraction,
i. e., whole numbers are not associative w.r.t. subtraction.
They are not equal.
So whole numbers do not satisfy Associative property w.r.t. Subtraction & Division.

Find using distributive property : (Pg. No. 22)
i) 2 × (5 + 6)
ii) 5 × (7 + 8)
Solution:
i) 2 × (5 + 6)
Given, 2 × (5 + 6) = (2 × 5) + (2 × 6)
By using distributive property of multiplication over addition.
2 × 11 = 10 + 12
22 = 22
L.H.S. = R.H.S

ii) 5 × (7 + 8)
Given, 5 × (7 + 8) = (5 × 7) + (5 × 8)
By using distributive property of multiplication over addition.
5 × 15 = 35 + 40
75 = 75
L.H.S = R.HS

iii) 19 × 7 + 19 × 3
Given, (19 × 7) + (19 × 3) = 19 × (7 + 3)
By using distributive property of multiplication over addition.
133 + 57 = 19 × 10
190 = 190
L.H.S = R.H.S

Find : i) 25 × 78 ii) 17 × 26 iii) 49 × 68 + 32 × 49 using distributive property. (Page. No. 22)
Solution:
i) 25 × 78
Given, 25 × 78 = 25 × (80 – 2)
By using distributive property of multiplication over subtraction.
= (25 × 80) – (25 × 2)
= 2000 – 50 = 1950
∴ 25 × 78 = 1950

ii) 17 × 26
Given, 17 × 26 = (10 + 7) × 26
By using distributive property of multiplication over addition.
= (10 × 26) + (7 × 26)
= 260 + 182 = 442
7.17 × 26 = 442

(OR)

= 17 × (30 – 4)
By using distributive property of multiplication over subtraction.
= (17 × 30) – (17 × 4)
= 510 – 68 = 442

iii) 49 × 68 + 32 × 49
Given, 49 × 68 + 32 × 49 = (49 × 68) + (49 × 32)
By using distributive property of multiplication over addition.
= 49 × (68 + 32) .
= 49 × 100
∴ (49 × 68) + (32 × 49) = 4900

Let’s Explore (Page. No. 25)

Question 1.
Which numbers can be shown as a line only?
Solution:
Two or more than two numbers can be shown as a line.
i.e., 2, 3, 4, 5, 6,

Question 2.
Which numbers can be shown as rectangles?
Solution:
6, 8, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 26, 27,.

Question 3.
Which numbers can be shown as squares?
Solution:
4, 9, 16, 25.

Question 4.
Which numbers can be shown as triangles?
Solution:
3, 6, 10, 15, 21, :
Note : Starting from 3; +3, +4, +5, +6, …………………. are all triangular numbers.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 4 Integers Ex 4.4 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 4th Lesson Integers Ex 4.4

Question 1.
Find:
i) 40 – (22)
ii) 84 – (98)
iii) (-16) + (-17)
iv) (-20) – (13)
v) (38) – (-6)
vi) (-17) – (-36)
Answer:
i) 40 – (22) = +40 – 22
= +(18 + 22)-22
= 18 +(22-22)
= 18 + 0
∴ 40-(22) = + 18

ii) 84 – (98) = 84 – 98
= + 84 – 84 – 14
= (84 – 84) – 14
= 0 – 14
∴ 84 – (98) = – 14

iii) (-16) + (-17) = -16 – 17 = – 33
∴ (-16) + (-17) = -33

iv) (-20) – (13) = – 20 – 13
= -33
∴ (-20) – (13) = – 33

v) 38 – (-6) = 38 + 6
We know – (-a) = a = + 44
∴ 38 – (-6) = + 44

vi) (-17) – (-36) = -17 + 36
We know – (- a) = a
= -17 + 17 + 19
= (-17+17) + 19
= + 19
∴ (-17) – (-36) = + 19

Question 2.
Fill in the boxes with >, < or = sign:
(i) (-4) + (-5) (-5) – (-4)
(ii) (-16) – (-23) (-6) + (-12)
(iii) 44 – (-10) 47 +(-3)
Answer:
(i) (-4) + (-5) (-5)- (-4)
-4-5  -5 + 4
-9 -1

(ii) (-16) – (-23) (-6) + (-12)
-16 + 23 -6-12  [∵ -(-a) = a]
-16 + 16 + 7 -18
+7 -18

(iii) 44 – (-10) 47 + (-3)
44+10 47-3.
54 44 + 3 – 3
54 44

Question 3.
Fill in the blanks:
i) (-13) + ———– = 0
ii) (-16) + 16 = ———–
iii) (-5) + ———– = -14
iv) ———– + (2 – 16) = – 22
Answer:
i) (-13) + ———– = 0
We know, additive inverse of a is -a (or) – a is a.
Additive inverse of -13 is 13. So, -13 + 13 = 0

ii) (-16) + 16 = ———–
We know, sum of a number and its additive inverse is 0.
i.e., (-a) + a = 0
So, (-16) + (16) = 0

iii) (-5) + ———– = -14
-5 + (-9) = -14

iv) ———– + (2 – 16) = – 22
———– + (-14) = -22
– 8 + (-14) = – 22

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 4 Integers Ex 4.3 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 4th Lesson Integers Ex 4.3

Question 1.
Add the following integers using number line.
i) 7 + (-6)
ii) (-8) + (-2)
iii) (-6) + (-5) + (+2)
Answer:
i) 7 + (-6)

On the number line, we first move 7 steps to the right of 0 to reach +7.
Then, we move 6 steps to the left of +7 and reach + 1.
So, 7 + (-6) = 1

ii) (-8) + (-2)

On the number line, we first move 8 steps to the left of 0 to reach -8.
Then, we move 2 steps to the left of -8 and reach -10.
So,(-8) + (-2) = -10

iii) (-6) + (-5) + (+2)

On the number line, we first move 6 steps to the left of 0 to reach -6.
We move 5 steps to the left of -6 and reach -11.
Then, we move 2 steps to the right of -11 and reach -9.
So, (-6) + (-5) + (+2) = -9

Question 2.
Add without using number line.
(i) 10 + (-3)
(ii) 10 + (+16)
(iii) (-8) + (+8)
Answer:
i) 10 + (-3)
10 + (-3) = 7 + 3 + (-3) = 7 + (3 + (-3))
= 7 + 3 – 3 = 7 + 0
∴ 10 + (-3) = +7

ii) -10 + (+16)
-10 + (+16)
= -10 + 10 + 6
= (-10 + 10) + 6
= 0 + 6
∴ -10 + (+16) = + 6

iii) (-8) + (+ 8)
-8 + (+8) = -8 + 8 = 0
∴ -8 + (+8) = 0

Question 3.
Find the sum of i) 120 and -274 ii) -68 and 28
Answer:
i) 120 and-274
Method -1: Sum = + 120 + (-274)
= + 120 + (- 120 – 154)
= + 120 – 120 – 154
∴ 120 + (-274) = -154

Method – II:
As the given numbers have opposite sign, we subtract one from other

As 274 is having negative (-) sign, the answer is – 154.

ii) -68 and 28
Sum = – 68 + (28)
= – 40 – 28 + 28
∴ – 68 + 28 = – 40

Question 4.
Simplify:
i) (-6) + (-10) + 5 + 17
ii) 30 + (-30) + (-60) + (-18)
Answer:
i) (-6) + (-10) + 5 + 17
– 6 – 10 + 5 + 17 = -16 + 22
= -16 + 16 + 6
= + 6
∴ (-6) + (-10) + 5 + 17 = + 6

ii) 30 + (-30) + (-60) + (-18)
= 30 + (-30 -60 -18)
= 30 + (-108)
= 30 – 108 = – 78
∴ 30 + (-30) + (-60) + (-18) = -78

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 6 Basic Arithmetic Ex 6.3 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 6th Lesson Basic Arithmetic Ex 6.3

Question 1.
If the cost of 3 apples is Rs. 60/-, then find the cost of 7 apples.
Answer:
Cost of 3 apples = Rs. 60
Cost of 1 apple = \(\frac{60}{3}\) = Rs. 20
∴ Cost of 7 apples = 7 × Rs. 20 = Rs. 140

Question 2.
Uma bought 8 books for a total of ? 120. How much would she pay for just 5 books?
Answer:
Cost of 8 books = Rs. 120
Cost of 1 book = \(\frac{120}{8}\) = Rs. 15
∴ Cost of 5 books = 5 × 15 = Rs. 75

Question 3.
The cost of 5 fans is Rs. 11,000/-. Find the number of funs that can be purchased for Rs. 4,400/-.
Answer:
Cost of 5 fans = Rs. 11000
Cost of 1 fan = \(\frac{11000}{5}\) = Rs. 2200
Number of fans can be purchased for Rs. 4400 = 4400 ÷ cost of 1 fan = \(\frac{4400}{2200}\) = 2

Question 4.
A car is moving at a constant speed covers a distance of 180 km in 3 hours. Find the time taken by the car to cover a distance of 420 km at the same speed.
Answer:
Distance covered = 180 km
Time taken = 3 Hrs.
Distance to be covered = 420 km
Time required = ? = x (say)
Since the car is moving at a constant speed, we have
180 : 3 is as to 420 : x
180 : 3 :: 420 : x
Its a proportion.
So, product of extremes = Product of means
180 × x = 3 × 420

∴ Time required = 7 Hrs.
(OR)
Distance covered by a car in 3 hours = 180 km
Distance covered by a car in 1 hour = 180 ÷ 3
Time taken to cover 60 km distance = \(\frac{180}{3}\) = 60 km
Time taken to cover 420 km distance = 420 ÷ 60 = \(\frac{420}{60}\) = 7 hours

Question 5.
A truck requires 108 litres of diesel for covering a distance of 594 km. How much diesel will be required by the truck to cover a distance of 1650 km?
Answer:
108 : 594 :: x : 1650
So, 108 × 1650 = x × 594
∴ x = \(\frac{108 \times 1650}{\hline 594}\) = 300 litres
(OR)
Distance covered by truck with 108 litres diesel = 594 km
Distance covered by truck with 1 litre of diesel = \(\frac{594}{108}\) km
Diesel required to cover 1650 km distance = 1650 ÷ \(\frac{594}{108}\) = 1650 × \(\frac{108}{594}\)
Diesel required to cover 1650 km distance = 300 litres.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 4 Integers Ex 4.2 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 4th Lesson Integers Ex 4.2

Question 1.
Put appropriate symbol > or < in the boxes given.
i) -1 0
ii) -3 -7
iii) -10  +10
Answer:
i) -1 < 0
ii) -3 > -7
iii) -10 < +10

Question 2.
Write the following integers in increasing and decreasing order:
i) -7, 5, -3
ii) -1, 3, 0
iii) 1, 3, -6
iv) -5, – 3, -1
Answer:

Question 3.
Write True or False.
i) Zero is on the right of -3 ( )
ii) -12 and +12 represent on the number line the same integer ( )
iii) Every positive integer is greater than zero ( )
iv) (-100) > (+100) ( )
Answer:
i) True
ii) False
iii) True
iv) False

Question 4.
Find all integers which lie between the given two integers. Represent them on number line:
i) -1 and 1
ii) -5 and 0
iii) -6 and -8
iv) 0 and -3
Answer:
i) Given integers -1 and +1

Integers between -1 and 1 is 0.

ii) Given integers -5 and 0

Integers between -5 and 0 are -4, -3, -2, -1.

iii) Given, integers -6 and -8

Integers between -6 and -8 is -7.

iv) Given integers 0 and -3

Integers between 0 and -3 are -1, -2.

Question 5.
The temperature recorded in Shimla is -4°C and in Kufri is -6°C on the same day. Which place is colder on that day? Why?
Answer:
Given temperatures of Shimla and Kufri are -4°C and -6°C.
We know that -6°C < – 4°C
Therefore, temperature in Kufri is colder than Shimla.