Class 6

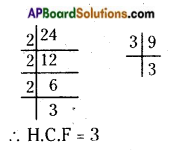
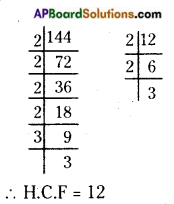
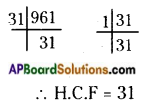
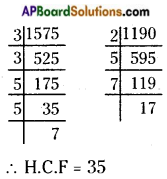
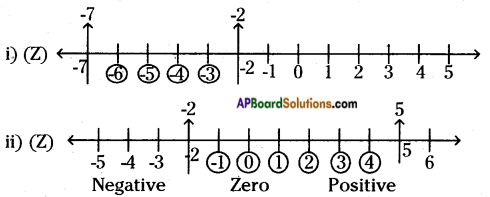
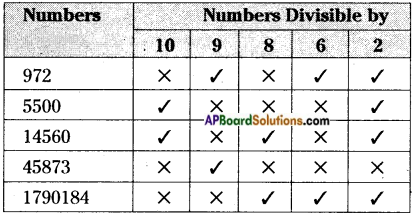
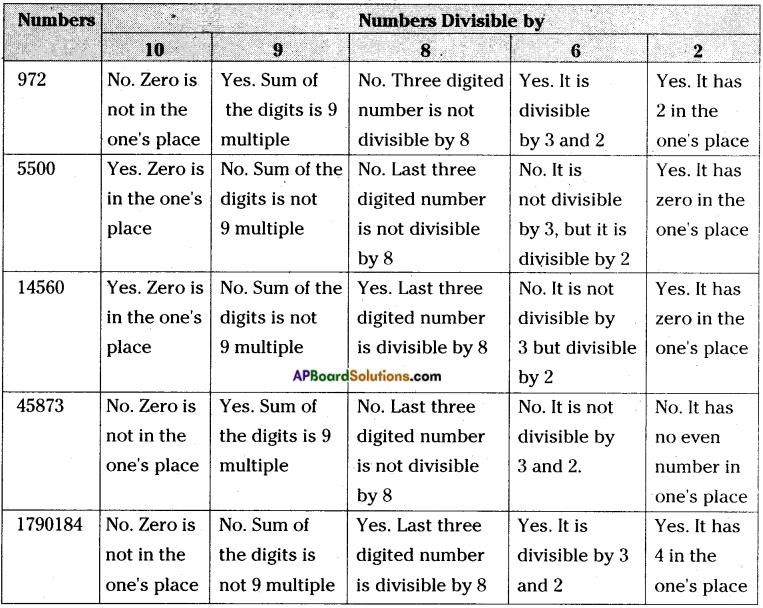
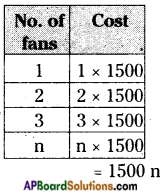AP State Syllabus AP Board 6th Class Maths Solutions Chapter 1 Numbers All Around us InText Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 1st Lesson Numbers All Around us InText Questions

Write the numbers in expanded form. (Page No. 5)

Question 1.
96,08,54,039
Solution:
96,08,54,039 = 9 × 10,00,00,000 + 6 × 1,00,00,000 + 8 × 10,00,000 + 5 × 10,000 + 4 × 1000 + 3 × 10 + 9 × 1
Ninety six crores eight lakhs fifty four thousand and thirty nine.

Question 2.
857,90,00,756
Solution:
857,90,00,756 = 8 × 100,00,00,000 + 5 × 10,00,00,000 + 7 × 1,00,00,000 + 9 × 10,00,000 + 7 × 100 + 5 × 10 + 6 × 1
Eight hundred fifty seven crores ninety lakhs seven hundred and fifty six.

1 Crore = 10 Ten Lakhs
= 100 Lakhs
= 1000 Ten Thousands
= 10,000 Thousands
= 1,00,000 Hundreds
= 10,00,000 Tens
= 1,00,00,000 Unit’s

Check Your Progress (Page No. 6)

Question 1.
Write 10 crores and 100 crores as in the above table.
Solution:
Ten crores = 10 One crores
= 100 Ten lakhs
= 1000 Lakhs
= ,10,000 Ten thousands
= 1,00,000 Thousands
= 10,00,000 Hundreds
= 1,00,00,000 Tens
= 10,00,00,000 Units

Hundred crores = 100 One crores
= 10 Ten crores
= 10,000 Lakhs
= 1.0. 000 Ten thousands
= 10.0. 000 Thousands
= 1.0. 00.000 Hundreds
= 10.0. 00.000 Tens
= 100.0. 00.000 Units

Check Your Progress (Page No. 8)

Question 1.
Write remaining numbers of the above table in the International System.
Solution:

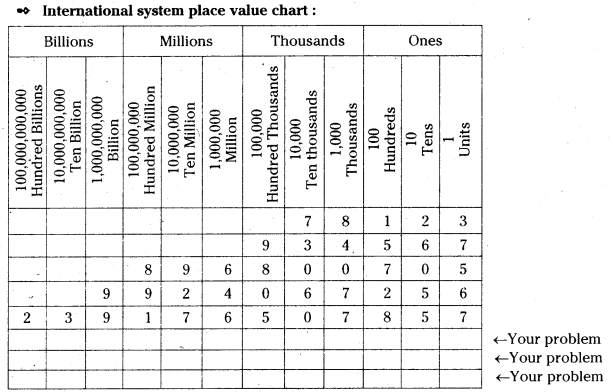
Question 2.
Fill the boxes in the table with your own numbers and write in words in the International system.
Solution:
a) 896800705

Put comma for each period 896,800,705 in International System.
In expanded form :
= 8 ×x 1,000,000,000 + 9 × 10,000,000 + 6 × 1,000,000 + 8 × 100,000 + 7 × 100 + 5 × 1

In word form :
Eight hundred ninety six millions eight hundred thousand seven hundred and five.

b) 239176507857
Put comma for each period 239,176,507,857 in International System.
In expanded form :
= 2 × 100,000,000,000 + 3 × 10,000,000,000 + 9 × 1,000,000,000 + 1 × 100,000,000 + 7 × 10,000,000 + 6 × 1,000,000 + 5 × 100,000 + 7 × 1,000 + 8 × 100 + 5 × 10 + 7 × 1
In word form :
Two hundred thirty nine billion one seventy six million five hundred seven thousand eight hundred and fifty seven.

c) 452069258932
Put comma for each period 452,069,258,932
In expanded form :
= 4 × 100,000,000,000 + 5 × 10,000,000,000 + 2 × 1,000,000,000 + 6 × 10,000,000 + 9 × 1,000,000 + 2 × 100,000 + 5 × 10,000 + 8 × 1,000 + 9 × 100 + 3 × 10 + 2 × 1
In word form :
Four hundred fifty two billion sixty nine million two hundred fifty eight thousand nine hundred and thirty two.

d) 839241367054
Put comma for each period 839,241,367,054
In expanded form :
8 × 100,000,000,000 + 3 × 10,000,000,000 + 9 × 1,000,000,000 + 2 × 100,000,000 + 4 × 10,000,000 + 1 × 1,000,000 + 3 × 100,000 + 6 × 10,000 + 7 × 1.000 + 5 × 10 + 4 × 1
In word form :
Eight hundred thirty nine billion two hundred forty one million three hundred sixty seven thousand and fifty four.

e) 342056743298
Put comma for each period 342,056,743,298
In expanded form :
3 × 100,000,000,000 + 4 × 10,000,000,000 + 2 × 1,000,000,000 + 5 × 10,000,000 + 6 × 1,000,000 + 7 × 100,000 + 4 × 10,000 + 3 × 1,000 + 2 × 100 + 9 × 10 + 8 × 1
In word form :
Three hundred forty two billion fifty six million seven hundred forty three thousand two hundred and ninety eight.

Check Your Progress (Page No.12)

Question 1.
Round off each to the nearest ten, hundred and thousands.
(1) 56,789 (2) 86,289 (3) 4,56,726 (4) 5,62,724
Solution:

Let’s Explore (Page No.12)

Question 1.
Discuss with your friends about rounding off numbers. Consider the population of A.P., Telangana and India in 2011. Round off the numbers to the nearest lakhs.
Solution:

Estimate the sum by rounding and verify the result. (Page No.12)

Question 1. 8756 + 723
Solution:
Given 8756 + 723
First estimate by rounding = 8800 + 700 = 9500

Thus sum is 9,479.
Think
9479 is close to the estimate of 9500.

Question 2.
56723 + 4567 + 72 + 5
Solution:
Given 56723 + 4567 + 72 + 5
First estimate by rounding = 56720 + 4570 + 70 + 10 = 61370

The sum is 61,367.
Think
61367 is close to the estimate of 61370.

Question 3.
656724 + 8567
Solution:
Given 656724 + 8567
First estimate by rounding = 657000 + 9000 = 666000

The sum is 6,65,291.

Think
665291 is close to the estimate of 666000.

Question 4.
60756 + 2562 + 72
Solution:
Given 60756 + 2562 + 72
First estimate by rounding = 60760 + 2560 + 70 = 63390

The sum is 63,390.
Think
63390 is equal to the estimate of 63390.

Estimate the difference by rounding and verify the result.Pg. No. 13)

Question 1.
7023 – 856
Solution:
Given, 7023 – 856
First estimate by rounding = 7000 – 900 = 6100

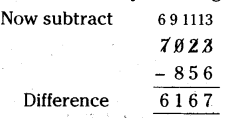
Think
6167 is close to the estimate of 6100

Question 2.
9563 – 2847
Solution:
Given, 9563 – 2847
First estimate by rounding = 10000 – 3000 = 7000

Think
6716 is close to the estimate of 7000

Question 3.
52007 – 6756
Solution:
Given, 52007 – 6756
First estimate by rounding = 52000 – 7000 = 45000

Think
45251 is close to the estimate of 45000

Question 4.
95625 – 4235
Solution:
Given, 95625 – 4235
First estimate by rounding = 95600 – 4200 = 91400 .

Think
91390 is close to the estimate of 91400.

Estimate the product by rounding and verify the result.

Question 1.
63 × 85
Solution:
Given, 63 × 85
First estimate by rounding = 60 × 90 = 5400,
Rounding the result to hundreds = 5400

Think
5355 is close to the estimate of 5400.

Question 2.
636 × 78
Solution:
Given, 636 × 78
First estimate by rounding = 640 × 80 = 51200
Rounding the result to hundreds = 51200

Think
49608 is close to the estimate of 51200.

Question 3.
506 × 85
Solution:
Given, 506 × 85
First estimate by rounding = 500 × 90 = 45000

Think
43010 is close to the estimate of 45000.

Question 4.
709 × 98
Solution:
Given, 709 × 98
First estimate by rounding = 700 × 100 = 70000

Think
69482 is close to the estimate of 70000.

Estimate the quotient by rounding and verify the result.

Question 1.
936 ÷ 7
Solution:
Given, 936 ÷ 7
Divide 936 ÷ 7
First estimate by rounding 1000 ÷ 10 = 100

Think
133 is close to the estimate of 100.

Question 2.
956 ÷ 17
Solution:
Given, 956 ÷ 17
Divide 956 ÷ 17
First estimate by rounding 1000 – 20 = 50

Think
56 is close to the estimate of 50.

Question 3.
859 ÷ 23
Given, 859 ÷ 23
Divide 859 ÷ 23
First estimate by rounding 860 ÷ 20 = 43

Think
37 is close to the estimate of 43.

Question 4.
708 ÷ 32
Given, 708 ÷ 32
Divide 708 ÷ 32
First estimate by rounding 710 ÷ 30 = 23

Think
22 is close to the estimate of 23.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 6 Basic Arithmetic Ex 6.1 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 6th Lesson Basic Arithmetic Ex 6.1

Question 1.
Express the following in the terms of ratios.
i) The length of a rectangle is 5 times to its breadth.
ii) For preparing coffee, 2 cups of water require to 1 cup of milk.
Answer:
i) Let the breadth of rectangle = x = 1 part
length of rectangle = 5x = 5 parts
Ratio = length : breadth = 5x : x = \(\frac{5x}{x}\) = \(\frac{5}{1}\) = 5 : 1

ii) To prepare coffee,
Required cups of water = 2
Required cups of milk = 1
Ratio = water : milk = 2 : 1

Question 2.
Express the following in the simplest form.
i) 24 : 9
ii) 144 : 12
iii) 961 : 31
iv) 1575 : 1190
Answer:
i) 24 : 9
Given ratio is 24 : 9
To write the given ratio in the simplest form.
First find the HCF of two terms.

HCF of 24 and 9 is 3.
Then, divide each term by their HCF.
Simplest form of the ratio = 24 ÷ 3 : 9 ÷ 3
Required ratio = 8 : 3

ii) 144 : 12
Given ratio is 144 : 12
To write the given ratio in the simplest form.
First find the HCF of two terms.

HCF of 144 and 12 is 12.
Then, divide each term by their HCF.
Simplest form of the ratio = 144 ÷ 12 : 12 ÷ 12
Required ratio = 12 : 1

iii) 961 : 31
Given ratio is 961 : 31
To write the given ratio in the simplest form.
First find the HCF of two terms.

HCF of 961 and 31 is 31.
Then, divide each term by their HCF.
Simplest form of the ratio = 961 ÷ 31 : 31 ÷ 31
Required ratio = 31 : 1

iv) 1575 : 1190
Given ratio is 1575 : 1190
To write the given ratio in the simplest form.
First find the HCF of two terms.

HCF of 1575 and 1190 is 35.
Then, divide each term by their HCF.
Simplest form of the ratio = 1575 ÷ 35 : 1190 ÷ 35
∴ Required ratio = 45 : 34

Question 3.
Write the antecedents and consequents of the following ratios.
(i) 36 : 73
(ii) 65 : 84
(iii) 58 : 97
(iv) 69 : 137
Answer:

Question 4.
Find the ratios of the following in their simplest form.
i) 25 minutes to 55 minutes
ii) 45 seconds to 30 minutes
iii) 4 m 20 cm to 8 m 40 cm
iv) 5 litres to 0.75 litres
v) 4 weeks to 4 days
vi) 5 dozen to 2 scores (1 score = 20 items)
Answer:
i) 25 minutes to 55 minutes
Given 25 minutes to 55 minutes = 25 : 55

HCF of 25 and 55 is 5 = 25 ÷ 5 : 55 ÷ 5 (Divide each term by 5)
∴ Required ratio = 5:11

ii) 45 seconds to 30 minutes
Given 45 seconds to 30 minutes.
To write the given ratio in the simplest form.
First convert the two terms into same units.
1 minute = 60 seconds
30 minutes = 30 × 60 = 1800 seconds
Then, find the HCF of two terms and divide them by their HCF.

HCF of 45 and 1800 is 45.
= 45 ÷ 45 : 1800 ÷ 45 (divide each term by 45)
∴ Required ratio = 1 : 40

iii) 4 m 20 cm to 8 m 40 cm
Given 4 m 20 cm to 8 m 40 cm
To write the given ratio in the simplest form.
First we convert them into cm.
1 m = 100 cm
4 m = 400 cm
8 m = 800 cm
4 m 20 cm = 400 + 20 = 420 cm
8 m 40 cm = 800 + 40 = 840 cm
Then, find the HCF of 420 and 840 and divide them by HCF.

HCF of 420 and 840 is 420.
= 420 ÷ 420 : 840 ÷ 420 (divide each term by 420)
Required ratio = 1 : 2.

iv) 5 litres to 0.75 litres
Given 5 litres to 0.75 litres
To write the given ratio in the simplest form, first we convert litres into millilitres.
1 litre = 1000 ml
5 litres = 5000 ml
0.75 litres = 750 ml
Then, find the HCF of 5000; 750 and divide them by HCF.

HCF of 5000 and 750 is 250,
= 5000 ÷ 250 : 750 ÷ 250 (divide each term by 250)
Required ratio = 20 : 3

v) 4 weeks to 4 days
Given 4 weeks to 4 days.
To write the given ratio in the simplest form, first we convert them into same units (days).
1 week = 7 days
4 weeks = 4 × 7 = 28 days
Then, find the HCF of 28 and 4, then divide them by HCF.

HCF of 28 and 4 is 4 = 28 ÷ 4 : 4 ÷ 4 (divide each term by 4)
Required ratio = 7 : 1

vi) 5 dozen to 2 scores (1 score = 20 items)
Given 5 dozen to 2 scores.
To write the given ratio in the simplest form, first we convert them into same units.
1 dozen = 12 items
5 dozens = 5 × 12 = 60 items
1 score = 20 items
2 scores = 2 × 20 = 40 items
Then, find the HCF of 60 and 40, divide them by HCF.

HCF of 60 and 40 is 20 = 60 ÷ 20 : 40 ÷ 20 (divide each term by 20)
Required ratio = 3 : 2

Question 5.
Rahim works in a software company and earns Rs. 75,000/- per month. He saves Rs. 28,000/- per month from his earnings. Find the ratio of
i) His savings to his income
ii) His income to his expenditure
iii) His savings to his expenditure
Answer:
Given Rahim’s monthly income = Rs. 75000
monthly savings = Rs. 28000
Monthly expenditure = income – savings
= 75000 – 28000 = 47,000/-
i) Ratio of savings to income = 28000 : 75000
To convert the ratio into the simplest form divide each term by their HCF is 1000
= 28000 ÷ 1000 : 75000 ÷ 1000 (divide by 1000)
= 28 : 75
Required ratio of savings to income = 28 : 75

ii) Ratio of income to expenditure = 75000 : 47000
To convert the ratio into the simplest form divide each term by their HCF is 1000 = 75000 ÷ 1000 : 47000 ÷ 1000 (divide by 1000)
= 75 : 47
Required ratio of income to expenditure = 75 : 47

iii) Ratio of savings to expenditure = 28000 : 47000
To convert the ratio into the simplest form divide each term by their HCF is 1000 = 28000 ÷ 1000 : 47000 ÷ 1000 (divide by 1000)
= 28 : 47
Required ratio of savings to expenditure = 28 : 47

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 4 Integers Ex 4.1 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 4th Lesson Integers Ex 4.1

Question 1.
Write True or False against each of the following statements.
i) -7 is on the right side of -6 on the number line.
ii) Zero is a positive number.
iii) 29 is on the right side of zero on the number line.
iv) -1 lies between the integers -2 and 1.
v) There are nine integers between -5 and +5.
Answer:
i) False
ii) False
iii) True
iv) True
v) True

Question 2.
Observe the following number line and answer the following questions.

i) Which is the nearest positive integer to -1?
ii) How many negative numbers you will find on the left side of Zero?
iii) How many integers are there in between -3 and 7?
iv) Write 3 integers lesser than -2.
v) Write 3 integers more than -2.
Answer:
i) +1 is the nearest positive integer to -1.
ii) On the given number line negative numbers to left of zero are -1, -2, -3, -4, -5.
So, there are 5 in number.
iii) On the number line integers between -3 and 7 are -2, -1, 0, 1, 2, 3, 4, 5, 6.
So, there are 9 in number.
iv) Integers less than -2 means numbers left side of -2.
They are -3, -4, -5, -6, -7, ………
So, 3 integers lesser than -2 are -3, -4, -5.
v) Integers more than -2 means numbers right side of -2.
They are -1, 0, 1, 2, 3, 4, ……..
So, 3 integers more than -2 are -1, 0, 1.

Question 3.
Represent the integers on a number line as given below.
i) Integers lies between -7 and -2.
ii) Integers lies Between -2 and 5.
Answer:

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 3 HCF and LCM Unit Exercise Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 3rd Lesson HCF and LCM Unit Exercise

Question 1.
Classify the given numbers according to their divisibility.

Answer:

(OR)

Question 2.
Write the divisibility rule by 11 with one example.
Answer:
Divisibility by 11:
A given number is divisible by 11, if the difference between the sum of the digits at odd places and the sum of the digits at even places (from the right) is either ‘O’ or a multiple of 11.
Ex: 123321
Sum of the digits at odd places = 1 + 3 + 2 = 6.
Sum of the digits at even places = 2 + 3 + 1 = 6
Their difference = 6 – 6 = 0
So, 123321 is divisible by 11.

Question 3.
Fill the table with correct answer.

Answer:

Question 4.
Find HCF of 70, 105 and 175 by prime factorization method.
Answer:
Given numbers are 70, 105 and 175.
The HCF of 70, 105 and 175 can be formed by prime factorization as follows:

Thus, 70 = 2 × 5 × 7
105 = 3 × 5 × 7
175 = 5 × 5 × 7
Common factors of 70, 105 and 175 are: 5, 7
Their product: 5 × 7 = 35
Hence, HCF of 70, 105 and 175 is 35.

Question 5.
Find HCF of 18, 54, 81 by continued division method.
Answer:
Given numbers are 18, 54 and 81 To find the HCF of 18, 54 and 81
First find the HCF of 18 and 54

HCF of 18 and 54 is 18.
Then find the HCF of the third number and the HCF of first two numbers.
i.e., let us find the HCF of 81 and 18

Last divisor is 9 when remainder is zero.
∴ HCF of 18, 54 and 81 is 9.

Question 6.
Find LCM of 4, 12, 24 by two methods.
Answer:
Given numbers are 4, 12 and 24
a) LCM by prime factors method:
Factors of 4 = 2 × 2
Factors of 12 = 2 × 2 × 3
Factors of 24 = 2 × 2 × 2 × 3
LCM of 4, 12 and 24= 2 × 2 × 2 × 3 = 24

b) Division method:

Thus, the LCM of 4, 12 and 24 is 2 × 2 × 2 × 3 = 24

Question 7.
What is the capacity of the largest vessel which can empty the oil from three vessels containing 32 liters, 24 liters and 48 liters respectively, an exact number of times?
Answer:
Given capacity of three vessels are 32 liters, 24 liters and 48 liters.
To find the capacity of the largest vessel.
We have to find the HCF of 32, 24 and 48.
First find the HCF of 32 and 24.
HCF of 32 and 24 is 8.

Then, find the HCF of third number and the HCF of first two numbers.
i.e., let us find the HCF of 48 and 8.

HCF of 32, 24 and 48 is 8.
Hence, the capacity of the largest vessel which can empty the oil, then the three vessels containing 32 l, 24 l and 48 l of exact number of times is 8 liters.

Question 8.
HCF, LCM of two numbers are 9 and 54 respectively. If one of those two numbers is 18, find the other number.
Answer:
Given, HCF of two numbers = 9
LCM of two numbers = 54
One of the two numbers a = 18
Then, the other number b = ?
We know, that the product of two numbers = LCM × HCF
a × b = LCM × HCF
18 × b = 54 × 9
b = \(\frac{54 × 9}{18}\) = 27
∴ The other number = 27

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 7 Introduction to Algebra Unit Exercise Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 7th Lesson Introduction to Algebra Unit Exercise

Question 1.
The cost of one fan is Rs. 1500. Then what is the cost of ‘n’ fans?
Answer:

Given cost of one fan = Rs. 1500
Number of fans = n
Cost of n fans = cost of one fan × no. of fans = 1500 × n
∴ Cost of n fans = 1500n

Question 2.
Srinu has number of pencils. Raheem has 4 times the pencils as of Srinu. How many pencils does Rahim has? Write an expression.
Answer:
Let number of pencils Srinu has = x
Number of pencils Raheem has = 4 times of Srinu
= 4 × x
∴ Number of pencils Raheem has = 4x

Question 3.
Parvathi has 5 more books than Sofia. How many books are with Parvathi? Write an expression choosing any variable for number of books.
Answer:
Let number of books Sofia has = y
Given Parvathi has 5 more books than Sofia
Number of books Parvathi has = 5 books more than Sofia
= y + 5
∴ Number of books Parvathi has = y + 5

Question 4.
Which of the following are equations?
i) 10 – 4p = 2
ii) 10 + 8x < – 22
iii) x + 5 = 8
iv) m + 6 = 2
v) 22x – 5 = 8
vi) 4k + 5 > – 100
vii) 4p + 7 = 23
viii) y < – 4
Answer:
i) 10 – 4p = 2
We know that, a mathematical statement involving equality symbol is called an equation.
10 – 4p = 2 has equality symbol.
So, it is an equation.

ii) 10 + 8x < – 22
We know that, a mathematical statement involving equality symbol is called an equation.
10 + 8x < – 22 has no equality symbol.
So, it is not an equation [so it is an inequation]

iii) x + 5 = 8 We know that, a mathematical statement involving equality symbol is called an equation.
x + 5 = 8 has equality symbol.
So, it is an equation.

iv) m + 6 = 2 We know that, a mathematical statement involving equality symbol is called an equation.
m + 6 = 2 has equality symbol.
So, it is an equation.

v) 22x – 5 = 8 We know that, a mathematical statement involving equality symbol is called an equation.
22x – 5 = 8 has equality symbol.
So, it is an equation.

vi) 4k + 5 > – 100
We know that, a mathematical statement involving equality symbol is called an equation.
4k + 5 > -100 has no equality symbol.
So, it is not an equation.
It is an inequation.

vii) 4p + 7 = 23
We know that, a mathematical statement involving equality symbol is ailed an equation.
4p + 7 = 23 has equality symbol.
So, it is an equation.

viii) y < – 4
We know that, a mathematical statement involving equality symbol is called an equation.
y < – 4 has no equality symbol.
So, it is not an equation.
It is an inequation.

Question 5.
Write L.H.S and R.H.S of the following equations:
i) 7x + 8 = 22
ii) 9y – 3 = 6
iii) 3k – 10 = 2
iv) 3p – 4q = -19
Answer:
i) 7x + 8 = 22
Given equation is 7x + 8 = 22
LHS = 7x + 8
RHS = 22

ii) 9y – 3 = 6
Given equation is 9y – 3 = 6
LHS = 9y – 3
RHS = 6

iii) 3k – 10 = 2
Given equation is 3k – 10 = 2
LHS = 3k – 10
RHS = 2

iv) 3p – 4q = -19
Given equation is 3p – 4q = -19
LHS = 3p – 4q
RHS = -19

Question 6.
Solve the following equations by trial and error method.
i) x – 3 = 5
ii) y + 6 = 15
iii) y = -1
iv) 2k – 1 = 3
Answer:
i) x – 3 = 5
Given equation is x – 3 = 5
If x = 1, then the value of x – 3 = 1 – 3 = -2 ≠ 5
If x = 2, then the value of x – 3 = 2 – 3 = -l ≠ 5
If x = 3, then the value of x – 3 = 3 – 3 = 0 ≠ 5
If x = 4, then the value of x – 3 = 4 – 3 = l ≠ 5
If x = 5, then the value of x – 3 = 5 – 3 = 2 ≠ 5
If x = 6, then the value of x – 3 = 6 – 3 = 3 ≠ 5
If x = 7, then the value of x – 3 = 7 – 3 = 4 ≠ 5
If x = 8, then the value of x – 3 = 8 – 3 = 5 = 5
From the above when x = 8, the both LHS and RHS are equal.
∴ Solution of the equation x – 3 = 5 is x = 8

ii) y + 6 = 15
Given equation is y + 6 = 15
If y = 1, then the value of y + 6 = 1 + 6 = 7 ≠ 15
If y = 2, then the value of y + 6 = 2 + 6 = 8 ≠ 15
If y = 3, then the value of y +6 = 3 + 6 = 9 ≠ 15
If y = 4, then the value of y + 6 = 4 + 6 = 10 ≠ 15
If y = 5, then the value of y + 6 = 5 + 6 = 11 ≠ 15
If y = 6, then the value of y + 6 = 6 + 6 = 12 ≠ 15
If y = 7, then the value hf y + 6 = 7 + 6 = 13 ≠ 15
If y = 8, then the value of y + 6 = 8 + 6 = 14 ≠ 15
If y = 9, then the value of y + 6 = 9 + 6 = 15 = 15
From the above when y = 9, the both LHS and RHS are equal.
∴ Solution of the equation y + 6 = 15 is y = 9

iii) \(\frac{m}{2}\) = -1
Given equation is \(\frac{m}{2}\) = -1
If m = 1, then the value of \(\frac{m}{2}\) = \(\frac{1}{2}\) ≠ -1
If m = 2, then the value of \(\frac{m}{2}\) = \(\frac{2}{2}\) = 1 ≠ -1
If m = 3, then the value of \(\frac{m}{2}\) = \(\frac{3}{2}\) ≠ -1
Here, we are not getting negative values.
If we take (substitute) m as a negative number we will get negative value.
If m = -1, then the value of \(\frac{m}{2}\) = \(\frac{-1}{2}\) ≠ -1
If m = -2, then the value of \(\frac{m}{2}\) = \(\frac{-2}{2}\) = -1 = -1
From the above when m = -2, the both LHS and RHS are equal.
∴ Solution of the equation \(\frac{m}{2}\) = -1 is m = -2.

iv) 2k – 1 = 3
Given equation is 2k – 1 = 3
If k = 1, then the value of 2k – 1 = 2(1) – 1 = 2 – 1 = 1 ≠ 3
If k = 2, then the value of 2k – 1 = 2(2) – 1 = 4 – 1 = 3 = 3
From the above when k – 2, the both LHS and RHS are equal.
Solution of the equation 2k – 1 = 3 is k = 2.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 5 Fractions and Decimals Unit Exercise Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 5th Lesson Fractions and Decimals Unit Exercise

Question 1.
The sum of two fractions is 5\(\frac{3}{9}\). If one fraction is 2\(\frac{3}{4}\), then find the other fraction.
Answer:
Given one fraction = 2\(\frac{3}{4}\) = \(\frac{11}{4}\)
Sum of two fractions = 5\(\frac{3}{9}\) = \(\frac{48}{9}\)
Now, \(\frac{11}{4}\) + second fraction = \(\frac{48}{9}\)
Second fraction = \(\frac{48}{9}\) – \(\frac{11}{4}\)
LCM of 9 and 4 is 36

Question 2.
A rectangle sheet of paper is of length 12\(\frac{1}{2}\) and breadth 10\(\frac{2}{3}\). Find its perimeter.
Answer:
Length of rectangular sheet = l = 12\(\frac{1}{2}\) = \(\frac{25}{2}\) m
Breadth of rectangular sheet = b = 10\(\frac{2}{3}\) = \(\frac{32}{3}\) m
Perimeter of rectangular sheet = 2(1 + b)

Question 3.
Simplify: \(\left(3 \frac{1}{6}-1 \frac{1}{3}\right)+\left(4 \frac{1}{6}-2 \frac{1}{3}\right)\)
Answer:
\(\left(3 \frac{1}{6}-1 \frac{1}{3}\right)+\left(4 \frac{1}{6}-2 \frac{1}{3}\right)\)
First convert the given mixed fractions into improper fractions.
\(\left(\frac{19}{6}-\frac{4}{3}\right)\) + \(\left(\frac{25}{6}-\frac{7}{3}\right)\)
Then subtract the fractions which are in brackets by making them like fractions.

Now add the fractions = \(\frac{11+11}{6}\) = \(\frac{22}{6}\) = 3\(\frac{4}{6}\)

Question 4.
By what number should 3\(\frac{1}{16}\) be multiplied to get 9\(\frac{3}{16}\)?
Answer:
Given fraction = 3\(\frac{1}{16}\) = \(\frac{49}{16}\)
Product = 9\(\frac{3}{16}\) = \(\frac{147}{16}\)
Fraction × fraction to be multiplied = \(\frac{147}{16}\)
\(\frac{49}{16}\) × other number = \(\frac{147}{16}\)
other number = \(\frac{147}{16}\) ÷ \(\frac{49}{16}\) = \(\frac{147}{16}\) × \(\frac{16}{49}\)
Other number = 3
∴ Number to be multiplied = 3.

Question 5.
The length of the staircase is 5\(\frac{1}{2}\) m. If one step is set at \(\frac{1}{4}\) m. then, how many steps will be there in the staircase?
Answer:
Given length of staircase = 5\(\frac{1}{2}\) m = \(\frac{11}{2}\) m
Length of each step = \(\frac{1}{4}\) m
Length of each step × number of steps = length of staircase
\(\frac{1}{4}\) × Number of steps = \(\frac{11}{2}\)
Number of steps = \(\frac{11}{2}\) ÷ \(\frac{1}{4}\) = \(\frac{11}{2}\) × \(\frac{4}{1}\) = 11 × 2 = 22
∴ Number of steps in the staircase = 22

Question 6.
Simplify: 23.5 – 27 + 35.4 – 17
Answer:
Given 23.5 – 27 + 35.4 – 17
First make them like decimals.
= 23.5 – 27.0 + 35.4 – 17.0
Add the positive numbers
= (+23.5 + 35.4) + (-27.0 – 17.0)
= 58.9 + (-44.0)
= 58.9 – 44.0
= 14.9

Question 7.
Sailaja bought 3.350kg of potatoes, 2.250kg of tomatoes and some onions. If the weight of the total items are 10.250 kg. Then, find the weight of onions.
Answer:
Weight of potatoes = 3.350 kg
Weight of tomatoes = 2.250 kg
Weight of total items = 10.250 kg
Weight of onions = ?
Weight of (potatoes + tomatoes + onions) = 10.250 kg
(3.350 + 2.250) + onions weight = 10.250
5.600 + onions weight = 10.250
Onions weight = 10.250 – 5.600
∴ Weight of onions = 4.650 kg.

Question 8.
What should be subtracted from 7.1 to get 0.713?
Answer:
Given number = 7.1
Difference = 0.713
Number to be subtracted = Number – difference
= 7.1 – 0.713
= 7.100 – 0.713
∴ Number to be subtracted = 6.387.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 7 Introduction to Algebra Ex 7.3 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 7th Lesson Introduction to Algebra Ex 7.3

Question 1.
Identify which of the following are equations.
i) x – 3 = 7
ii) l + 5 > 9
iii) p – 4 < 10
iv) 5 + m = -6
v) 2s – 2 = 12
vi) 3x + 5
Answer:
i) x – 3 = 7
We know that, a mathematical statement involving equality symbol is called an equation.
x – 3 = 7 has equality symbol. So, it is an equation.

ii) l + 5 > 9
We know that, a mathematical statement involving equality symbol is called an equation.
l + 5 > 9 has no equality symbol.
So, it is not an equation. [It is an inequation]

iii) p – 4 < 10
We know that, a mathematical statement involving equality symbol is called an equation.
p – 4 < 10 has no equality symbol.
So, it is not an equation. [It is an inequation]

iv) 5 + m = – 6
We know that, a mathematical statement involving equality symbol is called an equation.
5 + m = – 6 has equality symbol.
So, it is an equation.

v) 2s – 2 = 12
We know that, a mathematical statement involving equality symbol is called an equation.
2s – 2 = 12 has equality symbol.
So, it is an equation.

vi) 3x + 5
It is only an expression. It’s not an equation.

Question 2.
Write LHS and RHS of the following equations.
i) x – 5 = 6
ii) 4y = 12
iii) 2z + 3 = 7
Answer:
i) x – 5 = 6
Given equation is x – 5 = 6
LHS = x – 5
RHS = 6

ii) 4y = 12
Given equation is 4y = 12
LHS = 4y
RHS = 12

iii) 2z + 3 = 7
Given equation is 2z + 3 = 7
LHS = 2z + 3
RHS = 7

Question 3.
Solve the following equation by Trial & Error Method.
i) x + 3 = 5
ii) y – 2 = 7
iii) a + 4 = 9
Answer:
i) x + 3 = 5
Given equation is x + 3 = 5
If x = 1, then the value of x + 3 = 1 + 3 = 4 ≠ 5
If x = 2, then the value of x + 3 = 2 + 3 = 5 = 5
From the above when x = 2, then both LHS and RHS are equal.
∴ Solution of the equation x + 3 = 5 is x = 2

ii) y – 2 = 7
Given equation is y – 2 = 7
If y = 1, then the value of y – 2 = 1 – 2 = -1 ≠ 7
If y = 2, then the value of y – 2 = 2 – 2 = 0 ≠ 7
If y = 3, then the value of y – 2 = 3 – 2 = 1 ≠ 7
If y = 4, then the value of y – 2 = 4 – 2 = 2 ≠ 7
If y = 5, then the value of y – 2 = 5 – 2 = 3 ≠ 7
If y = 6, then the value of y – 2 = 6 – 2 = 4 ≠ 7
If y = 7, then the value of y – 2 = 7 – 2 = 5 ≠ 7
If y = 8, then the value of y – 2 = 8 – 2 = 6 ≠ 7
If y = 9, then the value of y – 2 = 9 – 2 = 7 = 7
From the above when y = 9, the both LHS and RHS are equal.
Solution of the equation y – 2 = 7 is y = 9

ii) a + 4 = 9
Given equation is a + 4 = 9
If a = 1, then the value of a + 4 = 1 + 4 = 5 ≠ 9
If a = 2, then the value of a + 4 = 2 + 4 = 6 ≠ 9
If a = 3, then the value of a + 4 = 3 + 4 = 7 ≠ 9
If a = 4, then the value of a + 4 = 4 + 4 = 8 ≠ 9
If a = 5, then the value of a + 4 = 5 + 4 = 9 = 9
From the above when a = 5, the both LHS and RHS are equal.
∴ Solution of the equation a + 4 = 9 is a = 5

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 7 Introduction to Algebra Ex 7.2 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 7th Lesson Introduction to Algebra Ex 7.2

Question 1.
Write the expressions for the following statements.
(i) 5 is added to three times z
(ii) 9 times ‘n’ is added to ’10’
(iii) 16 is subtracted from two times ‘y’
(iv) ‘y’ is multiplied by 10 and then x is added to the product
Answer:
i) Given 5 is added to three times z
three times z = 3z 5 is added to three times z = 3z + 5

ii) Given 9 times n is added to 10
9 times n = 9.n
9 times ‘n’ is added to 10 = 9n + 10

iii) Given 16 is subtracted from two times y
two times y = 2.y
16 is subtracted from two times y = 2.y – 16

iv) Given y is multiplied by 10 and then x is added to the product, y is multiplied by 10 = 10.y
x is added to the product = 10.y + x

Question 2.
Peter has ‘p’ number of balls. Number of balls with David is 3 times the balls with Peter. Write this as an expression.
Answer:
Given, number of balls with Peter = p
Number of balls with David = 3 times with the Peter
= 3.p
Expression is 3p.

Question 3.
Sita has 3 more note books than Geetha. Find the number of books that Sita has. Use any letter for the number of books that Geetha has.
Answer:
Given Sita has 3 more note books than Geetha.
Let the number of note books Geetha has = x
Number of note books Sita has = 3 more note books than Geetha
= x + 3

Question 4.
Cadets are marching in a parade. There are 5 cadets in each row. What is the rule for the number of cadets, for a given number of rows? Use ‘n’ for the number of rows.
Answer:
Given 5 cadets in each row.
Number of rows = n
Number of cadets in each row = 5
Number of cadets in n rows = 5 × n = 5n

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 5 Fractions and Decimals Ex 5.5 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 5th Lesson Fractions and Decimals Ex 5.5

Question 1.
Add the following:
i) 5.702, 5.2, 6.04 and 2.30
ii) 40.004; 44.444; 40.404 and 4.444
Answer:
i) 5.702, 5.2, 6.04 and 2.30
Given decimals fractions are 5.702; 5.2; 6.04 and 2.30
Convert the given decimals into like decimals.
5.702; 5.200; 6.040; 2.300
Then write the decimals in column with the decimal points directly below each other.
So, that tenth’s come under tenths, hundredths come under hundredths and so on, then add.

ii) 40.004; 44.444; 40.404 and 4.444
Given decimals are 40.004; 44.444; 40.404 and 4.444
They are like decimal fractions.
So, write the decimals in column with the decimal points directly below each other.
So, that tenths come under tenths, hundredths come under hundredths and so on, then add.

Question 2.
Do the following:
i) 426.326 – 284.482
ii) 5 – 3.009
iii) 2.107 – 0.31
Answer:
i) 426.326 – 284.482
Given decimals are 426.326 and 284.482.
They are like fractions.
So, write the decimals in column with the decimal points directly below each other.
So, that tenths come under tenths, hundredths come under hundredths and so on, then subtract.

ii) 5 – 3.009
Given decimals are 5 and 3.009 Make them as like fractions.
5.000 – 3.009
So, write the decimals in column with the decimal points directly below each other.
So, that tenths come under tenths, hundredths come under hundredths and so on. Then subtract.

iii) 2.107 – 0.31
Given decimals are 2.107 and 0.31, make them as like fractions.
2.107 – 0.310
So, write the decimals in column with the decimal points directly below each other.
So, that tenths come under tenths, hundredths come under hundredths and so on. Then subtract.

Question 3.
Akshara bought 3 m 40 cm cloth for her shirt and 1 m 10 cm cloth for skirt. Find the total cloth bought by her.
Answer:
Length of cloth bought for shirt = 3.40
Length of cloth bought for skirt = 1.10
Total length of cloth bought by Akshara = 3.40 + 1.10 = 4.50 cm

Question 4.
Write in decimals using the units written in brackets.
i) 90 rupees 75 paisa (Rs.)
ii) 49 m 20 cm (m)
iii) 12 kg 450 g (kg)
iv) 50 l 500 ml (l)
Answer:
i) 90 rupees 75 paisa = Rs. 90.75
ii) 49 m 20 cm = 49.20 m
iii) 12 kg 450 g = 12.450 kg
iv) 50 l 500 ml = 50.500 l

Question 5.
Convert into decimals and add.
i) 58 kg 100 g; 60 kg 350 g
ii) 80 m 15 cm; 72 m 30 cm
Answer:
i) 58 kg 100 g; 60 kg 350 g
Given values are 58 kg 100 g and 60 kg 350 g
First convert the given values into like decimal fractions.
58.100 kg and 60.350 kg
Then, write the decimals in column with the decimal points directly below each other.
So, that tenths come under tenths, hundredths come under hundredths and so on.
Then add:

ii) 80 m 15 cm; 72 m 30 cm
Given values are 80 m 15 cm and 72 m 30 cm.
First convert the given values into decimal fractions.
80.15 m and 72.30 m
Then, write the decimals in column with the decimal points directly below each other.
So, that tenths come under tenths, hundredths come under hundredths and so on. Then add:

Question 6.
Convert into decimals and subtract.
i) 14 kg 720 g from 16 kg 744 g
ii) 1 l 12 ml from 2 l 20 ml
Answer:
i) 14 kg 720 g from 16 kg 744 g
Given values are 14 kg 720 g and 16 kg 744 g.
First convert the given values into decimal fractions.
14.720 kg and 16.744 kg
Then, write the decimals in column with the decimal points directly below each other. So, that tenths come under tenths, hundredths come under hundredths and so on.
Then subtract:

ii) 1 l 12 ml from 2 l 20 ml
Given values are 1 l 12 ml and 2 l 20 ml
First convert the given values into decimal fractions.
1.012 l and 2.020 l
Then write the decimals in column with the decimal points directly below each other. So, that tenths come under tenths, hundredths come under hundredths and so on. Then subtract:

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 7 Introduction to Algebra Ex 7.1 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 7th Lesson Introduction to Algebra Ex 7.1

Question 1.
Find the rule which gives the number of matchsticks required to make the following matchstick patterns.
(i) A pattern of letter ‘T’
(ii) A pattern of letter ‘E’
(iii) A pattern of letter ‘Z’
Answer:

Question 2.
Make a rule between the number of blades required and the number of fans (say n) in a hall.
Answer:
Number of blades for one fan = 3 = 1 × 3
Number of blades for two fans = 3 + 3 = 2 × 3
Number of blades for three fans = 3 + 3 + 3 = 3 × 3
Number of blades for four fans = 3 + 3 + 3 + 3 = 4 × 3
………………………………………
Number of blades for n fans = 3 + 3 + …. (n times) = 3 × n
Rule of number of blades required for n fans = 3.n

Question 3.
The cost of one pen is Rs. 7, then what is the rule for the cost of ‘n’ pens ?
Answer:
Cost of one pen = Rs. 7 = 1 × 7
Cost of two pens = Rs. 7 + Rs. 7 = 2 × 7
Cost of three pens = Rs. 7 + Rs. 7 + Rs. 7 = 3 × 7
……………………………………..
Cost of n pens = Rs. 7 + Rs. 7 + Rs. 7 ….. n times = 7 × n
Rule for cost n pens = 7.n.

Question 4.
The rule for purchase of books is that the cost of q books is Rs. 25q, then find the price of one book.
Answer:
Given, rule for cost of q books = Rs. 25q
In this rule q is variable i.e., q = 1, 2, 3,….
To get the cost of one book, put q = 1 in rule 25q
∴ Cost of one book = 25 (q) = 25(1) = Rs. 25

Question 5.
Harshini says that she has 5 biscuits more than Padma has. How can you express the relationship using the variable ‘y’?
Answer:
Given, Harshini has 5 biscuits more than Padma.
Let number of biscuits Padma has = y
Number of biscuits Harshini has = 5 more than Padma
∴ Number of biscuits Harshini has = y + 5

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 6 Basic Arithmetic Unit Exercise Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 6th Lesson Basic Arithmetic Unit Exercise

Question 1.
Draw a four sided closed figure and divide it into some number of equal parts. Shade the figure with any colour so that the ratio of shaded parts to unshaded parts is 1 : 3.
Answer:

Given ratio of shaded parts: unshaded parts = 1 : 3
Total parts of a closed figure = 1 + 3 = 4
Consider a four sided closed figure square.
Divide it into 4 parts and shade one part.
Now, from the figure, shaded parts : unshaded parts = 1 : 3

Question 2.
Ramu spent \(\frac{2}{5}\)th of his money on a story book. Find the ratio of money spent to the money with him at present.
Answer:
Given money spent on story book = \(\frac{2}{5}\) th of his money.
That means from total 5 parts of money he spent 2 parts of money on story book. Then, out of 5 parts remaining parts of money with him is 3 parts.
So, ratio of money spent to the money with him at present
= parts of money spent : parts of money at him = 2 : 3

Question 3.
Divide Rs. 72,000 between Kesav and David in the ratio of 5 : 4.
Answer:
Amount to be divided = Rs. 72,000
Ratio of Kesav and David’s Shares = 5 : 4
Total shares = 5 + 4 = 9
Kesav’s share = \(\frac{5}{9}\) of 72000
\(\frac{5}{9}\) × 72,000 = 40,000/-
David’s share = \(\frac{4}{9}\) of 72,000
\(\frac{4}{9}\) × 72,000 = 32,000/-

Question 4.
The income of Kumar for 3 months is Rs. 15,000. If he earns the same amount for a month,
a) How much will he earn in 5 months?
b) In how many months, will he earn Rs. 95,000?
Answer:
Given Kumar’s 3 months income = Rs. 15,000
Kumar’s one month income = 15,000 ÷ 3
= \(\frac{15000}{3}\) = Rs. 5000
a) Kumar’s one month income = Rs. 5000
Kumar’s 5 months income = 5 × 5000 = Rs. 25,000
b) Time taken by Kumar to earn Rs. 5000 = 1 month
Time taken by Kumar to earn Rs. 95,000 = 95,000 ÷ 5000
= \(\frac{15000}{3}\) = 19 months = 1 year 7 months.

Question 5.
The cost of 16 chairs is Rs. 4,800. Find the number of chairs that can be purchased for Rs. 6,600.
Answer:
Cost of 16 chairs = Rs. 4800
Number of chairs that can be pruchased for Rs. 6600 = x (say)
∴ 16 : 4800 : : x : 6600
So, 16 x 6600 = 4800 x x
x = \(\frac{16 \times 6600}{4800}\) = 22 chairs
(OR)
Given cost of 16 chairs = Rs. 4800
Cost of one chair = 4800 ÷ 16
= \(\frac{4800}{3}\) = Rs. 300
Number of chairs can purchased for Rs. 6600 = 6600 ÷ cost of one chair
= 6600 ÷ 300
= \(\frac{6600}{300}\) = 22 chairs

Question 6.
What percentage of numbers from 1 to 30 has 1 or 9 in the unit’s digit?
Answer:
Total number from 1 to 30 = 30
Numbers ending with 1 or 9 are 1, 9,11, 19, 21, 29 = 6 numbers
Ratio = 6 : 30 = \(\frac{6}{30}\) = \(\frac{1}{5}\)
Percentage = \(\frac{1}{5}\) × 100% = 20%

Question 7.
In a college, 63% of students are less than 20 years of age. The number of students more than 20 years of age is — of number of students of 20 years of age which is 42. What is the total number of students in the college?
Answer:
Let the total number of students be x.
Then, number of students more than 20 years of age = (100 – 63)% of x
= 37% of x
Then, 37% of x = 42 + \(\frac{2}{3}\) of 48
\(\frac{37}{100}\) × x = 74
∴ x = 74 × \(\frac{100}{37}\) = 200

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 5 Fractions and Decimals Ex 5.4 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 5th Lesson Fractions and Decimals Ex 5.4

Question 1.
Which of the following are unlike decimal fractions ?
i) 5.03, 6.185
ii) 42.7, 7.42
iii) 16.003, 5.301
iv)15.81, 1.36
Answer:
i) 5.03, 6.185
5.3 has 2 decimal places
6.185 has 3 decimal places
Their decimal places are not equal.
So, these decimal fraction are unlike decimal fractions.

ii) 42.7, 7.42
42.7 has one decimal place
7.42 has two decimal places
Their decimal places are not equal.
So, these are unlike decimal fractions.

iii) 16.003, 5.301
16.3 has three decimal places
5.301 has three decimal places
Their decimal places are equal.
So, these are like decimal fractions.

iv) 15.81, 1.36
15.81 has two decimal places
1.36 has two decimal places
Their decimal places are equal.
So, these are like decimal fractions.

Question 2.
Change the following into like decimal fractions.
i) 0.802, 54.32, 873.274
ii) 4.78, 9.193, 11.3
iii) 16.003, 16.9, 16.19
Answer:
i) 0.802, 54.32, 873.274
Given decimal fractions are 0.802, 54.32, 873.274
The greatest number of decimal places is 3.
So, we convert all of them to equivalent decimals with 3 decimal places by placing sufficient zeroes.
0.802 = 0.802
54.32 = 54.320
873.274 = 873.274
Thus, 0.802, 54.32, 873.274 when converted to like decimals becomes 0.802, 54.320, 873.274.

ii) 4.78, 9.193, 11.3
Given decimal fractions are 4.78, 9.193, 11.3.
So, we convert all of them to equivalent decimals with 3 decimal places.
4.78 = 4.780
9.193 = 9.193
11.3 = 11.300
Thus, 4.78, 9.193, 11.3 when converted to like decimals becomes 4.780, 9.193, 11.300.

iii) 16.003, 16.9, 16.19
Given decimal fractions are 16.003, 16.9, 16.19
So, we convert all of them to equivalent decimals with three decimal places by providing sufficient zeroes.
16.3 = 16.003
16.9 = 16.900
16.19 = 16.190
Thus, 16.003, 16.9, 16.19 when converted to like decimals becomes 16.003, 16.900, 16.190.

Question 3.
Write the following in ascending order.
a) 7.26, 7.62, 7.2
b) 0.464, 0.644, 0.446, 0.664
c) 30.000, 30.060, 30.30
Answer:
a) 7.26, 7.62, 7.2
Given decimal fractions are 7.26, 7.62, 7.20
First compare the whole numbers.
Here whole numbers are equal. So, compare tenth’s place digits of the decimal fractions.
In 7.26 and 7.20 Tenths places are same.
But 7.62 Tenth place is more than the remaining numbers.
So,7.62 > 7.26 and 7.62 > 7.20
To compare 7.26 and 7.20 we should compare hundredth’s places. Then 7.26 > 7.20
∴ 7.62 > 7.26 > 7.20
(or) 7.20 < 7.26 < 7.62
Ascending order: 7.20; 7.26; 7.62

b) 0.464, 0.644, 0.446, 0.664
Given decimal fractions are 0.464, 0.644, 0.446, 0.664
Then, compare whole numbers.
Here whole numbers are same. Then, compare tenth’s place digits of the decimal fractions.
0.464, 0.446 are less than 0.644 and 0.664.
First make or check the given fraction are all like fractions or not?
Then, compare hundredth’s place digits
∴ 0.464 > 0.446, 0.664 > 0.644
and 0.664 > 0.644 > 0.464 > 0.446
(or) 0.446 < 0.464 < 0.644 < 0.664
Ascending order: 0.446; 0.464; 0.644; 0.664

c) 30.000, 30.060, 30.30
Given decimal fractions are 30.000, 30.060, 30.30
First make or check the given fractions are all like fractions or not?
So, 30.000; 30.060; 30.300 are like fractions.
Then, compare the whole numbers. They are same. So, compare, Tenth’s places of the decimal fractions.
30.300 > 30.060 > 30.000
(or) 30.000 < 30.060 < 30.300
Ascending order: 30.000; 30.060; 30.300

Question 4.
Arrange these numbers in descending order:
16.96; 16.42; 16.3; 16.03; 16.1; 16.99; 16.01
Answer:
Given decimal fractions are
16.96; 16.42; 16.3; 16.03; 16.1; 16.99; 16.01
First make or check the given fractions are all like fractions or not?
So, 16.96; 16.42; 16.30; 16.03; 16.10; 16.99; 16.01 are like fractions.
Then, compare whole numbers. They are same.
So, compare Tenth’s place digits of the decimal fractions.
16.96 < 16.99; 16.42 > 16.30 > 16.10 > 16.03 > 16.01
Then compare hundredth’s place digits.
So, 16.99 > 16.96 > 16.42 > 16.30 > 16.10 > 16.03 > 16.01 (or)
16.01 < 16.03 < 16.10 < 16.30 < 16.42 < 16.96 < 16.99
Descending order: 16.99; 16.96; 16.42; 16.30; 16.10; 16.03; 16.01.

Question 5.
Fill in the blanks by using appropriate symbols >, < or =.
i) 0.005 …… 0.0005
ii) 4.353 …… 4.2
iii) 58.3 …… 58.30
Answer:
i) 0.005 …… 0.0005
First make like decimal fractions
0.0050 …… 0.0005
By comparing Thousandth’s place digits.
So, 0.0050 > 0.0005

ii) 4.353 …… 4.2
First make like decimal fractions.
4.353 …… 4.200
Compare Tenth’s place digits, if whole numbers are same.
So, 4.353 > 4.200

iii) 58.3 …… 58.30
First make like decimal fractions.
58.30 …… 58.30
In these whole numbers and decimal place digits are same.
So, 58.30 = 58.30