Class 6

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 1 Numbers All Around us Ex 1.2 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 1st Lesson Numbers All Around us Exercise 1.2

Question 1.
Write each of the following in numeral form.
i) Sixty crores seventy five lakhs ninety two thousands five hundred and two.
Answer:
60, 75, 92, 502

ii) Nine hundred forty four crores six lakhs fifty five thousand four hundred and eighty six.
Answer:
944, 06, 55, 486

iii) Ten crores ten thousand and ten.
Answer:
10,00,10,010

Question 2.
Insert commas in the correct positions to separate periods and write the following numbers in words.
i) 57657560
ii) 70560762
iii) 97256775613
Answer:
i) 5,76,57,560: Five crores seventy six lakhs fifty seven thousands five hundred and sixty.
ii) 7,05,60,762: Seven crores five lakhs sixty thousands seven hundred and sixty two.
iii) 9725,67,75,613: Nine thousand seven hundred and twenty five crores sixty seven lakhs seventy five thousand six hundred and thirteen.

Question 3.
Write the following in expanded form.
i) 756723
ii) 60567234
iii) 8500756762
Answer:
i) 756723
Expanded form: 7 × 1,00,000 + 5 × 10,000 + 6 × 1,000 + 7 × 100 + 2 × 10 + 3 × 1
: 7 lakhs + 5 ten thousands + 6 thousands + 7 hundreds + 2 tens + 3 ones
Word form: Seven lakh fifty six thousand seven hundred and twenty three.

ii) 60567234
Expanded form: 6 × 1,00,00,000 + 5 × 1,00,000 + 6 × 10,000 + 7 × 1,000 + 2 × 100 + 3 × 10 + 4 × 1
: 6 crores + 5 lakhs + 6 ten thousands + 7 thousands + 2 hundreds + 3 tens + 4 ones
Word form: Six crore five lakh sixty seven thousand two hundred and thirty four.

iii) 8500756762
Expanded form: 8 × 1,00,00,00,000 + 5 × 10,00,00,000 + 7 × 1,00,000 + 5 × 10,000 + 6 × 1000 + 7 × 100 + 6 × 10 + 2 × 1
: 8 hundred crores + 5 ten crores + 7 lakhs & 5 ten thousands + 6 thousands + 7 hundreds + 6 tens + 2 ones
Word form: Eight hundred and fifty crore seven lakh fifty six thousand seven hundred and sixty two.

Question 4.
Determine the difference between the place value and the face value of 6 in 86456792.
Answer:
Given number is 86456792. By putting commas to separate periods the given number can be written as 8,64,56,792.
i) Place value of ‘6’ in thousand place = 6 x 1000 = 6,000
Face value of 6 = 6
Difference = 6,000 – 6 = 5,994
ii) Place value of ‘6’ in ten lakhs palce = 6 x 10,00,000 = 60,00,000
Face value of 6 = 6
Difference = 60,00,000 – 6 = 59,99,994

Students can go through AP Board 6th Class Maths Notes Chapter 12 Data Handling to understand and remember the concepts easily.

AP State Board Syllabus 6th Class Maths Notes Chapter 12 Data Handling

→ Data: Information which is in the shape of numbers or words or pictures which help us in taking decisions is called data.
If data is expressed in numbers it is called numerical data.
Eg: The marks obtained by five students at an examination is 25, 32, 28,14 & 24.
If data is expressed in words it is called data in words.
Eg : The colours liked by some students are Red, black, pink, white, etc.

→ Frequency: Number of times a particular observation occurs in a given data is called its frequency.

→ Frequency distribution table: A table showing the frequency or count of various items is called a frequency distribution table.
A data can be arranged in a tabular form using tally marks. The data arranged in a tally table is easy understood and interpret.

→ Pictograph: If a data is arranged using pictures, then it is called a pictograph.

→ Bar graph: If a data is arranged using rectangles, then it is called a bar graph.
The rectangles can be either vertical or horizontal in a bar graph.

→ Scale: Scale is a convenient way to represent the data. It quantifies what a single unit represents in a given bar graph or pictograph.

Students can go through AP Board 6th Class Maths Notes Chapter 11 Perimeter and Area to understand and remember the concepts easily.

AP State Board Syllabus 6th Class Maths Notes Chapter 11 Perimeter and Area

→ Perimeter: The perimeter of a polygon is sum of all its sides.
The perimeter of an equilateral triangle is P = 3 × side
The perimeter of a rectangle P = 2 (length + breadth)
And its area A = length × breadth A = l × b
The perimeter of a square is P = 4 × side And its area A = side × side (or)
A = s × s The circumference of a circle C = 2πr where r is the radius of the circle.

→ Area: The region occupied by a plane figure is called its area.
To find the area of a complex figure, we divide the given shape into the combination of rectangles, squares and triangles where ever necessary.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 2 Whole Numbers Ex 2.3 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 2nd Lesson Whole Numbers Exercise 2.3

Question 1.
Study the pattern.

1 × 8 + 1 = 9
12 × 8 + 2 – 98
123 × 8 + 3 = 987
1234 × 8 + 4 = 9876
12345 × 8 + 5 = 98765

Write the next four steps. Can you find out how the pattern works?
Answer:

12 × 8 + 2 = 98
123 × 8 + 3 = 987
1234 × 8 + 4 = 9876
12345 × 8 + 5 = 98765
123456 × 8 + 6 = 987654
1234567 × 8 + 7 = 9876543
12345678 × 8 + 8 = 98765432
123456789 × 8 + 9 = 987654321

The digits on the L.H.S. are in increasing order and the digits on the result (right side) are in decreasing order.

Question 2.
How would we multiply the numbers 13680347, 35702369 and 25692359 with 9 mentally? What is the pattern that emerges?
Answer:
i) 13680347 × 9 = 13680347 × (10 – 1)
Distributive property of multiplication over subtraction.
= 13680347 × 10 – 13680347 × 1
= 136803470 – 13680347
= 123123123

ii) 35702369 × 9 = 35702369 × (10 – 1)
Distributive property of multiplication over subtraction.
= 35702369 × 10 – 35702369 × 1
= 357023690 – 35702369
= 321321321

iii) 25692359 × 9 = 25692359 × (10 – 1)
Distributive property of multiplication over subtraction.
= 25692359 × 10 – 25692359 × 1
= 256923590 – 25692359
= 231231231

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 2 Whole Numbers Ex 2.2 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 2nd Lesson Whole Numbers Exercise 2.2

Question 1.
Find the sum by suitable rearrangement.
i) 238 + 695 + 162
ii) 154 + 197 + 46 + 203
Answer:
i) 238 + 695 + 162 = 238 + 162 + 695 (Commutative property)
= (238 + 162) + 695 (Associative property)
= 400 + 695
= 1095

ii) 154 + 197 + 46 + 203 = 154 + 46 + 197 + 203 (Commutative property)
= (154 + 46) + (197 + 203) (Associative property)
= 200 + 400
= 600

Question 2.
Find the product by suitable rearrangement.
i) 25 × 1963 × 4
ii) 20 × 255 × 50 × 6
Answer:
i) 25 × 1963 × 4 = 25 × (1963 × 4)
= 25 × (4 × 1963) (Commutative property)
= (25 × 4) × 1963 (Associative property)
= 100 × 1963 = 196300

ii) 20 × 255 × 50 × 6 = 20 × 50 × 255 × 6 (Commutative property)
= (20 × 50) × (255 × 6) (Associative property)
= 1000 × 1530
= 15,30,000

Question 3.
Find the product using suitable properties.
1)205 × 1989 ii) 1991 × 1005
Answer:
i) 205 × 1989 = (200 + 5) × 1989
(Distributive property of multiplication over addition)
= (200 × 1989) + (5 × 1989)
= 397800 + 9945
= 407745

ii) 1991 × 1005
= 1991 × (1000 + 5)
Distributive property of multiplication over addition.
= (1991 × 1000)+ (1991 × 5)
= 1991000 + 9955
= 2000955

Question 4.
A milk vendor supplies 56 liters of milk in the morning and 44 liters of milk in the evening to a hostel. If the milk costs Rs. 50 per liter, how much money he gets per day?
Answer:
Capacity of milk supplied in the morning = 56 l
Capacity of milk supplied in the evening = 44 l
Total capacity of milk supplied in one day = (56 + 44)l
Cost of one liter milk = Rs. 50
Cost of (56 + 44) liters milk =(56 + 44) × 50
= 100 × 50
= Rs. 5000
∴ Money got by vendor per day = Rs. 5000

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 2 Whole Numbers Ex 2.1 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 2nd Lesson Whole Numbers Exercise 2.1

Question 1.
How many whole numbers are there in between 27 and 46?
Answer:
Number of whole numbers upto 27 is 28 (from zero to 27)
Number of whole numbers upto 45 is 46 (excluding 46)
Number of whole numbers between 27 and 46 = 46 – 28 = 18
They are 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45.

Question 2.
Find the following using number line.
i) 6 + 7 + 7
ii) 18 – 9
iii) 5 × 3
Answer:
i) 6 + 7 + 7
Answer:
Draw the number line starting from zero (0).

Starting from 6, we make 7 jumps to the right of 6 on the number line. Then we reach 13. Again make 7 jumps to the right of 13. Then we reach 20.
So, 6 + 7 + 7 = 20

ii) 18 – 9
Answer:

Draw the number line starting from zero (0).
Start from 18. We make 9 jumps to the left of 18 on the number line.
Then we reach 9.
So, 18 – 9 = 9

iii) 5 × 3
Answer:

Draw the number line starting from zero (0).
Start from 0 and make 3 jumps to the right of the zero on the number line.
Now, treat 3 jumps as one step.
So, to make 5 steps (i.e., 3, 6, 9, 12 and 15) move on the right side, we read 15 on the number line.
So, 5 × 3 = 15

Question 3.
In each pair, state which whole number on the number line is on the right of the other number.
i) 895, 239
Answer:
As 239 < 895, we conclude that 895 is on the RHS of 239.

895 is right of 239 on the number line.

ii) 1001, 10001
Answer:
As 1001 < 10001, we conclude that 10001 is on the RHS of 1001.

10001 is right of 1001 on the number line.

iii) 15678, 4013
Answer:
As 4013 < 15678, we can say that 15678 is on the RHS of 4013.

15,678 is right of 4,013 on the number line.

Question 4.
Mark the smallest whole number on the number line.
Answer:
We know that zero is the smallest whole number mark it on the number line.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 1 Numbers All Around us Unit Exercise Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 1st Lesson Numbers All Around us Unit Exercise

Question 1.
Write each of the following in numeral form.
i) Hundred crores hundred thousands and hundred.
Answer:
Indian system: 100,01,00,100.

ii) Twenty billion four hundred ninety seven million pinety six thousands four hundred seventy two.
Answer:
20,497,096,472

Question 2.
Write each of the following in words in both Hindu-Arabic and International system.
i) 8275678960
ii) 5724500327
iii) 1234567890
Answer:
i) 8275678960
Hindu – Arabic system: 827,56,78,960
Eight hundred twenty seven crores fifty six lakhs seventy eight thousand nine hundred and sixty.
International system: 8,275,678,960
Eight billion two hundred seventy five million six hundred seventy eight thousand nine hundred and sixty.

ii) Hindu-Arabic system: 572,45,00,327
Five hundred seventy two crores forty five lakhs three hundred and twenty seven. International system: 5,724,500,327
Five billion seven hundred twenty four million five hundred thousand three hundred and twenty seven,

iii) 1234567890
Hindu-Arabic system: 123,45,67,890
One hundred twenty three crores forty five lakhs sixty seven thousand eight hundred and ninety.
International system: 1,234,567,890
One billion two hundred thirty four million five hundred sixty seven thousand eight hundred and ninety.

Question 3.
Find the difference between the place values of the two eight’s in 98978056.
Answer:
Place values of 8 in Hindu-Arabic system of the given number are 8,000 and 80,00,000
Difference = 80,00,000 – 8,000 = 79,92,000
Place values of 8 in International system of the given number are 8000 and 8,000,000
Difference = 8,000,000 – 8,000 = 79,92,000

Question 4.
How many 6 digit numbers are there in all?
Answer:
Number of 6 digit numbers = greatest 6 digit number – greatest 5 digit number
= 9,99,999 – 99,999 = 9,00,000.

Question 5.
How many thousands make one million?
Answer:
1000 thousands can make one million.
1 Million = 1000 Thousands.

Question 6.
Collect ‘5’ mobile numbers and arrange them in ascending and descending order.
Answer:
Let the 5 mobile numbers are: 9247568320, 9849197602, 8125646682, 6305481954, 7702177046
Ascending order: 6305481954, 7702177046, 8125646682, 9247568320, 9849197602
Descending older: 9849197602, 9247568320, 8125646682, 7702177046, 6305481954

Question 7.
Pravali has one sister and one brother. Pravali’s father earned one million rupees and wanted to distribute the amount equally. Estimate approximate amount each will get in lakhs and verify with actual division.
Answer:
One million = 10,00,000 = 10 lakhs
Pravali’s father distributed 10 lakhs amount to his 3 children equally.
So, the share of each children = 10 lakhs ÷ 3 = Rs. 3,33,333
= Rs. 3,00,000 (approximately)

Question 8.
Government wants to distribute Rs. 13,500 to each farmer. There are 2,27,856 farmers in a district. Calculate the total amount needed for that district. (First estimate, then calculate)
Answer:

Question 9.
Explain terms Cusec, T.M.C, Metric tonne, Kilometer.
Answer:
a) Cusec: A unit of flow equal to 1 cubic foot per second.
1 Cusec = 0.028316 cubic feet per second = 28.316 litre per second.
Cusec is the unit to measure the liquids in large numbers quantity.

b) TMC: TMC is the unit to measure the water in large quantity.
TMC means Thousand Million Cubic feet.
1 TMC = 0.28316000000 litre
= 28.316 billion litre
= 2831.6 crores litre

c) Metric tonne: Metric tonne is the unit of weight.
Metric tonne = 1000 kg = 10 quintals
We should use this unit in measuring crops, paddy, dall, etc.

d) Kilometer: Kilometre is the unit of length.
1 kilometer = 1000 meters.
We should use this unit is measuring distance between villages, towns, cities,…. etc.

AP State Syllabus AP Board 6th Class Maths Solutions Chapter 1 Numbers All Around us Ex 1.4 Textbook Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 1st Lesson Numbers All Around us Exercise 1.4

Question 1.
Write some daily life situation where we can use large numbers.
Answer:
We should use large number in our daily life in
a) Counting money at banks, etc.
b) Population of the city or state or country or world.
c) Austronautical distances, etc.

Question 2.
A box of medicine contains 3,00,000 tablets each weighing 15mg. What is the total weight of all the tablets in the box in grams and in kilograms?
Answer:
Weight of a tablet = 15 mg
Weight of 3,00,000 tablets = 300000 × 15
Weight of one box of tablets = 45,00,000 mg
we know 1000 mg = 1 gram
To convert mg into grams we have to divide grams by 1000 mg = 45,00,000 ÷ 1000
Weight of one box of tablets in grams = 4500 grams.
We know 1000g = 1kg
To convert ‘g’ into kilograms we have to divide kilograms by 1000g = \(\frac{4500}{1000}\) = 4.5 kg

Question 3.
Damodhar wants to buy onions in Kurnool market. Each onion bag weighs 45 kg. He loaded 326 onion bags with 45kg in a lorry. Find the total weight of onions in kilograms and quintals.
Answer:
Weight of one bag onions = 45 kg
Weight of 326 bag onions = 326 × 45 = 14,670 kg
We know, 100 kg = 1 quintal.
To convert kgs into quintal we have to divide kgs by 100
= 14670 ÷ 100 = 146.7 quintals.

Question 4.
The population of 4 South Indian States according to 2011 Census:
Andhra Pradesh: 8,46,65,533, Karnataka: 6,11,30,704, Tamil Nadu: 7,21,38,958 and Kerala: 3,33,87,677. What is the total population of South Indian States?
Answer:
Population of Andhra Pradesh = 8,46,65,533
Karnataka = 6,11,30,704
TamilNadu = 7,21,38,958
Kerala = 3,33,87,677
Total population of 4 states = 25,13,22,872

Question 5.
A famous cricket player has so far scored 28,754 runs in International matches. He wishes to complete 50,000 runs in his career. How many more runs does he need?
Answer:
Number of runs wishes to complete = 50,000
Number of runs scored by the player = 28,754
Number of runs needed = 50,000 – 28,754 = 21,246 runs

Question 6.
In an election, the successful candidate registered 1,32,356 votes and his nearest rival secured 42,246 votes. Find the majority of successful candidate.
Answer:
Number of votes secured by the winner = 1,32,356
Number of votes secured by the rival = 42,246
Number of more votes secured by the winner = 1,32,356 – 42,246 = 90,110
Majority of the winner = 90,110 votes.

Question 7.
Write the greatest and smallest six digit numbers formed by all the digits 6, 4, 0, 8, 7, 9 and find the sum and difference of those numbers.
Answer:
Given digits are 6, 4, 0, 8, 7, 9
The greatest number formed by the digits = 9,87,640
The smallest number formed by the digits = 4,06,789
Sum of the numbers = 9,87,640 + 4,06,789 = 13,94,429
Difference between numbers = 987640 – 406789 = 580851

Question 8.
Haritha has Rs. 1,00,000 with her. She placed an order for purchasing 124 ceiling fans at Rs. 726 each. How much money will remain with her after the purchase?
Answer:
Cost of each fan = Rs. 726
Cost of 124 fans = 726 × 124 = Rs. 90,024
Money with Haritha = Rs. 1,00,000
Cost of 124 fans = Rs. 90,024
Remaining money after purchasing = Rs. 9,976

Students can go through AP Board 6th Class Maths Notes Chapter 5 Fractions and Decimals to understand and remember the concepts easily.

AP State Board Syllabus 6th Class Maths Notes Chapter 5 Fractions and Decimals

→ Fraction: A fraction is a numerical representation of apart of a whole. The whole may be a single object or a group of objects.
Eg: \(\frac{4}{7}\).
The fraction \(\frac{4}{7}\) represents four out of seven.
In the fraction \(\frac{4}{7}\), 4 is called the numerator and 7 is called the denominator.

→ Proper fraction: A fraction in which the numerator is less than its denominator is called a proper fraction.
Eg: \(\frac{1}{7}\), \(\frac{2}{5}\), \(\frac{3}{11}\), …..
All proper fractions are less than 1.

→ Improper fraction: A fraction in which the numerator is greater than its denominator is called an improper fraction.
Eg: \(\frac{5}{11}\), \(\frac{4}{7}\), \(\frac{2}{3}\),….
All improper fractions are greater than or equal to 1.

→ Mixed fraction: A mixed fraction is a combination of a whole number and a proper fraction.
Fraction in lowest terms: A fraction is said to be in its lowest terms if the numerator and the denominator have no factors in common other than 1.
Eg: \(\frac{2}{11}\), \(\frac{3}{7}\), \(\frac{18}{25}\),……
Equivalent fractions: Two fractions are said to be equivalent if they have same numerators and same denominators respectively when expressed in their lowest terms.
Eg : \(\frac{2}{5}\) & \(\frac{8}{20}\)
Equivalent fractions have the same value.

→ Like fractions:
Fractions with the same denominators are called like fractions
Eg: \(\frac{3}{13}\), \(\frac{4}{13}\), \(\frac{7}{13}\), \(\frac{21}{13}\), ….

→ Un-like fractions:
Fractions with different denominators are called like fractions.
Eg: \(\frac{7}{11}\), \(\frac{3}{5}\), \(\frac{9}{17}\), ….

→ Comparison of fractions:

• Out of two fractions with the same denominators (like fractions), the fraction with the smallest numerator is smaller than the other.
• Similarly out of two fractions with the same denominators (like fractions), the fraction with the greatest numerator is greater than the other.
  Eg: \(\frac{2}{11}\) < \(\frac{5}{11}\) \(\frac{9}{17}\) > \(\frac{4}{17}\)
• Out of two given fractions with the same numerator, the fraction with smaller denominator is greater than the other.
• Similarly out of two given fractions with the same numerator, the fraction with greater denominator is smaller than the other.
  Eg: \(\frac{11}{2}\) > \(\frac{11}{5}\) \(\frac{13}{8}\) < \(\frac{13}{11}\)
• To compare unlike fractions, convert them in to like fractions with L.C.M. as the same denominators, and then compare the like fractions.
  Eg: \(\frac{2}{3}\) and \(\frac{4}{5}\).
  LCM of 2, 5 is 15
  \(\frac{2}{3}\) = \(\frac{10}{15}\) \(\frac{4}{5}\) = \(\frac{12}{15}\)
  Now \(\frac{10}{15}\) < \(\frac{12}{15}\) there by \(\frac{2}{3}\) < \(\frac{4}{5}\)

→ Addition and subtraction of like fractions:

• To add like fractions we add their numerators while retaining the common denominator. Eg: \(\frac{5}{7}\) + \(\frac{2}{7}\) = 5 + \(\frac{2}{7}\) = \(\frac{7}{7}\)
• To subtract like fractions we subtract their numerators while retaining the common denominator.
  Eg: \(\frac{6}{13}\) – \(\frac{2}{13}\) = 6 – \(\frac{2}{13}\) = \(\frac{4}{13}\)

→ Addition and subtraction of un-like fractions:

• Convert the given unlike fractions in to like fractions, (denominator = LCM of given denominators)
• Now add or subtract as we do in case of like fractions.
• To multiply a fraction with a whole number, first multiply the numerator of the fraction by the whole number while keeping the denominator the same.
  Eg: \(\frac{3}{4}\) × 5 = 3 × \(\frac{5}{4}\) = \(\frac{15}{4}\)
  8 × \(\frac{2}{3}\) = 8 × \(\frac{2}{3}\) = \(\frac{16}{3}\)

→ Multiplication of two fractions = product of numerators/product of denominators
Eg: \(\frac{5}{6}\) × \(\frac{4}{9}\) = 5 × \(\frac{4}{6}\) × 9 = \(\frac{20}{54}\)

• The product of any two proper fractions is always less than each of its fraction.
  Eg: \(\frac{1}{5}\) × \(\frac{2}{7}\) = \(\frac{2}{35}\), \(\frac{2}{35}\) < \(\frac{1}{5}\) & \(\frac{2}{35}\) < \(\frac{2}{7}\)
• The product of any two improper fractions is always greater than each of its fraction.
  Eg: \(\frac{7}{3}\) × \(\frac{5}{2}\) = \(\frac{35}{6}\) \(\frac{7}{3}\) < \(\frac{35}{6}\) \(\frac{5}{2}\) < \(\frac{35}{6}\)
• The product of a proper fraction and an improper fraction is always greater than its proper fraction and less than its improper fraction.
  Eg: \(\frac{2}{5}\) × \(\frac{7}{4}\) = \(\frac{14}{20}\) \(\frac{2}{5}\) < \(\frac{14}{20}\) < \(\frac{7}{4}\)

→ Reciprocal of a fraction: A fraction obtained by interchanging the numerator and the denominator of a given fraction is called its reciprocal fraction.
Eg: Reciprocal of \(\frac{3}{4}\) is \(\frac{4}{3}\)
\(\frac{1}{a}\) of b means \(\frac{1}{a}\) × b = \(\frac{b}{a}\)

→ Division of a whole number by a fraction: To divide a whole number by a fraction we multiply the given whole number by the reciprocal of the given fraction.
Eg: 5 ÷ \(\frac{3}{4}\) = 5 × \(\frac{20}{5}\) = \(\frac{4}{5}\)

• Any two non-zero numbers whose product is equal to 1 are called reciprocals to each other.
  Eg: \(\frac{3}{7}\) and \(\frac{7}{3}\) are reciprocals to each other.
• To divide a whole number by a mixed fraction, first convert the mixed fraction into improper fraction and then multiply the whole number with the reciprocal of the improper fraction.
  Eg: 7 ÷ 3\(\frac{2}{5}\) = 7 ÷ \(\frac{17}{5}\) = 7 × \(\frac{5}{17}\) = \(\frac{35}{17}\)

→ Division of a fraction by a whole number:

• To divide a fraction by a whole number we multiply the given fraction by the reciprocal of the given whole number.
  Eg: \(\frac{5}{4}\) ÷ 3 = \(\frac{5}{4}\) × \(\frac{1}{3}\) = \(\frac{5}{12}\)
• To divide a mixed fraction by a whole number, first convert the mixed fraction into an improper fraction and then multiply the improper fraction by the reciprocal of whole number.
  Eg : 4\(\frac{3}{4}\) ÷ 8 = \(\frac{19}{4}\) × \(\frac{1}{8}\) = \(\frac{19}{32}\)

→ Division of a fraction by another fraction: To divide a fraction by another fraction, we multiply the first fraction with the reciprocal of the second fraction.
E.g: \(\frac{3}{5}\) ÷ \(\frac{7}{11}\) = \(\frac{3}{5}\) × \(\frac{11}{7}\) = \(\frac{33}{35}\)

→ Decimal numbers or Decimal fractions: A decimal is a way of expressing a fraction.
The fraction \(\frac{1}{10}\) is written as 0.1 in decimal form.

Examples for decimal numbers: 0.7, 0.4, 0.23, ..etc The decimal number 0.7 is read as zero point seven.
The decimal number 5.8 is read as five point eight.
The dot or the point between the two digits is called the decimal point.
The number of digits after decimal point is called the number of decimal places. Decimal places of 5.247 is 3.
The decimal point separates a decimal number into two parts. The number on its left as integer part and the digits on its right as decimal part.
The decimal part of a decimal number is always less than 1. As we move from left to right each decimal place decreases by tenth of its previous value.
The decimal places after the decimal point are (\(\frac{1}{10}\)-tenths), (\(\frac{1}{100}\)-hundreths), (\(\frac{1}{1000}\)-thousandths) and so on.

These are also called the place values of the decimal part.
If we divide a whole number into ten equal parts each part of the whole represents tenths part. \(\frac{1}{10}\)
If we divide a whole number into hundred equal parts each part of the whole represents hundredths part. \(\frac{1}{100}\)
If we divide a whole number into thousand equal parts each part of the whole represents thousandths part. \(\frac{1}{1000}\)

→ Converting fractions into decimals and vice versa:
Fractions with denominators 10, 100, 1000 can be easily converted into decimals by placing decimal point in the numerator accordingly.

• If the denominator is 10, then we place the decimal point in the numerator after one digit from RHS. The number of decimal places is equal to 1.
  Eg: \(\frac{256}{10}\) = 25.6
• If the denominator is 100, then we place the decimal point in the numerator after two digits from RHS. The number of decimal places is equal to two.
  Eg: \(\frac{256}{100}\) = 2.56
• If the denominator is 1000, then we place the decimal point in the numerator after three digits from RHS, The number of decimal places is equal to three.
  Eg: \(\frac{256}{1000}\) = 0.256 and read as zero point two five six.

→ Decimals Can Also be converted into Conversion of simple fractions into decimal fractions:
To convert simple fractions into decimal numbers:
To convert simple fractions into decimal numbers first convert the denominators to 10/100/1000 accordingly and then place the decimal point in the numerator as required.
Eg: \(\frac{23}{2}\) = 23 × \(\frac{5}{10}\) = \(\frac{115}{10}\) = 11.5
\(\frac{7}{4}\) = 7 × \(\frac{25}{100}\) = \(\frac{175}{100}\) = 1.75
\(\frac{3}{5}\) = 3 × \(\frac{2}{10}\) = \(\frac{6}{10}\) = 0.6
Writing zeroes at the end of a decimal number does not change its value.
Eg: 5.2 = 5.20 = 5.200 = 5.2000 and so on
Like and unlike decimal fractions:
Decimals having the same number of decimal places are called like decimals.
Eg: 3.2,5.6,4.8.
Decimals having the different number of decimal places are called unlike decimals. Eg : 5.23, 8.3, 4.214
Unlike decimals can be converted into like decimals by converting them into equivalent decimals.
Eg: 2.7 & 6.54
2.7= 2.70 and now-2.70 and 6.54 are like decimals.

→ Comparing and ordering of decimals:
To compare the given decimals
a) First convert them to like decimals.
b) Now compare the integer / whole number part. The number with greater whole part is greater than the other.
c) If the whole / integer parts are equal, then compare the tenths digits. The number with greater tenths digit is greater than the other.
d) If the tenths digits are also equal, then compare the hundredths digits. The number with greater hundredths digit is greater than the other.
e) If the hundredths digits are also equal, then compare the thousandths digits. The number with greater thousandths digit is greater than the other.
Eg : 54.235 and 54.238
54.235 < 54.238

→ Addition and subtraction of decimal fractions:
To add or subtract the given decimal fractions first convert them into like decimals. Now add / subtract the digits in the corresponding place values.

→ Uses of decimals: Decimal fractions are used in expressing money, distance, weight and capacity.

Students can go through AP Board 6th Class Maths Notes Chapter 4 Integers to understand and remember the concepts easily.

AP State Board Syllabus 6th Class Maths Notes Chapter 4 Integers

→ Positive numbers: All numbers which are greater than zero are called positive numbers {1, 2, 3, …..}

→ Negative numbers: In our real life we come across many situations where in we have to use numbers whose value is less than zero; such numbers are called negative numbers.
Example: Very low temperature, loss in a business, depth below a surface, etc. Negative numbers are represented by the minus symbol

→ Zero is neither a negative number nor a positive number.

→ Integers: The set of positive numbers, zero along with the set of negative numbers are called Integers. The set of integers is denoted by I or Z.
I = Z = {…. 4, -3, -2, -1, 0, 1, 2, 3,…..}

→ Historical Notes: Brahma Gupta (598 – 670 AD), Indian mathematician first used a special sign (-) for negative numbers and stated rules for operations on negative numbers.
The letter ”Z” was first used by the Germans because the word for Integers in the language is Zehlen which means NUMBER.

→ Representation of Integers on a number line:

On a number line all negative numbers lie on the left side of zero. All positive numbers lie on right side of zero.
A number line extends on either side endlessly.
All whole numbers are called non-negative integers.
The natural numbers are called positive integers.

On a number, of the given two numbers the number on LHS is always less than the number on the RHS.

On a number line as we move from left to right the value of numbers goes on increasing and vice versa.
A number line can be written in a vertical direction as given below.

Students can go through AP Board 6th Class Maths Notes Chapter 3 HCF and LCM to understand and remember the concepts easily.

AP State Board Syllabus 6th Class Maths Notes Chapter 3 HCF and LCM

→ Divisibility Rules:
A divisibility rule is a process by which we can determine whether a given number is completely divisible by other given number or not without performing actual division.
Reasons behind the rules:
Our number system is based on base 10 system. Every place value increases by 10-times as move from right to left.

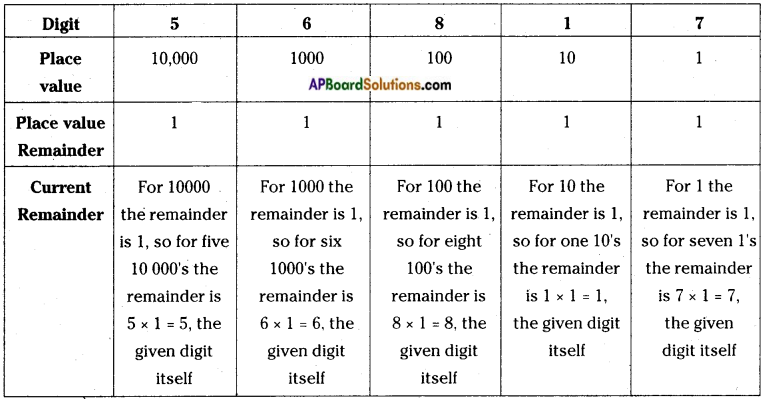
→ Divisibility rule for 2: In the above place value table except ones place all other places namely 100/1000/10 000…. are completely divisible by 2. So for divisibility by 2 we need to check the unit digit only.
A number is divisible by 2 if it has any of the digits 0, 2, 4 or 8 in its units place.
In other words all even numbers are divisible by 2.

→ Divisibility rule for 3:
10/3 → not divisible
100/3 → not divisible
1000/3 → not divisible and it goes on..
But in all the cases, the remainder is 1. As such if the number 56817 is divided by 3 we get remainder, 5, 6, 8, 1 and 7 respectively. The sum of these remainders 5 + 6 + 8 + 1 + 7 = 27 is divisible by 3 as is the number is divisible by 3.
In other words if the sum of the digits of a given number is divisible by 3, then the given number is also divisible by 3.
The digital root of natural number is the single digit value obtained by repeated process of summing digits.

Example: The digital root of 325698 is 3 + 2 + 5 + 6 + 9 + 8 = 33 = 3 + 3 = 6
Note: While adding the digits of a number we can ignore 9’s or combinations of digits summing up to 9.

Example: The digital root of 87459634572 is
By dropping (4+5), (9), (6+3), (4+5), (7+2), the remaining digits are 8 & 7. From these digits eliminate 9 that is 8 + 7 – 9 = 15 – 9 = 6
Therefore the digital root of 87459634572 is 6. Hence divisible by 3.

Now add these digits to get the total remainder. If this remainder is completely divisible by 3, then the given number is also divisible by 3.

Divisibility rule of 3 will add the digits and then check if its divisible by 3. This is applicable for numbers which leaves remainder 1 when 10 is divided by that number.

→ Divisibility rule for 4: In the place value table starting from 100, all other higher places namely 1000/10 000/100 000, …etc. are all completely divisible by 4. So we need to check the digits in ten’s and unit’s place for divisibility by 4.

A number is divisible by 4 if the number formed by the digits in its ten’s place and unit’s place taken in the same order is divisible by 4 and also zeros on both places.

Example: Is the number 87534 divisible by 4?
Number formed by last two digits 34 is not divisible by 4 and hence the given number is also not divisible by 4.

Example : Is the number 779956 divisible by 4?
Number formed by last two digits 56 is divisible by 4 and hence the given number is also divisible by 4.

→ Divisibility rule for 5: In the place value table starting from 10, all other higher places namely 10/100/1000/10000/1 00 000, ..’etc. are all completely divisible by 5. So we need to check the digits in unit’s place for divisibility by 5.
A number is divisible by 5 if the number ends in either zero of 5.

Example: Is the number 779956 divisible 5?
The digit in unit’s place is 6, so it is not divisible by 5.

Example: Is the number 77995 divisible by 5?
The digit in unit’s place is 5, so it is divisible by 5.

Example: Is the number 779950 divisible by 5?
The digit in unit’s place is 0, so it is divisible by 5.

→ Divisibility rule for 6 : If a number is divisible by both 2 and 3, then it is also divisible by 6.
Example: Is the number 612432 divisible by 6?
As the given number is an even number it is divisible by 2.
Also the digital root of the number is 3, it is divisible by 6.
Hence it is divisible by 6.
In other words if a number is divisible by two relatively prime numbers, then their product also divides the given number.

→ Divisibility rule for 8: In the place value table starting from 1000, all other higher places namely 10 000/1 00 000…etc., are all completely divisible by 8. So we need to check the digits in hundred’s, ten’s and unit’s place for divisibility by 8.
A number is divisible by 8 if the number formed by the digits in its hundred’s place, ten’s place and unit’s place taken in the same order is divisible by 8, are also zeros on three places.
Example: Is the number 875344 divisible by 8?
Number formed by last three digits 344 is divisible by 8 and hence the given number is also divisible by 8.

→ Divisibility rule for 9: The rule is same as rule for 3
10/9 → not divisible
100/9 → not. divisible
1000/9 → not divisible and it goes on ..
But in all the cases, the remainder is 1. As such if the number 56817 is divided by 9 we get remainder, 5, 6, 8, 1 and 7 respectively. The sum of these remainders 5 + 6 + 8 + 1 + 7 = 27 is divisible by 9 as is the number is divisible by 3.

In other words if the sum of the digits of a given number is divisible by 9, then the given number is also divisible by 9.
The digital root of natural number is the single digit value obtained by repeated process of summing digits.

Example: The digital root of 325698 is 3 + 2 + 5 + 6 + 9 + 8 = 33 = 3 + 3 = 6
Note: While adding the digits of a number we can ignore 9’s or combinations of digits summing up to 9.

Example: Is the number 7854963 divisible by 9?
The digital root of the given number is 7 + 8 + 5 + 4 + 9 + 6 + 3 = 42 = 4 + 2 = 6, not divisible by 9.

→ Divisibility rule for 10: In the place value table starting from 10, all other higher places namely 10/100/1000/10000/100000…etc., are all completely divisible by 10. So we need to check the digits in unit’s place for divisibility by 10.
A number is divisible by 10 if the number ends in zero.
Example: Is the number 779956 divisible 10?
The digit in unit’s place is 6, so it is not divisible by 10.

Example: Is the number 779950 divisible 10?
The digit in unit’s place is 0, so it is divisible by 10.

→ Divisibility rule for 11: A number is divisible by 11, if the difference between the sum of digits at even places and the sum of digits at odd place is either zero or a multiple of 11.
Example: Is the number 52487 divisible 11?
Sum of the digits at odd places = 7 + 4 + 5 = 16 Sum of the digits at even places = 8 + 2 = 10 Difference = 16 – 10 = 6, not divisible by 11.
Note: If two numbers are divisible by a given number, then their sum, difference and the product are also divisible by that number.

→ Factor: A factor of a number is an exact divisor of that number.
Example: 15 = 5 × 3, here 5 divides 15 completely and 3 divides 15 completely. As such 1, 3, 5, 15 are factors of 15.
Also 15 = 1 × 15. It means 1 is a factor of every number and every number is a factor of itself.
Every factor of a number is less than or equal to the number.
Perfect number: A number for which the sum of all its factors is equal to twice the number is called a perfect number.
Example: 6 = 1 × 6
= 2 × 3, here 1, 2,3 and 6 are factors whose sum is (1 + 2 + 3 + 6 = 12) 12, twice the given number 6. So 6 is a perfect number.
6, 28, 496, 8128…… are perfect numbers. Euclid has given a formula to derive perfect
numbers.
If q is a prime of the form 2p – 1 where p is a prime, then q(q+1)/2 is an even perfect number.

→ Multiple: Multiples of a given number can be obtained by multiplying the given number with natural numbers i.e. 1, 2, 3, 4, …. etc.
Example: Multiple of 6 are:
= 6 × 1, 6 × 2, 6 × 3, 6 × 4, …..
= 6, 12, 18, 24, …..

→ Prime number: Numbers having only two factors namely one and itself are called prime numbers.
A prime number is a whole number that has exactly two factors, 1 and itself.
Example: 2, 3, 5, 7, 11,
All the above numbers have only two factors namely 1 and itself.
We can write infinitely many prime numbers.
2 is the only even prime number. Also 2 is the smallest prime number.

→ Composite number: Numbers having more than two factors are called composite numbers.
Example: 4, 6, 8, 9, ….
1 is neither a prime number nor a composite number.
The Sieve of Eratosthenes is an ancient algorithm that can help us find all prime numbers up to any given limit.

→ How does the Sieve of Eratosthenes work?
The following example illustrates how the Sieve of Eratosthenes, can be used to find all the prime numbers that are less than 100.
Step 1: Write the numbers from 1. to 100 in ten rows as shown below.
Step 2: Cross out 1 as 1 is neither a prime nor a composite number.
Step 3: Circle 2 and cross out all the multiples of 2. (2, 4, 6, 8, 10, 12, ….)
Step 4: Circle 3 and cross out all the multiples of 3. (3, 6, 9, 12, 15, 18, ….)
Step 5: Circle 5 and cross out all the multiples of 5. (5, 10. 15, 20, 25, ….)
Step 6: Circle 7 and cross out all multiples of 7. (7, 14, 21. 28, 35, ….)
Circle all the numbers that are not crossed out and they are the required prime numbers less than 100.

Alternate method:
Finding prime numbers upto 100

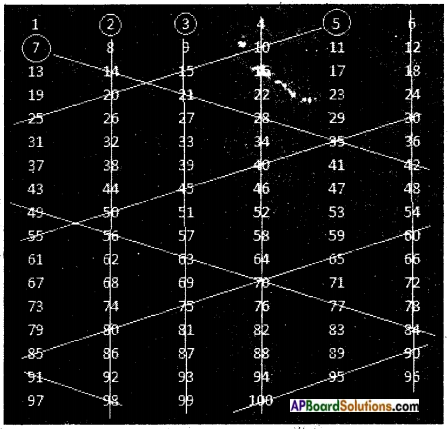
First arrange the numbers from 1 to 100 in a table as shown above.
Enter 6 numbers in each row until the last number 100 is reached.
First we select a number and we strike off all the multiples of it.
Start with 2 which is greater than 1.
Round off number 2 and strike off entire column until the end.
Similarly strike off 4th column and 6th column as they are divisible by 2.
Now round off next number 3 and strike off entire column until end.
The number 4 is already gone.
Now round off next number 5 and strike off numbers in inclined fashion as shown in the figure (they are all divisible by 5). When striking off ends in some row, start again striking off with number in another end which is divisible by 5. New striking off line should be parallel to previous strike off line as. shown in the figure.
The number 6 is already gone.
Now round off number 7 and strike off numbers as we did in case of number 5.
8,9,10 are also gone.
Stop at this point.
Count all remaining numbers. Answer will be 25.

→ Prime numbers
There are 25 prime numbers less than 100.
These are:

What if we go above 100? Around 400 BC the Greek mathematician. Euclid, proved that there are infinitely many prime numbers.

→ Co-primes: Two numbers are said to be co-prime if they have no factors in common. Example: (2, 9), (25, 28)
Any two consecutive numbers always form a pair of co-prime numbers.
Example: (7 & 8), (21 & 22), …..
Co-prime numbers are also called relatively prime number to one another.
Example: 3, 5, 8, 47 are relatively prime to one another/co-prime to each other.

→ Twin primes: Two prime numbers are said to be twin primes, if they differ by 2. Example: (3, 5), (5, 7), (11, 13), …etc.

→ Prime factorization: The process of expressing the given number as the product of prime numbers is called prime factorization.
Example: Prime factorization of 24 is
24 = 2 × 12 = 2 × 2 × 6
= 2 × 2 × 2 × 3, this way is unique.
Every number can be expressed as product of primes in a unique manner. We can factorize a given number in to product of primes in two methods. They are
a) Division method
b) Factor tree method

→ Common factors: The set of all factors which divides all the given numbers are called their common factors.
Example: Common factors to 24, 36 & 48 are 1, 2, 3, 4, 6 & 12
Factors of 24 = 1, 2, 3, 4, 6, 8, 12 & 24
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18 & 36
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24 & 48
Common factors to 24, 36 & 48 are 1, 2, 3, 4, 6 & 12
We can see that among their common factors 12 is the highest common factor. It is called H.C.F. of the given numbers. So H.C.F. of 24, 36 & 48 is 12.

→ H.C.F./G.C.D : The highest common factor or the greatest common divisor of given numbers is the greatest of their common factors.
H.C.F. of given two or more numbers can be found in two ways.
a) By prime factorization
b) By continued division
H.C.F. of any two consecutive numbers is always 1.
H.C.F. of relatively prime/co-prime numbers is always 1.
H.C.F. of any two consecutive even numbers is always 2.
H.C.F. of any two consecutive odd numbers is always 1.

→ Common multiples:
Multiples of 8: 8, 16, 24, 32, 40, 48, ….
Multiples of 12: 12, 24, 36, 48, ….
Multiples.common to 8 & 12: 24, 48; 72, 96, ….
Least among the common multiple is 24. This is called L.C.M. of 8 & 12. The number of common multiples of given two or more numbers is infinite, as such greatest common multiple cannot be determined.

→ L.C.M.: The least common multiple of two or more numbers is the smallest natural number among their common multiples.
L.C.M. of given numbers can be found by the
a) Method of prime factorization.
b) Division method.
L.C.M. of any two consecutive numbers is always equal to their product.
L.C.M. of 8 & 9 is 8 × 9 = 72
L.C.M. of co-prime numbers is always equal to their product.
L.C.M. of 8 & 15 is 8 × 15 = 120

→ Relation between the L.C.M. & H.C.F:
For a given two numbers N₁ & N₂, the product of the numbers is equal to the product of their L.C.M.(L) & H.C.F.(H)
N₁ × N₂ = L × H

Students can go through AP Board 6th Class Maths Notes Chapter 2 Whole Numbers to understand and remember the concepts easily.

AP State Board Syllabus 6th Class Maths Notes Chapter 2 Whole Numbers

→ Natural numbers: The numbers which we use for counting are called Natural numbers N= {1, 2, 3, 4, 5, 6,…} .

→ Successor: Every natural number has a successor, which is one more than it. Example : Successor of 15 is 15 + 1 = 16

→ Predecessor: Every natural number has a predecessor except 0. Predecessor of a number is one less than it.
Example: Predecessor of 56 is 56 – 1 = 55

→ Whole numbers: The natural numbers along with zero forms the set of Whole numbers.
W = {0, 1, 2, 3, 4, 5, 6,…}

• Every whole number has a successor and every whole number has a predecessor except zero.
• Every natural number is a whole number and every whole number is a natural number except zero.
• The smallest natural number is 1.
• The smallest whole number is 0.
• Addition, subtraction and multiplication can be represented on a number line.

→ Closure property: Sum of any two whole numbers is always a whole number.
Example : 5 + 3 = 8, a whole number.
This is called closure property of whole numbers w.r.t. addition.

→ Closure property: Product of any two whole numbers is always a whole number. Example : 5 × 3 = 15, a whole number.
This is called closure property of whole numbers w.r.t. multiplication.
In other words whole numbers are closed under addition and multiplication.
But whole numbers are not closed under subtraction and division.
Example: 7 – 12, is not a whole number.
9 ÷ 14, is not a whole number.
Division by zero is not defined.
Example: 5 ÷ 0, is not defined

→ Commutative property: Sum of any two whole numbers taken in any order is always same.
Example: 5 + 3 = 3 + 5 = 8
This is called commutative property of whole numbers w.r.t. addition.

→ Commutative property: Product of any two whole numbers taken in any order is always same.
Example: 5 × 3 = 3 × 5 = 15
This is called commutative property of whole numbers w.r.t. addition.
In other words whole numbers are commutative w.r.t. addition and multiplication. But whole numbers are not commutative w.r.t. subtraction and division.
Example: 4 – 9 ≠ 9 – 4 and 8 ÷ 11 ≠ 11 ÷ 8

→ Associative property: The sum of any three whole numbers taken in any or der is always same.
Example : 5 + (8 + 3) = (5 + 8) + 3 =16
This is called associative property of whole numbers w.r.t. addition.

→ Associative property: The product of any three whole numbers taken in any order is always same.
Example : 5 × (8 × 3) = (5 × 8) × 3 = 120
This is called associative property of whole numbers w.r.t. multiplication.
In other words whole numbers are associative w.r.t. addition and multiplication.
But whole numbers are not associative w.r.t. subtraction and division.
Example : 5 – (8 – 3) ≠ (5 – 8) – 3
: 5 ÷ (8 ÷ 3) ≠ (5 ÷ 8) ÷ 3

→ Distributive property of multiplication over addition:
(Example: 5 × (8 + 3) = (5 × 8) + (5 × 3) = 55

→ Additive identity: If zero is added to any whole number, then the result is the number itself.- Here zero is called the additive identity.
Example: 5 + 0 = 5, 7 + 0 = 7, 0 + 9 = 9 and so on.

→ Multiplicative identity: If any whole number is multiplied by 1, then the result is the number itself. Here one is called the multiplicative identity.
Example: 5 × 1 = 5, 7 × 1 = 7, 1 × 9 = 9 and so on.
If we represent the number 1 as a (.) dot, then a whole number can be represented either as an array of a triangle or a square.
The triangular numbers are 3, 6, 10, 15, 21, 28, ……. etc.

The square numbers are 4, 9, 16, 25, 36, …… etc.

→ Multiplication by 9/99/999/9999….etc.
74 × 99 = (74 – 1)/(9 – 7)(10 – 4) = 73/26
256 × 999 = (256 – 1)/(9 – 2)(9 – 5)(10 – 6) = 255/744
4267 × 9999 = (4267 – 1)/(9 – 4)(9 – 2)(9 – 6)(10 – 7) = 4266/5733
Here the number of 9’s in the multiplier is equal to number of digits in the multiplicand.
Answer has two parts: LHS/RHS
LHS: (Multiplicand-1)
RHS: Subtract all digits from 9 but the last digit from 10