Practice the AP 10th Class Maths Bits with Answers Chapter 12 Applications of Trigonometry on a regular basis so that you can attempt exams with utmost confidence.
AP SSC 10th Class Maths Bits 1st Lesson Chapter 12 Applications of Trigonometry with Answers
Question 1.
The ratio of the length of a rod and its shadow is 1 : √3 . Then find the angle of elevation of the sun.
Answer:
30°
Explanation:
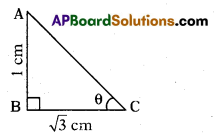
tan θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{1}{\sqrt{3}}\) = tan 30°
∴ θ = 30°
Question 2.
Find the angle ‘θ’ in the figure.
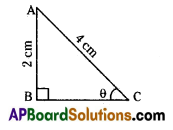
Answer:
30°
Explanation:
sin θ = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{2}{4}=\frac{1}{2}\) = sin 30°
∴ θ = 30°
Question 3.
Find the angle made by the minuteshand in a clock during a period of 20 minutes.
Answer:
120°
Explanation:
Angle made by minutes hand in 1 minute is 6°.
Angle made by minutes hand in 20 minutes is = 20 × 6 = 120°
Question 4.
If the angle of elevation of Sun is 45°, then find the length of the shadow of a 12 m high tree.
Answer:
12 m
Explanation:
tan 45° = \(\frac{\text { height of tree }}{\text { shadow of tree }}\)
⇒ Shadow of tree = 12 m
Question 5.
In the given figure, find measurement of BC.
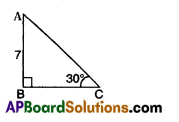
Answer:
7√3 cm
Explanation:
From figure, tan 30° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{7}{\mathrm{BC}}\) ⇒ BC = 7√3 cm
Question 6.
A boy observed 20 m away from the base of a 20 m high pole, find the angle of elevation of the top.
Answer:
45°
Explanation:
tan θ = \(\frac{20}{20}\) = 1 = tan 45° ⇒ θ = 45°
![]()
Question 7.
The length of shadow of a pole is equal to the length of the pole, then find the angle of the elevation of the Sun.
Answer:
45°
Question 8.
Ladder ‘x’ metres long is laid against a wall making an angle ‘θ’ with the ground. If we want to directly find the distance between the foot of ladder and foot of the wall, which trigonometrical ratio should be considered ?
Answer:
cos θ
Question 9.
Top of a building was observed at an angle of elevation ‘α’ from a point, which is at distance’d’ metres from the foot of the building. Which trigonometrical ratio should be considered for finding height of buildings?
Answer:
tan α
Question 10.
If the angle of elevation of sun in¬creases from 0° to 90°, then find the length of shadow of the tower.
Answer:
Decreases
Explanation:
Sine value decreases from 0° to 90°. So length of shadow of the tower also decreases.
Question 11.
A ladder touches a wall at a height of 5 m. Find the angle made by the ladder with the ground, if its length is 10 m.
Answer:
30°
Explanation:
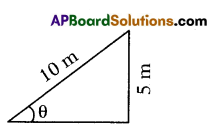
sin θ = \(\frac{5}{10}=\frac{1}{2}\)= sin 30°
∴ θ = 30°
Question 12.
x = (sec θ + tan θ), y = (sec θ – tan θ), then find xy.
Answer:
1
![]()
Question 13.
From the top of a building with height 30( √3 +1 )m two cars make angles of depression of 45° and 30° due east. What is the distance between two cars?
Answer:
60 m
Question 14.
At a point 15 m away from the base of a 15 m high pole, find the angle of elevation of the top.
Answer:
45°
Question 15.
If cosec θ + cot θ = k, then find cos θ.
Answer:
\(\frac{\mathrm{k}^{2}-1}{\mathrm{k}^{2}+1}\) = cos θ
Question 16.
A pole 6 m high casts a shadow 2√3 m long on the ground, then find the sun’s elevation.
Answer:
60°
Explanation:
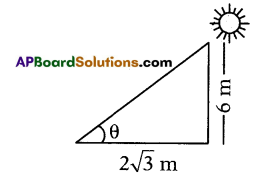
tan θ = \(\frac{6}{2 \sqrt{3}}\) = √3 = tan 60°
∴ θ = 60°
Question 17.
A tower is 50 m high. Its shadow is x m shorter when the sun’s altitude is 45°, then when it is 30°, then find x.
Answer:
100 cm
Question 18.
Suppose you are shooting an arrow from the top of a building at a height of 6m to a target on the ground at an angle of depression of 60°. What is the distance between you and the object?
Answer:
3√3 m
![]()
Question 19.
What change will be observed in the angle of elevation as.we move away from the object?
Answer:
Angle decreases.
Question 20.
In the given figure, the positions of the observer and the object are marked, find the angle of depression.
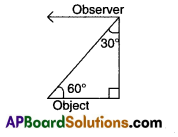
Answer:
60°
Question 21.
An object is placed above the observer’s horizontal, we call the angle between the line of sight and observer’s horizontal.
Answer:
Angle of elevation.
Question 22.
x = a sin θ, y = a cos θ, then find x2 + y2.
Answer:
a2
Question 23.
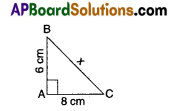
If AB = 4m and AC = 8 m, then find the angle of elevation of A as observed from C.
Answer:
30°
Explanation:
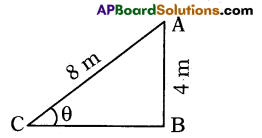
sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{4}{8}=\frac{1}{2}\) = sin 30°
∴ C = 30°
Question 24.
The given figure shows the observation of point ‘C’ from point A. Find the angle of depression from A.
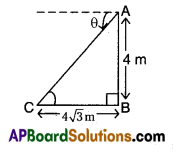
Answer:
30°
Explanation:
tan C = θ = \(\frac{4}{4 \sqrt{3}}=\frac{1}{\sqrt{3}}\) = tan = 30°
∴ θ = 30°
![]()
Question 25.
Find the angle of elevation of tower at a point 40 m apart from it is cot-1(\(\frac{3}{5}\)) . Obtain the height of the tower.
Answer:
\(\frac{200}{3}\) m
Explanation:

Question 26.
A ladder of 10 m length touches a wall at a height of 5 m. Find the angle made by it with the horizontal.
Answer:
30°
Question 27.
The ratio of length of a pole and its shadow is 1: √3 . Find the angle of elevation.
Answer:
30°
Question 28.
A wall of 8m long casts a shadow 5m long. At the same time, a tower casts a shadow 50 m long, then find the height of tower.
Answer:
80 m
Question 29.
In the below figure, find x.
Answer:
x = 10 m
Question 30.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After a flight of 10 seconds, its angle of elevation is observed to be 30° from the same point on the ground. Find the speed of the aeroplane.
Answer:
415.7 km/h
![]()
Question 31.
A building casts a shadow of length 50 √3m when the sun is 30° about the horizontal. Find the height of the building.
Answer:
50 m
Question 32.
A ladder 20 m long is placed against a vertical wall of height 10 m, then find the distance between the foot of the ladder and the wall.
Answer:
10√3 m
Question 33.
In the figure given below, if AB = 10 m and AC = 20 m, then find θ.
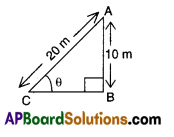
Answer:
30°
Question 34.
Find the length of the shadow of a tree is 8m long when the sun’s angle of elevation is 45°.
Answer:
8
Question 35.
Find the length of the string of a kite flying at 100m above the ground with the elevation of 60°.
Answer:
\(\frac{200}{\sqrt{3}}\)
Question 36.
In the figure given below, if AB = 10√3 m, then find CD. (take √3 = 1.732).
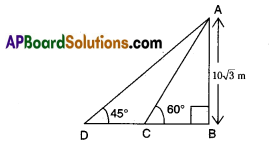
Answer:
7.32 m
![]()
Question 37.
From a bridge 25 m high, the angle of depression of a boat is 45°. Find the horizontal distance of the boat from the bridge.
Answer:
25 m
Question 38.
If the shadow of a tree is \(\frac{1}{\sqrt{3}}\) times the height of the tree, then find the angle of elevation of the sun.
Answer:
60°
Question 39.
A player sitting on the top of a tower of height 40m observes the angle of depression of a ball lying on the ground is 60°. Find the distance between the foot of the tower and ball.
Answer:
\(\frac{40}{\sqrt{3}}\)m
Question 40.
The length of the shadow of a tree is 7m high, when the sun’s elevation is
Answer:
45°
Explanation:
Length and shadow of a tree is same.
So sun’s elevation is 45°.
Question 41.
Write any one example of a Pythagorean triplet.
Answer:
5, 12, 13
Explanation:
5, 12, 13 (or) 3, 4, 5 (or) 7,24,25
Question 42.
When the angle of elevation of a light changes from 30° to 45°, the shadow of pole becomes 100 √3 m less. Find the height of the pole.
Answer:
100m
![]()
Question 43.
Find the elevation of the sun at the moment when the length of the shadow of a tower is just equal to its height.
Answer:
45°
Question 44.
The height of a tower is 10m. Find the length of its shadow when sun’s altitude is 45°.
Answer:
10 m
Question 45.
If the height and length of the shadow of a man are the same, then find the angle of elevation of the sun.
Answer:
45°
Question 46.
A boy observed the top of an electrical pole to be at angle of elevation of 60° when the observation point is 8m away from the foot of the pole, then find the height of the pole.
Answer:
8√3m
Question 47.
When the length of the shadow of a person is equal to his height, then find the elevation of source of light.
Answer:
45°
Question 48.
From the top of a building 50m from horizontal, the angle of depression made by a car is 30°. How far is the car from the building?
Answer:
50√3m
![]()
Question 49.
What change will be observed in the angle of elevation as we approach the foot of the tower ?
Answer:
Angle decreases.
Question 50.
The length of the shadow of a tower on the plane ground is √3 times the height of the tower. Find the angle of elevation of sun.
Answer:
30°
Question 51.
A pole of 12m high casts a shadow 4 √3 m on the ground, then find the sun’s angle of elevation.
Answer:
60°
Question 52.
Angle of elevation of the top of a build-ing from a point on the ground is 30°. Then find the angle of depression of this point from the top of the building.
Answer:
30°
Question 53.
In the figure given below, a man on the top of cliff observes a boat coming towards him. Then θ represents the angle of …………..

Answer:
Depression
Question 54.
The angle of elevation of a cloud from a point 200 m above the take is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud above the lake.
Answer:
400 m
![]()
Question 55.
In a rectangle, if the angle between a diagonal and a side is 30°, and the length of the diagonal is 6cm, find the area of the rectangle.
Answer:
9√3 cm2
Explanation:
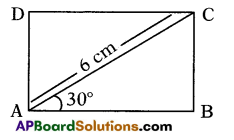
In ΔABC, sin 30°= \(\frac{\mathrm{BC}}{\mathrm{AC}}\) ⇒ \(\frac{1}{2}=\frac{\mathrm{BC}}{6}\) ⇒ BC = 3 cm,
cos 30° = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) ⇒ \(\frac{\sqrt{3}}{2}=\frac{\mathrm{AB}}{6}\)
⇒ AB = 3√3 cm.
∴ Area of rectangle = AB × BC
= 3√3 × 3 = 9√3 cm2
Question 56.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance between the top of the tree and the ground is 10m. Find the height of the tree.
Answer:
10√3 m
Question 57.
The angle of depression of the top of a tower at a point 100m from the house is 45°, then find the height of the tower.
Answer:
36.6 m
Question 58.
In the given figure, find the value of angle θ.
Answer:
30°
Question 59.
If the angle of elevation of a tower from a distance of 100m from its foot is 60°, then find the height of the tower.
Answer:
100√3 m
Question 60.
In the figure given below, if AD = 7 √3 m, then find BC.

Answer:
28 m
![]()
Question 61.
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm, then find the length of tangent.
Answer:
3√3 cm
Question 62.
An electric pole 20 m high stands up right on the ground with the help of steel wire to its top and affixed on the ground. If the steel wire makes 60° with the horizontal ground, find the length of steel wire.
Answer:
\(\frac{20}{\sqrt{3}}\)m
Question 63.
When the angle of elevation of a pole is 45°, what do you say about the length of the pole and its shadow.
Answer:
Both are equal.
Question 64.
If the ratio of height of a tower and the’length of its shadow on the ground is √3 : 1, then find the angle of elevation of the sun.
Answer:
60°
Question 65.
The ratio of the length of a rod and its shadow is 1 : √3, then find the angle of elevation of the sun.
Answer:
30°
Question 66.
In the figure given below, if AB = CD = 10√3m, then find BC.
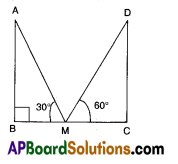
Answer:
40 m
Explanation:
From ΔABM, tan 30° = \(\frac{\mathrm{AB}}{\mathrm{BM}}\)
\(\frac{1}{\sqrt{3}}=\frac{10 \sqrt{3}}{\mathrm{BM}}\)
⇒ BM = 30m
From Δ CDM, tan 60°= \(\frac{\mathrm{CD}}{\mathrm{MC}}\)
√3 = \(\frac{10 \sqrt{3}}{\mathrm{MC}}\) ⇒ MC = 10m
∴ BC = BM + MC
= 30 + 10
= 40 m
![]()
Question 67.
The angle of elevation of top of a tree is 30°. On moving 20m nearer, the angle of elevation is 60°. Find the height of the tree.
Answer:
10√3 m
Question 68.
Two posts are 15m and 25m high and the line joining their tops make an angle of 45° with the horizontal. Find the distance between the two posts.
Answer:
10m
Question 69.
If a pole 6m high casts a shadow, 2 √3 m long on the ground, then find the sun’s angle of elevation.
Answer:
60°
Question 70.
If the length of the shadow of a tower \(\frac{1}{\sqrt{3}}\) is times the height of the tower, then find the angle of elevation of the sun.
Answer:
60°
Question 71.
In the figure given below, the imaginary line through the object and eye of the observer is called
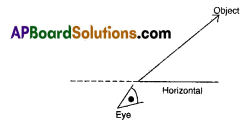
Answer:
Line of sight
Question 72.
A tower makes an angle of elevation equal to the angle of depression from the top of a cliff 25 m high. Find the height of the tower.
Answer:
50 m
![]()
Question 73.
If two towers of height X and Y subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find X : Y.
Answer:
1 : 3
Question 74.
An object is placed below the observer’s horizontal, then what is the angle between line of sight and observer’s horizontal?
Answer:
Angle of depression
Question 75.
The upper part of a tree is broken by wind and makes an angle of 30° with the ground and at a distance of 21 m from the foot of the tree. Find the total height of the tree.
Answer:
21√3 m
Question 76.
If the sun’s angle of elevation is 60°, then a pole of height 6 m, then find cast a shadow of length.
Answer:
2√3 m
Question 77.
A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60°. When he retires 40 in from the bank, he finds the angle to be 30°. Find the breadth of the river.
Answer:
20 m
❖ Choose the correct answer satisfying the following statements.
Question 78.
Statement (A) : If the below figure, if BC = 20m, then height AB is 11.56 m.
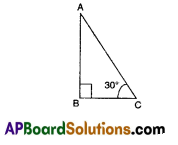
Statement (B) :
tan θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\text { perpendicular }}{\text { base }}\)
where θ is the ∠ACB.
(i) Both A and B are true
(ii) A istrue, B is false
(iii) A is false, B is true
(iv) Both A and B are false
Answer:
(i) Both A and B are true
Explanation:
Both A and B are correct, B is the correct explanation of the A.
tan30° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\) ⇒ \(\frac{1}{\sqrt{3}}=\frac{A B}{20}\)
AB = \(\frac{1}{\sqrt{3}}\) × 20 = \(\frac{20}{1.73}\) = 11.56 m.
So, option (i) is correct.
![]()
Question 79.
Statement (A) : If the length of shadow of a vertical pole is equal to its height, then the angle of elevation of the sun is 45°.
Statement (B) : According to Pythagoras theorem, h2 = l2 + b2, where h = hypotenuse, l = Length and b = base.
(i) Both A and B are true
(ii) A istrue, B is false
(iii) A is false, B is true
(iv) Both A and B are false
Answer:
(i) Both A and B are true
Explanation:
Both A and B are correct, but B is not the correct explanation of the A.
So, option (i) is correct.
❖ Read the below passages and answer to the following questions.
From the top of a tower, the angles of depresssion of two objects on the same side of the tower are found to be α and β where α > β.
Question 80.
If the distance between the objects is ‘P’ metres, then find the height ’h’ of the tower.
Answer:
\(\frac{P \tan \alpha \tan \beta}{\tan \alpha-\tan \beta}\)
Explanation:
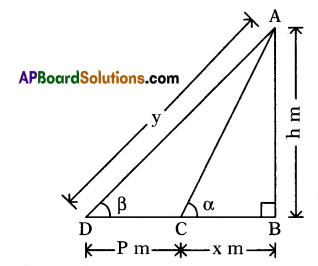
Height of the tower (AB) = h m
Distance (CD) = P m
Let distance (BC) = x m
∠ACB = α and∠ADB = β
In right ΔABC,\(\frac{\mathrm{AB}}{\mathrm{BC}}\) = tan α
⇒ \(\frac{\mathrm{h}}{\mathrm{x}}\) = tan α ⇒ h = x tan α …………….. (i)
In right ΔABD,\(\frac{\mathrm{AB}}{\mathrm{BD}}\) = tan β
⇒ \(\frac{\mathrm{h}}{\mathrm{BC}+\mathrm{CD}}\) = tan β
⇒ h = (x + P) tan β …………..(ii)
From (i), we get x = \(\frac{\mathrm{h}}{\tan \alpha}\)
Hence, h = \(\frac{P \cdot \tan \alpha \cdot \tan \beta}{\tan \alpha-\tan \beta}\) proved.
Question 81.
Find the height of the tower if P = 150 m, α = 60° and β = 30°.
Answer:
130 m
Explanation:
Putting P = 150 m, α = 60° and β = 30°, we get
h = \(\frac{150 \times \tan 60^{\circ} \times \tan 30^{\circ}}{\tan 60^{\circ}-\tan 30^{\circ}}\) m
= 129.9m ≅ 130m
Question 82.
The distance of the extreme object from the top of the tower is
Answer:
260 m
A straight highway leads to the foot of a tower of height 50m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60°.
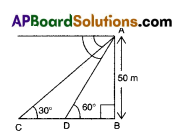
Explanation:
sin β = \(\frac{\mathrm{h}}{\mathrm{y}}\)
⇒ y = \(\frac{h}{\sin \beta}=\frac{130}{\sin 30^{\circ}}\) = 260m
Question 83.
Find the distance between the cars.
Answer:
57.7 m
Explanation:
From ΔABD, tan 60° = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
⇒ √3 = \(\frac{50}{\mathrm{BD}}\) ⇒ BD = \(\frac{50}{\sqrt{3}}\)
From ΔABC, tan 30° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{50}{\mathrm{BC}}\) ⇒ BC = 50√3
BC = BD + DC CD ⇒ BC – BD
= 50√3 = \(\frac{50}{\sqrt{3}}=\frac{150-50}{\sqrt{3}}=\frac{100}{\sqrt{3}}\) = 57.7 m
Question 84.
Find the distance between the second car from the tower.
Answer:
86.60 m
Explanation:
BC = 50 × 1.732 = 86.60 m
Question 85.
Which trignometrical concept was used to solve the given problem?
Answer:
Tangent and cosine.
The angle of elevation of a ladder against a wall is 60° and the foot of the ladder is 9.6 m from the wall.
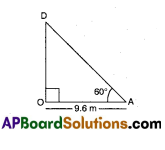
![]()
Question 86.
Find the length of the ladder.
Answer:
19.2 m
Explanation:
From ΔOAD, cos 60° = \(\frac{\mathrm{OA}}{\mathrm{DA}}\)
⇒ \(\frac{1}{2}=\frac{9.6}{\mathrm{DA}}\) ⇒ DA = 9.6 × 2 = 19.2m
Question 87.
Which trigonometrical concept was used to solve the problem?
Answer:
cos θ
Observe the below figure and answer to the following questions.
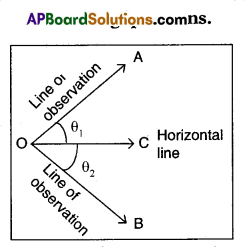
Question 88.
In the above figure θ1 is called
Answer:
Angle of elevation
Question 89.
In the above figure θ2 is called
Answer:
Angle of depression
Question 90.
θ1 and θ2 are measured from where?
Answer:
Always horizontal line.
Question 91.
What is the relation between θ1 and θ2?
Answer:
Both θ1 = θ2
Write the correct matching options.
![]()
Question 92.
From a window, ‘h’m high above the ground, of a house in a street, the angles of elevation and depression of the top and bottom of another house on the opposite side of the street are a and P respectively, then match the column.
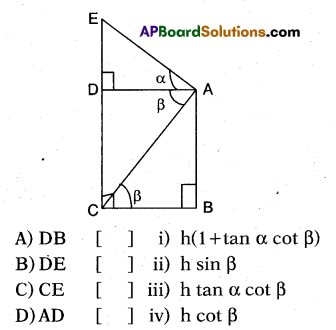
Answer:
A – (iv), B – (iii), C – (i), D – (ii)
Question 93.
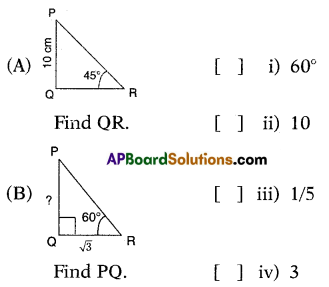
Answer:
A – (ii), B – (iv).
Question 94.
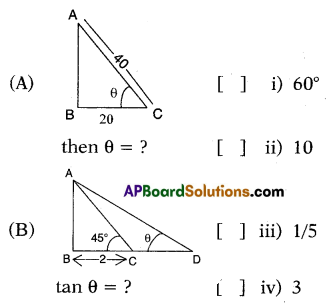
Answer:
A – (i), B – (iii).
Explanation:
(A) cos θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{20}{40}=\frac{1}{2}\) = cos 60°
∴ θ = 60°
(B) In ΔABC, tan 45° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ 1 = \(\frac{\mathrm{AB}}{2}\)
⇒ AB = 2
InΔABD, tan θ = \(\frac{\mathrm{AB}}{\mathrm{BD}}=\frac{2}{10}=\frac{1}{5}\)
Question 95.
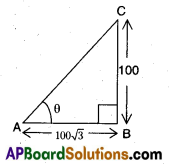
A tower of height 100√3m casts a shadow of length 10073 m then what is the angle of elevation of the sun at that time?
(OR)
In the given figure, what is the value of angle θ?
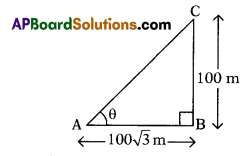
Solution .
In ΔABC
tan θ = \(\frac{\mathrm{BC}}{\mathrm{AB}}\) ⇒ tan θ = \(\frac{100}{100 \sqrt{3}}=\frac{1}{\sqrt{3}}\)
θ = 30°
Question 96.
Name the ‘angle of depression’ from the figure given below in which
∠B = 90°.
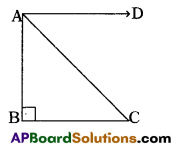
Answer:
∠DAC