AP 10th Class Maths Bits Chapter 14 Statistics with Answers

Practice the AP 10th Class Maths Bits with Answers Chapter 14 Statistics on a regular basis so that you can attempt exams with utmost confidence.

AP SSC 10th Class Maths Bits 1st Lesson Chapter 14 Statistics with Answers

Question 1.
If mean of 8, 6, 4, x, 3, 6 and ‘0’ is ‘4’, then find the value of x.
Answer:
1
Explanation:
\(\frac{6+8+4+x+3+6+0}{7}\) = 4
⇒ 27 + x = 28 ⇒ x = 1

Question 2.
Where the extreme values of some data influences high?
Answer:
In AM

Question 3.
In a data ‘n’ scores are given and if ‘n’ is odd, then find median.
Answer:
(\(\frac{n+1}{2}\))^th event

Question 4.
Find the class mark of 10 – 25.
Answer:
17.5

Question 5.
Mode of the data 5, 3, 4, – 2, 3, 2, 2, 1, p is 3, then the value of ‘p’.
Answer:
3

Question 6.
Find the class interval of the class 11 – 20.
Answer:
10

Question 7.
Mean of 1,2, x, 3 is ‘0’, then the value of ‘x’.
Answer:
-6

Question 8.
If the sum of 15 observations is 420, then find their mean.
Answer:
28
Explanation:
Mean = \(\frac{420}{15}\) = 28

Question 9.
Find the mid value of the class 10 – 19.
Answer:
14.5

Question 10.
Find the median of 2, 3, 4, 5, 6, 7.
Answer:
4.5
Explanation:
Median = \(\frac{4+5}{2}\) = 4.5

Question 11.
To elect the leader of your class from 3 contestants, which central measures is to be considered ?
Answer:
Mode

Question 12.
From the given graph of ogives, find median.

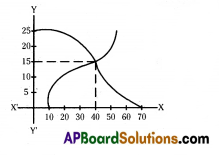
Answer:
40

Question 13.
Find median of the scores
1, 3, 5, 7, 9, ……………. 99.
Answer:
50

Question 14.
Find the mode of the values sin 0°, cos 0°, sin 90° and tan 45°.
Answer:
1
Explanation:
Mode in the values at 0, 1, 1, 1 is 1.

Question 15.
Find the mean of first four odd prime number.
Answer:
6.5

Question 16.
Find A.M. of x – 5, x, x + 5.
Answer:
x

Question 17.
Mode of 3, 4, 5 and x is 5, then find x.
Answer:
5
Explanation:
x = 5

Question 18.
Find the mode of the data
5, 6, 9, 10, 6, 11, 4, 6, 10, 4.
Answer:
6

Question 19.
The letter that represents \(\frac{\mathbf{x}_{\mathbf{i}}-\mathbf{a}}{\mathbf{h}}\)
which is used in measuring mean is …………….
Answer:
u_i

Question 20.
In “more than ogive curve” we consider in drawing …………………..
Answer:
More than cumulative frequency, lower limits.

Question 21.
Observe the following tables.


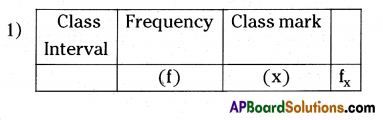
For finding Arithmetic Mean by Direct method, the suggested frequency distribution table is ……………….
Answer:
only (1) is true.

Question 22.
If \(\overline{\mathbf{x}}\), is the mean of x₁ x₂, x₃, ……………… x_n
(n times), then find \(\sum_{i=1}^{n}\)(x₁ – \(\overline{\mathbf{x}}\))
Answer:
0

Question 23.
Mode can be calculated by = l + (\(\frac{\mathbf{f}_{1}-\mathbf{f}_{0}}{2 \mathbf{f}_{1}-\mathbf{f}_{0}-\mathbf{f}_{2}}\)) × h
here f₁ represents ……………..
Answer:
Frequency of the modal class.

Question 24.
Find the x – coordinate of the point of intersection of the two ogives of grouped data.
Answer:
Median of the data.

Question 25.
3, 2, 4, 3, 5, 2, x, 6. If the mode of this data is 3, then find ‘x’.
Answer:
3

Question 26.
For the terms, x + 1, x + 2, x – 1, x + 3 and x – 2 (x G N), if the median of the data is 12, then find x.
Answer:
11

Question 27.
Which one of the following is NOT a measure of central tendency?
Mean, Median, Mode, Range
Answer:
Range

Question 28.
Find the most stable measure of central tendency.
Answer:
Mean

Question 29.
Find mode of 2004, 2005, 2006, ……………
2019.
Answer:
No mode

Question 30.
Mode = 24.5, Mean = 29.75, then find median.
Answer:
28

Question 31.
Unimodal data may have ……………… modes.
Answer:
1

Question 32.
Who is known as father of statistics ?
Answer:
Fisher

Question 33.
Find AM of \(\frac{1}{3}\),\(\frac{7}{12}\),\(\frac{3}{4}\),\(\frac{1}{2}\),\(\frac{5}{6}\)
Answer:
\(\frac{3}{5}\)

Question 34.
Find the mean of first 5 odd multiples of 5.
Answer:
25
Explanation:
\(\overline{\mathbf{x}}\) = \(\frac{5+15+25+35+45}{5}\) = \(\frac{125}{5}\) = 25

Question 35.
Find the mean of 6,-4,\(\frac{2}{3}\),\(\frac{5}{4}\),\(\frac{7}{6}\)
Answer:
\(\frac{11}{20}\)

Question 36.
In the figure, find the value of median of the data using the graph of less than ogive and more than ogive.

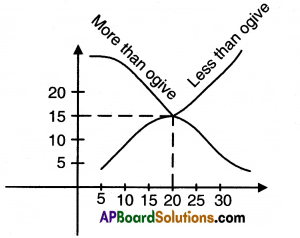
Answer:
20

Question 37.
Find mode of the following distribution.

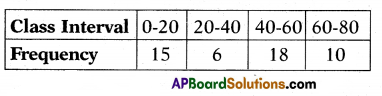
Answer:
52

Question 38.
Find the measure of central tendency which take into account all data terms.
Answer:
Mean

Question 39.
6, 3, 5, 6, 7, 5, 8, 7, 6, 2k + 1, 9, 7, 13. If the mode of this data is 7, then find ‘k’
Answer:
3
Explanation:
Mode = 7, so 2k + 1 = 7 ⇒ k = 3

Question 40.
For a given data with 50 observations ‘the less than ogive’ and the more than ogive intersect at (15.5, 20). Find the median of the data.
Answer:
15.5

Question 41.
Find median of first 8 prime numbers.
Answer:
9

Question 42.
In a data mean = 72.5 and median = 73.9, then find mode.
Answer:
76.7
Explanation:
Mode = 3 Median – 2 Mean
= 3 × 73.9 – 2 × 72.5
= 221.7 – 145 = 76.7

Question 43.
How much the sum of all deviations taken from AM?
Answer:
0

Question 44.
Find the modal class in the following frequency distribution.

Class	Frequency
0 – 10 10 – 20 20 – 30 30 – 40 40 – 50 50 – 60	3 9 15 30 18 5

Answer:
30 – 40

Question 45.
Mean – mode is equal to
Answer:
3 (Mean – Median)

Question 46.
In an arranged series of an even num¬ber 2n terms write the median.
Answer:
\(\frac{1}{2}\)(n^th and (n + 1)^th term)

Question 47.
In a data maximum value = x, minimum value = y, then find range.
Answer:
x – y

Consider the following frequency distribution.

Monthly income	Number of families
More than or equal to 10000 More than or equal to 13000 More than or equal to 16000 More than or equal to 19000 More than or equal to 22000	100 85 69 50 33

Question 48.
Find the number of families having income range from ₹ 16000 to ₹ 19000.
Answer:
19

Question 49.
C.I of 1 – 10 is …………….
Answer:
10

Question 50.
In calculating mode Δ₁ is equal to
Answer:
f – f₁

Question 51.
|| represents ………………
Answer:
7

Question 52.
Find mode of any 3 consecutive numbers.
Answer:
No mode.

Question 53.
Find the mean of the following data.

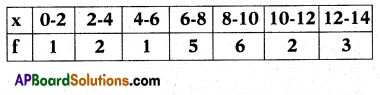
Answer:
8.1

Question 54.
Find AM of first n odd numbers.
Answer:
n

Question 55.
The class mark of 10 – 25 is ……………..
Answer:
17.5

Question 56.
Mean of 5,7,9,x is 9, then find ‘x’.
Answer:
15

Question 57.
Find AM of a – 2, a, a + 2.
Answer:
a

Question 58.
Cumulative frequency curves are called as ………………. curves.
Answer:
Ogive

Question 59.
Find the class marks of a class interval.
Answer:
\(\frac{\text { Upper boundary + lower boundary }}{2}\)

Question 60.
Write the abscissa of the point of intersection of the ‘less than’ type and ‘more than type’ cumulative frequency curves of a grouped data.
Answer:
Mode

Question 61.
Find AM of 1², 2², 3³, 4², …………….. , 20².
Answer:

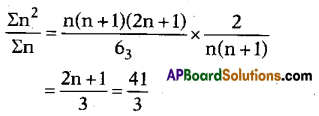
Question 62.
Write mode of first ‘n’ natural numbers.
Answer:
No mode.

Question 63.
Find mid value of the class 10 – 20.
Answer:
15

Question 64.
Mid values are used to calculate ……………
Answer:
Mean

Question 65.
Find mode of 1, 2, 3, ……………. 10, 10.
Answer:
10

Question 66.
Find the mean of the following data.

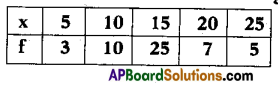
Answer:
15.1

Question 67.
Find the median of the data 5, 3, 10, 7, 2, 9, 11,2, 6.
Answer:
6

Question 68.
Histograiri’consists of ………………..
Answer:
Rectangles

Question 69.
Write empirical relation among mean, median and mode.
Answer:
Mode = 3 median – 2 mean

Question 70.
Write the class marks of a class x – y.
Answer:
\(\frac{x+y}{2}\)

Question 71.
Find mean of 1, 2, 3, …………… n.
Answer:
\(\frac{n+1}{2}\)

Question 72.
Find AM of 23, 24, 24, 22, 10.
Answer:
22.6

Question 73.
Find the modal class for the following distribution.

Answer:
30 – 40
Explanation:
Maximum frequency is 57,
i.e., 30 – 40 class.

Question 74.
For a given data with 60 observations, ‘the less than’ ogive and ‘the more than ogive’ intersect at (66.5, 30). Find the median of the data.
Answer:
66.5

Question 75.
Data having two modes is called ……………….
Answer:
Bimodal

Question 76.
pie diagram consists of …………….
Answer:
Sectors

Question 77.
Write the Range of first 5 natural num-bers.
Answer:
4

Question 78.
If the mean of 10, 12, 18, 13, P and 17 is 15, then find ‘P’.
Answer:
20
Explanation:
\(\frac{10+12+18+13+\mathrm{P}+17}{6}\) = 15
⇒ 70 + P = 90 ⇒ P = 20

Question 79.
Find range of 1,2,3, …………….. 10.
Answer:
9

Question 80.
For a distribution with odd numbers (n) of observations, find the median is ………………. observation.
Answer:
\(\frac{n+1}{2}\)^th

Question 81.
If each observation of a data is increased by ‘a’, then mean is increases by ……………….
Answer:
a

Question 82.
Find mode of 5, 6, 9,10,6,12,3,6,11, 10, 4, 6, 7.
Answer:
6

Question 83.
……………….. is effected by extreme values.
Answer:
Mean

Question 84.
1-8, 9-16, 17-24, ………………… then find C.I.
Answer:
8
Explanation:
9 – 1 = 8

Question 85.
Mode is the value of variate which occurs …………….. number of times.
Answer:
Maximum

Question 86.
Find the mean of first five prime numbers.
Answer:
5.6

Question 87.
Find mean of -8, -4 and 4, 8.
Answer:
0

Question 88.
Mean of n-observations x₁, x₂, …………….. x_n repeated , f₁,f₂, f₃, ……………. , f_n times is
Answer:

Question 89.
Find mean of 7, 6, 5, 0, 7, 8, 9.
Answer:
6

Question 90.
Representing the data with the help of pictures is called
Answer:
pictograph

Question 91.
If the mean of the data 2, a + 1, a, a – 2 is 4, then find a.
Answer:
5
Explanation:
\(\overline{\mathbf{x}}\) = \(\frac{2+a+1+a+a-2}{4}\) = 4
⇒ 3a + 1 = 16 ⇒ a = 5

Question 92.
£f(x) = 200, n=20, then find \(\overline{\mathbf{x}}\).
Answer:
10
\(\overline{\mathbf{x}}\) = \(\frac{\Sigma \mathrm{fx}}{\mathrm{n}}=\frac{200}{20}\) = 10

Question 93.
Median = 52.5, Mean = 54, then find Mode.
Answer:
49.5

Question 94.
In the formula of mode in the grouped ……………… data l represents
Answer:
Lower limit of the class with highest frequency.

Question 95.
Cumulative frequency is used to calculate in ……………….
Answer:
Median

Question 96.
Find the lower limit of the modal class of the following data.

Answer:
10

Question 97.
Construction of cumulative frequency table is useful in determining the ………………
Answer:
Median

Question 98.
\(\frac{\text { Sum of observations }}{\text { Number of observations }}\) is equal to
Answer:
Mean

Question 99.
If mode of a distribution is 8 and its mean is 8, then find median.
Answer:
8

Question 100.
Find mode of 0, 1, 2, 3, 3, 3, 7.
Answer:
3

Question 101.
For a distribution with even number (n) of observation, the median is ……………….
Answer:

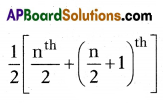
Question 102.
If the mean of x₁ x₂, …………….. x_n is \(\overline{\mathbf{x}}\), then find the mean of \frac{\mathbf{x}_{1}}{\mathbf{a}}, \(\frac{\mathbf{x}_{2}}{\mathbf{a}}\) ……………….. \(\frac{\mathbf{x}_{n}}{\mathbf{a}}\)
Answer:
\(\frac{\overline{\mathrm{x}}}{\mathrm{a}}\)

Question 103.
Find AM of 3 and 4.
Answer:
3.5

Question 104.
For a given data with 120 observations, the “less than ogive” and the “more than ogive” intersect at (42.5,60). Find the median of the data.
Answer:
42.5

Question 105.
Find the AM of 10 consecutive num¬bers starting with n + 1.
Answer:
x + 5.5

Question 106.
………………. is based on all observations.
Answer:
Mean

Question 107.
Mode of a continuous grouped distribution is ………………….
Answer:
l + \(\frac{\mathrm{f}_{1}-\mathrm{f}_{0}}{\left(\mathrm{f}_{1}-\mathrm{f}_{0}\right)+\left(\mathrm{f}_{1}-\mathrm{f}_{2}\right)}\) × h

Question 108.
Find mode of 20, 3, 7, 13, 3, 4, 6, 7, 19, 15, 7, 18, 3.
Answer:
3,7

Question 109.
Find the sum of lower limit of median class and upper limit of modal class is ………………

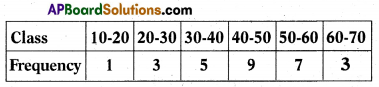
Answer:
90

Question 110.
The information collected is called ……………..
Answer:
data

Question 111.
Find AM of 1, 2, x, 3 is 0, then find ‘x’.
Answer:
-6

Question 112.
For a symmetrical distribution, which is correct?
A) Mean < Mode < Median B) Mean > Mode > Median
C) Mode = \(\frac{\text { Mean }+\text { Median }}{2}\)
D) Mean = Median = Mode
Answer:
D) Mean = Median = Mode

Question 113.
\(\overline{\mathbf{x}}\) = 2p + q, M = p + 2q, then find Z.
Answer:
4q – p

Question 114.
Find the median class of the following distribution.

Answer:
30 – 40

Question 115.
A data has 13 observations arranged in descending order which observation represents the median of data?
Answer:
7^th

Question 116.
For a continuous grouped frequency distribution, the median is given by
Answer:
l + (\(\frac{\frac{\mathrm{n}}{2}-\mathrm{cf}}{\mathrm{f}}\)) × h

Question 117.
A data arrange in descending order has 25 observations. Which observation represents the median?
Answer:
13^th

Question 118
……………… of all bars is same in bar graph.
Answer:
Width

Question 119.
Find mean of a + 1, a + 3, a + 4 and a + 8.
Answer:
a + 4
Explanation:
Mean = \(\frac{a+1+a+3+a+4+a+8}{4}\)
= \(\frac{4 a+16}{4}\) = a + 4

Question 120.
If assumed mean is ‘a’, then write the mean.
Answer:
a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)

Question 121.
Find the upper limit of median class of the following distribution.

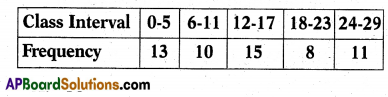
Answer:
18

❖ Choose the correct answer satisfying the following statements.
Question 122.
Statement (A) : The arithmetic mean of the following given frequency distribution table is 13.81.

Statement (B) : \(\overline{\mathbf{x}}\) = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i) Both A and B are true.
Explanation:
Both A and B are true, B is the correct explanation of the A.
Hence, (i) is the correct option.

Question 123.
Statement (A) : If the number of runs scored by 11 players of a cricket team of India are 5, 19, 42, 11, 50, 30, 21, 0, 52, 36, 27, then median is 30.
Statement (B) : Median = \(\frac{(n+1)^{t h}}{2}\)
value, if n is odd.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
iii) A is false, B is true.
Explanation:
Arranging the terms in ascending order, 0, 5, 11, 19, 21, 27, 30, 36, 42, 50, 52
Median value = (\(\frac{11+1}{2}\))^th = 6^th value = 27
∴ Option (iii) is true.

Question 124.
Statement (A) : If the value of mode and mean is 60 and 66 respectively, then the value of median is 64.
Statement (B) :
Median = \(\frac{1}{2}\)(mode + 2 mean)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
ii) A is true, B is false.
Explanation:
Median = \(\frac { 1 }{ 3 }\) (Mode + 2 Mean)
= \(\frac { 1 }{ 3 }\) (60 + 2 × 66) = 64
∴ Option (ii) is correct.

Read the below passages and answer to the following questions.
The following table gives the weekly wages of workers in a factory.

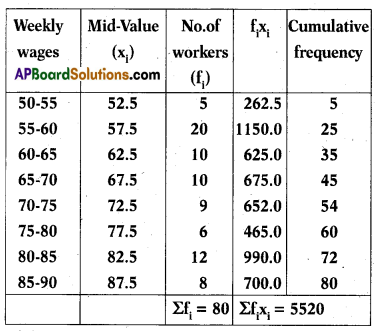
Question 125.
Find the mean.
Answer:
69
Explanation:
Mean = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{5520}{80}\) = 69

Question 126.
Find the modal class.
Answer:
55 – 60
Explanation:
Modal Class : We know that class of maximum frequency is called the modal class, i.e., 55 – 60 is the modal class.

Question 127.
Find the number of workers getting weekly wages, below ₹ 80.
Answer:
60
The marks of 20 students in a test were as follows : 5, 6, 8, 9, 10, 11, 11, 12, 13, 13, 14, 14, 15, 15, 15, 16, 16, 18, 19, 20.
Explanation:
Number of workers getting weekly wages below ₹ 80 according to table = 60 workers.

Question 128.
Calculate the mean.
Answer:
13
Explanation:
Arrange in ascending order

Question 129.
Calculate the median.
Answer:
13.5
Explanation:
Here, n = 20 which is an even number

= 13.5

Question 130.
Calculate the mode.
Answer:
15
A professor keeps data on students tabulated by performance and sex of the student. The data is kept on a computer disk.

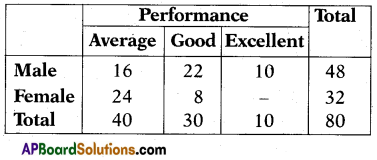
Explanation:
In the data, 15 occurs the maximum times i.e., 3 times.
∴ Mode = 15

Question 131.
How many students are both female and excellent?
Answer:
0
Explanation:
There is no female excellent student in the class.

Question 132.
What proportion of good students are male?
Answer:
0.73
Explanation:
Proportion of good male students
= \(\frac{22}{30}\) = 0.73

Question 133.
What proportion of female students are good?
Answer:
0.26
Explanation:
Proportion of good female students
\(\frac{8}{30}\) = 0.26

Question 134.
Write the short form of the expansion in symbolic form.
1 + 2 + 3 + 4 + ……………………. + n
Answer:
Σn