AP Board 10th Class Maths Solutions Chapter 11 త్రికోణమితి Exercise 11.1

SCERT AP 10th Class Maths Textbook Solutions Chapter 11 త్రికోణమితి Exercise 11.1 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 11th Lesson త్రికోణమితి Exercise 11.1

ప్రశ్న 1.
ఒక లంబకోణ త్రిభుజం ABCలో భుజాలు AB, BC మరియు CA ల పొడవులు వరుసగా 8 సెం.మీ., 15 సెం.మీ మరియు 17 సెం.మీ అయిన sinA, cos A మరియు tan A ల విలువలు కనుగొనుము.
సాధన.
∆ABC ఒక లంబకోణ త్రిభుజము.
భుజాల కొలతలు AB = 8 సెం.మీ. BC = 15 సెం.మీ. మరియు CA = 17 సెం.మీ.
ఇచ్చిన కొలతలలో \(\overline{\mathrm{CA}}\) పొడవైన భుజము కావున ∆ABC యొక్క కర్ణము CA అగును.

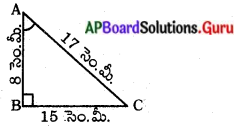
∠A పరంగా ఎదుటి భుజం = BC = 15 సెం.మీ.
ఆసన్న భుజము = AB = 8 సెం.మీ. మరియు కర్ణము = AC = 17 సెం.మీ.
A కు ఎదుటి భుజము = BC = 15

sin A = =\(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{15}{17}\)

cos A = 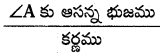=\(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{8}{17}\)

tan A = 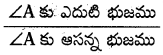=\(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{15}{8}\)
∴ sin A = \(\frac{15}{17}\); cos A = \(\frac{8}{17}\) మరియు tan A = \(\frac{15}{8}\)

ప్రశ్న 2.
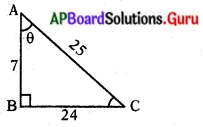
లంబకోణ త్రిభుజం POR యొక్క భుజాలు PQ = 7 సెం.మీ., QR = 25 సెం.మీ. మరియు ∠P = 90° అయిన tanQ – tan R విలువ కనుగొనుము.
సాధన.
దత్తాంశము ప్రకారం PORఒక లంబకోణ త్రిభుజము మరియు PQ = 7 సెం.మీ, PR = 25 సెం.మీ, మరియు ∠Q = 90°.

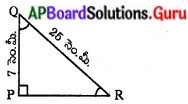
పైథాగరస్ సిద్ధాంతం ప్రకారము . PQ² + PR² = QR²
(7)² + PR² = (25)²
PR² = 625 – 49
PR² = 576
⇒ PR = √576 = 24
∴ tan Q =
= \(\frac{P R}{P Q}=\frac{24}{7}\)

tan R =
= \(\frac{P Q}{P R}=\frac{7}{24}\)

tan Q – tan R = \(\frac{24}{7}-\frac{7}{24}=\frac{(24)^{2}-(7)^{2}}{24 \times 7}\)
= \(\frac{576-49}{168}=\frac{527}{168}\)

ప్రశ్న 3.
B వద్ద లంబకోణం కల్గిన లంబకోణ త్రిభుజం ABCలో ‘ a = 24 యూనిట్లు, b = 25 యూనిట్లు మరియు ∠BAC = θ అయిన cos 6 మరియు tan 6 ల విలువలను కనుగొనుము.
సాధన.
దత్తాంశము ప్రకారం త్రిభుజం ABC లో B వద్ద లంబకోణం కలదు. మరియు a = BC = 24 యూనిట్లు, b = CA = 25 యూనిట్లు మరియు ∠BAC = θ అనుకొనిన

Bb 24 Ac పైథాగరస్ సిద్ధాంతం ప్రకారం
AC² = AB² + BC²
(25)² = AB² + 24²
AB² = 25² – 24²
= 625 – 576
AB² = 49
AB = √49 = 7
∠BAC = θ ప్రకారము
θకు ఎదుటి భుజము = BC = 24 యూనిట్లు
θకు ఆసన్న భుజము = AB = 7 యూనిట్లు
కర్ణము = AC = 25 యూనిట్లు

= \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{7^{\mathrm{\kappa}}}{25}\)

= \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{24^{\mathrm{\kappa}}}{7}\)
∴ cos θ = \(\frac{7}{25}\) మరియు tan θ = \(\frac{24}{7}\).

ప్రశ్న 4.
cos A = \(\frac{12}{13}\) అయిన sin A మరియు tan A ల విలువలను కనుగొనుము.
సాధన.
దత్తాంశము ప్రకారం Cos A = \(\frac{12}{13}\)
Cos A = = \(\frac{12}{13}\)
∴ఆసన్న భుజము : కర్ణము = 12 : 13.

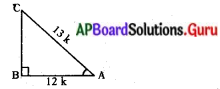
కోణం ‘A’ పరంగా, ఆసన్నభుజము = AB = 12k మరియు కర్ణము = AC = 13 k(‘k’ ఒక ధన సంఖ్య)
∆ABC నుండి
AC² = AB² + BC²
⇒ (13k)² = (12.k)² + BC²
⇒ 169 k² = 144 k² + BC²
⇒ BC² = 169 k² – 144 k²
⇒ (169 – 144) k² = 25 k²
⇒ BC = √(25k²)
⇒ 5k = ఎదుటి భుజము
ఇప్పుడు, మిగిలిన త్రికోణమితి నిష్పత్తులు
sin A =
= \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{5 \mathrm{k}}{13 \mathrm{k}}=\frac{5}{13}\)

tan A =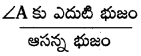
= \(\frac{B C}{A B}=\frac{5 k}{12 k}=\frac{5}{12}\)
ఆ విధముగా sinA = \(\frac{5}{13}\), tanA = \(\frac{5}{12}\) అగును.

ప్రశ్న 5.
3 tan A = 4 అయిన sin A మరియు Cos A ల విలువలను కనుగొనుము.
సాధన.
దత్తాంశము ప్రకారం 3 tan A = 4 ⇒ tan A = \(\frac{4}{3}\)
కాని tan A = = \(\frac{4}{3}\)
∠A కు ఎదుటి భుజము = 4k మరియు ∠A కు ఆసన్న భుజం = 3k.
ఈ విలువలను ∆ABC లో చూపగా

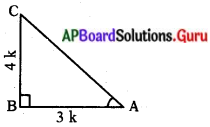
∆ABC ఒక లంబకోణ త్రిభుజము కావున AC² = AB² + BC² (∵ పైథాగరస్ సిద్ధాంతం ప్రకారం)
= (3k)² + (4k)² = 9k² + 16k²
AC² = 25k²
AC = √(25 k²) = 5k
sin A = \(\frac{B C}{A C}=\frac{4 k}{5 k}=\frac{4}{5}\)

cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{3 \mathrm{k}}{5 \mathrm{k}}=\frac{3}{5}\)

ప్రశ్న 6.
∆ABC, ∆XYZలలో cos A = cos X అయ్యేటట్లు 4A మరియు ∠Xలు లఘు కోణాలయిన ∠A = ∠X అని చూపుము.
సాధన.

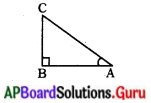
∆ABC లో
cos A =
= \(\frac{\mathrm{AB}}{\mathrm{AC}}\)

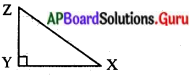
అలాగే ∆XYZ లో 2
cos X = \(\frac{\mathrm{XY}}{\mathrm{XZ}}\)
లెక్క ప్రకారం, cosA = cos X
∴ \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{XY}}{\mathrm{XZ}}\) = k అను
⇒ \(\frac{\mathrm{AB}}{\mathrm{XY}}=\frac{\mathrm{AC}}{\mathrm{XZ}}\) ………………(1)
∴ AB = kAC మరియు XY = kXZ
ఇప్పుడు

(1) మరియు (2) ల నుండి,
\(\frac{\mathrm{AB}}{\mathrm{XY}}=\frac{\mathrm{AC}}{\mathrm{XZ}}=\frac{\mathrm{BC}}{\mathrm{YZ}}\)
∴ రెండు త్రిభుజ భుజాలకు అనుపాతంలో కలవు.
∴ ∆ABC ~ ∆XYZ
⇒ ∠A = ∠X (∵ సరూప త్రిభుజాలలో అనురూప కోణాలు సమానాలు)

ప్రశ్న 7.
cot θ = \(\frac{7}{8}\) అయిన
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) \(\frac{(1+\sin \theta)}{\cos \theta}\) లను కనుగొనుము.
సాధన.
దత్తాంశము ప్రకారం cot θ = \(\frac{7}{8}\)

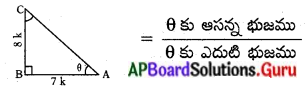
AB = 7k మరియు BC = 8k అనుకొనిన లంబకోణ త్రిభుజములో
AC² = AB² + BC² (పైథాగరస్ సిద్ధాంతం ప్రకారం)
= (7k)² + (8k)²
AC² = 49k² + 64k²
AC² = 113 k²
⇒ AC = √113k
ఇప్పుడు, sin θ =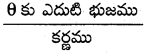
= \(\frac{8 k}{\sqrt{113} k}=\frac{8}{\sqrt{113}}\)
cos θ =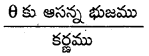
= \(\frac{7 k}{\sqrt{113} k}=\frac{7}{\sqrt{113}}\)

(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
= \(\frac{1^{2}-\sin ^{2} \theta}{1^{2}-\cos ^{2} \theta}\) [∵ (a + b) (a – b) = a² – b<sup.2)

= \(\frac{1-\left(\frac{8}{\sqrt{113}}\right)^{2}}{1-\left(\frac{7}{\sqrt{113}}\right)^{2}}=\frac{1-\frac{64}{113}}{1-\frac{49}{113}}=\frac{\frac{113-64}{113}}{\frac{113-49}{113}}=\frac{49}{64}\)

(ii) \(\frac{(1+\sin \theta)}{\cos \theta}\)
= \(\frac{1+\frac{8}{\sqrt{113}}}{\frac{7}{\sqrt{113}}}\)

= \(\frac{\frac{\sqrt{113}+8}{\sqrt{113}}}{\frac{7}{\sqrt{113}}}=\frac{\sqrt{113}+8}{7}\)

ప్రశ్న 8.
B వద్ద లంబకోణం కల్గిన, త్రిభుజం ABC లో tan A = √3 అయిన
(i) sin A cos.C + cos A sin C
(ii) cos A cos C-sin Asin C ల విలువలను కనుగొనుము.
సాధన.
దత్తాంశము : tan A = \(\frac{\sqrt{3}}{1}\\)
కాని tan A = 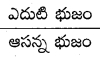= \(\frac{\sqrt{3}}{1}\\)
ఎదుటి భుజం = √3k మరియు ఆసన్న భుజం = 1k

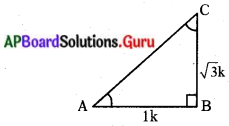
∆ABC లంబకోణ త్రిభుజములో
AC² = AB² + BC² (పైథాగరస్ సిద్ధాంతము ప్రకారం)
⇒ AC² = (1k)² + (J3k)²
⇒ AC² = 1k² + 3k²
⇒ AC² = 4k²
∴ AC = √4k² = 2k
BC
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{\sqrt{3} \mathrm{k}}{2 \mathrm{k}}=\frac{\sqrt{3}}{2}\)
cos A = \(=\frac{A B}{A C}=\frac{1 k}{2 k}=\frac{1}{2}\)
sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{1 \mathrm{k}}{2 \mathrm{k}}=\frac{1}{2}\)
cos C = \(\frac{B C}{A C}=\frac{\sqrt{3} k}{2 k}=\frac{\sqrt{3}}{2}\)

(i) sin A . cos C + cos A . sin C
= \(\frac{\sqrt{3}}{2} \cdot \frac{\sqrt{3}}{2}+\frac{1}{2} \cdot \frac{1}{2}=\frac{(\sqrt{3})^{2}}{4}+\frac{(1)^{2}}{4}\)
= \(\frac{3}{4}+\frac{1}{4}=\frac{3+1}{4}=\frac{4}{4}\) = 1

(ii) cos A. cos C-sin A. sin C
= \(\frac{1}{2} \cdot \frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2} \cdot \frac{1}{2}\)
= \(\frac{\sqrt{3}}{4}-\frac{\sqrt{3}}{4}\) = 0