AP SCERT 6th Class Maths Textbook Solutions Chapter 10 ప్రాయోజిక జ్యామితి InText Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 10th Lesson ప్రాయోజిక జ్యామితి InText Questions
ప్రయత్నించండి [పేజి నెం. 146]
ఒకే వ్యాసార్ధం గల రెండు వృత్తాలు నిర్మించండి.
(i) రెండు బిందువుల వద్ద ఖండించుకొనేలా నిర్మించండి.
(ii) ఒకే ఒక బిందువు వద్ద స్పర్శించుకొనేలా నిర్మించండి.

సాధన.

(i) P,Q కేంద్రంగా గల వృత్తాలు R, S అనే రెండు బిందువుల వద్ద ఖండించుకొంటున్నాయి.
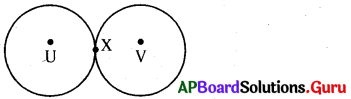
(ii) U,V కేంద్రాలుగా గల వృత్తాలు X అనే ఒకే బిందువు వద్ద స్పర్శించుకొంటున్నాయి. ఈ సందర్భంలో \(\overline{\mathrm{UX}}\) = \(\overline{\mathrm{XV}}\) అవుతుంది.
![]()
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 147]
పై రెండు పద్ధతులలోను \(\overline{\mathrm{AP}}\) = \(\overline{\mathrm{BP}}\) పొడవులు కొలవండి. ఏమి గమనించారు?
సాధన.
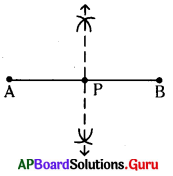
ఈ నిర్మాణంలో \(\overline{\mathrm{AP}}\) = \(\overline{\mathrm{PB}}\) అని మనం గమనించాము.
∴ AB ని ‘P’ రెండు భాగాలుగా విభజిస్తుంది.
ఆలోచించండి [పేజి నెం. 148]
రేఖాఖండానికి లంబ సమద్విఖండన రేఖ గీచే విధానంలో సోపానం-2లో \(\overline{\mathrm{AB}}\) సగం కంటే తక్కువ పొడవును వ్యాసార్ధంగా తీసుకుంటే ఏం జరుగుతుంది?
సాధన.
రేఖాఖండానికి లంబ సమద్విఖండన రేఖ గీచే విధానంలో సోపానం-2 లో \(\overline{\mathrm{AB}}\) సగం కంటే తక్కువ పొడవును వ్యాసార్ధంగా తీసుకొంటే చాపరేఖలు ఒకదానినొకటి ఖండించుకొనవు.
![]()
పేజి నెం. 152
180° , 240° , 300° కోణాలు నిర్మించండి.
సాధన.
(i) \(\angle \mathbf{A O B}\) = 180°
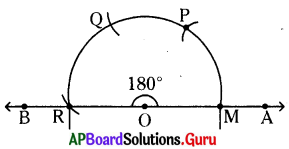
నిర్మాణం :
- కొంత పొడవుతో \(\overrightarrow{\mathrm{OA}}\) కిరణం గీయాలి.
- ‘O’ కేంద్రంగా కొంత వ్యాసార్ధంతో OA ను M వద్ద ఖండించేలా ఒక చాపం గీయాలి.
- M కేంద్రంగా అదే వ్యాసార్ధంతో పై చాపాన్ని P వద్ద ఖండించేలా ఒక చాపం గీయాలి.
- P కేంద్రంగా మరలా అదే వ్యాసార్ధంతో మొదటి చాపాన్ని Q వద్ద ఖండించేలా మరో చాపం గీయాలి.
- Q కేంద్రంగా మరలా. అదే వ్యాసార్ధంతో రెండవ చాపాన్ని R వద్ద ఖండించేలా మరో చాపం గీయాలి.
- OR (\(\overrightarrow{\mathrm{OB}}\)) లు కలపాలి. \(\angle \mathbf{A O B}\) కావలసిన కోణం .
(ii) \(\angle \mathbf{PQR}\) = 240°
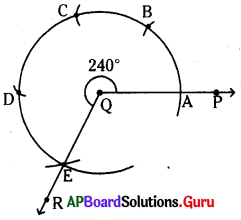
నిర్మాణం :
- కొంత పొడవుతో \(\overrightarrow{\mathrm{QP}}\) కిరణం గీయాలి.
- ‘Q’ కేంద్రంగా కొంత వ్యాసార్ధంతో QP ను A వద్ద ఖండించేలా ఒక చాపం గీయాలి.
- A కేంద్రంగా అదే వ్యాసార్ధంతో పై చాపాన్ని B వద్ద ఖండించేలా ఒక చాపం గీయాలి.
- B కేంద్రంగా మరలా అదే వ్యాసార్ధంతో మొదటి చాపాన్ని C వద్ద ఖండించేలా మరో చాపం గీయాలి.
- C కేంద్రంగా మరలా అదే వ్యాసార్ధంతో రెండవ చాపాన్ని D వద్ద ఖండించేలా మరో చాపం గీయాలి.
- D కేంద్రంగా మరలా అదే వ్యాసార్ధంతో మూడవ చాపాన్ని E వద్ద ఖండించేలా మరో చాపం గీయాలి.
- QE (\(\overrightarrow{\mathrm{QR}}\)) లు కలపాలి. \(\angle \mathbf{PQR}\) కావలసిన కోణం.
(iii) \(\angle \mathbf{XYZ}\) = 300°
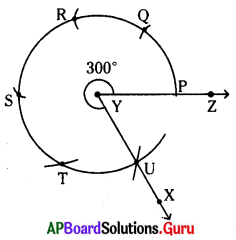
నిర్మాణం :
- కొంత పొడవుతో \(\overrightarrow{\mathrm{YZ}}\) కిరణం గీయాలి.
- Y కేంద్రంగా కొంత వ్యాసార్ధంతో YZను P వద్ద ఖండించేలా ఒక చాపం గీయాలి.
- P కేంద్రంగా అదే వ్యాసార్ధంతో పై చాపాన్ని Q వద్ద ఖండించేలా ఒక చాపం గీయాలి.
- Q కేంద్రంగా మరలా అదే వ్యాసార్ధంతో మొదటి చాపాన్ని R వద్ద ఖండించేలా మరొక చాపం గీయాలి.
- R కేంద్రంగా మరలా అదే వ్యాసార్ధంతో రెండవ చాపాన్ని ఏ వద్ద ఖండించేలా మరో చాపం గీయాలి.
- S కేంద్రంగా మరలా అదే వ్యాసార్ధంతో మూడవ ఛాపాన్ని T వద్ద ఖండించేలా మరో చాపం గీయాలి.
- T కేంద్రంగా మరలా అదే వ్యాసార్ధంతో నాలుగవ చాపాన్ని U వద్ద ఖండించేలా మరో చాపం గీయాలి.
- YU (\(\overrightarrow{\mathrm{YX}}\)) లు కలపాలి. \(\angle \mathbf{XYZ}\) కావలసిన కోణం .
![]()
పేజి నెం. 153
ప్రశ్న 1.
90° కోణం నిర్మించడానికి మరొక పద్ధతి ఆలోచించండి.
(\(\frac {180}{2}\) = 90°, 180° లకు కోణ సమద్విఖండనరేఖ గీయడం ద్వారా నిర్మించండి.)
సాధన.
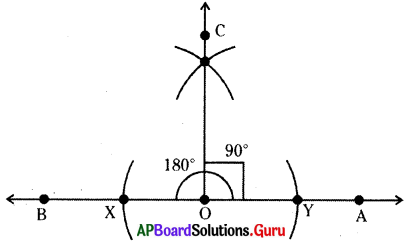
నిర్మాణ క్రమం :
- \(\angle \mathbf{AOB}\) = 180° కోణాన్ని నిర్మించాలి. (ఒక సరళరేఖ \(\overrightarrow{\mathrm{AB}}\) ని గీయాలి)
- “O” కేంద్రంగా ‘O’ కు ఇరువైపులా ఒకే వ్యాసార్ధంతో \(\overrightarrow{\mathrm{AB}}\) పై చాపరేఖలు గీచి, ఖండన బిందువులు X, Y లను గుర్తించాలి.
- \(\overrightarrow{\mathrm{XY}}\) పొడవులో సగం కన్నా ఎక్కువ వ్యాసార్ధంతో X, Y లు కేంద్రాలుగా \(\overrightarrow{\mathrm{AB}}\) పైన రెండు చాపరేఖలు గీయాలి. ఖండన బిందువును C గా గుర్తించాలి.
- O, C లను కలుపగా మనకు కావలసిన కోణం \(\angle \mathbf{AOC}\) = 90° ఏర్పడినది.
![]()
ప్రశ్న 2.
వృత్తలేఖిని సాయంతో 45° కోణాన్ని నిర్మించండి.
సాధన.
1వ పద్ధతి : (60°ల నుండి 30° + 15° నిర్మించడం ద్వారా)
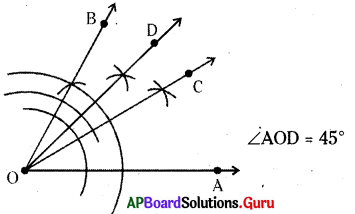
నిర్మాణక్రమం :
- వృత్తలేఖిని సహాయంతో 60° కోణం \(\angle \mathbf{AOB}\) ని గీయాలి.
- \(\angle \mathbf{AOB}\) యొక్క కోణ సమద్విఖండన కిరణం OC ని గీయాలి. ఇపుడు \(\angle \mathbf{AOC}\) = \(\angle \mathbf{COB}\) = 30° అవుతుంది.
- \(\angle \mathbf{COB}\) = 30° యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OD}}\) ని నిర్మించాలి.
- ఇపుడు \(\angle \mathbf{COD}\) = \(\angle \mathbf{DOB}\) = 15° కోణాలు ఏర్పడినవి.
- మనకు కావలసిన కోణం \(\angle \mathbf{AOD}\) = 45°, \(\angle \mathbf{AOD}\) = \(\angle \mathbf{AOC}\) + \(\angle \mathbf{COD}\) = 30° + 15° = 45° ఏర్పడినది.
2వ పద్ధతి : (90° లకు కోణ సమద్విఖండన రేఖ నిర్మించడం ద్వారా)
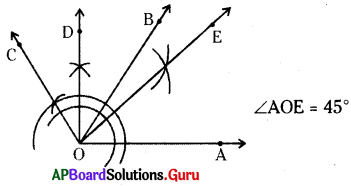
నిర్మాణక్రమం :
- \(\angle \mathbf{AOB}\) = 60°, \(\angle \mathbf{AOC}\) = 120° కోణాలను నిర్మించాలి.
- \(\angle \mathbf{BOC}\) = 60° కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OD}}\) ని గీయాలి.
- ఇపుడు \(\angle \mathbf{AOD}\) = \(\angle \mathbf{AOB}\) + \(\angle \mathbf{BOD}\) = 60° + 30° = 90° ఏర్పడినది.
- \(\angle \mathbf{AOD}\) = 90° యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OE}}\) ని గీయాలి. మనకు కావలసిన కోణం \(\angle \mathbf{AOE}\) = 45° ఏర్పడినది.
3వ. పద్దతి : (90° లను సరళకోణం నుండి నిర్మించి (మునుపటి సమస్యలో వలె) దాని కోణ సమద్విఖండనం చేయడం ద్వారా నిర్మించవచ్చును.)
4వ పద్దతి : (లంబకోణ సమద్విబాహు త్రిభుజ భావన నుండి)
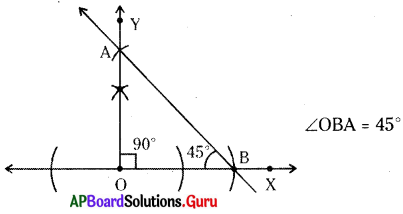
నిర్మాణక్రమం :
- \(\angle \mathbf{XOY}\) = 90° కోణాన్ని నిర్మించాలి. (పై సమస్యలోవలె)
- O కేంద్రంగా కొంత వ్యాసార్ధంలో \(\overrightarrow{\mathrm{OX}}\) మరియు \(\overrightarrow{\mathrm{OY}}\) లపై చాపరేఖలను గీచి, ఖండన బిందువులు A, B లుగా గుర్తించి, A, B లను కలపాలి.
- కావలసిన కోణం \(\angle \mathbf{OBA}\) = 45° ఏర్పడినది.