SCERT AP 7th Class Maths Solutions Pdf Chapter 11 Area of Plane Figures InText Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 11th Lesson Area of Plane Figures InText Questions
Check Your Progress [Page No: 84]
Question 1.
Fill the missing values in the following table.
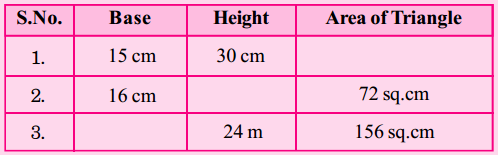
Answer:
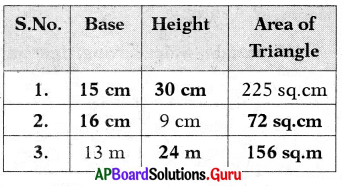
![]()
Question 2.
Anu has 4 right angled triangles with same size. Using those triangles, she makes a star like toy given below. Calculate the area of this toy star.

Answer:
Given base of the triangle b = 5 cm
Height of the triangle h = 12 cm
Area of the triangle = \(\frac{1}{2}\) × b × h
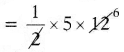
= 30 sq.cm
Area of star = Area of 4 triangles
∴ Area of the toy star = 4 × 30
= 120 sq.cm
Let’s Explore [Page No. 85]
Question 1.
The areas of triangular field ABC and rectangular field EFGH are equal. The length and breadth of EFGH are 15 m., 10 m. respectively. The base of ∆ABC 25 m. then find it’s height.
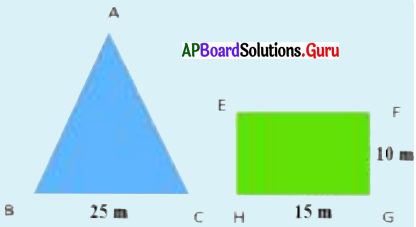
Answer:
Given length of rectangle l = 15 m
breadth of rectangle b = 10 m
Area of rectangle = l × b
= 15 × 10
= 150 sq.m.
Given base of the triangle b = 25 m
height of the triangle h = ? m
∴ Area of the triangle = \(\frac{1}{2}\) × b × h
⇒ \(\frac{1}{2}\) × 25 × h = 150
⇒ 25h = 150 × 2
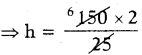
∴ Height of triangle h = 12 m.
![]()
Question 2.
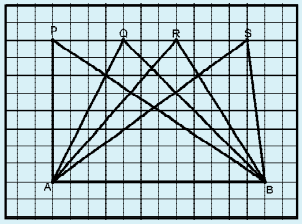
All the triangles in the given figure are on the base AB =12 cm. Find the height of each of the triangles corresponding to the base AB, by counting the grids and find the area of each triangle. What do you observe?
Answer:
Given in the figure,
Base of ∆ APB = 12 cm
Height = 8 cm
Area of ∆ APB = \(\frac{1}{2}\) × b × h
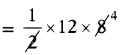
= 48 sq.cm
Base of ∆ AQB = 12 cm
Height = 8 cm
Area of ∆ AQB
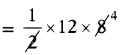
= 48 sq.cm
Base of ∆ ARB = 12 cm
Height = 8 cm
Area of ∆ ARB
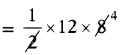
= 48 sq.cm
Base of ∆ ASB = 12 cm
Height = 8 cm
Area of ∆ ASB
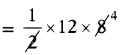
= 48 sq.cm
By observing area of each triangle is same.
![]()
Let’s Explore [Page No: 88]
Question 1.
5 cm width white tiles arranged between square shaped blue tiles along sides as shown in the figure. If the side of the total arrangement is 150 cm, find the area of the arranged white tiles.

Answer:
In the given figure side of total arrangement ABCD = 150 cm.
Width of white tile = 5 cm
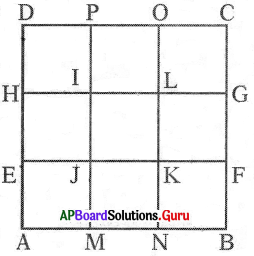
Area of white tile path EFGH = 150 × 5 = 750 sq.cm
Area of white tile path MNOP = 150 × 5 = 750 sq.cm
Area of common path IJKL = 5 × 5 = 25 sq.cm
Area of total white tile path
= Area of EFGH + Area of MNOP – Area of IJKL
= 750 + 750 – 25
∴ The area of the arranged white tiles
= 1475 sq.cm.
![]()
Question 2.
2 m wide path is present the outer side of the square grass land of side 80 m. Find the area of path and total expenditure of the path flooring with bricks, if the cost of flooring with bricks per sq.m is ₹ 200.

Answer:
Given side of the grass land = 80 m
Width of the path = 2 m
Path laid out side the grass land.
So, outer side of grassland
= side + 2 × width
= 80 + 2 × 2 = 84 m
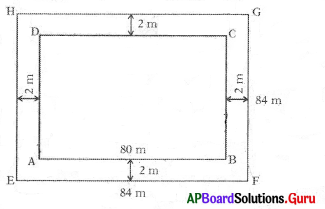
ABCD = 80 × 80 – 6400 sq.m
Area of the grass land with path
EFGH = 84 × 84 = 7056 sq.m
Area of the path = Area of EFGH – Area of ABCD
= 7056 – 6400 = 656 sq.m.
Cost of flooring per sq.m = ₹ 200
∴ Cost of flooring per 656 sq.m
= 656 × 200 = ₹ 1,31.200
![]()
Let’s Do Activity [Page No: 88]
Prepare two coloured rectangles one is red colour of length 25 cm, breadth 20 cm. Another one is green of length 20 cm, breadth 15 cm and place smaller rectangle middle to the bigger rectangle, so, that 2.5 cm red colour formed outside to green colour rectangle. Find the area of red colour path.

Answer:
Area of red rectangle = 25 × 20 = 500 cm2
Area of green rectangle = 20 × 15 = 300 cm2
∴ Area of the coloured path = (Area of red rectangle) – (Area of green rectangle)
= 500 – 300
= 200 cm2
[Page No: 89]
In the part of ‘Nadu-Nedu’ programme, Head master decided to arrange cir¬cular shape flower bed with radius 7 m in the premises of his school. How many flower plants needed if it takes 4 plants per sq. m. ?
Answer:
Here, length of the rectangle (l)
= Half of the perimeter of circle
= πr
breadth of the rectangle (b)
= radius of circle
= r
We know that the area of the rectangle = l × b = πr × r (∵ l = πr, b = r)
= πr2 – Area of the circle.
So, the area of the circle A = πr2
Now we solve above problem,
where ‘r’ = 7m
Area of flower bed = πr2
= \(\frac{22}{7}\) × 7 × 7
= 22 × 7
= 154 sq.m
Number of plants per sq.m = 4
Number of plants for 154 sq.m
= 154 × 4 = 616 plants.
So, Headmaster needs 616 plants for the flower bed.
![]()
Check Your Progress [Page No. 91]
Question 1.
The circumference of the circle shaped rangoli sheet is 88 cm. Find the radius of the circle and the area of the circle.
Answer:
Given circumference of the rangoli
2πr = 88 cm
⇒ 2 × \(\frac{22}{7}\) × r = 88
⇒ 44 r = 88 × 7
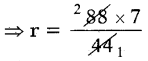
⇒ r = 14 cm
∴ Radius of rangoli r = 14 cm
Area of the rangoli = πr2
= \(\frac{22}{7}\) × 142
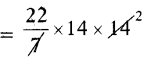
∴ Area of the circle = 616 sq.cm
![]()
Question 2.
Calculate the areas of circles shown in the figure.
(i)

Answer:
From the figure radius r = 7 cm
Area of the circle = πr2
= \(\frac{22}{7}\) × 72
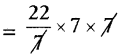
= 154 sq.cm
(ii)
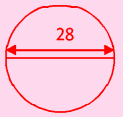
Answer:
From the figure diameter of circle d = 28 cm
Radius of circle r = \(\frac{\mathrm{d}}{2}\) = \(\frac{28}{2}\) = 14 cm.
Area of the circle = πr2
= \(\frac{22}{7}\) × 142
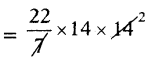
∴ Area of the circle = 616 sq.cm
![]()
(iii)
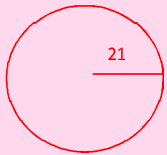
Answer:
From the figure radius of circle (r) = 21 cm
Area of the circle = πr2
= \(\frac{22}{7}\) × 212
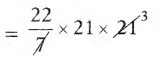
∴ Area of the circle = 1386 sq.cm
Let’s Explore [Page No: 93]
Radius of circular shaped grass land is 11 m. A goat is tied with a rope of length 4 m at the centre, then find the area of grass land that the goat cannot graze.
Answer:
Given the radius of grass land = 11 m
Area of grass land = πr2
= \(\frac{22}{7}\) × 11 × 11
= \(\frac{2662}{7}\)
∴ Area of grass land = 380.29 sq.m.
Radius of the small circle = length of rope to which goat tied = 4m
Area of land that the goat can graze = πr2
= \(\frac{22}{7}\) × 4 × 4
= \(\frac{352}{7}\) = 50.29 sq.m
∴ Area of land that the goat cannot graze
= Area of grass land – Area of grazed
= 380.29 – 50.29
= 330 sq.m.
![]()
Reasoning Corner (Non-Verbal) [Page No: 96 ]
Question 1.
Embedded Figures :
The problem figure (X) is given, answer figures as (a), (b), (c) & (d) given besides. The problem figures as a hidden figure of answer figure and one should identify that figure.

Answer:
Examples
Question 1.
Find the area of the given triangles.

Answer:
(i) In ∆PQR, Base (QR) = 6 cm,
Height (PS) = 4 cm
Area of ∆PQR = \(\frac{1}{2}\) x base x height
= \(\frac{1}{2}\) × QR × PS
= \(\frac{1}{2}\) × 6 cm × 4 cm
= 12 sq.cm.
(ii) In ∆LMN, Base (MN) = 3 cm,
Height (LO) = 2 cm
Area of ∆LMN = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × MN × LO
= \(\frac{1}{2}\) × 3 cm × 2 cm
= 3 sq.cm
![]()
Question 2.
The area of the ∆ XYZ is 12 sq.cm and the height XL is 3 cm, then find base YZ.
Answer:
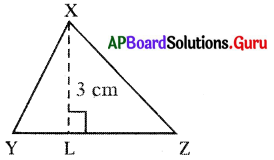
In ∆ XYZ, Base = YZ,
Height (XL) = 3 cm,
Area of the XYZ = 12 sq.cm.
Area of the ∆XYZ = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × YZ × XL
⇒ 12 = \(\frac{1}{2}\) × YZ × 3
⇒ YZ = 12 × \(\frac{2}{3}\)
So, YZ = 8 cm
Question 3.
In ∆ ABC, AC = 8 cm, BC = 4 cm and AE = 5 cm.
Find (i) the area of the AABC (ii) BD.
Answer:
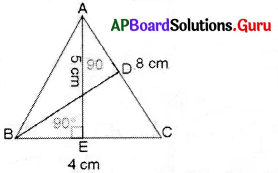
(i) In ∆ ABC, Base (BC) = 4 cm,
Height (AE) = 5 cm.
Area of the ∆ ABC = \(\frac{1}{2}\) × base × height
= = \(\frac{1}{2}\) × 4 × 5
10 sq.cm.
(ii) In ABAC, Base (AC) = 8 cm,
height (BD) = ?,
Area of ∆ BAC = 10 sq.cm
Area of the ∆ BAC = \(\frac{1}{2}\) × base × height
i. e. 10 = \(\frac{1}{2}\) × 8 × BD
BD = 10 × \(\frac{2}{8}\) = \(\frac{10}{4}\) = \(\frac{5}{2}\) = 2.5
So, height (BD) = 2.5 cm
![]()
Question 4.
Calculate the area of the given right-angled triangle with sides having right angle are 6 cm, 6 cm.
Answer:
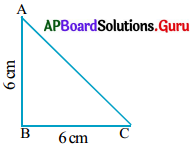
Method – 1: Sides having right angles are 6 cm, 6 cm.
Sides forming the right angle a = 6 cm, b = 6 cm
Area of a right-angled triangle
= \(\frac{1}{2}\) × Product of sides forming the right angle
= \(\frac{1}{2}\) × a × b
= \(\frac{1}{2}\) × 6 × 6
= 6 × 3 = 18 sq.cm.
(or)
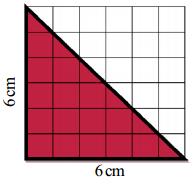
Method – 2: Observe the grid carefully, the right angled triangle covering half of the area of Square.
Area of a right-angled triangle
= \(\frac{1}{2}\) × Area of square
= \(\frac{1}{2}\) × 6 × 6 = 18 sq.cm.
Question 5.
Find the area of the triangle shaped lawn whose base and heights are 12m.,7m. respectively. Find the total cost of laying lawn, if cost of grass is ₹ 300 per Sq. m.

Answer:
Base of the triangle shaped lawn = 12 m.
Height = 7 m.
Area of triangle shaped lawn 1
= \(\frac{1}{2}\) × b × h
= \(\frac{1}{2}\) × 12 × 7
= 6 × 7 = 42 Sq.m
Cost of grass for laying in lawn per 1 Sq.m = ₹ 300
Cost of grass for laying in lawn for 42 Sq.m = ₹ 300 × 42 = ₹ 12,600
![]()
Question 6.
The length and breadth of a rectangular field is 65 m, 30 m respectively. A path of width 2.5 m is made around the park outside. Find the area of the path.
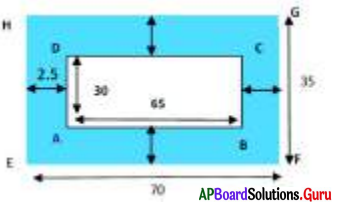
Answer:
In the fig, ABCD is a rectangular field and shaded area shows 2.5m. wide path. EFGH is a rectangle (field with path)
Length of ABCD (AB) = 65m.,
Breadth of ABCD (AD) = 30m.
Width of path = 2.5 m.
Area of path = Area of outer rectangular- field EFGH – Area of inner rectangular field ABCD
Length of rectangle EFGH = EF
= Length of field (AB) + (2 × Width of path)
= 65m + (2 × 2.5 m)
= 65m + 5m = 70m
Breadth of rectangle EFGH = EH
= Breadth of field (AD) + (2 × Width of path)
= 30 m + (2 × 2.5m)
= 30 m + 5m = 35m
Area of outer rectangle
EFGH = length × breadth
70m × 35m = 2450 Sq.m
Area of inner rectangle
ABCD = length × breadth
= 65 m × 30 m
= 1950 Sq.m
Area of path = Area of outer rectangle EFGH – Area of inner rectangle ABCD
= 2450 Sq.m – 1950 Sq.m
= 500 Sq.m.
Question 7.
A square shaped swimming pool of side 70m. It has 5m width path is present the outer side of the boundary. Find the area of this path. Find the expenditure of covering that path with tiles at the rate of ₹ 150 per sq.m.
Answer:
WXYZ shows a square shaped swimming pool of side 70m. 5m wide path to the outer side of the swimming pool.,
Area of the path = Area of swimming pool PQRS with path – Area of swimming pool WXYZ
PS = Side of swimming pool (WZ) + (2 × breadth of path)
= 70m + (2 × 5m)
= 70m + 10m = 80m
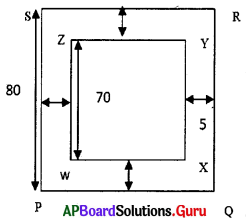
Area of swimming pool with path
PQRS = (Side)2 = (80 m)2
= 6400 Sq.m.
Area of swimming pool
WXYZ = (Side)2 = (70 m)2
= 4900 Sq.m.
Area of path = Area of swimming pool PQRS with path – Area of swimming pool WXYZ
= 6400 – 4900 = 1500 Sq.m.
If cost of covering tiles per 1 Sq.m.
= ₹ 150
Cost of covering tiles per 1500 Sq.m.
= ₹ 150 × 1500
= ₹ 2,25,000
![]()
Question 8.
The length of rectangular grass land is 55 m and breadth is 45 m in the centre of the grass land two paths of 3 m wide one parallel to the length and another parallel to breadth are situated in such a way that they intersect each other. Find the area of the path.
Answer:
In fig. ABCD is rectangular grass land.
Length of ABCD = 55 m
Breadth of ABCD = 45 m
Width of path = 3 m
Area of path EFGH = Length × Width
= 55 × 3
= 165 Sq.m
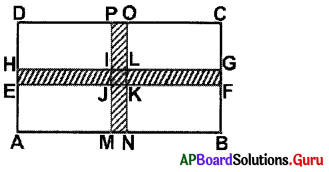
Area of path MNOP
= Breadth × Width
= 45 × 3 = 135 Sq.m.
Area of common path IJKL (situated on both paths)
= Width × Width = 3 m × 3 m = 9 Sq.m.
Area of square IJKL i.e., 9 Sq.m is included in both the paths. So we subtract one time.
Area of total path = Area of path EFGH + Area of path MNOP – Area of IJKL
= (165 Sq.m. + 135 Sq.m. – 9 Sq.m.)
= (300 9) Sq.m.
= 291 Sq.m.
Question 9.
Find the area of the rangoli of it’s radius is 21 cm.
(Use π = \(\frac{22}{7}\))
Answer:
Radius of rangoli (r) = 21 cm
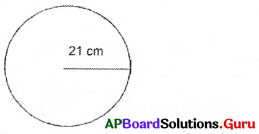
Area of circular shaped rangoli = πr2
= \(\frac{22}{7}\) × 21 cm × 21 cm
= 1386 sq. cm
∴ Area of the circle = 1386 sq. cm
![]()
Question 10.
Find the surface area of a circular shaped pool whose diameter is 28 m
(Use π = \(\frac{22}{7}\)).

Answer:
The diameter of circular shaped pool (d) = 28 m
Radius (r) = \(\frac{28}{2}\) m = 14 m
Area of a circular shaped pool = πr2
= \(\frac{22}{7}\) × (14m)2
= \(\frac{22}{7}\) × 14 m × 14 m
= 22 × 2 × 14 sq.m.
= 616 sq.m.
Question 11.
In a circular shaped park inner portion is given for kids to play and outer portion is given for walking to elders. If outer radius is 35 m, width of walking track is 14 m, then find the area of walking path.

Answer:
Outer radius of park (R) = 35 m,
Width of walking track = 14 m.
Radius of playground (r) = R – w = 35 – 14 = 21m.
Area of walking track = Area of the park – Area of playing ground
= πR2 – πr2
= \(\frac{22}{7}\) × 352 – \(\frac{22}{7}\) × 212
= \(\frac{22}{7}\) (352 – 212)
= \(\frac{22}{7}\) (1225 – 441)
= \(\frac{22}{7}\) × 784
= 22 × 112 = 2464 sq.m
![]()
Question 12.
A water fountain is in circular shaped whose radius is 10 m. Its inner portion of radius 3m is arranged for fountain and remaining part is cemented. Find the area of that cemented part and total cost of cementing if cost of cementing is ₹ 200 per sq.m.
Answer:
Radius for total water fountain (R) = 10m
Radius of fountain arranged portion (r) = 3 m
Area of cemented part = Area of total water fountain – Area of fountain arranged portion
= πR2 – πr2

= \(\frac{22}{7}\) × (10)2 – \(\frac{22}{7}\) × (3)2
= \(\frac{22}{7}\) [(10)2 – (3)2)
= \(\frac{22}{7}\) (100 – 9) sq.m.
= \(\frac{22}{7}\) × 91 sq.m.
= 22 × 13
= 286 sq.m
Given the cost of cementing per sq.m = ₹ 200
∴ Total cost of cementing = 286 × 200 = ₹ 57,200
Practice Questions [Page No: 96]
In each question below, you are given a figure (X) followed by four figures (a), (b), (c) and (d) such that (X) is embedded in one of them. Trace out the correct alternative.
Question 1.
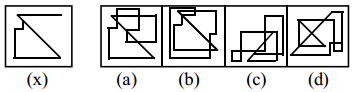
Answer:
a
Question 2.
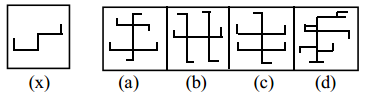
Answer:
c
Question 3.
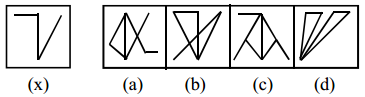
Answer:
b
![]()
Question 4.
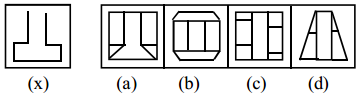
Answer:
a
Question 5.
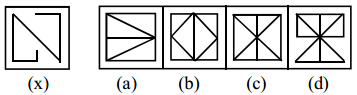
Answer:
c
Question 6.
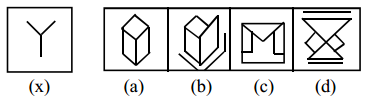
Answer:
a
Question 7.
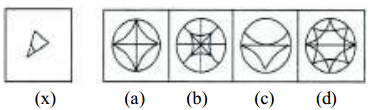
Answer:
b
Question 8.
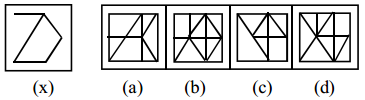
Answer:
b
![]()
Question 9.
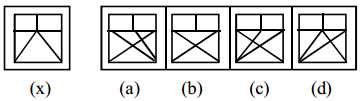
Answer:
d
Question 10.
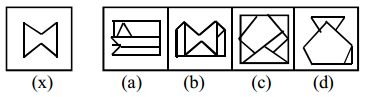
Answer:
b