AP State Syllabus AP Board 7th Class Maths Solutions Chapter 3 Simple Equations Ex 3 Textbook Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 3rd Lesson Simple Equations Exercise 3
![]()
Question 1.
Write the information given in the picture in the form of an equation. Also, find ‘x’ in the following figure.
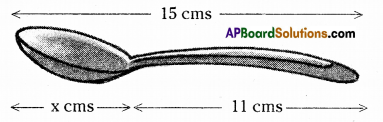
Solution:
From the figure x + 11 = 15
∴ x = 15 – 11 (transposing +11)
∴ x = 4cm
Question 2.
Write the information given in the picture in the form of an equation. Also, find ‘y in the following figure.
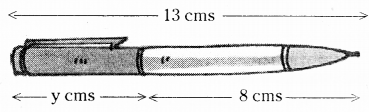
Solution:
From the figure y + 8 = 13
y = 13 – 8 (transposing 8)
∴ y = 5cm
![]()
Question 3.
If we add 7 to twice a number, we get 49. Find the number.
Solution:
Let the number be x
Then twice the number = 2x
Onaddingi = 2x + 7
By problem, 2x + 7 = 49
2x = 49 – 7 (transposing + 7)
2x = 42
x = \(\frac { 42 }{ 2 }\) (transposing x 2)
x = 21
Question 4.
If we subtract 22 from three times a number, we get 68. Find the number.
Solution:
Let the number be x
Then three times the number = 3x
On subtracting 22 ⇒ 3x – 22
By problem, 3x – 22 = 68
3x = 68 + 22 (transposing -22)
3x = 90
x = \(\frac { 90 }{ 3 }\)(transposingx3)
x = 30
∴ The required number 30
Question 5.
Find a number which when multiplied by 7 and then reduced by 3 is equal to 53.
Solution:
Let the number be x
Multiplied by 7 ⇒ 7x
Then reduced by 3 ⇒ 7x – 3
By problem, 7x – 3 = 53
7x = 53 + 3 (transposing – 3)
7x = 56
x = \(\frac { 56 }{ 7 }\) (transposing x 7)
x = 8 .
∴ The required number = 8
![]()
Question 6.
Sum of two numbers is 95. 1f one exceeds the other by 3, find the numbers.
Solution:
Let one number be = x.
Then the other number x – 3
Sumofthenumbers x + x – 3 = 2x – 3
By problem, 2x – 3 = 95
2x = 95 + 3 (transposing – 3)
2x = 98
x = \(\frac { 98 }{ 2 }\) (transposing x 2)
x = 49
∴if one number x 49 then the other number x – 3 = 49 – 3 = 46
![]()
Question 7.
Sum of three consecutive integers is 24. Find the integers.
Solution:
Let the three integers be = x, x + 1, x 2
Sumoftheintegers = x + x + 1 + x + 2 = 3x + 3
By problem, 3x + 3 = 24’
3x = 24 – 3 (Transposing + 3)
3x = 21
x = \(\frac { 21 }{ 3 }\) (transposing x 3)
x = 7
∴ The integers x = 7
x + 1 = 7 + 1 = 8
x + 2 = 7 + 2 = 9
Question 8.
Find the length and breadth of the rectangle given below if its perimeter is 72m.
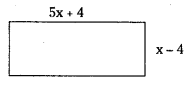
Solution:
Length of the rectangle = 5x + 4
Breadth of the rectangLe = x – 4
Perimeter of the rectangle = 2 x (length + breadth)
= 2x[(5x + 4)+(x – 4)]
= 2[5x + 4 + x – 4]
= 2(6x)
= 12x
Byproblem, 12x = 72
x = \(\frac { 72 }{ 12 }\) (transposing x 12)
x = 6
∴ Length of the rectangle = 5x + 4 = 5 x 6.4 = 34cm
Breadth of the rectangÌe = x – 4 = 6 – 4 = 2cm
![]()
Question 9.
Length of a rectangle exceeds its breadth by 4 m. 1f the perimeter of the rectangle is 84 m, find its length and breadth.
Solution:
Let the breadth be x
Then its length = x + 4
Perimeter of the rectangle = 2 x (length + breadth)
=2[x + 4 + x]
= 2 (2x + 4)
= 4x + 8
By problem, 4x + 8 = 84
4x = 84 – 8 (transposing + 8)
4x = 76
x = \(\frac{76}{4}\) (transposing x 4)
x = 19
∴ Length of the rectangle =x+4= 19+4 = 23m
Breadth of the rectangle = 19m
Question 10.
After 15 years, Hema’s age will become four times that of her present age. Find her present age.
Solution:
Let the preser age of Hema be x years
After 15 years Hema Age = 4x
By problem, x + 15 = 4x
x + 15 – 4x = 4x – 4x (Subtracting 4x from both sides)
– 3x + 15 = 0
– 3x = – 15
x = \(\frac{-15}{-3}\) transposing x ( – 3)]
x = 5
∴ Her present age is 5 years.
∴ Her present age is 5 years.
![]()
Question 11.
A sum of ₹.3000 is to be given in the form of 63 prizes. Ifthe prize money is either ₹. 100 or.25. Find the number of prizes of each type.
Solution:
Let the number of ₹ 100 prizes be x
Then the number of ₹ 25 prizes be = 63 – x
Value of the prizes = 100x + (63 – x) x 25
= 100x+ 1575 – 25x
= 75x + 1575
By problem, 75x + 1575 = 3000
75x = 3000 – 1575
75x = 1425
x = \(\frac { 1425 }{ 75 }\)
x = 19
∴ ₹ 100 prizes = 19
₹25 prizes= 63 – x =63 – 19 = 44
Question 12.
A number is divided into two parts such that one part is 10 more than the other. Ifthe two parts are in the ratio 5:3, find the number and the two parts.
Solution:
Let one part be x
Then the other part = x + 10
Ratio of these two parts = x + 10 : x
Byproblem, x + 10 : x=5:3
∴ \(\frac{x+10}{x}=\frac{5}{3}\)
3(x+ 10)=5x
3x + 30 = 5x
30 = 5x – 3x
2x = 30
x = \(\frac{30}{2}\)
x = 15
If one part is 15 then the other part must be x + 10 = 15 + 10 = 25
∴ The number is 15 + 25 40
![]()
Question 13.
Suhana said, “multiplying my number by 5 and adding 8 to it gives the same answer as subtracting my number from 20”. Find Suhana’s numbers.
Solution:
Let Suhana’s number be x
Muhtplying by S and adding 8 to that number 5x + 8
Subtracting that number from 20 = 20 – x
By problem above two are equal.
i.e. 5x + 8 = 20 – x
5x + x = 20 – 8
6x = 12
x = \(\frac{12}{6}\) = 2
x = 2
∴ Suhanas number is 2
Question 14.
The teacher tells the class that the highest marks obtained by a student in her class is twice the lowest marks plus 7. The highest mark is 87. What is the lowest mark?
Solution:
Let the Lowest mark of the class = x
Twice the least mark = 2x
On adding 7 = 2x + 7
By problem; 2x + 7 = 87
2x = 87 – 7
2x = 80
x = \(\frac{80}{2}\) = 40
x = 40
∴ The lowest mark = 40
![]()
Question 15.
In adjacent figure find the magnitude of each of the three angles formed?
(Hint: Sum of all angles at a point on a line is 180°)
Solution:
(Hint : Sum of all angles at a point on a line is 180°)
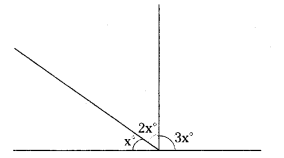
We know sum of angles at a point = 180°
∴ x° + 2x° + 3x° = 180
6x° = 180°
x = \(\frac{180}{6}\) = 30
∴ The angles are x = 30°
2x = 2 x 30 = 60°
3x° = 3 x 30° = 90°
Question 16.
Solve the following riddle:
I am a number
Tell my identity
Take me two times over
And add a thirty six.
To reach a century
Solution:
Let the number be x
Two times the number = 2x
On adding 36 = 2x 36
By problem, 2x + 36 = 100 – 4
2x 36 = 96
2x = 96 – 36
2x = \(\frac{60}{2}\)
x = 30