SCERT AP 7th Class Maths Solutions Pdf Chapter 5 త్రిభుజాలు Ex 5.2 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 5th Lesson త్రిభుజాలు Exercise 5.2
ప్రశ్న 1.
క్రింద ఇచ్చిన కోణాలలో ఏవి త్రిభుజమును ఏర్పరచును ?
(a) 60°, 70°, 80°
సాధన.
60°, 70, 80°.
మూడు కోణాల మొత్తం = 60° + 70° + 80°
= 210° ≠ 180°
కావున, ఇచ్చిన కోణాలు త్రిభుజమును ఏర్పరచవు.
![]()
(b) 65°, 45°, 70°
సాధన.
65°, 45°, 70°.
మూడు కోణాల మొత్తం
= 65° + 45° + 70° = 180°
కావున, ఇచ్చిన కోణాలు త్రిభుజాన్ని ఏర్పరుస్తాయి.
(c) 40°, 50°, 60°
సాధన.
40°, 50°, 60°
మూడు కోణాల మొత్తం = 40° + 50° + 60°
= 150° ≠ 180°
కావున, ఇచ్చిన కోణాలు త్రిభుజమును ఏర్పరచవు.
(d) 60°, 30°, 90°
సాధన.
60°, 30°, 90°.
మూడు కోణాల మొత్తం
= 60° + 30° + 90° = 180°
కావున, ఇచ్చిన కోణాలు త్రిభుజాన్ని ఏర్పరుస్తాయి.
(e) 38°, 102°, 40°
సాధన.
38°, 102°, 40°
మూడు కోణాల మొత్తం
= 38° + 102° + 40° = 180°
కావున, ఇచ్చిన కోణాలు త్రిభుజాన్ని ఏర్పరుస్తాయి.
(f) 100°, 30°, 45°
సాధన.
100°, 30°, 45°
మూడు కోణాల మొత్తం
= 100° + 30° + 45° = 175° = 180°
కావున, ఇచ్చిన కోణాలు త్రిభుజమును ఏర్పరచవు.
ప్రశ్న 2.
త్రిభుజంలోని రెండు అంతర కోణాల మొత్తము 105° అయిన మూడవకోణం కనుగొనండి.
సాధన.
∆ABC లో రెండు అంతర కోణాల మొత్తం 105°.
∠A + ∠B = 105° అనుకొనుము.
∆ABC లో, ∠A + ∠B + ∠C = 180° అని మనకు తెలుసు.
⇒ 105° + ∠C = 180°
⇒ 105° + ∠C – 105° = 180° – 105°
⇒ ∠C = 75°
∴ మూడవ కోనం = 75.
![]()
ప్రశ్న 3.
∆PQRలో ∠P = 65°మరియు ∠Q = 50° అయిన ∠Rను కనుగొనండి.
సాధన.
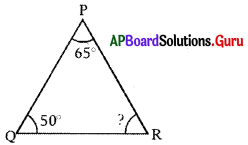
∆PQR లో ∠P = 65°, ∠Q = 50°, ∠R = ?
త్రిభుజంలోని మూడు కోణాల మొత్తం = 180°
∴ ∠P + ∠Q + ∠R = 180°
⇒ 65° + 50° + R = 180°
⇒ 115° + ∠R = 180°
⇒ ∠R = 180° – 115°
∴ ∠R = 65°
ప్రశ్న 4.
క్రింది త్రిభుజములలో మిగిలిన కోణమును కనుగొనండి.
(a)
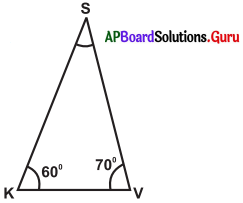
సాధన.
∠K = 60°, ∠V = 70°, ∠S = ?
⇒ ∠K + ∠V + ∠S = 180°
⇒ 60° + 70° + ∠S = 180°
⇒ 130° + ∠S = 180°
⇒∠S = 180° – 1300
∴ ∠S = 50°
![]()
(b)
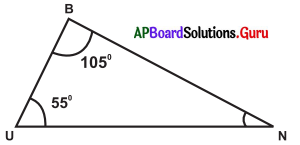
సాధన.
∠B = 105°, ∠U = 55°, ∠N = ?
⇒ ∠B + ∠U + ∠N = 180°
⇒ 105° + 55° + ∠N = 180°
⇒ 160° + ∠N = 180°
⇒ ∠N = 180° – 160°
∴ ∠N = 20°
(c)
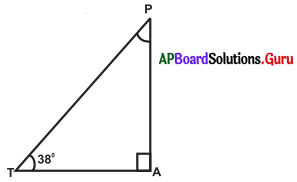
సాధన.
∠T = 38°, ∠A = 90°, ∠P = ?
⇒ ∠T +∠A + ∠P = 180°
⇒ 38° + 90° + ∠P = 180°
⇒ 128° + ∠P = 180°
⇒ ∠P = 180° – 128°
∴ ∠P = 52°
(లేదా)
లంబకోణ త్రిభుజంలో లంబకోణేతర కోణాలు పూరకాలు.
∴ ∠T + ∠P = 90°
⇒ 38° + ∠P = 90°
⇒ ∠P = 90° – 38°
∴ ∠P = 52°
ప్రశ్న 5.
క్రింద ఇచ్చిన త్రిభుజములలో ‘x’ విలువను కనుగొనండి.
(a)
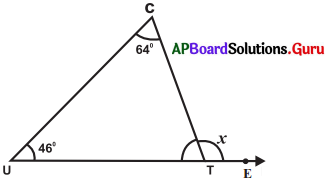
సాధన.
∆CUT లో, ∠C = 64°, ∠U = 46°
మరియు బాహ్యకోణం 2CTE = x = ?
∆CUT లో,
∠C + ∠U + ∠T = 180° అని మనకు తెలుసు.
⇒ 64° + 46° + ∠T = 180°
⇒ 110° + ∠T = 180°
⇒ 110° + ∠T – 110° = 180° – 110°
∴ ∠UTC = ∠T = 70°
∠UTC + ∠CTE = 180° (రేఖీయ కోణాల జత)
⇒ 70° + x° = 180°
⇒ 70° + x° – 70° = 180° – 70°
∴ x = 110°
![]()
(b)
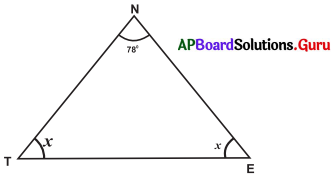
సాధన.
∠N = 78°, ∠T = x, ∠E = x
∠N + ∠T + ∠E = 180°
⇒ 78° + x + x = 180°
⇒ 78° + 2x = 180°
⇒ 2x = 180° – 78°
⇒ 2x = 102°
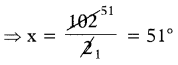
∴ x = 51°
ప్రశ్న 6.
క్రింద ఇచ్చిన త్రిభుజాలలో ‘x’ మరియు ‘y’ విలువలు కనుగొనండి.
(a)
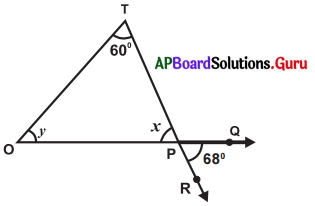
సాధన.
∠T = 60°, ∠0 = y
∠OPT = x మరియ ∠QPR = 68°
x = 68° (శీర్షాభిముఖ కోణాలు)
∆TOP లో,
∠T + ∠O + ∠P = 180°
⇒ 60° + y + x = 180°
⇒ 60° + y + 68° = 180°
⇒ y + 128° = 180
⇒ y = 180° – 128°
∴ y = 52°
(b)
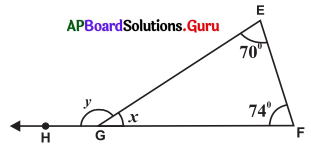
సాధన.
∠E = 70°, ∠F = 74°
∠FGE = x మరియు ∠EGH = y
∠E +∠F + ∠G = 180°
⇒ 70° + 74° + X = 180°
⇒ 144° + X = 180°
⇒ x = 180° – 144°
⇒ x = 36°
∴ x + y = 180° (రేఖీయద్వయం)
⇒ 36° + y = 180°
⇒ y = 180° – 36°
∴ y = 144°
![]()
ప్రశ్న 7.
ఒక లంబకోణ త్రిభుజంలో ఒక అల్ప కోణం 37° అయిన రెండవ అల్ప కోణం కనుగొనండి.
సాధన.
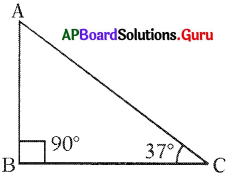
ఒక లంబకోణంలో ఒక అల్పకోణం = 37°
రెండవ అల్పకోణం = ?
లంబకోణ త్రిభుజంలోని రెండు అల్పకోణాల మొత్తం = 90°
∴ రెండవ అల్పకోణం = 90° – 37° = 53°
(లేదా)
లంబకోణ త్రిభుజంలోని రెండవ అల్పకోణం = x
అనుకొనుము ఇప్పుడు లంబకోణ త్రిభుజంలోని కోణాలు = 37°, 90°, x°
∴ 37° + 90° + x° = 180°
⇒ 127° + x° = 180°
⇒ x° = 180° – 127° = 53°
∴ రెండవ అల్పకోణము = 53°.
ప్రశ్న 8.
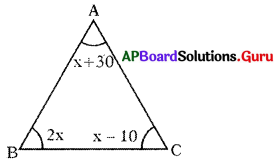
త్రిభుజాకారంలో ఉన్న సైన్ బోర్డ్ యొక్క మూడు అంతర కోణాలు వరుసగా 2x°, (x – 10)°, (x + 30)° అయిన ఆ కోణాలు కనుగొనండి.
సాధన.
త్రిభుజాకారంలోని సైన్ బోర్డ్ యొక్క మూడు అంతర .
కోణాలు 2x°, (x – 10)°, (x +30)°.
∴ 2x° + (x – 10)° + (x + 30)° = 180°
(∵ త్రిభుజంలోని మూడు అంతర కోణాల మొత్తం 180°)
⇒ 4x° + 20° = 180°
⇒ 4x° = 180° – 20°
⇒ 4x° = 160°
⇒ x° = \(\frac{160^{\circ}}{4}\)
∴ x = 40°
∴ త్రిభుజంలోని కోణాలు : –
1వ కోణం = 2x° = 2(40) = 80°
2వ కోణం = (x – 10° = (40 – 10)° = 30°
3వ కోణం = (x + 30)° = (40 + 30)° = 70°
సరిచూచుట:
80° + 30° + 70° = 180°
![]()
ప్రశ్న 9.
త్రిభుజం యొక్క ఒక కోణం 80° మరియు మిగిలిన రెండు కోణాలు సమానం అయిన వాటిని కనుగొనుము.
సాధన.
త్రిభుజం యొక్క ఒక కోణం = 80°
రెండు సమాన కోణాలను ఒక్కొక్కటి x° అనుకొందాం.
⇒ 80° + x° + x° = 180°
⇒ 80° + 2x° = 180°
⇒ 2x° = 180° – 80
⇒ 2x = 100°
⇒ x = \(\frac{100^{\circ}}{2}\) = 50°
∴ రెండు సమాన కోణాలు 50°, 50°.
(లేదా)
త్రిభుజంలో మూడు కోణాల మొత్తం = 180°
అందులో ఒక కోణం = 80°
∴ మిగిలిన రెండు కోణాల మొత్తం = 180° – 80° = 100°
మిగిలిన రెండు కోణాలు సమానం.
కావున, మిగిలిన రెండు కోణాలలో ఒక్కొక్క కోణం
= \(\frac{100^{\circ}}{2}\) = 50°
ప్రశ్న 10.
క్రింది ప్రవచనాలు సత్యమో, అసత్యమో వ్రాసి, అసత్య ప్రవచనాలను కారణంగా వివరించండి.
(i) త్రిభుజం రెండు లంబ కోణాలు కలిగి ఉండవచ్చు.
జవాబు
అసత్యం
కారణం: రెండు లంబకోణాల మొత్తం
90° + 90° = 180°
అపుడు త్రిభుజంలోని మూడు కోణాల మొత్తం 180° కన్నా ఎక్కువ అవుతుంది. కావున, త్రిభుజంలో రెండు లంబకోణాలు అసాధ్యము.
(ii) త్రిభుజం రెండు అల్ప కోణాలు కలిగి ఉండవచ్చు.
జవాబు
సత్యం
(iii) త్రిభుజం రెండు అధిక కోణాలు కలిగి ఉండవచ్చు.
జవాబు
అసత్యం
కారణం: రెండు అధిక కోణాల మొత్తం 180° కన్నా ఎక్కువ అవుతుంది. ఈ సందర్భంలో త్రిభుజంలోని మూడు కోణాల మొత్తం 180° కన్నా ఎక్కువ అవుతుంది. కావున, త్రిభుజంలో రెండు అధిక కోణాలు అసాధ్యము.
![]()
ప్రశ్న 11.
త్రిభుజం యొక్క కోణాలు 2:4:3 నిష్పత్తిలో ఉన్నచో, ఆ కోణాలు కనుగొనండి.
సాధన.
త్రిభుజం యొక్క కోణాల నిష్పత్తి = 2 : 4 : 3.
కావున, ఆ త్రిభుజ కోణాలు = 2x°, 4x°, 3x° అనుకొందాము.
∴ 2x° + 4x° + 3x° = 180° (త్రిభుజంలోని మూడు కోణాల మొత్తం 1809)
⇒ 9x° = 180°
⇒ x° = \(\frac{180^{\circ}}{9}\) = 20°
∴ త్రిభుజ కోణాలు :
1వ కోణం = 2x° = 2(20°) = 40°
2వ కోణం = 4x° = 4(20°) = 80°
3వ కోణం = 3x° = 3(20°) = 60°
(లేదా)
1వ కోణం = \(\frac{180}{(2+4+3)}\) × 2
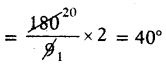
2వ కోణం = \(\frac{180}{(2+4+3)}\) × 4
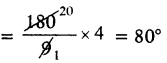
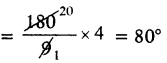
3వ కోణం = \(\frac{180}{(2+4+3)}\) × 3
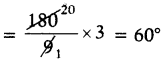
సరిచూచుట: 40° + 80° + 60° = 180°