AP State Syllabus AP Board 7th Class Maths Solutions Chapter 8 Congruency of Triangles InText Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 8th Lesson Congruency of Triangles InText Questions
![]()
Do This
Question 1.
Here are some shapes. See whether all the shapes given in row are congruent to each other or not. You can trace the figures and check. (Page No. 164 )

Solution:
All are congruent.
Question 2.
Which of the following pairs of figures are congruent ? (Page No. 164 )
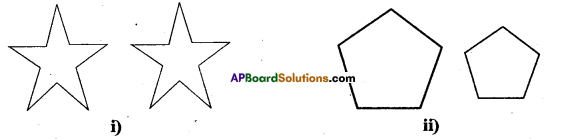
Solution:
Both is (i) and (iii) are congruent.
![]()
Question 3.
ΔEFG ≅ ΔLMN (Page No. 166)

Write the corresponding vertices, angles and sides of the two triangles.
Solution:
Corresponding Sides EF = LM; FG = MN; EG = LN
Angles ∠E = ∠L, ∠F = ∠M, ∠G = ∠N
Vertices E = L, F = M, G = N
Question 4.
If ΔABC ≅ ΔDEF, write the parts of AABC that correspond to (Page No. 166)
i) DE
ii) ∠E
iii) DF
iv) EF
v) ∠F
Solution:
i) \(\overrightarrow{\mathrm{DE}}=\overrightarrow{\mathrm{AB}}\)
ii) ∠E = ∠B
iii) \(\overrightarrow{\mathrm{DF}}=\overline{\mathrm{AC}}\)
iv) \(\overline{\mathrm{EF}}=\overline{\mathrm{BC}}\)
ii) ∠F = ∠C
![]()
Question 5.
Name the congruent triangles in each of the following pairs. Write the statement using ≅. (Page No. 166)
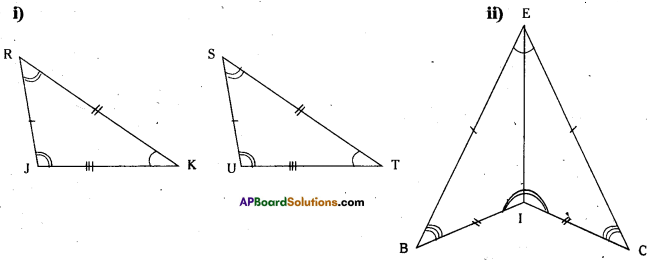
Solution:
i) ΔRJK ≅ ΔSUT
ii) ΔBIE ≅ ΔCIE
Question 6.
Name the congruent angles and sides for each pair of congruent triangles. (Page No. 166)
i) ΔCDG ≅ ΔRSW
Solution:
i) ΔTUV ≅ ΔXYZ
Sides: TU = XY
UV = YZ
TV = XZ
Angles :∠T = ∠X,
∠U = ∠Y,
∠V =∠Z
ii) ΔCDG ≅ ΔRSW
Sides : CD = RS
DG = SW
CG = RW
Angles : ∠C = ∠R,
∠D = ∠S,
∠G = ∠W
![]()
Try This
Question 1.
Is the following pair of triangles congurent ? Give reason to support your answer. (Page No. 174)
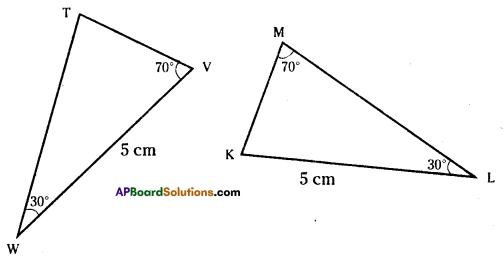
Solution:
The triangles are not congruent since the corresponding parts are not equal.
Try This
Question 1.
In the figures given below, measures of some parts of triangles are given. By applying RHS congruence rule state, which pairs of triangle are congruent. In case of congruent tri¬angles, write the result in symbolic form. (Page No. 177)
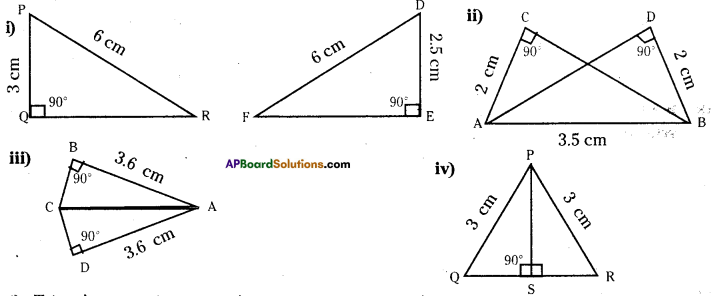
Solution:
i) Triangles are not congruent.
ii) ΔABC ≅ ΔBAD or ΔACB ≅ ΔBDA
iii) ΔABC ≅ ΔADC
iv) ΔPQS ≅ ΔPRS
![]()
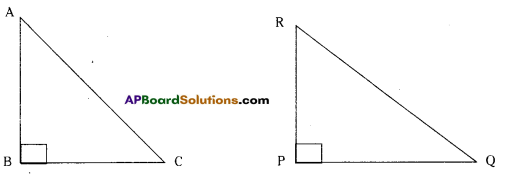
Question 2.
It is to be established by R.H.S congruence rule that ΔABC = ΔRPQ. What additional information is needed, if it is given that ∠B = ∠P = 90° and AB = RP ? (Page No. 177)
Solution:
∠B = ∠P (Right angle)
AB = RP (Side)
So we need AC = RQ
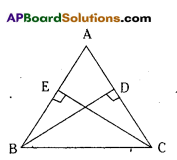
Question 3.
In the adjacent figure, BD and CE are altitudes of ΔABC such that BD = CE.
i) State the three pairs of equal parts in ΔCBD andΔBCE. (Page No. 177)
Solution:
∠CDB ≅ ∠BEC (Right angle)
BD = CE (Side)
BC = BC common/hypotenuse
ii) Is ΔCBD ≅ ΔBCE ? Why or why not ?
Solution:
Yes, ΔCBD ≅ ΔBCE by R.H.S congruence.
iii) Is ∠DBC = ∠EBC ? Why or why not ?
Solution:
No, ∠DBC ≠ ∠EBC
![]()
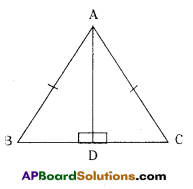
Question 4.
ABC is an isosceles triangle with AB = AC and AD is one of its altitudes. Page No. 177
i) State the three pairs of equal parts in ΔADB and ΔADC.
Solution:
∠ADB = ∠ADC Right angle
AB = AC hypotenuse; AD = AD common side
ii) Is ΔADB = ΔADC ? Why or why not ?
Solution:
Yes, by R.H.S congruence
iii) Is ∠B = ∠C ? Why or why not ?
Solution:
Yes by c.p.c.t
iv) Is BD ≅ CD ? Why or why not ?
Solution:
Yes, by c.p.c.t