Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 13th Lesson Thermodynamics Textbook Questions and Answers.
AP Inter 1st Year Physics Study Material 13th Lesson Thermodynamics
Very Short Answer Questions
Question 1.
Define Thermal equilibrium. How does it lead to the Zeroth Law of Thermodynamics?
Answer:
If the temperatures of the two systems are equal, then they are said to be in thermal equilibrium.
Zeroth law of thermodynamics: “If two systems (A, B) are in thermal equilibrium with the third system (c) separately, then two systems (A, B) thermal equilibrium with each other.”
Question 2.
Define Calorie. What is the relation between calorie and mechanical equivalent of heat?
Answer:
Calorie : It is defined to be the amount of heat required to raise the temperature of 1g of water from 14.5°C to 15.5°C.
The relation between calorie and mechanical equivalent of heat is given by 1 cal = 4186 J Kg-1K-1 or 1 cal = 4.186 J g-1K-1.
![]()
Qeustion 3.
What thermodynamic variables can be defined by
a) Zeroth Law
b) First Law ?
Answer:
a) Temperature
b) Internal energy.
Question 4.
Define specific heat capacity of the substance. On which factors does it depend ?
Answer:
Specific heat capacity :
The amount of heat required to raise the 1 gm of substance through 1°c or 1 k is called specific heat capacity (or) the heat capacity per unit mass is called specific heat.
S = \(\left(\frac{1}{m}\right) \frac{\Delta Q}{\Delta T}\)
It depends on 1) natuture of the substance 2) temperature.
Question 5.
Define molar specific heat capacity.
Answer:
Molar specific heat capacity : The amount of heat required to raise the 1gm mole of substance through 1°C or 1°K is called molar specific heat capacity.
Question 6.
For a solid, what is the total energy of an oscillator ?
Answer:
For a mole of a solid, the total energy of an oscillator, U = 3KB T × NA = 3RT.
![]()
Question 7.
Indicate the graph showing the variation of specific heat of water with temperature. What does it signify ?
Ans.
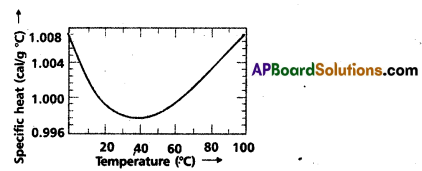
Significance : the specific heat of water varies slightly with temperature in the range 0 to 100°C.
Question 8.
Define state variables and equation of state.
Answer:
State variables : The state of a system is described by pressure P, temparature T, density p (intensive variables) and internal energy U, Volume V, total mass M (Extensive variables). These are called state variables.
Equation of state : The connection between the state variables is called the equation of state.
Question 9.
Why a heat engine with 100% efficiency can never be realised in practise ?
Answer:
The efficiency of heat engine is η = 1 – \(\frac{Q_2}{Q_1}\)
For Q2 = 0, η = 1, i.e., the engine will have 100% efficiency in converting heat into work.
The first law of thermodynamics does not rule out such an engine. But experience shows that such an ideal engine with η = 1 is never possible.
Question 10.
In summer, when the valve of a bicycle tube is opened, the escaping air appears cold.
Answer:
This happens due to adiabatic expansion of the air of the tube of the bicycle.
Question 11.
Why does the brake drum of an automobile get heated up while moving down at constant speed ?
Answer:
The work done by the brake drum on wheel is converted into heat due to friction.
![]()
Question 12.
Can a room be cooled by leaving the door of an electric refrigerator open ?
Answer:
No, a room can not be cooled by leaving the door of a refrigerator open, rather it will get slightly heated.
Question 13.
Which of the’ two will increase the pressure more, an adiabatic or an isothermal process, in reducing the volume to 50% ?
Answer:
Isothermal process obeys , P1V1 = P2V2
But V2 = \(\frac{\mathrm{v_1}}{2}\) ⇒ P1V1, = P2 \(\frac{\mathrm{v_1}}{2}\)
∴ P2 = 2P1
Adiabatic process obeys, P1V1γ = P2V2γ
P2 = \(P_1\left[\frac{v_1}{v_2}\right]^\gamma=p_1\left[\frac{v_1}{\frac{v_1}{2}}\right]\)
∴ P2 = 2γ P1 Where r = \(\frac{C_p}{C_v}\)
∴ pressure is more in adiabatic than isothermal.
Question 14.
A thermoflask containing a liquid is shaken vigorously. What happens to its temperature ? .
Answer:
Work is done by the liquid on the wall of flask, since it is vigorously shaken. Hence Internal energy and temperature of the liquid increases.
Question 15.
A sound wave is sent into a gas pipe. Does its internal energy change ?
Answer:
Yes, a sound wave is sent into a gas pipe internal energy increases.
![]()
Question 16.
How much will be the internal energy change in
- isothermal process
- adiabatic process
Answer:
- Change in internal energy during isothermal process is dU = 0 [∵ U is constant)]
- a) Change in internal energy during adiabatic compression increases,
b) Change in internal energy during adiabatic expansion decreases.
Question 17.
The coolant in a chemical or a nuclear plant should have.high specific heat. Why ?
Answer:
In chemical and nuclear plants more heat is liberated. To absorb this heat, the coolant should have a property of high specific heat for small rise in temperature.
Since S = \(\frac{1}{m} \frac{d Q}{d t}\) ⇒ S ∝ \(\frac{1}{d t}\)
Question 18.
Explain the following processes
- Isochoric process
- Isobaric process
Answer:
- Isochoric process : A process takes place at constant volume is called Isochoric process. During this process, no work is done on or by the gas, its internal energy and its temperature changes.
- Isoboric process : A process takes place at constant pressure is called isobaric process During this process temperature, internal energy changes. The heat absorbed goes partly to increase internal energy and partly to do work.
Short Answer Questions
Question 1.
State and explain first law of thermodynamics.
Answer:
Statement: The amount of heat supplied to system is equal to the algebraic sum of the change in internal energy of the system and the amount of external work-done.
Explanation : When ∆Q is the quantity of heat is supplied to system, a part of it is used to increase its internal energy ∆U and the rest is used in doing external work ∆W. The mathematical expressions of this law is ∆Q = ∆U – ∆W. It is a special case of law of conservation of energy.
![]()
Question 2.
Define two principal specific heats of a gas. Which is greater and why ?
Answer:
Two principal specific heats of a gas are
- Molar specific heat capacity at constant pressure
- molar specific heat capacity at constant volume.
1. Molar Specific heat capacity at constant pressure (Cp): The amount of heat required to raise the temperature of 1 gm – mole of a gas through 1°C at constant pressure is called molar specific heat at constant pressure.
i.e., Cp = \(\frac{1}{\mu} \frac{\Delta Q}{\Delta T}\) where μ is no of moles.
2. Molar Specific heat capacity at constant volume (Cv): The amount of heat required to raise the temperature of 1gm – mole of a gas through 1°C at constant volume is called molar specific heat at constant volume i.e., Cv = \(\frac{1}{\mu} \frac{\Delta Q}{\Delta T}\)
Explanation of Cp is greater that Cv: When a gas is heated at a constant pressure, it expands. The heat supplied to it is used partly in raising its temperature and partly in doing work against the external pressure. If, on the other hand, the gas is heated at constant volume, no work is done. Therefore, the heat supplied is to be used only in raising the temperature. Hence the amount of heat required to be supplied to a gas to raise its temperature by 1 °C (say) at constant pressure will be greater than the amount required at constant volume.
Question 3.
Derive a relation between the two specific heat capacities of gas on the basis of first law of thermodynamics
Answer:
The mathematical equation of first law of thermodynamics for 1 mole of gas is given by
∆Q = ∆U + P∆V
if ∆Q is absorbed heat at constant volume, ∆V = 0
Cv = \(\left[\frac{\Delta Q}{\Delta T}\right]_V=\left[\frac{\Delta U}{\Delta T}\right]_V=\left[\frac{\Delta U}{\Delta T}\right]\) ……………. (1)
Where the subscript V is dropped in the last step, since U of an ideal gas depends only on temperature. (The subscript denotes the quantity kept fixed.) If, on the other hand, ∆Q is absorbed heat at constant pressure,
Cp = \(\left[\frac{\Delta Q}{\Delta T}\right]_P=\left[\frac{\Delta U}{\Delta T}\right]_P+P\left[\frac{\Delta V}{\Delta T}\right]_P \Rightarrow\left[\frac{\Delta Q}{\Delta T}\right]_P=\left[\frac{\Delta U}{\Delta T}\right]+P\left[\frac{\Delta V}{\Delta T}\right]_P\) ………………… (2)
The subscript p.can be dropped from the first term since U of an ideal gas depends only on T. Now, for a mole of an ideal gas.
PV = RT
Which gives P\(\left[\frac{\Delta V}{\Delta T}\right]_P\) = R
Putting the equations (1) and (3) in (2), we get
Cp = Cv + R
∴ Cp – Cv = R
![]()
Question 4.
Obtain an expression for the work done by an ideal gas during isothermal change.
Answer:
Expression for the work done by an ideal gas during isothermal change : Let a certain mass of gas expands from volume V1 to V2 isothermally at constanst temperature T. Let the pressure changes form P1 to P2.
The work done during the small change in volume dv at a pressure ‘p’ is dw = pdv
The total work done during the change of volume from V1 to V2 is W = \(\int d w=\int_{V_1}^{V_2} p d v\) …………. (1)
The Isothermal change is represented by
PV = constant
PV = μRT ⇒ P =\(\frac{\mu \mathrm{RT}}{\mathrm{V}}\) where μ = no. of moles
substituting this value in equation (1)
W = \(\int_{V_1}^{v_2} p d v=\int_{V_1}^{V_2} \frac{\mu R T}{V} d V=\mu R T \int_{V_1}^{V_2} \frac{d v}{V}\)
W = μRT loge \(\frac{V_2}{V_1}\)
∴ Work done during the isothermal change W = 2.3026 RT log10 \(\frac{V_2}{V_1}\) .
Question 5.
Obtain an expression for the work done by an ideal gas during adiabatic change and explain.
Answer:
Expression for the work done by an ideal gas during adiabatic change :
During an adiabatic chnage the state of an ideal gas changes from (P1, V1, T1) to (P2, V2, T2)
The workdone during a small change in volume dV at a pressure p is dw = pdV
Total work done by gas from volume V1 to V2 is ,
W = \(\int\) dw = \(\int_{v_1}^{v_2}\) pdv ………………. (1)
The adiabatic relation between pressure and volume is given by PVr = constant K …………. (2)
P = \(\frac{k}{v^r}\) …………… (3)
and P1V1r = P2V2r = K
Substituting eg. (3) in (1) becomes

This is equal to the work done during the adiabatic change.
![]()
Question 6.
Compare isothermal and an adiabatic process.
Answer:
Isothermal change
- Changes in volume and pressure of a gas taking place at constant temperature are called isothermal changes,
- Temperature of the gas remains constant.
- The gas remains in good thermal contact with the surroundings and heat is exchanged.
- Internal energy remains constant. Change in internal energy ∆U = 0
- This process takes place slowly.
- Boyle’s law PV = Constant holds good.
- Work done W = RT loge\(\frac{V_2}{V_1}\) .
Adiabatic change
- Changes in volume and pressure of a gas taking place in a thermally isolated system are called adiabatic changes.
- Temperature of the gas changes.
- The gas is isolated from the surroundings and heat is not exchanged ∆Q = 0.
- Internal energy changes.
- This process takes place quickly.
- PVr = Constant
- Work done W = \(\frac{R}{(r-1)}\)(T1 – T2)
Question 7.
Explain the following processes
i) Cyclic process with example
ii) Non cyclic process with example
Answer:
i) Cyclic process: “A process in which the system after passing through various stages (of pressure, volume and temperature changes) returns to its initial state1′ is called as a cyclic process.
For cyclic process P.V graph is a closed curve. The area under P-V graph gives work done by the substance. In a cyclic process there will be no change in the internal energy i.e., ∆U = 0
The first law of thermodynamics states that
∆Q = ∆U + ∆W
∴ For cyclic process ∆Q = ∆W
In cyclic process, the total heat absorbed by the system equals the work done by the system. Example : Fleat engine is a device by which a system is made to undergo a cyclic process that results in conversion of heat to work.
ii) Non cyclic process : A process which is not cyclic is called Non-cyclic process. In Non-cydic process, the system does not attains its initial state. Irreversible process is a Non cyclic process. Workdone in non-cyclic process is given by the area between the curve and volume axis.
Example :
- Diffusion of liquids or gases
- Free expansion of a perfect gas.
![]()
Question 8.
Write a short note on Quasi – static process.
Answer:
A quasi-static process is defined as “an infinitesimally slow process in which at each and every intermediate stage the system remains in thermal and mechanical (thermodynamic) equilibrium with the surroundings through out the entire process.”
In this process the pressure and temperature of the surroundings at each and every stage will differ from those of the system only in a very small amount.
Any process taking place sufficiently slowly, not involving acceleration motions and large temperature gradients can be considered as quasi -static process.
Example : isothermal process, adiabatic process.
Question 9.
Explain qualitatively the working of a heat engine.
Answer:
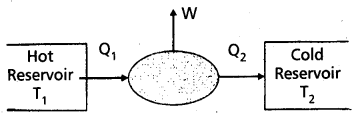
“A device used to convert heat energy into work (or mechanical energy)” is called heat engine. A heat engine converts heat into work.
A heat engine consists of the following essential parts :
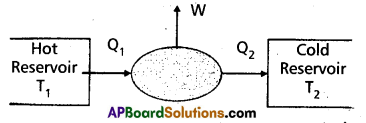
- A body at a higher temperature T1. Heat Q1 is extracted from this body and hence it is called a “hot reservior” (or source).
- The engine contains working substance. In a steam engine the working substance is the steam. In a diesel engine the working substance is a mixture of fuel vapour and air.
- A body at lower temperature T2. Heat Q2 is rejected by the working substance to this body and hence it is called a cold reservoir (or sink).
The difference in heat absorbed (Q1) and heat rejected (Q2) is equal to the workdone by the system (W). This is because the engine is operated in a cyclic process. W = Q1 – Q2.
The heat engine operates in a cyclic process and in each cycle, the work done (W) by the system is transferred to the environment via some arrangement (shaft) to drive vehicles.
The efficiency (η) of aheat engine is defined as the ratio of the workdone (W) by the engine to the amount of heat absorbed (Q1) by the engine.
Efficiency (η) = \(\frac{\mathrm{W}}{\mathrm{Q}_1}=\frac{\mathrm{Q}_1-\mathrm{Q}_2}{\mathrm{Q}_1}=1-\frac{\mathrm{Q}_2}{\mathrm{Q}_1}\)
Long Answer Questions
Question 1.
Explain reversible and irreversible processes. Describe the working of Carnot engine. Obtain an expression for the effieciency. [AP – Mar. ’18, ’17, ’16, 15; TS – Mar. ’17, ’15, ’14]
Answer:
Reversible process : A process that can be retraced back in the opposite direction in such away that the system passes through the same states as in the direct process, and finally the system and the surroundings return in their original states, is called a reversible process.
A reversible process is only a purely idealised process.
Examples:
- Slow isothermal and slow adiabatic changes
- Peltier effect and seeback effect.
- Fusion of ice and vaporisation of water.
Irreversible process : “A process that cannot be retraced back in the opposite direction” is called as irreversible process.
In this process the system does not pass through the same intermediate states as in the reversible process.
All natural processes such as conduction, radiation, radioactivity etc, are irreversible.
Example:
- Work done against friction.
- Heat produced in conductors by passing a current through it. (Joule heating)
- Diffusion of gases.
Carnot Engine : A reversible heat engine operating between two temperatures is called a carnot engine. The cycle operating it is known as carnot’s cycle. In this cycle the working substance(say an ideal gas) is taken through a cycle by means of two isothermals and two adiabatics. The four operations are shown in P-V (Indicator) diagram.
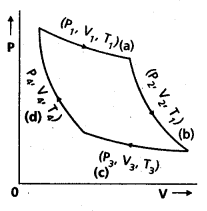
![]()
Step 1 → 2 : Isothermal expansion of the gas taking its state from (P1, V1, T1) to (P2, V2, T2). It is shown in curve (a).
The heat absorbed by the gas (Q1) from the reservoir at temperature
T1 equals the workdone by the gas. i.e.
W1 → 2 = Q1 = μRT1 loge \(\frac{V_2}{V_1}\)
Step 2 →3 : Adiabatic expansion of the gas from (P2, V2, T1) to (P3, V3, T2). It is shown in curve (b). The work done by the gas is gÑen by
W2 → 3 = \(\frac{\mu R\left(T_1-T_2\right)}{(r-1)}\)
Step 3 → 4: Isothermal compression of the gas from (P3, V3, T2) to (P4, V4, T2). It is shown in curve (c).
Heat released (Q2) by the gas to the reservoir at temperature T2 equals the work done on the goes.
i.e., W3 → 4;= μRT2 loge \(\frac{V_4}{V_3}\) = -μRT1 loge \(\frac{V_3}{V_4}\)
Step 4 → 1: Adiabatic compression of the gas from (P4, V4, T2) to (P1, V1, T1). It is shown in curve (d) Work done on the gas is given by.
W4 → 1 = μR \(\frac{\left(T_2-T_1\right)}{(r-1)}=-\mu R \frac{\left(T_1-T_2\right)}{(r-1)}\)
Total work done by the gas in one complete cycle is
W = W1 → 2 + W2 → 3 + W3 → 4 + W4 → 1
= \(\mu R T_1 \log _e \frac{V_2}{V_1}+\frac{\mu R\left(T_1-T_2\right)}{(r-1)}-\mu R T_2 \log _e \frac{V_3}{V_4}-\frac{\mu R\left(T_1-T_2\right)}{(r-1)}\)
∴ W = μRT1 loge \(\frac{V_2}{V_1}\) – μRT2 loge \(\frac{3}{V_4}\) = Q1 – Q2 …………… (2)
The efficiency of the cannot engine is
η = \(\frac{W}{Q_1}=\frac{Q_1-Q_2}{Q_1}\) ………… (3)
Now since step 2 → 3 is an adiabatic process,
T1V2r – 1 ≈ T2V3r – 1
Similarly, since step 4 → 1 is an adiabatic process,
T2V2r – 1 = T1V1r – 1 ⇒ T1V1r – 1 = T2V2r – 1
Question 2.
State second law of thermodynamics. How is heat engine different form a refrigerator. [TS – Mar. ’18, ’16; AP – Mar. ’15, ’13]
Answer:
Second law of thermodynamics gives the direction of flow of heat. Second law consists two statements.
- Kelvin – Planck statement: “No process is possible whose sole result is the absorption of heat from a reservoir and the complete conversion of the heat into work”.
(or)
“It is impossible to derive a continuous supply of engines in cooling a body below the coldest of its surroundings1′. - Clausius statement : “No process is possible whose sole result is the transfer of heat from a colder object to a hotter object”.
(or)
“Heat can not itself flow from cold body to hot body”.
Heat engine : A device which converts heat energy into work is called heat engine.
A heat engine consists of the essential parts.
- Source or hot reservoir: It is maintained at a very high temperature T1. Heat is extracted from this body.
- Working substance : In a steam engine working substance is steam. In a diesel engine working substance is mixture of fuel vapour and air.
- Sink or cold reservoir: It is maintained at a very low temperature T2. It absorbs heat energy, rejected by working substance.
Work done: The difference of heat absorbed from source and heat rejected to sink is equal to work done by the engine, i.e., W = Q1 – Q2.
Efficiency : The ratio of workdone (W) by the engine to the amount of heat absorbed (Q1) by the engine is called efficiency.
i.e., η = \(\frac{W}{Q_1}=\frac{Q_1-Q_2}{Q_1}=1-\frac{Q_2}{Q_1}\)
Refrigerator : Refrigerator is a heat pump which is the reverse of a heat engine.
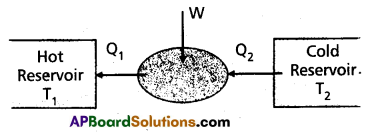
In refrigerator the working substance extracts (Q2) an amount of heat from sink of lower temperature and a external work W is done on the working substance and finally amount of heat (Q1) is transfered to source.
The coefficient of performance (α) of a refrigerator is given by
α = \(\frac{\mathrm{Q}_2}{\mathrm{~W}}=\frac{\mathrm{Q}_2}{\mathrm{Q}_1-\mathrm{Q}_2}\) (∴ heat released Q1 = Q2 + W)
For heat engine η can never exceed 1. For refregirator a can be greater than 1.
Therefore working of refrigerator is opposite to that of heat engine.
Problems
Question 1.
If a monoatomic ideal gas of volume 1 litre at N.T.P. is compressed (i) adia- batically to half of its volume, find the work done on the gas. Also find (ii) the work done if the cdmpression is iso- thermal, (γ = 5/3)
Solution:
i) During an adiabatic process
T1V1r – 1 = T2V2r – 1
Here T1 = 273 K
V2 = \(\frac{V_1}{2}\)
r = \(\frac{5}{3}\)
T2 = \(\left[\frac{V_1}{V_2}\right]^{\frac{5}{3}-1}=273\left[\frac{V_1}{V_1}\right]^{\frac{2}{3}}\)
T2 = (2)\(\frac{2}{3}\) = 273 = 431.6 K
Number of moles = \(\frac{1 \text { litre }}{22.4 \text { litre }}=\frac{1}{22.4}\)
Work done = \(\frac{\mu R}{(r-1)}\) [T1 – T2]
= \(\frac{8.314}{22.4\left[\frac{5}{3}-1\right]}\) × (273 – 431.6)
= \(\frac{8.314 \times 3}{22.4 \times 2}\) (-158.6)
= -89 J
![]()
ii) Work done during isothermal compression is
w = 2.3026 μRT log10\(\frac{V_2}{V_1}\)
μ = Number of moles = \(\frac{1}{22.4}\)
T = 273K
R = 8.314 Jmol-1K-2
\(\frac{V_2}{V_1}=\frac{1}{2}\) = 0.5
∴ W = \(\frac{2.3026 \times 8.314 \times 273 \log _{10}(0.5)}{22.4}\)
Or w = -70J
Question 2.
Five moles of hydrogren when heated through 20 K expand by an amount of 8.3 × 10-3m3 under a constant pressure of 105 N/m2. If Cv = 20.1/mole K, find Cp.
Solution:
Mayer’s relation Cp – Cv = R
Multiplying throughout by μ∆T
μCp∆T – μCv∆T = μ R∆T
μ ∆T(Cp – Cv) = P∆T [∴ μ R∆T = P∆V]
5 × 20 (Cp – 20) = 105 × 8.3 × (10 – 3)
[∴ μ = 5, ∆T = 20 K, P = 1 × 105 N/m2 Cv = 20 J/mole K and ∆V = 8.3 × 103 M3]
Cp – 20 = 8.3
∴ Cp = 28.3 J/mole-K
Additional Problems
Question 1.
A geyser heats water flowing at the rate of 3.0 litres per minute from 27 °C to 77 °C. If the geyser operate on a gas burner, what is the rate of consumption of the fuel if its heat of combustion is 4.0 × 104 J/g ?
Solution:
Here volume of water heated = 3.0 lit/min.
Mass of water heated m = 3000 g/min
Rise in temperature ∆T = 77 – 27 = 50°C
Sp. heat of water C = 4.2 Jg-1C-1
Amount of heat used
∆Q = mc∆T = 3000 × 4.2 × 50
= 63 × 104 J/min
Heat of combustion = 4 × 104 J/g
Rate of combustion of fuel = \(\frac{63 \times 10^4}{4 \times 10^4}\)
= 15.75 g/min
![]()
Question 2.
What amount of heat must be supplied t 2.0 × 10-2 kg of nitrogen (at room temperature) to raise its temperature by 45 °C at constant pressure ? (Molecular mass of N2 = 28; R = 8.3 J mol-1 K-1.)
Solution:
Here mass of gas m = 2 × 10-2kg = 20g
Rise in temperature ∆T = 45°C
Heat required ∆Q = ?
Molecular mass M = 28
Number of moles n = \(\frac{m}{M}=\frac{20}{28}\) = 0.714
As nitrogen is a diatomic gas, molecular specific heat of constant pressure is
Cp = \(\frac{7}{2}\) R = \(\frac{7}{2}\) × 8.3 J mole-1 K-1
As ∆Q = nCp∆T
∆Q = 0.714 × \(\frac{7}{2}\) × 8.3 × 45 J = 933.4 J
Question 3.
Explain why
a) Two bodies at different temperatures T1 and T2 if brought in thermal contact do not necessarily settle to the mean temperature (T1 + T2)/2.
b) The coolant in a chemical or nuclear plant (i.e., the liquid used to prevent the different parts of a plant from getting too hot) should have high specific heat.
c) Air pressure in a car tyre increases during driving.
d) The climate of a harbour town is more temperate then that of a town in a desert at the same latitude.
Solution:
a) In thermal contact heat flows from the body at higher temp to the body at lower temperature till temperatures becomes equal. The final temperature can be the mean temp (T1 + T2)/2 only when thermal capacities of the two bodies are equal.
b) This is because heat absorbed by a substance is directly proportional to the specific heat of the substance.
c) During, driving the temperature of air inside the tyre increases due to motion. According to Charles law, P α T. Therefore, air pressure inside the tyre increases.
d) This is because in a harbour town, the relative humidity is more than in a desert town. Hence the climate of a harbour town is without extremes of hot and cold.
![]()
Question 4.
A cylinder with a movable piston contains 3 moles of hydrogen at standard temperature and pressure. The walls of the cylinder are made of a heat insulator, and the piston is insulated by having a pile of sand on it. By what factor does the pressure of the gas increase if the gas is compressed to half its original volume ?
Solution:
As no heat is allowed to be exchanged, the process is adiabatic.
∴ P2V2r = P1V1r (or) \(\frac{P_2}{P_1}=\left(\frac{V_1}{V_2}\right)^r\)
As V2 = \(\frac{V_1}{2}\)
∴ P2/P1 = \(\left(\frac{V_1}{\frac{1}{2} V_1}\right)^{1 .4}\)
= 21.4 = 2.64
Question 5.
In changing the state of a gas adiabatically form an equilibrium state A to another equilibrium state B, and amount of work equal to 22.3 J is done on the system. If the gas is taken from state A to B via a process in which the net heat absorbed by the system is 9.35 cal. how much is the net work done by the system in the latter case ? (Take 1 cal = 4.19 J)
Solution:
Here, when the change is adiabatic, ∆Q = 0, ∆w = -22.3 J
If ∆u is change in internal energy of the system, then as
∆Q = ∆u + ∆w
O = ∆u – 22.3 (or) ∆u = 22.3 J
In the second case ∆Q = 9.35 cal
= 9.35 × 4.2 J = 39.3 J
∆w = ?
As ∆u + ∆w = ∆Q
∆w = ∆Q – ∆u
= 39.3 – 22.3 = 17.0 J
![]()
Question 6.
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following :
a) What is the final pressure of the gas in A and B ?
b) What is the change in internal energy of the gas ?
c) What is the change in the temperature of the gas ?
d) Do the intermediate states of the system (before settling to the final equilibrium state) lie on its P-V-T surface ?
Solution:
a) When the stopcock is suddenly opened, the volume available to the gas at 1 atm pressure will become two times. Therefore pressure will decrease to one-half i.e., 0.5 atm.
b) There will be no change in the internal energy of the gas as no work is done on/ by the gas.
c) Also there will be no change in temp of the gas as gas does no work in expansion.
d) No, because the process called free expansion is rapid and cannot be controlled. The intermediate states are non equilibrium states and do not satisfy the gas equation. In due course, the gas does return to an equilibrium state.
Question 7.
A steam engine delivers 5.4 × 108J . of work per minute and services 3.6 × 109J of heat per minute form its boiler, what is the efficiency of the engine ? How much heat is wasted per minute ? .
Solution:
Output i.e., useful workdone per min
= 5.4 × 108 J
Input i.e., heat absorbed per min
= 3.6 × 109 J
Efficiency = \(\frac{\text { Output }}{\text { Input }}=\frac{5.4 \times 10^8}{3.6 \times 10^9}\) = 0.15
= 0.15 × 100% = 15%
heat energy wasted / minute = Heat absorbed / minute – useful work done / minute
= 3.6 × 109 – 5.4 × 108 = 109 (3.6 – 0.54)
= 3.06 × 109
![]()
Question 8.
An electric heater supplies heat to a system at a rate of 100W. If system performs work at a rate of 75 joules per second. At what rate is the internal energy increasing ?
Solution:
Heat supplied, ∆Q = 100 w = 100 J/s
Useful workdone ∆w = 75 J/s
Increase in internal energy/ sec, ∆u = ?
As ∆Q = ∆u + ∆w
∴ ∆u = ∆Q – ∆w
= 100 – 75 = 25 J/S
Question 9.
A thermodynamic system is taken from an original state to an intermediate state by the linear process shown in Fig.
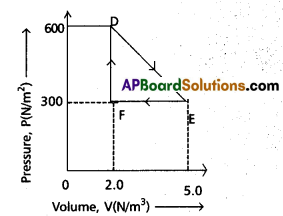
Its volume is then reduced to the original value form E to F by an isobaric process. Calculate the total work done by the gas from D to E to F
Solution:
A is clear from fig.
Change in pressure dp = EF = 5.0 – 2.0
= 3.0 atm = 3.0 × 1015 Nm-2
Change in volume dv = DF = 600 – 300
= 300 cc = 300 × 10-6 m3
Workdone by the gas from D to E to F = area of ∆DEF
w = \(\frac{1}{2}\) × DF × EF
= \(\frac{1}{2}\) × (300 × 10-6 ) × (3.0 × 105 ) = 45 J
![]()
Question 10.
A refrigerator is to maintain eatables kept inside at 9°C. If room temperature is 36°C. calculate the coefficient of performance.
Solution:
Here T1 = 36°C = 36 + 273 = 309 K
T2 = 10°C = 10 + 273 = 283 K
COP = \(\frac{T_2}{T_1-T_2}=\frac{283}{309-283}\)
= \(\frac{283}{26}\) = 10.9