AP Inter 2nd Year Maths 2A Solutions Chapter 2 డిమోయర్ సిద్ధాంతం Ex 2(b)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 2 డిమోయర్ సిద్ధాంతం Exercise 2(b) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2A Solutions Chapter 2 డిమోయర్ సిద్ధాంతం Exercise 2(b)

అభ్యాసం – 2(బి)

I.

ప్రశ్న 1.
క్రింది వాటికి అన్ని విలువలు కనుక్కోండి.
(i) \((1-i \sqrt{3})^{1 / 3}\)
సాధన:

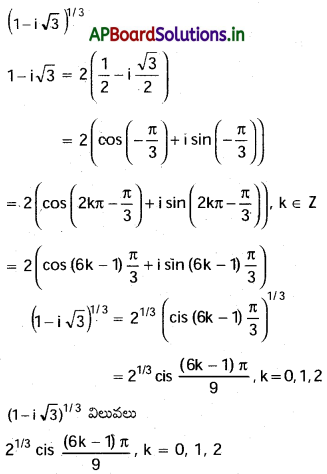
(ii) \((-i)^{1 / 6}\)
సాధన:

(iii) \((1+i)^{2 / 3}\)
సాధన:

(iv) \((-16)^{1 / 4}\)
సాధన:

(v) \((-32)^{1 / 5}\)
సాధన:

ప్రశ్న 2.
A, B, C లు త్రిభుజంలో కోణాలు, x = cis A, y = cis B, z = cis C అయితే xyz విలువ కనుక్కోండి. [A.P. Mar. ’16]
సాధన:
A, B, C లు త్రిభుజంలో కోణాలు
⇒ A + B + C = 180° ……(1)
x = cis A, y = cis B, z = cis C
⇒ xyz = cis (A + B + C)
= cos (A + B + C) + i sin (A + B + C)
= cos(180°) + i sin(180°)
= -1 + i(0)
= -1
∴ xyz = -1

ప్రశ్న 3.
(i) x = cis θ అయితే \(\left[x^6+\frac{1}{x^6}\right]\) విలువ కనుక్కోండి. [Mar. ’14]
సాధన:
x = cos θ + i sin θ
⇒ x⁶ = (cos θ + i sin θ)⁶ = cos 6θ + i sin 6θ
⇒ \(\frac{1}{x^6}\) = cos 6θ – i sin 6θ
∴ \(\left[x^6+\frac{1}{x^6}\right]\) = 2 cos 6θ

(ii) 8 యొక్క ఘన మూలాలు కనుక్కోండి.
సాధన:
x³ = 8 అనుకుందాం.
⇒ x = \((8)^{1 / 3}=\left(2^3 \cdot 1\right)^{1 / 3}\)
⇒ x = \(\left(2^3\right)^{1 / 3}(1)^{1 / 3}=2(1)^{1 / 3}\)
∴ 8 ఘన మూలాలు ω, 2ω, 2ω²

ప్రశ్న 4.
ఏకకపు (ఒకటి) ఘన మూలాలు 1, ω, ω² అయితే, క్రింది వాటిని నిరూపించండి.
(i) \(\frac{1}{2+\omega}+\frac{1}{1+2 \omega}=\frac{1}{1+\omega}\)
సాధన:
ఏకకపు ఘన మూలాలు 1, ω, ω²
1 + ω + ω² = 0, ω³ = 1

(ii) (2 – ω) (2 – ω²) (2 – ω¹⁰) (2 – ω¹¹) = 49
సాధన:
∵ ఏకకపు ఘన మూలాలు 1, ω, ω²
∴ ω³ = 1, 1 + ω + ω² = 0
2 – ω¹⁰ = 2 – ω⁹ . ω
= 2 – (ω³)³ . ω
= 2 – (1)³ ω
= 2 – ω
2 – ω¹¹ = 2 – (ω³)³ . ω²
= 2 – (1)³ ω²
= 2 – ω²
(2 – ω) (2 – ω²) = 4 – 2ω – 2ω² + ω³
= 4 – 2(ω + ω²) + 1
= 4 – 2(-1) + 1
= 4 + 2 + 1
= 7
∴ (2 – ω) (2 – ω²) (2 – ω¹⁰) (2 – ω¹¹) = (2 – ω) (2 – ω²) (2 – ω) (2 – ω²)
= ((2 – ω) (2 – ω²))²
= 7²
= 49

(iii) (x + y + z) (x + yω + zω²) (x + yω²+ zω) = x³ + y³ + z³ – 3xyz.
సాధన:
∵ ఏకకపు ఘనమూలాలు 1, ω, ω²
∴ 1 + ω + ω² = 0, ω³ = 1
ఇప్పుడు (x + yω + zω²) (x + yω² + zω) = x² + xyω² + zxω + xyω + y²ω3 + yzω² + zxω² + yzω⁴ + z²ω³
= x² + y² (1) + z² (1) + xy (ω + ω²) + yz (ω⁴ + ω²) + zx (ω + ω²)
= x² + y² + z² + xy(-1) + yz (ω + ω²) + zx (-1)
= x² + y² + z² – xy – yz – zx ………(1)
L.H.S. = (x + y + z) (x + yω + zω²) (x + yω² + zω)
= (x + y + z) (x² + y² + z² – xy – yz – zx)
(1) నుండి x³ + y³ + z³ – 3xyz = R.H.S.

ప్రశ్న 5.
ఏకకపు (ఒకటి) ఘన మూలాలు ω, ω² అయిన z² – z + 1 = 0 మూలాలు -ω, -ω² లు అవుతాయని చూపండి.
సాధన:
ω మరియు ω² సంకీర్ణ ఘనమూలాలు కావున
∴ 1 + ω + ω² = 0 మరియు ω³ = 1
z² – z + 1 = (-ω)² – (-ω) + 1
= ω² + ω + 1
= 0
∴ -ω అనేది z² – z + 1 = 0 సమీకరణం యొక్క మూలం
z² – z + 1 = (-ω²)² – (-ω²) + 1
= ω⁴ + ω² + 1
= ω³ . ω + ω² + 1
= ω + ω² + 1
= 0
∴ -ω² అనేది z² – z + 1 = 0 అనే సమీకరణం యొక్క మూలం.

ప్రశ్న 6.
ఏకకపు (ఒకటి) ఘన మూలాలు 1, ω, ω² లు అయిన, ఈ క్రింది విలువలు కనుక్కోండి.
(i) (a + b)³ + (aω + bω²)³ + (aω² + bω)³
సాధన:
ఏకకపు ఘన మూలాలు 1, ω, ω²
∴ 1 + ω + ω² = 0, ω³ = 1
ఇప్పుడు (a + b)³ = a³ + 3a²b + 3ab² + b³ …….(1)
(aω + bω²)³ = [ω(a + bω)]³
= ω³ (a + bω)³
= (1) (a + bω)³
= a³ + 3a²bω + 3ab²ω² + b³ω³
= a³ + 3a²bω + 3ab²ω² + b³ …….(2)
(aω² + bω)³ = [ω(aω + b)]³
= ω³(aω + b)³
= (1) (aω + b)³
= a³ω³ + 3a²bω² + 3ab²ω + b³
= a³(1) + 3a²b²ω² + 3ab²ω + b³
∴ (aω² + bω)³ = a³ + 3a²bω² + 3ab²ω + b³ …..(3)
(1), (2), (3) లను కలుపగా,
(a + b)³ + (aω + bω²)³ + (aω² + bω)³ = 3a³ + 3a²b (1 + ω + ω²) + 3ab² (1 + ω + ω²) + 3b³
= 3(a³ + b³) + 3a²b (0) + 3ab² (0)
= 3(a³ + b³)
∴ (a + b)² + (aω + bω²)³ + (aω² + bω)³ = 3(a³ + b³)

(ii) (a + 2b)² + (aω² + 2bω)² + (aω + 2bω²)²
సాధన:
(a + 2b)² = a² + 4ab + 4b² ……..(1)
(aω² + 2bω)² = a²ω⁴ + 4abω³ + 4b²ω²
= a²ω³ω + 4ab (1) + 4b²ω²
= a²ω + 4ab + 4b²ω² ……….(2)
మరియు (a + 2bω²)² = a²ω² + 4abω³ + 4b²ω⁴
= a²ω² + 4ab (1) + 4b² ω³ ω
= a²ω² + 4ab + 4b² (1) ω
∴ (aω + 2bω²)² = a²ω² + 4ab + 4b²ω ……..(3)
(1), (2), (3) లను కలుపగా
(a + 2b)² + (aω² + 2bω)² + (aω + 2bω²)² = a² (1 + ω + ω²) + 12ab + 4b² (1 + ω + ω²)
= a² (0) + 12ab + 4b² (0)
= 12ab
∴ (a + 2b)² + (aω² + 2bω)² + (aω + 2bω²)² = 12ab

(iii) (1 – ω + ω²)³
సాధన:
(1 – ω + ω²)³ = (-ω – ω)³ = (-2ω)³ = -8ω³
= -8(1)
= -8 (∵ 1 + ω + ω² = 0)

(iv) (1 – ω) (1 – ω²) (1 – ω⁴) (1 – ω⁸)
సాధన:
1 – ω⁴ = 1 – (ω³) ω = 1 – (1) ω = 1 – ω
1 – ω⁸ = 1 – (ω³)² ω² = 1 – (1) ω² = 1 – ω²
∴ (1 – ω) (1 – ω²) (1 – ω⁴) (1 – ω⁸)
= (1 – ω) (1 – ω²) (1 – ω) (1 – ω²)
= [(1 – ω) (1 – ω²)]²
= (1 – ω – ω² + ω³)²
= [1 – (ω + ω²) + 1]² [∵ 1 + ω + ω² = 0]
= [1 – (-1) + 1]²
= (3)²
= 9
∴ (1 – ω) (1 – ω²) (1 – ω⁴) (1 – ω⁸) = 9

(v) \(\left[\frac{a+b \omega+c \omega^2}{c+a \omega+b \omega^2}\right]+\frac{\left(a+b \omega+c \omega^2\right)}{\left(b+c \omega+a \omega^2\right)}\)
సాధన:
ఏకకపు ఘన మూలాలు 1, ω, ω²
ω³ = 1, 1 + ω + ω² = 0 ……..(1)

(vi) (1 + ω)³ + (1 + ω²)³
సాధన:
∵ ఏకకపు ఘన మూలాలు 1, ω, ω²
ω³ = 1, 1 + ω + ω² = 0
ఇప్పుడు (1 + ω)³ + (1 + ω²)³
= (-ω²)³ + (-ω)³ [∵ 1 + ω = -ω²]
= -ω⁶ – ω³ [∵1 + ω² = -ω, ω³ = 1]
= -(1)² – (1)
= -2

(vii) (1 – ω + ω²)⁵ + (1 + ω – ω²)⁵
సాధన:
∵ ఏకకపు ఘన మూలాలు 1, ω, ω²
1 + ω + ω² = 0, ω³ = 1
(1 – ω + ω²)⁵ + (1 + ω – ω²)⁵
= [(1 + ω²) – ω]⁵ + [(1 + ω) – ω²]⁵
= (-ω – ω)⁵ + (-ω² – ω²)⁵
= (-2ω)⁵ + (-2ω²)⁵
= (-2)⁵ [ω⁵ + ω¹⁰]
= -32 [ω³ . ω² + (ω³)³ ω]
= -32 [(1) ω² + (1)³ ω]
= -32 [ω + ω²]
= -32 (-1)
= 32
∴ (1 – ω + ω²)⁵ + (1 + ω – ω²)⁵ = 32

II.

ప్రశ్న 1.
క్రింది సమీకరణాలు సాధించండి.
(i) x² – 1 = 0
సాధన:
x⁴ – 1 = 0
x⁴ = 1
= cos 0° + i sin 0°
= cos 2k + i sin 2kr
x = (cos 2kπ + i sin 2kπ)^1/4
= cis \(\frac{k \pi}{2}\), k = 0, 1, 2, 3
= cis 0, cis \(\frac{\pi}{2}\), cis π, cis \(\frac{3 \pi}{2}\)
= cos 0° + i sin 0°, cos \(\frac{\pi}{2}\) + i sin \(\frac{\pi}{2}\), cos π + i sin π, cos \(\frac{3 \pi}{2}\) + i sin \(\frac{3 \pi}{2}\)
= 1, i, -1, -i
= ±1, ±i

(ii) x⁵ + 1 = 0
సాధన:
x⁵ + 1 = 0
x⁵ = -1 = cos π + i sin π
x⁵ = cos(2k + 1)π + i sin(2k + 1)π, k ∈ z
x = (cos (2k + 1)π + i sin (2k + 1)π)^1/5
x = cis \(\frac{(2 k+1) \pi}{5}\), k = 0, 1, 2, 3, 4

(iii) x⁹ – x⁵ + x⁴ – 1 = 0
సాధన:
x⁹ – x⁵ + x⁴ – 1 = 0
x⁵(x⁴ – 1) + 1(x⁴ – 1) = 0
(x⁴ – 1)(x⁵ + 1) = 0
x⁴ – 1 = 0
మూలాలు ±1, ±i (పై లెక్క నుండి)
x⁵ + 1 = 0
మూలాలు cis \(\frac{(2 k+1) \pi}{5}\), k = 0, 1, 2, 3, 4 (పై లెక్క నుండి)
∴ దత్త సమీకరణానికి మూలాలు ±1, ±i, cis(2k + 1)\(\frac{\pi}{5}\), k = 0, 1, 2, 3, 4

(iv) x⁴ + 1 = 0
సాధన:
x⁴ + 1 = 0
⇒ x⁴ = -1
⇒ x⁴ = cos π + i sin π
∴ x⁴ = cos (2kπ + π) + i sin (2kπ + π),
∴ x = [cis (2k + 1)π]^1/4
∴ x = cis (2k + 1)\(\frac{\pi}{4}\), k = 0, 1, 2, 3
∴ x = \({cis} \frac{\pi}{4}, {cis}\left(\frac{3 \pi}{4}\right), {cis}\left(\frac{5 \pi}{4}\right), {cis}\left(\frac{7 \pi}{4}\right)\)

ప్రశ్న 2.
x¹² – 1 = 0, x⁴ + x² + 1 = 0 లకు ఉమ్మడి మూలాలు కనుక్కోండి.
సాధన:
x¹² – 1 = 0
⇒ x¹² = 1
⇒ x¹² = (cos 0 + i sin 0)
⇒ x¹² = (cos 2kπ + i sin 2kπ), k ధన పూర్ణాంకం

ప్రశ్న 3.
ఏకకపు 15 వ మూలాలు, ఏకకపు 25వ మూలాలలో ఉమ్మడి మూలాల సంఖ్య కనుక్కోండి.
సాధన:
ఉమ్మడి మూలాల సంఖ్య = {15, 25} ల H.C.F = 5

ప్రశ్న 4.
ఏకకపు ఘన మూలాలు 1, ω, ω² అయితే, (x – 1)³ + 8 = 0 మూలాలను 1, ω, ω² లలో వ్యక్తపరచండి.
సాధన:
(x – 1)³ + 8 = 0
⇒ (x – 1)³ = -8
⇒ (x – 1)³ = (-2)³ (1)³
⇒ (x – 1) = (-2) (1)^1/3
⇒ x – 1 = -2, -2ω, -2ω²
⇒ x = 1 – 2, 1 – 2ω, 1 – 2ω²
⇒ x = -1, 1 – 2ω, 1 – 2ω²

ప్రశ్న 5.
(1 + i)^4/5 యొక్క అన్ని విలువల లబ్దాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 6.
z² + z + 1 = 0 ను ధ్రువపరిచే సంకీర్ణ సంఖ్య z అయిన, \(\left(z+\frac{1}{z}\right)^2+\left(z^2+\frac{1}{z^2}\right)+\left(z^3+\frac{1}{z^3}\right)^2\) \(+\left(z^4+\frac{1}{z^4}\right)^2+\left(z^5+\frac{1}{z^5}\right)^2+\left(z^6+\frac{1}{z^6}\right)\) = 12 అని చూపండి.
సాధన:
ఇచ్చినది z² + z + 1 = 0

III.

ప్రశ్న 1.
ఏకకపు (ఒకటి) n వ మూలాలు 1, α, α², α³, …. α^n-1 లు అయిన,
1^P + α^P + (α²)^P + (α³)^P + ….. + (α^n-P)^P = \(\left\{\begin{array}{l}
\mathbf{0} ; \mathbf{p} \neq \mathbf{k n} \text { అయితే } \\
\mathbf{n} ; \mathbf{p}=\mathbf{k n} అయితే
\end{array}\right.\), అని చూపండి (p, k ∈ N)
సాధన:
ఏకకపు nవ మూలాలు 1, α, α², ………., α^n-1

ప్రశ్న 2.
x⁷ – 1 = 0 మూలాల యొక్క 99వ ఘాతాల మొత్తం. శూన్యం అని చూపండి. దీని నుంచి x⁶ + x⁵ + x⁴ + x³ + x² + x + 1 = 0 యొక్క మూలాలను రాబట్టండి.
సాధన:
ఇచ్చిన సమీకరణం x⁷ – 1 = 0
⇒ x⁷ = 1
⇒ x = (1)^1/7
= (cos 0 + i sin 0)^1/7
= \(\cos \left(\frac{2 \pi}{7}\right)+i \sin \left(\frac{2 \pi}{7}\right)\)
ఏకకపు 7వ మూలాలు 1, α, α², α³, α⁴, α⁵, α⁶

∴ x⁷ – 1 = 0 యొక్క 99వ ఘాతాల మొత్తం శూన్యం.
అప్పుడు x = α అనుకుంటే,
అప్పుడు x⁶ + x⁵ + x⁴ + x³ + x² + x + 1
= α⁶ + α⁵ + α⁴ + α³ + α² + α + 1
= \(\frac{1\left[1-\alpha^7\right]}{1-\alpha}\)
= \(\frac{1-x^7}{1-x}\)
= \(\frac{0}{1-x}\)
= 0
∴ x⁶ + x⁵ + x⁴ + x³ + x² + x + 1 = 0

ప్రశ్న 3.
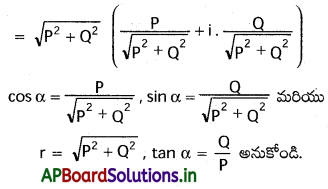
‘n’ ధన పూర్ణాంకం అయితే, (P + iQ)^1/n + (P – iQ)^1/n = 2(P² + Q²)^1/2n . \(\cos \left(\frac{1}{n} \tan \frac{Q}{P}\right)\) అని చూపండి.
సాధన:
P + iQ అనుకోండి.

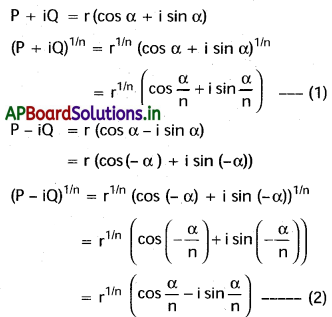
ప్రశ్న 4.
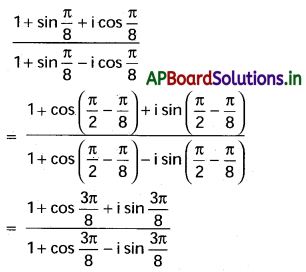
\(\left(\frac{1+\sin \frac{\pi}{8}+i \cos \frac{\pi}{8}}{1+\sin \frac{\pi}{8}-i \cos \frac{\pi}{8}}\right)^{8 / 3}\) యొక్క విలువ -1 అని చూపండి. [T.S. Mar. ’16]
సాధన:

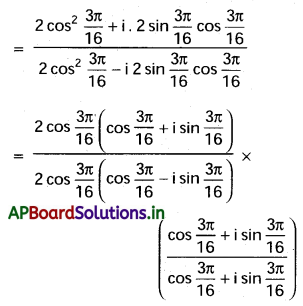
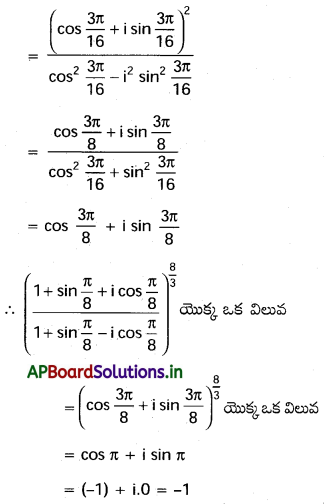
ప్రశ్న 5.
(x – 1)ⁿ = xⁿ, (n ధన పూర్ణాంకం) సాధించండి.
సాధన:
దత్త సమీకరణానికి x = 0 ఒక సాధన కాదు కావున \(\left(\frac{x-1}{x}\right)^n\) = 1
⇒ \(\frac{x-1}{x}=(1)^{1 / n}\)
⇒ \(\frac{x-1}{x}\) మూలం 1 కాని ఏకకపు ఘనమూలం
ఏకకపు nవ మూలకము ‘ω’ అనుకొంటే, (ω ≠ 1)