Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 4 సమీకరణ వాదం Exercise 4(c) will help students to clear their doubts quickly.
AP Inter 2nd Year Maths 2A Solutions Chapter 4 సమీకరణ వాదం Exercise 4(c)
అభ్యాసం – 4(సి)
I.
ప్రశ్న 1.
క్రింది మూలాలు గల బహుపది సమీకరణాలను రూపొందించండి.
(i) 2 + 3i, 2 – 3i, 1 + i, 1 – i
సాధన:
కావలసిన సమీకరణం [x – (2 + 3i)] [x – (2 – 3i)] [x – (1 + i)] [x – (1 – i)] = 0
⇒ [(x – 2) – 3i)] [(x – 2) + 3i] [(x – 1) – i] [(x – 1) + i] = 0
⇒ [(x – 2)2 – 9i2] [(x – 1)2 – i2] = 0
⇒ (x2 – 4x + 4 + 9) (x2 – 2x + 1 + 1) = 0
⇒ (x2 – 4x + 13) (x2 – 2x + 2) = 0
⇒ x4 – 4x3 + 13x2 – 2x3 + 8x2 – 26x + 2x2 – 8x + 26 = 0
⇒ x4 – 6x3 + 23x2 – 34x + 26 = 0
(ii) 3, 2, 1 + i, 1 – i
సాధన:
కావలసిన సమీకరణం (x – 3) (x – 2) [x – (1 + i)] [x – (1 – i)] = 0
⇒ (x2 – 5x + 6) [(x – 1) – i] [(x – 1) + i) = 0
⇒ (x2 – 5x + 6) [(x – 1)2 – i2] = 0
⇒ (x2 – 5x + 6) (x2 – 2x + 1 + 1) = 0
⇒ (x2 – 5x + 6) (x2 – 2x + 2) = 0
⇒ x4 – 5x3 + 6x2 – 2x3 + 10x2 – 12x + 2x2 – 10x + 12 = 0
⇒ x4 – 7x3 + 18x2 – 22x + 12 = 0
(iii) 1 + i, 1 – i, -1 + i, -1 – i
సాధన:
కావలసిన సమీకరణం [x – (1 + i)] [x – (1 – i)] [x – (-1 + i)] [x – (-1 – i)] = 0
⇒ [(x – 1) – i] [(x – 1) + i] [(x + 1) – i] [(x + 1) + i) = 0
⇒ [(x – 1)2 – i2] [(x + 1)2 – i2] = 0
⇒ (x2 – 2x + 1 + 1) (x2 + 2x + 1 + 1) = 0
⇒ (x2 – 2x + 2) (x2 + 2x + 2) = 0
⇒ x4 – 2x3 + 2x2 + 2x3 – 4x2 + 4x + 2x2 – 4x + 4 = 0
⇒ x4 + 4 = 0
(iv) 1 + i, 1 – i, 1 + i, 1 – i
సాధన:
కావలసిన సమీకరణం [x – (1 + i)] [x – (1 – i)]
⇒ [x – (1 + i)] [x – (1 – i)] = 0
⇒ [(x – 1) – i]2 [(x – 1) + i]2 = 0
⇒ [(x – 1)2 – i2] = 0
⇒ (x2 – 2x + 1 + 1)2 = 0
⇒ x4 + 4x2 + 4 – 4x3 + 4x2 – 8x = 0
⇒ x4 – 4x3 + 8x2 – 8x + 4 = 0
![]()
ప్రశ్న 2.
కింది మూలాలు గల అకరణీయ గుణకాలు గల బహుపది సమీకరణాన్ని రూపొందించండి.
(i) 4√3, 5 + 2i
సాధన:
బహుపది సమీకరణ గుణకాలు అకరణీయ సంఖ్యలైన, దాని మూలాలు సంయుగ్మ కరణులు మరియు సంయుగ్మసంకీర్ణ సంఖ్యలు.
α = 4√3 అయిన β = -4√3 మరియు γ = 5 + 2i అయిన δ = 5 – 2i
α, β, γ, δ లు మూలాలు
α + β = 0, αβ = -48
γ + δ = 10, γδ = 25 + 4 = 29
కావలసిన సమీకరణం [x2 – (α + β)x + αβ] [x2 – (γ + δ)x + γδ] = 0
⇒ (x2 – 48) (x2 – 10x + 29) = 0
⇒ x4 – 10x3 + 29x2 – 48x2 + 480x – 1932 = 0
⇒ x4 – 10x3 – 19x2 + 480x – 1932 = 0
(ii) 1 + 5i, 5 – i
సాధన:
బహుపది సమీకరణ గుణకాలు అకరణీయ సంఖ్యలైన, దాని మూలాలు సంయుగ్మ కరణులు మరియు సంయుగ్మసంకీర్ణ సంఖ్యలు.
α = 1 + 5i అయిన β = 1 – 5i
మరియు γ = 5 + i అయిన δ = 5 – i లు మూలాలు.
α + β = 2, αβ = 26
γ + δ = 10, γδ = 26
కావలసిన సమీకరణం [x2 – (α + β)x + αβ] [x2 – (γ + δ)x + γδ] = 0
⇒ (x2 – 2x + 26) (x2 – 10x + 26) = 0
⇒ x4 – 12x3 + 72x2 – 312x + 676 = 0
(iii) i – √5
సాధన:
బహుపది సమీకరణ గుణకాలు అకరణీయ సంఖ్యలైన, దాని మూలాలు సంయుగ్మ కరణులు మరియు సంయుగ్మసంకీర్ణ సంఖ్యలు.
α = i – √5, β = i + √5, γ = -i – √5, δ = -i + √5 లు మూలాలు
α + β = 2i, αβ = -6
γ + δ = -2i, γδ = -6
కావలసిన సమీకరణం [x2 – (α + β)x + αβ] [x2 – (γ + δ)x + γδ] = 0
⇒ (x2 – 2ix – 6) (x2 + 2ix – 6) = 0
⇒ [(x2 – 6) – 2ix] [(x2 – 6) + 2ix] = 0
⇒ (x2 – 6)2 + 4x2 = 0
⇒ x4 + 36 – 12x2 + 4×2 = 0
⇒ x4 – 8x2 + 36 = 0
(iv) -√3 + i√2
సాధన:
α = -√3 + i√2, β = -√3 – i√2, γ = √3 – i√2, δ = √3 + i√2 లు మూలాలు
α + β = -2√3
αβ = (-√3)2 – (i√2)2
= 3 – i2 (2)
= 5
γ + δ = 2√3, γδ = 5
కావలసిన సమీకరణము [x2 – (α + β)x + αβ] [x2 – (γ + δ)x + γδ] = 0
⇒ (x2 + 2√3x + 5) (x2 – 2√3x + 5) = 0
⇒ (x2 + 5)2 – (2√3x)2 = 0
⇒ x4 + 25 + 10x2 – 12x2 = 0
⇒ x4 – 2x2 + 25 = 0
![]()
II.
ప్రశ్న 1.
x4 + 2x3 – 5x2 + 6x + 2 = సమీకరణపు ఒక మూలం 1 + i అయిన, సమీకరణాన్ని సాధించండి.
సాధన:
1 + i ఒక మూలం ⇒ 1 – i ఇంకొక మూలం అవుతుంది.
1 ± i మూలాలుగా గల సమీకరణం
x2 – 2x + 2 = 0
∴ x2 – 2x + 2 ఒక కారణాంకము
x4 + 2x3 – 5x2 + 6x + 2 = 0
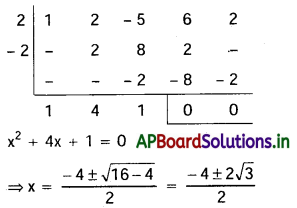
x = -2 ± √3
∴ మూలాలు 1 ± i, -2 ± √3
ప్రశ్న 2.
3x3 – 4x2 + x + 88 = 0 సమీకరణపు ఒక మూలం 2 – √-7 అయిన, సమీకరణాన్ని సాధించండి.
సాధన:
2 – √-7 ⇒ 2 – √7i ఒక మూలం
⇒2 + √7i ఇంకొక మూలం
2 ± √7i మూలాలుగా గల సమీకరణం x2 – 4x + 11 = 0
∴ x2 – 4x + 11 దత్త సమీకరణానికి ఒక కారణాంకము
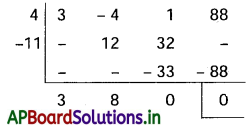
3x + 8 = 0
⇒ x = \(\frac{-8}{3}\)
∴ దత్త సమీకరణానికి మూలాలు 2 ± √7i, \(\frac{-8}{3}\)
![]()
ప్రశ్న 3.
x4 – 4x2 + 8x + 35 = 0 సమీకరణపు ఒక మూలం 2 + i√3 అయితే, సమీకరణాన్ని సాధించండి.
సాధన:
2 + i√3 ఒక మూలం ⇒ 2 – i√3 ఇంకొక మూలం
2 ± i√3 మూలాలుగాగల సమీకరణం x2 – 4x + 7 = 0
∴ x2 – 4x + 7 దత్త సమీకరణానికి ఒక మూలం
x4 – 4x2 + 8x + 35

∴ దత్త సమీకరణానికి మూలాలు 2 ± i√3, -2 ± i
ప్రశ్న 4.
x4 – 6x3 + 11x2 – 10x + 2 = 0 సమీకరణపు ఒక మూలం 2 + √3 అయితే, సమీకరణాన్ని సాధించండి.
సాధన:
2 + √3 ఒక మూలం ⇒ 2 – √3 ఇంకొక మూలం.
2 ± √3 మూలాలుగాగల సమీకరణం x2 – 4x + 1 = 0
∴ x2 – 4x + 1 ఒక కారణాంకము
x4 – 6x3 + 11x2 – 10x + 2 = 0

∴ దత్త సమీకరణానికి 2 ± √3, 1 ± i
ప్రశ్న 5.
x4 + 2x2 – 16x + 77 = 0 సమీకరణపు ఒక మూలం -2 + √-7 అయితే, సమీకరణాన్ని పూర్తిగా సాధించండి.
సాధన:
-2 – √-7 (i.e.) -2 + i√7 ఒక మూలం.
⇒ -2 – i√7 ఇంకొక మూలం -2 + i√7
-2 ± i√7 మూలాలుగా గల సమీకరణం x2 + 4x + 11 = 0
∴ x2 + 4x + 11 ఒక కారణాంకము
x4 + 2x2 – 16x + 77 = 0
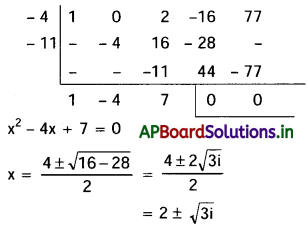
∴ దత్త సమీకరణానికి మూలాలు -2 ± i√7, 2 ± √3i
![]()
ప్రశ్న 6.
x4 + 2x3 – 16x2 – 22x + 7 = 0 సమీకరణపు ఒక మూలం 2 – √3 అయితే, సమీకరణాన్ని సాధించండి.
సాధన:
2 – √3 ఒక మూలం ⇒ 2 + √3 ఇంకొక మూలం
2 ± √3 లు మూలాలుగా గల వర్గ సమీకరణం
x2 – (2 + √3 + 2 – √3)x + (2 + √3) (2 – √3) = 0
⇒ x2 – 4x + 1 = 0

∴ దత్త సమీకరణానికి మూలాలు 2 ± √3, -3 ± √2
ప్రశ్న 7.
3x5 – 4x4 – 42x3 + 56x2 + 27x – 36 = 0 సమీకరణానికి ఒక మూలం √2 + √5 అయితే, సమీక రణాన్ని సాధించండి.
సాధన:
√2 + √5 ఒక మూలం
⇒ √2 – √5, -√2 + √5, -√2 – √5 లు కూడా దత్తసమీకరణానికి మూలాలు.
√2 ± √5 మూలాలుగా గల వర్గ సమీకరణం
x2 – (√2 + √5 + √2 – √5)x + (√2 + √5) (√2 – √5) = 0
⇒ x2 – 2√2x – 3 = 0
-√2 ± √5 లు మూలాలుగా గల వర్గ సమీకరణం
x2 – (-√2 + √5 – √2 – √5)x + (-√2 + √5)(-√2 – √5) = 0
⇒ x2 + 2√2x – 3 = 0
±√2±√5 లు మూలాలుగా గల సమీకరణం
(x2 + 2√2x – 3) (x2 – 2√2x – 3) = 0
⇒ (x2 – 3)2 – (2√2x)2 = 0
⇒ x4 – 6x2 + 9 – 8×2 = 0
⇒ x4 – 14x2 + 9 = 0
3x5 – 4x4 – 42x3 + 56x2 + 27x – 36 = 0
⇒ 3x(x4 – 14x2 + 9) – 4(x4 – 14x2 + 9) = 0
⇒ (x4 – 14x2 + 9) (3x – 4) = 0
⇒ x = ±√2 ± √5 లేదా \(\frac{4}{3}\)
∴ దత్త సమీకరణానికి మూలాలు ±√2 ± √5, \(\frac{4}{3}\)
ప్రశ్న 8.
x4 – 9x3 + 27x2 – 29x + 6 = 0 సమీకరణపు ఒక మూలం 2 – √3 అయితే, సమీకరణాన్ని సాధించండి.
సాధన:
2 – √3 ఒక మూలం ⇒ 2 + √3 ఇంకొక మూలం.
2 ± √3 లు మూలాలుగా గల సమీకరణం
x2 – 4x + 1 = 0
∴ x2 – 4x + 1 ఒక కారణాంకము
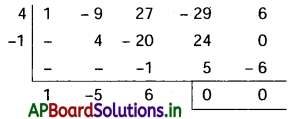
x2 – 5x + 6 = 0
⇒ (x – 2) (x – 3) = 0
⇒ x = 2, 3
∴ దత్త సమీకరణానికి మూలాలు 2 ± √3, 2, 3
![]()
ప్రశ్న 9.
a, b, c…. k, m, a’, b’, c’….k’ లు అన్నీ వాస్తవ సంఖ్యలైనపుడు \(\frac{a^2}{x-a^{\prime}}+\frac{b^2}{x-b^{\prime}}+\frac{c^2}{x-c^{\prime}}\) +…..+ \(\frac{k^2}{x-k^{\prime}}\) = m సమీకరణం వాస్తవేతర మూలాన్ని కలిగి ఉండదని చూపండి.
సాధన:
దత్త సమీకరణానికి α + iβ ఒక మూలం అనుకోండి.
β ≠ 0 అనుకుందాం.
అపుడు α – iβ కూడా దత్త సమీకరణానికి మూలం అవుతుంది.
దత్త సమీకరణంలో α + iβ వ్రాయగా

= 0
⇒ β = 0
ఇది అనుకొన్నదానికి విరుద్ధం.
∴ దత్త సమీకరణానికి వాస్తవేతర మూలాలు ఉండవు.