Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 8 అవకలన సమీకరణాలు Exercise 8(a) will help students to clear their doubts quickly.
AP Inter 2nd Year Maths 2B Solutions Chapter 8 అవకలన సమీకరణాలు Exercise 8(a)
అభ్యాసం – 8(ఎ)
I.
ప్రశ్న 1.
xy = c ex + b e-x + x2 నుంచి యాదృచ్ఛిక స్థిర సంఖ్యలు b, c లను తొలగిస్తే వచ్చే అవకలన సమీకరణం పరిమాణం కనుక్కోండి.
సాధన:
పరిమాణము = 2
ప్రశ్న 2.
మూలబిందువు కేంద్రంగా గల వృత్తాల కుటుంబపు అవకలన సమీకరణం పరిమాణం కనుక్కోండి. (Mar. ’11)
సాధన:
మూల బిందువు కేంద్రంగా గల వృత్తం x2 + y2 = r2
పరిమాణం = యాదృశ్చిక స్థిరాంకాల సంఖ్య = 1
![]()
II.
ప్రశ్న 1.
బ్రాకెట్లలో చూపిన పరామితులతో కింది ఇచ్చిన వక్రాల కుటుంబాల అవకలన సమీకరణాలను కనుక్కోండి. (T.S. Mar. ’16)
i) y = c(x – c)2; (c)
ii) xy = aex + be-x; (a, b)
iii) y = (a + bx)ekx; (a, b)
iv) y = a cos (nx + b); (a, b)
సాధన:
i) y = c(x – c)2 ——- (1)
x దృష్ట్యా అవకలనం చేయగా
(2) ను (1) తో భాగించగా
\(\frac{\mathrm{y}_1}{\mathrm{y}}\) = \(\frac{2 c(x-c)}{c(x-c)^2}\)
x – c = \(\frac{2 y}{y_1}\)
c = x – \(\frac{2 y}{y_1}\)
(1) లో ప్రతిక్షేపించగా
У = \(\left(x-\frac{2 y}{y_1}\right)\left(\frac{2 y}{y_1}\right)^2\)
= \(\frac{x y_1-2 y}{y_1} \cdot \frac{4 y^2}{y_1^2}\)
y.\(\mathrm{y}_1^3\) = 4y2 (xy1 -2y)
i.e., \(\mathrm{y}_1^3\) = 4y (xy1 – 2y)
= 4xyy1 – 8y2
\(\left(\frac{d y}{d x}\right)^3\) – 4xy \(\frac{d y}{d x}\) + 8y2 = 0
ii) xy = aex + be-x ; (a, b)
సాధన:
xy = aex + be-x
x దృష్ట్యా అవకలనం చేయగా
x. y1 + y = aex + b. e-x
x దృష్ట్యా మరల అవకలనం చేయగా
xy2 + y1 + y1 = aex + be-x
= xy
x\(\frac{d^2 y}{d x^2}\) + 2\(\frac{d y}{d x}\) – xy = 0
iii) y = (a + bx)ekx; (a, b)
సాధన:
y = (a + bx)ekx
x దృష్ట్యా అవకలనం చేయగా
y1 = (a + bx) ekx. k + ekx. b
= k. y + b.ekx
y1 – ky = b.ekx —– (1)
x దృష్ట్యా మరల అవకలనం చేయగా
y2 – ky1 = kb ekx
= k(y1 – ky) —– (2)
= ky1 – k2y
\(\frac{d^2 y}{d x^2}\) – 2k\(\frac{d y}{d x}\) + k2y = 0
iv) y = a cos (nx + b) ; (a, b)
సాధన:
y = a cos (nx + b)
y1 = -a sin (nx + b) n
y2 = – an. cos (nx + b) n
= – n2. y
\(\frac{d^2 y}{d x^2}\) + n2.y = 0
![]()
ప్రశ్న 2.
కింది వక్రాల కుటుంబాలకి అనుగుణంగా ఉండే అవకలన సమీకరణాలను కనుక్కోండి.
i) నిరూపకాక్షాలు అనంత స్పర్శరేఖలుగా ఉన్న లంబ అతిపరావలయాలు.
సాధన:
లంబ అతి పరావలయ సమీకరణము
xy = c2, c యాదృశ్చిక స్థిరాంకం
x దృష్ట్యా అవకలనం చేయగా
x\(\frac{d y}{d x}\) + y = 0
ii) మూల బిందువు వద్ద కేంద్రం ఉండి నిరూపకాక్షాలు అక్షాలుగా ఉన్న దీర్ఘ వృత్తాలు.
సాధన:
దీర్ఘవృత్త సమీకరణము
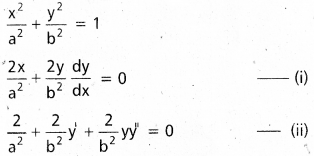
(ii) ను X తో గుణించి (i) నుండి తీసివేయగా
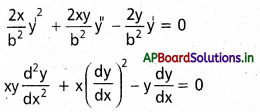
III.
ప్రశ్న 1.
బ్రాకెట్లలో చూపిన పరామితులతో కింద ఇచ్చిన వక్రాల కుటుంబాల అవకలన సమీకరణాలను కనుక్కోండి.
i) ae3x + be4x; (a, b)
సాధన:
x దృష్ట్యా అవకలనం చేయగా
y1 = 3ae3x + 4be3x
y1 – 3a. e3x = 4b.e3x
= 4(y – a. e3x)
= 4y – 4a. e3x
y1 – 4y = -a.e3x —- (1)
x దృష్ట్యా మరల అవకలనం చేయగా
y2 – 4y1 = -3a. e3x
= 3 (y1 -4y) by (1)
= 3y1 – 12y
\(\frac{d^2 y}{d x^2}\) – 7\(\frac{d y}{d x}\) + 12y = 0
![]()
ii) y = ax2 + bx; (a, b)
సాధన:
\(\frac{d y}{d x}\) = 2ax + b
\(\frac{d^2 y}{d x^2}\) = 2a
x2 \(\frac{d^2 y}{d x^2}\) = 2ax2 —- (i)
– 2x\(\frac{d y}{d x}\) = -4ax2 – 2bx —— (ii)
2y = 2ax2 + 2bx —— (iii)
ఈ మూడు సమీకరణాలు కూడగా
x2 \(\frac{d^2 y}{d x^2}\) – 2x \(\frac{d y}{d x}\) + 2y = 0
iii) ax2 + by2 = 1; (a, b)
సాధన:
ax2 + by2 = 1
by2 = 1 – ax2 — (1)
x దృష్ట్యా అవకలనం చేయగా
2by. y1 = – 2ax —- (2)
(2) ను (1) తో భాగించగా
\(\frac{\text { by. } y_1}{\text { by }^2}\) = \(\frac{-a x}{1-a x^2}\)
\(\frac{1-a x^2}{a x}\) = \(\frac{-y}{y_1}\)
y1 – ax2y1 = -axy1
y1 = ax2y1 – axy1
= ax(xy1 – y)
a = \(\frac{y_1}{\left(x^2 y_1-x y\right)}\)
x దృష్ట్యా అవకలన సమీకరణాలు.
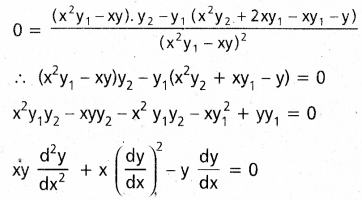
iv) xy = ax2 + \(\frac{\mathbf{b}}{\mathbf{x}}\) ; (a, b)
సాధన:
xy = ax2 + \(\frac{b}{x}\)
x2y = ax3 + b
x దృష్ట్యా అవకలనం చేయగా
x2y1 + 2xy = 3ax2
x తో భాగించగా
xy1 + 2y = 3ax —— (1)
x దృష్ట్యా మరల అవకలనం చేయగా
xy2 + y1 + 2y1 = 3a
xy2 + 3y1 = 3a —- (2)
(1) ను (2) తో భాగించగా
\(\frac{x y_1+2 y}{x y_2+3 y_1}\) = \(\frac{3 a x}{3 a}\) = x
అడ్డగుణకారము చేయగా
xy1 + 2y = x2 y2 + 3xy
x2y2 + 2xy1 – 2y = 0
x2\(\frac{d^2 y}{d x^2}\) – 2x\(\frac{d y}{d x}\) – 2y = 0
ప్రశ్న 2.
కింది వక్రాల కుటుంబాలకు అనుగుణంగా ఉండే అవకలన సమీకరణాలను కనుక్కోండి.
i) మూల బిందువు వద్ద Y – అక్షాన్ని స్పృశించే వృత్తాలు.
సాధన:
కావలసిన వృత్త సమీకరణం
x2 + y2 + 2gx = 0
x2 + y2 = -2gx —- (1)
x దృష్ట్యా అవకలనం చేయగా
2x + 2yy1 = – 2g. —- (2)
(1) తో ప్రతిక్షేపించగా
(2) నుండి x2 + y2 = x(2x + 2yy1)
= 2x2 + 2xyy1
yy2 – 2xyy1 – 2x2 = 0
y2 – x2 = 2xy \(\frac{d y}{d x}\)
ii) ప్రతిదాని అక్షం x – అక్షానికి సమాంతరంగానూ, నాభి లంబం 4a గానూ ఉన్న పరావలయాలు.
సాధన:
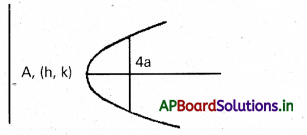
కావలసిన పరావలయ సమీకరణం
(y – k)2 = 4a(x – h) —- (1)
x దృష్ట్యా అవకలనం చేయగా
2 (y – k) y1 = 4a — (2)
x దృష్ట్యా అవకలనం చేయగా
(y – k) y2 + \(\mathrm{y}_1^2\) = 0 — (3)
(2) నుండి y – k = \(\frac{2 a}{y_1}\)
(3) లో ప్రతిక్షేపిస్తే
\(\frac{2 a}{y_1}\)· y2 + \(\mathrm{y}_1^2\) = 0
2ay2 + \(y_1^3\) = 0
![]()
iii) మూల బిందువు వద్ద నాభి, X – అక్షం గుండా అక్షం గల పరావలయాల కుటుంబం.
సాధన:
పరావలయ సమీకరణం y2 = 4a (x + a)