Students get through AP Inter 2nd Year Physics Important Questions 3rd Lesson Wave Optics which are most likely to be asked in the exam.
AP Inter 2nd Year Physics Important Questions 3rd Lesson Wave Optics
Short Answer Questions
Question 1.
Explain Doppler effect in light. Distinguish between red shift and blue shift. [T.S. Mar. 16]
Answer:
Doppler effect in light : The change in the apparent frequency of light, due to relative motion between source of light and observer. This phenomenon is called Doppler effect.
The apparent frequency of light increases when the distance between observer and source of light is decreasing and the apparent frequency of light decreases, if the distance between source of light and observer increasing.
Doppler shift can be expressed as = \(\frac{\Delta v}{v}=\frac{-v_{\text {radial }}}{c}\)
Applications of Doppler effect in light:
- It is used in measuring the speed of a star and speed of galaxies.
- Measuring the speed of rotation of the sun.
Red shift: The apparent increase in wave length in the middle of the visible region of the spectrum moves towards the red end of the spectrum is called red shift.
Blue shift: When waves are received from a source moving towards the observer, there is an apparent decrease in wave length, this is called blue shift.
![]()
Question 2.
Derive the expression for the intensity at a point where interference of light occurs. Arrive at the conditions for maximum and zero intensity. [A.P. Mar. 16; T.S. Mar. 15]
Answer:
Let y1 and y2 be the displacements of the two waves having same amplitude a and <|> is the phase difference between them.
y1 = a sin ωt …………… (1)
y2 = a sin (ωt + Φ) …………….. (2)
The resultant displacement y = y1 + y2
y = a sin ωt + a sin (ωt + Φ)
y = a sin ωt + a sin ωt cos Φ + a cos ωt sin Φ
y = a sin ωt [1 + cos Φ] + cos ωt (a sin Φ)
Let R cos θ = a(1+ cos Φ) ……………….. (4)
R sin θ = a sin Φ ………………. (5)
y = R sin ωt. cos θ + R cos ωt. sin θ
y = R sin (ωt + θ) ………………… (6)
where R is the resultant amplitude at P, squaring equations (4) and (5), then adding
R2 [cos2 θ + sin2 θ] = a2[l + cos2 Φ + 2 cos Φ + sin2 Φ]
R2 [1] = a2 [1 + 1 + 2 cos Φ]
I = R2 = 2a2 [1 + cos Φ] = 2a2 × 2 cos2 \(\frac{\phi}{2}\);
I = 4a2 cos2 \(\frac{\phi}{2}\) …………. (7)
i) Minimum intensity (Imax)
cos2 \(\frac{\phi}{2}\) = 1
Φ = 2nπ Where n = 0, 1, 2, 3 ……….
Φ = 0, 2π, 4π, 6π
∴ Imax = 4a2.
ii) Minimum intensity (Imin)
cos2 \(\frac{\theta}{2}\) = 1
Φ = (2n + 1)π Where n = 0, 1, 2, 3 ……….
Φ = π, 3π, 5π, 7π …………..
∴ Imin = 0
Question 3.
Does the principle of conservation of energy hold for interference and diffraction phenomena? Explain briefly. [Mar. 14]
Answer:
Yes, law of conservation of energy is obeyed. In case of constructive interference, intensity becomes maximum. Hence bright fringes are formed on the screen where as in the case of destructive interference, intensity becomes minimum. Hence dark fringes are formed on the screen.
This establishes that in the interference and diffraction pattern, the intensity of light is simply being redistributed i.e., energy is being transferred from dark fringe to bright fringe. No energy is being created (or) destroyed in the process. Hence energy is redistributed.
Thus the principle of conservation of energy is being obeyed in the process of interference and diffraction.
![]()
Question 4.
How do you determine the resolving power of your eye ? [A.P. Mar. 17]
Answer:
Make black strips of equal width separated by white strips. All the black strips having same width, while the width of white strips should increase from left to right.
Now watch the pattern with one eye. By moving away (or) closer to the wall, find the position where you can just see some two black strips as separate strips.
All black strips to the left of this strips would merge into one another and would not be distinguishable on the other hand, the black strips to the right of this would be more and more clearly visible.
Note the width d of the white strips and measure the distance D of the wall from eye.
Then resolution of your eye = \(\frac{\mathrm{d}}{\mathrm{D}}\)
Question 5.
Explain polarisation of light by reflection and arrive at Brewster’s law from it.
Answer:
Polarisation of light by reflection : When unpolarized light is incident on the boundary of a denser medium, at a particular angle of incidence the reflected light is completely plane polarised. This incident angle is called Brewster’s angle (iB).
Brewster’s law:
When light is incident on a transparent surface at Brewster s angle, then reflected and refracted rays are at right angles to each other.
From snell’s law, refractive index,
∴ iB + r = \(\frac{\pi}{2}\) ⇒ r = \(\frac{\pi}{2}\) – iB
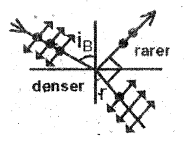
n = \(\frac{\sin \mathrm{i}_B}{\sin \mathrm{r}}=\frac{\sin \mathrm{i}_B}{\sin \left(\frac{\pi}{2}-\mathrm{i}_B\right)}=\frac{\sin \mathrm{i}_B}{\cos \mathrm{i}_B}\) = tan iB
n = taniB, This is known as Brewster’s law.
Brewster’s law – statement: The refractive index of a denser medium is equal to tangent of the polarising angle.
![]()
Question 6.
Discuss the intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids. [T.S. Mar. 17; Mar. 12]
Answer:
Let I0 be the intensity of polarised light after passing through the first polariser P1. Then the intensity of light after passing through second polariser P2 will be I = I0cos2θ.
Where θ is the angle between pass axes P1 and P2. Since P1 and P2 are crossed the angle between the pass axes of P2 and P3 will be (\(\frac{\pi}{2}\) – θ)
Hence the intensity of light emerging from P3 will be
I = I0cos2θ . cos2(\(\frac{\pi}{2}\) – θ)
= I0cos2θ . sin2θ
I = \(\frac{\mathrm{I}_0}{4}\) sin2 2θ
∴ The transmitted intensity will be maximum when θ = \(\frac{\pi}{4}\).
Long Answer Questions
Question 1.
Distinguish between Coherent and Incoherent addition of waves. Develop the theory of constructive interferences.
Answer:
Coherent sources : The two sources which maintain zero (or) any constant phase relation between themselves are known as Coherent sources.
Incoherent sources : If the phase difference changes with time, the two sources are known as incoherent sources.
Theory of constructive and destructive interference :
Let the waves of two coherent sources be
y1 = a sin ωt ………………….. (1)
y2 = a sin (ωt + Φ) …………….. (2)
where a is amplitude and Φ is the phase difference between two displacements.
According to superposition principle, y = y1 + y2
y = a sin ωt + a sin (ωt + Φ) = a sin ωt + a sin ω cos Φ + a cos ωt sin Φ
y = a sin ωt [1 + cos Φ] + cos ωt [a sin Φ] ………………….. (3)
Let A cos θ = a(1 + cos Φ], ………………. (4)
A sin θ = a sin Φ ……………… (5)
Substituting equations (4) and (5) in equation (3)
y = A sin ωt. cos θ + A cos ωt sin θ
y = A sin (ωt + θ) …………………… (6)
Where A is resultant amplitude. Squaring equations (4) and (5), then adding
A2[cos2 θ + sin2 θ] = a2[1 + cos2 Φ + 2 cos Φ + sin2 Φ]
A2 [1] = a2 [1 + 1 + 2 cos Φ]
I = A2 = 2a2 [1 + cos Φ]
I = 2a2 × 2 cos2 \(\frac{\phi}{2}\)
I = 4a2 cos2 \(\frac{\phi}{2}\)
I = 4I0 cos2 \(\frac{\phi}{2}\) …………….. (7) [∵ I0 = a2]
Case (i) For constructive interference: Intensity should be maximum.
cos \(\frac{\phi}{2}\) = 1 ⇒ Φ = 2nπ
Where n = 0, 1, 2, 3 ⇒ Φ = 0, 2π, 4π, 6π ………….. Imax = 4I0
Case (ii) For destructive interference: Intensity should be minimum
i.e., cos Φ = 0 ⇒ Φ = (2n + 1) π ; where π = 0, 1, 2, 3 ; Φ = π, 3π, 5π ⇒ Imin = 0.
![]()
Question 2.
Describe Young’s experiment for observing interference and hence arrive at the expression for ‘fringe width’.
Answer:
Interference: The modification of intensity obtained by the super position of two (or) more light waves is called interference.
Description :
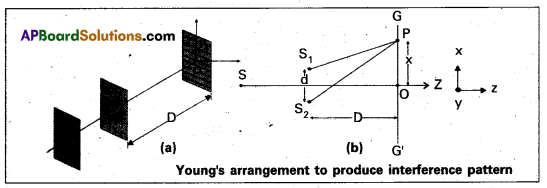
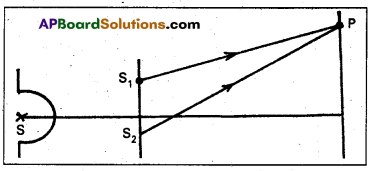
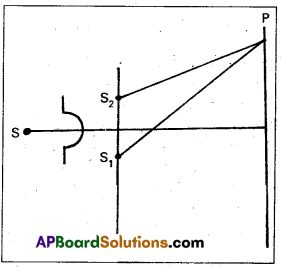
- Thomas Young experimentally observed the phenomenon of interference of light using two coherent sources.
- A small pin hole ‘S’ illuminated by monochromatic source of light which produces a spherical wave.
- S1 and S2 are two narrow pin holes equidistant from S.
- Screen is placed at a distance D.
- The points at which any two crests (or) any two troughs are superimposed, constructive interference takes place bright fringe will be observed on the screen.
- The points at which crest of one wave and trough of another wave are superimposed, destructive interference takes place dark fringe will be observed on the screen.
- Thus on the screen alternately bright and dark frings are observed.
Expression for fringe width :
1. It is the distance between two successive bright (or) dark fringes, denoted by β.
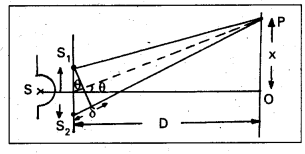
The path difference (δ) = d sin θ
2. If θ is very small then from figure sin θ ≈ tan θ = \(\frac{x}{D}\)
3. For bright fringes path difference S2P – S1P = nλ
∴ d sin θ = nλ
d × \(\frac{x}{D}\) = nλ
x = \(\frac{\mathrm{n} \lambda \mathrm{D}}{\mathrm{d}}\) ……………. (1) where n = 0, 1, 2, 3 …………….
This equation represents the position of bright fringe.
When n = 0, x0 = 0.
n = 1, x1 = \(\frac{\lambda \mathrm{D}}{\mathrm{d}}\) and n = 2, x2 = \(\frac{2\lambda \mathrm{D}}{\mathrm{d}}\)
The distance between any two consecutive bright fringes is
x2 – x1 = \(\frac{2 \lambda D}{d}-\frac{\lambda D}{d} \Rightarrow \beta=\frac{\lambda D}{d}\) ………… (2)
4. For dark fringes path difference S2P – S1P = (2n + 1) \(\frac{\lambda}{2}\) ∴ d sin θ = (2n + 1) \(\frac{\lambda}{2}\)
d × \(\frac{x}{D}\) = (2n + 1) \(\frac{\lambda}{2}\) ⇒ x = \(\frac{(2 n+1) \lambda D}{2 d}\) ………….. (3) where n = 0, 1, 2, 3…………
This equation (3) represents, position of dark fringe.
When n = 0, x0 = \(\frac{\lambda D}{2 d}\) ⇒ n = 1, x1 = \(\frac{3 \lambda D}{2 d}\); n = 2, x2 = \(\frac{5 \lambda D}{2 d}\) ………….
The distance between any two consecutive dark fringes is x2 – x1 = \(\frac{5 \lambda \mathrm{D}}{2 \mathrm{~d}}-\frac{3 \lambda \mathrm{D}}{2 \mathrm{~d}}=\frac{5 \lambda \mathrm{D}-3 \lambda \mathrm{D}}{2 \mathrm{~d}}\)
β = \(\frac{\lambda \mathrm{D}}{\mathrm{d}}\) …………………….. (4)
Hence fringe width is same for bright and dark fringes.
Problems
Question 1.
What speed should a galaxy move with respect to us so that the sodium line at 589.0 nm is observed at 589.6 nm ? .
Solution:
Since vλ = c, \(\frac{\Delta v}{v}=\frac{\Delta \lambda}{\lambda}\)
(for small changes in v and λ). For
∆λ = 589.6 – 589.0 = + 0.6 nm
we get [usmg Equation \(\frac{\Delta v}{v}=\frac{v_{\text {radial }}}{c}\)]
\(\frac{\Delta v}{v}=-\frac{\Delta \lambda}{\lambda}=-\frac{v_{\text {radial }}}{\dot{c}}\)
or, υradial ≅ + c(\(\frac{0.6}{589.0}\)) = +3.06 × 105 m s-1
= 306 km/s
Therefore, the galaxy is moving away from us.
![]()
Question 2.
Unpolarised light is incident on a plane glass surface. What should be the angle of the incidence so that the reflected and refracted rays are perpendicular to each other ?
Solution:
For i + r to be equal to π/2, we should have tan iB = μ = 1.5. This gives iB = 57°. This is the Brewster’s angle for air to glass interface.
Question 3.
What is the Brewster angle for air to glass transition ? (Refractive index of glass = 1.5.)
Solution:
Here, ip = ? μ = 1.5; As tan ip = μ = 1.5
∴ ip = tan-1 (1.5); ip = 56.3
Question 4.
In Young’s double-slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. What is the intensity of light at a point where path difference is λ/3 ?
Solution:
Let I1 = I2 = I. If Φ is phase difference between the two light waves, then resultant intensity,
IR = I1 + I2 + \(2 \sqrt{\mathrm{I}_1 \mathrm{I}_2}\) . cos Φ
When path difference = λ, Phase difference Φ = 0°
∴ IR = I + I + 2\(\sqrt{\text { II }}\) . cos 0° = 4I = k
When path difference = \(\frac{\lambda}{3}\), phase difference Φ = \(\frac{2 \pi}{3}\) rad
∴ IR = I + I + 2\(\sqrt{\text { II }}\) cos \(\frac{2 \pi}{3}\) ⇒ I’R = 2I + 2I(\(\frac{-1}{2}\)) = I = \(\frac{\mathrm{k}}{4}\)
![]()
Question 5.
Assume that light of wavelength 6000Å is coming from a star. What is the limit of resolution of a telescope whose objective has a diameter of 100 inch ?
Solution:
A 100 inch telescope implies that 2a = 100 inch = 254 cm. Thus if,
λ = 6000 Å = 6 × 10-5 cm
then ∆θ ≈ \(\frac{0.61 \times 6 \times 10^{-5}}{127}\)
= 2.9 × 10-7 radians.
Question 6.
In a Youngs double-slit experiment, the slits are separated by 0.28 mm and the screen is placed 1.4 m away. The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm. Determine the wavelength of light used in the experiment.
Solution:
d = 0.28 mm = 0.28 × 10-3 m, D = 1.4 m, β = 1.2 × 10-2 m, n = 4
Since, β = \(\frac{\mathrm{D}}{\mathrm{d}}\) nλ ⇒ \(\frac{\beta}{n} \cdot \frac{d}{D}\) ⇒ λ = \(\frac{1.2 \times 10^{-2} \times 2.8 \times 10^{-2}}{4 \times 1.4}\)
⇒ λ = 600 × 10-9 m
⇒ λ = 600 nm.
Textual Examples
Question 1.
What speed should a galaxy move with respect to us so that the sodium line at 589.0 nm is observed at 589.6 nm ?
Solution:
Since vλ = c, \(\frac{\Delta \mathrm{v}}{\mathrm{v}}=\frac{\Delta \lambda}{\lambda}\)
(for small changes in v and λ). For
∆λ = 589.6 – 589.0 = + 0.6 nm
we get [usmg Equation \(\frac{\Delta v}{v}=\frac{v_{\text {radial }}}{c}\)]
\(\frac{\Delta v}{v}=-\frac{\Delta \lambda}{\lambda}=-\frac{v_{\text {radial }}}{\dot{c}}\)
or, υradial ≅ + c(\(\frac{0.6}{589.0}\)) = +3.06 × 105 m s-1
= 306 km/s
Therefore, the galaxy is moving away from us.
![]()
Question 2.
(a) When monochromatic light is incident on a surface separating, two media, the reflected and refracted light both have the same frequency as the incident frequency. Explain why ?
(b) When light travels from a rarer to a denser medium, the speed decreases. Does the reduction in speed imply a reduction in the energy carried by the light wave ?
(c) In the wave picture of light, intensity of light is determined by the square of the amplitude of the wave. What determines the intensity of light in the photon picture of light.
Solution:
a) Reflection and refraction arise through interaction of incident light with the atomic constituents of matter. Atoms may be viewed as oscillators, which take up the frequency of the external agency (light) and undergo forced oscillations. The frequency of light emitted by a charged oscillator equals its frequency of oscillation. Thus, the frequency of scattered light equals the frequency of incident light.
b) No. energy carried by a wave depends on the amplitude of the wave, not on the speed of wave propagation.
c) For a given frequency, intensity of light in the photon picture is determined by the number of photons crossing ah unit area per unit time.
Question 3.
Two slits are made one millimetre apart and the screen is placed one metre away. What is the fringe separation when blue*: green light of wavelength 500 nm is used ?
Solution:
Fringe spacing = \(\frac{\mathrm{D} \lambda}{\mathrm{d}}=\frac{1 \times 5 \times 10^{-7}}{1 \times 10^{-3}}\) m
= 5 × 10-4 m = 0.5 mm
Question 4.
What is the effect on the interference fringes in a Young’s double-slit experiment due to each of the following operations :
(a) the screen is moved away from the plane of the slits;
(b) the (monochromatic) source is replaced by another (monochro-matic) source of shorter wavelength;
(c) the separation between the two slits is increased;
(d) the source slit is moved Closer to the double-slit plane;
(e) the width of the source slit is increased;
(f) the monochromatic source is replaced by a source of white light ?
(In each operation, take all parameters, other than the one specified, to remain unchanged.)
Solution:
a) Angular separation of the fringes remains constant (= λ/d). The actual separation of the fringes increases in proportion to the distance of the screen from the plane of the two slits.
b) The separation of the fringes (and also angular separation) decreases. See, however, the condition mentioned in (d) below.
c) The separation of the fringes (and also angular separation) decreases. See however, the condition mentioned in (d) below.
![]()
d) Let s be the size of the source and S its distance from the plane of the two slits. For interference fringes to be seen, the condition s/S < λ/d should be satisfied; otherwise, interference patterns produced by different parts of the source overlap and no fringes are seen. Thus, as S decreases (i.e., the source slit is brought closer), the interference pattern gets less and less sharp, and when the source is brought too close for this condition to be valid, the fringes disappear. Till this happens, the fringe separation remains fixed.
e) Same as in (d). As the source slit which increases, fringe pattern gets less and less sharp. When the source slit is so wide that the condition s/S ≤ λ/d is not satisfied, the interference pattern disappears.
f) The interference patterns due to different component colours of white light overlap (incoherently). The central bright fringes for different colours are at the same position. Therefore, the central fringe is white. For a point P for which S2P – S1P = λb/2, where λb (≈ 4000 Å) represents the wavelength for the blue colour, the blue component will be absent and the fringe will appear red in colour. Slightly farther away where S2Q – S1Q = λb = λr/2 where λr (≈ 8000 Å) is the wavelength for the red colour, the fringe will be predominantly blue.
Thus, the fringe closest on either side of the central white fringe is red and the farthest will appear blue. After a few fringes, no clear fringe pattern is seen.
Question 5.
In Textual Example 3, what should the width of each slit be to obtain 10 maxima of the double slit pattern within the central maximum of the single slit pattern ?
Solution:
We want aθ = λ, θ = \(\frac{\lambda}{\mathrm{a}}\)
10 \(\frac{\lambda}{\mathrm{d}}\) = 2\(\frac{\lambda}{\mathrm{a}}\), a = \(\frac{\mathrm{d}}{5}\) = 0.2 mm
Question 6.
Assume that light of wavelength 6000 Å is coming from a star. What is the limit of resolution of a telescope whose objective has a diameter of 100 inch ?
Solution:
A 100 inch telescope implies that 2a =100 inch = 254 cm.
Thus if,
λ = 6000 Å = 6 × 10-5 cm
then
∆θ ≈ \(\frac{0.61 \times 6 \times 10^{-5}}{127}\)
≈ 2.9 × 10-7 radians.
![]()
Question 7.
For what distance is ray optics a good approximation when the aperture is 3 mm wide and the wavelength is 500 nm ?
Solution:
ZF = \(\frac{\mathrm{a}^2}{\lambda}=\frac{\left(3 \times 10^{-3}\right)^2}{5 \times 10^{-7}}\) = 18 m
Question 8.
Discuss the intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids ?
Solution:
Let I0 be the intensity of polarised light after passing through the first polariser P1. Then the intensity of light after passing through second polariser P2 will be I = I0cos2θ,
where θ is the angle between pass axes of P1 and P2. Since P2 and P3 are crossed the angle between the pass axes of P2 and P3 will be (π/2 – θ). Hence the intensity of light emerging from P3 will be
I = I0cos2θ cos2 (\(\frac{\pi}{2}\) – θ)
= I0 cos2 θ sin2 θ = (I0/4) sin2 2θ
Therefore, the ‘transmitted intensity will be maximum when θ = π/4.
Question 9.
Unpolarised light is incident on a plane glass surface. What should be the angle of the incidence so that the reflected and refracted rays are perpendicular to each other ?
Solution:
For i + r to be equal to π/2, we should have tan iB = μ = 1.5. This gives iB = 57°. This is the Brewster’s angle for air to glass interface.