AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 8 Similar Triangles Ex 8.2 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 8th Lesson Similar Triangles Exercise 8.2
10th Class Maths 8th Lesson Similar Triangles Ex 8.2 Textbook Questions and Answers
Question 1.
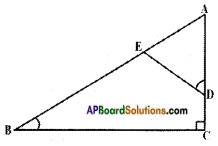
In the given figure, ∠ADE = ∠B
i) Show that △ABC ~ △ADE
ii) If AD = 3.8 cm, AE = 3.6 cm, BE = 2.1 cm, BC = 4.2 cm, find DE.
Answer:
i) Given: △ABC and ∠ADE = ∠B
R.T.P: △ABC ~ △ADE.
Proof: In △ABC and △ADE
∠A = ∠A [∵ Common]
∠B = ∠ADE [∵ Given]
∴ ∠C = ∠AED [∵ By Angle Sum property of triangles] △ABC ~ △ADE by AAA similarity condition.]
ii) AD = 3.8 cm, AE = 3.6 cm, BE = 2.1 cm, BC = 4.2 cm, find DE.
To find DE; △ABC ~ △ADE
Hence,
\(\frac{AB}{AD}\) = \(\frac{BC}{DE}\) = \(\frac{AC}{AE}\)
[∵ Ratios of corresponding sides are equal]

![]()
Question 2.
The perimeters of two similar triangles are 30 cm and 20 cm respectively. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
Answer:
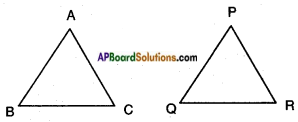
Given: △ABC ~ △PQR
Perimeter of △ABC = 30 cm.
Perimeter of △PQR = 20 cm.
AB = 12 cm.
To find: \(\overline{\mathrm{PQ}}\)
Ratio of perimeters = 30 : 20 = 3 : 2
Let the length of the side corresponding to the side with length 12 cm be x.
Then 30 : 20 : : 12 : x
30x = 20 x 12
\(x = \frac{20 \times 12}{30}\) = 8 cm
Question 3.
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/sec. If the lamp-post is 3.6 m above the ground, find the length of her shadow after 4 seconds.
Answer:
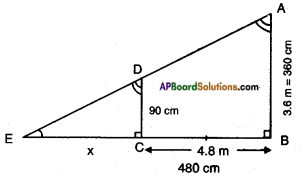
Given:
A lamp-post \(\overline{\mathrm{AB}}\) of height = 3.6 m
= 360 cm.
Speed of the girl = 1.2 m/sec.
Distance travelled in 4 sec = Speed x Time = 1.2 × 4 = 4.8 m = 480 cm.
\(\overline{\mathrm{CD}}\), height of the girl = 90 cm.
Let the length of the shadow at a distance of 4.8 m from the lamp post = x cm.
From the figure,
△ABE ~ △DCE
[∵ ∠B = ∠C = 90°
∠E = ∠C common
(A.A. similarity)]
Hence,
\(\frac{AB}{DC}\) = \(\frac{BE}{CE}\) = \(\frac{AE}{DE}\)
∴ \(\frac{360}{90}\) = \(\frac{480+x}{x}\)
⇒ 4 = \(\frac{480+x}{x}\)
⇒ 4x = 480 + x
⇒ 4x – x = 480
⇒ 3x = 480
⇒ x = 160 cm = 1.6 m
∴ Length of the shadow = 1.6 m
![]()
Question 4.
CM and RN are respectively the medians of similar triangles △ABC and △PQR. Prove that
i) △AMC ~ △PNR
ii) \(\frac{CM}{RN}\) = \(\frac{AB}{PQ}\)
iii) △CMB ~ △RNQ
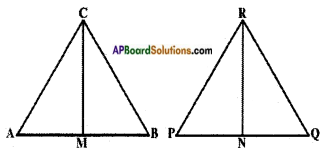
Answer:
Given : △ABC ~ △PQR
CM is a median through C of △ABC.
RN is a median through R of △PQR.
R.T.P:
i) △AMC ~ △PNR.
Proof: In △AMC and △PNR,
\(\frac{AC}{PR}\) = \(\frac{AM}{PN}\) and ∠A = ∠P [∵ In △ABC, △PQR 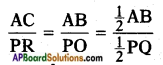 and M, N are the mid-points of AB and PQ]
and M, N are the mid-points of AB and PQ]
∴ △AMC ~ △PNR
[∵ SAS similarity condition]
ii) \(\frac{CM}{RN}\) = \(\frac{AB}{PQ}\)
Proof: From (i) we have
△AMC ~ △PNR
Hence \(\frac{AC}{PQ}\) = \(\frac{AM}{PN}\) = \(\frac{CM}{RN}\)
[∵ Ratio of corresponding sides of two similar triangles are equal]
Thus, \(\frac{CM}{RN}\) = \(\frac{AM×2}{PN×2}\)
[Multiplying both numerator and the denominator by 2]
\(\frac{CM}{RN}\) = \(\frac{AB}{PQ}\) [2AM = AB; 2PN = PQ]
iii) △CMB ~ △RNQ
Proof: In △CMB and △RNQ
∠B = ∠Q [Corresponding angles of △ABC and △PQR]
Also, \(\frac{BC}{RQ}\) = \(\frac{BM}{QN}\)

Thus, △CMB ~ △RNQ by S.A.S similarity condition.
![]()
Question 5.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point ‘O’. Using the criterion of similarity for two triangles, show that \(\frac{OA}{OC}\) = \(\frac{OB}{OD}\).
Answer:
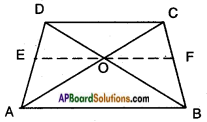
Given : □ ABCD, AB || DC
The diagonals AC and BD intersect at ‘O’.
R.T.P: \(\frac{OA}{OC}\) = \(\frac{OB}{OD}\)
Construction: Draw EF || AB, passing through ‘O’.
Proof: In △ACD, OE || CD [∵ Construction]
Hence \(\frac{OA}{OC}\) = \(\frac{EA}{ED}\) …….. (1)
(∵ Line drawn parallel to one side of a triangle divides other two sides in the same ratio – Basic proportionality theorem)
Also in △ABD, EO || AB [Construction] Hence,
\(\frac{EA}{ED}\) = \(\frac{OB}{OD}\) ……… (2)
(∵ Basic proportionality theorem) From (1) and (2), we have
\(\frac{OA}{OC}\) = \(\frac{OB}{OD}\)
∴ Hence proved.
Question 6.
AB, CD, PQ are perpendicular to BD. AB = x, CD = y and PQ = z, prove that \(\frac{1}{x}+\frac{1}{y}=\frac{1}{z}\).
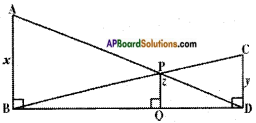
Answer:
Given ∠B = ∠Q = ∠D = 90°
Thus, AB || PQ || CD.
Now in △BQP, △BDC
∠B = ∠B (Common)
∠Q = ∠D (90°)
∠P = ∠C [∵ Angle Sum property of triangles]
∴ △BQP ~ △BDC
(by A.A.A similarity condition)
Hence \(\frac{BQ}{BD}\) = \(\frac{PQ}{CD}\)
[∵ Ratio of corresponding sides is equal] Also in △DQP and △DBA
∠D = ∠D (Common)
∠Q = ∠B (90°)
∴ △DQP ~ △DBA (by A.A. similarity condition)
\(\frac{QD}{BD}\) = \(\frac{PQ}{AB}\)
[ Ratio of corresponding sides is equal]
Adding (1) and (2), we get

![]()
Question 7.
A flag pole 4 m tall casts a 6 m., shadow. At the same time, a nearby building casts a shadow of 24 m. How tall is the building?
Answer:
Given: 4 m length flag pole casts a shadow 6 m.
Let x m length/tall building casts a shadow 24 m.
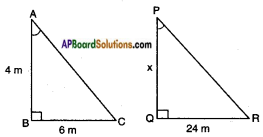
Let AB be the length of flag pole = 4 m.
Shadow of AB = BC = 6 m.
PQ be the building = x m (say)
QR, the shadow of the building = 24 m
From the figure,
∠A = ∠P
∠B = ∠Q
∴ △ABC ~ △PQR by A.A. similarity condition
Hence \(\frac{AB}{PQ}\) = \(\frac{BC}{QR}\)
[∵ Ratio of corresponding angles is equal]
\(\frac{4}{6}\) = \(\frac{x}{24}\)
x = \(\frac{24 \times 4}{6}\) = 16 m
∴ Height of the building = 16 m.
Question 8.
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of △ABC and △FEG respectively. If △ABC ~ △FEG then show that
i) \(\frac{CD}{GH}\) = \(\frac{AC}{FG}\)
ii) △DCB ~ △HGE
iii) △DCA ~ △HGF
Answer:
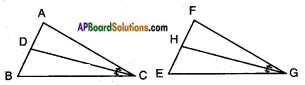
Given: △ABC ~ △FEG.
CD is the bisector of ∠C and GH is the bisector of ∠G.
R.T.P.:
i) \(\frac{CD}{GH}\) = \(\frac{AC}{FG}\)
In △ACD and △FGH
∠A = ∠F
[∵ Corresponding angles of △ABC and △FEG]
∠ACD = ∠FGH
[∵ ∠C = ∠G ⇒ \(\frac{1}{2}\)∠C = \(\frac{1}{2}\)∠G ⇒ ∠ACD = ∠FGH]
∴ By A.A. similarity condition, △ACD ~ △FGH
\(\frac{AC}{FG}\) = \(\frac{CD}{GH}\) = \(\frac{AD}{FH}\)
[∵ Ratio of the Corresponding angles is equal]
⇒ \(\frac{AC}{FG}\) = \(\frac{CD}{GH}\) [Q.E.D]
![]()
ii) △DCB ~ △HGE
In △DCB and △HGE,
∠B = ∠E
[∵ Corresponding angles of △ABC and △FEG]
∠DCB = ∠HGE
[∵ ∠C = ∠G ⇒ \(\frac{1}{2}\)∠C = \(\frac{1}{2}\)∠G ⇒ ∠DCB = ∠HGE]
∴ △DCB ~ △HGE . (by A.A. similarity condition)
iii) △DCA ~ △HGF
In △DCA and △HGF
∠A = ∠F
\(\frac{1}{2}\)∠C = \(\frac{1}{2}\)∠G ⇒ ∠DCA = ∠HGF
[∵ Corresponding angles of the similar triangles]
∴ △DCA ~ △HGF
[ A.A. similarity condition]
Question 9.
AX and DY are altitudes of two similar triangles △ABC and △DEF. Prove that AX : DY = AB : DE.
Answer:
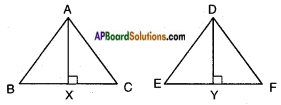
Given: △ABC ~ △DEF.
AX ⊥ BC and DY ⊥ EF.
R.T.P.: AX : DY = AB : DE.
Proof: In △ABX and △DEY ∠B = ∠E [∵ Corresponding angles of △ABC and △DEF]
∠AXB = ∠DYE [given]
∴ △ABX ~ △DEY
(by A.A. similarity condition)
Hence \(\frac{AB}{DE}\) = \(\frac{BX}{EY}\) = \(\frac{AX}{DY}\)
[∵ Ratios of corresponding sides of similar triangles are equal]
⇒ AX : DY = AB : DE [Q.E.D.]
Question 10.
Construct a triangle shadow similar to the given △ABC, with its sides equal to \(\frac{5}{3}\) of the corresponding sides of the triangle ABC.
Answer:
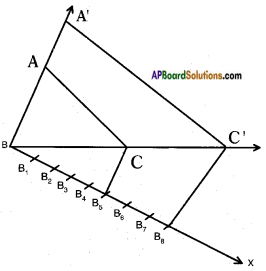
Steps of construction :
- Draw a △ABC with certain measures.
- Draw a ray \(\overrightarrow{\mathrm{BX}}\) making an acute angle with BC on the side opposite to vertex A.
- Locate 8 points (B1, B2, …., B8) on \(\overrightarrow{\mathrm{BX}}\) such that BB1 = B1B2 = B2B3 = B3B4 = B4B5 = B5B6 = B6B7 = B7B8.
- Join B5, C.
- Draw a line parallel to B5C through which it intersects BC extended at C’.
- Draw a line parallel to AC through ‘C’ which meets \(\overrightarrow{\mathrm{BA}}\) produced at A’.
- △A’BC’ is the required triangle.
![]()
Question 11.
Construct a triangle of sides 4 cm, 5 cm and 6 cm. Then, construct a triangle similar to it,whose sides are 2/3 of the corresponding sides of the first triangle.
Answer:
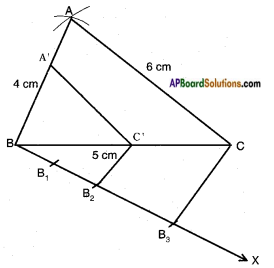
Steps of construction:
- Draw △ABC with AB = 4 cm, BC = 5 cm and CA = 6 cm.
- Draw a ray BX making an acute angle with BC on the side opposite to vertex A.
- Mark three points B1, B2 and B3 on \(\overrightarrow{\mathrm{BX}}\) such that BB1 = B1B2 = B2B3.
- Join B3, C.
- Draw a line parallel to B3C through B2 meeting BC at C’.
- Draw a line parallel to BA through C’ meeting BA at A’.
- △A’BC’ is the required triangle.
Question 12.
Construct an isosceles triangle whose base is 8 cm and altitude is 4 cm. Then, draw another triangle whose sides are 1\(\frac{1}{2}\) times the corresponding sides of the isosceles triangle.
Answer:
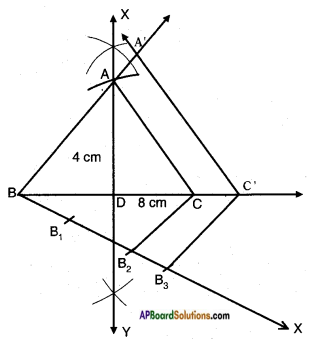
Steps of construction:
- Draw AABC in which BC = 8 cm and altitude AD = 4 cm.
- Draw a ray BX making an acute angle with BC on the side opposite to vertex A.
- Mark three points B1, B2 and B3 such that BB1 = B1B2 = B2B3.
- Join B2C.
- Draw a line parallel to B2C through B3 meeting BC produced C’.
- Draw a line paral1e1 to AC through C’ meeting BA produced at A’.
- △A’BC’ is the required triangle.