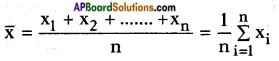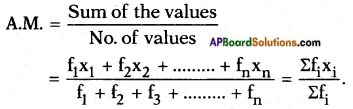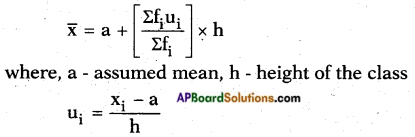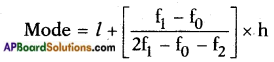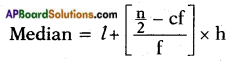Mahesh

Students can go through AP Board 9th Class Maths Notes Chapter 8 Quadrilaterals to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 8 Quadrilaterals

→ A quadrilateral is a simple closed figure bounded by four line segments.

→ The line segments joining any two opposite vertices are called diagonals.

→ The sum of the four interior angles of a quadrilateral is 360° or four right angles.

→ A quadrilateral in which one pair of opposite sides are parallel is called a trapezium.

→ A quadrilateral in which both pairs of opposite sides are parallel is called a parallelogram.

→ A parallelogram in which the adjacent sides are equal is called a rhombus.

→ A parallelogram in which one angle is right angle is called a rectangle.

→ A parallelogram in which adjacent sides are equal and one angle is right angle is called a square.

→ A quadrilateral in which the two pairs of adjacent sides are equal is called a ‘kite’.

→ In, a parallelogram

• diagonals bisect each other.
• adjacent/consecutive angles are supplementary.
• opposite angles are equal.
• both pairs of opposite sides are equal.
• diagonal divides the parallelogram into two congruent triangles.

→ In a rhombus, diagonals bisect each other at right angles and the diagonals are unequal.

→ In a square diagonals are equal and bisect each other at right angles.

→ In a rectangle diagonals are equal and bisect each other.

→ The line segment joining the mid points of two side of a triangle is parallel to third side and also half of it.

→ The line drawn through the mid point of one side of a triangle and parallel to another side will bisect the third side.

→ The intercepts made by the transversal on three or more parallel lines are equal to one another.

Students can go through AP Board 8th Class Maths Notes Chapter 1 Rational Numbers to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 1 Rational Numbers

→ The numbers which are expressed in the form of \(\frac{p}{q}\) where p and q are integers and q ≠ 0, are called “Rational Numbers” which are denoted by the letter ‘Q’.

→ Rational numbers are closed under the operations of addition, subtraction and multiplication.

→ Rational numbers are not closed on division.

→ Whole numbers:

→ Whole numbers:

→ The additive inverse of a is – a. (∵ a + (-a) = 0)

→ The multiplicative inverse of a is \(\frac{1}{a}\). (∵ a × \(\frac{1}{a}\) = 1)

→ The operations addition and multiplications are

1. Commutative for rational numbers.
2. Associative for rational numbers.

→ ‘0’ is the additive identity for rational number.

→ ‘1’ is the multiplicative identity for rational number.

→ A rational number and its additive inverse are opposite in their sign.

→ The multiplicative inverse of a rational number is its reciprocal.

→ Distributivity of rational numbers a, b and c is a(b + c) = ab + ac and a(b – c) = ab – ac.

→ Rational numbers can be represented on a number line.

→ There are infinite number of rational numbers between any two given rational numbers.

→ The concept of mean help us to find rational numbers between any two rational numbers.

→ The decimal representation of rational numbers is either in the form of terminating decimal or non-terminating recurring decimals.

Students can go through AP Board 8th Class Maths Notes Chapter 14 Surface Areas and Volume to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 14 Surface Areas and Volume

→ If l, b, h are-the dimensions of cuboid, then:

(i) its lateral surface area is 2h (l+ b)
(ii) its total surface area is 2 (lb + bh + hl)
(iii) its volume is l × b × h

→ Lateral surface area of a cube is 4a²

→ Total surface area of a cube is 6a²

→ Volume of a cube is side × side × side = a³

→ 1 cm³ = 1 ml

→ 1 l = 1000 cm³

→ 1 m³ = 1000000 cm³ = 1000 l = 1 kl (kilolitre)

Students can go through AP Board 9th Class Maths Notes Chapter 7 Triangles to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 7 Triangles

→ Two line segments are congruent if they have equal length.

→ Two squares are congruent if they have same side.

→ Squares that have same measure of diagonals are also congruent.

→ Two triangles are congruent if they cover each other exactly.

→ If two triangles are congruent then Corresponding Parts of Congruent Triangles (CPCT) are equal.

→ Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and included angle of the other triangle (S.A.S. congruence rule).

→ Two triangles are congruent, if two angles and the included side of one triangle are equal to two angles and the included side of the other triangle (A.S.A. congruence rule).

→ Two triangles are congruent if any two pairs of angles and one pair of corresponding sides are equal (A.A.S.).

→ Angles opposite equal sides of a triangle are equal.

→ The sides opposite to equal angles of a triangle are equal.

→ If three sides of one triangle are respectively equal to the corresponding three sides of another triangle, then the two triangles are congruent (SSS).

→ If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the another triangle, then the two triangles are congruent (RHS).

→ In a triangle, of the two sides, side opposite to greater angle is greater.

→ Sum of any two sides of a triangle is greater than the third side.

Students can go through AP Board 8th Class Maths Notes Chapter 13 Visualizing 3-D in 2-D to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 13 Visualizing 3-D in 2-D

→ Polyhedron: Solid objects having flat surfaces.

→ Prism: The polyhedra have top and base as same polygon and other faces are rectangular (parallelogram).

→ Pyramid: Polyhedron which have a polygon as base and a vertex, rest of the faces are triangles. 4 3-D objects could be make by using 2-D nets.

→ Euler’s formula for polyhedra : E + 2 = F + V.

→ 3-D Objects made with cubes:
Observe the following solid shapes. Both are formed by arranging four unit cubes. If we observe them from different positions, it seems to be different. But the object is same.

→ Faces, Edges and Vertices of 3D-Objects:
Observe the walls, windows, doors, floor, top, corners etc of our living room and tables, boxes etc. Their faces are flat faces. The flat faces meet at its edges. Two or more edges meet at corners. Each of the corner is called vertex. Take a cube and observe it where the faces meet?

→ There are only five regular polyhedra, all of them are complex, often referred as Platonic solids as a tribute to Plato.

Note: Cube is the only polyhedron to completely fill the space.

→ Net diagrams of Platonic Solids

→ No. of Edges, Faces and Vertices of Polyhedrons:

By observing the last two columns of the above table, we can conclude that F + V = E + 2 for all polyhedra.

Students can go through AP Board 9th Class Maths Notes Chapter 6 Linear Equation in Two Variables to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 6 Linear Equation in Two Variables

→ Equations like x + 7 = 10; y + √3 = 8 are examples of linear equations in one variable.

→ If a linear equation has two variables then it is called a linear equation in two variables. Eg.: 3x – 5y = 8; 5x + 7y = 6 ….

→ The general form of a linear equation in two variables x and y is ax + by + c = 0; where a, b, c are real numbers and a, b are not simultaneously zero.

→ Any pair of values of x and y which satisfy ax + by + c = 0 is called the solution of linear equation.

→ An easy way of getting two solutions is put x = 0 and get the corresponding value of y. Similarly put y = 0 and get the value for x.

→ The line obtained by joining all points which are solutions of a linear equation is called graph of linear equation.

→ Equation of a line parallel to X-axis is y = k. (at a distance ‘k’ units)

→ Equation of a line parallel to Y-axis at a distance of k – units is x = k.

→ Equation of X-axis is y = 0 and Y-axis is x = 0.

→ The graph of x = k is a line parallel to Y-axis at a distance of ‘k’ units and passing through the point (k, 0).

→ The graph of y = k is a line parallel to X-axis at a distance of k – units and passing through the point (0, k).

Students can go through AP Board 9th Class Maths Notes Chapter 5 Co-Ordinate Geometry to understand and remember the concepts easily.

AP State Board Syllabus 9th Class Maths Notes Chapter 5 Co-Ordinate Geometry

→ To locate the exact position of a point on a number line we need only a single reference.

→ To describe the exact position of a point on a Cartesian plane we need two references.

→ Rene Descartes a French mathematician developed the new branch of mathematics called Co-ordinate Geometry.

→ The two perpendicular lines taken in any direction are referred to as co-ordinate axes. © The horizontal line is called X – axis.

→ The vertical line is called Y – axis.

→ The meeting point of the axes is called the origin.

→ The distance of a point from Y – axis is called the x co-ordinate or abscissa.

→ The distance of a point from X – axis is called the y co-ordinate or ordinate.

→ The co-ordinates of origin are (0, 0).

→ The co-ordinate plane is divided into four quadrants namely Q₁, Q₂, Q₃, Q₄ i.e., first, second, third and fourth quadrants respectively.

→ The signs of co-ordinates of a point are as follows.
Q₁: (+, +) Q₂: (-, +) Q₃: (-, -) Q₄: (+, -).

→ The x co-ordinate of a point on Y – axis is zero.

→ The y co-ordinate of a point on X – axis is zero.

→ Equation of X – axis is y = 0

→ Equation of Y – axis is x = 0

→ In a co-ordinate plane (x₁; y₁) ≠ (x₂, y₂) unless x₁ = x₂ and y₁ = y₂.

Students can go through AP Board 8th Class Maths Notes Chapter 12 Factorisation to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 12 Factorisation

→ Factorisation is a process of writing the given expression as a product of its factors.

→ A factor which cannot be further expressed as product of factors is an irreducible factor.

→ Expressions which can be transformed into the form:
a² + 2ab + b²;
a² – 2ab + b²;
a² – b² and x² + (a + b)x + ab can be factorised by using identities.

→ If the given expression is of the form x² + (a + b) x + ab, then its factorisation is (x + a)(x + b).

→ Division is the inverse of multiplication. This concept is also applicable to the division of algebraic expressions.

Gold Bach Conjecture:

→ Gold Bach found from observation that every odd number seems to be either a prime or the sum of a prime and twice a square.
Thus 21 = 19 + 2 or 13 + 8 or 3 + 18.

→ It is stated that up to 9000, the only exceptions to his statement are
5777 = 53 × 109 and 5993 = 13 × 641,
which are neither prime nor the sum of a primes and twice a square.

Students can go through AP Board 8th Class Maths Notes Chapter 11 Algebraic Expressions to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 11 Algebraic Expressions

→ There are number of situations in which we need to multiply algebraic expressions.

→ A monomial multiplied by a monomial always gives a monomial.

→ While multiplying a polynomial by a monomial, we multiply every term in the polynomial by the monomial.

→ In carrying out the multiplication of an algebraic expression with another algebraic expression (monomial/ binomial/ trinomial etc.) we multiply term by term i.e. every term of the expression is multiplied by every term in the another expression.

→ An identity is an equation, which is true for-all values of the variables in the equation. On the other hand, an equation is true only for certain values of its variables. An equation is not an identity.

→ The following are identities:
I. (a + b)² = a² + 2ab + b²
II. (a – b)² = a² – 2ab + b²
III. (a + b) (a -b) = a² – b²
IV. (x + a) (x + b) = x² + (a + b)x + ab

→ The above four identities are useful in carrying out squares and products of algebraic expressions. They also allow easy alternative methods to calculate products of numbers and so on.
Note:
We know that
(+) × (+) = +
(+) × (-) = –
(-) × (+) = –
(-) × (-) = +

Students can go through AP Board 8th Class Maths Notes Chapter 10 Direct and Inverse Proportions to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 10 Direct and Inverse Proportions

→ If x and y are in direct proportion, the two quantities vary in the same ratio.
i.e. if \(\frac{x}{y}\) = k or x = ky. We can write \(\frac{x_{1}}{y_{1}}\) = \(\frac{x_{2}}{y_{2}}\) [y₁, y₂ are values of y corresponding to the values x₁, x₂ of x respectively]

→ Two quantities x and y are said to vary in inverse proportion, if there exists a relation of the type xy = k between them, k being a constant. If y₁, y₂ are the values of y corresponding to the values x₁ and x₂ of x respectively, then x₁y₁ = x₂y₂ (= k), or = \(\frac{x_{1}}{x_{2}}\) = \(\frac{y_{2}}{y_{1}}\)

→ If one quantity increases (decreases) as the other quantity decreases (increases) in same proportion, then we say it varies in the inverse ratio of the other quantity. The ratio of the first quantity (x₁ : x₂) is equal to the inverse ratio of the second quantity (y₁ : y₂). As both the ratios are the same, we can express this inverse variation as proportion and it is called inverse proportion.

→ Sometimes change in one quantity depends upon the change in two or more other quantities in same proportion. Then we equate the ratio of the first quantity to the compound ratio of the other two quantities.

Students can go through AP SSC 10th Class Maths Notes Chapter 14 Statistics to understand and remember the concepts easily.

AP State Syllabus SSC 10th Class Maths Notes Chapter 14 Statistics

→ Statistics is a branch of mathematics which deals with collection, organisation, presentation, analysis and interpretation of numerical data.

→ Data is a collection of actual information which is used to make logical inferences.

→ Arithmetic Mean of raw data:
The Arithmetic Mean (A.M.) of a raw data viz. x₁, x₂, x₃, ……., x_n is the sum of values of all observations divided by the number of observations.
Arithmetic Mean (A.M.) =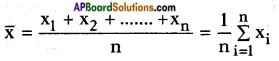
Eg.: Sita secured 23, 24, 24, 22 and 20 marks in a test. Her mean marks are
A.M. = \(\frac{23+24+24+22+20}{5}\) = \(\frac{113}{5}\) = 22.6

→ A.M. by direct method:
Let x₁, x₂, x₃, ……., x_n be observations with respective frequencies f₁, f₂, ……, f_n
i.e., x₁ occurs for f₁ times, x₂ occurs for f₂ times, ….., x_n occurs for f_n times.

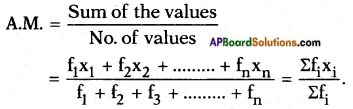
→ For a grouped data, it is assumed that the frequency of each class interval is centered around its mid-point and the A.M. is given by A.M. = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)

→ A.M. by deviation method, \(\overline{\mathbf{x}}=\mathbf{a}+\frac{\Sigma \mathbf{f}_{\mathbf{i}} \mathbf{d}_{\mathbf{i}}}{\Sigma \mathbf{f}_{\mathbf{i}}}\)
where, a – assumed mean
d_i – deviation = x_i – a.
Step – 1: Choose ‘a’ from the central values.
Step – 2: Obtain d_i by subtracting a from x_i.
Step – 3: Multiply f_i and d_i.
Step – 4: Find ∑f_id_i and ∑f_i .
Step – 5: Find \(\overline{\mathbf{x}}=\mathbf{a}+\frac{\Sigma \mathbf{f}_{\mathbf{i}} \mathbf{d}_{\mathbf{i}}}{\Sigma \mathbf{f}_{\mathbf{i}}}\)

→ A.M. by step-deviation method:

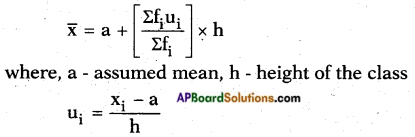
Step – 1: Choose ‘a’ from mid values.
Step – 2: Obtain u_i = \(\frac{x_{i}-a}{h}\).
Step – 3: Multiply f_i and u_i.
Step – 4: Find Ef_iu_i and Sf_i.
Step – 5: Find \(\overline{\mathrm{x}}=\mathrm{a}+\left(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\right) \times \mathrm{h}\)

→ Mode : Mode is the size of variable which occurs most frequently.

→ Mode of a grouped data:

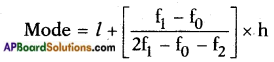
Where, l – lower boundary of the modal class,
h – size of the modal class interval,
f₁ – frequency of modal class.
f₀ – frequency of the class preceding the modal class.
f₂ – frequency of the class succeeding the modal class.

→ Median: Median is defined as the measure of the central items when they are in descending or ascending order of magnitude.

→ Median for a grouped data:

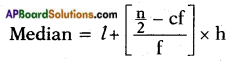
where,
l – lower boundary of median class,
n – number of observations.
cf – cumulative frequency of class preceding the median class.
f – frequency of median class.
h – size of the median class.

→ Cumulative frequency curve or an ogive:
First we prepare the cumulative frequency table, then the cumulative frequencies are plotted against the upper or lower limits of the corresponding class intervals. By joining the points the curve so obtained is called a cumulative frequency or ogive.
Ogives are of two types.

1. Less than ogive: Plot the points with the upper limits of the classes as abscissa and the corresponding less than cumulative frequencies as ordinates. The points are joined by free hand smooth curve to give less than cumulative frequency curve or the less than ogive. It is a rising curve.
2. Greater than ogive: Plot the points with the lower limits of the classes as abscissa and the corresponding greater than cumulative frequencies as ordinates. Join the points by a free hand smooth curve to get the greater than ogive. It is a falling curve.

When the points are joined by straight lines, the figure obtained is called cumulative frequency polygon.

→ Median can be obtained from cumulative frequency curve: From \(\frac{n}{2}\) frequency draw a line parallel to X-axis cutting the curve at a point. From this point draw a perpendicular to the axis. The point at which the perpendicular meets the X – axis determines the median.

Less than type and greater than type curves intersects at a point. From this point of intersection if we draw a perpendicular on the X-axis then this cuts X-axis at some point. This point gives the median.

Students can go through AP Board 8th Class Maths Notes Chapter 8 Exploring Geometrical Figures to understand and remember the concepts easily.

AP State Board Syllabus 8th Class Maths Notes Chapter 8 Exploring Geometrical Figures

→ Shapes are said to be congruent if they have same shape and size.

→ Shapes are said to be similar if they have same shapes but in different size.

→ If we flip, slide or turn the congruent/similar shapes their congruence/similarity remain the same.

→ Some figures may have more than one line of symmetry.

→ Symmetry is of three types namely line symmetry, rotational symmetry and point symmetry.

→ With rotational symmetry, the figure is rotated around a central point so that it appears two or more times same as original.

→ The number of times for which it appears the same is called the order.

→ The method of drawing enlarged or reduced similar figures is called Dialation.

→ The patterns formed by repeating figures to fill a plane without gaps or overlaps are called tessellations.

→ Flip: Flip is a transformation in which a plane figure is reflected across a line, creating a mirror image of the original figure.

→ After a figure is flipped or reflected, the distance between the line of reflection and each point on the original figure is the same as the distance between the line of reflection and the corresponding point on the mirror image.

→ Rotation: “Rotation “means turning around a center.
The distance from the center to any point on the shape stays the same. Every point makes a circle around the center.

There is a central point that stays fixed and everything else moves around that point in a circle.
A “Full Rotation” is 360°.

→ Now observe the following geometrical figures.

In all the cases if the first figure in the row is moved, rotated and flipped do you find any change in size and shape? No, the figures in every row are congruent they represent the same figure but oriented differently.

→ If two shapes are congruent, still they remain congruent if they are moved or rotated. The shapes would also remain congruent if we reflect the shapes by producing their mirror images.

→ We use the symbol ≅ to represent congruency.