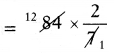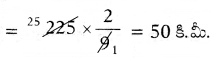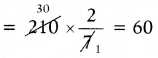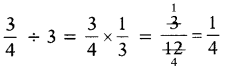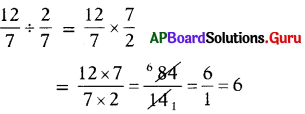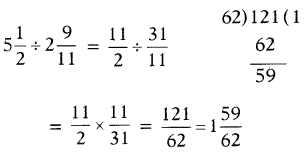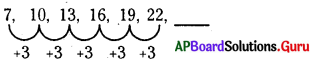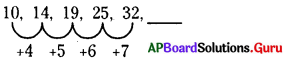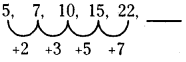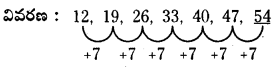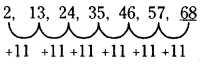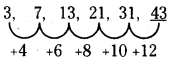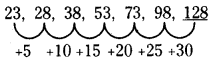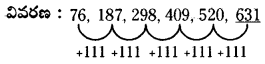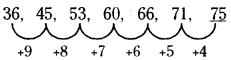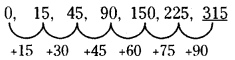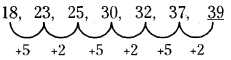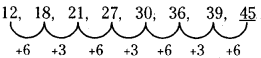Mahesh

SCERT AP 7th Class Maths Solutions Pdf Chapter 2 భిన్నాలు మరియు దశాంశాలు Ex 2.3 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 2nd Lesson భిన్నాలు మరియు దశాంశాలు Exercise 2.3

ప్రశ్న 1.
పట్టికలోని ఖాళీలను నింపండి. ఒకటి మీ కొరకు చేయబడింది.

సాధన.

ప్రశ్న 2.
క్రింది వాటిని సాధించండి.
(i) 5.51 ÷ 2
సాధన.
5.51 ÷ 2

∴5.51 ÷ 2 = 2.755

(ii) 38.4 ÷ 3
సాధన.
38.4 ÷ 3

∴38.4 ÷ 3 = 12.8

(iii) 57.39 ÷ 6
సాధన.
57.39 ÷ 6

∴57.39 ÷ 6 = 9.565

(iv) 562.1 ÷ 11
సాధన.
562.1 ÷ 11

∴562.1 ÷ 11 = 51.1

(v) 0.7005 ÷ 5
సాధన.
0.7005 ÷ 5

∴0.7005 ÷ 5 = 0.1401

(vi) 9.99 ÷ 3
సాధన.
9.99 ÷ 3

∴9.99 ÷ 3 = 3.33

(vii) 13 ÷ 6.5
సాధన.
13 ÷ 6.5 = 13 × 10 ÷ 6.5 × 10

(viii) 10.01 ÷ 11
సాధన.
10.01 ÷ 11

∴10.01 ÷ 11 = 0.91

(ix) 8 ÷ 0.32
సాధన.
8 ÷ 0.32

∴8 ÷ 0.32 = 25

(x) 320.1 ÷ 33
సాధన.
320.1 ÷ 33
= \(\frac{3201}{10}\) ÷ 33

∴320.1 ÷ 33 = 9.7

ప్రశ్న 3.
క్రింది పేర్కొన్న భాగాహారాలను చేయండి.
(i) 78.24 ÷ 0.2
సాధన.
78.24 ÷ 0.2

(ii) 4.845 ÷ 1.5
సాధన.
4.845 ÷ 1.5
= \(\frac{4845}{1000} \div \frac{15}{10}\)

(iii) 0.246 ÷ 0.6
సాధన.
0.246 ÷ 0.6

(iv) 563.2 ÷ 2.2
సాధన.
563.2 ÷ 2.2

(v) 0.026 ÷ 0.13
సాధన.
0.026 ÷ 0.13

(vi) 4.347 ÷ 0.09
సాధన.
4.347 ÷ 0.09

(vii) 3.9 ÷ 0.13
సాధన.
3.9 ÷ 0.13

(viii) 20.32 ÷ 0.8
సాధన.
20.32 ÷ 0.8

(ix) 24.4 ÷ 6.1
సాధన.
24.4 ÷ 6.1

(x) 2.164 ÷ 0.008
సాధన.
2.164 ÷ 0.008

ప్రశ్న 4.
క్రింది వాటిని సాధించండి.
(i) 39.54 ను 6తో భాగించండి.
సాధన.
39.54 ÷ 6

∴39.54 ÷ 6 = 6.59

(ii) 7.2ని 10తో భాగించండి.
సాధన.
7.2 ÷ 10
= \(\frac{72}{10}\) ÷ 10
= \(\frac{72}{10} \times \frac{1}{10}\) = \(\frac{72}{100}\) = 0.72

(iii) 5.2ని 1.3 తో భాగించండి.
సాధన.
5.2 ÷ 1.3
= \(\frac{52}{10} \div \frac{13}{10}\)

(లేదా)
5.2 × 10 ÷ 1.3 × 10
52 ÷ 13 = 4

ప్రశ్న 5.
శేఖర్ తన బైక్ పై సమవేగంతో 5 గంటల్లో 154.5 కి.మీ. ప్రయాణించాడు. ఒక గంటలో ఎంత దూరం ప్రయాణించగలడు?
సాధన.
5 గంటలలో శేఖర్ బైక్ పై ప్రయాణించిన దూరం = 154.5 కి.మీ.
1 గంటలో శేఖర్ ప్రయాణించగల దూరం = 154.5 ÷ 5
= \(\frac{1545}{10} \div \frac{5}{1}\)

= \(\frac{309}{10}\) = 30.9 కి.మీ.

ప్రశ్న 6.
ఒక తాపి మేస్త్రీ గోడను నిర్మించడానికి 12.5 రోజుల్లో 100 గంటలు పనిచేస్తే, అతను రోజుకు ఎన్ని గంటలు పనిచేశాడు?

సాధన.
తాపి మేస్త్రి 12.5 రోజులలో పనిచేసిన గంటలు = 100 గంటలు
∴తాపీ మేస్త్రి రోజుకు పని చేసిన గంటలు
= 100 ÷ 12.5
= 100 ÷ \(\frac{125}{10}\)

ప్రశ్న 7.
డజన్ గుడ్లు ఖరీదు ₹61.80 అయితే ఒక గుడ్డు యొక్క ధర కనుగొనండి.
సాధన.
డజన్ గుడ్లు ఖరీదు = ₹61.80
(∵1 డజన్ గుడ్లు = 12 గుడ్లు)
∴ ఒక గుడ్డు ఖరీదు = 61.80 ÷ 12
= \(\frac{6180}{100}\) ÷ 12

ఒక గుడ్డు ఖరీదు = ₹ 5.15

ప్రశ్న 8.
10 టాబ్లెట్ (మాత్ర) లను కలిగి ఉన్న టాబ్లెట్ స్క్రిప్ ధర ₹ 26.5 అయితే ఒక టాబ్లెట్ ధరను కనుగొనండి.
సాధన.
10 టాబ్లెట్లను కలిగిన స్ట్రిప్ ధర = ₹ 26.5
ఒక టాబ్లెట్ ధర = 26.5 ÷ 10
= \(\frac{265}{10}\) ÷ 10
= \(\frac{265}{10} \times \frac{1}{10}\)
= \(\frac{265}{100}\)
= 2.65
∴ ఒక టాబ్లెట్ ధర = ₹ 2.65

SCERT AP 7th Class Maths Solutions Pdf Chapter 2 భిన్నాలు మరియు దశాంశాలు Ex 2.2 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 2nd Lesson భిన్నాలు మరియు దశాంశాలు Exercise 2.2

ప్రశ్న 1.
క్రింది వాటి లబ్దాన్ని కనుగొనండి.
(i) 23.4 × 6
సాధన.
23.4 × 6
= \(\frac{234}{10} \times \frac{6}{1}\)
= \(\frac{1404}{10}\)
∴ 23.4 × 6 = 140.4

(ii) 681.25 × 9
సాధన.
681.25 × 9

(iii) 53.29 × 14
సాధన.
53.29 × 14

∴ 53.29 × 14 = 746.06

(iv) 8 × 2.52
సాధన.
8 × 2.52
= 8 × \(\frac{252}{100}\)
= \(\frac{8 \times 252}{100}\) = \(\frac{2016}{100}\)
∴8 × 2.52 = 20.16

(v) 25 × 2.013
సాధన.
25 × 2.013
= 25 × \(\frac{2013}{1000}\)
= \(\frac{25 \times 2013}{1000}\)
= \(\frac{50325}{1000}\)
1000 50325 – 1000 .
∴ 25 × 2.013 = 50.325

ప్రశ్న 2.
పట్టికలో ఖాళీలను నింపండి.

సాధన.

ప్రశ్న 3.
లబ్దాన్ని కనుగొనండి.
(i) 5.1 × 8.1
సాధన.

(ii) 63.205 × 0.27
సాధన.

(iii) 1.321 × 0.9
సాధన.

(iv) 6.51 × 0.99
సాధన.

(v) 837.6 × 0.006
సాధన.

ప్రశ్న 4.
రితేష్ ప్రతిరోజూ 2.5 గం.ల పాటు ఒక పుస్తకాన్ని చదువుతాడు. ఒక వారంలో ఆ పుస్తకంను అతను పూర్తిగా చదివితే, మొత్తం ఎన్ని గంటలు చదివాడు?

సాధన.
రితేష్ ప్రతిరోజు పుస్తకాన్ని చదివే సమయం = 2.5 గం.లు
= 7 × 2.5
= 7 × \(\frac{25}{10}\)
= \(\frac{175}{10}\)
= 17.5 గంటలు.

ప్రశ్న 5.
పొడవు మరియు వెడల్పులు వరుసగా 5.3 సెం.మీ. మరియు 2.7 సెం.మీ.గా ఉన్న దీర్ఘచతురస్రం యొక్క వైశాల్యం కనుగొనండి.
సాధన.

దీర్ఘచతురస్ర పొడవు (1) = 5.3 సెం.మీ.
వెడల్పు (b) = 2.7 సెం.మీ.
∴దీర్ఘచతురస్ర వైశాల్యం = lb

ప్రశ్న 6.
ఒక సిమెంట్ బస్తా ధర ₹ 326.50 అయినచో 24 బ్యాగుల సిమెంట్ బస్తాల ధరను కనుగొనండి.
సాధన.
ఒక సిమెంట్ బస్తా ధర = ₹ 326.50
24 సిమెంట్ బస్తాల ధర = 326.50 × 24

∴24 సిమెంట్ బస్తాల ధర = ₹ 7,836.

ప్రశ్న 7.
ధార్మిక చుడిధార్ మెటీరియల్ ను, ఒక మీ.కు ₹152.5 చొప్పున 1.40 మీ. కొనుగోలు చేసింది. చెల్లించాల్సిన మొత్తాన్ని కనుగొనండి.

సాధన.
ఒక మీటరు చుడిధార్ మెటీరియల్ ధర = ₹152.5
1.40 మీ. చుడిధార్ మెటీరియల్ కొనుగోలు చేయుటకు ధార్మిక చెల్లించాల్సిన మొత్తం = 152.5 × 1.40

ప్రశ్న 8.
అమృత ఒక ఆల్బమ్ తయారు చేయడానికి 16 175 ఛార్జులను కొనుగోలు చేయాలని అనుకుంటుంది. ఒక పిక్చర్ ఛార్టు ధర ₹4.25 అయితే ఆమె ఎంత డబ్బు చెల్లించాల్సి ఉంటుంది ?
సాధన.
అమృత కొనుగోలు చేసిన ఛార్టుల సంఖ్య = 16
ఒక ఛార్టు ధర = ₹ 4.25
∴అమృత చెల్లించాల్సిన డబ్బు = 16 × 4.25
= 16 × \(\frac{425}{100}\)
= \(\frac{6800}{100}\)
= ₹68.00

SCERT AP 7th Class Maths Solutions Pdf Chapter 2 భిన్నాలు మరియు దశాంశాలు Ex 2.1 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 2nd Lesson భిన్నాలు మరియు దశాంశాలు Exercise 2.1

ప్రశ్న 1.
జగనన్న గోరు ముద్ద (MDM) పథకంలో ఒక్కొక్క విద్యార్థి రోజుకు \(\frac{3}{20}\) కి.గ్రా. బియ్యం పొందిన, తరగతిలో గల మొత్తం 60 మంది విద్యార్థులకు ఒక రోజుకు కావలసిన బియ్యం బరువు కనుగొనండి.
సాధన.
జగనన్న గోరు ముద్ద పథకంలో ఒక్కొక్క విద్యార్థి రోజుకు పొందు బియ్యం \(\frac{3}{20}\) = కి.గ్రా.
తరగతిలోని మొత్తం విద్యార్థులు = 60
∴ ఒక రోజుకు ఆ తరగతికి కావలసిన బియ్యం

= 9 కి.గ్రా.

ప్రశ్న 2.
ఒక సమబాహు త్రిభుజం యొక్క ప్రతి 5\(\frac{3}{10}\) సెం.మీ. అయితే త్రిభుజం యొక్క చుట్టుకొలత ఎంత?
సాధన.
సమబాహు త్రిభుజం యొక్క భుజం = 5\(\frac{3}{10}\) సెం.మీ.

సమబాహు త్రిభుజం యొక్క చుట్టుకొలత
= 3 × 5\(\frac{3}{10}\)
= 3 × \(\frac{53}{10}\) = \(\frac{159}{10}\) = 15\(\frac{9}{10}\) సెం.మీ.
(లేదా)
సమబాహు త్రిభుజ భుజం = 5\(\frac{3}{10}\) = \(\frac{53}{10}\) సెం.మీ.
సమబాహు త్రిభుజం చుట్టుకొలత
= \(\frac{53}{10}+\frac{53}{10}+\frac{53}{10}\)
= \(\frac{159}{10}\) = 15\(\frac{9}{10}\) సెం.మీ.

ప్రశ్న 3.
సూర్య ఒక గంటలో \(\frac{18}{5}\) కిలో మీటర్లు నడవగలడు 2\(\frac{1}{2}\) గంటల్లో ఎంత దూరం నడవగలదు?
సాధన.
సూర్య ఒక గంటలో నడవగల దూరం = \(\frac{18}{5}\) కి.మీ.
సూర్య 2\(\frac{1}{2}\) గంటల్లో నడవగల దూరం = 2\(\frac{1}{2}\) × \(\frac{18}{5}\)

ప్రశ్న 4.
ఒక దీర్ఘచతురస్రాకార తోట పొడవు మరియు వెడల్పులు వరుసగా \(\frac{27}{2}\) మీ. మరియు \(\frac{15}{2}\) మీ. అయిన అప్పుడు ఆ తోట యొక్క వైశాల్యం కనుగొనండి.

సాధన.
దీర్ఘ చతురస్రాకార తోట పొడవు = \(\frac{27}{2}\) మీ
వెడల్పు = \(\frac{15}{2}\) మీ
దీర్ఘచతురస్రాకార తోట వైశాల్యం = పొడవు × వెడల్పు
= \(\frac{27}{2}\) × \(\frac{15}{2}\)
= \(\frac{405}{2}\)
= 101\(\frac{1}{4}\)చ.మీ.

ప్రశ్న 5.
గోపాల్ మార్కెట్లో 3\(\frac{1}{2}\) కి.గ్రా. బంగాళదుంపలు కొనుగోలు చేశాడు. వాటికి అతడు ₹84 చెల్లించినచో, 1 కి.గ్రా. బంగాళదుంపల వెల కనుగొనండి.
సాధన.
గోపాల్ మార్కెట్లో కొనుగోలు చేసిన బంగాళ దుంపలు = 3\(\frac{1}{2}\) కి.గ్రా.
గోపాల్ చెల్లించిన డబ్బు = ₹84
∴ 1 కి.గ్రా. బంగాళ దుంపల వెల = 84 ÷ 3\(\frac{1}{2}\)
= 84 ÷ \(\frac{7}{2}\)

= ₹ 24

ప్రశ్న 6.
ఒక కారు సమవేగంతో 47 గం.లలో 225 కి.మీ. ప్రయాణించింది. అది ఒక గంటలో ప్రయాణించిన దూరాన్ని కనుగొనండి.

సాధన.
ఒక కారు సమవేగంతో 4, గం.లలో ప్రయాణించిన
దూరం = 225 కి.మీ.
∴ కారు ఒక గంటలో ప్రయాణించిన దూరం
= 225 ÷ 4\(\frac{1}{2}\) = 225 ÷ \(\frac{9}{2}\)

ప్రశ్న 7.
24 మంది విద్యార్థులు 4\(\frac{4}{5}\) కి.గ్రా.ల కేకేను సమానంగా పంచుకుంటే, అప్పుడు ప్రతి ఒక్కరూ ఎంత కేక్ ను పొందుతారు ?

సాధన.
24 మంది విద్యార్థులు పంచుకొన్న కేకు = 4\(\frac{4}{5}\) కి.గ్రా.
∴ ప్రతి ఒక్కరూ పొందు కేకు = 4\(\frac{4}{5}\) ÷ 24
= \(\frac{24}{5}\) ÷ \(\frac{24}{1}\)

ప్రశ్న 8.
ఒక డ్రమ్ లో 210 లీ. నీరు కలదు. మొక్కలకు నీరు పోయుటకు బాలుడు 3\(\frac{1}{2}\) లీ. సామర్థ్యం గల నిండు బక్కెట్టుతో ఆ డ్రమ్ నుంచి ఎన్నిసార్లు నీటిని పొందగలడు?

సాధన.
ఒక డ్రమ్ లో గల నీరు = 210 లీ.
మొక్కలకు నీరు పోయుటకు బాలుడు ఉపయోగిస్తున్న బకెట్ సామర్థ్యం = 3\(\frac{1}{2}\) లీ.
= 210 ÷ 3\(\frac{1}{2}\)
= 210 ÷ \(\frac{7}{2}\)

∴ డ్రమ్ నుంచి నీటిని 60 సార్లు పొందగలడు.

SCERT AP 7th Class Maths Solutions Pdf Chapter 2 భిన్నాలు మరియు దశాంశాలు Review Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 2nd Lesson భిన్నాలు మరియు దశాంశాలు Review Exercise

ప్రశ్న 1.
క్రింది భిన్నాలను గమనించండి మరియు వాటిని పట్టికలోనింపండి. \(\frac{1}{2}, \frac{5}{3}, \frac{11}{9}, \frac{23}{25}, \frac{19}{100}, \frac{99}{70}\).

సాధన.

ప్రశ్న 2.
క్రింది భిన్నాలను ఆరోహణ క్రమంలో రాయండి.
(i) \(\frac{3}{2}, \frac{5}{2}, \frac{1}{2}, \frac{17}{2}, \frac{9}{2}\)
సాధన.
ఆరోహణ క్రమం: \(\frac{1}{2}, \frac{3}{2}, \frac{5}{2}, \frac{9}{2}, \frac{17}{2}\)

(ii) \(\frac{6}{5}, \frac{11}{10}, \frac{19}{5}, \frac{7}{10}, \frac{5}{10}\)
సాధన.
5, 10 ల క.సా.గు = 10

(iii) \(\frac{8}{3}, \frac{7}{6}, 3 \frac{1}{4}, \frac{5}{3}, \frac{11}{4}\)
సాధన.
3, 4, 6ల క.సా.గు = 12

ప్రశ్న 3.
క్రింది వాటిని లెక్కించండి.

(i) \(\frac{3}{5}+\frac{7}{4}\)
సాధన.
\(\frac{3}{5}+\frac{7}{4}\)
= \(\frac{12+35}{20}\) = \(\frac{47}{20}\)

(ii) \(\frac{5}{6}+\frac{7}{12}\)
సాధన.

(iii) 1\(\frac{7}{8}\) – \(\frac{1}{5}\)
సాధన.

(iv) 4\(\frac{1}{2}\) + 3\(\frac{1}{3}\)
సాధన.

ప్రశ్న 4.
క్రింది వాటిని సూక్ష్మీకరించండి.

(i) 3 లో \(\frac{1}{4}\) వ వంతు
సాధన.
3 × \(\frac{1}{4}\) = \(\frac{3}{4}\)

(ii) \(\frac{2}{3}\) లో \(\frac{5}{8}\) వ వంతు
సాధన.

(iii) \(\frac{15}{4}\) × 2\(\frac{1}{7}\)
సాధన.

(iv) 3\(\frac{1}{3}\) × 2\(\frac{2}{5}\)
సాధన.

ప్రశ్న 5.
క్రింది వాటిని లెక్కించండి.
(i) \(\frac{3}{4}\) ÷ 3
సాధన.

(ii) 8 ÷ 2\(\frac{1}{7}\)
సాధన.

(iii) \(\frac{12}{7}\) ÷ \(\frac{2}{7}\)
సాధన.

(iv) 5\(\frac{1}{2}\) ÷ 2\(\frac{9}{11}\)
సాధన.

SCERT AP 7th Class Maths Solutions Pdf Chapter 1 పూర్ణ సంఖ్యలు InText Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 1st Lesson పూర్ణ సంఖ్యలు InText Questions

[పేజి నెం. 6]

ఖాళీలను పూరించుము.

ప్రశ్న 1.
7 × (- 4) = – (7 × 4) = ________
సాధన.
– 28

ప్రశ్న 2.
2 × (- 6) = – (2 × 6) = ________
సాధన.
– 12

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 8]

(i) 4 × (- 8)
సాధన.
4 × (- 8) = – (4 × 8) = – 32

(ii) 5 × (- 20)
సాధన.
5 × (20) = – (5 × 20) = – 100

(iii) 7 × (- 8)
సాధన.
7 × (- 8) = (7 × 8) = – 56

(iv) 10 × (- 9) ల విలువలను కనుక్కోండి.
సాధన.
10 × (- 9) = – (10 × 9) = – 90

[పేజి నెం. 8]

ఖాళీలను పూరించుము.

ప్రశ్న 1.
– 3 × 4 = _______ = 3 × (-4)
సాధన.
– 12

ప్రశ్న 2.
-4 × 4 = ________ = 4 × (4)
సాధన.
– 16

సుందరి

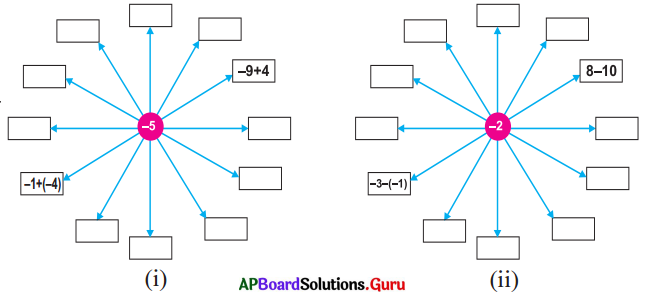
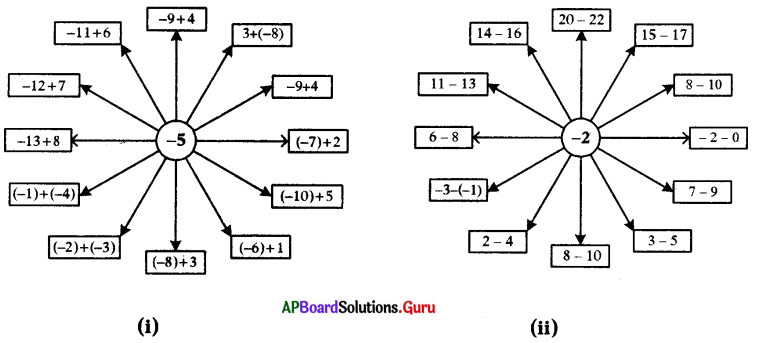
అన్వేషిద్దాం [పేజి నెం. 8]

ప్రశ్న 1.
4 × 5 నుంచి ప్రారంభించి (- 3) ×5 విలువ కనుగొనుటకు అమరికను వ్రాయుము.
సాధన.
4 × 5 = 20
3 × 5 = 15
2 × 5 = 10
1 × 5 = 5
0 × 5 = 0

(- 1) × 5 = -5
(-2) × 5 = – 10
(- 3) × 5 = – 15

ప్రశ్న 2.
5 × 3 నుంచి ప్రారంభించి (-7) × 3 విలువ కనుగొనుటకు అమరికను వ్రాయుము.
సాధన.
5 × 3 = 15
4 × 3 = 12
3 × 3 = 9
2 × 3 = 6
1 × 3 = 3
0 × 3 = 0

(- 1) × 3 = – 3
(- 2) × 3 = – 6
(- 3) × 3 = 9
(- 4) × 3 = – 12
(- 5) × 3 = – 15
(- 6) × 3 = – 18
(- 7) × 3 = – 21

[పేజి నెం: 8]

క్రింది విలువలను కనుగొనుము.
ప్రశ్న 1.
(- 6) × 7 = ________ = (6 × 7) = – 42
సాధన.
6 × (- 7)

ప్రశ్న 2.
(- 2) × 5 = ________ = – (2 × 5) = – 10
సాధన.
2 × (- 5)

ప్రశ్న 3.
(- 3) × 6 = ________ = – (3 × 6) = – 18
సాధన.
3 × (- 6)

ప్రశ్న 4.
(-4) × 5 = ________ = – (4 × 5) = – 20
సాధన.
4 × (- 5)

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 8]

ప్రశ్న 1.
(i) (- 6) × 5
సాధన.
(- 6) × 5 = (6 × 5) = – 30

(ii) (-15) × 2
సాధన.
(- 15) × 2 = -(15 × 2) = – 30

(iii) (-12) × 8
సాధన.
(- 12) × 8 = -(12 × 8) = – 96

(iv) (-10) × 6 ల విలువలను కనుక్కోండి.
సాధన.
(- 10) × 6 = (10 × 6) = – 60

క్రింది విలువలను కనుగొనుము. [పేజి నెం. 8]

ప్రశ్న 1.
(- 2) × (- 4) = _____
సాధన.
8

ప్రశ్న 2.
– 2 × (- 5) = _____
సాధన.
10

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 10]

ప్రశ్న 1.
(- 5) × 3 నుంచి ప్రారంభించి (-5) × (- 4) విలువ కనుగొనుటకు అమరికను వ్రాయుము.
సాధన.
(- 5) × 3 = – 15
(- 5) × 2 = – 10
(- 5) × 1 = – 5
(- 5) × 0 = 0
(- 5) × (- 1) = 5
(- 5) × (- 2) = 10
(- 5) × (- 3) = 15
(- 5) × (- 4) = 20

ప్రశ్న 2.
(- 7) × 5 నుంచి ప్రారంభించి (-7) × (-2) విలువ కనుగొనుటకు అమరికను వ్రాయుము.
సాధన.
(- 7) × 5 = – 35
(- 7) × 4 = – 28
(- 7) × 3 = – 21
(- 7) × 2 = – 14
(- 7) × 1 = – 7
(- 7) × 0 = 0
(- 7) × (- 1) = 7
(- 7) × (- 2) = 14

ఇవి చేయండి కృత్యం [పేజి నెం. 12]

క్రింది పట్టికలో మొదటి నిలువు వరుసలో ప్రతి సంఖ్యను, మొదటి అడ్డు వరుసలోని ప్రతి సంఖ్యతో గుణిస్తూ పట్టికను పూరించుము మరియు ఇవ్వబడిన ప్రశ్నలకు సమాధానాలు ఇవ్వండి.

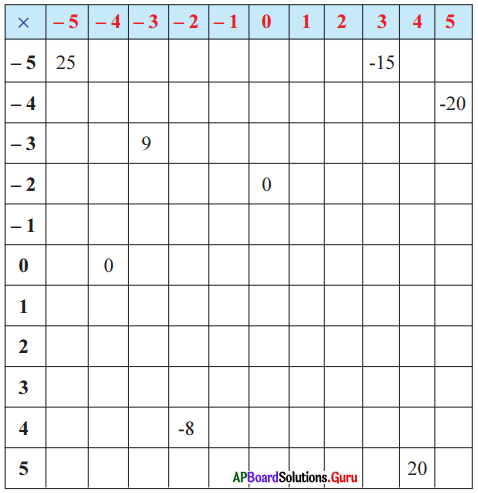
సాధన.

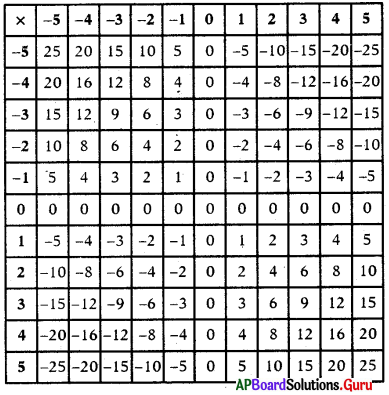
ప్రశ్న 1.
పట్టిక నుండి మీరు ఏమి గమనించారో వ్రాయండి.
సాధన.
పై పట్టిక నుండి గమనించిన అంశాలు :

• రెండు ధన పూర్ణ సంఖ్యల లబ్దం ధనపూర్ణసంఖ్య.
• ఒక ధన పూర్ణ సంఖ్య, ఒక రుణ పూర్ణ సంఖ్యల లబ్దం రుణ పూర్ణ సంఖ్య.
• పూర్ణ సంఖ్య, ‘O’ (సున్న) ల లబ్దము సున్న.
• ఒక పూర్ణ సంఖ్యను 1 చే గుణించిన లబ్దము అదే పూర్ణసంఖ్య అవుతుంది.

ప్రశ్న 2.
పూర్ణసంఖ్యను (-1) చే గుణకారం చేసినపుడు ఏమవుతుంది ?
సాధన.
పూర్ణసంఖ్యను (-1)చే గుణకారము చేసినపుడు ఆ పూర్ణ సంఖ్య యొక్క గుర్తు మారుతుంది.

ప్రశ్న 3.
రెండు పూర్ణసంఖ్యల లబ్ధము సున్నా ఎప్పుడు అవుతుంది ?
సాధన.
రెండు పూర్ణ సంఖ్యలలో ఏదేని ఒక్కటి సున్న అయినపుడు, లేదా ఆ రెండు పూర్ణ సంఖ్యలు సున్నా అయినపుడు ఆ రెండు పూర్ణ సంఖ్యల లబ్ధము సున్న అవుతుంది.

[పేజి నెం. 16]

పూర్ణసంఖ్యల భాగహారము:
క్రింది పట్టికను పరిశీలించి, మిగిలిన ఖాళీలను పూరించండి.

Answer:

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 18]

ప్రశ్న 1.

సాధన.

ఇవి చేయండి కృత్యం [పేజి నెం. 20]

ప్రశ్న 1.
పక్క కొలనులోని చేపలపై కొన్ని సంఖ్యలు ఉన్నవి. ఏవేని 4 జతల సంఖ్యలను ఎన్నుకొని, 4 గుణకార వాక్యాలు రాయుము. తరువాత 4 జతల ఇతర సంఖ్యలను ఎన్నుకొని, 4 భాగహార వాక్యాలు రాయుము.

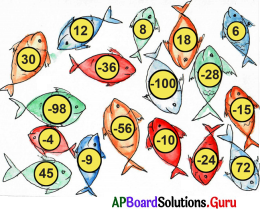
సాధన.
గుణకార వాక్యాలు:

• (-10) × 6 = – 60
• 12 × 8 = 96
• 6 × (-4) = – 24
• (4) × (-9) = 36
• (-56) × (- 10) = 560

భాగహార వాక్యాలు:

• – 36 + 6 = – 6
• 72 + 8 = 9
• (- 24) + 6 = 4
• (- 100) + (- 10) = 10
• 18 + (- 9) = – 2

పజల్ టైమ్ [పేజి నెం. 22]

జశ్వి తన ఇష్టమైన సంఖ్యను ఒక పజిల్ రూపములో చెప్పినది. ఆ సంఖ్యను కనుగొనండి.

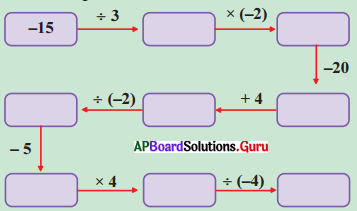
సాధన.

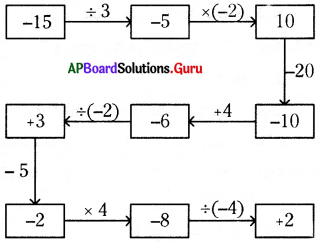
పేజి నెం. 22

(i) సంవృత ధర్మము : కింది పట్టికలను పరిశీలించండి మరియు వాటిని పూరించుము.

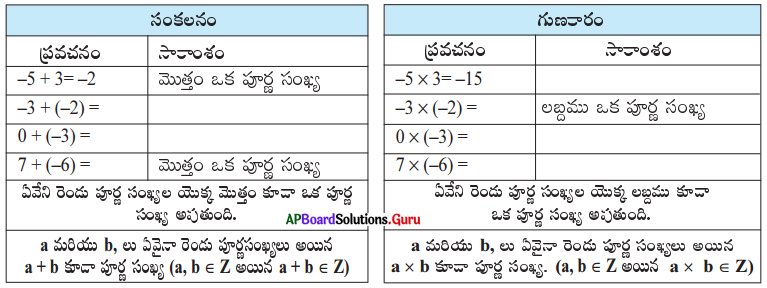
సాధన.

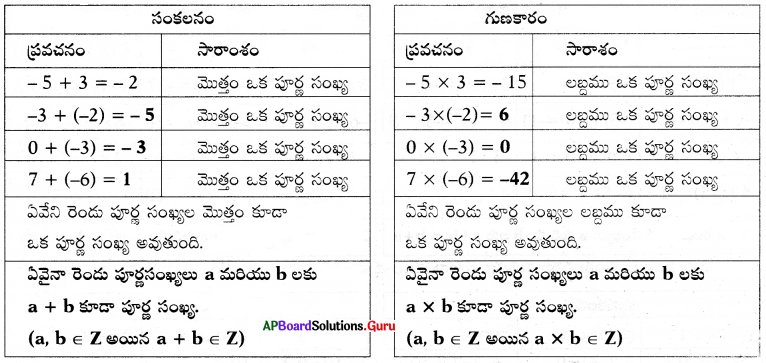
∴ పూర్ణ సంఖ్యలు సంకలనము, గుణకారముల దృష్ట్యా సంవృత ధర్మాన్ని పాటిస్తాయి.

ఆలోచించండి [పేజి నెం. 22]

మొత్తము లేదా లబ్దము పూర్ణ సంఖ్య కాని సంఖ్య అగునట్లు కనీసం ఒక పూర్ణ సంఖ్యల జత చెప్పగలమా ?
సాధన.
మొత్తము లేదా లబ్దము పూర్ణ సంఖ్య కాని సంఖ్య అగునట్లు కనీసం ఒక పూర్ణ సంఖ్యల జత సాధ్యము కాదు.

[పేజి నెం. 24]

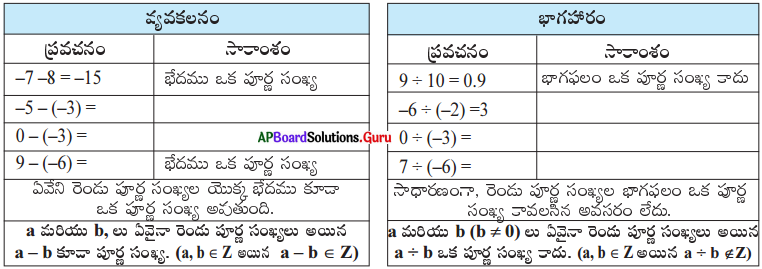
సాధన.

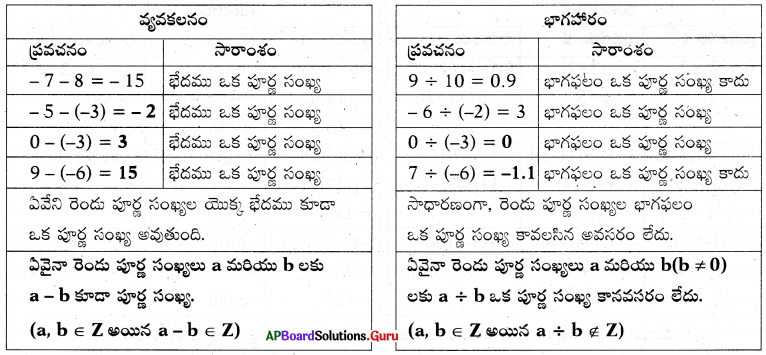
∴ పూర్ణ సంఖ్యలు వ్యవకలనం దృష్ట్యా సంవృత ధర్మాన్ని పాటిస్తాయి. కానీ భాగహారము దృష్ట్యా సంవృత ధర్మాన్ని పాటించనవసరం లేదు.

(ii) వినిమయ (స్థిత్యంతర) న్యాయము: కింది పట్టికలను పరిశీలించండి మరియు వాటిని పూరించుము. సంకలనం

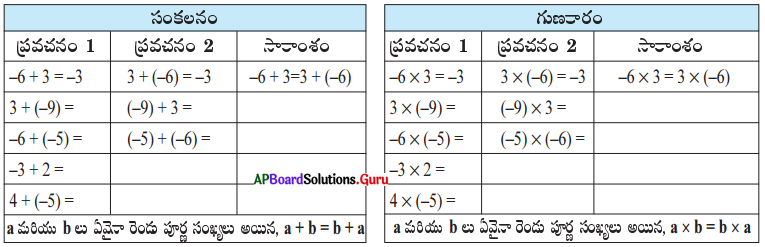
సాధన.

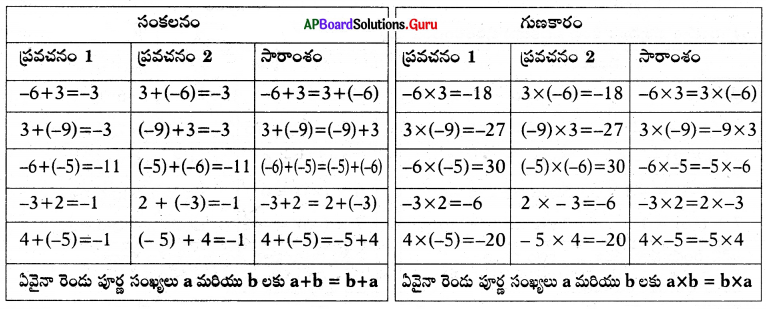
∴ పూర్ణ సంఖ్యలు సంకలనము మరియు గుణకారముల దృష్ట్యా వినిమయ (స్థిత్యంతర) న్యాయమును పాటిస్తాయి.

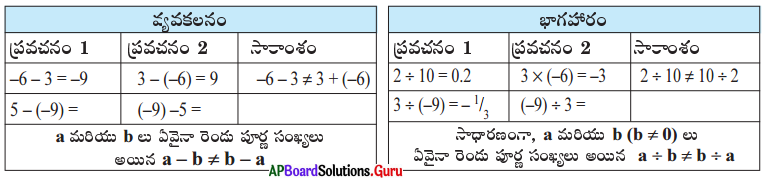
సాధన.

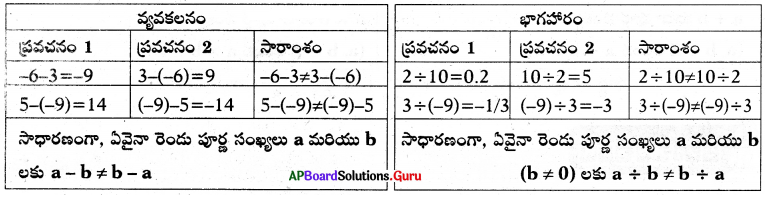
∴ పూర్ణ సంఖ్యలు వ్యవకలనము మరియు భాగహారముల దృష్ట్యా వినిమమ (స్థిత్యంతర) న్యాయమును పాటించవు.

(iii) సహచర న్యాయము: కింది పట్టికలను పరిశీలించండి మరియు వాటిని పూరించుము.

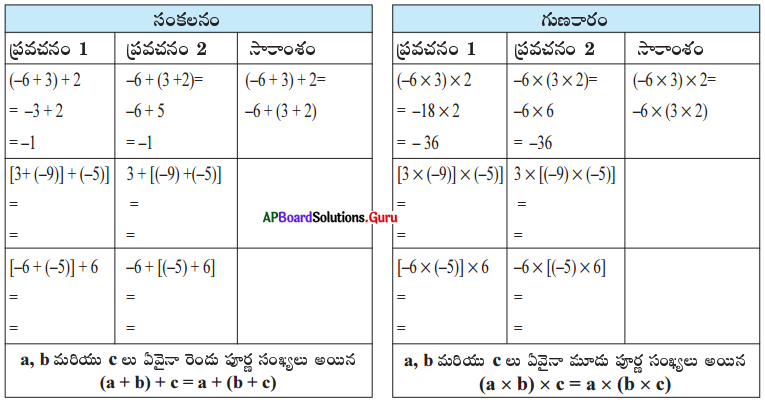
సాధన.

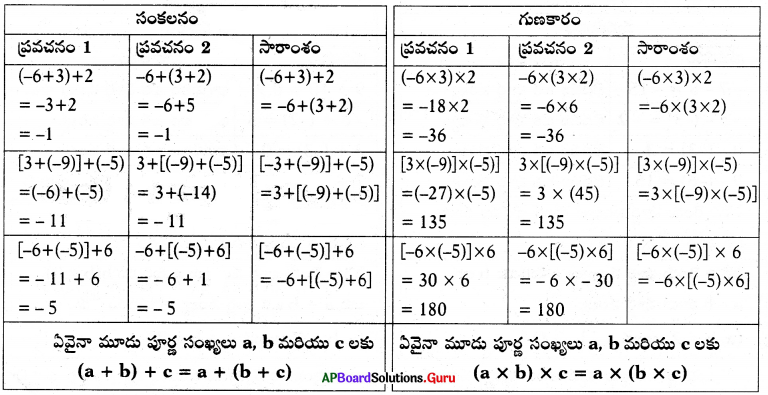
∴ పూర్ణ సంఖ్యలు సంకలనము మరియు గుణకారముల దృష్ట్యా సహచర న్యాయము పాటిస్తాయి.

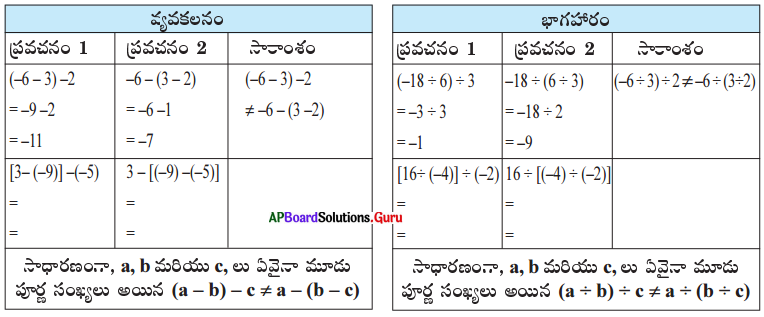
సాధన.

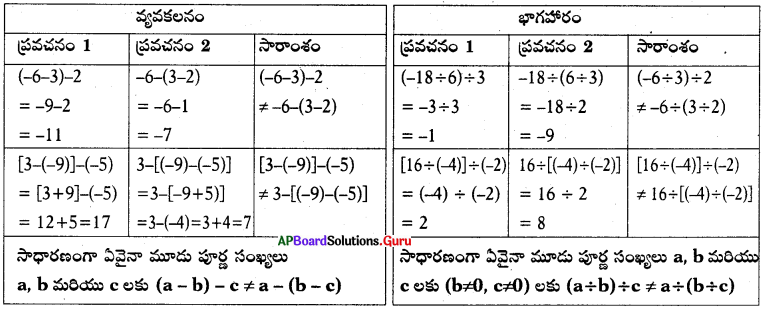
∴ పూర్ణ సంఖ్యలు వ్యవకలనము మరియు భాగహారముల దృష్ట్యా సహచర న్యాయమును పాటించవు.

(iv) తత్సమ ధర్మము: ఈ క్రింది పట్టికలను గమనించి, పూరించండి.

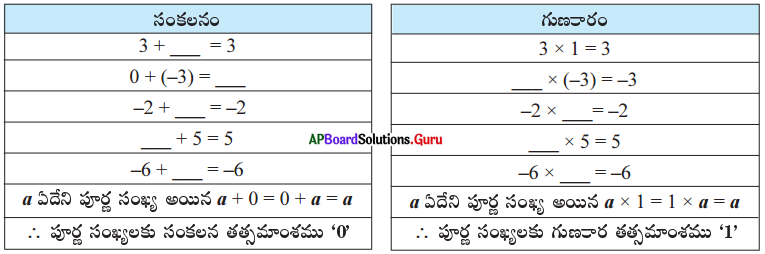
సాధన.

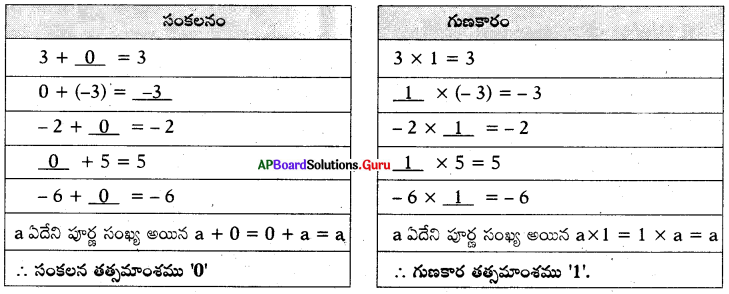
[పేజి నెం. 28]

v. సంకలన విలోమ న్యాయము :
– 3 కు ఎంత కలిపిన సంకలన తత్సమాంశము ‘0’ వచ్చును ?
సాధన.
జ. పరిశీలన :

• 4 + (- 4) = 0
• (- 5) + 5 = 0
• (- 6) + 6 = 0

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 28 ఉదాహరణ]

5, -8, 1, 0 ల సంకలన విలోమాలను వ్రాయుము.
సాధన.
5 యొక్క సంకలన విలోమం = – (5) = – 5
-8 యొక్క సంకలన విలోమం = – (-8) = 8
1 యొక్క సంకలన విలోమము = – (1) = – 1
0 యొక్క సంకలన విలోమము = – (0) = 0

ఆలోచించండి [పేజి నెం. 28]

ప్రశ్న 1.
6ను ఏ సంఖ్యతో గుణించిన గుణకార తత్సమాంశము ‘1’ వస్తుంది ? అది పూర్ణ సంఖ్యలలో వుంటుందా?
సాధన.
6 ను \(\frac{1}{6}\) తో గుణించిన గుణకార తత్సమాంశము 1 వస్తుంది.
6 × \(\frac{1}{6}\) = 1
\(\frac{1}{6}\) పూర్ణ సంఖ్యలలో ఉండదు.

ప్రశ్న 2.
– 3 × [(- 4) – 2] = [(- 3) × (-4)] – [(- 3) × 2)ను సరిచూడుము. పూర్ణసంఖ్యలు వ్యవకలనముపై గుణకారము విభాగ న్యాయమును పాటిస్తాయా ? మీ పరిశీలనలను వ్రాయండి.
సాధన.
– 3 × [(- 4) – 2] = [(- 3) × (- 4)] – [(- 3) × 2]
– 3 × (-6) = 12 — (-6)
18 = 18
ప్రతి సందర్భములోనూ ఎడమచేతి వైపు ఉన్న విలువ, కుడిచేతి వైపు ఉన్న విలువకు సమానము.
కావున, పూర్ణసంఖ్యలు వ్యవకలనముపై గుణకారము విభాగ న్యాయమును పాటిస్తాయి.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 34]

సూక్ష్మీకరించుము:
(i) 5 × 6 – 6
సాధన.
5 × 6 – 6
= 30 – 6
= 24
(BODMAS నియమం ప్రకారం గుణకారం, ఆ తర్వాత వ్యవకలనం)

(ii) 24 ÷ 3 × 3 – 30
సాధన.
24 ÷ 3 × 3 – 30
= 8 × 3 – 30
= 24 – 30
= – 6
(BODMAS నియమం ప్రకారం మొదట భాగహారం, ఆ తరువాత గుణకారం, ఆ తరువాత వ్యవకలనం)

(iii) 5 × 5 – 5 ÷ 5 + 5
సాధన.
5 × 5 – 5 ÷ 5 + 5
= 5 × 5 – 1 + 5
= 25 – 1 + 5
= 30 – 1
(BODMAS నియమం ప్రకారం సూక్ష్మీకరణ క్రమం: భాగహారం, గుణకారం, సంకలనం, వ్యవకలనం)

అన్వేషిద్దాం [పేజి నెం. 38]

|x| = 15 అయిన x యొక్క విలువ ఏమవుతుంది ? చర్చించండి.
సాధన.
|x| = 15 అయిన x = 15 లేదా X = – 15 అవుతుంది.
వివరణ (i): .
ఎందుకనగా, |15| = 15 మరియు |- 15| = 15

వివరణ (ii):
x > 0 అయిన |x| = x
x < 0 అయిన |x| = – x .
|x| = 15 లో
x > 0 అనగా x ధనాత్మకం అయిన x = 15
x < 0 అనగా x రుణాత్మకం అయిన x = – 15

తార్కిక విభాగం

సంఖ్యాశ్రేణులు – 1 [పేజి నెం. 40]

ఒక ప్రత్యేక నియమము లేదా ప్రత్యేక అమరిక ఆధారంగా ఏర్పడిన సంఖ్యల సమాహారమే సంఖ్యా శ్రేణులుగా పరిగణించవచ్చు. ఒక పదమునకు దాని ముందు పదమునకు మధ్య సంబంధం ఏ విధంగా ఉందో, ఆ శ్రేణిలోని అన్ని పదాల మధ్య అదే విధంగా ఉండును. మనం శ్రేణిలోని పదాలు ఏ నియమం ప్రకారం ఏర్పడ్డాయో కనుగొని, ఆ నియమం ఆధారంగా మనకు తెలియని సంఖ్యను కనుగొనాలి. కొన్ని రకాల శ్రేణులు కింద ఇవ్వబడ్డాయి.

1. ప్రధాన సంఖ్యలు శ్రేణి : ,ఇందులో ప్రధాన సంఖ్యలు క్రమంలో ఉండును.
ఉదా (i) : 2, 3, 5, 7, 11, 13, ____.
ఈ శ్రేణిలో వరుస ప్రధాన సంఖ్యలు ఉన్నాయి. 13 తర్వాత వచ్చు ప్రధాన సంఖ్య 17.
కావున, సమాధానము 17.

ఉదా (ii): 2, 5, 11, 17, 23,
ఈ శ్రేణిలో ప్రత్యామ్నాయ (ఒకటి వదిలి మరొకటి) ప్రధాన సంఖ్యలు ఉన్నాయి. 23 తర్వాత వచ్చు ప్రధాన సంఖ్యలు 29, 31. కావున, సమాధానము 31.

2. సంకలన శ్రేణి : ఈ శ్రేణిలో ప్రతి సంఖ్య దాని ముందున్న సంఖ్యకు, ఒక ప్రత్యేక సంఖ్య లేదా శ్రేణిని కలుపగా ఏర్పడును.
ఉదా (i) : 7, 10, 13, 16, 19, 22, ____.
కావున, సమాధానము = 22 + 3 = 25

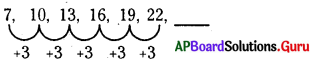
ఉదా (ii): 10, 14, 19, 25, 32, _____.
కావున, సమాధానము = 32 + 8 = 40

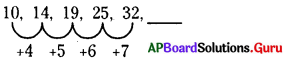
ఉదా (iii) : 5, 7, 10, 15, 22, ______.

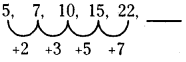
ప్రతి సంఖ్య వరుస ప్రధాన సంఖ్యలను కలుపగా ఏర్పడుచున్నది. కావున, సమాధానము
= 22 + 11 = 33.

3. ఫిబోనాకి శ్రేణి : ఇందులో మూడవ సంఖ్య నుండి ప్రతీ సంఖ్య దాని ముందున్న రెండు సంఖ్యల మొత్తముగా ఉండును.
ఉదా (i) : 3, 5, 8, 13, 21, ______.
ఇక్కడ మూడవ సంఖ్య నుండి,
3 + 5 = 8,
5 + 8 = 13,
8 + 13 = 21,
కావున, సమాధానము = 13 + 21 = 34
ఉదా (ii): 6, 10, 16, 26, 42, ______.
ఇక్కడ మూడవ సంఖ్య నుండి,
6 + 10 = 16,
10 + 16 = 26,
16 + 26 = 42,
కావున, సమాధానము = 26 + 42 = 68

ఉదాహరణలు:

ప్రశ్న 1.
నీటి గుంట(సంప్) పూర్తిగా నీటితో నిండి వుంది. మోటారుతో నీటిని తోడడం వలన నీటి స్థాయి నిముషానికి 2 అంగుళాల చొప్పున తగ్గిన 20 నిముషాల తరువాత నేలమట్టము నుండి నీరు ఎంత లోతులో ఉంటుంది ?
సాధన.
ఒక నిముషములో నీటి మట్టములో మార్పు = -2 అంగుళాలు (2 అంగుళాలు తగ్గినది)
20 నిముషాల తరువాత నీటి మట్టములో మార్పు = 20 × (- 2) = – 40 అంగుళాలు
కావున, నీటి గుంటలో నీరు నేల మట్టము నుండి 40 అంగుళాల లోతులో ఉండును.

ప్రశ్న 2.
భూమి నుంచి 20 మీ. ఎత్తు నుంచి ఒక లిఫ్ట్ ప్రారంభమయింది. అది గని లోపలికి నిముషానికి 6 మీ. చొప్పున కిందికి వెళ్ళిన, 15 నిముషాల తరువాత దాని స్థానము ఏమిటి ?
సాధన.
లిఫ్ట్ కిందికి వెళ్తున్నది కావున అది వెళ్ళే దూరాన్ని ఋణ పూర్ణ సంఖ్యతో సూచిస్తాము.
ఒక నిముషంలో లిఫ్ట్ యొక్క స్థానములో మార్పు = – 6 మీ.
15 నిముషాలలో లిఫ్ట్ యొక్క స్థానములో మార్పు = 15 × (- 6) = – 90 మీ.
కనుక, లిఫ్ట్ యొక్క చివరి స్థానము = 20 + (- 90) = -70 మీ.
∴ లిఫ్ట్ నేల మట్టము నుండి 70 మీ. లోతులో ఉండును.

ప్రశ్న 3.
ఒక పరీక్షలో రాయబడిన సరైన సమాధానానికి (+5) మార్కులు మరియు తప్పు అయిన సమాధానానికి (-3) మార్కులు కేటాయించడం జరిగింది. లక్ష్మి రాసిన సమాధానాలలో 45 సరైనవి మరియు 15 తప్పు అయిన ఆమెకు వచ్చిన మార్కులు ఎన్ని?
సాధన.
ఒక సరైన సమాధానానికి ఇవ్వబడ్డ మార్కులు = 5
45 సరైన సమాధానాలకు మార్కులు = 45 × 5 = 225
ఒక తప్పు సమాధానానికి ఇవ్వబడ్డ మార్కులు = – 3
15 తప్పు సమాధానాలకి ఇవ్వబడ్డ మార్కులు = 15 × (- 3) = – 45
∴ లక్ష్మికి వచ్చిన మార్కులు = 225 + (- 45) = 180

ప్రశ్న 4.
భూ ఉపరితలం నుంచి ఒక బోర్ వెల్ యంత్రం ప్రతి గంటకు 72 అడుగుల లోతును త్రవ్వగలదు. భూ ఉపరితలం నుంచి 360 అడుగుల లోతులో ఉన్న నీటి పొరను చేరుటకు ఆ యంత్రానికి ఎంత సమయం పడుతుంది ?

సాధన.
ఒక గంటలో త్రవ్వు లోతు = – 72 అడుగులు
భూ ఉపరితలము నుండి నీటిపొర గల దూరము = -360 అడుగులు
నీటిని చేరుటకు పట్టు సమయము = -360 ÷ (- 72) = 5
కావున, బోర్‌వెల్ యంత్రం నీటి పొరను చేరుటకు 5 గంటల సమయం పడుతుంది.

ప్రశ్న 5.
ఒక పరీక్షలో, ప్రతి సరైన సమాధానానికి (+ 4) మార్కులు మరియు ప్రతి తప్పు సమాధానానికి (- 2) మార్కులు ఇవ్వబడతాయి. శశి అన్ని ప్రశ్నలకు సమాధానం ఇచ్చాడు మరియు అతను వ్రాసిన 8 సరైన సమాధానాల ద్వారా 26 మార్కులు సాధించాడు. శశి రాసిన తప్పు సమాధానాలు ఎన్ని ?
సాధన.
ఒక్కొక్క సరైన సమాధానానికి మార్కులు = 4
కనుక, 8 సరైన సమాధానాలకు మార్కులు = 4 × 8 = 32
శశికి వచ్చిన మార్కులు = 26
తప్పు సమాధానాలకు ఇవ్వబడిన మార్కులు = 26 – 32 = – 6
ఒక్కొక్క తప్పు సమాధానానికి మార్కులు = – 2
∴ తప్పు సమాధానాల సంఖ్య = (- 6) ÷ (- 2) = 3

ప్రశ్న 6.
దుకాణదారుడు యాసిన్ ఒక సోనా మసూరి బియ్యపు బస్తాపై ₹20 లాభముతో మరియు హంస బియ్యపు బస్తాపై ₹12 నష్టముతో అమ్మాడు. ఒక నెలలో 1440 సోనా మసూరి బియ్యపు బస్తాలు అమ్మిన లాభము కానీ, నష్టము కానీ రాలేదు. అయిన ఆ నెలలో ఎన్ని హంస బియ్యపు బస్తాలు అమ్మాడు ?
సాధన.
ఇచ్చిన సమస్యలో, లాభము కానీ, నష్టము కానీ లేదు.
కావున, వచ్చిన లాభము + వచ్చిన నష్టము = 0
వచ్చిన లాభము = – వచ్చిన నష్టము
ఒక సోనా మసూరి బియ్యపు బస్తాపై వచ్చు లాభము = ₹ 20
1440 సోనా మసూరి బియ్యపు బస్తాలపై వచ్చు లాభము = 1440 × 20 = ₹ 28800
హంస బియ్యపు బస్తాలపై వచ్చు నష్టము = ₹ – 28800
ఒక హంస బియ్యపు బస్తాపై వచ్చు నష్టము = ₹ 12, దీనిని మనం – 12గా సూచిస్తాం.
ఆ నెలలో అమ్మిన హంస బియ్యపు బస్తాల సంఖ్య = (-28800) ÷ (-12) = 2400 బస్తాలు.

ప్రశ్న 7.
(+2) మరియు (-3)ల సంకలన విలోమాలను వ్రాయుము.
సాధన.
+2 సంకలన విలోమము = -(+2) = – 2
-3 సంకలన విలోమము = -(-3) = + 3

ప్రశ్న 8.
క్రింది వాటిని సహచర న్యాయము ఆధారంగా గుణకారము చేయండి.
(i)
– 25 ×(4) × 2 × (-8)
సాధన.
– 25 × (4) × 2 × (- 8)
= [- 25 × (-4)] × 2 × (- 8)
= [100 × 2] × (- 8)
= 200 × (- 8) = – 1600

(ii) (- 20) × (-2) × (- 5) × 1
సాధన.
(- 20) × (- 2) × (- 5) ×7
= (- 20) × [(- 2) × (- 5)] × 7
= [(- 20) × 10] ×7
= – 200 × 7 = – 1400

ప్రశ్న 9.
(-42) × (-7) మరియు (-7) × (-42) లు సమానమా ? ఇది ఏ న్యాయము ?
సాధన.
(- 42) × (-7) = + 294
(- 7) × (42) = + 294
∴ (- 42) × (- 7) = (- 7) × (42)
ఇది గుణకార వినిమయ (స్థిత్యంతర) న్యాయము.

ప్రశ్న 10.
26 × (- 48) + (- 48) × (- 36) ను తగిన న్యాయాలను ఉపయోగించి సూక్ష్మీకరించుము.
సాధన.
26 × (-48) + (- 48) × (- 36)
= (- 48) × 26 + (- 48) × (- 36) (వినిమయ న్యాయము)
= (- 48) × [26 + (- 36)] (విభాగ న్యాయము)
= (48) × (- 10) = 480

ప్రశ్న 11.
3 × 2 + 8 ÷ 4 సూక్ష్మీకరించుము.
సాధన.
3 × 2 + 8 ÷ 4 (భాగహారము)
= 3 × 2 + 2 (గుణకారము)
= 6 + 2 (సంకలనము)
= 8

ప్రశ్న 12.
1 × 6 – \(\overline{8-4}\) సూక్ష్మీకరించుము.
సాధన.
7 × 6 – \(\overline{8-4}\) (విన్కులం)
= 7 × 6 – 4 (గుణకారము)
= 42 – 4 (వ్యవకలనము)

ప్రశ్న 13.
18 + 64 – 4 {26 – (14 – \(\overline{7-3}\)} సూక్ష్మీకరించుము.
సాధన.
18 + 64 -4 {26 – (14 – \(\overline{7-3}\))} (విన్కులం)
= 18 + 64 ÷ 4 {26 – (14 – 4)} (సాధారణ బ్రాకెట్)
= 18 + 64 ÷ 4 {26 – 10} (కర్లీ బ్రాకెట్)
= 18 + 64 ÷ 4 {16} (ఆఫ్)
= 18 + 64 ÷ 64 (భాగహారము)
= 18 ÷ 1 (సంకలనము)
= 19

సాధనా ప్రశ్నలు [పేజి నెం. 42]

ప్రశ్న 1.
12, 19, 26, 33, 40, 47, ______
(a) 57
(b) 54
(c) 52
(d) 50
సాధన.
(b) 54

వివరణ:

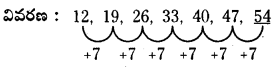
ప్రశ్న 2.
2, 13, 24, 35, 46, 57, _____
(a) 65
(b) 67
(c) 68
(d) 72
సాధన.
(c) 68

వివరణ:

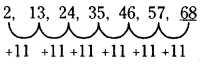
ప్రశ్న 3.
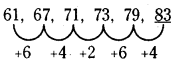
61, 67, 71, 73, 79, ______
(a) 89
(b) 87
(c) 85
(d) 83
సాధన.
(d) 83

వివరణ:

ప్రశ్న 4.
3, 7, 13, 21, 31,
(a) 43
(b) 48
(c) 51
(d) 53
సాధన.
(a) 43

వివరణ:

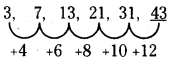
ప్రశ్న 5.
8, 12, 20, 32, 52, 84, _______
(a) 111
(b) 126
(c) 136
(d) 174
సాధన.
(c) 136

వివరణ: 8, 12, 20, 32, 52, 84, 136 (ఫిబోనాకి శ్రేణ)
8 + 12 = 20
12 + 20 = 32
20 + 32 = 52
32 + 52 = 84
52 + 84 = 136

ప్రశ్న 6.
23, 28, 38, 53, 73, 98, __
(a) 121
(b) 128
(c) 135
(d) 146
సాధన.
(b) 128

వివరణ:

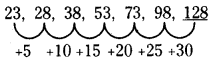
ప్రశ్న 7.
101, 97, 89, 83, 79, 73, 71, _____
(a) 61
(b) 65
(c) 66
(d) 67
సాధన.
(d) 67

వివరణ: వరుస ప్రధాన సంఖ్యలు.
71 కి వెంటనే ముందున్న ప్రధాన సంఖ్య = 67

ప్రశ్న 8.
4, 7, 11, 18, 29, 47, __
(a) 67
(b) 76
(c) 84
(d) 92
సాధన.
(b) 76

వివరణ: ఫిబోనాకి శ్రేణి
4 + 7 = 11,
7 + 11 = 18,
11 + 18 = 29,
18 + 29 = 47,
29 + 47 = 76
4, 7, 11, 18, 29, 47, 76

ప్రశ్న 9.
76, 187, 298, 409, 520, ______
(a) 631
(b) 656
(c) 701
(d) 724
సాధన.
(a) 631

వివరణ: 61, 67, 71, 73, 79, 83

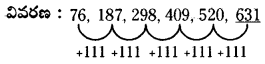
ప్రశ్న 10.
0, 2, 5, 10, 17, 28, 41, ______
(a) 50
(b) 53
(c) 57
(d) 58
సాధన.
(d) 58

వివరణ:

ప్రశ్న 11.
36, 45, 53, 60, 66, 71, ____
(a) 84
(b) 78
(c) 75
(d) 73
సాధన.
(c) 75

వివరణ:

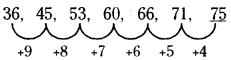
ప్రశ్న 12.
0, 15, 45, 90, 150, 225, _____
(a) 295
(b) 300
(c) 315
(d) 360
సాధన.
(c) 315

వివరణ:

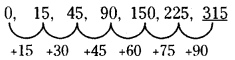
15, 30, 45, 60, 75 లు 15 గుణిజాలు.
కావున, 75 తరువాత గల 15 గుణిజము 90.

ప్రశ్న 13.
18, 23, 25, 30, 32, 37, _____ .
(a) 43
(b) 41
(c) 39
(d) 38
సాధన.
(c) 39

వివరణ:

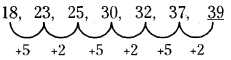
ప్రశ్న 14.
4, 7, 11, 18, 29, 47, ______
(a) 71
(b) 76
(c) 77
(d) 82
సాధన.
(b) 76

వివరణ: ఫిబోనాకి శ్రేణి
4 + 7 = 11,
7 + 11 = 18,
11 + 18 = 29,
18 + 29 = 47,
∴ 29 + 47 = 76
4, 7, 11, 18, 29, 47, 76

ప్రశ్న 15.
12, 18, 21, 27, 30, 36, 39, _____
(a) 43
(b) 45
(c) 49
(d) 52
సాధన.
(b) 45

వివరణ:

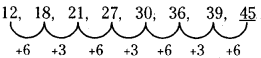
SCERT AP 7th Class Maths Solutions Pdf Chapter 1 పూర్ణ సంఖ్యలు Unit Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 1st Lesson పూర్ణ సంఖ్యలు Unit Exercise

ప్రశ్న 1.
క్రింది వాటిని లెక్కించుము. సాధన.
(i) 8 × (- 1)
సాధన.
8 × (-1)
a × (-b) = – (a × b) అని మనకు తెలుసు.
= – (8 × 1) = – 8

(ii) (- 2) × 175
సాధన.
(- 2) × 175
(- a) × b = – (a × b) అని మనకు తెలుసు.
= – (2 × 175)
= – 350

(iii) (- 3) × (- 40)
సాధన.
(- 3) × (40)
(- a) × (- b) = (a × b) అని మనకు తెలుసు.
= (- 3) × (40)
= 3 × 40 = 120

(iv) (- 24) × (- 7)
సాధన.
(- 24) × (27)
(- a) × (- b) = (a × b) అని మనకు తెలుసు.
= 24 × 7 = 168

(v) (- 7) ÷ (- 1)
సాధన.
(- 7) ÷ (- 1)
(- a) ÷ (-b) = a ÷ b అని మనకు తెలుసు.
= (- 7) ÷ (- 1) = 7 ÷ 1 = 7

(vi) (- 12) ÷ (+ 6)
సాధన.
(- 12) ÷ (+ 6)
(- a) ÷ b = – (a ÷ b) అని మనకు తెలుసు.
= (- 12) ÷ 6 = – 2

(vii) (- 49) ÷ (-7)
సాధన.
(49) ÷ (-7)
(- a) ÷ (- b) = a ÷ b అని మనకు తెలుసు.
= (- 49) ÷ (- 7) = 49 ÷ 7 = 7

(viii) (+ 63) ÷ (- 9)
సాధన.
(+ 63) ÷ (- 9)
a ÷ (- b) = – (a ÷ b) అని మనకు తెలుసు.
= 63 ÷ (- 9) = – (63 ÷ 9) = – 7

ప్రశ్న 2.
క్రింది వాక్యాలు సత్యమయ్యే విధముగా ఖాళీలను పూర్ణసంఖ్యలతో భర్తీ చేయుము.
(i) (- 7) × _____ = 21
సాధన.
(- 7) × x = 21
x = 21 ÷ (-7)
a ÷ (- b) = – (a ÷ b) అని మనకు తెలుసు.
x = – (21 ÷ 7)
∴ x = – 3

(ii) 7 x _______= – 42
సాధన.
7 × x = 42
x = (- 42) ÷ 7.
(- a) ÷ b = – (a ÷ b) అని మనకు తెలుసు.
x = – (42 ÷ 7)
∴ x = – 6

(iii) _______ × (9) = – 72
సాధన.
x × (- 9) = – 72
x = (- 72) ÷ (- 9)
(- a) ÷ (-b) = (a ÷ b) అని మనకు తెలుసు.
x = (72 ÷ 9)
∴ x = 8

(iv) _______ × (- 11) = 132
సాధన.
x × (- 11) = 132
x = 132 ÷ (- 11)
a ÷ (-b) = – (a ÷ b) అని మనకు తెలుసు.
x = – (132 ÷ 11)
∴ x = – 12

(v) (- 25) ÷ ______ = 1.
సాధన.
(- 25) ÷ x = 1 .
x = (- 25) ÷ 1
(- a) ÷ b = – (a ÷ b) అని మనకు తెలుసు.
x = (- 25 ÷ 1)
∴ x = – 25

(vi) 42 ÷ ____ = – 6
సాధన.
42 ÷ x = – 6
42 = (- 6) × x
x = 42 ÷ (- 6)
a ÷ (- b) = – (a ÷ b) అని మనకు తెలుసు.
x = – (42 ÷ 6)
∴ x = – 7

(vii) __ ÷ (- 15) = 6
సాధన.
x ÷ (- 15) = 6 .. x = -3
x = 6 × (- 15)
a × (-b) = – (a × b) అని మనకు తెలుసు.
x = – (6 × 15)
∴ x = – 90

(viii) _____ ÷ (- 9) = 16
సాధన.
_x_ + (-9) = 16
x = 16 × (9)
a × (-b) = – (a × b) అని మనకు తెలుసు.
x = – (16 × 9)
∴ x = – 144

ప్రశ్న 3.
లబ్దము – 50 అయ్యే విధముగా వీలైనన్ని పూర్ణ సంఖ్యల జతలు వ్రాయండి.
సాధన.

ప్రశ్న 4.
పండ్ల వ్యాపారి శంకర్, 100 కి.గ్రా. కమలా పండ్లు మరియు 75 కి.గ్రా. దానిమ్మ పండ్లు అమ్మాడు. అతను ఒక కి.గ్రా. దానిమ్మ పండ్లపై ₹ 11 లాభాన్ని, ఒక కి.గ్రా. కమలా పండ్లపై ₹8 నష్టాన్ని పొందిన మొత్తము మీద అతనికి ఎంత లాభము లేదా నష్టము ?

సాధన.
పండ్ల వ్యాపారికి దానిమ్మ పండ్లపై కి.గ్రా. కు లాభం = ₹11
కావున, 75 కి.గ్రా. దానిమ్మ పండ్ల అమ్మకంపై లాభము = 75 × 11 = ₹ 825
కమలాపండ్లు అమ్మకంపై కి.గ్రా. కు నష్టం = – ₹8
100 కి.గ్రా. కమలాపండ్ల అమ్మకంపై నష్టం = 100 × (- 8) = – ₹800
వ్యాపారికి లాభం లేదా నష్టం = ₹825 + (- ₹800) = ₹ 25
∴ ₹25 ధన సంఖ్య కావున వ్యాపారికి ₹ 25 లాభం వస్తుంది.

ప్రశ్న 5.
భార్గవి జూన్ నెలలో యోగా ద్వా రా 5700 కేలరీలను తగ్గించుకొంది. కేలరీల తగ్గుదల స్థిరంగా వున్న, ఆ నెలలో రోజువారి సరాసరి కేలరీల తగ్గుదల ఎంత?

సాధన.
భార్గవి జూన్ నెలలో యోగా ద్వారా తగ్గిన కేలరీలు = – 5700
జూన్ నెలలోని రోజుల సంఖ్య = 30
జూన్ నెలలో రోజువారి సరాసరి కేలరీల తగ్గుదల
= (- 5700) ÷ 30

∴ సరాసరి కేలరీల తగ్గుదల = 190

ప్రశ్న 6.
625 × (- 35) + 625 × 30 ను తగిన న్యాయాలను ఉపయోగించి సూక్ష్మీకరించుము.
సాధన.
625 × (- 35) + 625 × 30
= 625 × [[- 35) + 30]
(సంకలనంపై గుణకార విభాగ న్యాయము)
= 625 × (- 5)
= – 3125

ప్రశ్న 7.
BODMAS ను ఉపయోగించి సూక్ష్మీకరించుము.
(i) 12 – 36 ÷ 3
సాధన. 1
2 – 36 ÷3 (భాగహారం)
= 12 – 12 (వ్యవకలనం)
= 0

(ii) 6 × (- 7) + (- 3) ÷ 3
సాధన.
6 × (- 7) + (-3) ÷ 3
= 6 × (- 7) + (- 1) (భాగహారం)
= (42) + (- 1) (గుణకారం)
= – 43 (సంకలనం)

(iii) 38 – {35 – (36 – \(\overline{34-37}\))}
సాధన.
38 – {35 – (36 – \(\overline{34-37}\)) }
= 38 – {35 – (36 + 3)} (విన్కులం)
= 38 – {35 – 39} (సాధారణ బ్రాకెట్)
= 38 + 4 (కర్లీ బ్రాకెట్)
= 42 (సంకలనం)

ప్రశ్న 8.
కింది సంఖ్యలకు పరమ మూల్య విలువను వ్రాయండి.
(i) – 700
సాధన.
|- 700| = 700

(ii) 150
సాధన.
|150| = 150

(iii) – 150
సాధన.
|- 150| = 150

(iv) – 35
సాధన.
|- 35| = 35

(v) p< 10 అయిన |p – 10|
సాధన.
p < 10 అయిన |p – 10|
= – (p – 10) = 10 – p

(vi) y > 7 అయిన |7 – y|
సాధన.
y > 7 అయిన |7 – y|
= – (7 – y) = y – 7
(y > 7 అయిన 7 – y < 0)

SCERT AP 7th Class Maths Solutions Pdf Chapter 1 పూర్ణ సంఖ్యలు Ex 1.4 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 1st Lesson పూర్ణ సంఖ్యలు Exercise 1.4

ప్రశ్న 1.
కింది వాటిని సూక్ష్మీకరించుము.
(i) 6 × 9 – 6 ÷ 3
సాధన.
6 × 9 – 6 ÷ 3
= 6 × 9 – 2 (భాగహారం)
= 54 – 2 (గుణకారం)
= 52 (వ్యవకలనం)

(ii) 12 ÷ 4 – 8 + 5
సాధన.
12 ÷ 4 – 8 + 5
= 3 – 8 + 5 (భాగహారం)
= 8 – 8 (సంకలనం)
= 0 (వ్యవకలనం)

(iii) 80 – 56 ÷ 8 × 9
సాధన.
80 – 56 ÷ 8 × 9
= 80 – 7 × 9 (భాగహారం)
= 80 – 63 (గుణకారం)
= 17 (వ్యవకలనం)

(iv) 15 ÷ 5 + 17 – 30
సాధన.
15 ÷ 5 + 17 – 30
= 3 + 17 – 30 (భాగహారం )
= 20 – 30 (సంకలనం)
= – 10 (వ్యవకలనం)

(v) 8 + 8 – 8 × 8 ÷ 8
సాధన.
8 + 8 – 8 × 8 ÷ 8
= 8 + 8 – 8 × 1 (భాగహారం )
= 8 + 8 – 8 (గుణకారం)
= 16 – 8 (సంకలనం)
= 8 (వ్యవకలనం)

ప్రశ్న 2.
కింది వాటిని సూక్ష్మీకరించుము.
i) 8 × 3 – \(\overline{13-7}\)
సాధన.
8 × 3 – \(\overline{13-7}\)
= 8 × 3 – 6 (విన్కులం)
= 24 – 6 (గుణకారం)
= 18 (వ్యవకలనం)

(ii) {12 – \(\overline{14-8}\) + 7} – 15
సాధన.
{12 – \(\overline{14-8}\) + 7} – 15
= {12 – 6+7} – 15 (విన్కులం)
= {19 – 6} – 15 (కర్లీ బ్రాకెట్లో సంకలనం)
= 13 – 15 (కర్లీ బ్రాకెట్ లో వ్యవకలనం)
= – 2 (వ్యవకలనం)

(iii) 16 – (4 + 18 ÷ 6 – \(\overline{7-5}\)) × 5
సాధన.
16 – (4 + 18 ÷ 6 – \(\overline{7-5}\)) × 5
= 16 – (4 + 18 ÷ 6 – 2) × 5(విన్కులం)
= 16 – (4 + 3 – 2) × 5 (భాగహారం)
= 16 – (7 – 2) × 5
= 16 – 5 × 5 (సాధారణ బ్రాకెట్)
= 16 – 25 (గుణకారం)
= – 9 (వ్యవకలనం)

(iv) {6 of 145 ÷ (3 + 2)} ÷ 2 – 4 of 20
సాధన.
{6 of 145 ÷ (3 + 2)} ÷ 2 – 4 of 20
= {6 of 145 ÷ 5} + 2 – 4 of 20 (సాధారణ బ్రాకెట్)
= {870 ÷ 5} ÷ 2 – 4 of 20 (ఆఫ్)
= 174 ÷ 2 – 4 of 20 (కర్లీ బ్రాకెట్)
= 174 + 2 – 80 (ఆఫ్)
= 87- 80 (భాగహారం)
= 7 (వ్యవకలనం)

(v) 25 + [14 – 18+ {12 of 5 -( 4 + 14)}]
సాధన.
25 + [14 – 18 + {12 of 5 -(-4 + 14)}]
= 25 + [14 – 18 + {12 of 5 – 10}] (సాధారణ బ్రాకెట్)
= 25 + [14 – 18 + {60 – 10}] (ఆఫ్ )
= 25 + [14 – 18 + 50] (కర్లీ బ్రాకెట్)
= 25 + [64 – 18]
= 25 + 46 (చతురస్ర బ్రాకెట్)
= 71 (సంకలనం)

ప్రశ్న 3.
కింది వాటిలో సత్య వాక్యాలను గుర్తించుము.
(i) 48 ÷ 6 – 4 = 24
సాధన.
48 ÷ 6 – 4 = 24
8 – 4 = 24 (భాగహారం)
4 ≠ 24 (వ్యవకలనం)
∴ అసత్యం

(ii) – 18 + 12 ÷ 3 = – 14
సాధన.
– 18 + 12 ÷ 3 = – 14
– 18 + 4 = – 14 (భాగహారం)
– 14 = – 14 (వ్యవకలనం)
∴ సత్యం

(iii) -11 + 3 ×7 = – 56
సాధన.
– 11 + 3 × 7 = – 56
-11 + 21 = – 56 (గుణకారం)
10 ≠ – 56 (వ్యవకలనం)
∴ అసత్యం

(iv) 2020 – 20 – 100 = 1
సాధన.
2020 + 20 – 100 = 1 (భాగహారం)
101 – 100 = 1 (వ్యవకలనం)
1 = 1
∴ సత్యం

ప్రశ్న 4.
కింది వాక్యాలు సత్యమయ్యే విధముగా ఖాళీలను +, -, ×, ÷ లతో పూరించుము.
(i) 9 __ 3 __ 6 = – 3
సాధన.
9 ÷ 3 – 6 = – 3

(ii) – 6 __ 12 __ 6 = – 4
సాధన.
– 6 + 12 ÷ 6 = -4

(iii) – 15 __ 3 __ 6 = – 30
సాధన.
– 15 ÷ 3 × 6 = – 30

SCERT AP 7th Class Maths Solutions Pdf Chapter 1 పూర్ణ సంఖ్యలు Ex 1.3 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 1st Lesson పూర్ణ సంఖ్యలు Exercise 1.3

ప్రశ్న 1.
కింది వాటిలో ఉన్న ధర్మాలను గుర్తించి రాయండి. విభాగ న్యాయమును పాటిస్తాయి.
(i) – 3 + 5 = 5 + (- 3)
సాధన.
– 3 + 5 = 5 + (- 3) సంకలన వినిమయ (స్థిత్యంతర) ధర్మము.

(ii) – 2 × 1 = 1 × (- 2) = – 2
సాధన.
(- 2) × 1 = 1 × (- 2) = – 2 గుణకార తత్సమ ధర్మము.

(iii) [[- 5) × 2] × 3 = (- 5) × [[2 × 3)]
సాధన.
[(- 5) × 2] × 3 = (- 5) × [(2 × 3)] గుణకార సహచర న్యాయము

(iv) 18 × [7 + (- 3)] = [18 × 7] + [18 × (-3)]
సాధన.
18 × [7 + (- 3)] = [18 × 7] + [18 × (- 3)] సంకలనం పై గుణకార విభాగ న్యాయము

(v) – 5 × 6 = – 30
సాధన.
(- 5) × 6 = – 30 గుణకార సంవృత ధర్మము

(vi) – 3 + 0 = 0 + (-3) = – 3
సాధన.
-3 + 0 = 0 + (-3) = – 3 సంకలన తత్సమ ధర్మము

ప్రశ్న 2.
కింది సందర్భాలలో లబ్దము యొక్క సంజ్ఞ (గుర్తు)ను రాయండి.
(i) ఋణ పూర్ణ సంఖ్యకు 24 రెట్లు
సాధన.
(- 1) × (- 1) ×…………… 24 రెట్లు = + 1 (ధనాత్మకం)

(ii) ఋణ పూర్ణ సంఖ్యకు 35 రెట్లు
సాధన.
(- 1) × (- 1) × ………………. 35 రెట్లు = – 1 (ఋణాత్మకం)

ప్రశ్న 3.
కింది ఖాళీల నందు సరైన పూర్ణ సంఖ్యలను తగిన న్యాయాల ఆధారంగా పూరించుము.
(i) – 3 + ________ = – 3.
సాధన.
– 3 + 0 = – 3

(ii) 2 × (- 3) = (- 3) × ________
సాధన.
2 × (- 3) = (- 3) × 2

(iii) – 6 + [3 + (- 2)] = [[- 6) + ________] + ________
సాధన.
– 6 + [3 + (-2)] = [(- 6) + 3 ] + (- 2)

(iv) – 6 × ________ = – 6
సాధన.
– 6 × 1 = – 6

(v) 5 × [[- 6) + 9] = ________ × (-6) + 5 × ________
సాధన.
5 × [(- 6) + 9] = 5 × (- 6) + 5 × 9

ప్రశ్న 4.
కింది వాక్యాలు సత్యమా ? అసత్యమా ? తెల్పండి. కారణాలు వ్రాయండి.
(i) 2 యొక్క గుణకార తత్సమాంశము – 2.
సాధన.
అసత్యం. 2 యొక్క గుణకార తత్సమాంశం \(\frac{1}{2}\).

(ii) పూర్ణ సంఖ్యలు వ్యవకలనము దృష్ట్యా వినిమయ న్యాయము పాటిస్తాయి.
సాధన.
అసత్యం . (-5) – 3 ≠ 3 – (-5)

(iii) a మరియు bలు ఏవైనా రెండు పూర్ణ సంఖ్యలు అయిన a × b = b × a.
సాధన.
సత్యం .
4 × (-5) = (- 5) × 4 .
-(4 × 5) = – (5 × 4)
– 20 = -20
పూర్ణ సంఖ్యలు గుణకార వినిమయ ధర్మాన్ని పాటిస్తాయి.

(iv) సున్నాతో పూర్ణసంఖ్యల భాగహారము నిర్వచించబడదు.
సాధన.
సత్యం
6 ÷ 0 (సాధ్యం కాదు)

(v) 6 + (-6) = (-6) + 6 = 0 అనునది సంకలన తత్సమ ధర్మమును సూచించును.
సాధన.
అసత్యం.
6 + (-6) = (-6) + 6 = 0 అనునది సంకలన విలోమ ధర్మము.

ప్రశ్న 5.
కింది వాటిని తగిన న్యాయాలనుపయోగించి సూక్ష్మీ కరించుము.
(i) – 11 × ( 25) × (- 4)
సాధన.
– 11 × (- 25) × (4)
a × (b × c)
= (- 11) × [[- 25) × (- 4)]
= (- 11) × (25 × 4)
= – 11 × 100
= – (11 × 100)
= – 1100

(ii) 3× (- 18) + 3 × (- 32)
సాధన.
3 × (- 18) + 3 × (- 32)
(a × b) + (a × c) = a × (b + c)
= 3 × [[- 18) + (- 32)]
= 3 × (- 18 – 32)
= 3 × (- 50)
= – (3 × 50)
= – 150

ప్రశ్న 6.
పూర్ణ సంఖ్యలు వ్యవకలనము దృష్ట్యా సహచర న్యాయమును పాటిస్తాయా ? ఉదాహరణ ద్వారా వివరించుము.
సాధన.
పాటించవు.
మూడు పూర్ణసంఖ్యలు a = 2, b = -3, c = 5 అనుకొందాం.
(i) (a – b) – c = [2 – (-3)] – (5)
= (2 + 3) – 5 = 5 – 5 = 0

(ii), a – (b – c) = 2 – [[-3) – (5)] = 2 – [- 3 – 5]
= 2 – (- 8) = 2 + 8 = 10
(a – b) – c ≠ a – (b – c)
∴ [2 – (-3)] – (5) ≠ 2 – [[-3) – (5)]
కావున, పూర్ణసంఖ్యలు వ్యవకలనం దృష్ట్యా సహచర న్యాయమును పాటించవు.

ప్రశ్న 7.
[(-5) × 2] × 3 = (-5) × [[2 × 3)] సరిచూడుము.
సాధన.
[(-5) × 2)] × 3 = (-5) × [(2 × 3)]
(a× b) × c = a × (b × c)
(- 10) × 3 = (-5) × 6
– 30 = – 30
∴ పూర్ణసంఖ్యలు గుణకారము దృష్ట్యా సహచర న్యాయమును పాటిస్తాయి.

SCERT AP 7th Class Maths Solutions Pdf Chapter 1 పూర్ణ సంఖ్యలు Ex 1.2 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 1st Lesson పూర్ణ సంఖ్యలు Exercise 1.2

ప్రశ్న 1.
క్రింది వాటిని లెక్కించండి.
(i) (- 96) ÷ 16
సాధన.
(-96) ÷ 16 = – 6

(ii) 98 ÷ (- 49)
సాధన.
98 ÷ (- 49) = – 2

(iii) (- 51) ÷ 17.
సాధన.
(- 51) ÷ 17 = – 3

(iv) 38 ÷ (- 19)
సాధన.
38 ÷ (- 19) = – 2

(v) (- 80) ÷ 20
సాధన.
(- 80) ÷ 20 = – 4.

(vi) (- 150) ÷ (- 25)
సాధన.
(- 150) ÷ (- 25) = 6

(vii) (- 600) ÷ 60
సాధన.
(- 600) ÷ 60 = – 10

(viii) (- 54) ÷9
సాధన.
(- 54) ÷ 9 = – 6

(ix) 130 ÷ 65
సాధన.
130 ÷ 65 = 2

(x) (- 315) ÷ (- 315)
సాధన.
(- 315) ÷ (- 315) = 1

ప్రశ్న 2.
రెండు పూర్ణ సంఖ్యల లబ్దము – 165. అందులో ఒక సంఖ్య -15 అయిన రెండవ సంఖ్య కనుగొనుము.
సాధన.
రెండు పూర్ణ సంఖ్యల లబ్దము = -165
అందులో ఒక సంఖ్య = -15
రెండవ సంఖ్య = (-165) + (-15)

∴ రెండవ సంఖ్య = 11

ప్రశ్న 3.
2020 సం||లో కోవిడ్-19 వలన ఒక కంపెనీ 6 నెలలు లాక్ డౌన్ లో వుండినది మరియు ₹ 1,32,000 నష్టపోయినది. నెలసరి సరాసరి నష్టమును కనుగొనుము.

సాధన.
6 నెలల లాక్ డౌన్ సమయంలో వచ్చిన నష్టము = ₹(- 1,32,000)
నెలసరి సరాసరి నష్టము = – 1,32,000 ÷ 6
= \(\frac{-1,32,000}{6}\) = ₹ – 22,000
∴ ప్రతినెల సరాసరి ₹ 22,000 నష్టం వచ్చినది.

ప్రశ్న 4.
మధ్యాహ్నం 12 గంటలకు ఉష్ణోగ్రత 0° పైన 10°C అని గుర్తించబడినది. ఉష్ణోగ్రత ప్రతి గంటకు 2°C చొప్పున అర్ధరాత్రి వరకు తగ్గుతుంది. ఏ సమయానికి 0° కన్నా 8°C తక్కువగా ఉంటుంది ? అర్ధరాత్రి ఉష్ణోగ్రత ఎంత ?
సాధన.
మధ్యాహ్నం 12 గంటలకు ఉష్ణోగ్రత = + 10°C
ప్రతి గంటకు తగ్గుతున్న ఉష్ణోగ్రత = – 2°C
0° కన్నా 8°C తక్కువగా ఉండుటకు (- 8°C) అవుటకు తగ్గవలసిన ఉష్ణోగ్రత = (-8) – (10) = – 18°C
– 18°C ఉష్ణోగ్రత తగ్గుటకు పట్టుకాలము = -18 + (-2) = 9 గంటలు
∴ రాత్రి 9 గంటలకు 0° కన్నా 8°C తక్కువగా ఉంటుంది.
∴ అర్ధరాత్రి ఉష్ణోగ్రత = (- 8°C) + (- 2°C × 3 గంటలు) = (- 8°C + – 6°C) = – 14°C

ప్రశ్న 5.
ఒక కూరగాయల వ్యాపారి ఒక కి.గ్రా. టమోటాపై ₹7 లాభముతో, ఒక కి.గ్రా. వంకాయలపై ₹ 4 నష్టముతో అమ్మాడు. అతను సోమవారము 68 కి.గ్రా.ల టమోటాలు అమ్మినా లాభము కానీ నష్టము కానీ రాలేదు. అయిన అతను ఆ రోజు ఎన్ని కి.గ్రా.ల వంకాయలు అమ్మాడు?

సాధన.
కూరగాయల వ్యాపారికి ఒక కి.గ్రా. టమోటాపై వచ్చు లాభము = ₹7
1 కి.గ్రా. వంకాయలపై వచ్చు నష్టము = ₹(4)
వ్యాపారి అమ్మిన టమోటాలు = 68 కి.గ్రా.
టమోటా కిలోల సంఖ్య = x కి.గ్రా. అనుకొనుము
వంకాయలు కిలోల సంఖ్య = y కి.గ్రా. అనుకొనుము
7x – 4y = 0
⇒ 7 × 68 – 4y = 0
⇒ – 4y = – 7 × 68
⇒ y = \(\frac{-7 \times 68}{-4}\)
∴ ఆ రోజు వ్యాపారి అమ్మవలసిన వంకాయలు
= + 7 × 17 = + 119 కిలోలు.

ప్రశ్న 6.
ఒక పరీక్షలో, ప్రతి సరైన సమాధానానికి + 3 మార్కులు మరియు ప్రతి తప్పుకు -1 మార్కులు ఇవ్వబడతాయి. సోనా అన్ని ప్రశ్నలకు సమాధానాలు వ్రాయగా, అందులో 10 సరియైనవి మరియు ఆమె 20 మార్కులు పొందినది.
(i) ఆమె రాసిన తప్పు సమాధానాలు ఎన్ని ?
సాధన.
ప్రతి సరైన సమాధానానికి మార్కులు = + 3 .
కావున, 10 సరైన సమాధానాలకు మార్కులు = 10 × 3 = 30
ఇవ్వబడిన లెక్క ప్రకారం, సోనాకు వచ్చిన మార్కులు = 20
తప్పు సమాధానాలకు మార్కులు = 20 – 30 = – 10
ప్రతి తప్పు సమాధానానికి మార్కులు = – 1
∴ తప్పు సమాధానాలు రాసిన ప్రశ్నల సంఖ్య = (- 10) ÷ (- 1) = 10

(ii) పరీక్షలో ఇవ్వబడిన మొత్తం ప్రశ్నలు ఎన్ని ?
సాధన.
పరీక్షలోని మొత్తం ప్రశ్నల సంఖ్య = సరైన సమాధానాలు రాసిన ప్రశ్నలు + తప్పు సమాధానం రాసిన ప్రశ్నలు
= 10 + 10 = 20

ప్రశ్న 7.
a ÷ b = – 4 అగునట్లు 5 పూర్ణ సంఖ్యల జత (a, b) లు వ్రాయుము.
(ఉదా: (12, – 3) ఎందుకనగా 12 ÷ (- 3) = – 4).
సాధన.
(i) (16, – 4)
(ii) (- 48, 12)
(iii) (40, – 10)
(iv) (- 64, 16)

SCERT AP 7th Class Maths Solutions Pdf Chapter 1 పూర్ణ సంఖ్యలు Ex 1.1 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 1st Lesson పూర్ణ సంఖ్యలు Exercise 1.1

ప్రశ్న 1.
కింది వాటిని గుణించండి.
(i) 5 × 7
సాధన.
5 × 7 = 35

(ii) (-9) × (6)
సాధన.
(-9) × 6 = – 54

(iii) (9) × (- 4)
సాధన.
9 × (4) = – 36

(iv) (8) × (-7)
సాధన.
8 × (-7) = – 56

(v) (-124) × (-1)
సాధన.
(-124) × (-1) = + 124

(vi) (-12) × (-7)
సాధన.
(-12) × (-7) = + 84

(vii) (- 63) × 7,
సాధన.
(- 63) × 7 = – 441

(viii) 7 × (- 15)
సాధన.
7 × (- 15) = – 105

ప్రశ్న 2.
కింది వాటిలో పెద్దది ఏది ?
(i) 2 × (- 5) లేదా 3 × (-4)
సాధన.
2 × (- 5) లేదా 3 × (4)
– (2 × 5) = – 10, – (3 × 4) = – 12
– 10 > – 12
∴ 2 × (-5) పెద్దది

(ii) (- 6) × (- 7) లేదా (-8) × 5
సాధన.
(- 6) × (- 7) లేదా (-8) × 5
+ (6 × 7) = 42, – (8 × 5) = – 40
42 > – 40
∴ (- 6) × (- 7) పెద్దది

(iii) (- 6) × 10 లేదా (-3) × (- 21)
సాధన.
(- 6) × 10 లేదా (-3) × (-21).
– (6 × 10) = – 60, + (3 × 21) = 63
63 > – 60
∴ (- 3) × (- 21) పెద్దది

(iv) 9 × (- 11) లేదా 6 × (- 16)
సాధన.
9 × (-11) లేదా 6 × (-16)
– (9 × 11) = – 99, – (6 × 16) = – 96
– 96 > – 99
∴ 6 × (-16) పెద్దది

(v) (- 8) × (- 5) లేదా (-9) × (-4)
సాధన.
(- 8) × (- 5) లేదా (-9) × (4)
+ (8 × 5) = 40, + (9 × 4) = 36
40 > 36
∴ (- 8) × (-5) పెద్దది

ప్రశ్న 3.
రెండు పూర్ణసంఖ్యల లబ్దము i) ఒక ధన పూర్ణ సంఖ్య ii) ఒక రుణ పూర్ణ సంఖ్య iii) సున్నా అగునట్లు పూర్ణ సంఖ్యలను వ్రాయుము.
సాధన.
లబ్దము (i) ఒక ధన పూర్ణ సంఖ్య:
(i) 4 × 3
(ii) (+ 4) × (- 3)
(iii) (- 10) × (- 5)

లబ్దము (ii) ఒక రుణ పూర్ణ సంఖ్య:
(i) (4) × 3
(ii) 4 × (-3)
(iii) (- 10) × 5

లబ్దము (iii) సున్న:
(i) 0 × 5
(ii) (- 5) × 0
(iii) 0 × 0

ప్రశ్న 4.
ఒక కప్ప నిముషానికి 3 మీటర్ల వంతున బావి పై ఉపరితలం నుండి లోపలికి జారుతున్నది. కప్ప 5 నిముషాల తరువాత బావిలో ఏ స్థానములో ఉంటుంది?

సాధన.
కప్ప నిముషానికి బావి లోపలికి జారుతున్న లోతు = -3 మీటర్లు
5 నిముషాలలో కప్ప జారు లోతు = 5 × (-3) = -15 మీటర్లు
∴ 5 నిమిషాల తరువాత కప్ప బావి ఉపరితలం నుండి 15 మీటర్ల లోతులో ఉంటుంది.

ప్రశ్న 5.
వేసవిలో ఒక కొలనులో నీటిమట్టము బాష్పీభవనం వలన ఒక వారానికి 5 అంగుళాల చొప్పున తగ్గుతున్నది. నీటి స్థాయి స్థిర పరిమాణములో తగ్గుచున్నచో, 6 వారాల తరువాత కొలనులో నీటి మట్టములో మార్పు ఎంత ఉండును?

సాధన.
బాష్పీభవనం వలన ఒక వారానికి తగ్గు నీటి మట్టము = – 5 అంగుళాలు
6 వారాల తరువాత కొలనులో నీటి మట్టంలో మార్పు = 6 × (- 5) = -30 అంగుళాలు
∴ 6 వారాల తరువాత నీటి మట్టం 30 అంగుళాలు తగ్గుతుంది.

ప్రశ్న 6.
ఒక దుకాణదారుడు ఒక్కొక్క పుస్తకం అమ్మడం వలన ₹5లు లాభాన్ని మరియు ఒక్కొక్క పెన్ను అమ్మడం వలన ₹3లు నష్టము పొందును. జూలై నెలలో అతను 1500 పుస్తకాలు మరియు 1500 పెన్నులు అమ్మిన అతనికి వచ్చిన లాభము లేదా నష్టమును కనుగొనుము.
సాధన.
ఒక్కొక్క పుస్తకం అమ్మడం వలన దుకాణదారునకు వచ్చు లాభము = ₹5
1500 పుస్తకాలు అమ్మడం వలన వచ్చు లాభం = 1500 × 5 = ₹7500
ఒక్కొక్క పెన్ను అమ్మడం వలన దుకాణదారునకు వచ్చు నష్టం = ₹(-3)
1500 పెన్నులు అమ్మడం వలన వచ్చు నష్టం = 1500 × (-3) = ₹ – 4500
1500 పుస్తకాలు, 1500 పెన్నులు అమ్మడం వలన వచ్చు లాభము లేదా నష్టము = 7500 + (- 4500) = ₹3000
ఫలితం ధన సంఖ్య కావున ₹ 3000 లాభం వస్తుంది.

ప్రశ్న 7.
ఒక సిమెంటు కంపెనీ ఒక్కొక్క తెలుపు రంగు బస్తా సిమెంటుపై ₹8 లాభం మరియు బూడిద రంగు బస్తా సిమెంటుపై ₹6 నష్టముతో అమ్మింది. ఒక నెలలో 2,000 బస్తాల తెలుపు రంగు సిమెంటు, 3,000 బస్తాల బూడిద రంగు సిమెంటు అమ్మిన దానికి వచ్చినది లాభమా లేదా నష్టమా ఏమిటో కనుగొనండి.
సాధన.
సిమెంటు కంపెనీకి ఒక్కొక్క తెలుపు రంగు సిమెంటు బస్తాపై వచ్చు లాభము = ₹8
2000 తెలుపు రంగు సిమెంటు బస్తాలపై వచ్చు లాభము = 2000 × 8 = ₹ 16,000
సిమెంటు కంపెనీకి ఒక్కొక్క బూడిదరంగు సిమెంటు బస్తాపై వచ్చు నష్టము = ₹ (- 6)
3,000 బూడిద రంగు సిమెంటు బస్తాలపై వచ్చు నష్టము = 3000 × (- 6) = ₹ – 18000
2,000 బస్తాల తెలుపు రంగు సిమెంట్, 3000 బస్తాల బూడిద రంగు సిమెంట్ అమ్మడం వలన వచ్చు లాభం లేదా నష్టము = (16000) + (-18000) = ₹ – 2000
∴ ఫలితం రుణసంఖ్య కావున ₹ 2000 నష్టం వస్తుంది.

ప్రశ్న 8.
ప్రవచనం సరియగునట్లు కింది ఖాళీలను సరైన పూర్ణ సంఖ్యచే పూరించుము.
(i) (-4) ×________ = – 20
సాధన.
(- 4) × 5 = – 20

(ii) ________ × 5 = – 35
సాధన.
(- 7) × 5 = – 35

(iii) (-6) × ________ = 48
సాధన.
(- 6) × (-8) = 48

(iv) ________ × (-9) = 45
సాధన.
(5) × (-9) = 45

(v) ________ × 1 = – 42
సాధన.
(-6) × 7 = – 42

(vi) 8 × ________ = – 8
సాధన.
8 × (- 1) = – 8

SCERT AP 7th Class Maths Solutions Pdf Chapter 1 పూర్ణ సంఖ్యలు Review Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 1st Lesson పూర్ణ సంఖ్యలు Review Exercise

ప్రశ్న1.
కింది వాక్యాలను సరైన పూర్ణ సంఖ్యతో సూచించండి.
(i) స్నేహ తన పొదుపు ఖాతాలో ₹2000 జమ చేసినది.
సాధన.
+ ₹ 2000

(ii) జలాంతర్గామి సముద్ర మట్టము నుండి 350 అడుగుల లోతులో ఉంది.
సాధన.
– 350 అడుగులు

(iii) ఎవరెస్టు శిఖరం సముద్ర మట్టము నుండి 8848 మీ. ఎత్తులో ఉంది.
సాధన.
+ 8848 మీ.

(iv) 0°C కన్నా 14 డిగ్రీల తక్కువ ఉష్ణోగ్రత ఉంది.
సాధన.
– 14°C

ప్రశ్న2.
క్రింది సంఖ్యారేఖపై లేని పూర్ణసంఖ్యలను గుర్తించండి.

సాధన.

ప్రశ్న3.
క్రింది పూర్ణ సంఖ్యలను అవరోహణ మరియు ఆరోహణ క్రమంలో వ్రాయండి.

(i) -9, -1, 0, – 10, -6
సాధన.
అవరోహణ క్రమం: 0, -1, -6, -9, -10
ఆరోహణ క్రమం: -10, -9, -6, -1, 0

(ii) -6, 6, -9, 5, 10, -3
సాధన.
అవరోహణ క్రమం: 10, 6, 5, -3, -6, -9
ఆరోహణ క్రమం: -9, -6, -3, 5, 6, 10

(iii) -15, -20, -35, 0, 2
సాధన.
అవరోహణ క్రమం: 2, 0, -15, -20, -35
ఆరోహణ క్రమం: -35, -20, -15, 0, 2

ప్రశ్న4.
క్రింది వాటిని లెక్కించుము.
(i) – 2 + 3
సాధన.
– 2 + 3 = + 1

(ii) -6 + (-2)
సాధన.
– 6 + (-2) = – 8

(iii) 8 – (-6)
సాధన.
8 – (-6) = 8 + 6 = + 14

(iv) -9 + 4
సాధన.
-9 + 4 = -5

(v) – 23 – (-30)
సాధన.
– 23 – (-30) = – 23 + 30 = + 7

(vi) 50 – 153
సాధన.
50 – 153 = – 103

(vii) 71 + (-10) – 8
సాధన.
71 + (-10) – 8 = 71 + (-18) = + 53

(viii) – 30 + 58 – 38
సాధన.
– 30 + 58 – 38 = – 68 + 58 = – 10

ప్రశ్న5.
సియాచిన్ వద్ద 5 a.m ఉష్ణోగ్రత 0°C కన్నా 10°C తక్కువ ఉంది. ఆరు గంటల తర్వాత అది 14°C పెరిగినది. 11 a.m వద్ద ఉష్ణోగ్రత ఎంత ఉంటుంది?

సాధన.
సియాచిన్ వద్ద 5 a.m ఉష్ణోగ్రత = – 10°C
ఆరు గంటల తర్వాత పెరిగిన ఉష్ణోగ్రత = + 14°C
∴ 11 a.m వద్ద ఉష్ణోగ్రత = (-10) + 14 = + 4°C

ప్రశ్న6.
ఒక చేప సముద్ర ఉపరితలం నుండి 16 అడుగుల లోతులో ఉంది మరియు మరొక 17 అడుగుల కిందకు వెళ్ళింది. ప్రస్తుతం సముద్ర మట్టం నుండి చేప స్థానం ఏమిటి ?
సాధన.
సముద్రమట్టం నుండి మొదట చేపగల స్థానం = -16 అడుగులు
చేప మరొక 17 అడుగులు క్రిందకు వెళితే చేప ప్రస్తుత స్థానం = (-16) + (-17) = – 33 అడుగులు
అనగా చేప ప్రస్తుతం సముద్ర మట్టం నుండి 33 అడుగుల లోతులో ఉంటుంది.

ప్రశ్న7.
ఒక ఆకుకూరల వ్యాపారి సోమవారం నాడు ₹250 లాభం, మంగళవారం నాడు ₹ 120 నష్టం మరియు బుధవారం నాడు ₹180 నష్టం పొందాడు. మూడు రోజుల తరువాత వచ్చిన మొత్తం లాభం లేదా నష్టం ఎంతో కనుగొనుము.
సాధన.
ఆకుకూరల వ్యాపారికి
సోమవారం లాభం = ₹250
మంగళవారం నష్టం = ₹120
బుధవారం నష్టం = ₹180
∴ మూడు రోజుల తర్వాత వచ్చిన మొత్తం లాభం లేదా నష్టం = + 250 + (-120) + (-180)
= 250 + (-300) = -50
∴ వ్యాపారికి మూడు రోజుల తరువాత ₹ 50 నష్టం వస్తుంది.

ప్రశ్న8.
మొదటి పటంలో రెండు పూర్ణసంఖ్యల యొక్క సంకలనం ఆధారంగా మరియు రెండో పటంలో రెండు పూర్ణసంఖ్యల వ్యవకలనం ఆధారంగా పూర్తి చేయుము.

పాదన.