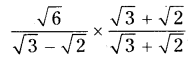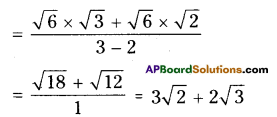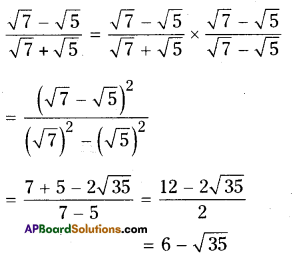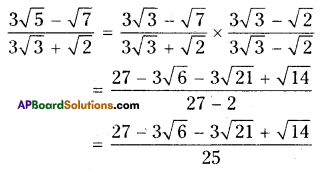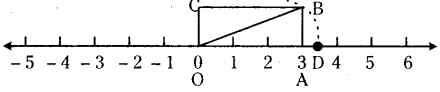Srinivas

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 3 The Elements of Geometry Ex 3.1 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 3rd Lesson The Elements of Geometry Exercise 3.1

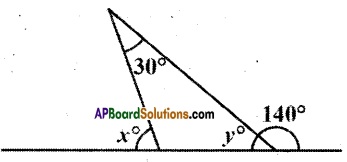
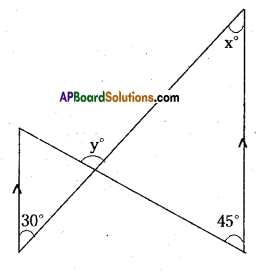
Question 1.
Answer the following:
i) How many dimensions a solid has ?
Solution:
A solid has three dimensions namely length, breadth and height or depth.

ii) How many books are there in Euclid’s Elements ?
Solution:
There are 13 volumes in Euclid’s elements.

iii) Write the number of faces of a cube and cuboid.
Solution:
Cube : 6 faces
Cuboid : 6 faces

iv) What is the sum of interior angles of a triangle ?
Solution:
The sum of interior angles of a triangle is 180°.

v) Write three undefined terms of geometry.
Solution:
Point, line and plane are three undefined terms in geometry.

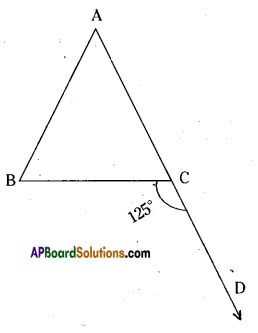
Question 2.
State whether the following statements are true or false. Also give reasons for your answers.
a) Only one line can pass through a given point
b) All right angles are equal
c) Circles with same radii are equal
d) A finite line can be extended on its both sides endlessly to get a straight line

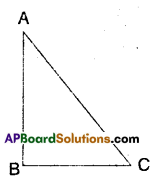
e) From figure AB > AC
Solution:
a) Only one line can pass through a given point – False.
Reason : (Since, infinitely many lines can pass through a given point)
b) All right angles are equal – True.
c) Circles with same radii are equal – True.
d) A finite line can be extended on its both sides endlessly to get a straight line – True.
e) From figure AB > AC – True.

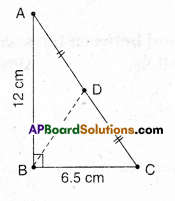
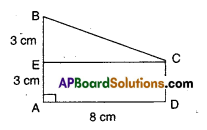
Question 3.
In the figure given below, show that the length AH > AB + BC + CD.

Solution:
Given a line \(\stackrel{\leftrightarrow}{\mathrm{AH}}\)
To prove AH > AB + BC + CD
From the figure AB + BC + CD = AD
AD is a part of whole AH.
From Euclid’s axiom whole is greater than part.
∴ AH > AD
⇒ AH > AB + BC + CD

Question 4.
If a point Q lies between two points P and R such PQ = QR, prove that PQ = \(\frac{1}{2}\)PR.

Let PR be a given line.
Given that PQ = QR
i. e., Q is a point on PR.
⇒ PQ + QR = PR
⇒ PQ + PQ = PR [∵ PQ = QR]
⇒ 2PQ = PR
⇒ PQ = \(\frac{1}{2}\) PR
Hence proved.

Question 5.
Draw an equilateral triangle whose sides are 5.2 cm
Soluton:
Step – 1 : Draw a line segment AB of length 5.2 cm. *
Step – 2 : Draw an arc of radius 5.2 cm with centre A.
Step – 3 : Draw an arc of radius 5.2 cm with centre B.
Step – 4 : Two arcs intersect at C; join C to A and B.

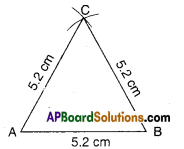
Δ ABC is the required triangle.

Question 6.
What is a conjecture? Give an example for it.
Solution:
Mathematical statements which are neither proved nor disproved are called conjectures. Mathematical discoveries often start out as conjectures. This may be an educated guess based on observations.
Eg : Every even number greater than 4 can be written as sum of two primes. This example is called Gold Bach Conjecture

Question 7.
Mark two points P and Q. Draw a line through P and Q. Now how many lines are parallel to PQ, can you draw ?
Solution:

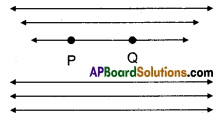
Infinitely many lines parallel to PQ can be drawn.

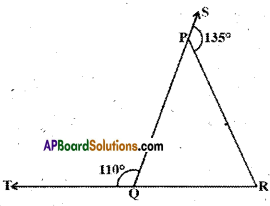
Question 8.
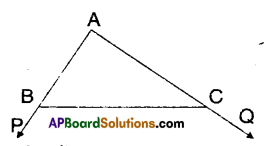
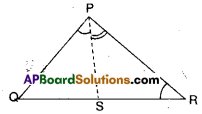
In the figure given below, a line n falls on lines / and m such that the sum of the interior angles 1 and 2 is less than 180°, then what can you say about lines l and m ?

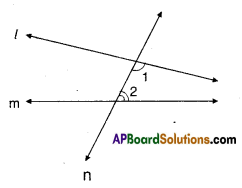
Solution:
Given : l, m and n are lines, n is a transversal.
∠1 < 90°
∠2 < 90°
If the lines l and m are produced on the side where angles 1 and 2 are formed, they intersect at one point.

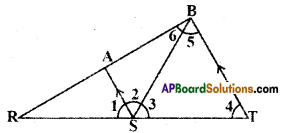
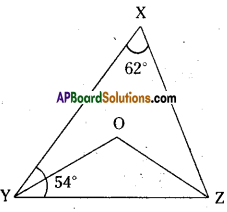
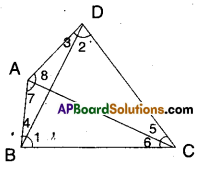
Question 9.
In the figure given below, if ∠1 = ∠3, ∠2 = ∠4 and ∠3 = ∠4 write the rela-tion between ∠1 and ∠2 using Euclid’s postulate.

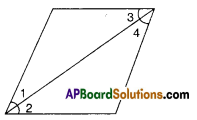
Solution :
Given : ∠1 = ∠3
∠3 = ∠4
∠2 = ∠4
∴∠1 = ∠2

∵Both ∠1 and ∠2 are equal to ∠4. (By Euclid’s axiom things which are equal to same things are equal to one another).

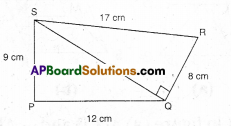
Question 10.
In the figure given below, we have BX = \(\frac{1}{2}\) AB, BY= \(\frac{1}{2}\) BC and AB = BC. Show that BX = BY.

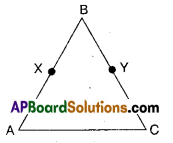
Solution:
Given : BX = \(\frac{1}{2}\) AB
BY = \(\frac{1}{2}\)BC
AB = BC
To prove : BX = BY
Proof: Given AB = BC [ ∵ By Euclid’s axiom things which are halves of the same things are equal to one another]
\(\frac{1}{2}\) AB = \(\frac{1}{2}\) BC
BX = BY
Hence proved.

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 6 Linear Equation in Two Variables Ex 6.1 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 6th Lesson Linear Equation in Two Variables Exercise 6.1

Question 1.
Express the following linear equations in the form of ax + by + c = 0 and indicate the values of a, b and c in each case.
i) 8x + 5y – 3 = 0
Solution:
8x + 5y – 3 = 0
⇒ 8x + 5y + (- 3) = 0
Here a = 8, b = 5 and c = – 3

ii) 28x – 35y = – 7
Solution:
28x – 35y = – 7
⇒ 28x + (- 35) y + 7 = 0
Here a = 28, b = – 35 and c = 7

iii) 93x = 12- 15y
Solution:
93x = 12 – 15y
⇒ 93x + 15y -12 = 0
⇒ 93x + 15y + (- 12) = 0
Here a = 93, b = 15 and c = – 12

iv) 2x = – 5y
Solution:
2x = – 5y
⇒ 2x + 5y = 0
Here a = 2, b = 5 and c = 0

v) \(\frac{x}{3}+\frac{y}{4}=7\)
Solution:
\(\frac{x}{3}+\frac{y}{4}=7\)
⇒ \(\frac{x}{3}+\frac{y}{4}-7=0\)
⇒\(\frac{4 x+3 y-84}{12}=0\)
⇒ 4x + 3y – 84 = 0
Here a = 4, b = 3 and c = – 84

vi) y = \(-\frac{3}{2} x\)
Solution:
y = \(-\frac{3}{2} x\)
⇒ 2y = -3x
⇒ 3x + 2y = 0
Here a = 3, b = 2 and c = 0

vii) 3x + 5y = 12
Solution:
3x + 5y = 12
⇒ 3x + 5y + (- 12) = 0
Here a = 3, b = 5 and c = – 12

Question 2.
Write each of the following in the form of ax + by + c = 0 and find the values of a, b and c.
i) 2x = 5
Solution:
2x – 5 = 0
a = 2
b = 0
c = -5

ii) y – 2 = 0
Solution:
y – 2 = 0
a = 0
b = 1
c = – 2

iii) \(\frac{y}{7}\) = 3
Solution:
\(\frac{y}{7}\) = 3
y = 21
y – 21 = 0
a = 0
b = 1
c = -21

iv) x = \(-\frac{14}{13}\)
x = \(-\frac{14}{3}\)
⇒ 13x = – 14
⇒ 13x + 14 = 0
a = 13
b = 0
c = 14

Question 3.
Express the following statements as a linear equation in two variables,
i)The sum of two numbers is 34.
Solution:
x + y = 34; x, y are any two numbers ⇒ x + y – 34 = 0

ii) The cost of a ball pen is ?5 less than half the cost of a fountain pen.
Solution:
Let the cost of a fountain pen = x
Let the cost of ball pen = y
Then y = x – 5 or x – y – 5 = 0

iii) Bhargavi got 10 more marks than double of the marks of Sindhu. |l M)
Solution:
Let Sindhu’s marks = x
Bhargavi’s marks = y
Then by problem y = 2x + 10 or 2x – y + 10 = 0

iv) The cost of a pencil is ₹2 and one ball point pen costs ₹15. Sheela pays ₹100 for the pencils and pens she purchased.
Solution:
Giver: that cost of a pencil = ₹2
Cost of a ball point pen = ₹15
Let the number of pencils purchased = x
Let the number of pens purchased = y
Then the total cost of x – pencils = 2x
Then the total cost of y – pens = 15y
By problem 2x + 15y = 100

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 5 Co-Ordinate Geometry Ex 5.3 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 5th Lesson Co-Ordinate Geometry Exercise 5.3

Question 1.
Plot the following points on the Cartesian plane whose x, y co-ordinates are given.

Solution:

Question 2.
Are the positions of (5, -8) and (-8, 5) Is same ? JustIfy your answer.
Solution:
The positions of (5, -8) and (-8, 5) are not same. They are two distinct points. (5, -8) lies at a distance of 5 units from Y – axis and 8 units from X – axis on down side of the origin. So it lies in Q₄. Where as (- 8, 5) lies in Q₂. The point is at a distance of 8 units from Y – axis on left side of the origin and 5 units from X – axis.

Question 3.
What can you say about the position of the points (1, 2), (1, 3), (1, – 4), (1, 0) and (1, 8), Locate on a graph sheet.
Solution:

All the given points lie on a line parallel to Y-axis at a distance of 1 cm.

Question 4.
What can you say about the position of the points (5, 4), (8, 4), (3, 4), (0, 4), (-4, 4), (-2,4)? Locate the points on a graph sheet and justify your answer.
Solution:
The points (5, 4), (8, 4), (3, 4), (0, 4), (- 4, 4) and (- 2, 4) all lie on a line parallel to X-axis at a distance of 4-units from it.

Question 5.
Plot the points (0, 3), (4, 3), (3, 4) (4, 0) in graph sheet. Join the points with straight lines to make a rectangle. Find the area of the rectangle.
Solution:

From the graph, area of the rectangle =12 square units (OR)
Length = 4 units ; breadth = 3 units
A = l/b = 4 × 3 = 12 sq. units.

Question 6.
Plot the points (2, 3), (6, 3) and (4, 7) in a graph sheet. Join them to make it a triangle. Find the area of the triangle.
Solution:

From the graph
Base of the triangle = 4 units
Height of the triangle = 4 units
∴ Area of the triangle = \(\frac{1}{2}\) × base × height = \(\frac{1}{2}\) × 4 × 4 = 8sq. units.

Question 7.
Plot at least six points in a graph sheet, each having the sum of its co-ordinates equal to 5. [Hint: (- 2, 7), (1, 4)………….]
Solution:
Given that (x co-ordinate) + (y co-ordinate) = 5
Let the points be

Question 8.
Look at the graph. Write the co-ordinates of the points
A, B, C, D, E, F. G. H, 1, J, K, L, M, N, O, P and Q.

Solution:
A(- 3, 4) ; B(0, 5) : C (3, 4) ; D (2, 4) ; E (2, 0) ;
F (3, 0) ; G (3, – 1) ; H (0, – 1) ; I (- 3, – 1) ;
J (- 3, 0) ; K (- 2, 0) ; L (- 2, 4) ; M (- 1, 0) ;
N (-1, 3); O (0, 0) ; P (1. 3) and Q (1, 0)

Question 9.
In a graph sheet plot each pair of points, join them by line segments.
i) (2, 5), (4, 7)
ii) (-3, 5) (-1,7)
iii) (-3, -4), (2, -4)
iv) (-3, -5) (2, -5)
v) (4, -2), (4, -3)
vi) (-2, 4), (-2, 3)
vii) (-2, 1), (-2, 0)
Now join the following pairs of points by straight line segments, in the same graph.
viii) (-3, 5), (-3, 4)
ix) (2, 5), (2, -4)
x) (2, -4), (4, -2)
xi) (2, -4), (4, -3)
xii) (4, -2), (4, 7)
xiii) (4, 7), (-1, 7)
xiv) (-3, 2), (2, 2)
Now you will get a surprise figure. What is it ?
Solution:

AP Board 9th Class Maths Solutions

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 5 Co-Ordinate Geometry Ex 5.2 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 5th Lesson Co-Ordinate Geometry Exercise 5.2

Question 1.
Write the quadrant in which the following points lie.
i) (- 2, 3)
ii) (5, – 3)
iii) (4, 2)
iv) (- 7, – 6)
v) (0, 8)
vi) (3, 0)
vii) (-4,0)
viii) (0, – 6)
Solution:
i) (- 2, 3) – Q₂ (second quadrant)
ii) (5, – 3) – Q₄ (fourth quadrant)
iii) (4, 2) – Q₁ (Iirst quadrant)
iv) (- 7, – 6) – Q₃ (third quadrant)
v) (0, 8) – on Y-axis
vi) (3, 0) – on X-axis
vii) (-4,0) – on X’ – axis
viii) (0, – 6) – on Y’: axis

Question 2.
Write the abscissae and ordinates of the following points.
i)(4,-8)
ii)(-5,3)
iii)(0,0)
iv)(5, 0)
v)(0, -8)
Note: Plural of abscissa is abscissae.
Solution:

Question 3.
Which of the following points lie on the axes ? Also name the axis.
i) (-5,-8)
ii) (0, 13)
iii) (4, – 2)
iv) (- 2,0)
v) (0, – 8)
vi) (7,0)
vii) (0,0)
Solution:
The points (ii) (0,13) ; (v) (0,- 8) lie on Y – axis.
The points (iv) (- 2, 0), (vi) (7, 0) lie on X – axis.
The point (vii) (0, 0) lie on both X – axis and Y – axis.
The points (i) (- 5, – 8); (iii) (4, – 2) do not lie on any axis.

Question 4.
Write the following based on the graph.
i) The ordinate of L
ii) The ordinate of Q
iii) The point denoted by (- 2,-2)
iv) The point denoted by (5, – 4)
v) The abscissa of N
vi) The abscissa of M

Solution:
i) – 7
ii) 7
iii) The point ’R’
iv) The point P
v) 4
vi) – 3

Question 5.
State true or false and write correct statement.
i) In the Cartesian plane the horizon-tal line is called Y – axis, if) in the Cartesian plane, the vertical line is called Y – axis.
iii) The point which lies on both the axes is called origin.
iv) The point (2, – 3) lies in the third quadrant.
v) (-5, -8) lies in the fourth quadrant.
vi) The point (- x, – y) lies in the first quadrant where x < 0; y < 0.
Solution:
i) False
Correct statement: In the Cartesian plane the horizontal line is called X – axis.
ii) True
iii) True
iv) False
Correct statement: The point (2, -3) lies in the fourth quadrant.
v) False
Correct statement: (- 5, – 8) lies in the third quadrant.
vi) True

Question 6.
Plot the following ordered pairs on a graph sheet. What do you observe ?
i) (1, 0), (3, 0), (- 2, 0), (- 5, 0), (0, 0), (5, 0), (- 6, 0)
ii) (0, 1), (0, 3), (0, – 2), (0, – 5), (0, 0), (0,5), (0,-6)
Solution:
i) All points lie on X – axis,
ii) All points lie on Y – axis.

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 5 Co-Ordinate Geometry Ex 5.1 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 5th Lesson Co-Ordinate Geometry Exercise 5.1

Question 1.
In a locality, there is a main road along North – South direction. The map is given below. With the help of the picture answer the following questions.

i) What is the 3rd object on the left side in street no. 3 while going in east direction ?
ii) Find the name of the 2nd house which is on right side of street 2 while going in east direction.
iii) Locate the position of Mr. K’s house.
iv) How do you describe the position of the post office ?
v) How do you describe the location of the hospital ?
Solution:
i) Water tank
ii) Mr. J’s house
iii) In street No. 2, 3rd house on right side.
iv) In street No. 4, the first house on right side.
v) In street No. 4, the last house on left side.

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 4 Lines and Angles Ex 4.4 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 4th Lesson Lines and Angles Exercise 4.4

Question 1.
In the given triangles, find out ∠x, ∠y and ∠z

Solution:
In fig(i)
x° = 50° + 60°
(∵ exterior angle is equal to sum of the opposite interior angles)
∴ x= 110°

In fig (ii)
z° = 60° + 70°
(∵ exterior angle is equal to sum of the opposite interior angles)
∴ z = 130°

In fig (iii)
y° = 35° + 45° = 80°
(∵ exterior angle is equal to sum of the opposite interior angles)

Question 2.
In the given figure AS // BT; ∠4 = ∠5, \(\overline{\mathbf{S B}}\) bisects ∠AST. Find the measure of ∠1.

Solution:
Given AS // BT
∠4 = ∠5 and SB bisects ∠AST.
∴ By problem
∠2 = ∠3 …………..(1)
For the lines AS // BT
∠2 = ∠5 ( ∵alternate interior angles)
∴ In ΔBST
∠3 = ∠5 = ∠4
Hence ΔBST is equilateral triangle and each of its angle is equal to 60°.
∴∠3 = ∠2 = 60° [by eq. (1)]
Now ∠1 + ∠2 + ∠3 = 180°
∠1 + 60° + 60° = 180°
[ ∵ angles at a point on a line]
∴∠1 = 180° – 120° = 60°

Question 3.
In the given figure AB // CD; BC // DE then find the values of x and y.

Solution:
Given that AB // CD and BC // DE.
∴ 3x = 105° (∵ alternate interior angles for AB // CD)
x = \(\frac { 105° }{ 3 }\) = 35°
Also BC // DE
∴∠D = 105°
(∵ alternate interior angles)
Now in ΔCDE
24° + 105° + y = 180°
(∵ angle sum property)
∴ y = 180° – 129° = 51°

Question 4.
In the given figure BE ⊥ DA and CD ⊥ DA then prove that m∠1 = m∠3.

Solution:
Given that CD ⊥ DA and BE ⊥ DA.
⇒ Two lines CD and BE are perpendicular to the same line DA.
⇒ CD // BE (or)
∠D =∠E ⇒ CD // BE
(∵ corresponding angles for CD and BE and DA are transversal)
Now m∠1 = m∠3
(∵alternate interior angles for the lines CD // BE ; DB are transversal)
Hence proved.

Question 5.
Find the values of x, y for which lines AD and BC become parallel.

Solution:
For the lines AD and BC to be parallel x – y = 30° (corresponding angles) ……… (1)
2x = 5y ………….(2)
(∵ alternate interior angles)
Solving (1) & (2)

y = \(\frac{60}{3}\) = 20°
Substituting y = 20° in eq. (1)
x – 20° = 30°
⇒ x = 50°
∴ x = 50° and y = 20°

Question 6.
Find the values of x and y in the figure.

Solution:
From the figure y + 140° = 180°
(∵ linear pair of angles)
∴ y = 180° – 140° = 40°
And x° = 30° + y°
(∵ exterior angle = sum of the opposite interior angles)
x° = 30° + 40° = 70°

Question 7.
In the given figure segments shown by arrow heads are parallel. Find the values of x and y.

Solution:
From the figure
x° = 30° (∵ alternate interior angles)
y° = 45° + x° (∵ exterior angles of a triangle = sum of opp. interior angles)
y = 45° + 30° – 75°

Question 8.
In the given figure sides QP and RQ of ∠PQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.

Solution:
Given that ∠SPR = 135° and ∠PQT =110°
From the figure
∠SPR + ∠RPQ = 180°
∠PQT + ∠PQR = 180°
[∵ linear pair of angles]
⇒ ∠RPQ = 180° – ∠SPR
= 180° – 135° = 45°
⇒ ∠PQR = 180° – ∠PQT
= 180°-110° = 70°
Now in APQR
∠RPQ + ∠PQR + ∠PRQ = 180°
[∵ angle sum property]
∴ 45° + ’70° + ∠PRQ = 180°
∴ ∠PRQ = 180°-115° = 65°

Question 9.
In the given figure ∠X = 62° ; ∠XYZ = 54°. In ΔXYZ. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respec-tively find ∠OZY and ∠YOZ.

Solution:
Given that ∠X = 62° and ∠Y = 54°
YO arid ZO are bisectors of ∠Y and ∠Z.
In ΔXYZ
∠X + ∠XYZ + ∠XZY = 180° .
62° + 54° + ∠XZY = 180°
=> ∠XZY = 180°- 116° = 64°
Also in Δ????OYZ
∠OYZ = 1/2 ∠XYZ = 1/2 x 54° = 27°
(∵ YO is bisector of ∠XYZ)
∠OZY = 1/2 ∠XZY = 1/2 x 64° = 32
(∵ OZ is bisector of ∠XYZ)
And ∠OYZ + ∠OZY + ∠YOZ = 180°
(∵ angle sum property, ΔOYZ)
⇒ 27 + 32° + ∠YOZ = 180°
⇒ ∠YOZ = 180° – 59° = 121°

Question 10.
In the given figure if AB // DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE.

Solution:
Given that AB // DE, ∠CDE = 53°;
∠BAC = 35°
Now ∠E = 35°
( ∵ alternate interior angles)
Now in ∆CDE
∠C + ∠D + ∠E = 180°
(∵angle sum property, ACDE)
∴ ∠DCE + 53° + 35° = 180°
⇒ ∠DCE = 180° – 88° = 92°

Question 11.
In the given figure if line segments PQ and RS intersect at point T, such that∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°, find ∠SQT.

Solution:
Given that ∠PRT = 40°; ∠RPT = 95°;
∠TSQ = 75°
In ∆PRT ∠P + ∠R + ∠PTR = 180°
(∵angle sum property)
95° + 40° + ∠PTR = 180°
⇒ ∠PTR = 180° – 135° = 45°
Now ∠PTR = ∠STQ
(∵ vertically opposite angles)
In ΔSTQ ∠S + ∠Q + ∠STQ = 180°
(∵ angle sum property)
75° + ∠SQT + 45° = 180°
∴ ∠SQT = 180° – 120° = 60°

Question 12.
In the given figure, ABC is a triangle in which ∠B = 50° and ∠C = 70°. Sides AB and AC are produced. If ∠ is the measure of angle between the bisec¬tors of the exterior angles so formed, then find ‘z’.

Solution:
Given that ∠B = 50°; ∠C = 70°
Angle between bisectors of exterior angles B and C is ∠.
From the figure
50° + 2x = 180°
70° + 2y = 180°
(∵ linear pair of angles)
∴ 2x= 180°-50°
2x= 130°
x = \(\frac{130}{2}\)
= 65°

2y= 180°-70°
2y= 110°
x = \(\frac{110°}{2}\)
= 55°

Now in ΔBOC
x + y + ∠ = 180° (∵ angle sum property)
65° + 55° + ∠ = 180°
z = 180° -120° = 60°

Question 13.
In the given figure if PQ ⊥ PS; PQ // SR, ∠SQR = 28° and ∠QRT = 65°, then find the values of x and y.

Solution:
Given that PQ ⊥ PS ; PQ // SR
∠SQR = 28°, ∠QRT = 65°
From the figure
∠QSR = x° (∵ alt. int. angles for the lines PQ // SR)
Also 65° = x + 28° (∵ ext. angles = sum of the opp. interior angles)
∴ x° = 65° – 28° = 37°
And x° + y° = 90°
[ ∵ PQ ⊥ PS and PQ // SR. ⇒ ∠P = ∠S]
37° + y = 90°
∴ y = 90° – 37° = 53°

Question 14.
In the given figure ΔABC side AC has been produced to D. ∠BCD = 125° and ∠A: ∠B = 2:3, find the measure of ∠A and ∠B

Solution:
Given that ∠BCD = 125°
∠A : ∠B = 2 : 3
Sum of the terms of the ratio
∠A : ∠B = 2 + 3 = 5
We know that ∠A + ∠B = ∠BCD
(∵ exterior angles of triangle is equal to sum of its opp. interior angles)
∴ ∠A = \(\frac{2}{5}\) x 125° = 50°
∠B = \(\frac{3}{5}\) x 125° = 75°

Question 15.
In the given figure, it is given that, BC // DE, ∠BAC = 35° and ∠BCE = 102°. Find the measure of 0 ∠BCA i0 ∠ADE and iii) ∠CED.

Solution:
Given that BC // DE ; ∠BAC = 35°;
∠BCE = 102°

i) From the figure
102° + ∠BCA = 180°
(∵ linear pair of angles)
∴ ∠BCA = 180° – 102° = 78°

ii) ∠ADE + ∠CBD = 180°
(∵ interior angles on the same side of the transversal)
∠ADE + (78° + 35°) = 180°
(∵ ∠CBD = ∠BAC + ∠BCA)
∴ ∠ADE = 180° – 113° = 67°

iii) From the figure .
∠CED = ∠BCA = 78°
(∵ corresponding angles)

Question 16.
In the given figure, it is given that AB = AC; ∠BAC = 36°; ∠ADB = 45° and ∠AEC = 40°. Find i) ∠ABC
i) ∠ACB iii) ∠DAB iv) ∠EAC.

Solution:
Given that AB = AC; ∠BAC = 36°,
∠ADB = 45°, ∠AEC = 40°
(i) & (ii)
In ∆ABC ; AB = AC
⇒ ∠ABC = ∠ ACB
And 36° + ∠ABC + ∠ACB = 180°
(∵ angle sum property)
∴ ∠ABC = \(\frac{180^{\circ}-36^{\circ}}{2}=\frac{144^{\circ}}{2}=72^{\circ}\)
∠ACB = 72°

iii) From the figure
∠ABD + ∠ABC = 180°
∠ABD = 180° – 72° = 1086
In ΔABD
∠DAB + ∠ABD + ∠D = 180°
∠DAB + 108° + 45° = 180°
∠DAB = 180° – 153° = 27°

iv) In ΔADE
∠D + ∠A + ∠E = 180°
45° + ∠A + 40° = 180°
⇒ ∠A = 180° -85° = 95°
But ∠A = ∠DAB + 36° + ∠EAC
95° = 27°, + 36° + ∠EAC
∴ ∠EAC = 95° – 63° = 32°

Question 17.
Using information given in the figure, calculate the values of x and y.

Solution:
From the figure In ∆ACB
34° + 62° + ∠ACB = 180°
(∵ angle sum property)
∴ ∠ACB = 180° – 96° = 84° .
And x + ∠ACB = 180°
(∵ linear pair of angles) .
∴ x + 84° = 180°
x = 180°-84° = 96°
(OR)
x = 34° + 62° = 96°
( ∵ x is exterior angle, ∆ABC)
y = 24° + x°
= 24° + 96° = 120°
(∵ y is exterior angle, ∆DCE)

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 6 Linear Equation in Two Variables Ex 6.4 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 6th Lesson Linear Equation in Two Variables Exercise 6.4

Question 1.
Give the graphical representation of the following equation
a) on the number line and b) on the Cartesian plane.
l) x = 3
ii) y + 3 = 0
iii) y = 4
iv) 2x – 9 = 0
v) 3x + 5 = 0
Solution:
i) x = 3 is a line parallel to Y-axis at a distance of 3 units on the right side of the origin.
ii) y + 3 = 0 y = – 3 is a line parallel to X-axis, below the origin.
iii) y = 4 is a line parallel to X-axis at a distance of 4 units above the origin.
iv) 2x – 9 = 0
⇒ x = \(\frac{9}{2}\) = 4.5 is a line parallel to Y-axis at a distance of 4.5 units, right side of the zero.
v) 3x + 5 = 0
⇒ 3x = -5 x = \(\frac{-5}{3}\) is a line parallel to Y – axis at a distance of \(\frac{5}{3}\)units on the left side of the origin.

x = 3

y + 3 = 0

y = 4

2x – 9 = 0

3x + 5 = 0

Question 2.
Give the graphical representation of 2x – 11 = 0 as an equation in i) one variable ii) two variables
Solution:
2x – 11 = 0

Question 3.
Solve the equation 3x + 2 = 8x – 8 and represent the solution on
i) the number line ii) the Cartesian plane.
Solution:
Given that 3x + 2 = 8x – 8
3x – 8x = – 8 – 2
– 5x = -10
x = \(\frac{-10}{-5}\) = 2

Question 4.
Write the equation of the line parallel to X-axis and passing through the point i) (0, – 3) ii) (0,4) iii) (2, – 5) iv) (3,4)
Solution:
i) The given point is (0, – 3)
Equation of a line parallel to X-axis is y = k
∴ Required equation is y = – 3 or y + 3 = 0

ii) The given point is (0, 4)
Equation of a line parallel to X-axis is y = k
∴ Required equation isy = 4ory-4 = 0

iii) The given point is (2, – 5)
Equation of a line parallel to X-axis is y = k
∴ Required equation isy = -5 or y + 5 = 0

iv) The given point is (3, 4)
Equation of a line parallel to X-axis is y = k
∴ Required equation isy = 4 or y – 4 = 0

Question 5.
Write the equation of the line parallel to Y-axis passing through the point
i) (- 4, 0)
ii) (2,0)
iii) (3, 5)
(iv) (- 4, – 3)
Solution:
Equation of a line parallel to Y-axis is x = k
∴ The required equations are
i) Through the point (- 4, 0) ⇒ the equation is x = – 4 or x + 4 = 0
ii) Through the point (2, 0) ⇒ the equation isx = 2orx-2 = 0
iii) Through the point (3, 5) ⇒ the equation isx = 3orx-3 = 0
iv) Through the point (- 4,-3) ⇒ the equation is x = – 4 or x + 4 = 0

Question 6.
Write the equation of three lines that are
1) Parallel to the X-axis
Solution:
y = 3
y = -4
y = 6

ii) Parallel to the Y-axis
Solution:
x = – 2
x = 3
x = 4

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 11 Areas Ex 11.1 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 11th Lesson Areas Exercise 11.1

Question 1.
In ΔABC, ∠ABC = 90°; AD = DC; AB =12 cm, BC = 6.5 cm. Find the area of ΔADB

Solution:
ΔADB = \(\frac { 1 }{ 2 }\) ΔABC [ ∵ AD is a median of ΔABC]
\(\frac { 1 }{ 2 }\) = [ \(\frac { 1 }{ 2 }\) AB x BC]
= \(\frac { 1 }{ 4 }\) x 12 x 6.5
= 19.5 cm²

Question 2.
Find the area of a quadrilateral PQRS in which ∠QPS = ∠SQR = 90°, PQ = 12 cm, PS = 9 cm, QR = 8 cm and SR =17 cm.
[Hint: PQRS has two parts]

Solution:
Area of ΔQPS = \(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) x 9 x 12
= 54cm²
In ΔQPS
QS² = PQ² + PS²
QS = \(\begin{aligned}
\sqrt{12^{2}+9^{2}} &=\sqrt{144+81} \\
&=\sqrt{225}=15
\end{aligned}\)
Area of ΔQSR =\(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) x 15 x 8 = 60 cm²
∴ □PQRS = ΔQPS + ΔQSR
= 54 + 60= 114 cm²

Question 3.
Find the area of trapezium ABCD as given in the figure in which ADCE is a rectangle.
[Hint: ABCD has two parts]

Solution:
Area of trapezium 1
= \(\frac { 1 }{ 2 }\) (sum of parallel sides) x (distance between the parallel sides)
= \(\frac { 1 }{ 2 }\) (a + b) h
From the figure, a = 3 + 3 = 6 cm
b = 3 cm
(∵ Opp. sides of rectangle)
h = 8 cm
∴ A = \(\frac { 1 }{ 2 }\)(6 + 3)x8 = 36cm²

Question 4.
ABCD is a parallelogram. The diago-nals AC and BD intersect each other at O. Prove that ar (ΔAOD) = ar (ΔBOQ. [Hint: Congruent figures have equal area]

Solution:
Given that □ABCD is a parallelogram.
Diagonals AC and BD meet at ‘O’.
In ΔAOD and ΔBOC
AD = BC [ ∵ Opp. sides of a ||gm]
AO = OC [ ∵ diagonals bisect each
OD = OB other]
ΔAOD = ΔBOC [S.S.S. congruence]
∴ ΔAOD = ΔBOC (i.e., have equal area)

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 1 Real Numbers Ex 1.3 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 1st Lesson Real Numbers Exercise 1.4

Question 1.
Simple the following expressions.
i) (5 + √7) (2 + √5)
Solution:
(5 + √7) (2 + √5)
= 10 + 5√5 + 2√7 + √35

ii) (5 + √5) (5 – √5)
Solution:
(5 + √5) (5 – √5)
= 5² + (√5)²
= 25 – 5 = 20

(iii) (√3 + √7)²
Solution:
(√3 + √7)²
= (√3)² + (√7)² + 2(√3)(√7)
= 3 + 7 + 2√21
= 10 + 2√21

iv) (√11 – √7) (√11 + √7)
= (√11)² – (√7)²
= 11 – 7 = 4

Question 2.
Classify the following numbers as rational or irrational.
i) 5 – √3
ii) √3 + √2
iii) (√2 – 2)²
iv) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\)
v) 2π
vii) (2 +√2) (2 – √2)
Solution:
i) 5 – √3 – irrational
ii) √3 + √2 – irrational
iii) (√2 – 2)² – irrational
iv) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\) – rational
v) 2π – Transcendental number. (not irrational)
vi) \(\frac{1}{\sqrt{3}}\)– irrational
vii) (2 +√2) (2 – √2) – rational

Question 3.
In the following equations, find whether variables x, y, z etc., represents rational or irrational numbers.
i) x² = 7
ii) y² = 16
iii) z² = 0.02
iv) u² = \(\frac{17}{4}\)
v) w² = 27
vi) t⁴ = 256
Solution:
i) x² = 7
⇒ x = √7 is an irrational number.
ii) y² = 16 ⇒ y = 4 is a rational number.
iii) z² = 0.02 ⇒ z = \(\sqrt{0.02}\) is an irrational number.
iv) u² = \(\frac{17}{4}\) ⇒ x = \(\frac{\sqrt{17}}{2}\) is an irrational number.
v) w² = 27 ⇒ w = \(3 \sqrt{3}\) an irrational number.
vi) t⁴ = 256 ⇒ t² = \(\sqrt{256}\) = 16
⇒ t = \(\sqrt{16}\) = 4 is a rational number

Qeustion 4.
The ratio of circumference to the diameter of a circle c/d is represented by π. But we say that π is an irrational number. Why?

Question 5.
Rationalise the denominators of the following.
i) \(\frac{1}{3+\sqrt{2}}\)
Solution:

ii) \(\frac{1}{\sqrt{7}-\sqrt{6}}\)
Solution:

iii) \(\frac{1}{\sqrt{7}}\)
Solution:

iv) \(\frac{\sqrt{6}}{\sqrt{3}-\sqrt{2}}\)
Solution:

Question 6.
Simplify each of the following by rationalising the denominator.
i) \(\frac{6-4 \sqrt{2}}{6+4 \sqrt{2}}\)
Solution:

ii) \(\frac{\sqrt{7}-\sqrt{5}}{\sqrt{7}+\sqrt{5}}\)
Solution:

iii) \(\frac{1}{3 \sqrt{2}-2 \sqrt{3}}\)
Solution:

iv) \(\frac{3 \sqrt{5}-\sqrt{7}}{3 \sqrt{3}+\sqrt{2}}\)
Solution:

Question 7.
Find the value of \(\frac{\sqrt{10}-\sqrt{5}}{2 \sqrt{2}}\) upto three decimal places. (take \(\sqrt{2}\) = 1.414, \(\sqrt{3}\) = 1.732 and \(\sqrt{5}\) = 2.236).
Solution:

Question 8.
Find
i) 64^1/6
Solution:
= (2⁶)^1/6
= 6

ii) 32^1/5
Solution:
32^1/5
= (2⁵)^1/5
= 2

iii) 625^1/4
625^1/5
= (5⁴)^1/4
= 5

iv) 16^3/2
Solution:
16^3/2
= (4²)^3/2

v) 243^2/5
Solution:
243^2/5
= (3⁵)^2/5

vi) (46656)^-1/6
Solution:

Question 9.
Simplify \(\sqrt[4]{81}-8 \sqrt[3]{343}+15 \sqrt[5]{32}+\sqrt{225}\)
Solution:

Question 10.
If ‘a’ and ‘b’ are rational numbers, find the values of a and b in each of the following equations.
i) \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}=\mathbf{a}+\mathbf{b} \sqrt{6}\)
Solution:
Given that \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}=\mathbf{a}+\mathbf{b} \sqrt{6}\)
Rationalising the denominator we get

Comparing 5 + 2√6 with a + b√6
We have a = 5 and b = 2

ii) \(\frac{\sqrt{5}+\sqrt{3}}{2 \sqrt{5}-3 \sqrt{3}}=a-b \sqrt{15}\)
Solution:
Given that \(\frac{\sqrt{5}+\sqrt{3}}{2 \sqrt{5}-3 \sqrt{3}}=a-b \sqrt{15}\)
Rationalising the denominator we get

AP Board 9th Class Maths Solutions

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 1 Real Numbers Ex 1.3 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 1st Lesson Real Numbers Exercise 1.3

Question 1.
Visualise \(2.8 \overline{74}\) on the number line, using successive magnification.
Solution:

Question 2.
Visualise \(5 . \overline{28}\) on the number line, upto 3 decimal places.
Solution:

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 1 Real Numbers Ex 1.2 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 1st Lesson Real Numbers Exercise 1.2

Question 1.
Classify the following numbers as rational or irrational.
i) \(\sqrt{27}\)
ii) \(\sqrt{441}\)
iii) 30.232342345
iv) 7.484848
v) 11.2132435465
vi) 0.3030030003
Solution:
i) \(\sqrt{27}\) – irrational number
ii) \(\sqrt{441}\) = 21 – rational
iii) 30.232342345 – irrational number
iv) 7.484848 – rational number
v) 11.2132435465 – irrational number
vi) 0.3030030003 – irrational number

Question 2.
Explain with an example how irrational numbers differ from rational numbers ?
Solution:
Irrational numbers can’t be expressed in \(\frac { p }{ q }\) form where p and q are integers and q ≠ 0.
E.g.\(\sqrt{2}, \sqrt{3} ; \sqrt{5}, \sqrt{7}\) etc.
Where as a rational can be expressed in \(\frac { p }{ q }\) form
E.g. :- -3 = \(\frac { -3 }{ 1 }\) and \(\frac { 5 }{ 4 }\) etc.

Question 3.
Find an irrational number between \(\frac { 5 }{ 7 }\) and \(\frac { 7 }{ 9 }\). How many more there may be ?
Solution :
The decimal forms of \(\frac { 5 }{ 7 }\) and \(\frac { 7 }{ 9 }\) are
\(\frac{5}{7}=0 . \overline{714285} \ldots ., \frac{7}{9}=0.7777 \ldots \ldots=0 . \overline{7}\)
∴ An irrational between \(\frac { 5 }{ 7 }\) and \(\frac { 7 }{ 9 }\) is 0.727543…………
There are infinitely many irrational numbers between \(\frac { 5 }{ 7 }\) and \(\frac { 7 }{ 9 }\).

Question 4.
Find two irrational numbers between 0.7 and 0.77.
Solution:
Two irrational numbers between 0.7 and 0.77 can take the form
0.70101100111000111…………. and 0.70200200022……………

Question 5.
Find the value of √5 uPto 3 decimal places.
Solution:

[√5 is not exactly equal to 2.2350679………….. as shown ¡n calculators]

Question 6.
Find the value of √7 upto six decimal places by long division method.
Solution:

Question 7.
Locate \(\sqrt{\mathrm{10}}\) on number line.

Step – 1 : Draw a number line.
Step – 2 : Draw a rectangle OABC at zero with measures 3 x 1. i.e., length 3 units and breadth 1 unit.
Step – 3 : Draw the diagonal OB.
Step – 4 : Draw an arc with centre ‘O’ and radius OB which cuts the number line at D.
Step – 5 : ‘D’ represents \(\sqrt{\mathrm{10}}[latex] on the number line.

Question 8.
Find atleast two irrational numbers between 2 and 3.
Solution:
An irrational number between a and b is Tab [latex]\sqrt{\mathrm{ab}}\) unless ab is a perfect square.
∴ Irrational number between 2 and 3 is √6

∴ Required irrational numbers are 6^1/2, 24^1/4

Method – II:
Irrational numbers between 2 and 3 are of the form 2.12111231234………….. and 3.13113111311113…….

Question 9.
State whether the following statements are true or false. Justify your answers.
Solution:

1. Every irrational number is a real number – True (since real numbers consist of rational numbers and irrational numbers)
2. Every rational number is a real number – True (same as above)
3. Every rational number need not be a rational number – False (since all rational numbers are real numbers).
4. \(\sqrt{n}\) is not irrational if n is a perfect square – True. (since by definition of an irrational number).
5. \(\sqrt{n}\) is irrational if n is not a perfect square – True. (same as above)
6. All real numbers are irrational – False (since real numbers consist of rational

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 7 Triangles Ex 7.4 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 7th Lesson Triangles Exercise 7.1

Question 1.
Show that in a right angled triangle, the hypotenuse is the longest side.
Solution:

Let a ΔABC be right angled at ∠B.
Then ∠A + ∠C = 90°
(i.e.,) ∠A and ∠C are both acute.
Now, ∠A < ∠B ⇒ BC < AC
Also ∠C < ∠B ⇒ AB < AC
∴ AC, the hypotenuse is the longest side.

Question 2.
In the given figure, sides AB and AC of ΔABC are extended “to points P and Q respectively. Also ∠PBC < ∠QCB. Show that AC > AB.

Solution:
From the figure,
∠PBC = ∠A + ∠ACB
∠QCB = ∠A + ∠ABC
Given that ∠PBC < ∠QCB
⇒∠A + ∠ACB < ∠A + ∠ABC
⇒ ∠ACB < ∠ABC
⇒ AB < AC
⇒ AC > AB
Hence proved.

Question 3.
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

Solution:
Given that ∠B < ∠A; ∠C < ∠D
∠B < ∠A ⇒ AO < OB [in ΔAOB] ……………… (1)
∠C < ∠D ⇒ OD < OC [in ΔCOD]…… (2)
Adding (1) & (2)
AO + OD < OB + OC
AD < BC
Hence proved.

Question 4.
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see figure). Show that ∠A >∠C and ∠B > ∠D.

Solution:

Given that AB and CD are the smallest and longest sides of quadrilateral ABCD.
From the figure,
In ΔBCD
∠1 > ∠2 [∵ DC > BC] ………………(1)
In ΔBDA
∠4 > ∠3 [∵ AD > AB] ………….(2)
Adding (1) & (2)
∠1 + ∠4 > ∠2 + ∠3
∠B > ∠D
Similarly,
In ΔABC, ∠6 < ∠7 [ ∵AB < BC] ……………….(3)
In ΔACD
∠5 < ∠8 …………. (4)
Adding (3) & (4)
∠6 + ∠5 < ∠7 + ∠8
∠C < ∠A ⇒ ∠A > ∠C
Hence proved.

Question 5.
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that
∠PSR > ∠PSQ.

Solution:
Given that PR > PQ;
∠QPS =∠RPS
PR> PQ
∠Q > ∠R
Now ∠Q +∠QPS > ∠R + ∠RPS
⇒ 180° – (∠Q + ∠QPS) < 180° – (∠R + ∠RPS)
⇒ ∠PSQ < ∠PSR ⇒ ∠PSR > ∠PSQ
Hence proved.

Question 6.
If two sides of a triangle measure 4 cm and 6 cm find all possible measurements (positive integers) of the third side. How many distinct triangles can be obtained ?
Solution:
Given that two sides of a triangle are 4 cm and 6 cm.
∴ The measure of third side > Differ-ence between other two sides.
third side > 6 – 4
third side > 2
Also the measure of third side < sum of other two sides
third side <6 + 4 < 10
∴ 2 < third side <10
∴ The measure of third side may be 3 cm, 4 cm, 5 cm, 6 cm, 7 cm, 8 cm, 9 cm
∴ Seven distinct triangles can be obtained.

Question 7.
Try to construct a triangle with 5 cm, 8 cm and 1 cm. Is it possible or not ? Why ? Give your justification.
Solution:
As the sum (6 cm) of two sides 5 cm and 1 cm is less than third side. It is not possible to construct a triangle with the given measures.