Srinivas

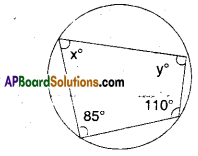
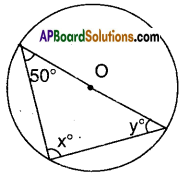
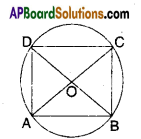
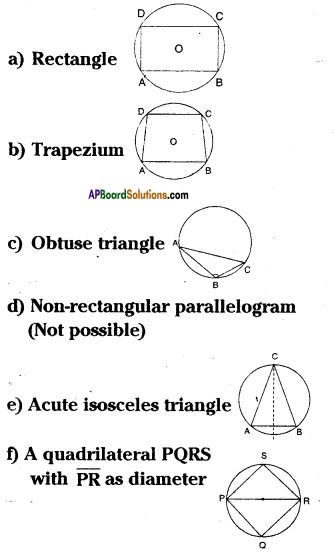
AP State Syllabus AP Board 9th Class Maths Solutions Chapter 14 Probability InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 14th Lesson Probability InText Questions

Do This

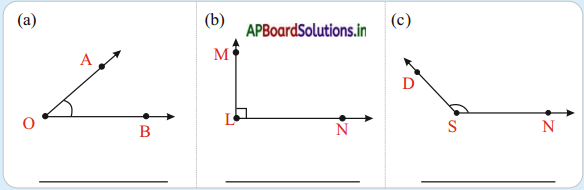
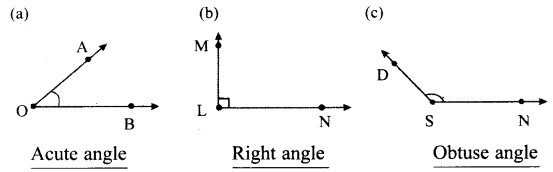
Question 1.
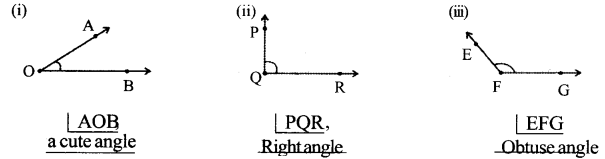
Observe the table given in the previous page (Textbook Page No. 293) and give some other example for each term. [Page No. 294]
Solution:
Certain : Independence day on 15th Aug.
More likely : When a die is thrown, the chance of getting a number less than or equal to 5. Equally likely : When a coin is tossed, getting a head.
Less likely : When a die is thrown, the chance of getting neither prime nor composite. Impossible : When a die is thrown, getting a negative number.

Question 2.
Classify the following statements into the categories less likely, equally . likely, more likely. [Page No. 294]

a) Rolling a die and getting a number 5 on the top face.
b) Getting a cold wave in your village in the month of November.
c) India winning the next soccer (foot ball) world cup.
d) Getting a tail or head when a coin is tossed.
e) You buy a lottery ticket and win the jackpot.
Solution:
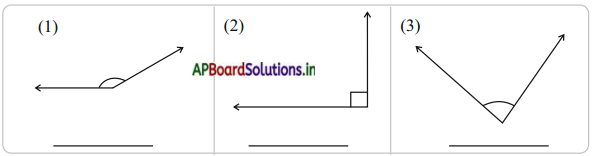
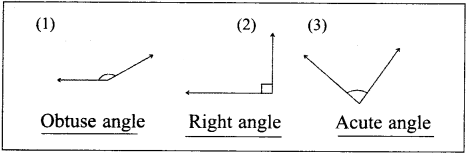
a) less likely
b) more likely
c) less likely
d) equally likely
e) more likely

Try These

Question 1.
If you try to start a scooter, what are the possible outcomes ? [Page No. 295]
Solution:
[Starts], [Doesn’t start]

Question 2.
When you roll a die, what are the six possible outcomes ? [Page No. 295]
Solution:
1, 2, 3, 4, 5 and 6.

Question 3.
When you spin the wheel shown, what are the possible outcomes ? (Outcomes here means the possible sector where the pointer stops) [Page No.295]

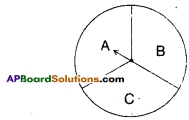
Solution:
A, B and C.

Question 4.
You have ajar with five identical balls of different colours. [White, Red, Blue, Grey and Yellow] and you have to pick up (draw) a ball without looking at it. List the possible outcomes you get. [Page No. 295]

Solution:
White ball, Red ball, Blue ball. Grey ball and Yellow ball.

Think, Discuss and Write

In rolling a die [Page No. 295]

Question
Does the first player have a greater chance of getting a six on the top face ?
Solution:
No. The chance of getting 6 on the top face is independent of the turn of the player.

Question
Would the player who played after him have a lesser chance of getting a six on the top face?
Solution:
No.

Question
Suppose the second player got a six on the top face. Does it mean that the third player would not have a chance of getting a six on the top face ?
Solution:
No. The third player may or may not get six on the top face. It is indepen¬dent of 2nd player’s outcome.

Do This

Question
Toss a coin for number of times as shown in the table. And record your findings in the table [Page No. 296]
Solution:

Question
What hapens if you increase the num- her of tosses more and more.
Solution:
If you increase the number of tosses more and more they are equally likely chances to get a head or a tail.
Note : This could also be done by the students with a die, roll it for large number of times and observe!

Do This

If three coins are tossed simulta¬neously : [Page No. 299]

a) Write all possible outcomes.
Solution:
HHH, HHT, HTH, THH, HTT, THT, TTH, TTT, total 8 outcomes.

b) Number of possible outcomes.
Solution:
8

c) Find the probability of getting at least one head, (getting one or more than one head)
Solution:
P = \(\frac{\text { favourable outcomes }}{\text { total outcomes }}=\frac{7}{8}\)

d) Find the probability of getting at most two heads, (getting two or less than two heads)
Solution:
P = \(\frac{\text { favourable outcomes }}{\text { total outcomes }}=\frac{7}{8}\)

e) Find the probability of getting no tails.
Solution:
P = \(\frac{\text { favourable outcomes }}{\text { total outcomes }}=\frac{1}{8}\)

Try This

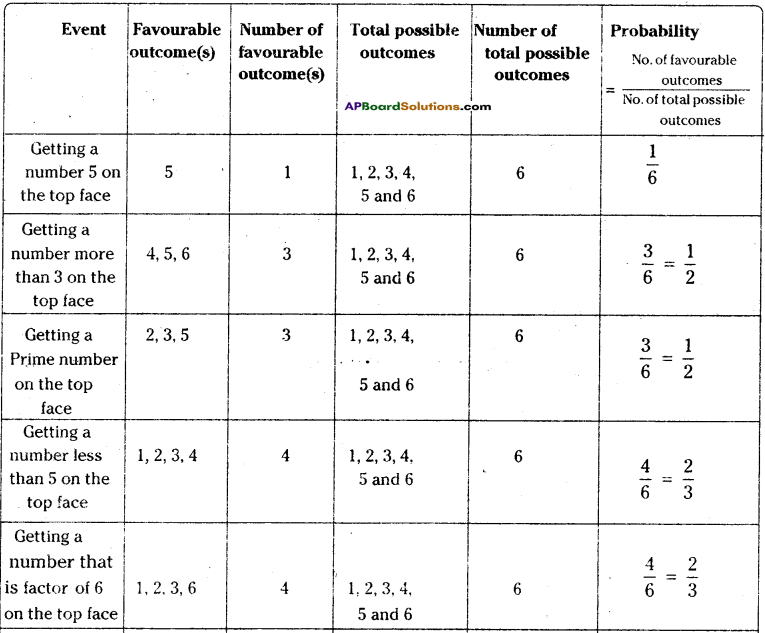
Find the probability of each event when a die is rolled once. [Page No. 300]

Try These

From the figure given below [Page No. 306]

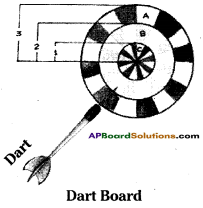
Question 1.
Find the probability of the dart hit¬ting the board in the circular region B. (i.e., ring B)
Solution:
Area of innermost ‘C’ circle = πr²
= π x 1² = π sq. units.
Area of the middle ‘B’ circle
= π (2² – 1²) = π (4 – 1) = 3π sq.units.
Area of the outermost ’A’ circle
= π (3² – 2²) = π (9 – 4) = 5π sq.units.
Probability of hitting the circle B

Question 2.
Without calculating, write the percent¬age of probability of the dart hitting the board in circular region ‘C’ (Le., ring C).
Solution:
\(\frac{1}{9}\) x 100% = 11\(\frac{1}{9}\)

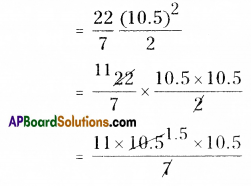
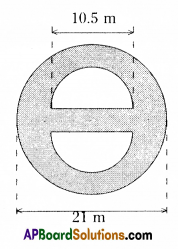
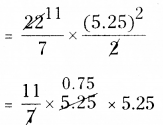
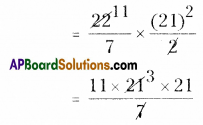
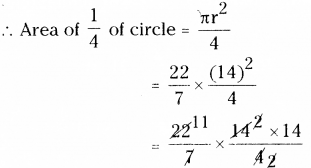
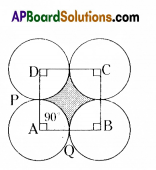
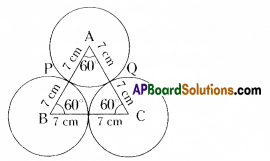
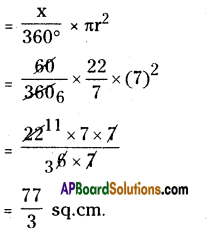
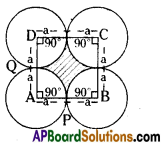
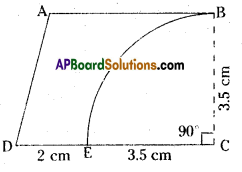
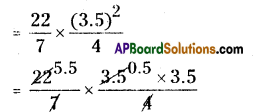
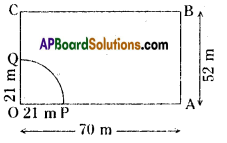
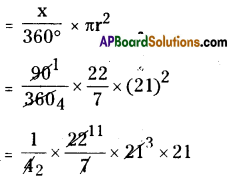
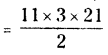
AP State Syllabus AP Board 9th Class Maths Solutions Chapter 4 Lines and Angles InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 4th Lesson Lines and Angles InText Questions

Question
Observe your surroundings carefully and write any three situations of your daily life where you can observe lines and angles. [Page No. 71]
Solution:
The edges of a blackboard; the edges of a ruler/scale and the edges of a table gives the idea of lines and their corners give the idea of angles.

Question
Draw the pictures in your notebook and collect some pictures. [Page No. 71]
Solution:

Think, Discuss and Write

What is the difference between inter-secting lines and concurrent lines ? [Page No. 74]
Solution:
If the number of lines meeting at a point are only two then they are said to be intersecting lines whereas if the lines are three or more than three meeting at a point then they are said to be concurrent lines.

Do These

Question 1.
Write the complementary, supplementary and conjugate angles for the following angles, a) 45° b) 75° c) 215° d) 30° e) 60° f) 90° g) 180° [Page No. 76]
Solution:

Question 2.
Which pairs of the following angles become complementary or supplementary. [Page No. 76]

Solution:
The angles formed by the figures (i) and (ii) are complementary.
The angles formed by the figures (ii) and (iii) are supplementary.

Try This

Question 1.
Find the pairs of adjacent and non- adjacent angles in the given figures. [Page No. 77]

Solution:
In figure (i) ∠1 and ∠2 are pair of adjacent angles.
In figure (ii), no adjacent angles.
In figure (iii) (∠1, ∠2), (∠2, ∠3) are pairs of adjacent angles.
In figure (iv) ∠1 and Z2 are adjacent angles.

ii) List the adjacent angles in the given figure. [Page No. 77]

Solution:
In the given figure
(∠1, ∠2), (∠3, ∠4), (∠4,∠5) and (∠3, ∠5) are the pairs of adjacent angles.

Think Discuss and Write

Question
Linear pair of angles are always supplementary. But supplementary angles need not form a linear pair. Why ? [Page No. 77]
Solution:
A pair of supplementary angles need not necessarily a linear pair because they may exists in separate figures.

Activity

Measure the angles in the following figure and complete the table.
[Page No. 78]

Solution:

Measure the four angles 1,2,3,4 in each of the above figure and complete the table:
[Page No. 79]

Solution:

Do This

Question 1.
Classify the given angles as pairs of complementary, linear pair, vertically opposite and adjacent angles. [Page No. 80]

Solution:
The pairs of angles a and b in the fig.(i) are linear pair of angles.
The pairs of angles a and b in the fig.(ii) are adjacent angles.
The pairs of angles a and b in the fig.(iii) are complementary angles*
The pairs of angles a and b in the fig.(iv) are vertically opposite angles.

Question 2.
Find the measure of angle ‘a’ in each figure. Give reasons in each case. [Page No. 81]
i)

a = 180° – 50° = 130°
(linear pair of angles)

ii)

a = 43°
( ∵ vertically opposite angles)

iii)

a = 360° – (209° + 96°)
= 360° – 305° = 55°
(∵ complete angle = 360°)

iv)

a = 90° – 63° = 27°
(pair of complementary angles )

Do These

Question 1.
Find the measure of each angle indi-cated in each figure where / and m are parallel lines intersected by a transversal n. [Page No. 87]

Solution:
x = 110° (alternate exterior angles)

Solution:
y = 84° (alternate interior angles)

Solution:
z = 180° – 100° = 80° .
(interior angles on the same side of transversal)

Solution:
s° = 53° (pair of corresponding angles)

Question 2.
Solve for x and give reasons. [Page No. 88]

11x + 2 = 75°
11x = 75 – 2 = 73
∴ x = \(\frac{73}{11}\)
(∴ pair of corresponding angles are equal).

Solution:
8x – 4 = 60°
8x = 60 + 4 = 64
∴ x = \(\frac{64}{8}\) = 8
(∴ alternate interior angles are equal)

Solution:
(14x- 1)°.= (12x + 17)°
14x – 12x = 17 + 1
2x = 18
x = \(\frac{18}{2}\) = 9
(∴ alternate exterior angles are equal)

Solution:
13x- 5 = 17x + 5
13x- 17x = 5 + 5
– 4x = 10
x = \(\frac{10}{-4}=\frac{-5}{2}\)
(∴ Pair of, corresponding angles are equal).

Activity

Question 1.
Take a scale and a ‘set sqaure’. Arrange the set sqare on the scale as shown in figure. Along the slant edge of set sqare draw a line with the pencil. Now slide your set square along its horizontal edge and again draw a line. We observe that the lines are parallel. Why are they parallel ? Think and discuss with your friends. [Page No. 88]
Solution:

A. Student Activity (For Reference .)
All slant lines are parallel making an angle of 60° with the horizontal line. In this figure horizontal line is transversal to the slant line and corresponding angles are equal.

Do This

Question
Draw a line \(\overline{\mathbf{A D}}\) and mark points B and C on it. At B and C, construct ∠ABQ and ∠BCS equal to each other as shown. Produce QB and SC on the other side of AD to form two lines PQ and RS.

Draw common perpendiculars EF and GH for the two lines PQ and RS. Measure the lengths of EF and GH. What do you observe ? What can you conclude from that ? Recall that if the perpendicular distance between two lines is the same, then they are parallel lines. [Page No. 89]


Solution:
As ∠ABQ =∠BCS and they lie on the same line AD we can say that BQ // CS. Now EF and GH are the perpendicular distances between two parallel lines PQ and R, we say EF = GH.

Try This

Question i)
Find the measure of the question marked angle in the given figure. [Page No. 90]

Solution:
? = 70°
[ ∵ from the figure, these two angles are exterior angles on the same side of the transversal]

ii) Find the angles which are equal to ∠P.
Solution:
∠P = ∠Q = ∠R = 110°
(corresponding angles)

Activity

Question
Draw and cut out a large triangle as shown in the figure.
Number the angles and tear them off.
Place the three angles adjacent to each other to form one angle as shown below. [Page No. 97]

1. Identify angle formed by the three adjacent angles ? What is its mea-sure ?
2. Write about the sum of the measures of the angles of a triangle. Now let us prove this statement
using the axioms; and theorems related to parallel lines.
Solution:
Student Activity.

Think, Discuss and Write

Question
If the sides of a triangle are produced in order, what will be the sum of exterion angles formed ? [Page No. 99]
Solution:
Let ΔABC and the sides of the triangle is formed by exterior angles.

∠3 = ∠B + ∠C
∠1 + ∠2 + Z∠3 = 2[∠A + ∠B + ∠C]
= 2 x 180° = 360°
∴ Sum of the exterior angles are 360°.

AP Board 9th Class Maths Solutions

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 13th Lesson Geometrical Constructions InText Questions

Try These

Question
Observe the sides, angles and diagonals of quadrilateral BEFD. Name the figures given below and write properties of figures. [Page No. 283]

Solution:
In fig. (1)
\(\overrightarrow{\mathrm{BF}}\) is the bisector of ∠B and ∠F.
In quad BEFD
BE = BD = DF = EF
It is a rhombus

In fig. (2)
BD = BE
FD = FE
∴ BEFD is a kite.
BF is bisector of ∠B and ∠F.

Try This

Question
Draw a circle, identify a point on it. Cut arcs on the circle with the length of the radius in succession. How many parts can the circle be divided into ? Give reasons. [Page No. 284]
Solution:

Let P be the centre of the circle.
A is any point on its circumference.
It can be divided into 2π parts
∴ \(\frac{\text { Circumference }}{\text { Radius }}=\frac{2 \pi r}{r}=2 \pi\)

Think, Discuss and Write

Question
Can you construct a triangle ABC with BC = 6 cm, ∠B = 60° and AB + AC = 5 cm? If , not, give reasons. (Page No. 286)
Solution:
We can’t construct a triangle with measures ∠B = 60°; BC = 6 cm and AB + AC = 5 cm.
∵ AB + AC < BC
Sum of any two sides of a triangle must be greater than the third side.

Think, Discuss and Write

Question
Can you construct the triangle ABC with the same measures by changing the base angle ∠C instead of ∠B ? Draw a rough sketch and construct it.
BC = 4.2cm. ∠C = 30°, AB – AC = 1.6 cm (Page No. 287)

Solution:

Steps of construction:

1. Construct ΔBCD where BC = 4.2 cm and ∠C = 30° and AC – AB = 1.6 cm.
2. Draw perpendicular bisector of BD which meets \(\overline{\mathrm{CD}}\) produced at A.
3. Join B, D.
4. ΔABC is the required triangle.

Try These

Can you draw the triangle with the same measurements as shown in the figure in alternate way ? (Page No. 289)
[Measurements : ∠B = 6Q°, ∠C = 45° and AB + BC + CA =11 cm]
[Hint: Take ∠YXL = 60°/2 = 30° and ∠XYM = 45°/2 = 22 \(\frac { 1 }{ 2 }\) ]

Solution:
→ Draw XY = 11 cm [AB + BC + CA = 11 cm]
Construct ∠YXP = 30° at X \(\left[\frac{B}{2}=\frac{60^{\circ}}{2}=30^{\circ}\right]\)
Construct ∠XYQ = 22\(\frac { 1 }{ 2 }\) at Y \(\left[\frac{\mathrm{C}}{2}=\frac{45^{\circ}}{2}=22 \frac{1}{2}^{\circ}\right]\)
→ \(\overrightarrow{\mathrm{XP}}\) and \(\overrightarrow{\mathrm{YQ}}\) meet at A.
→ At A, draw \(\overrightarrow{\mathrm{AB}}\) such that ∠XAB = 30° where B is a point on XY.
→ Also draw \(\overrightarrow{\mathrm{AC}}\) such that ∠YAC = 22\(\frac{1}{2}^{\circ}\) where C is a point on XY.
→ Δ ABC is the required triangle.

Try These

Question
What happens if the angle in the. circle segment is right angle ? What kind of segment do you obtain ? Draw the figure and give reason. [Page No. 290]
Solution:
If the angle in the circle segment is right angle i.e., 90°, then the angle subtended by it at the centre is 2 x 90° = 180°
Thus the line segment becomes the diameter and the circle segment becomes the semi-circle.

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.1 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 2nd Lesson Linear Equations in One Variable Exercise 2.1

Question
Solve the following Simple Equations:

(i) 6m = 12
(ii) 14p -42
(iii) -5y = 30
(iv) – 2x = – 12
(v) 34x = – 51
(vi) \(\frac{n}{7}\) = -3
(vn) \(\frac{2x}{3}\) = 8
(vui) 3x+1 = 16
(ix) 3p – 7 = 0
(x) 13 – 6n = 7
(xi) 200y – 51 = 49
(xii) 11n + 1 = 1
(xiii) 7x – 9 = 16
(xiv) 8x + \(\frac{5}{2}\) =13
(xv) 4x – \(\frac{5}{3}\) = 9
(xvi) x – \(\frac{4}{3}\) = 3\(\frac{1}{2}\)
Solution:
i) 6m = 12 ⇒ m = \(\frac{12}{6}\) ⇒ m = 2

ii) 14p = – 42p ⇒ P = \(\frac{-42}{14}\)
∴ p = -3

iii) -5y = 30 ⇒ y = \(\frac{30}{-5}\) = -6
∴ y = -6

iv) -2x = -12
⇒ 2x = 12
x = \(\frac{30}{-5}\)
= 6
∴ x = 6

v) 34x = -51
⇒ \(\frac{-3}{2}\) = \(\frac{-3}{2}\)
∴ x = \(\frac{-3}{2}\)

vi) \(\frac{n}{7}\) = -3
⇒ n = -3 x 7 = -21
∴ n = -21

vii) \(\frac{2x}{3}\) = 18 ⇒ 18 x \(\frac{3}{2}\) = 27
∴ x = 27

viii) 3x + 1 = 16
3x = 16 – 1 = 15
3x = 15
x = \(\frac{15}{3}\)
∴ x = 5

ix) 3p – 7 = 0
⇒ 3p = 7
∴ p = \(\frac{7}{3}\)

x) 13 – 6n = 7 ⇒ -6n = 7 – 13
⇒ -6n = -6 ⇒ n= \(\frac{-6}{-6}\)
∴ n = 1

xi) 200y – 51 = 49
⇒ 200y = 49 + 51
⇒ 200y = 100
⇒ y = \(\frac{100}{200}\)
∴ y = \(\frac{1}{2}\)

xii) 11n + 1 = 1
⇒ 11n = 1 – 1
= 11n = 0
⇒ n = \(\frac{0}{11}\) = 0
∴ n = 0

xiii) 7x – 9 = 16
⇒ 7x = 16 + 9
⇒ 7x = 25
∴ x = \(\frac{25}{7}\)

xiv) 8x + \(\frac{5}{2}\) = 13

xv) 4x – \(\frac{5}{3}\)

xvi) x + \(\frac{4}{3}\) = 3\(\frac{1}{2}\)
⇒ \(x+\frac{4}{3}=\frac{7}{2}\)
⇒\(\frac{7}{2}-\frac{4}{3}=\frac{21-8}{6}\)
∴ x = \(\frac{13}{6}\)

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 9 Area of Plane Figures Ex 9.2 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 9th Lesson Area of Plane Figures Exercise 9.2

Question 1.
A rectangular acrylic sheet is 36 cm by 25 cm. From it, 56 circular buttons, each of diameter 3.5 cm have been cut out. Find the area of the remaining sheet.
Solution:
The dimensions of a rectangular acrylic sheet = 36 cm × 25 cm.
∴ Its area = l × b
= 36 × 25 = 900 sq.cm
The diameter of a circular button = 3.5 cm
radius = r = \(\frac{d}{2}=\frac{3.5}{2}\) = 1.75 cm.
∴ Area of each button = πr²
= \(\frac{22}{7}\) × (1.75)²
= \(\frac{22}{7}\) × 1.75 × 1.75
= 9.625 sq.cm.
The area of 56 such buttons = 56 × 9.625 = 539 sq.cm.
∴ The area of remaining sheet
= Area of a rectangular sheet – Area of 56 buttons
= 900 – 539
= 361 sq.cm

Question 2.
Find the area of a circle inscribed in a square of side 28 cm.
[Hint. Diameter of the circle is equal to the side of the square]

Solution:
Diameter of a circle = d = side of a square = 28 cm.
∴ d = 28 cm
⇒ r = \(\frac{d}{2}=\frac{28}{2}\) = 14 cm
∴ Area of a circle = \(\frac{22}{7}\) × 14 × 14
= 22 × 28
= 616 sq.cm.

Question 3.
Find the area of the shaded region in each of the following figures.
[Hint:d + \(\frac{d}{2}\) + d/2 = 42]
d = 21
∴ side of the square 21 cm
i)

Solution:

∴ Side of a square, d = 21 cm.
Radius of a semicircle = r = \(\frac{\mathrm{d}}{2}=\frac{21}{2}\) = 10.5 cm
∴ Area of a semi-circle = \(\frac{\pi r^{2}}{2}\)

= 11 × 1.5 × 10.5
= 173.250 sq.cm.

∴ Area of 4 shaded semi-circles
= 4 × Area of each semi-circle
= 4 × 173.25 = 693 sq.cm.

Diameter of a big circle = 21 m

Diameter of a semicircle = 10.5 m.
Radius = \(\frac{10.5}{2}\) = 5.25 m.
∴ Area of semi-circle = \(\frac{\pi r^{2}}{2}\)

= 11 × 0.75 × 5.25
= 43.3125 sq.m.
Area of two semicircles
= 2 × 43.3125 = 86.6250 sq.m.
∴ Area of shaded region
= Area of big circle – Area of 2 semicircles
= 346.5 – 86.6250
= 259.8750 sq.m.

Question 4.
The adjacent figure consists of four small semi-circles of equal radii and two big semi-circles of equal radii (each 42 cm). Find the area of the shaded region
Solution:
Diameter of a bigger semi circle d = 42 cm
Radius, r = \(\frac { 42 }{ 2 }\) = 21 cm
Area of a bigger semi circle = \(\frac{\pi r^{2}}{2}\)

= 11 × 3 × 21
= 693 sq.cm

∴ Area of the shaded region
= Area of two bigger semi circles – Area of two smaller semi circles + Area of two smaller semi circles
= Area of two bigger semi circles
= 2 × Area of bigger semi circles
= 2 × 693 = 1386 sq.cm.

Question 5.
The adjacent figure consists of four half circles and two quarter circles.
If OA=OB=OC=OD= 14cm. Find the area of the shaded region.

Solution:

OA = OB = OC = OD = 14CM
Radius of \(\frac { 1 }{ 4 }\) of circle BXD, r = 14cm

= 154 sq.cm.
∴ Area of the quarter circle AYC
= 154 sq.cm
.’. Area of the shaded region = Area of quarter circle BXD – Area of semi circle OPB + Area of semi circle OQD + Area of quarter circle AYC – Area of semi circle ARO + Area of semi circle OSC
= Area of quarter circle BXD + Area of quarter circle AYC
= 154 + 154
= 308 sq.cm.

Question 6.
In adjacent figure A, B, C and D are centres of equal circles which touch externally is pairs and ABCD is a square of side 7 cm. Find the area of the shaded region.

Solution:

Side of a square,
AB = BC = CD = DA = 7 cm
Area of a square = s × s
= 7 × 7 = 49 sq.cm.
From the above figure,
Radius of a circle, r = \(\frac{\text { Side of a square }}{2}\)
= \(\frac{7}{2}\) = 3.5
Areas of 4 equal sectors are equal.
Angle of a sector APQ, x = 90°
Radius, r = 3.5 cm
Area of sector APQ

= 5.5 × 0.5 × 3.5
= 9.625 sq.cm.
Total area of 4 equal sectors = 4 × 9.625 = 38.5 sq.cm.
∴ Area of shaded region = Area of square ABCD – Area of 4 equal sectors
= 49 – 38.5
= 10.5 sq.cm.

Question 7.
The area of an equilateral triangle is 49√ cm². Taking each angular point as centre, a circle is described with radius equal to half the length of the side of the triangle as shown in the figure. Find the area of the portion in the triangle not included in the circles.

Solution:
From the given figure,
Δ ABC is an equilateral triangle.
∴ Area of an equilateral triangle
= 49√3 sq.em (given)
3 equal circles (whose radii are equal) are touch externally.
Each angle of a sector in the circle = 60°,
Radius r = 7 cm.
∴ The areas of 3 sectors are equal.
∴ Area of a sector APQ

∴ The area of 3 sectors
= 3 × \(\frac { 77 }{ 3 }\) = 77 sq. cm
∴ The area of the portion in the triangle not included in the circles
= area of ΔABC — area of 3 equal sectors
=49√3 – 77
=49 × 1.7321 – 77 (∵√3 = 1.7321)
= 84.8729 – 77
= 7.8729 sq.cm.

Question 8.
(i) Four equal circles, each of radius ‘a’ touch one another. Find the area between them.
(ii) Four equal circles are described about the four corners of a square so that each circle
touches two of the others. Find the area of the space enclosed between the circumferences
of the circles, each side of the square measuring 14 cm.
Solution:

The side of a square ABCD
AB = BC = CD = DA = a + a = 2a units.
∴ Area of a square = s × s
= 2a × 2a = 4a2 sq.units.
4 equal sectors are there.
In each sector,
The angle of a sector APQ, x = 90°
Radius, r = a units
Area of each sector APQ

∴ Area of 4 equal sectors
= 4 × \(\frac{\pi \mathrm{a}^{2}}{4}\) = πa² sq. units
= 2a × 2a = 4a2 sq.units. 4 equal sectors are there.
∴ The area between the circles
= Area of square sectors
= 4a² – πa²
= a² (4 – π) sq. units
= a² (4 – \(\frac { 22 }{ 7 }\) ) = \(\frac{6 a^{2}}{7}\) sq. units

Question 9.
From a piece of cardbord, in the shape ofa trapezium ABCD, and AB||CD and ∠BCD = 90°,= quarter circle is removed. Given AB = BC = 3.5 cm and DE =2 cm. Calcualte the area of the remaining piece of the cardboard. (Take π to be \(\frac{22}{7}\) )

Solution:
ABCD is a trapezium
AB || CD and ZBCD = 90°
AB = BC = 3.5 cm; DE = 2 cm.
Area of a trapezium ABCD :
Length of parallel sides, AB = 3.5 cm
CD = DE + EC
= 2 + 3.5 = 5.5 cm.

Distance between parallel sides,
BC = 3.5 cm.
∴ Area of a trapezium
= \(\frac { 1 }{ 2 }\) h (a + b)
= \(\frac { 1 }{ 2 }\) × BC (AB + CD)
= \(\frac { 1 }{ 2 }\) × 3.5 (3.5 + 5.5)
= \(\frac { 1 }{ 2 }\) × 3.5 × 9
= 3.5 × 4.5
= 15.75 sq.cm.

Area of quarter circle EBC :
Radius, r = 3.5 cm
∴ Area of quarter circle

= 5.5 × 0.5 × 3.5
= 9.625 sq.cm.

Area of the remaining piece of card board = Area of a trapezium – \(\frac { 1 }{ 2 }\) th of area of a circle
= 15.75 – 9.625
= 6.125 sq.cm.

Question 10.
A horse is placed for grazing inside a rectangular field 70 m by 52 m and is tethered to one corner by a rope 21 m long. How much area can it graze?

Solution:
From the above figure,
The sector represents the grazing area of a horse.
The angle of a sector OPQ, x = 90°
Radius of a sector OPQ, r = 21 m .
∴ Area of a sector


= 346.5 sq.m.
∴ The area of grazing = 346.5 sq.m.

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.1 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 13th Lesson Geometrical Constructions Exercise 13.1

Question 1.
Construct the following angles at the initial point of a given ray and justify the construction.
a) 90°
Solution:

• Let AB be the given ray.
• Produce BA to D.
• Taking A as centre draw a semi circle with some radius.
• With X and Y as Center draw two intersecting arcs of same radius.

Or

|

• Let \(\overrightarrow{\mathrm{AB}}\) be the given ray.
• With A as centre draw an arc of any radius.
• Mark off two equal arcs from X as shown in the figure with the same radius taken as before.
• Bisect the second segment.
• Join the point of intersection of above arcs, with A.
• ∠BAC is the required right angle.
• Join the point of intersection ‘C’ and ‘A’.
• ∠BAC = 90°

In ΔAXY; ∠YAX = 60° and
in ΔAYC ∠YAC = 30° ∠BAC = 90°

b) 45°
Solution:
Steps:

• Construct 90° with the given ray AB.
• Bisect it from ∠BAD = 45°

Or

Steps:

• Construct ∠BAC = 60°
• Bisect ∠BAC = ∠DAC = 30°
• Bisect ∠DAC such that ∠DAE = ∠FAC = 15°
• ∠BAE=45°

ΔAXZ is equilateral
and ∠YAZ = 15°
∴∠XAY = 45°

Question 2.
Construct the following angles using ruler and compass and verify by measuring them by a protractor.
a) 30°
Solution:

• Construct ∠ABY = 60°
• Bisect ∠ABY = 60°
• Such that ∠ABC = ∠CBY = 30°

b) 22\(\frac{1}{2}^{\circ}\)
Solution:

• Construct ∠ABD = 90°.
• Bisect ∠ABD such that ∠ABC = ∠CBD = 45°
• Bisect ∠ABC such that
  ∠ABE = ∠EBC = 22\(\frac{1}{2}^{\circ}\)

c) 15°
Solution:

Steps of construction : ,

• Construct ∠BAE = 60°
• Bisect ∠BAE such that ∠BAC = ∠CAE = 30°
• Bisect ∠BAC such that ∠BAF = ∠FAC = 15°

d) 75°
Solution:

Steps of construction :

• Construct ∠BAC = 60°
• Construct ∠CAD = 60°
• Bisect ∠CAD such that ∠BAE = 90°
• Bisect ∠CAE such that ∠BAF = 75°

e) 105°
Solution:

Steps of construction:

• Construct ∠ABC = 90°
• Construct ∠CBE = 30°
• Bisect ∠CBE such that the angle formed ∠ABD = 105°

f) 135°
Solution:

Steps of construction:

• Construct ∠ABC = 120°
• Construct ∠CBD = 30°
• Bisect ∠CBD such that the angle formed ∠ABE = 135°

Question 3.
Construct an equilateral triangle, given its side of length of 4.5 cm and justify the constraction.
Solution:
A.

• Draw a line segment AB = 4.5 cm.
• With B and A as centres draw two arcs of radius 4.5 cm meeting at C.
• Join C to A and B.
• ΔABC is the required triangle.

Justification:
In ΔABC
AB = ∠C ⇒ ∠C = ∠B
Also AB = BC ⇒ ∠C = ∠A
Hence ∠A = ∠B = ∠C
But ∠A + ∠B + ∠C = 180°
∴ ∠A = ∠B = ∠C = \(\frac{180^{\circ}}{3}\) = 60°

Question 4.
Construct an isosceles triangle, given its base and base angle and justify the construction. [Hint: You can take any measure of side and angle]
Solution:
A.

Steps:

• Draw a line segment AB of any given length.
• Construct ∠BAX and ∠ABY at A and B such that ∠A = ∠B.
• \(\overrightarrow{\mathrm{AX}}\) and \(\overrightarrow{\mathrm{BY}}\) will intersect at C.
• ΔABC is the required triangle.

Justification:
Drop a perpendicular CM to AB from C.
Now in ΔAMC and ΔBMC
∠AMC = ∠BMC [Right angle]
∠A = ∠B [Construction]
CM = CM (Common)
∴ ΔAMC ≅ ΔBMC
⇒ AC = BC [CPCT]

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 1 Real Numbers InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 1st Lesson Real Numbers InText Questions

Do This

Question 1.
Represent \(\frac{-3}{4}\) on a number line. (Page No.3)
Solution:

Step – 1: Divide each unit into four equal parts to the right and left side of zero on the number line.
Step – 2 : Take 3 parts after zero on its left side.
Step -3 : It represents \(\frac{-3}{4}\)

Question 2.
Write 0, 7, 10, -4 in p/q form (Page No.2)
Solution:

Question 3.
Guess my number : Your friend chooses an integer between 0 and 100. You have to find out that number by asking questions, but your friend can only answer ‘Yes’ or ‘No’. What strategy would you use ? (Page No.3)
Solution:
Let my friend choosen 73; then my questions may be like this.

Q : Does it lie in the first 50 numbers ?
A: No .

Q : Does it lie between 50 and 60 ?
A: No

Q : Does it lie between 60 and 70 ?
A: No

Q : Does it lie between 70 and 80 ?
A: Yes
[then my guess would be “it is a number from 70 to 80]

Q : Is it an even number ?
A: No
[my guess : it should be one of the numbers 71, 73, 75, 77 and 79]

Q : Is it a prime number ?
A: Yes
[my guess : it may be 71, 73 or 79]

Q : Is it less than 75 ?
A: Yes
[my guess : it may be either 71 or 73]

Q : Is it less than 72 ?
A: No

Then the number is 73.
Therefore the strategy is
→ Use number properties such as even, odd, composite or prime to determine the number.

Do This

Question (i)
Find five rational numbers between 2 and 3 by mean method. (Page No.4)
Solution:
We know that \(\frac{a+b}{2}\) is a rational
between any two numbers a and b.
Let a = 2 and b = 3

Question (ii)
Find 10 rational numbers between \(\frac{-3}{11}\) and \(\frac{8}{11}\) (Page No.4)
Solution:
\(\frac{-3}{11}<\left[\frac{-2}{11}, \frac{-1}{11}, \frac{0}{11}, \frac{1}{11}, \frac{2}{11}, \frac{3}{11}, \frac{4}{11}, \frac{5}{11}, \frac{6}{11}, \frac{7}{11}\right]<\frac{8}{11}\)

Do This

Question
Find the decimal form of
(i) \(\frac{1}{17}\) (Page No.5)
Solution:

\(\frac{1}{19}\) = 0.052631

(ii) \(\frac{1}{19}\)(Page No.5)
Solution:

Try These

Question 1.
Find the decimal values of the following. (Page No.6)
Solution:
i) \(\frac{1}{2}\) = 0.5
ii) \(\frac{1}{2^{2}}=\frac{1}{4}\) = 0.25
iii) \(\frac{1}{5}\) = 0.2
iv) \(\frac{1}{5 \times 2}=\frac{1}{10}\) = 0.1
v) \(\frac{3}{10}\) = 0.3
vi) \(\frac{27}{25}\)

vii) \(\frac{1}{3}\)
Solution:

viii) \(\frac{7}{6}\)
Solution:

ix) \(\frac{5}{12}\)
Solution:

x) \(\frac{1}{7}\)
Solution:

Think, Discuss and Write

Question 1.
Kruthi said √2 can be written as \(\frac{\sqrt{2}}{1}\) which is in form. So √2 is a rational number. Do you agree with her argument ? (Page No.10)
Solution:
No.
Writing √2 = \(\frac{\sqrt{2}}{1}\) is not in the \(\frac { p }{ q }\) form.
Since p and q are integers and √2 is not an integer.

Try These

Question 1.
Find the value of √3 upto six decimals.(Page No.10)
Solution:

Step 1 :
Write 3 as 3.00 00 00 00 00 00 00
Step – 2 :
Group the zeros in pairs (i.e.) make periods.
Step – 3 :
Find the square root using long division method.
∴ √3 = 1.732050

Try These

Question 1.
Locate √5 and -√5 on the number line [Hint 5 = 2² + 1²](Page No.12)
Solution:
Step – 1 :
At zero draw a rectangle of length 2 units and breadth 1 unit.

Step – 2 :

Step – 3 :
Using compass draw an arc of radius OB with centre ‘O’ which cuts the num-ber line at D and D¹.

Step – 4 :
D represents √5 and D¹ represents – √5 on the number line.

Activity

Question
Constructing the ‘Square root spiral’. (Page No. 15)
Solution:
Take a large sheet of paper and construct the ‘Square root spiral’ in the following manner.
Step – 1 : Start with point ‘O’ and draw a line segment \(\overline{\mathrm{OP}}\) of 1 unit length.
Step – 2 : Draw a line segment \(\overline{\mathrm{PQ}}\) perpendicular to \(\overline{\mathrm{OP}}\) of unit length (where OP = PQ = 1) (see Fig.)
Step – 3 : Join 0, Q. (OQ = √2 )
Step – 4 : Draw a line segment OR of unit length perpendicular to \(\overline{\mathrm{OQ}}\)
Step – 5 : Join O, R. (OR = √3 )
Step – 6 : Draw a line segment RS of unit length perpendicular to \(\overline{\mathrm{OR}}\).
Step – 7 : Continue in this manner for some more number of steps, you will create a
beautiful spiral made of line segment \(\overline{\mathrm{PQ}}, \overline{\mathrm{QR}}, \overline{\mathrm{RS}}, \overline{\mathrm{ST}}, \overline{\mathrm{TU}}\) …………etc. Note that the line segments \(\overline{\mathrm{OQ}}, \overline{\mathrm{OR}}, \overrightarrow{\mathrm{OS}}, \overline{\mathrm{OT}}, \overline{\mathrm{OU}}\) …… etc., denote the lengths √2,√3, √4, √5, √6 respectively.

Do This

Question 1.
Find rationalising factors of the denominators of (Page No. 20)
i) \(\frac{1}{2 \sqrt{3}}\)
Solution:
\(\frac{1}{2 \sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{\sqrt{3}}{2 \times 3}=\frac{\sqrt{3}}{6}\)
∴ The R.F is √3

ii) \(\frac{1}{\sqrt{5}}\)
Solution:
\(\frac{3}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}}=\frac{3 \sqrt{5}}{5}\)
∴ The R.F is √5

iii) \(\frac{1}{\sqrt{8}}\)
Solution:

Do This;

Question
Simplify : (Page No. 23)

i) (16) ^1/2
Solution:
(16)^1/2 = (4 x 4)^1/2 = (42)^1/2 = 4^2/2 = 4

ii) (128)^1/7
Solution:
(128)^1/7 =(2 X 2 X 2 X 2 X 2 X 2 X 2)^1/7 = (2⁷)^1/7 = 2

iii) (343)^1/5
Solution:
(343)^1/5= (3 x 3 x 3 x 3 x 3)^1/5 = (3⁵)^1/5= 3

Question 1.
Write the following surds in exponen-tial form (Page No. 24)
i) √2
Solution:
√2 = 2^1/2

ii) 3√9
Solution:
\(\sqrt[3]{9}=\sqrt[3]{3 \times 3}=\sqrt[3]{3^{2}}=3^{\frac{2}{3}}\)

iii) \(\sqrt[5]{20}\)
Solution:
\(\begin{aligned}
\sqrt[5]{20}=\sqrt[5]{2 \times 2 \times 5} &=\sqrt[5]{2^{2} \times 5} \\
&=2^{\frac{2}{5}} \times 5^{\frac{1}{5}}
\end{aligned}\)

iv) 17√19
Solution:
\(\sqrt[17]{19}=19^{\frac{1}{17}}\)

Question 2.
Write the surds in radical form. (Page No. 24)
i) 5^1/7 = \(\sqrt[7]{5}\)
ii) 17^1/6 = \(\sqrt[6]{17}\)
iii) 5^2/5 = \(\sqrt[5]{5^{2}}=\sqrt[5]{5 \times 5}=\sqrt[5]{25}\)
iv) 142^1/2 = \(\sqrt{142}\)

Andhra Pradesh AP Board 5th Class Maths Solutions 6th Lesson Geometry Textbook Exercise Questions and Answers.

AP State Syllabus 5th Class Maths Solutions Chapter 6 Geometry

Do these: (TextBook Page No.87)

Question 1.
Read the following points.

Answer:
Point – M, Point – S, Point – U, Point – G, Point – P, Point – R, Point – D.

Question 2.
Write any 5 distinct points from the above.
Answer:
Point – A, Point – B, Point – C, Point – E, Point – F.

Question 3.
Note down any 3 points in your note book and name them.
Answer:

Point – Q, Point – S, Point – T.

Do this: (TextBook Page No. 88)

Question 1.
Read the following line segments.

Answer:
Line segment – AB, line segment – CD, line segment – PQ, line segment – ST.

Question 2.
Draw some line segments by joining following points and name them.

Answer:

Line segment \(\overline{\mathrm{AB}}\)
Line segment \(\overline{\mathrm{BC}}\)
Line segment \(\overline{\mathrm{CM}}\)
Line segment \(\overline{\mathrm{DK}}\)

Question 3.
Find the line segments in the figures given below.

Answer:
Fig (i): \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\), \(\overline{\mathrm{CD}}\), \(\overline{\mathrm{DA}}\)
Fig (ii): \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\), \(\overline{\mathrm{CD}}\), \(\overline{\mathrm{DA}}\), \(\overline{\mathrm{EF}}\), \(\overline{\mathrm{GH}}\), \(\overline{\mathrm{FG}}\), \(\overline{\mathrm{EH}}\), \(\overline{\mathrm{AE}}\), \(\overline{\mathrm{BF}}\), \(\overline{\mathrm{CG}}\), and \(\overline{\mathrm{DH}}\).

Do this: (TextBook Page No. 90)

Observe the following rays and name them.

Answer:

OA ray, BC ray, DE ray and PQ ray.

Do this: (TextBook Page No. 91)

Question 1.
Read the following lines.

Answer:
Line AB, Line PQ, Line MN, Line XY.

Question 2.
Take any two points and draw a line.
Answer:

Exercise 1:

Question 1.
Take any six points on a paper and name them.
Answer:

Question 2.
Join the points given below. Name the line segments so formed in the figures.

Answer:

Line segment — AB
Line segment — AC
Line segment — BC

Line segment — PQ
Line segment — PR
Line segment — RS
Line segment — QS

Line segment — EF
Line segment — EG
Line segment — FH
Line segment — GI
Line segment — HI.

Question 3.
Classify the following as ray, line and line segment. Also name them.

Answer:
a) Line
b) Line segment
c) Ray

Question 4.
Check whether the statements are True (T) or False (F). If it is false, give the reason.

a) A ray has a definite length. ( )
Answer:
F

b) A ray has one end point. ( )
Answer:
T

c) A line segment has a fixed length. ( )
Answer:
T

d) A line segment has no end points. ( )
Answer:
F

e) A line has no end points. ( )
Answer:
T

Question 5.
Represent the rays from the figure given below.

Answer:
From figure, Ray – and Ray – .

Question 6.
Find rays, lines and line segments from the figure given below.

Answer:
Rays : \(\overrightarrow{\mathrm{BA}}\), \(\overrightarrow{\mathrm{BE}}\), \(\overrightarrow{\mathrm{CD}}\), \(\overrightarrow{\mathrm{CF}}\)
Lines : \(\overleftrightarrow{\mathrm{AE}}\), \(\overleftrightarrow{\mathrm{DF}}\)
Line segment: \(\overline{\mathrm{BC}}\)

Question 7.
How many straight lines can be drawn through ?
a) One point
b) Two distinct points.
Answer:
a) From one point many straight lines can be possible to draw.
b) From two distinct points only one line can be possible to draw.

Question 8.
a) Write any three points.
b) Write any Two rays.
c) Write any five line segments.

Answer:
a) Point – K, Point – P, Point – A
b) Ray – \(\overleftrightarrow{\mathrm{KY}}\), Ray – \(\overleftrightarrow{\mathrm{AT}}\)
c) Line segments : \(\overline{\mathrm{KP}}\), \(\overline{\mathrm{PA}}\), \(\overline{\mathrm{AT}}\), \(\overline{\mathrm{TY}}\) and \(\overline{\mathrm{KA}}\)

Do these: (TextBook Page No. 94)

Question 1.
Observe the adjacent figure and fill in the blanks.

a) Vertex is …………….
Answer:
O

b) Arms are ……………
Answer:
\(\overrightarrow{\mathrm{OA}}\) and \(\overrightarrow{\mathrm{OB}}\)

c) Angle is ……………..
Answer:
∠AOB

Question 2.
Observe the various items in your classroom and write the things where angles occur.
Answer:
Corners of black board.
Corners of table.
Corners of book.
Edges of room door etc.

Do this: (TextBook Page No.94)

Answer:

Do this: (TextBook Page No.95)

Question 1.
Observe the angles given below and classify them as acute, obtuse and right angles.

Answer:

Do this: (TextBook Page No.97)

Classify the angles given below.
25°, 30°, 45°, 120°, 150°, 90°, 160°, 95°, 100°, 60°, 80°, 75°, 110°

Acute angles : _____________
Answer:
25°, 30°, 45°, 60°, 75° and 80°.

Right angle: ______________
Answer:
90°

Obtuse angles: _____________
Answer:
95°, 100°, 110°, 120°, 150°.

Exercise 2:

Question 1.
Observe the following angles and write them.

Answer:

Question 2.
Observe the following. Name the type of angle.

Answer:

Question 3.
Observe the picture given below. Count the number of acute angles, obtuse angles and right angles.

No. of Right angles ___________
No. ofAcute angles ___________
No. of Obtuse angles ___________
Answer:
No. of Right angles 10
No. of Acute angles 10
No. of Obtuse angles 4.

Exercise 3:

Question 1.
State what figures are open and which are closed.

Answer:

Question 2.
Draw three simple closed figures by using straight lines only.
Answer:

Question 3.
Draw three simple closed figures by using both straight lines and curved lines.
Answer:

Question 4.
What is angle in a rectangle?
Answer:
A rectangle has right angle in its corners.

Question 5.
Square is a special case of rectangle.
What is its speciality in terms of sides?
Answer:
In square all sides are equal in lengths.

Question 6.
Why there are four angles in a rectangle?
Answer:
In a rectangle four line segments are joined at corners. So, it has four angles.

Question 7.
What are the properties of a rect angle?
Answer:
In a rectangle, opposite sides are equal in Lengths. Each angle is right angle.

Question 8.
Give some examples of articles in a square shape.
Answer:
Place of chalk box, Dice, Cube etc.

Do this: (TextBook Page No.103)

Question 1.
Here are some letters. Tick the letters which look different in the mirror.

Answer:

Do this: (TextBook Page No.104)

Question 1.
Put (✓) mark to the picture which have line of symmetry.

Answer:

Question 2.
Draw possible number of symmetrical lines for the given figures.

Answer:

Complete the following table.

Answer:

Do this: (TextBook Page No.107)

Complete the following table.

Answer:

Exercise 4:

Question 1.
Match each letter with its mirror image. The dotted line with every letter shows the mirror.

Answer:

Question 2.
Check whether the dotted line represents the line of symmetry or not and put a tick mark under the figure with line of symmetry.

Answer:

Question 3.
Draw possible lines of symmetry for the figures given below, wherever possible.

Answer:

Question 4.
Complete the following table.

Answer:

Try these: (TextBook Page No.109)

Question 1.
Arrange some patterns using .
Answer:

Question 2.
What should come next?

Answer:

Do this: (TextBook Page No.110)

Question 1.
Find the perimeter of the following.

Answer:
i) Perimeter of given figure = 10 cm + 3 cm + 10 cm + 3 cm = 26 cm
ii) Perimeter of given figure = 4 cm + 4 cm + 4 cm + 4 cm = 16 cm
iii) Perimeter of given figure = 3 cm + 5 cm + 4 cm = 12 cm
iv) Perimeter of given figure = 8 cm + 4 cm + 5 cm + 4 cm = 21 cm.

Question 2.
Find the perimeter of the following rectangles.

Answer:

Do these: (TextBook Page No.112)

Question 1.
Find the perimeter of a square with a side of 3 ems.
Answer:
Length of side of square 3 cm
Perimeter of a square = 4 × 3 cm = 12 cm.

Question 2.
Find the perimeter of a square with a side of 12 ems.
Answer:
Length of side of square = 12 cm
Perimeter of a square 4 × 12 = 48 cm.

Exercise 5:

Question 1.
Find the perimeter of a rectangular field whose length is 40 m and breadth is 25 m.
Answer:
Length of rectangular field l = 40 cm
Breadth of rectangular field b = 25 m
Perimeter of rectangular field = P
= 2l + b
= 2 × 40 + 2 × 25
= 80 + 50 = 130 m.

Question 2.
Find the perimeter of a park in square shape side with 25m.
Answer:
Side of square = 25 m
Perimeter of a square = 4 × 25 = 100 m

Question 3.
Find the area of a square whose one side is 13 cms.
Answer:
Side of square = 13 cm
Area of a square = 13 × 13 = 169 sq cm

Question 4.
Find the area of a black board with a length of 240 cms and breadth 120 cms.
Answer:
Length of black board = 240 cm
Breadth of black board = 120 cm
Area of black board = 240 × 120 = 28,800 sq cm.

Question 5.
Find the cost of fencing to a square park whose side is 200 m. Cost for lm is ^ 30.
Answer:
Side of a square park = 200 m
Area of a square = 200 × 200 = 40,000 sq m
Fencing cost per 1 m = ₹ 30
Cost of fencing 40,000 sq m = 40,000 × 30 = ₹ 12,00,000.

Question 6.
A piece of wire is 28 cm long. What will be the length of each side, if the wire is used to form a square?
Answer:
Length of a piece of wire = 28 cm
Required length of wire for making square = 4 × 28 = 112 cm

Andhra Pradesh AP Board 3rd Class EVS Solutions 4th Lesson Our Body Parts Textbook Exercise Questions and Answers.

AP State Syllabus 3rd Class EVS Solutions Lesson 4 Our Body Parts

I. Conceptual Understanding:

Question 1.
Name the parts that you see on the your face.
Answer:
I can see eyes, nose, mouth, ears, cheeks, chin hair, forehead on my face in the mirror.

Question 2.
Name the parts of the body that you use to speak over the phone ?
Answer:
I use the following body parts when I speak over the phone.

1. Ears to hear others voice.
2. Mouth and tongue to speak
3. Hands to handle the phone.

Question 3.
Write three good habits you have.
Answer:
I have the following good habits.

1. I will brush my teeth twice a day.
2. I will wash my hands properly before and after eating.
3. I will trim my nails once in a week.

II. Questioning and Hypothesis:

Question 4.
What will happen if you are silent when someone gives you a bad touch ?
Answer:

1. If you are silent when some one gives you a bad touch you feel uncomfortable.
2. It will become habit to them to give bad touch.
3. Do not allow anyone to touch or tickle you. Say no to bad touch.
4. Never be afraid to shout and say “Don’t touch me”.

III. Experiments & Field Observations:

Question 5.
Ravi observed his dress in the mirror and wrote his feelings / appreciation.
I look good, my dress is clean and healthy.
Observe your dress in the mirror and write your observations as Ravi.
Answer:

1. I look so good in this dress.
2. My good appearance also increases my confidence level.
3. I also look healthy with my clean & neat dressing.

IV. Information Skills – Project Work:

Question 6.
Observe your friends and write some good habits practised by them.
Answer:
I have observed the following good habits practised by my friends to be healthy.

1. They brush their teeth twice a day.
2. They trim their nails once in a week.
3. They drink plenty of water.
4. Some of them exercise daily.
5. They eat fresh fruits and vegetables.
6. They wash their hands properly before and after eating.

V. Drawing Pictures and Model Making:

Question 7.
Label the parts.

Answer:
Student Activity.

VI. Appreciation, values and creating awareness towards bio-diversity:

Question 8.
What will you do after using a toilet ?
Answer:

1. After using a toilet wash it properly with water and with toilet cleaner if necessary.
2. Wash your hands and legs with soap.
3. Turn off the taps properly to avoid wastage of water.

Additional Questions:

I. Conceptual Understanding:

Question 1.
Basically our body is divided into how many parts ?
Answer:
Basically our body is divided into three parts they are head, trunk and limbs (legs and hands)

Question 2.
Look at these pictures. And answer the following.

1) What are they doing ?
Answer:
They are reading, eating, clapping, cutting, walking, running and playing.

2) How do you clap ?
Answer:
I clap with my hands.

3) What activities can we do with our hands ?Answer:
Answer:
Holding things, clapping, cutting.

4) What activities can we do with our legs ?
Answer:
Walking, running and playing.

Question 3.
Mention the names of fingers.

Answer:

Thumb, Index finger, Middle finger, Ring finger and Little finger are the names of fingers.

Question 4.
What are the activities related to good touch ?
Answer:

“A good touch” is that cares for us and makes us feel safe.
The activities that related to good touch are

1. Hugs and kisses by parents.
2. Friendly hugs by family members.
3. Patting by father.
4. Shaking hands.

Question 5.
What is a “Bad touch” and what are the activities related to “bad touch”.
Answer:
“Bad touch” is any touch that we don’t want or makes us feel scared.
Activities related to ‘Bad touch’ are :

children must know which touch is good and which is bad and be away from bad touch.

II. Experiments & Field Observations:

Question 6.
Students activity 1 :
Name the parts that help us to :
1. Watch T.V.: __________
2. Listening music: __________
3. Sing songs: __________
4. Taste chocolate: __________
5. Smell flowers: __________
6. Draw pictures: __________
7. Kick the ball: __________

Answer:
Student activity.

III. Appreciation, Values:

Question 7.
Who are physically challenged ? What is our responsibility towards physically challenged ?
Answer:

1. “Physically challanged” persons are those who will have disabilities to do work due to an accident or birth defects.
2. We should be kind to them and help them. It is our responsibility.

Question 8.
Children do you know how to wash your hands ?
Answer:
“Children it is essential to know how to wash your hands in this ‘Carona’ time.

See the above pictures and follow while washing your hands, to prevent us from harmful viral diseases like ‘Carona’.

Question 10.
Children check how good you are.
Write (✓) mark (or) wrong (✗) mark against each.
1. Eat good food. ( )
2. Play video games. ( )
3. Drink plenty of water daily. ( )
4. Wash hands after using toilet. ( )
5. Wash hands before taking food. ( )
6. Take bath monthly. ( )
7. Do not brush teeth daily. ( )
8. Trim nails once a month. ( )
9. Stand before mirror to see how neat & fresh I am after bath and dressing. ( )
Answer:
Student Activity.

Multiple Choice Questions:

Question 1.
________ connects the head with the trunk.
a) Head
b) Neck
c) Hand
d) Legs
Answer:
b) Neck

Question 2.
________ sense organs are used to taste.
a) Nose
b) Eyes
c) Skin
d) Tongue
Answer:
d) Tongue

Question 3.
Our nose help us to ________ and ________
a) breathe and smell
b) smell and taste
c) a & b
d) none
Answer:
a) breathe and smell

Question 4.
We should keep our body ________ and stay strong.
a) dirty
b) clean
c) healthy
d) none
Answer:
b) clean

Question 5.
We should take ________ food to be strong.
a) dirty
b) clean
c) healthy
d) none
Answer:
c) healthy

Question 6.
We have ________ sense organs.
a) five
b) four
c) three
d) none
Answer:
a) five

Question 7.
If someone touches your private parts it is called ________.
a) touch
b) good touch
c) bad touch
d) none
Answer:
c) bad touch

Question 8.
________ touch cares for us and makes us feel safe.
a) Good
b) Bad
c) Both
d) None
Answer:
a) Good

Question 9.
________ covers the internal organs of our body.
a) Skin
b) Eyes
c) Trunk
d) Legs
Answer:
a) Skin

Question 10.
Our body parts need ________ to perform different works.
a) Coordination
b) difference
c) permission
d) all
Answer:
a) Coordination

Question 11.
Child line free emergency No. to protect children is ________.
a) 1098
b) 1048
c) 1038
d) 1068
Answer:
a) 1098

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 12 Circles Ex 12.5 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 12th Lesson Circles Exercise 12.5

Question 1.
Find the values of x and y in the figures given below.
i)

Solution:
From the figure x = y [ ∵ angles opp. to opp. to equal sides]
But x + y + 30° = 180°
∴ x + y = 180° – 30° = 150°
⇒ x + y = \(\frac { 150° }{ 2 }\) = 75°

ii)

Solution:
From the figure x° + 110° = 180°
[ ∵ Opp. angles of a cyclic quad, are supplementary]
y + 85°= 180°
∴ x= 180° – 110°; y = 180° – 85°
x = 70°; y = 95°

iii)

Solution:
From the figure x = 90° [angle in a semi-circle]
∴ y = 90° – 50° [∵ angle sum property]
= 40°

Question 2.
Given that the vertices A, B, C of a quadrilateral ABCD lie on a circle. Also ∠A + ∠C = 180°, then prove that the vertex D also lie on the same circle.
Solution:
Given : ∠A + ∠C = 180°
∴ ∠B + ∠D = 360° – 180°
[ ∵ sum of the four angles of a quad. is 360 ].
Now in □ABCD, sum of the pairs of opp. angles is 180°.
∴ □ABCD must be a cyclic quadrilateral, i.e., D also lie on the same circle on which the vertices A, B and C lie. Hence proved.

Question 3.
Prove that a cyclic rhombus is a square.
Solution:

Let □ABCD be a cyclic rhombus,
i.e., AB = BC = CD = DA and
∠A + ∠C = ∠B + ∠D = 180°
But a rhombus is basically a parallelo-gram.

Question 4.
For each of the following, draw a circle and inscribe the figure given. If a poly¬gon of the given type can’t be in-scribed, write not possible.
a) Rectangle
b) Trapezium .
c) Obtuse triangle
d) Non-rectangular parallelogram
e) Acute isosceles triangle
f) A quadrilateral PQRS with PR as diameter.
Solution:

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 15 Proofs in Mathematics Ex 15.4 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 15th Lesson Proofs in Mathematics Exercise 15.4

Question 1.
State which of the following are mathematical statements and which are not ? Give reason.
i) She has blue eyes.
Solution:
This is not a mathematical statement. no mathematics is involved in it.

ii) x + 7 = 18
Solution:
This is not a statement, as its truthness cant be determined.

iii) Today is not Sunday.
Solution:
This is not a statement. This is an am biguous open sentence.

iv) For each counting number x, x + 0 = x.
Solution:
This is a mathematical statement.

v) What tune is it?
Solution:
This is not a riathematical statement.

Question 2.
Find counter examples to disprove the following statements.
i) Every rectangle is a square.
Solution:

A rectangle and square are equiangular i.e., all the four angles are right angles. This doesn’t mean that they have equal sides.

ii) For any integers x and y,
\(\sqrt{x^{2}+y^{2}}\) = x + y
Solution:
Let x = 3; y = 8
\(\sqrt{x^{2}+y^{2}}=\sqrt{3^{2}+8^{2}}\)
= \(\sqrt{9+64}=\sqrt{73}\)

x + y = 3 + 8 = 11
Here, √73 ≠ 11
i.e., \(\sqrt{x^{2}+y^{2}}\) ≠ x + y

iii) If n is a whole number then 2n² +11 is a prime.
Solution:
If n = 11 then 2n²+ 11 = 2 (11)² + 11
= 11 (2 × 11 + 1) = 11 × (22 + 1)
= 11 × 23 is not a prime.

iv) Two triangles are congruent if all their corresponding angles are equal.
Solution:

If the corresponding angles are equal then the triangles are only similar.

v) A quadrilateral with all sides are equal is a square.
Solution:
A rhombus is not a square, but all its sides are equal.

Question 3.
Prove that the sum of two odd numbers is even.
Solution:

Question 4.
Prove that the product of two even numbers is an even number.
Solution:

Question 5.
Prove that if x is odd, then x² is also odd.
Solution:
Let x be an odd number.
Then x = 2m + 1
(general form of ah odd number) Squaring on both sides,
x² = (2m + 1)²
= 4m² + 4m +1
= 2 (2m² + 2m) + 1
= 2K + 1 where K = 2m²+ 2
Hence x² is also odd.

Question 6.
Examine why they work ?
Choose a number. Double it. Add nine. Add your original number. Divide by three. Add four. Subtract your original number. Your result is seven.
Solution:
Choose a number = x say
Double it = 2x
Add nine = 2x + 9
Add your original number
= 2x + 9 + x = 3x + 9
Divide by 3 = (3x + 9) ÷ 3
= \(\frac{3 x}{3}+\frac{9}{3}\) = x + 3
Add 4 ⇒ x + 3 + 4 = x + 7
Subtract your original number =
x + 7 – x = 7
Your result is 7 – True.

ii) Write down any three digit number (for example, 425). Make a six digit number by repeating these digits in the same order 425425. Your new number is divisible by 7, 11 and 13.
Solution:
Let a three digit number be xyz.
Repeat the digit = xyzxyz
= xyz × (1001)
= xyz × (7 × 11 × 13)
Hence the given conjecture is true.

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 15 Proofs in Mathematics Ex 15.3 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 15th Lesson Proofs in Mathematics Exercise 15.3

Question 1.
Take any three consecutive odd numbers and find their product, for example 1 × 3 × 5 = 15;
3 × 5 × 7 = 105: 5 × 7 × 9 = ……………
ii) Take any three consecutive even numbers and add them, say,
2 + 4 + 6 = 12; 4 + 6 + 8 = 18:
6 + 8 + 10 = 24; 8 + 10 + 12 = 30 ….
so on. Is there any pattern you can guess in these sums ? What can von conjecture about them ?
Solution:
i) 1 × 3 × 5 = 15
3 × 5× 7 = 105
5 × 7 × 9 = 315
7 × 9 × 11 = 693

1. The product of any three consecutive odd numbers is odd.
2. The product of any three consecutive odd numbers is divisible by ’3′.
3. 2 + 4 + 6 = 12; 4 + 6 + 8= 18;
   6 + 8 + 10 = 24; 8 + 10 + 12 = 30
4. The sum of any three consecutive even numbers is even.
5. The sum of any three consecutive even numbers is divisible by 6
6. The sum of any three consecutive even numbers is a multiple of 6.

Question 2.
Go back to Pascal’s triangle.
Line-1: 1=11°
Line-2: 11 = 11¹
Line-3 : 121 = 11²
Make a conjecture about line – 4 and line – 5.

Does your conjecture hold ? Does your conjecture hold for line – 6 too ?
Solution:
Line-4 : 1331 = 11³
Line-5 : 14641 = 11⁴
Line – 6 : 11⁵
∴ Line – n = 11^n-1
Yes the conjecture holds good for line – 6 too.

Question 3.
Look at the following pattern.
i) 28 = 2² × 7¹;
Total number of factors
(2+ 1)(1 + 1) = 3 × 2 = 6
28 is divisible by 6 factors i.e.,
1, 2, 4, 7, 14, 28.
ii) 30 = 2¹ × 3¹ × 5¹, Total number of .
factors (1 + 1) (1 + 1) (1 + 1) = 2 × 2 × 2 = 8
30 Is divisible by 8 factors i.e., 1, 2, 3, 5, 6, 10, 15 and 30
Find the pattern.
[Hint : Product of every prime base exponent +1)
Solution:
24 = 2³ × 3¹
24 has (3+1) (1 + 1) = 4 × 2 = 8 factors
[1, 2, 3, 4, 6, 8, 12 and 24]
36 = 2² × 3²
Number of factors = (2 + 1) (2 + 1)
3 × 3 = 9 [ 1, 2, 3. 4, 6, 9, 12, 18 and 36]
If N = a^p. b^q . c^r…….. where N is a natural number.
a. b, c … are primes and p, q, r ……. are positive integers then, the number of factors of N =(p- 1)(q+ 1)(r + 1)

Question 4.
Look at the following pattern :
1² = 1
11² = 121
111² = 12321;
1111² = 1234321
11111² = 123454321
Make a conjecture about each of the following
111111² =
1111111² =
Check if your conjecture is true.
Solution:
111111² = 12345654321
1111111² = 1234567654321
(111………. n-times)² = (123 … (n- 1) n (n – 1) (n – 2) 1)
The conjecture is true.

Question 5.
List five axioms (postulates) used in text book.
Solution:

1. Things which are equal to the same things are equal to one another.
2. If equals are added to equals, the sums are equal.
3. If equals are subtracted from equals, the differences are equal.
4. When a pair of parallel lines are in-tersected by a transversal, the pairs of corresponding angles are equal.
5. There passes infinitely many lines through a given point.

Question 6.
In a polynomial p(x) = x² + x + 41 put different values of x and find p(x). Can you conclude after putting different values of x that p(x) is prime for all. Is ‘x’ an element of N ? Put x = 41 in p(x). Now what do you find ?
Solution:
p(x) = x² + x + 41
p(0) = 0² + 0 + 41 = 41 – is a prime
p(1) = 1² + 1 + 41 = 43 – is a prime
p(2) = 2² + 2 + 41 = 47 – is a prime
p(3) = 3² + 3 + 41 = 53 – is a prime
p(41) = 41² + 41 + 41
= 41(41 + 1 + 1)
= 41 x 43 is not a prime.
∴ p(x) = x²+ x + 41 is not a prime for all x.
∴ The conjecture “p(x) = x² + x + 41 is a prime” is false.