Class 10

SCERT AP 10th Class Physics Study Material Pdf 9th Lesson విద్యుత్ ప్రవాహం Textbook Questions and Answers.

AP State Syllabus 10th Class Physical Science 9th Lesson Questions and Answers విద్యుత్ ప్రవాహం

10th Class Physical Science 9th Lesson విద్యుత్ ప్రవాహం Textbook Questions and Answers

అభ్యసనాన్ని మెరుగుపరుచుకోండి

ప్రశ్న 1.
లోరెంజ్ – డ్రూడ్ ఎలక్ట్రాన్ సిద్ధాంతం సహాయంతో విద్యుత్ ప్రవాహానికి ఎలక్ట్రానులు ఎలా కారణమో వివరించండి. (AS1)
జవాబు:
1) లోహాల వంటి వాహకాలలో అధిక సంఖ్యలో స్వేచ్ఛా ఎలక్ట్రాన్లు, ధనాత్మక అయాన్లు నిర్దిష్ట స్థానాలలో ఉంటాయని 19వ శతాబ్దానికి చెందిన శాస్త్రవేత్తలైన డ్రూడ్ మరియు లోరెంజ్ ప్రతిపాదించారు. ఈ ధనాత్మక అయానుల అమరికను లాటిస్ అంటాము.

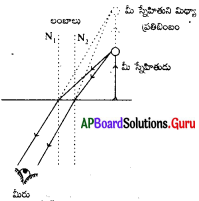
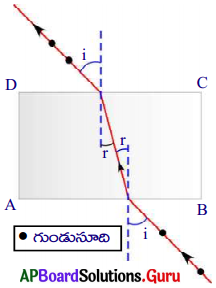
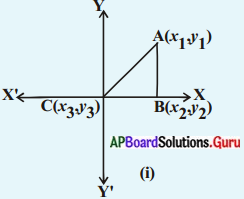
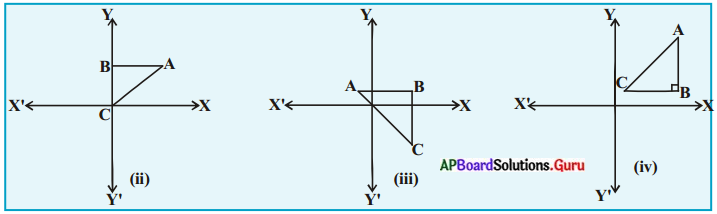
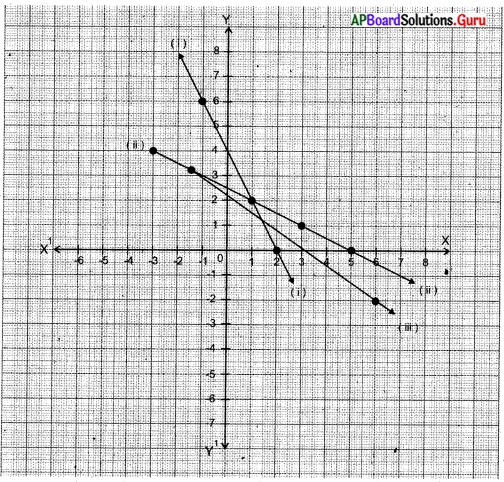
2) వాహకాన్ని తెరచిన వలయంగా భావించిన, పటంలో చూపిన విధంగా వాహకంలో ఎలక్ట్రాన్లు స్వేచ్ఛగా ఏ దిశలో కదులుతాయో నిర్ణయించలేని విధముగా చలిస్తాయి. ఈ చలనమును క్రమరహిత చలనం అంటాము.

3) పటం (i) లో చూపినట్లు వాహకంలో ఏదైనా మధ్యచ్ఛేదాన్ని ఊహిస్తే, ఒక సెకను కాలంలో ఆ మధ్యచ్ఛేదాన్ని ఎడమ నుండి కుడికి దాటి వెళ్ళే ఎలక్ట్రానుల సంఖ్య, ఒక సెకను కాలంలో ఆ మధ్యచ్ఛేదాన్ని కుడి నుండి ఎడమకి దాటి వెళ్ళే ఎలక్ట్రాన్ల సంఖ్యకు సమానం.

4) అనగా తెరచిన వలయం వంటి వాహకంలో ఏదేని మధ్యచ్ఛేదం వెంబడి కదిలే ఫలిత ఆవేశం శూన్యమవుతుంది.

5) ఒక బల్బ్ తో సహా వాహకం రెండు చివరలను బ్యాటరీకి కలిపితే, బ్యాటరీ నుండి బల్బ్ కు శక్తి సరఫరా జరగడం వల్ల బల్బ్ వెలుగుతుంది.

6) ఈ విధమైన శక్తి సరఫరాకు కారణము ఎలక్ట్రానులు.

7) పటం (ii) లో చూపిన విధంగా ఎలక్ట్రాన్లు క్రమపద్ధతిలో చలిస్తే, వాహకంలోని ఏదేని మధ్యచ్ఛేదాన్ని దాటి వెళ్ళే ఫలిత ఆవేశం వ్యవస్థితమవుతుంది.

8) ఈ విధముగా ఎలక్ట్రానులు క్రమమైన పద్ధతిలో చలించడాన్ని విద్యుత్ ప్రవాహం అంటారు.

9) కనుకనే ఆవేశాల క్రమ చలనాన్ని విద్యుత్ ప్రవాహం అంటారు.

ప్రశ్న 2.
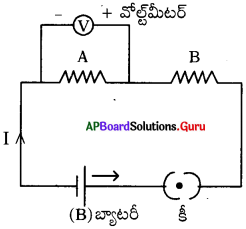
బ్యాటరీ ఎలా పని చేస్తుంది? వివరించండి. (AS1)
(లేదా)
ఒక బ్యాటరీనందు టెర్మినళ్ల మధ్య పొటెన్షియల్ భేదం ఏ విధముగా స్థిరంగా ఉండునో వివరింపుము.
జవాబు:

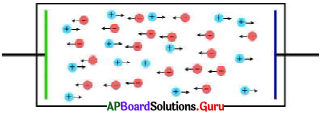
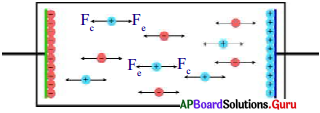
1. బ్యాటరీలో రెండు లోహపు పలకలు (ఎలక్ట్రోడులు, ఒక రసాయనం (విద్యుత్ విశ్లేష్యం) ఉంటాయి.
2. బ్యాటరీ యొక్క రెండు ఎలక్ట్రోడుల మధ్య ఉండే విద్యుద్విశ్లేష్యంలో పరస్పరం వ్యతిరేకదిశల్లో చలించే ధన, ఋణ అయాన్లు పటంలో చూపినట్లుగా ఉంటాయి.
3. ఈ అయాన్లపై విద్యుద్విశ్లేష్యం కొంత బలాన్ని ప్రయోగించడం వల్ల అవి నిర్దిష్ట దిశలో చలిస్తాయి. ఈ బలాన్ని రసాయన బలం (F_c) అంటాము.
4. రసాయన స్వభావమును బట్టి, ధన అయాన్లు బ్యాటరీలో ఏదో ఒక లోహపు పలకవైపు కదిలి, ఆ పలకపై పోగవుతాయి. దీని ఫలితంగా ఆ లోహపు పలక ధనావేశపూరితమవుతుంది. దీనిని ఆనోడ్ అంటాము.
5. ధనావేశ అయాన్లకు వ్యతిరేకదిశలో ఋణావేశ అయాన్లు చలించి రెండవ లోహపు పలకపై పోగవుతాయి. ఆ పలక ఋణావేశపూరితమవుతుంది. దీనిని కాథోడ్ అంటాము.
6. లోహపు పలకలపై ఆవేశం సంతృప్త స్థితిని చేరే వరకు, ఇలా ఆవేశాలు పోగవుతూనే ఉంటాయి.
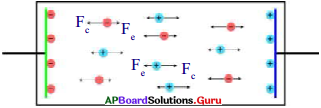
7. లోహపు పలకలపై ఆవేశం సంతృప్త స్థితికి చేరాక, కదిలే అయానులపై విద్యుత్ బలం (F_e) పని చేస్తుంది.
8. విద్యుత్ బలదిశ రసాయన బలదిశకు వ్యతిరేకదిశలో ఉంటుంది.
9. విద్యుత్ బలం పరిమాణం, లోహపు పలకలపై పోగైన ఆవేశంపై ఆధారపడును.
10. విద్యుత్ బలం కన్నా రసాయన బలం ఎక్కువగా ఉంటే, ఆవేశాలు అవి చేరవలసిన పలకలవైపు పటంలో చూపినట్లుగా కదులుతాయి.
11. విద్యుత్ బలం, రసాయన బలం సమానమైనపుడు ఆవేశాల చలనం పటంలో చూపినట్లుగా ఆగిపోవును.
12. క్రొత్త బ్యాటరీ యొక్క రెండు ధృవాల మధ్య స్థిర పొటెన్షియల్ భేదం ఉంటుంది.
13. ఒక వాహక తీగను బ్యాటరీ ధృవాలకు కలిపినప్పుడు వాహక తీగ రెండు చివరల మధ్య పొటెన్షియల్ భేదం ఏర్పడుతుంది.
14. ఈ పొటెన్షియల్ భేదం వల్ల వాహకం అంతటా విద్యుత్ క్షేత్రం ఏర్పడుతుంది.
15. బ్యాటరీ యొక్క ధన ధృవం దగ్గరలోని ఎలక్ట్రానులను ఆకర్షించడం వల్ల వాహకంలోని ఎలక్ట్రానులు ధన ధృవం వైపు కదులుతాయి. ఫలితంగా ధన ధృవం యొక్క ధనావేశ పరిమాణం తగ్గును. ఈ సందర్భంలో రసాయన బలం (F_c), కంటే విద్యుత్ బలం (F_e) తక్కువ అవుతుంది.
16. అప్పుడు రసాయన బలం, ఋణావేశ అయానులను ధనావేశ పలక (ఆనోడు) నుండి బయటకు లాగి వాటిని ఋణావేశ పలక (కాథోడ్) వైపు కదిలేటట్లు చేస్తుంది.
17. ఈ ఋణావేశ అయానులు (ఎలక్ట్రానులు), ఋణ ధృవం మధ్య ఉండే బలమైన వికర్షణ కారణంగా ఋణధృవం ( కాథోడ్) వాహకంలోనికి ఎలక్ట్రాను నెట్టును.
18. కనుక విద్యుత్ ప్రవహిస్తున్నపుడు వాహకంలో ఎలక్ట్రాన్ల సంఖ్య స్థిరంగా ఉంటుంది.
19. రసాయన, విద్యుత్ బలాల మధ్య సమతాస్థితి ఏర్పడే వరకు పైన తెలిపిన ప్రక్రియ కొనసాగుతూనే ఉంటుంది.

ప్రశ్న 3.
విద్యుచ్ఛాలక బలము (emf), పొటెన్షియల్ భేదాల మధ్య తేడాలను రాయండి. (AS1)
(లేదా)
పొటెన్షియల్ భేదం మరియు విద్యుచ్ఛాలక బలముల మధ్యగల భేదాలను వ్రాయుము.
జవాబు:

ప్రశ్న 4.
ఎలక్ట్రిక్ షాక్ (విద్యుత్ ఘాతం) అంటే ఏమిటి? ఇది ఎలా సంభవిస్తుంది? (AS1)
(లేదా)
విద్యుత్ ఘాతం అర్థం ఏమిటో వ్రాయుము? ఇది ఏ విధంగా సంభవించునో వ్రాయుము.
జవాబు:

1. మన శరీరంలోని ఏవేని రెండు అవయవాల మధ్య పొటెన్షియల్ భేదం ఉన్నప్పుడు మనం విద్యుత్ ఘాతానికి లోనైనట్లు చెప్పవచ్చును.
2. మానవ శరీరం గుండా విద్యుత్ ప్రవహించేటప్పుడు తక్కువ నిరోధాన్ని కలిగించే మార్గాన్ని ఎన్నుకొంటుంది.
3. మన శరీరం అంతటా నిరోధం ఒకే విధముగా ఉండదు.
4. శరీరంలో విద్యుత్ ప్రవాహం జరుగుతున్న కొలదీ, శరీర నిరోధం, విద్యుత్ ప్రవాహ విలువలు పరస్పరం విలోమముగా మారుతుంటాయి.
5. కాబట్టి విద్యుత్ ఘాతాన్ని విద్యుత్ పొటెన్షియల్ భేదం, విద్యుత్ ప్రవాహం మరియు శరీరం నిరోధాల ఫలిత ప్రభావంగా చెప్పవచ్చును.

ప్రశ్న 5.
\(\mathbf{R}=\frac{\rho l}{\mathbf{A}}\) ను ఉత్పాదించండి. (AS1)
జవాబు:
1) పొటెన్షియల్ భేదం స్థిరంగా ఉన్నప్పుడు వాహకం నిరోధం (R), దాని పొడవు (l) కు అనులోమానుపాతంలో ఉంటుంది.
R ∝ l …………………….. (1)

2) వాహక ఉష్ణోగ్రత, పొడవు స్థిరంగా ఉన్నప్పుడు వాహక నిరోధం, వాహక మధ్యచ్ఛేద వైశాల్యానికి విలోమానుపాతంలో ఉంటుంది.
R ∝ \(\frac{l}{A}\) …………………….. (2)

3) సమీకరణాలు (1) మరియు (2) ల నుండి
R ∝ \(\frac{l}{A}\)ఉష్ణోగ్రత స్థిరంగా ఉన్నప్పుడు) R = ρ \(\frac{l}{A}\)
ఇక్కడ ρ = అనుపాత స్థిరాంకము, దీనిని విశిష్ట నిరోధం లేదా నిరోధకత అంటాము.

4) ఈ విశిష్ట నిరోధం ఉష్ణోగ్రత, పదార్థ స్వభావంలపై మాత్రమే ఆధారపడి ఉంటుంది.
దీనికి ప్రమాణాలు ఓమ్ – మీటరు ( Ω – m).

ప్రశ్న 6.
స్థిర ఉష్ణోగ్రత, స్థిర మధ్యచ్ఛేద వైశాల్యం గల వాహక నిరోధం, దాని పొడవుకు అనులోమానుపాతంలో ఉంటుందని మీరెలా పరీక్షిస్తారు? (కృత్యం – 4) (AS1)
జవాబు:

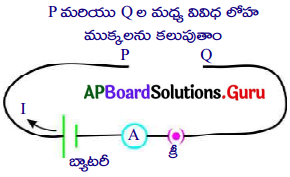
1. ఒకే మధ్యచ్చేద వైశాల్యం, వివిధ పొడవులు గల కొన్ని మాంగనిన్ తీగలను తీసుకొంటిని.
2. పటంలో చూపినట్లు వలయాన్ని ఏర్పాటు చేసితిని.
3. మాంగనిన్ తీగను ఒకదానిని P, Q ల మధ్య కలిపితిని.
4. అమ్మీటర్ సహాయంతో వలయంలో ప్రవహించే విద్యుత్ ను కొలిచి నమోదు చేసితిని.
5. మిగిలిన తీగలను ఉపయోగిస్తూ ఈ కృత్యాన్ని మరలా చేసితిని.
6. ప్రతి సందర్భంలోని విద్యుత్ ప్రవాహాన్ని కొలిచి క్రింది పట్టికలో నమోదు చేసితిని.
   
7. మాంగనిన్ తీగ పొడవు పెరుగుతున్న కొలదీ వలయంలో ప్రవహించే విద్యుత్ విలువ తగ్గడం గమనించవచ్చును.
8. పొటెన్షియల్ భేదం స్థిరంగా ఉన్నప్పటికీ చువ్వ పొడవు పెరిగితే, నిరోధం పెరుగుతుంది.
9. పై కృత్యాన్ని బట్టి పొటెన్షియల్ భేదం స్థిరంగా ఉన్నప్పుడు వాహకం నిరోధం (R), దాని పొడవు (l)కు అనులోమానుపాతంలో ఉంటుంది. R ∝ l (ఉష్ణోగ్రత, మధ్యచ్ఛేద వైశాల్యం స్థిరంగా ఉన్నప్పుడు)

ప్రశ్న 7.
కిర్చాఫ్ నియమాలను తెలిపి, ఉదాహరణలతో వివరించండి. (AS1)
(లేదా)
ఏవైనా రెండు ఉదాహరణలతో కిర్ఛాఫ్ నియమాలను వివరించుము.
జవాబు:

1. ఒక DC వలయంలో కొన్ని బ్యాటరీలు, నిరోధాలను ఏ విధంగా కలిపినా, దాని ఫలితంను అవగాహన చేసుకునేందుకు అవసరమగు సరళ నియమాలను కిర్ఛాఫ్ నియమాలంటారు.
2. కిర్ఛాఫ్ నియమాలు రెండు రకాలు. అవి :
   a) జంక్షన్ నియమం, b) లూప్ నియమం.

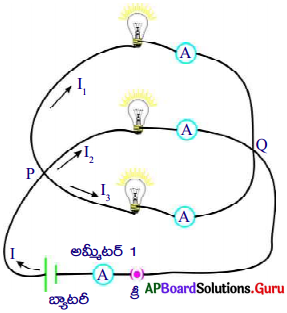
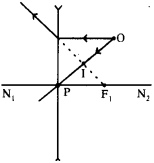
జంక్షన్ నియమం :
వలయంలో విద్యుత్ ప్రవాహం విభజించబడే ఏ జంక్షన్ వద్దనైనా, ఆ జంక్షన్‌కు చేరే విద్యుత్ ప్రవాహాల మొత్తం, ఆ బ్యాటరీ జంక్షన్ ను వీడిపోయే విద్యుత్ ప్రవాహాల మొత్తానికి సమానము.

ఉదాహరణ :
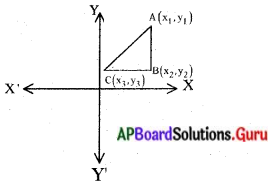
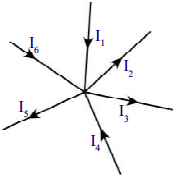
a) పటంలో చూపిన విధంగా మూడు లేదా అంతకంటే ఎక్కువ వాహక తీగలు కలిసే బిందువును జంక్షన్ ‘P’ అంటారు.
b) వలయంలో విద్యుత్ ప్రవాహం విభజించబడే ఏ జంక్షన్ వద్దనైనా, జంక్షన్ ను చేరే విద్యుత్ ప్రవాహాల మొత్తం ఆ జంక్షన్ ను వీడిపోయే విద్యుత్ ప్రవాహాల మొత్తానికి సమానము.
c) అనగా వలయంలోని ఏ జంక్షన్ వద్దనైనా ఆవేశాలు పోగుకావడం అనేది జరుగదు.
అందుచే I₁ + I₄ + I₆ = I₂ + I₃ + I₅.

లూప్ నియమం :
ఒక మూసిన వలయంలోని పరికరాల రెండు చివరల మధ్య పొటెన్షియల్ భేదాల్లో పెరుగుదల, తగ్గుదలల బీజీయ మొత్తం శూన్యం.

ఉదాహరణ :
లూప్ నియమాన్ని ప్రక్క పటంలోని వలయానికి అన్వయించగా

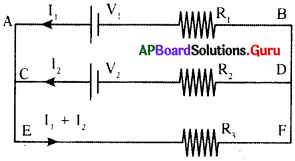
ACDBA లూప్ నందు,
-V₂ + I₂R₂ – I₁R₁ + V₁ = 0

EFDCE లూప్ నందు,
– (I₁ + I₂) R₃ – I₁ R₁ + V₁ = 0

EFBAE లూప్ నందు,
– (I₁ + I₂) R₃ – I₁R₁ + V₁ = 0

ప్రశ్న 8.
1 KWH విలువను ఔళ్ళలో తెలపండి. (AS1)
(లేదా)
1 KWH విలువను ఔళ్ళలో వ్రాయుము.
జవాబు:
1 KW = 1000 W = 1000 J/s
1 KWH = (1000 J/s) (60 × 60 సెకన్లు) = 3600 × 1000 J = 3.6 × 10⁶ J.
సామర్థ్య వినియోగంనకు’ పెద్ద ప్రమాణం కిలోవాట్ (KW).

ప్రశ్న 9.
ఇంటిలోకి వచ్చే కరెంటు ఓవర్ లోడ్ కావడం గూర్చి వివరించండి. (AS1)
(లేదా)
ఓవర్ లోడ్ లేక షార్ట్ సర్క్యూట్లను ఉదాహరణతో వివరించుము.
జవాబు:

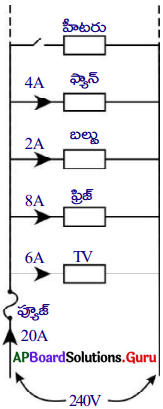
1. మన ఇంటిలోకి విద్యుత్ రెండు తీగల ద్వారా వస్తుంది. వీటిని కరెంట్ లైన్ అంటాము.
2. ఈ తీగల నిరోధం చాలా తక్కువ. వీటి మధ్య పొటెన్షియల్ భేదం దాదాపుగా 240 V ఉంటుంది.
3. మన ఇంటిలోని విద్యుత్ సాధనాలన్నీ సమాంతర సంధానంలో వుంటాయి.
4. కాబట్టి ప్రతీ సాధనం రెండు చివరల మధ్య పొటెన్షియల్ భేదం 240V అవుతుంది.
5. ప్రతి విద్యుత్ సాధనం దాని నిరోధాన్ని బట్టి, లైన్స్ నుండి కొంత విద్యుత్ ను వినియోగించుకుంటుంది.
6. లైన్స్ నుండి వినియోగించుకున్న మొత్తం విద్యుత్, వివిధ సాధనాల గుండా ప్రవహించే విద్యుత్ ల మొత్తానికి సమానము.
7. మన ఇంటిలో వాడే విద్యుత్ సాధనాల సంఖ్యను పెంచితే, అవి లైన్స్ నుండి వినియోగించుకునే విద్యుత్ కూడా పెరుగుతుంది.
8. దీని వలన ఇంటిలోని వలయం బాగా వేడెక్కి మంటలు ఏర్పడే అవకాశం ఉంది. దీనినే ఓవర్ లోడ్ అంటాము.

ప్రశ్న 10.
మూడు నిరోధాలు శ్రేణిలో కలిపినప్పుడు వాటి ఫలిత నిరోధాన్ని ఉత్పాదించండి. (కృత్యం – 6) (AS1)
(లేదా)
మూడు నిరోధాలను శ్రేణిలో కలిపినప్పుడు వాటి ఫలిత నిరోధానికి సూత్రంను ఉత్పాదించి, వివరించుము.
జవాబు:
శ్రేణి సంధానం :
ఒక వలయంలో, చివరి నుండి – చివరికి కలిపిన నిరోధాల గుండా ఒకే విద్యుత్ ప్రవాహం ఒకే మార్గంలో ప్రవహిస్తున్నట్లయితే అవి శ్రేణి సంధానంలో ఉన్నాయంటాము.

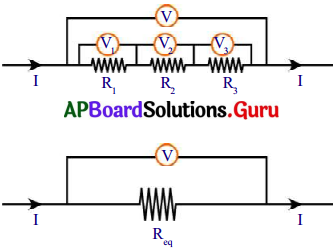
1. ‘V’ పొటెన్షియల్ భేదం ఉన్న ఘటాన్ని తీసుకొని శ్రేణి సంధానంలో ఉన్న మూడు నిరోధాలను పటంలో చూపిన విధముగా కలుపుము.
2. నిరోధాలను శ్రేణిలో కలిపినప్పుడు విద్యుత్ ప్రవాహానికి ఒకటే మార్గం, కావున వలయంలో విద్యుత్ ప్రవాహం (I) ఒకటే ఉండును.
3. శ్రేణిలో గల నిరోధాల వల్ల వలయంలో ఏర్పడే విద్యుత్ ప్రవాహానికి సమానమైన విద్యుత్ ప్రవాహాన్ని కలుగజేసే మరొక నిరోధంను ఆ నిరోధాల ఫలిత నిరోధం (R_eq) అంటాము.
4. శ్రేణి సంధానంలో గల ఫలిత నిరోధం విలువను ఓమ్ నియమం ద్వారా R_eq = \(\frac{V}{I}\) ⇒ V = IR_eq గా వ్రాయవచ్చును.
5. R₁, R₂, R₃ అను నిరోధాల చివరల యందు గల పొటెన్షియల్ భేదాలు వరుసగా V₁, V₂, V₃ లు అయిన ఓమ్ నియమం ప్రకారము,
   V₁ = IR₁ ; V₂ = IR₂ మరియు V₃ = IR₃
6. శ్రేణి సంధానంలో గల వేర్వేరు పొటెన్షియల్ భేదాల మొత్తం, వాటి ఫలిత పొటెన్షియల్ భేదానికి సమానం.
   V = V₁ + V₂ + V₃ ………………. (1)
7. V₁, V₂, V₃ ల మరియు V విలువలను సమీకరణం (1) లో ప్రతిక్షేపించగా
   I R_eq = IR₁ + IR₂ + IR₃        I Ra_eq = I (R₁ + R₂ + R₃)
   R_eq = R₁ + R₂ + R₃ + ……………. + R_n

పై సమీకరణాన్ని బట్టి శ్రేణిలో కలిపిన నిరోధాల వల్ల ఏర్పడే ఫలిత నిరోధం, ఆయా విడివిడి నిరోధాల మొత్తానికి సమానము.

ప్రశ్న 11.
మూడు నిరోధాలు సమాంతరంగా కలిపినప్పుడు వాటి ఫలిత నిరోధాన్ని ఉత్పాదించండి. (AS1)
(లేదా)
మూడు నిరోధాలను సమాంతరంగా సంధానం చేసినప్పుడు వాటి ఫలిత నిరోధమునకు సూత్రంను ఉత్పాదించి, వివరించుము. (కృత్యం – 7)
జవాబు:
సమాంతర సంధానం :
ఒక వలయంలో నిరోధాలు ఉమ్మడి టెర్మినల్ కి కలపబడి, వాటి మధ్య ఒకే పొటెన్షియల్ భేదం ఉంటే అవి సమాంతర సంధానంలో ఉన్నాయంటాము.

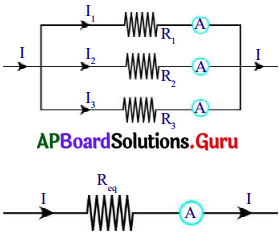
1) ‘V’ పొటెన్షియల్ భేదం ఉన్న ఘటమును తీసుకుని సమాంతర సంధానంలో ఉన్న మూడు నిరోధాలను పటంలో చూపిన విధముగా కలుపుము.

2) వలయంలో ప్రవహించే ఫలిత విద్యుత్ ప్రవాహం విడివిడి నిరోధాల ద్వారా ప్రవహించు విద్యుత్ ప్రవాహాల మొత్తానికి సమానము.
దీనిని బట్టి I = I₁ + I₂ + I₃ అగును.

3) నిరోధాల సమాంతర సంధానంలో పొటెన్షియల్ భేదం ‘V’ మారదు, మూడు నిరోధాల ఫలిత నిరోధాన్ని ‘R_eq‘ తో సూచిస్తాము.

4) సమాంతర సంధానంలో ఫలిత నిరోధం ‘R_eq‘. ఓమ్ నియమం ప్రకారం,

పై సమీకరణం నుండి సమాంతర సంధానంలో ఉన్న నిరోధాల ఫలిత నిరోధం విలువ, ఆ విడివిడి నిరోధాల విలువ కన్నా తక్కువగా ఉంటుంది. (లేదా) సమాంతర సంధానంలో ఫలిత నిరోధం యొక్క వ్యుత్రమణం, విడి నిరోధాల వ్యుత్ర్కమణాల మొత్తానికి సమానము.

ప్రశ్న 12.
కాపర్ కంటే సిల్వర్ మంచి విద్యుత్ వాహకం. అయినా, విద్యుత్ తీగగా కాపర్‌ను వాడతాం ఎందుకు? (AS1)
(లేదా)
సిల్వర్‌ కు బదులుగా కాపర్‌ను ఎందుకు విద్యుత్ తీగగా వాడతారో కారణం వివరించుము.
జవాబు:

1. సిల్వర్ యొక్క విశిష్ట నిరోధం విలువ 1.59 × 10^-8 Ωm మరియు కాపర్ యొక్క విశిష్ట నిరోధం విలువ 1.68 × 10^-8 Ωm.
2. కాపర్ యొక్క విశిష్ట నిరోధం కన్నా సిల్వర్ విలువ తక్కువ.
3. తక్కువ విశిష్ట నిరోధం గల లోహాలను మంచి వాహకాలుగా ఉపయోగిస్తారు. కాని, సిల్వర్ అత్యధిక ఖరీదైన లోహము కావటం చేత కాపర్‌ను వాడుతున్నాము.
4. కాపర్ తీగ గుండా విద్యుత్ ప్రవహించునపుడు ఉష్ణరూపంలో కోల్పోయే శక్తి సిల్వర్ కన్నా చాలా తక్కువ.
5. కాపర్ లోహంను చాలా సన్నని తీగలుగా మార్చవచ్చును. దీనికి పెళుసుతనం తక్కువ.

ప్రశ్న 13.
100 W, 220V మరియు 60 W, 220 V గల రెండు బల్బులున్నవి. దేని నిరోధం ఎక్కువ? (AS1)
జవాబు:
దత్తాంశము ప్రకారము,
మొదటి బల్బు యొక్క వివరాలు 100W, 220V
రెండవ బల్బు యొక్క వివరాలు 60W, 220V

∴ 60 W, 220 V ల విలువ గల బల్బు అనగా రెండవది అధిక నిరోధమును కలిగి ఉన్నది.

ప్రశ్న 14.
ఇండ్లలో విద్యుత్ పరికరాలను ఎందుకు శ్రేణిలో కలపము? (AS1)
(లేదా)
ఇండ్లలో వాడు విద్యుత్ పరికరాలను శ్రేణిలో కలుపకుండుటకు గల కారణంను వివరించుము.
జవాబు:

1. మన నిత్య జీవితంలో ఉపయోగించే ఫ్యాన్, ఫ్రిజ్, హీటర్, కుక్కర్ వంటి విద్యుత్ సాధనాలను సమాంతర సంధానంలోనే కలుపుతారు.
2. ఎందుకనగా, శ్రేణిలో కలిపిన విద్యుత్ పరికరాలలో ఏదైనా ఒకటి పని చేయకపోతే, వలయం తెరవబడి వలయంలో విద్యుత్ ప్రవాహం జరుగదు. దీనితో మిగిలినవి కూడా పని చేయవు.
3. సమాంతర సంధానంలో కలుపుట వలన, పరికరాల మధ్య పొటెన్షియల్ భేదం సమానంగా ఉండి, వాటికి సరిపడేంత విద్యుతను వినియోగించుకుంటాయి.

ప్రశ్న 15.
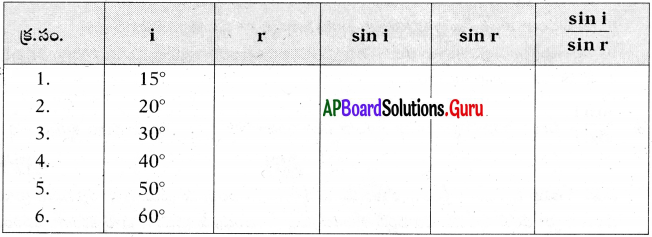
1 మీ పొడవు, 0.1 మి.మీ. వ్యాసార్ధం గల వాహక నిరోధం 100 Ω అయిన దీని నిరోధకత ఎంత? (AS1)
జవాబు:
వాహక నిరోధము R = 100 Ω.
వాహక పొడవు l = 1 మీ. = 1000 మి.మీ.
వాహక వ్యాసార్ధము r = 0.1 మి.మీ.

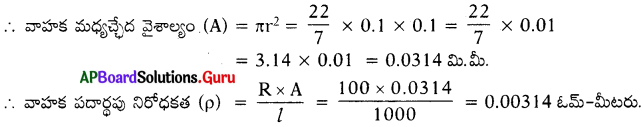
ప్రశ్న 16.
బల్బులోని ఫిలమెంట్ తయారీకి టంగ్ స్టనను వినియోగిస్తారు. ఎందుకు? (AS2)
(లేదా)
ఫిలమెంట్ తయారీకి టంగ్ స్టనను వాడుటకు గల కారణమేమిటో సవివరంగా తెలుపుము.
జవాబు:

1. సాధారణంగా విద్యుత్ బల్బులో వాడే ఫిలమెంట్ ను “టంగ్ స్టన్” తో తయారుచేస్తారు.
2. దీనికి కారణం, టంగ్ స్టన్ విశిష్ట నిరోధం, ద్రవీభవన స్థానం విలువలు చాలా ఎక్కువ.
3. విశిష్ట నిరోధం ఎక్కువగా గల లోహాలు మంచి విద్యుత్ నిరోధాలుగా పని చేస్తాయి. కనుకనే టంగ్ స్టన్ వంటి లోహాలను ఫిలమెంట్ల తయారీకి ఉపయోగిస్తాము.

ప్రశ్న 17.
కారు హెడ్ లైట్లను శ్రేణిలో కలుపుతారా? లేక సమాంతరంగా కలుపుతారా? ఎందుకు? (AS2)
(లేదా)
వాహనాలకు వాడు హెడ్ లైట్లను సమాంతరంగా అనుసంధానం చేయుటకు గల కారణంను వ్రాయుము.
జవాబు:

1. కారు హెడ్ లైటు సమాంతరంగా కలుపుతారు.
2. ఎందుకనగా సమాంతర సంధానంలో గల లైటులు సమాన విద్యుత్ సామర్థ్యంను పొందుతాయి.
3. వాటిలో ఒక దానిలో ఏదైనా లోపము సంభవించి పని చేయకపోయినా మరొకటి పని చేయును.
4. ఈ సౌలభ్యం శ్రేణి సంధానంలో ఉండదు.

ప్రశ్న 18.
ఇండ్లలో విద్యుత్ పరికరాలను సమాంతరంగా ఎందుకు కలుపుతారు? శ్రేణిలో కలిపితే ఏమి జరుగుతుంది? (AS2)
(లేదా)
ఇండ్లలోని విద్యుత్ పరికరాలను శ్రేణిలో ఎందుకు అనుసంధానం చేరో? ఎందుకు సమాంతరంగా అనుసంధానం చేస్తారో తెలుపుము.
జవాబు:

1. మన ఇంటిలోని విద్యుత్ సాధనాలన్నీ కరెంట్ లైన్లకు వివిధ బిందువుల వద్ద సమాంతర సంధానంలో కలుపుతారు.
2. ఎందుచేతనంటే శ్రేణిలో కలిపితే ఆ విద్యుత్ పరికరాలలో ఏదైనా ఒక పరికరాన్ని ఆపివేస్తే మిగతా పరికరాలు కూడా పని చేయటం ఆగిపోతాయి.
3. ఇదియే కాకుండా ఆ పరికరాలలో మొత్తం పొటెన్షియల్ భేదం విభజించబడును. కానీ ఇండ్లలోని పరికరాలకు పొటెన్షియల్ భేదం సమానముగా ఉండాలి.

ప్రశ్న 19.
ఓమ్ నియమం తెల్పండి. దానిని సరిచూడడానికి ప్రయోగాన్ని తెల్పి, ప్రయోగ విధానాన్ని వివరించండి. (AS3)
(లేదా)
ఓమ్ నియమమును పరీక్షించుము. దీనికై ఒక కృత్యంను వ్రాయుము. (ప్రయోగశాల కృత్యం)
జవాబు:
ఓమ్ నియమము :
స్థిర ఉష్ణోగ్రత వద్ద, వాహకం రెండు చివరల మధ్య పొటెన్షియల్ భేదం వాహకం గుండా ప్రవహించే విద్యుత్ ప్రవాహానికి అనులోమానుపాతంలో ఉంటుంది.

ఓమ్ నియమంను సరిచూచుట :
ఉద్దేశ్యం :
ఒక వాహకానికి సంబంధించిన V/I విలువ స్థిరమని చూపడము.

కావలసిన వస్తువులు :
6V బ్యాటరీ ఎలిమినేటర్, 0-1 A అమ్మీటర్, 0-67/1, మాంగనీస్ తీగ . ఓల్డ్ టరు, వాహక తీగలు (రాగి తీగలు), 50 సెం.మీ. పొడవు గల సర్పిలాకార మాంగనీస్ తీగ, రియోస్టాట్, స్విచ్ మరియు UV LED.

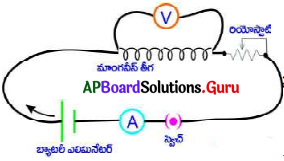
నిర్వహణ పద్దతి :

1. పటంలో చూపిన విధముగా వలయాన్ని కలపండి. (బ్యాటరీ ఎలిమినేటర్ లో గరిష్ఠంగా 4.5V దగ్గర నాబ్ ను ఉంచాలి.
2. రియోస్టాట్ ను ఉపయోగించి మాంగనీస్ తీగ రెండు కొనల వద్ద పొటెన్షియల్ భేదమును OV నుంచి గరిష్ఠంగా 4.5V మధ్య వరకు మార్చాలి.
3. రియోస్లాట్ ఉపయోగించి మాంగనీస్ తీగ రెండు కొనల వద్ద కనీసం 10 పొటెన్షియల్ భేదం ఉంచాలి.
4. ఈ సందర్భానికి వలయంలో విద్యుత్ ప్రవాహంను అమ్మీటరు ద్వారా గుర్తించి పట్టికలో నమోదు చేయండి.
5. రియోస్టాట్ ను ఉపయోగించి పొటెన్షియల్ భేదం (V) 4.5V వరకు మార్చుతూ విద్యుత్ ప్రవాహం (I) విలువలను గుర్తించండి.
6. ఈ విధంగా V మరియు I విలువలను కనీసం 5 రీడింగులను గుర్తించి పట్టికలో నమోదు చేయండి.
7. ప్రతి సందర్భానికి \(\frac{V}{I}\) విలువను కనుగొనండి.
8. \(\frac{V}{I}\) విలువ స్థిరమని మనము గమనించవచ్చును. V ∝ I అయిన \(\frac{V}{I}\) = స్థిరము
9. ఈ స్థిరాంకంను వాహక విద్యుత్ నిరోధం అంటాము. దీనిని ‘R’ తో సూచిస్తాము.
   \(\frac{V}{I}\) = R ⇒ V = IR
   ∴ ఓమ్ నియమము నిరూపించబడినది.

II. ఉద్దేశ్యం :
LED వంటి వాహకాలకు \(\frac{V}{I}\) స్థిరం కాదు అని చూపడం.

నిర్వహణ పద్దతి :
మాంగనిన్ తీగ బదులుగా 3V LED (Light Emitting diode) వాడి పై కృత్యాన్ని మరలా చేయండి.

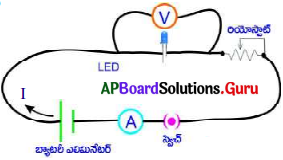
→ LED యొక్క పొడవైన ధృవాన్ని బ్యాటరీ ధన ధృవానికి, పొట్టి దానిని బ్యాటరీ ఋణ ధృవానికి కలపండి.
→ రియోస్టాట్ ను ఉపయోగించి పొటెన్షియల్ భేదాన్ని మార్చుతూ (గరిష్ఠంగా 39 వరకు) ప్రతి సందర్భంలోను విద్యుత్ ప్రవాహం (I) మరియు పొటెన్షియల్ భేదం (V) విలువలు గుర్తించి పట్టికలో పొందుపరచండి.
→ \(\frac{V}{I}\) విలువలు లెక్కించండి.
→ \(\frac{V}{I}\) విలువ స్థిరం కాదని గుర్తిస్తారు.

రియోస్టాట్ తయారీ :

30 సెం.మీ. ల పొడవు గల చెక్క స్కేలు తీసుకొని దానికి రెండు చివరల రెండు రంధ్రాలు చేయాలి. ఆ రంధ్రాల గుండా రెండు బోల్టులను నట్టుల సహాయంతో బిగించాలి. తరువాత విద్యుత్ ఇస్త్రీ పెట్టె ఫిలమెంట్ లోని పలుచని నిక్రోమ్ తీగ తీసుకొని, ఒక కొనను మొదటి బోల్టుకు బిగించి, స్కేలు చుట్టూ సమాన దూరాలలో తీగను వలయాకారంలో బిగుతుగా చుట్టి, రెండవ కొనను రెండవ బోలుకు | బిగించాలి. ఈ స్కేలును మరొక స్కేలుపై లంబంగా, పటంలో చూపిన విధంగా జిగురుతో అతికించాలి. మీ రియోస్టాట్ తయారైనది. విద్యుత్ వలయంలో రియోస్టాట్ ను ఎలా ఉపయోగించాలో మీ ఉపాధ్యాయుని అడిగి తెలుసుకోండి.

ప్రశ్న 20.
a) ఒక 30Ω బ్యాటరీని తీసుకొని, పొటెన్షియల్ భేదాన్ని కొలవండి. ఆ బ్యాటరీని ఏదైనా వలయంలో ఉంచి, పొటెన్షియల్ భేదాన్ని కొలవండి. మీ రీడింగులలో ఏమైనా తేడా ఉందా? ఎందుకు?
జవాబు:
ఘటమును వలయంలో సంధానం చేసినప్పుడు పొటెన్షియల్ భేదాన్ని గమనించలేము.

b) బల్బు విడిగా ఉన్నప్పుడు మల్టీమీటరు సహాయంతో దాని నిరోధాన్ని కొలవండి. ఈ బల్బ్ 12V బ్యాటరీ, స్విలను శ్రేణిలో కలిపి, స్విచ్ ఆన్ చేయండి. ప్రతి 30 సెకనులకొకసారి బల్పు యొక్క నిరోధాన్ని కొలవండి. సరైన పట్టికను గీసి దానిలో నమోదు చేయండి. పై పరిశీలనల నుండి ఏమి నిర్ధారిస్తారు? (AS4)
జవాబు:
బల్బును వలయంలో ఉంచి, ప్రతి 30 సెకనులకొకసారి బల్బు యొక్క నిరోధాన్ని కొలిచిన దాని విలువ పెరుగుచుండును.

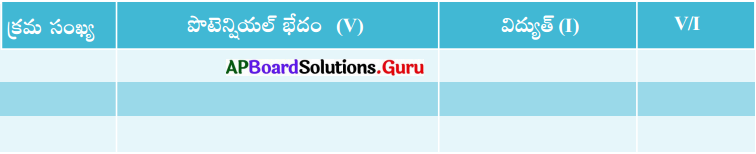
పై పట్టిక నుండి i) మూసిన, తెరిచిన వలయంలో బ్యాటరీ యొక్క పొటెన్షియల్ భేదంలో మార్పుండదు.
ii) ఉష్ణోగ్రత తగ్గిన, పెరిగిన వాహక నిరోధం తగ్గును.

ప్రశ్న 21.
ఇండ్లలో వాడే వివిధ విద్యుత్ పరికరాలు పాడవకుండా కాపాడడంలో వలయంలోని ఫ్యూజ్ పాత్రను ఎలా అభినందిస్తావు? (AS7)
జవాబు:

1. ఓవర్ లోడ్ వలన కలిగే ప్రమాదాన్ని నివారించడానికి, మన ఇండ్లలోని వలయంలో ఫ్యూజ్ ని ఉపయోగిస్తాము.
2. ఇంటి వలయంలో లైన్స్ ద్వారా వచ్చే మొత్తం విద్యుత్ ఫ్యూజ్ గుండా ప్రవహించవలసి ఉంటుంది.
3. ఫ్యూజ్ అనేది అతి తక్కువ ద్రవీభవన స్థానం కలిగిన ఒక సన్నని తీగ.
4. పరిమితికి మించిన ఎక్కువ విద్యుత్ ఫ్యూజ్ ద్వారా ప్రవహించినపుడు సన్నని తీగ వేడెక్కి కరిగిపోతుంది.
5. కరిగిపోయిన ఫ్యూజ్ వల్ల ఇంటిలోని మొత్తం వలయం తెరవబడి విద్యుత్ ప్రవాహం ఆగిపోతుంది.
6. ఆ విధముగా వలయంలో ఫ్యాన్, టి.వి., ఫ్రిజ్ వంటి విద్యుత్ సాధనాలకు ఇబ్బంది కలగకుండా ఉంచుటలో ఫ్యూజ్ పాత్ర ఎంతగానో అభినందనీయమైనది.

ప్రశ్న 22.
పటంను గమనించండి. కింది ప్రశ్నలకు సమాధానాలు తెల్పండి.

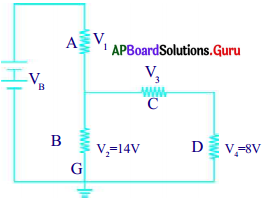
i) C, D నిరోధాలు శ్రేణిలో ఉన్నాయా?
ii) A, B నిరోధాలు శ్రేణిలో ఉన్నాయా?
iii) ఏదైనా నిరోధంతో బ్యాటరీ శ్రేణి సంధానంలో ఉందా?
iv) నిరోధం C పై పొటెన్షియల్ భేదం ఎంత?
v) నిరోధం A పై పొటెన్షియల్ భేదం 6V అయిన వలయంలో ఫలిత emf ఎంత?
జవాబు:
i) అవును, 3 మరియు 4 నిరోధాలు చివర – నుండి – చివరకు సంధానం చేసినందున అవి శ్రేణి సంధానంలో ఉన్నాయి.
ii) కాదు, 1 మరియు 2 నిరోధాలు చివర – నుండి – చివరకు సంధానం చేయలేనందున అవి శ్రేణిలో లేవు.
iii) అవును, V₁ నిరోధంతో (A) బ్యాటరీ శ్రేణిలో సంధానం చేయబడి ఉంది.
iv) 3వ నిరోధం పై ఉన్న పొటెన్షియల్ భేదం 6 వోల్ట్లు . 3 మరియు 4 నిరోధాలు శ్రేణిలో ఉన్నాయి.
మొత్తం పొటెన్షియల్ V₄ + V₃ = 8 + V₃
3 మరియు 4 నిరోధాలు రెండూ 2వ నిరోధానికి సమాంతరంగా ఉన్నాయి.
V₂ = V₃ + 8 ⇒ 14 = V₃ + 8 ⇒ V₃ = 6V
v) మొత్తం ఫలిత emf విలువ V = V₁ + V₂
V= 6 + 14 = 20V
V = 20V

(లేదా)
V = V₁ + V₂ + V₄
= 6 + 6 + 18
V = 20V

ప్రశ్న 23.
ఒక ఇంటిలో మూడు బల్బులు, రెండు ఫ్యాన్లు, ఒక టెలివిజన్‌ను వాడుతున్నారు. ప్రతి బల్బు 40 W విద్యుత్ ను వినియోగిస్తుంది. టెలివిజన్ 60 W, ఫ్యాన్ 80 W విద్యుత్ ను వినియోగిస్తున్నాయి. సుమారు ప్రతి బల్బును ఐదు గంటలు, ప్రతి ఫ్యానును 12 గంటలు, టెలివిజనను 5 గంటల చొప్పున ప్రతిరోజు వినియోగిస్తున్నారు. ఒక యూనిట్ (KWH) కు 3 రూ. చొప్పున విద్యుత్ ఛార్జీ వేస్తే 30 రోజుల్లో చెల్లించాల్సిన సొమ్ము ఎంత? (AS7)
జవాబు:

1. 40 W ల 3 బల్బులు రోజుకి 5 గం||ల చొప్పున వినియోగించు విద్యుత్ శక్తి = 3 × 40 × 5 = 600 WH
2. 80 W ల 2 ఫ్యానులు రోజుకి 12 గం||ల చొప్పున వినియోగించు విద్యుత్ శక్తి = 2 × 80 × 12 = 1920 WH
3. 60 W ల.టెలివిజన్ రోజుకు 5 గం||ల చొప్పున వినియోగించు విద్యుత్ శక్తి = 1 × 60 × 5 = 300 WH
   1 రోజుకు వినియోగించిన మొత్తం విద్యుత్ శక్తి = 600 + 300 + 1920 = 2,820 WH
   WH ను KWH లోకి మార్చగా
   \(\frac{2820}{1000}\) = 2.82 KWH

30 రోజులలో వాడిన విద్యుత్ శక్తి = 2.82 x 30 = 84.6 KWH
1 యూనిట్ (KWH) ధర = ₹ 3.00
84.6 యూనిట్లకు చెల్లించవలసిన సొమ్ము = 84.6 × 3 = ₹ 253.80

ప్రశ్న 24.
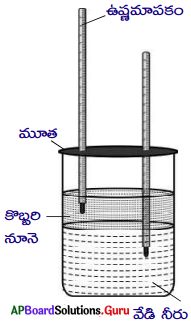
వాహక నిరోధం ఉష్ణోగ్రతపై ఆధారపడుతుందని మీరెలా పరీక్షిస్తారు? (కృత్యం – 2) (AS1)
(లేదా)
వాహక నిరోధము ఉష్ణోగ్రతపై ఆధారపడునని నీవు ఏ విధముగా నిరూపించెదవో వ్రాయుము.
జవాబు:

1) పటంలో చూపిన విధంగా వలయం పూర్తి చేయండి.
2) బ్యాటరీ ఎలిమినేటర్ 1.5V పొటెన్షియల్ భేదం ఉండే విధంగా నాబ్ ను ఉంచండి.
3) స్విచ్ ఆన్ చేసి వలయంలో అమ్మీటర్ రీడింగ్ గుర్తించి పట్టికలో నమోదు చేయండి.
4) ఈ సందర్భంలో బల్బును తాకి ఉష్ణాన్ని గుర్తించండి.

5) ఇదే విధంగా 3V, 4.5V, 6V లతో ప్రయోగం చేసి V మరియు I విలువలు కనుగొని పట్టికలో నమోదు చేయండి.
6) బల్బును తాకి విడుదల చేసే ఉష్ణాన్ని పరిశీలించండి.

పరిశీలనలు :

1. ప్రతి సందర్భంలో బల్బు ద్వారా ప్రవహించే విద్యుత్ ప్రవాహం సరాసరి పెరుగుదల తగ్గి విద్యుత్ నిరోధం పెరగడం గమనిస్తారు.
2. పై కృత్యం నుంచి మీరు బల్బులోని టంగ్ స్టన్ తీగ (ఫిలమెంట్) ఉష్ణోగ్రత పెరిగే కొలదీ ఆ తీగ నిరోధం పెరగడం గమనించి ఉంటారు.

ఫలితం :
దీనిని బట్టి బల్బులోని తీగ నిరోధానికి మరియు దాని ఉష్ణోగ్రతకు సంబంధం ఉందని చెప్పవచ్చు. కాబట్టి ఓమ్ నియమాన్ని ఎల్లప్పుడూ స్థిర ఉష్ణోగ్రత వద్ద మాత్రమే పరిశీలించాలి.

ప్రశ్న 25.
ఇండ్లలో ఫ్యూజ్ ఎందుకు వాడతాం? (AS1)
(లేదా)
ఇళ్ళలో విద్యుత్ సాధనాలు, సంధానాలు పాడవకుండా ప్యూజ్ కాపాడుతుంది. ప్యూజ్ పాత్రను ప్రశంసిస్తూ నాలుగు వాక్యాలు వ్రాయండి.
(లేదా)
ఇంటి పరికరాలను కలుపు వలయంలో ఫ్యూజ్ లను ఎందుకు వాడతారో వివరింపుము.
(లేదా)
ఫ్యూజ్ ల వలన ఉపయోగమేమి?
జవాబు:

1. ఫ్యూజ్ అనునది అతి తక్కువ ద్రవీభవన స్థానం కల్గిన ఒక సన్నని తీగ.
2. ఓవర్ లోడ్ వలన కలిగే ప్రమాదాన్ని నివారించడానికి మన ఇండ్లలోని వలయంలో ఫ్యూజ్ ని ఉపయోగిస్తాము.
3. ఈ అమరికలో, లైన్స్ ద్వారా వచ్చే మొత్తం విద్యుత్ ఫ్యూజ్ గుండా ప్రవహించవలసి ఉంటుంది.
4. ఫ్యూజ్ గుండా ప్రవహించే విద్యుత్ అధికం అయితే ఆ సన్నని తీగ వేడెక్కి కరిగిపోతుంది.
5. అప్పుడు ఇంటిలోని మొత్తం వలయం తెరవబడి విద్యుత్ ప్రవాహం ఆగిపోతుంది.
6. దీని వలన ఇంటిలోని విద్యుత్ సాధనాలకు ఇబ్బంది కలగకుండా ఉంటుంది.

ప్రశ్న 26.
30 Ω నిరోధం గల మూడు నిరోధాలు నీ దగ్గర ఉన్నవి అనుకుందాం. ఈ మూడింటిని వాడి ఎన్ని రకాల నిరోధాలు పొందగలం ? వాటికి సంబంధించిన పటాలను గీయండి. (AS2)
జవాబు:
R₁ R₂ మరియు R₃ లను మూడు నిరోధాలనుకొనుము.
ఇచ్చిన నిరోధాల విలువలు R₁ = R₂ = R₃ = 30 Ω
ఈ మూడు నిరోధాలను క్రింది విధాలుగా సంధానం చేయవచ్చును.

1) మూడు నిరోధాలను శ్రేణి సంధానం చేసిన,
2) మూడు నిరోధాలను సమాంతర సంధానం చేసిన,

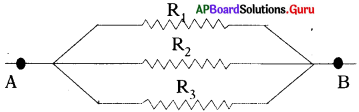
3) రెండు నిరోధాలను సమాంతరంగానూ, ఒక నిరోధాన్ని శ్రేణిలో సంధానం చేసిన,

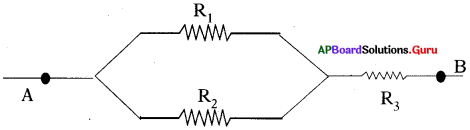
4) రెండు నిరోధాలను శ్రేణిలోను, ఒక నిరోధంను సమాంతరంగాను సంధానం చేసిన,

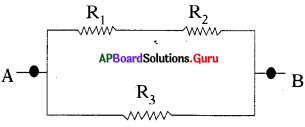
ప్రశ్న 27.
A, B అనే రెండు నిరోధాలు బ్యాటరీతో శ్రేణిలో కలపబడి ఉన్నాయి. A నిరోధంపై పొటెన్షియల్ భేదాన్ని కొలవడానికి వోల్టు మీటరు ఉంది. ఈ సందర్భాన్ని వివరించే పటాన్ని గీయండి. (AS5)
జవాబు:

A మరియు B లు రెండు నిరోధములు.

ప్రశ్న 28.
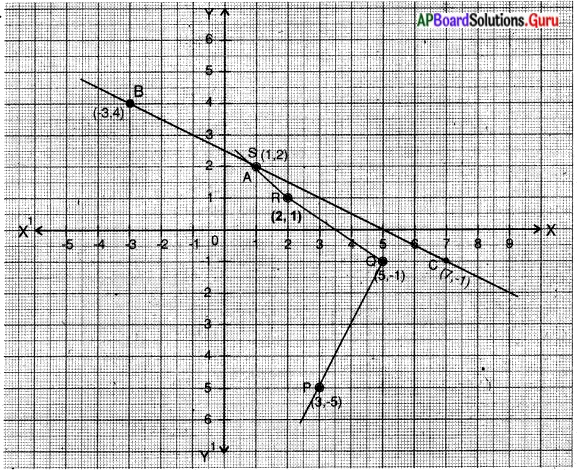
పటంలో B వద్ద పొటెన్షియల్ శూన్యమయిన A వద్ద పొటెన్షియల్ …..
(లేదా)
పటంలో A వద్ద ఎంత పొటెన్షియల్ వున్న B వద్ద పొటెన్షియల్ శూన్యమగును?

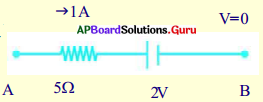
జవాబు:
ఇచ్చిన పటంకు కిర్ ఛాఫ్ లూప్ నియమంను అన్వయించగా,
V_A – (5 × 1) – 2 – V_B = 0 ⇒ V_A – 5 – 2 – 0 = 0 ⇒ V_A = 7
B వద్ద పొటెన్షియల్ శూన్యమయిన ‘A’ వద్ద పొటెన్షియల్ విలువ 7V ఉండును.

ప్రశ్న 29.
మీ శరీర నిరోధం 1,00,000 Ω అయిన మీరు 12V బ్యాటరీని ముట్టుకున్నప్పుడు మీ శరీరం గుండా ప్రవహించే విద్యుత్ ప్రవాహం ఎంత? (AS7)
జవాబు:
శరీరం యొక్క నిరోధము = R = 1,00,000 Ω
బ్యాటరీ యొక్క విద్యుత్ పొటెన్షియల్ (V) = 12V

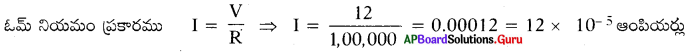
ప్రశ్న 30.
100 Ω నిరోధం గల ఏకరీతి మందం గల వాహకం కరిగి, మొదటి వాహక పొడవుకు రెట్టింపు పొడవు గల దానిగా మారింది. క్రొత్తగా తయారైన వాహకం నిరోధం ఎంత? (AS7)
జవాబు:
వాహకము యొక్క తొలి పొడవు = l₁ = l
వాహకము యొక్క తుది పొడవు = l₂ = 2l
వాహకము యొక్క తొలి మధ్యచ్ఛేద వైశాల్యం = A₁ = A
వాహకము యొక్క తుది మధ్యచ్ఛేద వైశాల్యం = A₂ = ?
స్థూపము యొక్క వైశాల్యం A₁l₁ = A₂l₂ {∵ πr² =h = Al; πr² = a, h = l}

∴ వాహకపు పొడవు రెట్టింపైన, దాని నిరోధము 4 రెట్లుగా మారును.

ఖాళీలను పూరించండి

1. కిలోవాట్ అవర్ ………….. కు ప్రమాణం. అందుకు (విద్యుత్ శక్తి)
2. మందంగా ఉన్న వాహకం యొక్క నిరోధం, సన్నని వాహకం యొక్క నిరోధం కంటే …………….. (తక్కువ)
3. 12 V బ్యాటరీ 2 A విద్యుత్ ప్రవాహాన్ని ఒక వలయంలోకి పంపుతుంది. అయితే ఆ వలయ ఫలిత నిరోధం ……….. (6Ω)
4. పొటెన్షియల్ భేదానికి SI ప్రమాణం …….. (ఓల్ట్)
5. విద్యుత్ ప్రవాహానికి SI ప్రమాణం ……… (ఆంపియర్)
6. 22, 42, 692 నిరోధాలను శ్రేణిలో కలిపారు. ఆ వలయ ఫలిత నిరోధం …………… (12Ω)
7. 22, 42, 692 నిరోధాలను సమాంతరంగా కలిపారు. ఆ వలయం ఫలిత నిరోధం ……………. (11/12Ω)
8. 10 V బ్యాటరీ ఇచ్చే సామర్థ్యం 10 W బ్యాటరీ నుండి బయటకు వచ్చే విద్యుత్ ప్రవాహం ……… (1 ఆంపియర్)

సరైన సమాధానాన్ని ఎన్నుకోండి

1. 50 2 నిరోధం గల ఏకరీతి నిరోధాన్ని ఐదు సమాన భాగాలుగా విభజించారు. వీటిని సమాంతరంగా కలిపారు. దాని ఫలిత నిరోధం …..
A) 2 Ω
B) 12 Ω
C) 250 Ω
D) 6250 Ω
జవాబు:
A) 2 Ω

2. వాహకంలో ఒక ఆవేశాన్ని A నుండి B కు కదిలించారు. ఈ విధంగా ప్రమాణ ఆవేశాన్ని ఆ బిందువుల మధ్య కదల్చడానికి విద్యుత్ బలాలు చేయవలసిన పనిని …… అంటాం.
A) A వద్ద పొటెన్షియల్
B) B వద్ద పొటెన్షియల్
C) A, B ల మధ్య పొటెన్షియల్ భేదం
D) A నుండి B కు ప్రవహించే విద్యుత్
జవాబు:
C) A, B ల మధ్య పొటెన్షియల్ భేదం

3. కౌలు / కూలుంబ్ … కు సమానం.
A) వాట్
B) వోల్ట్
C) ఆంపియర్
D) ఓమ్
జవాబు:
B) వోల్ట్

4. తీగలో విద్యుత్ ప్రవాహం ……… పై ఆధారపడుతుంది.
A) కేవలం తీగ కొనల మధ్య ఉన్న పొటెన్షియల్ భేదం
B) కేవలం తీగ నిరోధం
C) A మరియు B
D) దేనిపై ఆధారపడదు
జవాబు:
C) A మరియు B

5. కింది వాక్యాలను గమనించండి.
a) శ్రేణి సంధానంలో, ప్రతి విద్యుత్ పరికరం నుండి ఒకే విద్యుత్ ప్రవహిస్తుంది.
b) సమాంతర సంధానంలో, ప్రతి విద్యుత్ పరికరంపై పొటెన్షియల్ భేదం ఒకేలా ఉంటుంది.
A) a, b లు సరైనవి
B) a సరైనది; b సరైనది కాదు
C) a సరైనది కాదు; b సరైనది
D) a, b లు రెండునూ సరైనవి కావు
జవాబు:
A) a, b లు సరైనవి

10th Class Physical Science 9th Lesson విద్యుత్ ప్రవాహం Textbook InText Questions and Answers

10th Class Physical Science Textbook Page No. 209

ప్రశ్న 1.
లఘువలయం (short circuit) అంటే ఏమిటి?
జవాబు:

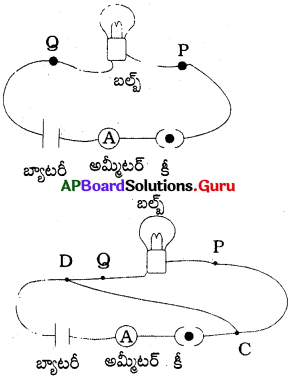
1. పటంలో చూపినట్లుగా వలయంను ఏర్పాటు చేయుము.
2. వలయంను మూసిన బల్బ్ వెలుగును.
3. పటంలో చూపినట్లు C మరియు D ల మధ్య రాగి తీగను కల్పుము.
4. వలయంను మూసిన బల్బ్ వెలగదు.
   పై సందర్భంలో అమ్మీటర్ మొదట రీడింగు కన్నా ఎక్కువ రీడింగును చూపును.
5. రెండవ సందర్భంలో బల్బ్ ఫిలమెంట్ రాగి తీగకన్నా ఎక్కువ నిరోధంను ప్రదర్శించును.
6. కావున కరెంటు CD మార్గంను ఎన్నుకొనును. కావున బల్బ్ వెలగదు.
7. దీనిని బట్టి వలయంలో విద్యుత్ తక్కువ నిరోధము గల మార్గముకు ప్రాధాన్యతనిచ్చును.
8. ఈ విధంగా C మరియు D ల మధ్య తీగను కలుపు పద్ధతిని లఘువలయం అంటారు.

ప్రశ్న 2.
షార్ట్ సర్క్యూట్ వలన ఇంటిలోని వలయం, సాధనాలు ఎందుకు పాడవుతాయి?
జవాబు:

1. వలయంలో విద్యుత్ ప్రవాహం కనిష్ఠ నిరోధమార్గంను ఎంచుకొనును.
2. లఘువలయం ఏర్పడిన తర్వాత వలయంలో అధిక విద్యుత్ ప్రవాహం ఏర్పడును.
3. ఈ అధిక కరెంటు విద్యుత్ సాధనాలను పాడయ్యేటట్లుగా చేస్తుంది.

10th Class Physical Science Textbook Page No. 185

ప్రశ్న 3.
విద్యుత్ ప్రవాహం అంటే ఏమిటి?
జవాబు:
ఆవేశాల క్రమచలనాన్ని విద్యుత్ ప్రవాహం అంటారు.

ప్రశ్న 4.
వలయంలో కలిపిన వాహకం గుండా ఏ ఆవేశం (ధనావేశం/ఋణావేశం) ప్రవహిస్తుంది?
జవాబు:
వలయంలో కలిపిన వాహకం గుండా ఋణావేశం ప్రవహించును.

ప్రశ్న 5.
ఆవేశాల చలనాన్ని స్పష్టం చేసే సందర్భాలు మన నిత్యజీవితంలో ఏవైనా ఉన్నాయా?
జవాబు:
మేఘాల మధ్య లేదా మేఘం, భూమి మధ్య ఆవేశాల ఉత్సర్గం వలన మెరుపులు రావటం ఒక ఉదాహరణ.

ప్రశ్న 6.
ఆవేశాల చలనం వల్ల, ఎల్లప్పుడూ విద్యుత్ ప్రవాహం ఏర్పడుతుందా?
జవాబు:
ఏర్పడుతుంది.

10th Class Physical Science Textbook Page No. 186

ప్రశ్న 7.
అన్ని పదార్థాలూ వాహకాలుగా ఎందుకు పని చేయలేవు?
జవాబు:
అన్ని పదార్థాలలో స్వేచ్ఛా వాహకాలు ఉండవు. కనుక వాహకాలుగా పనిచేయవు.

10th Class Physical Science Textbook Page No. 187

ప్రశ్న 8.
ఎలక్ట్రాన్లు ఏ దిశలో కదులుతాయి?
జవాబు:
విద్యుత్ క్షేత్ర దిశకు వ్యతిరేకదిశలో ఎలక్ట్రాన్లు కదులుతాయి.

ప్రశ్న 9.
ఎలక్ట్రాన్లు త్వరణాన్ని పొందుతాయా?
జవాబు:
ఎలక్ట్రాన్లు అభిఘాతాల వలన శక్తిని కోల్పోతాయి. తిరిగి విద్యుత్ క్షేత్రం వలన త్వరణాన్ని పొందుతాయి.

ప్రశ్న 10.
ఎలక్ట్రాన్లు స్థిరవేగంతో చలిస్తాయా?
జవాబు:
ఎలక్ట్రాన్లు స్థిరవేగంతో చలిస్తాయి. దానినే అపసర వేగం లేదా అపసర వడి అంటారు.

10th Class Physical Science Textbook Page No. 188

ప్రశ్న 11.
విద్యుత్ ప్రవాహ దిశను మనం ఎలా నిర్ణయిస్తాం?
జవాబు:
దీనికి I = nqv_dA ద్వారా సమాధానమివ్వచ్చు. ఆవేశం ‘q’, డ్రిప్ట్ వడి v_d గుర్తులపై విద్యుత్ ప్రవాహదిశ ఆధారపడి ఉంటుంది.

1) ఋణావేశంకు :
q – ఋణాత్మకము, v_d – ధనాత్మకము ఐతే I-ఋణాత్మకం అగును. అనగా ఋణావేశాల ప్రవాహదిశకు వ్యతిరేక దిశలో విద్యుత్ ప్రవాహం ఉండును.

2) ధనావేశంకు :
q- ధన్మాతకము, v_d – ధనాత్మకము ఐతే I- ధనాత్మకం అగును. అనగా ధనావేశాల ప్రవాహదిశలోనే విద్యుత్ ప్రవాహం ఉండును.

10th Class Physical Science Textbook Page No. 189

ప్రశ్న 12.
విద్యుత్ ప్రవాహాన్ని మనం ఎలా కొలుస్తాం?
జవాబు:
వలయంలో విద్యుత్ ప్రవాహాన్ని అమ్మీటరుతో కొలుస్తాం.

10th Class Physical Science Textbook Page No. 190

ప్రశ్న 13.
పొటెన్షియల్ భేదం ప్రకారం విద్యుత్ ప్రవాహం ఏ దిశలో ఉంటుంది?
జవాబు:
పొటెన్షియల్ భేదం ప్రకారం విద్యుత్ ప్రవాహం ఎక్కువ పొటెన్షియల్ నుండి తక్కువ పొటెన్షియల్ దిశలో ఉంటుంది.

ప్రశ్న 14.
వాహకంలో ధనావేశాలు కదులుతాయా? దీనికి మీరు ఒక ఉదాహరణ ఇవ్వగలరా?
జవాబు:
ద్రవాల గుండా విద్యుత్ ప్రవహిస్తున్నపుడు ధన అయాన్లు, ఋణ అయాన్లు పరస్పరం వ్యతిరేకదిశలో చలిస్తాయి.

10th Class Physical Science Textbook Page No. 192

ప్రశ్న 15.
పొటెన్షియల్ భేదం లేదా emfను ఎలా కొలుస్తాం?
జవాబు:
ఓల్ట్ మీటర్ ను పయోగించి పొటెన్షియల్ భేదం లేదా emfను కొలుస్తాము.

10th Class Physical Science Textbook Page No. 194

ప్రశ్న 16.
LED విషయంలో V, I ల నిష్పత్తి ఎందుకు స్థిరంగా లేదో ఊహించగలరా?
జవాబు:
LED అనునది అర్ధవాహకము. అర్ధవాహకాలలో V మరియు I లు అనుపాతంలో ఉండవు మరియు ఓమ్ నియమంను పాటించవు కనుక.

ప్రశ్న 17.
అన్ని పదార్థాలు ఓమ్ నియమాన్ని పాటిస్తాయా?
జవాబు:
వాయువులు, అర్ధవాహకాలు ఓమ్ నియమమును పాటించవు.

ప్రశ్న 18.
ఓమ్ నియమం ఆధారంగా మనం పదార్థాలను వర్గీకరించగలమా?
జవాబు:
ఓమ్ నియమం ఆధారముగా పదార్థాలను రెండు రకాలుగా వర్గీకరించవచ్చును. అవి :

1. ఓమీయ వాహకాలు,
2. అఓమీయ వాహకాలు

ప్రశ్న 19.
నిరోధం అంటే ఏమిటి?
జవాబు:
వాహకంలో ఎలక్ట్రాన్ల చలనానికి కలిగే ఆటంకాన్ని నిరోధం అంటాం.

10th Class Physical Science Textbook Page No. 185

ప్రశ్న 20.
మన నిత్యజీవితంలో ఓమ్ నియమం ఉపయోగమేమైనా ఉందా?
జవాబు:
పదార్థాల మధ్య వ్యత్యాసము, వాటి రకాలను తెలుసుకొనుటకు ఓమ్ నియమం ఉపయోగపడును.

ప్రశ్న 21.
మన శరీరానికి విద్యుత్ ఘాతం (electric shock) కలగడానికి కారణం విద్యుత్ ప్రవాహమా? లేక ఓల్టేజా?
జవాబు:
మన శరీరానికి విద్యుత్ ఘాతం కలగడానికి కారణం .విద్యుత్ ప్రవాహం, ఓల్టేజ్ మరియు మన శరీర నిరోధంలో కలిగే మార్పు.

ప్రశ్న 22.
మన ఇళ్లలో వాడే ఓల్టేజ్ ఎంతో మీకు తెలుసా?
జవాబు:
మన ఇళ్లలో 240 V ఓల్టేజ్ ను వాడతాము.

ప్రశ్న 23.
240 V తీగను తాకితే ఏం జరుగుతుంది?
జవాబు:
240 V తీగను తాకినపుడు, మన శరీరం గుండా 0.0024 A విద్యుత్తు ప్రవహించును. దీని వలన మన అవయవాలు నిర్వహించు పనులకు ఆటంకం కలుగును.

10th Class Physical Science Textbook Page No. 197

ప్రశ్న 24.
అధిక ఓల్టేజ్ తీగపై నిలుచున్న పక్షికి విద్యుత్ ఘాతం ఎందుకు కలుగదు?
జవాబు:
అధిక ఓల్టేజ్ తీగపై పక్షి నిలబడినప్పుడు, దాని కాళ్ళ మధ్య పొటెన్షియల్ భేదం లేదు. ఎందుకంటే అది ఒకే తీగపై నిలబడింది. అందువల్ల పక్షి గుండా విద్యుత్ ప్రవాహం జరుగదు. కనుక పక్షికి విద్యుత్ ఘాతం కలుగదు.

10th Class Physical Science Textbook Page No. 200

ప్రశ్న 25.
విద్యుత్ పరికరాలను వలయంలో ఎలా కలుపుతాం?
జవాబు:
విద్యుత్ పరికరాలను వలయంలో సమాంతరంగా కానీ, శ్రేణిలో కానీ కలుపుతాము.

10th Class Physical Science Textbook Page No. 202

ప్రశ్న 26.
మన ఇళ్ళలోని విద్యుత్ పరికరాలను ఎలా కలుపుతారు?
జవాబు:
మన ఇండ్లలోని విద్యుత్ పరికరాలను సమాంతర సంధానం చేస్తారు.

10th Class Physical Science Textbook Page No. 207

ప్రశ్న 27.
“ఈ నెల మనం 100 యూనిట్ల విద్యుత్ (కరెంట్) వాడాము” వంటి మాటలు మీరు వినే ఉంటారు. దీని అర్థమేంటి?
జవాబు:
ఈ నెల మనము 100 KWHల విద్యుత్ శక్తిని వినియోగించామని అర్థము.

10th Class Physical Science Textbook Page No. 208

ప్రశ్న 28.
యూనిట్ అంటే ఏమిటి?
జవాబు:
ఒక యూనిట్ అంటే ఒక కిలోవాట్ (KWH) అవర్ అని అర్థము.

ప్రశ్న 29.
ఓవర్ లోడ్ అంటే ఏమిటి?
జవాబు:
విద్యుత్ వలయంలో పరిమితిని మించిన పరిమాణంలో విద్యుత్తు ప్రవహించు సందర్భము.

ప్రశ్న 30.
ఓవర్ లోడ్ వల్ల విద్యుత్ సాధనాలు ఎందుకు చెడిపోతాయి?
జవాబు:
పరిమితిని మించిన విద్యుత్తు ప్రవాహం వలన అధిక ఉష్ణం విడుదలై, తీగలు వేడెక్కడం వల్ల మంటలు సంభవిస్తాయి.

10th Class Physical Science Textbook Page No. 209

ప్రశ్న 31.
ఓవర్ లోడ్ వలన కలిగే ప్రమాదాన్ని మనం ఎలా నివారించగలం?
జవాబు:
ఓవర్ లోడ్ వల్ల కలిగే ప్రమాదాన్ని ఫ్యూజ్ ను వాడడం వల్ల నివారించవచ్చును.

పరికరాల జాబితా

బల్బు, ఘటము, స్విచ్, రాగి తీగలు, అమ్మీటరు, వోల్టుమీటరు, బ్యాటరీ ఎలిమినేటర్, బల్బు, మల్టీమీటరు, కీ, రాగి, అల్యూమినియం, మాంగనిన్ తీగలు, వివిధ పొడవులు గల మాంగనిన్ తీగలు, ఒకే పొడవు కలిగి వేరు వేరు మధ్యచ్ఛేద వైశాల్యాలు గల అల్యూమినియం తీగలు, గ్రాఫ్ కాగితాలు, నిరోధాలు.

10th Class Physical Science 9th Lesson విద్యుత్ ప్రవాహం Textbook Activities

కృత్యములు

కృత్యం – 1

ప్రశ్న 1.
విద్యుత్ ప్రవాహంకు జనకము మరియు వాహకము అవసరమని కృత్యం ద్వారా తెలుపుము.
(లేదా)
ఆవేశాల చలనం వలన విద్యుత్ ప్రవాహం ఏర్పడునని కృత్యం ద్వారా వివరింపుము.
జవాబు:
సందర్భం -1:

1. ఒక బల్బు, ఘటం (బ్యాటరీ), స్విచ్ మరియు ఉష్ణ బంధక పొర కలిగిన రాగి తీగలను కొన్నింటిని తీసుకొనుము.
2. వీటిని వలయంలో కలిపి స్విచ్ ఆన్ చేయుము.
3. బల్బును పరిశీలించుము. అది వెలుగును.

సందర్భం – 2:

1. పైన తయారు చేయబడిన వలయం నుండి ఘటాన్ని తొలగించుము.
2. మిగిలిన పరికరాలతో వలయం పూర్తి చేయుము.
3. ఇప్పుడు స్విచ్ ఆన్ చేయుము.
4. బల్బు వెలగదు, దీనికి కారణము వలయంలో శక్తి జనకం (బ్యాటరీ) లేకపోవుటయే.

సందర్భం – 3:

1. ఇప్పుడు వలయంలో రాగి తీగకు బదులుగా నైలాన్ తీగను తీసుకొనుము.
2. నైలాన్ తీగను బల్బు, స్విచ్ ద్వారా బ్యాటరీ యొక్క రెండు చివరలకు కలుపుము.
3. ఇప్పుడు స్విచ్ ఆన్ చేసి బల్బును పరిశీలించుము.
4. బల్బు వెలగదు.
5. వలయంలో సామర్థ్య జనకమైన ఘటమున్నప్పటికీ నైలాన్ తీగలు శక్తిని తీసుకోలేకపోవడం వలన బల్బ్ వెలగలేదు.

పరిశీలన :
దీనిని బట్టి పై సందర్భాల ద్వారా వలయంలో విద్యుత్తును సరఫరా చేయడంలో, వలయంలో బ్యాటరీ, వాహక తీగలు అవసరమని తెలుస్తుంది.

కృత్యం – 3

ప్రశ్న 2.
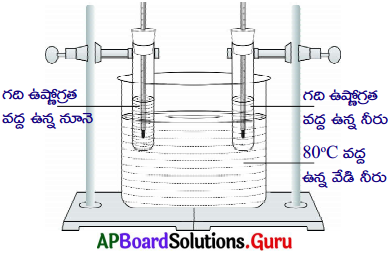
వాహక నిరోధం, ఆ వాహక స్వభావంపై ఆధారపడి ఉంటుందని ఒక కృత్యం ద్వారా నిరూపించండి.
జవాబు:

1. రాగి, నిక్రోమ్, మాంగనిన్ (కనీసం 2మీ) వంటి వివిధ రకాల లోహపు తీగలను తీసుకోండి. వాటి పొడవులు, మధ్యచ్ఛేద వైశాల్యాలు సమానంగా ఉండేట్లు జాగ్రత్త వహించండి.
2. పటంలో చూపినట్లు వలయాన్ని ఏర్పాటు చేయండి.
3. లోహపు తీగలలో ఏదో ఒకదానిని P, Q ల మధ్య ఉంచండి.
4. స్విచ్ ఆన్ చేసి, వలయంలో విద్యుత్ ప్రవాహాన్ని అమ్మీటర్ తో కొలిచి మీ నోట్ బుక్ లో రాసుకోండి.
5. మిగిలిన లోహపు తీగలతో ఈ కృత్యాన్ని నిర్వహించి, ప్రతీ సందర్భంలో బ్యాటరీ విద్యుత్ ప్రవాహాన్ని కొలవండి.
6. పొటెన్షియల్ భేదం స్థిరంగా ఉన్నప్పటికీ విద్యుత్ ప్రవాహం విలువ వివిధ లోహపు తీగలకు వివిధ రకాలుగా ఉండడం మీరు గుర్తిస్తారు.
7. ఈ కృత్యాన్ని బట్టి వాహక నిరోధం, ఆ వాహక స్వభావంపై ఆధారపడి ఉంటుందని చెప్పవచ్చు.

కృత్యం – 5

ప్రశ్న 3.
వాహక నిరోధము ఆ వాహక మధ్యచ్చేద వైశాల్యంకు విలోమానుపాతంలో ఉంటుందని ఒక కృత్యం ద్వారా వివరింపుము.
జవాబు:

1. ఒకే పొడవు, వివిధ మధ్యచ్ఛేద వైశాల్యాలు గల ఇనుప కడ్డీలను తీసుకొనుము.
2. పటంలో చూపిన విధముగా వలయాన్ని ఏర్పాటు చేయుము.
3. మనము ఎంచుకున్న కడ్డీలలో ఏదో ఒకదానిని P, Qల మధ్య ఉంచి వలయంను పూర్తిచేయుము.
4. వలయంలో ఉంచిన అమ్మీటర్ సహాయంతో విద్యుత్ ప్రవాహాన్ని కొలిచి రీడింగ్ ను నమోదు చేయుము.
5. మిగిలిన కడ్డీలతో ఈ కృత్యాన్ని మరలా చేయుము.
6. ప్రతీ సందర్భంలో విద్యుత్ ప్రవాహాన్ని కొలిచి రీడింగ్ ను నమోదు చేయుము.
7. ఇనుప కడ్డీ మధ్యచ్ఛేద వైశాల్యం పెరుగుతున్న కొలదీ అందులో విద్యుత్ ప్రవాహం కూడా పెరుగుటను మనము గమనించవచ్చు.
8. అంటే కడ్డీ మధ్యచ్ఛేద వైశాల్యం పెరిగే కొలదీ దాని నిరోధం తగ్గును.
9. ఈ కృత్యాన్ని బట్టి వాహక నిరోధము, వాహక మధ్యచ్ఛేద వైశాల్యంకు విలోమానుపాతంలో ఉంటుందని చెప్పవచ్చును.
   i.e. R ∝ \(\frac{l}{A}\) (ఉష్ణోగ్రత స్థిరంగా ఉన్నప్పుడు)

SCERT AP 10th Class Physics Study Material Pdf 5th Lesson మానవుని కన్ను-రంగుల ప్రపంచం Textbook Questions and Answers.

AP State Syllabus 10th Class Physical Science 5th Lesson Questions and Answers మానవుని కన్ను-రంగుల ప్రపంచం

10th Class Physical Science 5th Lesson మానవుని కన్ను-రంగుల ప్రపంచం Textbook Questions and Answers

అభ్యసనాన్ని మెరుగుపరుచుకోండి

ప్రశ్న 1.
హ్రస్వదృష్టి లోపాన్ని మీరెలా సవరిస్తారు?
(లేదా)
కన్ను యొక్క హ్రస్వ దృష్టిని మీరు ఏ విధంగా సవరిస్తారు?
జవాబు:
1) ఒక వ్యక్తి గరిష్ఠ దూర బిందువుకు ఆవల ఉన్న వస్తువును చూడలేకపోవు దోషాన్ని “హ్రస్వదృష్టి” అంటారు.

2) ఏ దూరం వద్ద నున్న బిందువుకు లోపల గల వస్తువుకు మాత్రమే కంటి కటకం రెటీనా పై ప్రతిబింబాన్ని ఏర్పరచుకోగలదో ఆ బిందువును గరిష్ఠ దూర బిందువంటారు.

3) గరిష్ఠ దూరబిందువుకు, స్పష్ట దృష్టి కనీస దూరాన్ని తెలిపే బిందువుకు మధ్య వస్తువు ఉన్నప్పుడు కంటి కటకం రెటీనా పై ప్రతిబింబమును ఏర్పరచగలదు.

|4) గరిష్ఠ దూరబిందువు ఆవల ఉన్న వస్తువు యొక్క ప్రతిబింబాన్ని కంటి కటకం రెటీనా కంటే ముందు ఏర్పరుస్తుంది.

5) కావున ఒక కటకంను ఉపయోగించి గరిష్ఠ దూర బిందువుకు ఆవల ఉన్న వస్తువు యొక్క ప్రతిబింబాన్ని గరిష్ఠ దూర బిందువు మరియు స్పష్ట దృష్టి కనీస దూరాన్ని తెలిపే బిందువుల మధ్యకు తేగలిగితే ఆ ప్రతిబింబం కంటి కటకానికి వస్తువులా పని చేస్తుంది.

6) హ్రస్వదృష్టిని నివారించేందుకు అనంతదూరంలో ఉండే వస్తువు యొక్క ప్రతిబింబాన్ని గరిష్ఠ దూర బిందువు వద్ద ఏర్పరచగలిగే కటకాన్ని ఎంచుకోవాలి.

7) దీని కొరకు ద్విపుటాకార కటకమును వాడాలి.

8) ఈ ద్విపుటాకార కటకం ఏర్పరిచే ప్రతిబింబం కంటి కటకానికి వస్తువు వలె పనిచేసి, చివరకు వస్తు ప్రతిబింబంను రెటీనా పై ఏర్పరచును.

ప్రశ్న 2.
దీర్ఘదృష్టి లోపాన్ని సవరించే విధానాన్ని వివరించండి.
(లేదా)
కన్ను యొక్క దీర్ఘదృష్టిని మీరు ఏ విధంగా సవరిస్తారు?
జవాబు:
1) దీర్ఘదృష్టి గల వ్యక్తి దూరంలో వున్న వస్తువులను స్పష్టంగా చూడగలడు. కానీ దగ్గరి వస్తువులను చూడలేడు.
2) దీనికి గల కారణము కంటి కటక కనిష్ఠ నాభ్యంతరం 2.27 సెం.మీ. కన్నా ఎక్కువగా ఉండడమే.

3) పై పటంలో చూపినట్లుగా ఈ సందర్భంలో దగ్గరలోని వస్తువు నుండి వచ్చే కాంతి కిరణాలు కంటి కటకం ద్వారా వక్రీభవనం చెంది ప్రతిబింబం రెటీనాకు ఆవల ఏర్పడుతుంది.
4) వస్తువు కనిష్ఠ దూర బిందువుకు ఆవల ఉంటే, కంటి కటకం రెటీనా పై ప్రతిబింబాన్ని ఏర్పరచగలదు.

5) కనుక దీర్ఘదృష్టిని నివారించడానికి ద్వికుంభాకార కటకాన్ని ఉపయోగించాలి.
6) ఈ కటకం వలన ఏర్పడే ప్రతిబింబం కంటి కటకానికి వస్తువుగా పనిచేస్తుంది.
7) అందువలన చివరకు కంటి కటకం వలన ఏర్పడే ప్రతిబింబం పటంలో చూపినట్లుగా రెటీనా పై ఏర్పడును.

ప్రశ్న 3.
పట్టక పదార్థ వక్రీభవన గుణకాన్ని ప్రయోగపూర్వకంగా ఎలా కనుగొంటారు?
(లేదా)
పట్టకపు వక్రీభవన గుణకమును కనుగొను కృత్యంను వ్రాయుము. (ప్రయోగశాల కృత్యం)
జవాబు:
ఉద్దేశ్యం : పట్టక వక్రీభవన గుణకాన్ని కనుగొనడము.

కావలసిన వస్తువులు :
పట్టకం, తెల్లని డ్రాయింగ్ చార్ట్ (20 X 20 సెం.మీ.), పెన్సిల్, గుండుసూదులు, స్కేలు మరియు కోణమానిని.

నిర్వహణ పద్దతి :

1. ఒక గాజు పట్టకాన్ని తీసుకొని, దాని త్రిభుజాకార పతనకిరణం, AM ఆధారం డ్రాయింగ్ చార్ట్ పై ఉండే విధముగా అమర్చుము.
2. పట్టక ఆధారం చుట్టూ పెన్సిల్ తో గీత గీసి పట్టకాన్ని తీసివేయాలి.
3. త్రిభుజ భుజం PQ పై ఒక బిందువు ‘M’ ను గుర్తించుము.
4. M వద్ద PQ కు లంబాన్ని గీయాలి.
5. M వద్ద PQ తో 30° కోణాన్ని గుర్తించి, ఒక రేఖను గీయుము. ఇదియే పతన కిరణం అగును.
6. ఈ కోణమును “పతన కోణము” అంటారు.
7. పట్టకాన్ని తిరిగి దాని స్థానంలో ఉంచి పతన కిరణం AB పై రెండు గుండు సూదులను నిలువుగా గుచ్చుము.
8. పట్టకం రెండోవైపు నుండి గుండుసూదుల ప్రతిబింబాలతో ఒకే వరుసలో ఉండునట్లు C, D బిందువుల వద్ద మరో రెండు గుండు సూదులను గుచ్చుము.
9. ఇప్పుడు C, D లను కలుపుము. ఇది బహిర్గత కిరణమును సూచించును.
10. పతన కిరణం, బహిర్గత కిరణాలను వెనుకకు పొడిగించిన అవి రెండూ ‘O’ వద్ద ఖండించుకుంటున్నాయి.
11. ‘O’ బిందువు వద్ద ఈ రెండు కిరణాల మధ్య కోణమును కొలిచిన, అది విచలన కోణం (d) అగును.
12. ఈ విధంగా వివిధ పతన కోణాలకు, విచలన కోణాల విలువలను తెలుసుకొని, వాటిని నమోదు చేయుము.
13. ఈ ప్రయోగం ద్వారా పతన కోణం పెరుగుతున్న కొలదీ కొంతమేర విచలన కోణం విలువ తగ్గి తర్వాత పతన కోణంతో పాటుగా పెరగడం గమనించవచ్చును.
    
14. పతన కోణంను X-అక్షం వెంబడి, విచలన కోణంను Y-అక్షం వెంబడి తీసుకొని గ్రాఫును గీసిన సున్నిత వక్రం ఏర్పడుతుంది.
15. ఈ వక్రం ద్వారా కనిష్ట విచలన కోణం ‘D’ ను కనుగొనవచ్చును.
16. ‘పట్టక కోణం ‘A’ కనిష్ఠ విచలన కోణం ‘D’ అయితే పట్టక వక్రీభవన గుణకము \(n=\frac{\sin \left[\frac{(A+D)}{2}\right]}{\sin \frac{A}{2}}\) అగును.

ప్రశ్న 4.
ఇంద్రధనుస్సు ఏర్పడే విధానాన్ని వివరించండి. (కృత్యం – 5)
జవాబు:

1. ప్రకృతిలోని తెల్లని సూర్యకాంతి, అనేక లక్షల నీటి బిందువుల చేత విక్షేపణం చెందడం వల్ల ఇంద్రధనుస్సు ఏర్పడును.
2. పటంలో చూపినట్లుగా నీటి బిందువు పై ప్రాంతం నుండి సూర్యుని కాంతికిరణం లోపలికి ప్రవేశించును.
3. అక్కడ జరిగే మొదటి వక్రీభవనంలో తెల్లని కాంతి వివిధ రంగులుగా విక్షేపణం చెందును.
4. అన్ని రంగులు నీటి బిందువు రెండో వైపుకు చేరాక, సంపూర్ణాంతర పరావర్తనం వల్ల నీటి బిందువులోనే వెనుకకు పరావర్తనం చెందుతాయి.
5. ఫలితముగా నీటి బిందువు మొదటి ఉపరితలాన్ని చేరాక, ప్రతీ రంగు మరలా గాలిలోకి వక్రీభవనం చెందును.
6. నీటి బిందువులోకి ప్రవేశించే కిరణాలు, బయటకు వెళ్ళే కిరణాల మధ్య కోణం (0° నుండి 42° మధ్య ఎంతైనా ఉండవచ్చు.
7. ఆ కోణం 42° లకు దాదాపు సమానంగా ఉన్నప్పుడు ప్రకాశవంతమైన ఇంద్రధనుస్సును మనం చూడగలము.
8. ప్రతి నీటి బిందువు కాంతిని ఏడు రంగులలోకి విడగొట్టినా, ఒక పరిశీలకుడు తాను ఉన్న స్థానాన్ని బట్టి, ఒక నీటి బిందువు నుండి వచ్చే రంగులలో ఏదో ఒకదానిని మాత్రమే చూడగలడు.
9. సూర్యకాంతి పుంజానికి, నీటి బిందువుచే వెనుకకు పంపబడిన కాంతికి మధ్యకోణం 42° ఉన్నప్పుడే మనకు ఎరుపు రంగు కనబడుతుంది.
10. 40° ల నుండి 42°ల మధ్య కోణంలో VIBGYOR లోని మిగిలిన రంగులు కనిపిస్తాయి.
    
11. ఈ విధముగా ప్రకృతిలో ఇంద్రధనుస్సు ఏర్పడును.

ప్రశ్న 5.
ఆకాశం నీలి రంగులో కనబడటానికి గల కారణాన్ని క్లుప్తంగా వివరించండి.
(లేదా)
మనకు ఆకాశము నీలముగా కనబడుటకు గల కారణమును వివరింపుము.
జవాబు:

1. ఆకాశం నీలిరంగుగా ఉండుటకు కారణము కాంతి యొక్క పరిక్షేపణము.
2. కాంతి పరిక్షేపణమనగా ఒక కణం శోషించుకున్న కాంతిని తిరిగి అన్ని దిశలలో వివిధ తీవ్రతలతో విడుదల చేయడాన్ని “కాంతి పరిక్షేపణం” అంటాము.
3. వాతావరణంలో వివిధ పరిమాణాలు గల కణాలుంటాయి.
4. వాతావరణంలోని నైట్రోజన్, ఆక్సిజన్ అణువు పరిమాణం నీలిరంగు కాంతి తరంగదైర్ఘ్యంతో పోల్చదగిన విధముగా ఉంటుంది.
5. ఈ అణువులు నీలిరంగు కాంతికి పరిక్షేపణ కేంద్రాలుగా పనిచేస్తాయి.
6. వాతావరణంలో నైట్రోజన్, ఆక్సిజన్ అణువులు ఎక్కువగా వుండటం వల్ల, అవి నీలిరంగు కాంతికి పరిక్షేపణ కేంద్రాలుగా పనిచేయడం వల్ల ఆకాశం నీలిరంగులో కనిపిస్తుంది.

ప్రశ్న 6.
అంశం (A) : కాంతి పరిక్షేపణం వలన ఆకాశం నీలిరంగులో కనబడుతుంది.
కారణం (R) : తెల్లని కాంతిలోని వివిధ కాంతులలో నీలిరంగు కాంతి తరంగదైర్ఘ్యం తక్కువ.
a) A, R రెండూ సరియైనవి. మరియు A కు R సరైన వివరణ.
b) A, R రెండూ సరియైనవి. కానీ A కు R సరైన వివరణ కాదు.
c) A సరియైనది. కానీ R సరియైనది కాదు.
d) A మరియు R సరైనవి కావు.
e) A సరియైనది కాదు కానీ R సరైనది.
జవాబు:
a) A, R లు రెండూ సరియైనవి. మరియు A కు R సరైన వివరణ.

కారణము :
ఆకాశం నీలిరంగుకు కాంతి పరిక్షేపణమే కారణము. తక్కువ తరంగదైర్ఘ్యం గల కాంతికి, అధిక తరంగదైర్ఘ్యం గల కాంతితో పోల్చితే పరిక్షేపణ సామర్థ్యం ఎక్కువ.

ప్రశ్న 7.
తరగతి గదిలో ఇంద్రధనుస్సును ఏర్పరిచేందుకు ఒక ప్రయోగాన్ని తెల్పండి. ప్రయోగ విధానాన్ని వివరించండి. (కృత్యం-4)
జవాబు:

1. ఒక లోహపు పళ్ళాన్ని తీసుకొని; నీటితో నింపుము.
2. నీటి ఉపరితలంతో కొంతకోణం చేసే విధంగా ఒక సమతల దర్పణమును పటంలో చూపిన విధంగా ఉంచుము.
3. పటంలో చూపినట్లుగా నీటి గుండా అద్దం పై తెల్లని కాంతిని ప్రసరింపజేయుము.
4. ఈ అమరికకు కొంత ఎత్తులో తెల్లటి కార్డుబోర్డుపై వివిధ రంగులతో ఇంద్రధనుస్సు ఏర్పడుటను గమనించవచ్చును.

ప్రశ్న 8.
కొన్ని బైనాక్యులర్లందు పట్టకాలను వినియోగిస్తారు. బైనాక్యులర్లలో పట్టకాలు ఎందుకు వినియోగిస్తారో తెలియజేసే – సమాచారాన్ని సేకరించండి.
(లేదా)
పట్టకములకు సంబంధించిన సమాచారాన్ని సేకరించుము. వాటిని బైనాక్యులలో ఎందుకు వాడుతారో వివరింపుము.
జవాబు:

1. పరిశీలకునికి దూరపు వస్తువులను పరీక్షించుటకు సమాంతరంగా కదిలే విధంగా రెండు కటకాలను అమర్చుతారు.
2. అధిక -పరావర్తనం కోసం బైనాక్యులర్లలో పట్టకాలను ఉపయోగిస్తారు.
3. పట్టకాలను ఉపయోగించి బైనాక్యులర్ యొక్క పరిమాణంను తగ్గిస్తారు.
4. పట్టకములను ఉపయోగించి వస్తు పరిమాణం మరియు దృక్ తీవ్రతలను పెంచవచ్చును.
5. సాధారణంగా బైనాక్యులర్లలో లంబకోణ పట్టకం లేదా ద్విపట్టకాలను ఉపయోగిస్తారు.
6. బైనాక్యులలో పట్టకాలను ఉపయోగించి తక్కువ ఖర్చుతోనే వాటి పరావర్తన సామర్థ్యాన్ని 95% వరకు పెంచవచ్చును.

ప్రశ్న 9.
పటంలో పట్టక తలం AB పై పడిన పతన కిరణాన్ని, పట్టక తలం AC నుండి వచ్చే బహిర్గత కిరణాన్ని చూపడం జరిగింది. పటంలో లోపించిన వాటిని గీయండి.

జవాబు:
AB, AC లు వక్రీభవన తలాలు మరియు BC పరావర్తన తలము.

ప్రశ్న 10.
ఆకాశం నీలిరంగులో కనబడడానికి కారణమైన వాతావరణంలోని అణువుల పాత్రను మీరెలా అభినందిస్తారు?
(లేదా)
ఆకాశం నీలి రంగులో కనబడుటకు కారణం ఏమిటి ? ఈ విషయంలో వాతావరణంలోని అణువుల పాత్రను మీరెలా అభినందిస్తారు?
జవాబు:

1. ఆకాశం నీలిరంగులో ఉండుటకు ముఖ్యకారణము కాంతి పరిక్షేపణమే.
2. వాతావరణంలోని N₂, O₂ అణువుల పరిమాణం నీలిరంగు కాంతి తరంగదైర్ఘ్యంతో పోల్చదగిన విధముగా ఉంటుంది.
3. ఈ అణువులు నీలిరంగు కాంతికి పరిక్షేపణ కేంద్రాలుగా పనిచేస్తాయి.
4. వాతావరణంలో నైట్రోజన్, ఆక్సిజన్ అణువుల శాతము ఎక్కువగా ఉండటం వలన, అవి నీలిరంగు కాంతికి పరిక్షేపణ కేంద్రాలుగా పనిచేయడం వలన ఆకాశం నీలిరంగులో కనిపిస్తుంది.
5. ఈ విధమైన ఆకాశపు నీలిరంగుకి కారణమైన వాతావరణంలోని N₂ మరియు O₂ల పాత్రను నేను అభినందించుచున్నాను.

ప్రశ్న 11.
కంటిలోని సిలియరి కండరాల పనితీరును మీరెలా అభినందిస్తారు?
(లేదా)
సిలియరి కండరాల పనితీరు మన కంటికి ఏ విధమైన అవసరమో అభినందించుము.
జవాబు:
కంటిలోని సిలియరి కండరాల పనితీరు కంటిపై ప్రతిబింబంను ఏర్పరుచుటలో ఎంతో అభినందనీయమైనది. ఎందుకనగా

1. కంటిలోని కటకానికి ఆనుకొని ఉన్న ఈ కండరాలు కటక వక్రతా వ్యాసార్ధాన్ని మార్చడం ద్వారా కటకం తన నాభ్యంతరమును మార్చుకోవడానికి దోహదపడతాయి.
2. దగ్గరలో వున్న వస్తువును కన్ను చూస్తున్నప్పుడు, సిలియరి కండరాలు ఒత్తిడికి గురికావడం వల్ల కంటి కటక నాభ్యంతరం తగ్గుతుంది.
3. దూరంలో ఉన్న వస్తువును కన్ను చూస్తున్నప్పుడు, సిలియరి కండరాలు విశ్రాంత స్థితిలో ఉండటం వల్ల కంటి కటక నాభ్యంతరం గరిష్ఠమవుతుంది.
4. ఈ విధమైన సర్దుబాటును సిలియరి కండరాలు చేస్తాయి.

ప్రశ్న 12.
కొన్ని సందర్భాలలో ఆకాశం తెలుపురంగులో కనబడుతుంది. ఎందుకు?
(లేదా)
అప్పుడప్పుడు ఆకాశం తెలుపు రంగులో కనబడుటకు వెనుకన గల కారణాలేమిటో వ్రాయుము.
జవాబు:

1. వాతావరణంలో వివిధ పరిమాణాలు గల కణాలుంటాయి.
2. ఆ కణాలు వాటి పరిమాణాలకనుగుణంగా వివిధ తరంగదైర్ఘ్యాలు గల కాంతిని పరిక్షేపణం చేస్తాయి.
3. వేసవి రోజుల్లో ఉష్ణోగ్రత ఎక్కువగా ఉండడం వల్ల వాతావరణంలోకి నీటి ఆవిరి చేరుతుంది.
4. దీని ద్వారా వాతావరణంలో నీటి అణువులు ఇతర పౌనఃపున్యాలు గల కాంతులను పరిక్షేపణం చేస్తాయి.
5. N₂, O₂ ల పరిక్షేపణం వల్ల వచ్చే నీలిరంగు కాంతి, నీటి అణువుల పరిక్షేపణం వల్ల వచ్చే ఇతర రంగుల కాంతులన్నీ కలిసి మన కంటిని చేరినప్పుడు తెలుపురంగు కాంతి కనబడుతుంది.

ప్రశ్న 13.
తెల్లకాగితానికి నూనె పూస్తే, అది పాక్షిక పారదర్శకంగా పనిచేస్తుంది. ఎందుకు?
(లేదా)
కాగితం (లేదా) న్యూస్ పేపర్ కు నూనెను పూసిన అది పాక్షిక పారదర్శకంగా పని చేయుటకు గల కారణాలను వ్రాయుము.
జవాబు:

1. తెల్లని కాగితం కాంతినిరోధములా ప్రవర్తించును.
2. తెల్లని కాగితానికి నూనె పూస్తే అది పాక్షిక పారదర్శక పదార్థంగా పనిచేయును.
3. కాగితము మరియు నూనెల వక్రీభవన గుణకాలు సమానమైతే, దానిమీద పడిన కాంతి సమాన వక్రీభవన గుణకాల వలన కాగితం నుండి నూనెలోనికి ప్రవేశించునపుడు ఎటువంటి పరిక్షేపణం చెందకుండా ప్రయాణించును.
4. ఈ కారణం చేత నూనె పూసిన కాగితము పాక్షిక పారదర్శకముగా పనిచేయును.

ప్రశ్న 14.
“దీర్ఘదృష్టి” గల ఒక వ్యక్తికి 100 సెం.మీ. నాభ్యంతరం గల కటకాన్ని వాడమని డాక్టర్ సలహా ఇచ్చారు. కనిష్ఠ దూరబిందువు యొక్క దూరాన్ని, కటక సామర్థ్యాన్ని కనుగొనండి. (జవాబు : 33.33 సెం.మీ., 1D)
జవాబు:
వస్తు దూరము u =- 25 సెం.మీ. –
ప్రతిబింబదూరం V = కనిష్ఠ దూరము = -d
నాభ్యంతరము f = 100 సెం.మీ.
కనిష్ఠ దూరము ‘d’ మరియు నాభ్యంతరం ‘f అయిన

ప్రశ్న 15.
ఒక వ్యక్తి దూరంలో ఉన్న వస్తువును చూస్తున్నాడు. అతని కంటిముందు కేంద్రీకరణ కటకాన్ని ఉంచితే, అతనికి వస్తువు పెద్దదిగా కనబడుతుందా? కారణాన్ని తెల్పండి.
(లేదా)
రావు, అతనికి దూరంగా గల వస్తువును చూస్తున్నప్పుడు అతని స్నేహితుడు శ్రీను ఒక కుంభాకార కటకంను అతని కంటి ముందు ఉంచిన అది అతనికి వస్తువును పెద్దదిగా కనబడేటట్లు చేస్తుందా? దీనికి గల కారణాలను వ్రాయుము.
జవాబు:

1. ఒక వ్యక్తి దూరంలో వున్న వస్తువును చూస్తున్నప్పుడు, అతని కంటి ముందు కేంద్రీకరణ కటకాన్ని ఉంచిన, వస్తు ప్రతిబింబం మసకబారుతుంది.
2. కేంద్రీకరణ (లేక) కుంభాకార కటకపు ప్రతిబింబ విషయం వస్తు స్థానంపై ఆధారపడును.
3. దూరంగా ఉన్నటువంటి వస్తువులను చూస్తున్నపుడు కుంభాకార కటకం వలన అవి మసకగా కనిపిస్తాయి.
4. ఒకవేళ వస్తువును కుంభాకార కటకపు విషయంలో కటకనాభి, కటక కేంద్రముల మధ్య ఉంచినపుడు నిటారైన, వృద్ధీకరణ చెందిన ప్రతిబింబం ఏర్పడును.

ప్రశ్న 16.
కృత్రిమ ఇంద్రధనుస్సును పొందే విధానాన్ని రెండు కృత్యాల ద్వారా వివరించండి. (AS1)
(లేదా)
మీ ఉపాధ్యాయుడు నిన్ను ఒక ఇంద్రధనుస్సును ఏర్పరచమన్న నీవు ఏ విధంగా ఏర్పరచెదవో ఒక కృత్యంను వ్రాయుము. (కృత్యం : 1)
జవాబు:

1. తెల్లని గోడకు దగ్గరగా ఒక టేబుల్ ను ఉంచుము.
2. ఒక కార్డ్ బోర్డు షీట్ కు మధ్యలో సన్నని రంధ్రం చేసి, దానిని టేబుల్ పై నిలువుగా అమర్చుము.
3. కార్డ్ బోర్డుకు, గోడకు మధ్యలో ఒక పట్టకాన్ని ఉంచుము.
4. తెలుపురంగు కాంతినిచ్చే కాంతి జనకాన్ని కార్డ్ బోర్డ్ కు దగ్గరగా ఉంచి, దాని రంధ్రం గుండా కాంతిని ప్రసరింపజేయుము.
5. ఈ కాంతి సన్నని పుంజంగా ఉంటుంది. దీనిని పట్టకం యొక్క ఏదో ఒక దీర్ఘచతురస్రాకార తలంపై పడే విధముగా పట్టుకొని పట్టకాన్ని త్రిప్పుతూ ఉంటే, గోడపై ఇంద్రధనుస్సు ఏర్పడుతుంది.

కృత్యం : 2
జవాబు:
7వ ప్రశ్న జవాబు చూడుము.

ప్రశ్న 17.
పట్టక వక్రీభవన గుణక సూత్రాన్ని ఉత్పాదించండి. (AS1)
(లేదా)
పట్టకపు వక్రీభవన గుణకంను కనుగొను సూత్రంను వ్రాసి, రాబట్టుము.
జవాబు:

1) పటంలో PQR అను పట్టకం యొక్క పట్టక కోణము ‘A’, పట్టక పదార్థపు వక్రీభవన గుణకము ‘n’, PQ, PRలు వక్రీభవన తలాలు.
2) AB పతన కిరణము, CD బహిర్గామి కిరణము పతన కోణము i₁ బహిర్గామి కోణం i₂ అనుకొనుము.

3) త్రిభుజము OMN నుండి,
d= i₁ – r₁ + i₂ – r₂
∴ d = (i₁ + i₂) – (r₁ + r₂) ………. (1)

4) త్రిభుజము PMN నుండి,
A + (90° = r₁) + (90° – r₂) = 180°
r₁ + r₂ = A ……………… (2)
5) (1), (2) సమీకరణాల నుండి
=d = (i₁ + i₂) – A
= A+ d = i₁ + i₂ ……………………… (3)

6) పతన కోణం, బహిర్గత కోణం, విచలన కోణము మరియు పట్టక కోణాల మధ్య సంబంధమును సమీకరణం- (3) తెలియజేస్తుంది.

7) స్నెల్ నియమం n₁ sin i = n₂ sin r కనుక, M బిందువు వద్ద, గాలి వక్రీభవన గుణకము n₁ = 1, పట్టక వక్రీభవన గుణకము n₂ = n, పతన కోణము i = i₁, వక్రీభవన కోణం r = r₁ లను స్నెల్ నియమంలో ప్రతిక్షేపించగా
sin i₁ = n sin r₁ ………. (4)

8) అదే విధముగా N బిందువు వద్ద, పట్టక వక్రీభవన గుణకము n₁ = n, గాలి వక్రీభవన గుణకము n₂ = 1, పతన కోణం i = r₂, వక్రీభవన కోణం r= i₂, స్నెల్ నియమంలో ప్రతిక్షేపించగా
n sin r₂ = sin i₂ ………. (5)

9) కనిష్ఠ విచలన కోణం (D) వద్ద పతన కోణం, బహిర్గామి కోణాల విలువలు సమానం. అనగా i₁ = i₂

10) సమీకరణం (3) నుండి కనిష్ఠ విచలన కోణంకు A + D = i + i
⇒ A + D = 2i₁
∴ \(\mathrm{i}_{1}=\frac{\mathrm{A}+\mathrm{D}}{2}\)

ప్రశ్న 18.
λ₁ తరంగదైర్ఘ్యం గల కాంతి n₁ వక్రీభవన గుణకం గల యానకం నుండి n₂ వక్రీభవన గుణకం గల యానకంలోకి ప్రవేశించింది. రెండవ యానకంలో ఆ కాంతి తరంగదైర్ఘ్యం ఎంత? (AS1)
జవాబు:

2) రెండు యానకాలలో తరంగదైర్ఘ్యాలు వరుసగా λ₁ మరియు λ₂ అనుకొనుము.

3) రెండు యానకాల వక్రీభవన గుణకాలు వరుసగా n₁ మరియు n₂ అనుకొనుము.

4) ఒక యానకపు వేగము (v), తరంగదైర్ఘ్యం (λ) మరియు పౌనఃపున్యాల (υ) మధ్య సంబంధము v = υλ.

5) కాంతి ఒక యానకం నుండి వేరొక యానకంలోకి ప్రవేశించినపుడు, దాని పౌనఃపున్యంలో మార్పు ఉండదు.

6) కావున v₁ = υλ₁ మరియు v₂ = υλ₂ అగును.

ప్రశ్న 19.
అంశం (A) : పట్టక వక్రీభవన గుణకం, ఆ పట్టక తయారీకి వాడిన గాజురకంపై మరియు కాంతి రంగుపై మాత్రమే ఆధారపడుతుంది. (AS2)
కారణం (R) : పట్టక వక్రీభవన గుణకం, పట్టక వక్రీభవన కోణంపై మరియు కనిష్ఠ విచలన కోణంపై ఆధారపడుతుంది.
a) A, R రెండూ సరియైనవి. మరియు A కు R సరైన వివరణ.
b) A, R రెండూ సరియైనవి. కానీ Aకు R సరైన వివరణ కాదు.
c) A సరియైనది. కానీ R సరియైనది కాదు.
d) A మరియు R సరైనవి కావు.
e) A సరియైనది కాదు కానీ R సరైనది.
జవాబు:
b) ‘A, R’ లు రెండూ సరియైనవే, కాని A కు R సరైన వివరణ కాదు.
కారణము :
పట్టక వక్రీభవన సూత్రము ప్రకారం వక్రీభవన గుణకము, పట్టకం తయారీకి వాడిన గాజురకంపై మరియు కాంతి రంగుపై ఆధారపడుతుంది.

ప్రశ్న 20.
మన చుట్టూ ఉన్న రంగుల ప్రపంచాన్ని మనం చూడడానికి ఉపయోగపడేది కన్ను. కంటి కటకానికి గల సర్దుబాటు లక్షణం వల్ల ఇది సాధ్యమవుతుంది. ఈ విషయంపై మీ స్పందనను తెలియజేసే విధంగా ఆరు వాక్యాల పద్యాన్ని రాయండి. (AS6)
జవాబు:
ఇంద్రియాలన్నింటిలో కన్నే మిన్నరా
అది లేకపోతే బ్రతుకే సున్నరా
సృష్టిని చూడగల్గడమే మహాభాగ్యంరా
దృష్టిని కల్గి ఉండడమే గొప్ప అదృష్టంరా
మన్నువంటి ఆధారం లేదురా
కన్నువంటి ప్రకాశం లేదురా
‘A’ విటమిన్ లోపిస్తే అంధత్వమేరా
అంధులైతే జీవితమే వృధారా
అందుకే కంటిని జాగ్రత్తగా కాపాడుకోవాలిరా.

ప్రశ్న 21.
గాజు పారదర్శక పదార్థం. ఒక తలం గరుకుగా చేయబడిన గాజు పాక్షిక పారదర్శకంగానూ, తెలుపురంగులోనూ కనబడుతుంది. ఎందుకు?
(లేదా)
సమరీతి, నునుపైన గాజు పారదర్శక పదార్థంగానూ, గరుకు చేయబడిన గాజు పాక్షిక పారదర్శకంగానూ, తెలుపు రంగులో కనబడుటకు గల కారణాలను వ్రాయుము.
జవాబు:

1. గాజు ఒక పారదర్శక పదార్థం. ఇది తన గుండా కాంతిని ప్రసారం చేయును.
2. గాజును ఒక తలం గరుకుగా చేయడం వల్ల ఆ ఉపరితలంలో అనేక ఎత్తు పల్లాలు అనగా అసమతలం ఏర్పడుతుంది.
3. ఇటువంటి అసమతలం క్రమరహిత పరావర్తనమును ఏర్పరుస్తుంది.
4. దీనివల్ల కొంతి ప్రసారం జరుగదు.
5. దీని ప్రభావం వలన గాజు పాక్షిక పారదర్శకముగా పని చేస్తుంది.
6. అందుకనే గరుకుతలం తెలుపురంగులో కనబడుతుంది.

ప్రశ్న 22.
పట్టకం యొక్క ఒక తలంపై 40° కోణంతో పతనమైన కాంతి కిరణం, 30° కనిష్ఠ విచలనాన్ని పొందింది. అయిన పట్టక కోణాన్ని, ఇచ్చిన తలం వద్ద వక్రీభవన కోణాన్ని కనుగొనండి. (జవాబు : 50°, 25°) (AS7)
జవాబు:
పట్టకపు తలంపై పతనమయ్యే కాంతి పతన కోణము = i = 40°
కనిష్ఠ విచలన కోణము = D = 30°

ఖాళీలను పూరించండి

1. స్పష్ట దృష్టి కనిష్ఠ దూరం విలువ …………. (25 సెం.మీ.)
2. రెటీనా, కంటి కటకాల మధ్య దూరం ………….. (2.5 సెం.మీ.)
3. కంటి కటకం యొక్క గరిష్ఠ నాభ్యంతరం విలువ …………… (2.5 సెం.మీ.)
4. మానవుని కంటి యొక్క నాభ్యంతరం మారటానికి దోహదపడే కండరాలు ………………. (సిలియరి)
5. కటకం యొక్క సామర్థ్యం 1D అయిన, ఆ కటక నాభ్యంతరం …………….. (100 సెం.మీ.)
6. హ్రస్వ దృష్టిని నివారించేందుకు ………………….. కటకాన్ని వాడుతారు. (పుటాకార)
7. దీర్ఘదృష్టిని నివారించేందుకు ……………… కటకాన్ని వాడుతారు. (కుంభాకార)
8. పట్టకం కనిష్ఠ విచలన స్థానంలో ఉన్నప్పుడు పతన కోణం ………………….. కు సమానం. (బహిర్గామికోణం)
9. తెల్లని కాంతి వివిధ రంగులుగా (VIBGYOR) విడిపోవడాన్ని ………………… అంటాం. (కాంతి విక్షేపణం)
10. వక్రీభవనం జరిగినప్పుడు కాంతి ………………….. లో మార్పు రాదు. (పౌనఃపున్యం)

సరైన సమాధానాన్ని ఎన్నుకోండి

1. మానవుని కన్ను గ్రహించే వస్తు పరిమాణం ప్రాథమికంగా …. పై ఆధారపడుతుంది.
A) వస్తువు నిజ పరిమాణం
B) కన్ను నుండి వస్తువుకు గల దూరం
C) నల్లగుడ్డు రంధ్రం
D) రెటీనాపై ఏర్పడ్డ ప్రతిబింబ పరిమాణం
జవాబు:
B) కన్ను నుండి వస్తువుకు గల దూరం

2. వివిధ దూరాలలో గల వస్తువులను చూస్తున్నప్పుడు కింది వాటిలో ఏది స్థిరంగా ఉంటుంది?
A) కంటి కటక నాభ్యంతరం
B) కంటి కటకం నుండి వస్తువుకి గల దూరం
C) కంటి కటక వక్రతా వ్యాసార్ధం
D) కంటి కటకం నుండి ప్రతిబింబ దూరం
జవాబు:
D) కంటి కటకం నుండి ప్రతిబింబ దూరం

3. కింది వాటిలో వక్రీభవన సమయంలో మారని విలువ
A) తరంగదైర్ఘ్యం
B) పౌనఃపున్యం
C) కాంతివేగం
D) పైవన్నీ
జవాబు:
B) పౌనఃపున్యం

4. పటంలో చూపిన విధంగా టేబుల్ పై ఉంచిన ఒక సమద్విబాహు పట్టకంపై కాంతి పతనమైంది. కనిష్ఠ విచలనానికి సంబంధించి కింది వాటిలో ఏది సరియైనది?

A) ఆధారానికి సమాంతరరేఖ PQ
B) ఆధారానికి సమాంతరరేఖ QR
C) ఆధారానికి సమాంతరరేఖ RS
D) ఆధారానికి సమాంతర రేఖ PQ లేదా RS
జవాబు:
B) ఆధారానికి సమాంతరరేఖ QR

5. హ్రస్వదృష్టితో బాధపడే వ్యక్తి యొక్క గరిష్ఠ దూరం 5 మీ. దీనిని నివారించి సాధారణ దృష్టి వచ్చేట్లు చేయాలంటే …. ను వినియోగించాలి.
A) 5 మీ. నాభ్యంతరం గల పుటాకార కటకం
B) 10 మీ. నాభ్యంతరం గల పుటాకార కటకం
C) 5 మీ. నాభ్యంతరం గల కుంభాకార కటకం
D) 2.5 మీ. నాభ్యంతరం గల కుంభాకార కటకం
జవాబు:
A) 5 మీ. నాభ్యంతరం గల పుటాకార కటకం

6. సూర్యకాంతిని శోషించుకున్న అణువు వివిధ కాంతి తీవ్రతలతో అన్ని దిశలలోనూ కాంతిని విడుదల చేయడాన్ని …….. అంటాం.
A) కాంతి పరిక్షేపణం
B) కాంతి విక్షేపణం
C) కాంతి పరావర్తనం
D) కాంతి వక్రీభవనం
జవాబు:
A) కాంతి పరిక్షేపణం

10th Class Physical Science 5th Lesson మానవుని కన్ను-రంగుల ప్రపంచం Textbook InText Questions and Answers

10th Class Physical Science Textbook Page No. 90

ప్రశ్న 1.
విమానంలో ప్రయాణించే వ్యక్తికి ఇంద్రధనుస్సు ఏ ఆకారంలో కనిపిస్తుందో ఊహించగలరా? మీ స్నేహితులతో చర్చించండి. సమాచారాన్ని సేకరించండి.
జవాబు:
విమానంలో ప్రయాణించే వ్యక్తికి ఇంద్రధనుస్సు పూర్తిగా వృత్తాకారంలో కన్పించును.

10th Class Physical Science Textbook Page No. 90

ప్రశ్న 2.
మన కంటిముందున్న అన్ని వస్తువులనూ మనం స్పష్టంగా చూడగలమా?
జవాబు:
మన కంటి ముందు 25 సెం.మీ. దూరానికి అవతల ఉన్న అన్ని వస్తువులను మనం స్పష్టంగా చూడగలం.

10th Class Physical Science Textbook Page No. 91

ప్రశ్న 3.
స్పష్ట దృష్టి యొక్క సరాసరి దూరం విలువ ఎంత?
జవాబు:
స్పష్ట దృష్టి యొక్క కనీస దూరం 25 సెం.మీ.

ప్రశ్న 4.
మీ కంటికి 25 సెం.మీ. దూరంలో ఉంచిన వస్తువు ఆకారం ఎలా ఉన్నా, దానిని పై నుండి కింది వరకు మీరు చూడగలరా?
జవాబు:
చూడలేము. ఎందుకనగా స్పష్ట దృష్టి కనీస దూరం విలువ వయస్సుపై ఆధారపడి ఉంటుంది. అదే విధంగా కంటి వద్ద 60° కోణంతో కనబడే వస్తుభాగం మాత్రమే మనం చూడగలం.

10th Class Physical Science Textbook Page No. 92

ప్రశ్న 5.
స్పష్ట దృష్టి కనీస దూరం, దృష్టికోణం విలువలు వ్యక్తినిబట్టి, వయసునుబట్టి ఎందుకు మారతాయి?
జవాబు:
ఈ విలువలన్నీ కంటి నిర్మాణం మరియు సిలియరి కండరాల పనితీరుపై ఆధారపడి ఉంటాయి కాబట్టి.

10th Class Physical Science Textbook Page No. 93

ప్రశ్న 6.
వివిధ వస్తుదూరాలకు ఒకే ప్రతిబింబదూరం ఉండడం ఎలా సాధ్యం?
జవాబు:
కటకనాభ్యంతరం విలువను మారుస్తూ ఉంటే వివిధ వస్తు దూరాలకు ఒకే ప్రతిబింబ దూరం ఉండటం సాధ్యపడుతుంది.

ప్రశ్న 7.
కటకాల గుండా వక్రీభవనం గురించి మీకున్న అవగాహనతో పై ప్రశ్నకు సమాధానం చెప్పగలరా?
జవాబు:
చెప్పగలము. వస్తుదూరం మారినప్పుడు ప్రతిబింబ దూరం స్థిరంగా ఉండాలంటే కటక నాభ్యాంతరం మారాలి.

10th Class Physical Science Textbook Page No. 94

ప్రశ్న 8.
కన్ను తన నాభ్యంతరాన్ని ఎలా మార్చుకుంటుంది? కనుగుడ్డులో ఈ మార్పు ఎలా జరుగుతుంది?
జవాబు:
కనుగుడ్డులోని కటకానికి ఆనుకుని ఉన్న సిలియరి కండరాలు కటక వక్రతా వ్యాసార్థాన్ని మారుస్తాయి. ఈ మార్పు ద్వారా కన్ను తన నాభ్యంతరాన్ని మార్చుకుంటుంది.

ప్రశ్న 9.
కంటి కటకం నిజ ప్రతిబింబాన్ని ఏర్పరుస్తుందా? మిథ్యా ప్రతిబింబాన్ని ఏర్పరుస్తుందా?
జవాబు:
కంటి కటకం వస్తువు నిజ ప్రతిబింబాన్ని రెటీనా పై తలక్రిందులుగా ఏర్పరుస్తుంది.

ప్రశ్న 10.
కంటి కటక నాభ్యంతరం మార్పుకు ఏదైనా హద్దు ఉందా?
జవాబు:
అవును. కటక నాభ్యంతరానికి గరిష్ఠ, కనిష్ఠ విలువలుంటాయి.

10th Class Physical Science Textbook Page No. 95

ప్రశ్న 11.
కంటి కటకం తన నాభ్యంతరాన్ని మార్చుకోలేకపోతే ఏం జరుగుతుంది?
జవాబు:
కంటి కటకం తన నాభ్యంతరాన్ని మార్చుకోలేకపోతే వస్తువును సులభంగా, స్పష్టంగా చూడలేము.

ప్రశ్న 12.
కంటి కటక నాభ్యంతరం 2.27 – 2.5 సెం.మీ.లకు మధ్యస్థంగా లేకపోతే ఏమవుతుంది?
జవాబు:
కంటి కటక నాభ్యంతరం 2.27 – 2.5 సెం.మీ. లకు మధ్యస్థంగా లేకపోతే కంటి దోషాలు ఏర్పడతాయి.

10th Class Physical Science Textbook Page No. 97

ప్రశ్న 13.
‘కంటి కటక కనిష్ఠ నాభ్యంతరం 2.27 సెం.మీ. కంటే ఎక్కువైతే ఏం జరుగుతుంది?
జవాబు:

1. కంటి కటక కనిష్ఠ నాభ్యంతరం 2.27 సెం.మీ. కంటే ఎక్కువైతే దీర్ఘదృష్టి ఏర్పడుతుంది.
2. అంటే ఆ వ్యక్తి దూరంలో ఉన్న వస్తువులను స్పష్టంగా చూడగలదు కాని దగ్గరి వస్తువులను చూడలేదు.

10th Class Physical Science Textbook Page No. 98

ప్రశ్న 14.
దీర్ఘదృష్టిని సవరించడానికి ఏం చేయాలి?
జవాబు:
దీర్ఘదృష్టి సవరణ :

1. వస్తువు కనిష్ఠదూర బిందువుకు ఆవల ఉంటే, కంటికటకం రెటీనా పై ప్రతిబింబాన్ని ఏర్పరచగలదు.
2. కనుక కనిష్ఠదూర బిందువు (H) కు స్పష్ట దృష్టి కనీస దూరాన్ని తెలిపే బిందువు (L) కు మధ్యనున్న వస్తువు యొక్క ప్రతిబింబాన్ని కనిష్ఠదూర బిందువుకు ఆవల ఏర్పరచగలిగే కటకాన్ని అంటే ద్వికుంభాకార కటకాన్ని ఉపయోగించాలి.
3. ద్వికుంభాకార కటకాన్ని వాడటం వల్ల ఇది సాధ్యపడుతుంది.

10th Class Physical Science Textbook Page No. 99

ప్రశ్న 15.
కంటి డాక్టర్ రాసే ప్రిస్క్రిప్షన్ లోని వివరాలను మీరెప్పుడైనా పరిశీలించారా?
జవాబు:
కంటి డాక్టర్ రాసే ప్రిస్క్రిప్షన్లోని వివరాలను పరిశీలించాను. అవి +, – గుర్తులతో సూచింపబడి ఉంటాయి.

ప్రశ్న 16.
సైట్ పెరగడం లేదా తగ్గడం అంటే ఏమిటి?
జవాబు:
కంటి చూపులోని పెరుగుదల లేదా తగ్గుదల.

ప్రశ్న 17.
కటక సామర్థ్యం అంటే ఏమిటి?
జవాబు:
కటక సామర్థ్యం :
ఒక కటకం కాంతికిరణాలను కేంద్రీకరించే స్థాయి లేదా వికేంద్రీకరించే స్థాయిని కటక సామర్థ్యం అంటాం. (లేదా) కటక నాభ్యంతరం యొక్క విలోమ విలువను కటక సామర్థ్యం అంటాం.

ఒక కటక నాభ్యంతరం గ అనుకుంటే,
కటక సామర్థ్యం P = 1/f (మీటర్లలో) ; P = 100/f (సెం.మీ.లలో)
కటక సామర్థ్యానికి ప్రమాణం డయాప్టర్ (Dioptre). దీనిని D తో సూచిస్తాం.

10th Class Physical Science Textbook Page No. 100

ప్రశ్న 18.
పట్టకం అంటే ఏమిటి?
జవాబు:
ఒకదానికొకటి కొంత కోణం చేసే కనీసం రెండు సమతలాలతో పరిసరయానకం నుండి వేరుచేయబడి ఉన్న పారదర్శక యానకాన్ని “పట్టకం” అంటారు.

10th Class Physical Science Textbook Page No. 105

ప్రశ్న 19.
తెల్లని కాంతి రంగులుగా విడిపోవడాన్ని కిరణ సిద్ధాంతంతో వివరించగలమా?
జవాబు:
తెల్లని కాంతి రంగులుగా విడిపోవడాన్ని కిరణ సిద్ధాంతంతో వివరించలేము.

ప్రశ్న 20.
వివిధ రంగులు గల కొంతుల వేగాలు వేర్వేరుగా ఉంటాయా?
జవాబు:
శూన్యంలో వివిధ రంగులు గల కాంతుల వేగాలు స్థిరంగా ఉంటాయి. యానకంలో వివిధ రంగులు గల కాంతుల వేగాలు వేర్వేరుగా ఉంటాయి.

ప్రశ్న 21.
పట్టకం గుండా తెలుపురంగు కాంతిని పంపితే అది వివిధ రంగులుగా ఎందుకు విడిపోతుందో ఇప్పుడు మీరు ఊహించగలరా?
జవాబు:
శూన్యంలో అన్ని రంగుల కాంతి వేగాలు ఒకటే అయినప్పటికీ, ఒక యానకంలో ప్రయాణించేటప్పుడు కాంతివేగం దాని తరంగదైర్యంపై ఆధారపడును. అందువల్ల కాంతి వివిధ రంగులుగా విడిపోతుంది.

10th Class Physical Science Textbook Page No. 106

ప్రశ్న 22.
పట్టకం గుండా తెలుపురంగు కాంతిని పంపితే అది వివిధ రంగులుగా ఎందుకు విడిపోతుందో ఇప్పుడు మీరు ఊహించగలరా?
జవాబు:
యానకంలో ప్రయాణించేటప్పుడు కాంతి వేగం దాని తరంగదైర్ఘ్యంపై ఆధారపడుతుంది. అందువల్ల కాంతి వివిధ రంగులుగా విడిపోతుంది.

ప్రశ్న 23.
కృత్యం – 3లో చూసినట్లు ప్రకృతిలో మీరు రంగులు చూడగలిగే సందర్భానికి ఒక ఉదాహరణ ఇవ్వగలరా?
జవాబు:
ప్రకృతిలో రంగులు చూడగలిగే సందర్భం ఇంద్రధనుస్సు.

10th Class Physical Science Textbook Page No. 108

ప్రశ్న 24.
ఆకాశం నీలిరంగులో ఎందుకు కనిపిస్తుంది?
జవాబు:
వాతావరణంలోని N₂, O₂ అణువులు సూర్యుని కాంతిలోని నీలం రంగు కాంతిని పరిక్షేపణం చెందించడం వల్ల ఆకాశం నీలి రంగులో కనిపిస్తుంది.

10th Class Physical Science Textbook Page No. 109

ప్రశ్న 25.
పరిక్షేపణం అంటే ఏమిటి?
జవాబు:
ఒక కణం శోషించుకున్న కాంతిని తిరిగి అన్ని దిశలలో వివిధ తీవ్రతలతో విడుదల చేయడాన్ని “కాంతి పరిక్షేపణం” అంటారు.

ప్రశ్న 26.
స్వేచ్ఛా పరమాణువు లేదా అణువుపై నిర్దిష్ట పౌనఃపున్యం గల కాంతి పతనం చెందితే ఏం జరుగును?
జవాబు:
పరమాణువులు లేదా అణువులపై కాంతి పతనం చెందినపుడు అవి కాంతి శక్తిని శోషించుకుని, అందులో కొంత భాగాన్ని వివిధ దిశల్లో ఉద్గారం చేస్తాయి. ఇదే కాంతి పరిక్షేపణంలోని ప్రాథమిక నియమము.

10th Class Physical Science Textbook Page No. 94

ప్రశ్న 27.
వస్తువు ఆకారం, పరిమాణం మరియు రంగులలో ఏ మార్పు లేకుండా వస్తువును మనం గుర్తించే విధంగా రెటీనాపై ప్రతిబింబం ఎలా ఏర్పడుతుంది?
జవాబు:

1. రెటీనా అనేది ఒక సున్నితమైన పొర.
2. దీనిలో దండాలు (rods) మరియు శంఖువులు (cones) అనబడే దాదాపు 125 మిలియన్ల గ్రాహకాలు (receptors) ఉంటాయి.
3. ఇవి కాంతి సంకేతాలను (signals) గ్రహిస్తాయి. శంఖువులు రంగును గుర్తిస్తాయి. దండాలు కాంతి తీవ్రతను గుర్తిస్తాయి.
4. ఈ సంకేతాలు దాదాపు 1 మిలియన్ దృక్ నాడుల (optic – nerve fibres) ద్వారా మెదడుకు చేరవేయబడతాయి.
5. వాటిలోని సమాచారాన్ని మెదడు విశ్లేషించడం ద్వారా వస్తువు ఆకారం, పరిమాణం మరియు రంగులను మనం గుర్తిస్తాం.

ప్రశ్న 28.
కంటి కటకం యొక్క కనిష్ఠ, గరిష్ఠ నాభ్యంతరాలు ఎంత? వాటిని మనం ఎలా కనుగొంటాము?
జవాబు:
గరిష్ఠ నాభ్యంతరం

1. పటంలో చూపినట్లు అనంతదూరంలో ఉన్న వస్తువు నుండి వచ్చే
   సమాంతర కాంతి కిరణాలు కంటి కటకంపై పడి వక్రీభవనం చెందాక
   రెటీనా పై ఒక బిందురూప ప్రతిబింబాన్ని ఏర్పరుస్తాయి.
2. ఈ సందర్భంలో కంటి కటక నాభ్యంతరం గరిష్టంగా ఉంటుంది.
3. దీని విలువ f_{గరిష్ఠ} = 2.5 సెం.మీ. ఉండును.

కనుగొనే విధానం :
వస్తుదూరం = µ = α
ప్రతిబింబ దూరం = v = 2.5 సెం.మీ (కంటికటకం నుండి రెటీనాకు దూరం)
నాభ్యంతరం = f = ?

కనిష్ఠ నాభ్యంతరము :

1. పటంలో చూపినట్లు కంటి ముందు 25 సెం.మీ. దూరంలో వస్తువు ఉందనుకొనుము.
2. ఈ సందర్భంలో కంటి కటక నాభ్యంతరం కనిష్ఠంగా ఉంటుంది.
3. దీని విలువ f_{కనిష్ఠ} = 2.27 సెం.మీలుగా ఉండును.

కనుగొనే విధానం :
వస్తు దూరం = u = 25 సెం.మీ.
ప్రతిబింబ దూరం = v = 25 సెం.మీ. (కంటి కటకం నుండి రెటీనాకు గల దూరం)
నాభ్యంతరం = f = ?

10th Class Physical Science Textbook Page No. 96

ప్రశ్న 29.
హ్రస్వదృష్టిని సవరించడానికి ఏం చేయాలి?
జవాబు:
హ్రస్వదృష్టికి సవరణ :

1. గరిష్ఠదూర బిందువుకు, స్పష్ట దృష్టి కనీస దూరాన్ని తెలిపే బిందువుకు మధ్య వస్తువు ఉన్నప్పుడు కంటికటకం రెటీనా పై ప్రతిబింబాన్ని ఏర్పరచగలదు.
2. కాబట్టి ఒక కటకాన్ని ఉపయోగించి గరిష్ఠ దూర బిందువుకు ఆవల ఉన్న వస్తువు యొక్క ప్రతిబింబాన్ని గరిష్ఠ దూరబిందువు (M) మరియు స్పష్ట దృష్టి కనీస దూరాన్ని తెలిపే బిందువు (L) ల మధ్యకు తేగలిగితే, ఆ ప్రతిబింబం కంటి కటకానికి వస్తువులా పనిచేస్తుంది.
3. పుటాకార కటకాన్ని వాడడం వల్ల ఇది సాధ్యపడుతుంది.

10th Class Physical Science Textbook Page No. 97

ప్రశ్న 30.
హ్రస్వదృష్టిని నివారించడానికి వాడవలసిన పుటాకార కటక నాభ్యంతరం ఎంత ఉండాలనేది ఎలా నిర్ణయిస్తాం?
జవాబు:

1. హ్రస్వదృష్టిని నివారించడానికి, అనంతదూరంలో ఉండే వస్తువు యొక్క ప్రతిబింబాన్ని గరిష్ఠ దూరబిందువు వద్ద ఏర్పరచగలిగే కటకాన్ని అంటే ద్విపుటాకార కటకాన్ని ఎంచుకోవాలి.
2. ఈ కటకం ఏర్పరచే ప్రతిబింబం కంటి కటకానికి వస్తువులా పనిచేసి చివరగా ప్రతిబింబం రెటీనాపై ఏర్పడుతుంది.
3. ఈ సందర్భంలో వస్తుదూరం (u) అనంతం. ప్రతిబింబదూరం (v) గరిష్ఠ దూర బిందువుకు గల దూరానికి సమానం. కావున
   u = – ∞, v = -D (గరిష్ఠ దూరబిందువుకు, కంటికి గల దూరం)
4. ద్విపుటాకార కటక నాభ్యంతరం గ అనుకుంటే..
   1/f = 1/v – 1/4 సూత్రాన్ని ఉపయోగించినపుడు 1/f = 1/-D ⇒ f = -D
5. ఇక్కడ f కు ‘ఋణ విలువ’ రావడమనేది పుటాకార కటకాన్ని తెలియజేస్తుంది.

10th Class Physical Science Textbook Page No. 108

ప్రశ్న 31.
వాననీటి బిందువులతో విక్షేపణం చెందిన కాంతి అర్ధవలయాకారంలో ఎందుకు కన్పిస్తుంది?
జవాబు:

1. ఇంద్రధనుస్సు అనునది మనకు కనబడే విధంగా పలుచని ద్విమితీయ చాపం కాదు.
2. ఇంద్రధనుస్సు అనేది మీ కంటి వద్ద తన కొనభాగాన్ని కల్గి వున్న త్రిమితీయ శంఖువు.
3. పటంలో చూపినట్లు శంఖువు అక్షం వెంబడి మనం భాగం భూమి పైని వాతావరణంలోని కణాల నుండి, శంఖువు కింది సగ భాగం నేలపైని వస్తువుల నుండి వచ్చే కాంతులను మన కంటికి చేరవేస్తున్నాయి.
4. కావున గాలిలోని నీటి బిందువుల నుండి వచ్చే కాంతి (శంఖువు పై సగం) మనకు ఇంద్రధనుస్సును అర్ధ చంద్రాకారంలో ఏర్పరుస్తుంది.
5. మనం భూమి నుండి నిర్ణీత ఎత్తుకు వెళ్తే ఇంద్ర ధనుస్సును పూర్తి వలయంగా చూడవచ్చు.

10th Class Physical Science Textbook Page No. 110

ప్రశ్న 32.
వేసవి రోజుల్లో (ఉష్ణోగ్రత ఎక్కువగా ఉన్న రోజుల్లో) ఒక నిర్దిష్ట దిశలో చూస్తున్నపుడు కొన్ని సందర్భాలలో ఆకాశం తెలుపురంగులో కనిపిస్తుంది. ఎందుకు?
జవాబు:

1. వాతావరణంలో వివిధ పరిమాణాలు గల కణాలుంటాయి. వాటి పరిమాణాల కనుగుణంగా అవి వివిధ తరంగదైర్యాలు గల కాంతిని పరిక్షేపణం చేస్తాయి.
2. ఉదాహరణకు N₂, O₂ అణువుల కన్నా నీటి అణువు పరిమాణం ఎక్కువ. కాబట్టి అది నీలిరంగుకాంతి కంటే తక్కువ పౌనఃపున్యాలు (ఎక్కువ తరంగదైర్యాల) గల కాంతులకు పరిక్షేపణ కేంద్రంగా పనిచేస్తుంది.
3. వేసవి రోజుల్లో ఉష్ణోగ్రత ఎక్కువగా ఉండడం వల్ల వాతావరణంలోకి నీటి ఆవిరి చేరుతుంది.
4. తద్వారా వాతావరణంలో నీటి అణువులు అధిక స్థాయిలో ఉంటాయి.
5. ఈ నీటి అణువులు ఇతర పౌనఃపున్యాలు (నీలిరంగు కానివి) గల కాంతులను పరిక్షేపణం చేస్తాయి.
6. N₂, O₂, ల పరిక్షేపణం వల్ల వచ్చే నీలిరంగుకాంతి, నీటి అణువుల పరిక్షేపణం వల్ల వచ్చే ఇతర రంగుల కాంతులు అన్నీ కలిసి మన కంటిని చేరినప్పుడు తెలుపు రంగు కాంతి కనబడుతుంది.

10th Class Physical Science Textbook Page No. 111

ప్రశ్న 33.
సూర్యోదయం, సూర్యాస్తమయ సమయాలలో సూర్యుడు ఎర్రగా కనబడడానికి గల కారణం మీకు తెలుసా?
జవాబు:

1. సూర్యోదయం, సూర్యాస్తమయ సమయంలో సూర్యుని నుండి వెలువడే కాంతి మీ కంటిని చేరడానికి భూ వాతావరణంలో అధిక దూరం ప్రయాణించాల్సి ఉంటుంది.
2. ఎరుపు రంగు కాంతి తప్ప మిగిలిన అన్ని రంగుల కాంతులు అధికంగా పరిక్షేపణం చెంది కాంతి మీ కంటిని చేరే లోపే ఆ రంగులన్నీ కనుమరుగవుతాయి.
3. ఎరుపు రంగు కాంతి తక్కువగా పరిక్షేపణం చెందడం వల్ల అది మీ కంటిని చేరును.
4. ఫలితంగా సూర్యుడు, సూర్యోదయం మరియు సూర్యాస్తమయ సమయాలలో ఎరుపుగా కన్పిస్తాడు.

ప్రశ్న 34.
మధ్యాహ్న వేళల్లో సూర్యుడు ఎర్రగా ఎందుకు కనబడడో ఊహించగలరా?
జవాబు:

1. ఉదయం, సాయంత్రం వేళల కంటే మధ్యాహ్నం సమయంలో వాతావరణంలో సూర్యకాంతి ప్రయాణించే దూరం తక్కువ.
2. కాబట్టి కాంతి ఎక్కువగా పరిక్షేపణం చెందక పోవడం వల్ల అన్ని రంగులూ మీ కంటిని చేరతాయి.
3. కాబట్టి మధ్యాహ్న వేళల్లో సూర్యుడు తెల్లగా కనబడతాడు.

10th Class Physical Science Textbook Page No. 98

ప్రశ్న 35.
దీర్ఘదృష్టిని నివారించడానికి వాడవలసిన కుంభాకార కటక నాభ్యంతరం ఎంత ఉండాలనేది ఎలా నిర్ణయిస్తాం?
జవాబు:
1) కటక నాభ్యంతరాన్ని కనుగొనడానికి, స్పష్ట దృష్టి కనీస దూరాన్ని తెలిపే బిందువు (L) వద్ద ఒక వస్తువు ఉన్నదని ఊహించవలెను.

2) పటంలో చూపినవిధంగా L వద్ద ఉన్న వస్తువు ప్రతిబింబాన్ని కనిష్ఠదూర బిందువు (H) వద్ద ఏర్పరచగలిగే ద్వికుంభాకార కటకాన్ని ఉపయోగిస్తే దృష్టిదోషం సవరించబడుతుంది.

3) ఆ ప్రతిబింబం కంటికటకానికి వస్తువుగా పనిచేస్తుంది.

4) కనుక చివరగా కంటి కటకం వలన ఏర్పడే ప్రతిబింబం రెటీనా పై ఏర్పడుతుంది.

5) ఈ సందర్భంలో, వస్తుదూరం

(u) = -25 సెం.మీ.
ప్రతిబింబం దూరం (v) = – d
(కంటికి, కనిష్ఠ దూరబిందువుకు గల దూరం)
మనం వాడే ద్వికుంభాకార కటక నాభ్యంతరం f అనుకుంటే.
1/f = 1/v – 1/4 సూత్రాన్ని ఉపయోగించినపుడు :
1/f = 1/-d – 1/(-25) ⇒ 1/f = -1/d + 1/25
1/f = (d – 25)/25d ⇒ f = 25d(d – 25)
d > 25 కాబట్టి గ విలువ ధనాత్మకం అవుతుంది. అనగా కుంభాకార కటకం వాడాలని తెలుస్తుంది.

పరికరాల జాబితా

పొడవైన కర్ర లేదా పివిసి పైపు ముక్కలు (20, 30, 35, 40, 50 సెం.మీ.,) అడ్డు కడ్డీ, రిటారు స్టాండు, కంటి నిర్మాణం ప్రదర్శించే నమూనా, డ్రాయింగ్ షీట్, పెన్సిల్, గుండుసూదులు, స్కేలు, కోణమానిని, పట్టకం, చిన్న రంధ్రం కలిగిన కార్డుబోర్డు, తెల్లని కాంతి జనకం (టార్చిలైటు), లోహపు పళ్లెం, అద్దం, నీరు, గాజుబీకరు, సోడియం’
థయో సల్ఫేట్, సల్ఫూరికామ్ల ద్రావణాలు

10th Class Physical Science 5th Lesson మానవుని కన్ను-రంగుల ప్రపంచం Textbook Activities

కృత్యములు

కృత్యం – 1

ప్రశ్న 1.
స్పష్ట దృష్టి కనీస దూరమును కనుగొనుటకు ఒక కృత్యాన్ని వ్రాయుము.
జవాబు:

1. ఒక పుస్తకాన్ని తెరచి మీ కంటి ముందు కొంతదూరంలో పట్టుకొని చదవడానికి ప్రయత్నించండి.
2. నెమ్మదిగా ఆ పుస్తకాన్ని మీ కంటివైపుగా, కంటికి అతి దగ్గరగా చేరే వరకు కదిలించండి.
3. పుస్తకంలోని అక్షరాలు మసకబారినట్లుగా అనిపిస్తాయి లేదా మీ కన్ను ఒత్తిడికి గురైనట్లు అనిపిస్తుంది.
4. పుస్తకంలోని అక్షరాలను మీ ‘కన్ను ఏ ఒత్తిడి లేకుండా చూడగలిగే స్థానం వరకు నెమ్మదిగా పుస్తకాన్ని వెనుకకు . జరపండి.
5. ఈ సందర్భంలో పుస్తకానికి, మీ కంటికి గల దూరాన్ని కొలిస్తే అది దాదాపు 25 సెం.మీ. ఉంటుంది.
6. ఈ దూరం వ్యక్తికి, వ్యక్తికీ వయస్సును బట్టి మారుతుంది.
7. మన కంటికి ఏ ఒత్తిడి లేకుండా, స్పష్టంగా ఒక వస్తువును మనము చూడాలంటే ఉండవలసిన కనీస దూరాన్ని “స్పష్ట దృష్టి కనీస దూరం” అంటారు.

కృత్యం – 2

ప్రశ్న 2.
“దృష్టికోణం” ను కనుగొనేందుకు ఒక కృత్యాన్ని తెల్పుము.
జవాబు:

1. బట్టలషాప్ లో బట్టల చుట్టలకు వచ్చే కర్రలను లేదా PVC పైపులను సేకరించుము.
2. ఈ వస్తువులను 20 సెం.మీ., 30 సెం.మీ., 35 సెం.మీ., 40 సెం.మీ., 50 సెం.మీ. పొడవు గల ముక్కలుగా ఆ కత్తిరించుము.
3. ఒక రిటార్ట్ స్టాండును బల్లపై ఉంచి, రిటార్ట్ స్టాండు నిలువు కడ్డీ ప్రక్కన మీ తల ఉండే విధముగా బల్ల దగ్గర నిలబడండి.
4. మీ కంటి నుండి 25 సెం.మీ. దూరంలో రిటార్టు స్టాండ్ అడ్డుకడ్డీకి క్లాంప్ ను బిగించి, 30 సెం.మీ. పొడవు గల కర్రను కట్టమని మీ స్నేహితునికి చెప్పుము.
5. ఇప్పుడు అడ్డుకడ్డీ వెంబడి మీ దృష్టి సారిస్తూ, కర్రముక్కను పై అంచు నుండి క్రింది అంచు వరకు మొత్తంగా చూడడానికి ప్రయత్నించుము.
6. కర్రముక్క 25 సెం.మీ. దూరంలో ఉన్నప్పుడు దాని రెండు చివరలను మీరు స్పష్టంగా చూడలేకపోతే, అడ్డుకడ్డీ వెంబడి కర్రముక్కను వెనుకకు జరుపుము.
7. ఏ కనీస దూరం వద్ద మీరు దానిని పూర్తిగా చూడగలరో అక్కడ దానిని అడ్డుకడ్డీకి ఇంప్ సహాయంతో బిగించండి.
8. వస్తువు యొక్క చివరి బిందువుల నుండి వచ్చే కిరణాలు కంటి వద్ద కొంత కోణం చేస్తాయి.
9. ఈ కోణం 60° కంటే తక్కువగా ఉంటే ఆ వస్తువును పూర్తిగా మనము చూడగలము.
10. ఈ కోణం 60° కంటే ఎక్కువగా ఉంటే ఆ వస్తువులో కొంతభాగం మాత్రమే మనము చూడగలము.
11. ఏ గరిష్ఠ కోణము వద్ద మనము పూర్తిగా చూడగలమో, ఆ కోణాన్ని “దృష్టికోణం” అంటారు.
12. ఈ విధముగా దృష్టికోణమును కనుగొంటారు.

కృత్యం – 6

ప్రశ్న 3.
కాంతి పరిక్షేపణాన్ని ప్రయోగ పూర్వకముగా వ్రాయుము.
జవాబు:

1. ఒక బీకరులో సోడియం థయోసల్ఫేట్ (హైపో) మరియు సల్ఫ్యూరిక్ ఆమ్లాల ద్రావణాన్ని తీసుకొనుము.
2. ఈ గాజు బీకరును ఆరుబయట సూర్యుని వెలుగులో ఉంచుము.
3. బీకరులో సల్ఫర్ స్పటికాలు ఏర్పడటాన్ని గమనించుము.
4. రసాయన చర్య జరుగుతున్న కొలదీ సల్ఫర్ అవక్షేపం (precipitation) ఏర్పడటం గమనించవచ్చును.
5. ప్రారంభంలో సల్ఫర్ స్పటికాలు చాలా చిన్నవిగానూ చర్య జరిగే కొలదీ వాటి పరిమాణం పెరుగును.
6. మొదట సల్ఫర్ స్పటికాలు నీలిరంగులో ఉం, వాటి పరిమాణం పెరుగుతున్నకొలదీ తెలుపు రంగులోకి మారును. దీనికి కారణం కాంతి పరిక్షేపణము.
7. ప్రారంభంలో సల్ఫర్ స్పటికాల పరిమాణం చాలా తక్కువగా ఉండి, అది నీలిరంగు కాంతి తరంగదైర్ఘ్యంతో పోల్చడానికి వీలైనదిగా ఉంటుంది. కావున అపుడు అవి నీలిరంగులో కనబడతాయి.
8. సల్పర్ స్పటికాల పరిమాణం పెరుగుతున్న కొలదీ వాటి పరిమాణం ఇతర రంగు కాంతుల తరంగదైర్యాలతో పోల్చడానికి వీలయ్యేదిగా ఉంటుంది.
9. అప్పుడు ఆ స్పటికాలు ఇతర రంగుల కాంతులకు పరిక్షేపణ కేంద్రాలుగా పనిచేస్తాయి.
10. ఈ అన్ని రంగులూ కలిసి తెలుపు రంగులా కనబడుతుంది.

SCERT AP 10th Class Physics Study Material Pdf 4th Lesson వక్రతలాల వద్ద కాంతి వక్రీభవనం Textbook Questions and Answers.

AP State Syllabus 10th Class Physical Science 4th Lesson Questions and Answers వక్రతలాల వద్ద కాంతి వక్రీభవనం

10th Class Physical Science 4th Lesson వక్రతలాల వద్ద కాంతి వక్రీభవనం Textbook Questions and Answers

అభ్యసనాన్ని మెరుగుపరుచుకోండి

ప్రశ్న 1.
కంచరగాడిద (Zebra) ఫోటో కావాలనుకున్న వ్యక్తి కెమెరా కటకానికి నల్లచారలున్న గాజుపలకను అమర్చి తెల్ల గాడిదను ఫోటో తీశాడు. అతనికి ఏ ఫోటో లభిస్తుంది? వివరించండి. (AS1)
జవాబు:

1. కెమెరా కటకానికి నల్లచారలున్న గాజుపలకను అమర్చాడు. కావున అతను తెల్ల గాడిద ఫోటోను మాత్రమే పొందగలడు.
2. దీనికి కారణము వస్తువు (గాడిద) నుండి వచ్చిన కాంతికిరణాల తీవ్రత గాజుపలక వలన తగ్గుతాయి. కావున అతను తెల్లని గాడిద’ ఫోటోనే (ప్రతిబింబం) పొందగలిగాడు.

ప్రశ్న 2.
20 సెం.మీ. నాభ్యంతరం గల కేంద్రీకరణ కటకం ముందు 60 సెం.మీ. దూరంలో వస్తువు వుంది. ప్రతిబింబం ఎక్కడ ఏర్పడుతుంది ? దాని లక్షణాలు తెలపండి. (AS1)
(లేదా)
వస్తువు 20 సెం.మీ.ల నాభ్యంతరం గల కుంభాకార కటకంకు 60 సెం.మీ.ల దూరంలో ఉంచిన, దాని ప్రతిబింబం ఎక్కడ ఏర్పడును? ఆ ప్రతిబింబ లక్షణాలను తెలుపుము.
జవాబు:
కేంద్రీకరణ కటక నాభ్యంతరం = f = 20 సెం.మీ.
వస్తుదూరము = u = 60 సెం.మీ.
ప్రతిబింబదూరము = v = ?

లక్షణాలు :
కటకానికి రెండోవైపు 30 సెం.మీ. దూరంలో తలక్రిందులుగా ఉన్న నిజప్రతిబింబం, వస్తుపరిమాణం కంటే తక్కువ పరిమాణంతో ఏర్పడుతుంది.

ప్రశ్న 3.
ఒక ద్వికుంభాకార కటకపు రెండు వక్రతలాల వక్రతా వ్యాసార్ధాలు సమానం (R). కటక వక్రీభవన గుణకం n = 1.5 అయిన కటక నాభ్యంతరాన్ని కనుగొనండి. (AS1)
(లేదా)
రెండు వక్రతా వ్యాసార్ధాలు సమానముగా గల ద్వికుంభాకార కటకపు వక్రీభవన గుణకం విలువ 1.5 అయిన ఆ కటక నాభ్యంతరం విలువ ఎంత?
జవాబు:
ద్వికుంభాకార కటకాల రెండు వక్రతలాల వక్రతావ్యాసార్ధాలు సమానము.
రెండు వక్రతలాలు వరుసగా R₁ మరియు R₂ లు అనుకొనుము. ∴ R₁ = R₂ = R అగును.
కటక వక్రీభవన గుణకము = n = 1.5 ; కటక నాభ్యంతరం = f = ?
రెండు కటకాల మధ్య దూరం వాటి నాభ్యాంతరాల మొత్తానికి సమానమయ్యే విధంగా కటకాలను అమర్చాలి.

∴ కటక నాభ్యంతరము విలువ ‘R’ అగును. ∴ కటక నాభ్యంతరము వక్రతా వ్యాసార్ధానికి సమానము.

ప్రశ్న 4.
కటక సూత్రాన్ని రాయండి. అందులోని పదాలను వివరించండి. (AS1)
(లేదా)
రవి ఒక కటకాన్ని తయారు చేయాలనుకున్నాడు. దానికి అతను ఏ సూత్రాన్ని ఉపయోగిస్తాడు ? ఆ సూత్రం వ్రాసి అందలి పదాలను వివరింపుము.
జవాబు:
కటక తయారీ సూత్రము : 1) \(\frac{1}{f}=(n-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
ఈ సూత్రమును కటకంను గాలిలో ఉంచిన సందర్భంలో వాడతారు. దీనిలో
R₁, R₂ లు వక్రతావ్యాసార్ధాలు ; n – వక్రీభవన గుణకము ; f – నాభ్యంతరము

2) కటకంను ఏదైనా యానకంలో ఉంచిన సందర్భం దీనిలో \(\frac{1}{f}=\left(n_{b a}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
R₁, R₂లు వక్రతా వ్యాసార్ధాలు.
f – నాభ్యంతరం
n_ba – యానకం పరంగా కటకపు వక్రీభవన గుణకం.
n_b – కటకం తయారుచేసిన పదార్థపు వక్రీభవన గుణకం.
n_a – కటకం ఉంచిన యానకపు వక్రీభవన గుణకం.

ప్రశ్న 5.
ఒక కటక నాభ్యంతరాన్ని ప్రయోగపూర్వకంగా ఎలా కనుగొంటారు ? (ప్రయోగశాల కృత్యం-1) (AS1)
(లేదా)
కటక నాభ్యాంతరాన్ని UV పద్ధతిలో కనుగొనే ప్రయోగాన్ని రాయండి.
జవాబు:
ఉద్దేశ్యం : కుంభాకార కటక నాభ్యంతరమును UV పద్ధతిలో కనుగొనుట.

కావలసిన పరికరాలు :
టేబుల్, V – స్టాండ్, కుంభాకార కటకం, మీటరు స్కేలు, కొవ్వొత్తి (వస్తువు), తెర.

పద్ధతి : ఉజ్జాయింపుగా కటక నాభ్యంతరంను కనుగొనుట :

1. కటకంను V – స్టాండుపై ఉంచుము.
2. కటకంకు చాలా దూరంగా కటక ప్రధానాక్షం పై వెలుగుతున్న కొవ్వొత్తి నుంచుము.
3. కటకంకు రెండోవైపున కొవ్వొత్తి ప్రతిబింబంను తెరపై ఏర్పడునట్లు అమర్చుము.
4. ఇప్పుడు కటకం నుండి ప్రతిబింబానికి గల దూరంను కొలిచిన మనకు ఉజ్జాయింపు కటక నాభ్యంతరం తెలియును.

ప్రయోగ లెక్కింపు పద్ధతి (లేదా) u – v పద్ధతి :

1. ఈ పద్ధతిలో కొవ్వొత్తిని కటకంకు 60 సెం.మీ. దూరంలో కటక ప్రధానాక్షంపై, ఉంచుము.
2. కటకమునకు మరోవైపున తెరపై స్పష్టమైన ప్రతిబింబాన్ని ఏర్పరచు స్థానంలో ఉంచుము.
3. ఇపుడు ప్రతిబింబదూరము (v) ను కొలువుము.
4. ఈ విధంగా వస్తువును కటకమునకు 50 సెం.మీ., 40 సెం.మీ., 30 సెం.మీ. మొ॥గు దూరాలలో ఉంచుతూ, ప్రతి సందర్భంలో ప్రతిబింబదూరం (V) ను కొలువుము.
5. పైన పొందిన u, v విలువలను పట్టికలో నమోదు చేయుము.

6. u, v విలువల నుండి f = \(\mathrm{f}=\frac{\mathrm{uv}}{\mathrm{u}+\mathrm{v}}\) ద్వారా కటక నాభ్యంతరంను లెక్కించి ప్రతి సందర్భంలోనూ స్థిరమని గమనించుము.

మరొక పద్ధతి :

1. కుంభాకార కటకాన్ని సూర్యునికి అభిముఖంగా ఉంచండి.
2. కటకానికి రెండోవైపు ఒక తెరని అమర్చి, ఆ తెరను కటకం వద్ద నుండి మెల్లగా వెనుకకు జరుపుతూ తెరపై ఎక్కడ ప్రకాశవంతమైన, దాదాపు బిందురూపంలో ఉండే సూర్యుని ప్రతిబింబం ఏర్పడుతుందో గుర్తించండి. కటకంపైన పడిన సూర్యకిరణాలన్నీ ఒక చోట కేంద్రీకరింపబడటం వలన ఇలా జరుగుతుంది.
3. ఇప్పుడు కటకం నుండి తెరకు గల దూరాన్ని కొలవండి. ఈ విలువే కటక నాభ్యాంతరం అవుతుంది.

ప్రశ్న 6.
ద్వికుంభాకార కటకం కేంద్రీకరణ కటకంగా పనిచేస్తుందని సిద్దూతో హర్ష చెప్పాడు. హర్ష చెప్పేది నిజం కాదని తెలిసిన సిద్దూ, హర్షని కొన్ని ప్రశ్నలు అడిగి అతని భావనను సరిచేశాడు. ఆ ప్రశ్నలేమై ఉంటాయి? (AS2)
జవాబు:

1. కుంభాకార కటకం గుండా కాంతికిరణాలు ప్రసరించిన ఏమగును?
2. ద్వికుంభాకార కటక ఆకారమేమి?
3. ద్వికుంభాకార కటకం గుండా ప్రసరించు కాంతి లక్షణం ఏమిటి?
4. సమతల కుంభాకార కటకం గుండా ప్రసరించు కాంతి లక్షణం ఏమిటి?
5. ఈ రెండు కటకాల ప్రతిబింబాల మధ్య గల తేడాలేమిటి?

ప్రశ్న 7.
పటంలో చూపినట్లు ఒక కుంభాకార కటకం మూడు వేర్వేరు పదార్థాలతో తయారుచేయబడింది. అది ఎన్ని ప్రతిబింబాలను ఏర్పరుస్తుంది? (AS2)
(లేదా)
మూడు వేర్వేరు పదార్థాలతో తయారుచేయబడిన కటకంతో ఏర్పడు ప్రతిబింబాల సంఖ్యను తెల్పుము.

జవాబు:

1. ఇచ్చిన కటకం మూడు వేర్వేరు పదార్థాలతో తయారు చేయబడినది. కావున వాటి వక్రీభవన గుణకాలు వేర్వేరుగా ఉండును.
2. ఈ లక్షణం వలన కాంతి ఈ కటకం గుండా ప్రయాణించిన, మూడు ప్రతిబింబాలను ఏర్పరచును.

ప్రశ్న 8.
మీ దగ్గరలోని కళ్ళజోళ్ళ షాపులో దొరికే కటకాల గురించి సమాచారాన్ని సేకరించండి. కటకం యొక్క సామర్థ్యాన్ని (power) బట్టి దాని నాభ్యంతరం ఎలా కనుగొంటారో తెలుసుకోండి. (AS4)
జవాబు:

1. కళ్ళజోళ్ళ షాపునందు అనేక రకాల కటక సామర్థ్యం గల కటకాలను మనము చూడవచ్చును.
2. వాటిని మానవుని దృష్టి లోపమును బట్టి డాక్టర్ సలహా మేరకు వివిధ కటక సామర్థ్యాలు గల కటకాలతో కూడిన కళ్ళజోళ్ళను వాడేందుకు సలహా ఇస్తారు.
3. కటక సామర్థ్యం : కటక నాభ్యంతరం యొక్క విలోమమును కటక సామర్థ్యం అంటారు.
4. కుంభాకార కటకంకు ఈ విలువ ధనాత్మకము, పుటాకార కటకంకు ఈ విలువ ఋణాత్మకము.
5. కటక సామర్థ్యంను డయాఫ్టర్లలో కొలుస్తారు.
6. 
   ఉదా : కటక సామర్థ్యము \(+\frac{1}{4}\) డయాప్టర్లు అయిన దాని నాభ్యంతరం 25 సెం.మీ. లుండును.

ప్రశ్న 9.
గెలీలియో తన టెలిస్కోప్ లో వాడిన కటకాలను గురించి సమాచారాన్ని సేకరించండి. (AS4)
(లేదా)
ఏ రకపు టెలిస్కోపులను గెలీలియో తన టెలిస్కోపులో ఉపయోగించెను?
జవాబు:

1. గెలీలియో టెలిస్కోప్ లో రెండు వేర్వేరు నాభ్యంతరాలు గల కటకాలను వాడినారు.
2. ఈ కటకాలలో ఒకటి వస్తుకటకంగాను, మరొకటి అక్షికటకంగాను పనిచేస్తాయి.
3. అక్షికటకం పరిశీలకుని కంటికి దగ్గరగా ఉంటుంది.
4. వస్తుకటకం వస్తువు ఉన్నవైపు, దానికి దగ్గరగా ఉంటుంది.
5. అక్షికటకపు నాభ్యంతరం తక్కువగా ఉంటుంది.
6. వస్తుకటకపు నాభ్యంతరం అక్షికటకం కంటే ఎక్కువగా ఉంటుంది.
7. వస్తు ప్రతిబింబం వస్తుకటకపు నాభి వద్ద ఏర్పడును.
8. ఈ ప్రతిబింబం అక్షికటకంకు వస్తువుగా పనిచేసి, దాని ప్రతిబింబం వృద్దీకరణం చెందిన, నిటారుగా ఏర్పడును.
9. ప్రక్కన గెలీలియో టెలిస్కోప్రలోని కటకాల అమరిక నమూనాను ఇవ్వడమైనది.

ప్రశ్న 10.
వికేంద్రీకరణ కటకం గుండా ప్రయాణించే AB కిరణాన్ని పటం చూపుతుంది. పటంలో కటక నాభుల స్థానాలను బట్టి కటకం వరకు ఆ కిరణ పథాన్ని గీయండి. (AS5)

జవాబు:

ఇచ్చిన కటకం. వికేంద్రీకరణ కటకం. వక్రీభవన కిరణం (AB) ని వెనుకకు పొడిగించిన ప్రధానాక్షంపై గల నాభి (F) వద్ద ఖండించును. కావున పతన కిరణం ప్రధానాక్షానికి సమాంతరంగా వచ్చిందని తెలుస్తుంది.

ప్రశ్న 11.
ఒక బిందురూప వస్తువును, N₁ N₂ ప్రధానాక్షం గల కటకంతో ఏర్పడిన ప్రతిబింబాన్ని పటం చూపుతుంది. కిరణచిత్రం ద్వారా కటకస్థానాన్ని, దాని నాభులను కనుగొనండి. (AS5)

జవాబు:
పుటాకార కటకం వాడినప్పుడు :

O – వస్తువు
I – ప్రతిబింబం
F₁ – నాభి
P – దృక కేంద్రం
N₁N₂ – ప్రధానాక్షం

ప్రశ్న 12.
పటంలో చూపిన వస్తువు స్థానం S, ప్రతిబింబస్థానం S’ లను ఉపయోగించి కిరణచిత్రాన్ని గీసి, నాభిని కనుక్కోండి. (AS5)

జవాబు:
కటకం : కుంభాకార కటకం

S – వస్తువు
S’ – ప్రతిబింబం
P – దృక కేంద్రం
F₁ – నాభి
N₁N₂ – ప్రధానాక్షం

ప్రశ్న 13.
కింది సందర్భాలకు సంబంధించిన కిరణచిత్రాలను గీయండి. ప్రతిబింబస్థానం, లక్షణాలను వివరించండి. (కుంభాకార కటకాన్ని వాడినప్పుడు)
i) 2F₂ వద్ద వస్తువు ఉన్నప్పుడు ii) F₂ మరియు దృక్ కేంద్రం (P)ల మధ్య వస్తువు ఉన్నప్పుడు (AS5)
జవాబు:
i) వస్తువును వక్రతా కేంద్రం (2F₂) వద్ద ఉంచినప్పుడు 2F₁ వద్ద ప్రతిబింబం ఏర్పడుతుంది.

ప్రతిబింబ లక్షణాలు :
a) నిజప్రతిబింబం
b) వస్తువు పరిమాణంకు సమాన పరిమాణం గల ప్రతిబింబం.
c) తలక్రిందులుగా గల ప్రతిబింబం ఏర్పడును.

ii) వస్తువును నాభికి, కటక దృక కేంద్రానికి మధ్య ఉంచినపుడు వస్తువున్న వైపునే ప్రతిబింబం ఏర్పడును.

లక్షణాలు :
a) మిథ్యా ప్రతిబింబం
b) వస్తువు పరిమాణం కంటే ఎక్కువ పరిమాణం గల ప్రతిబింబం
c) వృద్దీకరణం చెందిన ప్రతిబింబం ఏర్పడును.

ప్రశ్న 14.
ఒక సౌష్టవ కేంద్రీకరణ కటకం యొక్క నాభ్యంతరం, వక్రతా వ్యాసార్ధం సమానమైన, దాని వక్రీభవన గుణకొన్ని కనుగొనండి. (AS7)
జవాబు:
కటకం యొక్క నాభ్యంతరం =f
కటకం యొక్క వక్రతా వ్యాసార్ధం = R అనుకొనుము.
దత్తాంశం నుండి
కటకం యొక్క నాభ్యంతరం, వక్రతావ్యాసార్ధాలు సమానము. కావున f = R

ఇచ్చిన కటకం సౌష్ఠవ కేంద్రీకరణ కటకం, కావున దీనికి రెండు వక్రతావ్యాసార్ధాలుండును.
అవి R₁ మరియు R₂ అనుకొనుము.
R₁ = R₂ = R అనుకొనుము.
R₁ = R మరియు R₂ = – R అనుకొనుము.

∴ సౌష్ఠవ కేంద్రీకరణ కటక వక్రీభవన గుణకం విలువ = n = 1.5

ప్రశ్న 15.
రెండు బిందురూప వస్తువులు ఒకదానికొకటి 24 సెం.మీ. దూరంలో ఉన్నాయి. 9 సెం.మీ. నాభ్యంతరం గల కేంద్రీకరణ కటకాన్ని వాటి మధ్య ఎక్కడ ఉంచితే, వాటి రెండు ప్రతిబింబాలు ఒకే స్థానంలో ఏర్పడతాయి? (AS7)
జవాబు:
బిందురూప వస్తువుల మధ్య దూరము d = 24 సెం.మీ.
కటక నాభ్యంతరం విలువ = f = 9 సెం.మీ.

పటంలో చూపినట్లుగా మొదటి బిందు జనకము నుండి కటకము X సెం.మీ.ల దూరము ఉందనుకొనుము.
ఇక్కడ వస్తుదూరము = u= -x; ప్రతిబింబదూరము = v = v ; నాభ్యంతరము = f = 9

∴ కేంద్రీకరణ కటకంను మొదటి వస్తువుకు 6 లేక 18 సెం.మీ.ల దూరం ఉంచిన వాటి రెండు ప్రతిబింబాలు ఒకే స్థానంలో ఏర్పడతాయి.

ప్రశ్న 16.
సమాంతర కిరణాల మార్గంలో రెండు కేంద్రీకరణ కటకాల నుంచి, రెండు కటకాల గుండా ప్రయాణించాక కూడా కాంతి కిరణాలు సమాంతరంగానే ఉండాలంటే ఆ కటకాలను ఎలా అమర్చాలి? పటం సహాయంతో వివరించండి. (AS1)
జవాబు:
1) సమాంతర కాంతికిరణాల మార్గంలో రెండు కేంద్రీకరణ కటకాలనుంచారు.

2) సమాంతర కాంతికిరణపుంజము కేంద్రీకరణ కటకంపై పడిన, అవి నాభి వద్ద కేంద్రీకరించబడతాయి.

3) నాభి నుండి ప్రయాణించే కాంతికిరణం వక్రీభవనం చెందాక ప్రధానాక్షానికి సమాంతరంగా ప్రయాణిస్తుంది.

4) పటంలో చూపినట్లుగా రెండు కటకాలను ఒకే ప్రధానాక్షంపై ఉంచిన, వక్రీభవనం తర్వాత కూడా కాంతికిరణాలు సమాంతరంగానే ప్రయాణిస్తాయి. రెండు కటకాల మధ్య దూరం వాటి నాభ్యంతరాల మొత్తానికి సమానమయ్యే విధంగా కటకాలను అమర్చాలి.

పై పటంలో f₁ మరియు f₂లు కటక నాభ్యంతరాలు.

5) దీనినిబట్టి కాంతికిరణాలు మొదటి కటకంలో వక్రీభవనం చెంది నాభి వద్ద కేంద్రీకరించబడ్డాయి. నాభి నుండి రెండవ కటకం ద్వారా వక్రీభవనం తర్వాత ప్రధానాక్షానికి సమాంతరంగా ప్రయాణించాయి. రెండు కటకాల నాభి బిందువులు ఏకీకృతం కాబడ్డాయి.

ప్రశ్న 17.
కుంభాకార కటకాన్ని నీటిలో ఉంచినపుడు, దాని నాభ్యంతరం పెరుగుతుందని ప్రయోగపూర్వకంగా మీరు ఎలా సరిచూస్తారు? (కృత్యం – 2) (AS1)
(లేదా)
ఒక కుంభాకార కటకంను నీటిలో ఉంచిన, దాని నాభ్యంతరంలో మార్పు సంభవించునో లేదో? ఒక కృత్యం ద్వారా వివరింపుము.
(లేదా)
కటకపు నాభ్యంతరము పరిసర యానకంపై ఏ విధంగా ఆధారపడునో ప్రయోగం ద్వారా వివరింపుము.
జవాబు:
ఉద్దేశ్యం : కుంభాకార కటకంను నీటిలో ఉంచినపుడు, నాభ్యంతరం పెరుగుతుందని పరిశీలించుట.

కావలసిన పరికరాలు :
నాభ్యంతరం తెలిసిన కుంభాకార కటకం, కటకంను ఉంచే రింగు, రాయి, స్థూపాకార గాజు పాత్ర మరియు నీరు.

పద్ధతి :

1. నాభ్యంతరం తెలిసినటువంటి కుంభాకార కటకంను తీసుకొని, దాని విలువను నోట్ చేసుకొనుము.
2. గాజు గ్లాసు వంటి ఒక స్థూపాకార పాత్రను తీసుకొనుము.
3. పాత్ర ఎత్తు కటకపు నాభ్యంతరం కంటే చాలా ఎక్కువ (దాదాపు 4 రెట్లు) ఉండేటట్లు చూడాలి.
4. పాత్ర అడుగున నల్లటి రాయిని ఉంచుము.
5. రాయిపై నుండి కటక నాభ్యంతరం కన్నా ఎక్కువ ఎత్తు వరకు ఉండునట్లు పాత్రలో నీరు నింపుము.
6. పటంలో చూపినట్లుగా కటకాన్ని నీటి ఉపరితలానికి సమాంతరంగా ఉండేటట్లు నీటిలో కొద్ది లోతు వరకు కటకాన్ని సమాంతరంగా ముంచుము.
7. రాయి ఉపరితలం నుండి కటకానికి గల దూరం కటక నాభ్యంతరానికి ఎక్కువగా ఉండే విధంగా కటకాన్ని పట్టుకొనుము.
8. కటకం గుండా రాయిని గమనించుము.
9. కటకం గుండా రాయిని చూడగలము, కానీ గాలిలో రాయి, కటకంకు మధ్య దూరం నాభ్యంతరం కంటే తక్కువ దూరం లోపే రాయి ప్రతిబింబాన్ని చూడగలిగాము. దీనినిబట్టి నీటిలో ఉన్నప్పుడు కటక నాభ్యంతరం పెరిగిందని తెలుస్తుంది.
10. ఈ కృత్యం ద్వారా కటక నాభ్యంతరం పరిసర యానకంపై ఆధారపడుతుందని మనం నిర్ధారించవచ్చును.

ప్రశ్న 18.
భావన (A) : నీటిలో ఉన్న చేపకు ఒడ్డున ఉన్న మనిషి అతని వాస్తవ ఎత్తు కంటే ఎక్కువ ఎత్తుగా కనిపిస్తాడు.
కారణం (R) : నీటి నుండి వచ్చే కాంతికిరణం గాలిలోకి ప్రవేశించేటప్పుడు లంబానికి దూరంగా విచలనమవుతుంది. కింది వాటిలో ఏది సరియైనది? వివరించండి. (AS2)
a) A, R లు రెండూ సరియైనవి. మరియు A కు R సరైన వివరణ.
b) A, R లు రెండూ సరియైనవి. కానీ A కు R సరైన వివరణ కాదు.
c) A సరియైనది. R సరియైనది కాదు.
d) A, R లు రెండూ సరైనవి కావు.
e) A సరైనది కాదు. కానీ R సరియైనది.
జవాబు:
‘C’ సరియైన సమాధానము.

వివరణ :
1) కాంతి విరళ యానకం నుండి సాంద్రతర యానకంలోకి ప్రయాణించునపుడు లంబానికి దగ్గరగా వంగును.
2) ఈ లక్షణం వలన చేపకు వాస్తవ ఎత్తు కంటే ఎక్కువ ఎత్తుగా మనిషి కనిపిస్తాడు.

ప్రశ్న 19.
మిథ్యా ప్రతిబింబాన్ని కెమెరాతో ఫోటో తీయగలమా? (AS2)
(లేదా)
కెమెరాతో మిథ్యా ప్రతిబింబంను తీసిన అది ఏ విధముగా ఏర్పడును?
జవాబు:
మిథ్యా ప్రతిబింబాన్ని మనము కెమెరాతో ఫోటో తీయగలము.
ఉదా :
1) సమతల దర్పణం(అద్దం)లో ఏర్పడిన మన ప్రతిబింబంను ఫోటో తీయగలగడం.
2) మిథ్యా ప్రతిబింబంను కెమెరా సూత్రంపై పనిచేయు మన కన్ను చూడగలగడం మొ||నవి.

ప్రశ్న 20.
మీ దగ్గరున్న కటకం యొక్క నాభ్యంతరం కనుక్కోవడానికి చేసే ప్రయోగంలో తీసుకోవలసిన జాగ్రత్తలు సూచించండి. (AS3)
జవాబు:
జాగ్రత్తలు :

1. కటకం యొక్క ప్రధానాక్షాన్ని ఊహించడంలో జాగ్రత్త వహించవలెను.
2. వెలుగుతున్న క్రొవ్వొత్తి కటకానికి ఎదురుగా పట్టుకొనవలెను.
3. ప్రతిబింబాన్ని తెరపై ఏర్పరచునపుడు తెరను నెమ్మదిగా ముందుకు, వెనుకకు జరపవలెను.
4. నాభ్యాంతరం విలువ ఒకేలా రాలేదంటే, ప్రయోగం నిర్వహించినప్పుడు దోషాలు (errors) జరిగి ఉండవచ్చు. అటువంటప్పుడు గణించిన నాభ్యాంతరం విలువల సరాసరి తీసుకొనవలెను.

ప్రశ్న 21.
ఒక వ్యవస్థలో f₁, f₂ నాభ్యంతరాలు గల రెండు కటకాలున్నాయి. కింది సందర్భాలలో ఆ వ్యవస్థ యొక్క నాభ్యంతరాన్ని ప్రయోగపూర్వకంగా ఎలా కనుగొంటారు? (AS3)
i) రెండూ ఒకదానినొకటి ఆనుకొని ఉన్నప్పుడు
ii) రెండూ ఒకే ప్రధానాక్షంపై d దూరంలో ఉన్నప్పుడు
జవాబు:
కటకాల యొక్క నాభ్యంతరాలు f₁ మరియు f₂ లు

i) రెండు కటకాలు ఒకదానికొకటి ఆనుకొని ఉన్నప్పుడు :
మనకు ఇచ్చిన కటకాలు కుంభాకార కటకాలు అనుకొనుము. వాటి నాభ్యంతరాలు f₁ మరియు f₂ లు అనుకొనుము.

1. ఈ రెండు కటకాలను ఒకదానితో ఒకటి ఆనుకొని ఉండునట్లు అమర్చి వాటిని సూర్యునికి అభిముఖంగా ఉంచాలి.
2. ఆ కటకాలకు మరోవైపు తెరను ఉంచి దానిపై సూర్యుని యొక్క బిందురూప ప్రతిబింబం ఏర్పరచాలి.
3. రెండో కటకం నుండి తెరకు గల దూరం కొలిసే అదే ఆ వ్యవస్థ యొక్క నాభ్యాంతరం అవుతుంది.

ii) రెండూ ఒకే ప్రధానాక్షంపై ‘d’ దూరంలో ఉన్నపుడు :
కటకాలను మధ్య దూరం ‘d’లో ఉంచినపుడు వాటి ఫలిత నాభ్యంతరం.

1. కటకాలను d దూరంలో ఉండునట్లు ఒక గొట్టంలో అమర్చాలి.
2. ఈ వ్యవస్థతో సూర్యుని బిందురూప ప్రతిబింబం తెరపై ఏర్పరచాలి.
3. రెండో’ కటకం నుండి తెరకు గల దూరమే ఈ వ్యవస్థ యొక్క నాభ్యంతరం అవుతుంది.

ప్రశ్న 22.
పాఠంలోని పట్టిక – 19 (ప్రయోగశాల కృత్యం – 1) ఉపయోగించి u మరియు V లకు, 1/u మరియు 1/v లకు లు గీయండి. (AS5)
జవాబు:
పట్టిక – 1లోని విలువల నుండి 1 విలువలను X – అక్షంపై, V – విలువలను Y – అక్షంపై తీసుకుని గీసిన గ్రాఫ్

\(\frac{1}{\mathrm{u}}\) విలువలను X – అక్షంపై, \(\frac{1}{\mathrm{v}}\) విలువలను Y – అక్షం పై తీసుకుని గీసిన గ్రాఫ్

ప్రశ్న 23.
40 సెం.మీ. నాభ్యంతరం గల కేంద్రీకరణ కటకంపై సమాంతర కిరణాలు పతనం చెందాయి. 15 సెం.మీ. నాభ్యంతరం గల వికేంద్రీకరణ కటకాన్ని ఎక్కడ ఉంచితే, రెండు కటకాల గుండా ప్రయాణించిన తర్వాత ఆ కిరణాలు తిరిగి సమాంతరంగా ఉంటాయి. కిరణచిత్రాన్ని గీయండి. (AS5)
జవాబు:
కిరణచిత్రము :

కుంభాకార కటకం నుండి 25 సెం.మీ. దూరంలో పుటాకార దర్పణాన్ని ఉంచాలి.

వివరణ : కుంభాకార దర్పణానికి :
u = ∞ (ప్రధానాక్షానికి సమాంతరంగా కాంతి కిరణాలు వస్తున్నాయి)
v = f (అవి నాభి వద్ద కేంద్రీకరింపబడుతున్నాయి)
f = + 40 సెం.మీ.

పుటాకార దర్పణానికి :
u = ?
v = ∞ (వక్రీభవన కిరణాలు ప్రధానాక్షానికి సమాంతరంగా వెళ్తున్నాయి)
f = – 15 సెం.మీ.

అనగా కటకం అవతల 15 సెం.మీ. దూరంలో వస్తువు ఉన్నట్లు భావించాలి. కనుక కుంభాకార దర్పణం వలన కాంతికిరణాలు ఎక్కడ కేంద్రీకరింపబడతాయో (f = 40) ఆ బిందువు కన్నా 15 సెం.మీ. ముందు పుటాకార దర్పణాన్ని ఉంచాలి. అప్పుడు రెండు కటకాల మధ్య దూరం 25 సెం.మీ. అవుతుంది.

ప్రశ్న 24.
ప్రయోగఫలితాలు, కిరణచిత్రాల ఫలితాలు ఒకే విధంగా ఉండడాన్ని మీరెలా అభినందిస్తారు? (AS6)
జవాబు:
ప్రయోగ ఫలితాలు, కిరణ చిత్ర ఫలితాలు ఒకే విధంగా ఉంటాయి. కనుక ప్రయోగం చేయకుండానే కిరణచిత్రాల ద్వారా వివిధ వస్తుదూరాలకు ప్రతిబింబ స్థానాలను, లక్షణాలను తెలుసుకోవచ్చును.
కావున కిరణ చిత్రాలు మనకు ఎంతో ఉపయోగపడతాయి.

ప్రశ్న 25.
వక్రీభవన గుణకం n = 1.5 గల గాజుతో ఒక కుంభాకార – పుటాకార కేంద్రీకరణ కటకం తయారు చేయబడింది. దాని నాభ్యంతరం 24 సెం.మీ. దాని ఒక వక్రతావ్యాసార్ధం మరొక వక్రతా వ్యాసార్ధానికి రెట్టింపైన ఆ రెండు వక్రతా వ్యాసార్ధాలను కనుగొనండి. (R₁ = 6 సెం.మీ. R₂ = 12 సెం.మీ.) (AS7)
జవాబు:
గాజు యొక్క వక్రీభవన గుణకం = n = 1.5
కుంభాకార – పుటాకార కేంద్రీకరణ కటకం నాభ్యంతరం = f = 24 సెం.మీ.

పుటాకార – కుంభాకార కటక వక్రతావ్యాసార్ధాలు R₁ మరియు R₂ లు అనుకొనుము. ఇవి రెండూ ఒకే సంజ్ఞను కలిగి ఉంటాయి.

ఒక వక్రతా వ్యాసార్ధం మరొక వక్రతా వ్యాసార్ధానికి రెట్టింపు కావున R₂ = 2R₁

ప్రశ్న 26.
ఒక ఈతకొలనులో అంచువెంబడి నీటిలో మునిగి మీరు ఈదుతున్నారనుకుందాం. ఒడ్డుపై మీ స్నేహితుడు నిలబడి ఉన్నాడు. మీకు మీ స్నేహితుడు, అతని వాస్తవ ఎత్తుకన్నా ఎక్కువ ఎత్తుగా కనబడతాడా లేక తక్కువ ఎత్తుగా కనబడతాడా? ఎందుకు? (AS7)
(లేదా)
రాజు అతని స్నేహితులు కొలనులో ఈత కొడుతున్నారు. వారిలో ఒకరు ఒడ్డుపై నిలబడి ఉన్నాడు. వారికి ఆ స్నేహితుడు, అతని వాస్తవ ఎత్తుకన్నా ఎక్కువ ఎత్తుగా కనబడతాడా? లేదా? ఎందుకు?
జవాబు:
అతని వాస్తవ ఎత్తుకన్నా ఎక్కువ ఎత్తుగా కనబడతాడు.

కారణం :
కాంతి విరళ యానకం నుండి సాంద్రతర యానకంలోనికి ప్రయాణించునపుడు లంబానికి దగ్గరగా వక్రీభవనం చెందును.

ఖాళీలను పూరించండి

1. దూరంలో ఉన్న వస్తువు నుండి వచ్చే కిరణాలు కుంభాకార కటకం వల్ల వక్రీభవనం చెంది …………… గుండా ప్రయాణిస్తాయి. (నాభి వద్ద)
2. కటకం యొక్క ……….. గుండా ప్రయాణించే కిరణం విచలనం పొందదు. (దృక్ కేంద్రం)
3. కటక సూత్రం ….. \(\left(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\right)\)
4. ఒక సమతల కుంభాకార కటక నాభ్యంతరం 28, వక్రతా వ్యాసార్ధం R అయిన కటక తయారీకి వాడిన పదార్థ వక్రీభవన గుణకం …………… (1.5)
5. నిజ మరియు మిథ్యా ప్రతిబింబాలను ఏర్పరచే కటకం ………………. (కుంభాకార కటకం)

సరైన సమాధానాన్ని ఎన్నుకోండి

1. కింది పదార్థాలలో కటక తయారీకి పనికిరానిది
A) నీరు
B) గాజు
C) ప్లాస్టిక్
D) బంకమన్ను
జవాబు:
D) బంకమన్ను

2. కింది వాటిలో ఏది సరియైనది?
A) కుంభాకార కటకంతో ఏర్పడ్డ మిథ్యా ప్రతిబింబ దూరం ఎల్లప్పుడూ వస్తుదూరం కంటే ఎక్కువ.
B) కుంభాకార కటకంతో ఏర్పడ్డ మిథ్యా ప్రతిబింబ దూరం ఎల్లప్పుడూ వస్తుదూరం కంటే తక్కువ లేదా సమానం.
C) కుంభాకార కటకం వల్ల ఎల్లప్పుడూ నిజప్రతిబింబం ఏర్పడుతుంది.
D)కుంభాకార కటకం వల్ల ఎల్లప్పుడూ మిథ్యా ప్రతిబింబం ఏర్పడుతుంది.
జవాబు:
A) కుంభాకార కటకంతో ఏర్పడ్డ మిథ్యా ప్రతిబింబ దూరం ఎల్లప్పుడూ వస్తుదూరం కంటే ఎక్కువ.

3. n వక్రీభవన గుణకం, R వక్రతావ్యాసార్ధం గల ఒక సమతల కుంభాకార కటకం యొక్క నాభ్యంతరం …
A) f= R
B) f = R/2
C) f = R(n – 1)
D) F = (n – 1)/R
జవాబు:
C) f = R(n – 1)

4. ఏ సందర్భంలో కటకనాభ్యంతర విలువకు ప్రతిబింబ దూరం విలువ సమానం?
A) కిరణాలు దృక కేంద్రం గుండా ప్రయాణించినప్పుడు
B) కిరణాలు ప్రధానాక్షానికి సమాంతరంగా ప్రయాణించినప్పుడు
C) కిరణాలు నాభి గుండా ప్రయాణించినప్పుడు
D) అన్ని సందర్భాలలో
జవాబు:
B) కిరణాలు ప్రధానాక్షానికి సమాంతరంగా ప్రయాణించినప్పుడు

5. కింది వాటిలో కటక తయారీ సూత్రం ఏది?
A) 1/f = (n – 1) (1/R₁ + 1/R₂)
B) 1/f = (n + 1) (1/R₁ – 1/R₂)
C) 1/f = (n – 1) (1/R₁ – 1/R₂)
D) 1/f = (n + 1) (1/R₁ + 1/R₂)
జవాబు:
C) 1/f = (n – 1) (1/R₁ – 1/R₂)

పరికరాల జాబితా

వివిధ రకాల కటకాలు, V – స్టాండు, కుంభాకార కటకం, తెర, కొవ్వొత్తి, గాజు బీకరు, కటకం ఉంచే రింగు.

10th Class Physical Science 4th Lesson వక్రతలాల వద్ద కాంతి వక్రీభవనం Textbook InText Questions and Answers

10th Class Physical Science Textbook Page No. 68

ప్రశ్న 1.
రెండు యానకాలను వేరు చేసే వక్రతలంపై కాంతికిరణం పతనమైతే ఏం జరుగుతుంది?
జవాబు:
కాంతి వక్రతలం వద్ద వక్రీభవనం చెందుతుంది.

ప్రశ్న 2.
వక్రతలంపై పతనమైన కాంతికిరణాలు ఎలా విచలనం పొందుతాయి?
జవాబు:
విరళ యానకం నుండి సాంద్రతర యానకంలోనికి ప్రయాణించేటప్పుడు లంబానికి దగ్గరగా జరుగుతాయి.

10th Class Physical Science Textbook Page No. 69

ప్రశ్న 3.
ప్రధానాక్షం వెంట ప్రయాణించే కిరణం ఏమవుతుంది? అలాగే వక్రతా కేంద్రం గుండా ప్రయాణించే కిరణం ఏమవుతుంది?
జవాబు:
రెండు కిరణాలు లంబం వెంటే ప్రయాణిస్తాయి.
విచలనం పొందవు.

10th Class Physical Science Textbook Page No. 74

ప్రశ్న 4.
రెండు వక్రతలాలున్న పారదర్శక పదార్థాన్ని కాంతికిరణ మార్గంలో ఉంచితే, ఆ కిరణం ఏమవుతుంది?
జవాబు:
కాంతికిరణం రెండుసార్లు వక్రీభవనం చెందుతుంది.

ప్రశ్న 5.
కటకం గుండా ప్రయాణించిన కాంతి కిరణం ఎలా ప్రవర్తిస్తుంది?
జవాబు:

10th Class Physical Science Textbook Page No. 76

ప్రశ్న 6.
నాభి గుండా ప్రయాణించే కాంతి కిరణం ఎలా ప్రవర్తిస్తుంది?
జవాబు:
నాభి గుండా ప్రయాణించే కాంతి కిరణం వక్రీభవనం పొందాక ప్రధానాక్షానికి సమాంతరంగా ప్రయాణిస్తుంది.

10th Class Physical Science Textbook Page No. 77

ప్రశ్న 7.
ప్రధానాక్షానికి కొంత కోణం చేస్తూ వచ్చే సమాంతర కాంతి కిరణాలు కటకంపై పతనం చెందితే ఏం జరుగుతుంది?
జవాబు:
ప్రధానాక్షానికి కొంత కోణం చేస్తూ వచ్చే సమాంతర కాంతి కిరణాలు నాభీయతలంపై ఏదేని బిందువు వద్ద కేంద్రీకరించ బడతాయి. (లేదా) నాభీయ తలంపై నున్న బిందువు నుండి బయలుదేరి వస్తునట్లు కనిపిస్తాయి.

ప్రశ్న 8.
వస్తువు అనంతదూరంలో ఉండటం అంటే ఏమిటి?
జవాబు:
వస్తువు కటకానికి బాగా దూరంగా ఉంటే అనంత దూరంలో ఉందని అంటాం. అనంతదూరంలో వస్తువు ఉన్నప్పుడు కటకంపై పడే కాంతి కిరణాలు ప్రధానాక్షానికి సమాంతరంగా ఉంటాయి.

10th Class Physical Science Textbook Page No. 83

ప్రశ్న 9.
u – V పద్ధతిలో అన్ని సందర్భాలలోనూ కటక నాభ్యంతరం ఒకే విలువ వచ్చునా?
జవాబు:

1. u, v విలువలు మారిన అన్ని సందర్భాలలోనూ ఒకే విలువ ఉండును.
2. నాభ్యంతరం విలువ ఒకేలా రాకుంటే గణించిన నాభ్యంతరం విలువల సరాసరిని తీసుకోవాలి.

10th Class Physical Science Textbook Page No. 84

ప్రశ్న 10.
కటకం యొక్క నాభ్యంతరం ఏ ఏ అంశాలపై ఆధారపడుతుంది?
జవాబు:
కటకం యొక్క నాభ్యంతరం

1. కటకం తయారైన పదార్థ లక్షణంపై
2. కటక వక్రతా వ్యాసార్ధాలపై
3. పరిసర యానకంపైన ఆధారపడుతుంది.

10th Class Physical Science Textbook Page No. 69

ప్రశ్న 11.
ప్రధానాక్షానికి సమాంతరంగా ప్రయాణించే కిరణం ఏమవుతుంది?

జవాబు:
a, C లలో వక్రీభవన కిరణం ప్రధానాక్షం పై ఒక నిర్దిష్ట బిందువును చేరుతుంది. Ab, d లలో ప్రధానాక్షానికి దూరంగా జరిగింది. వెనుకకు పొడిగిస్తే అది ప్రధానాక్షాన్ని అదే బిందువు వద్ద ఖండిస్తుంది.

ప్రశ్న 12.
i) 4(ఎ), 4(బి) పటాలలో వక్రీభవన కిరణాల మధ్య ఏం తేడా గమనించారు?
జవాబు:
4(ఎ) లో వక్రీభవన కిరణం ప్రధానాక్షంపై నిర్దిష్ట బిందువు వద్ద చేరింది.
4(బి) లో వక్రీభవన కిరణం ప్రధానాక్షానికి దూరంగా జరిగింది.

10th Class Physical Science Textbook Page No. 70

ii) ఈ (4(ఎ), 4(బి) మధ్య తేడాకు కారణం ఏమై ఉంటుంది?
జవాబు:
దీనికి ముఖ్యకారణం కాంతికిరణం వేర్వేరు యానకాలలో వక్రీభవనం చెందుట.

iii) 4(సి), 4(డి) పటాలలో వక్రీభవన కిరణాల మధ్య ఏం తేడా గమనించారు?
జవాబు:
4(సి) లో వక్రీభవన కిరణం ప్రధానాక్షంపై నిర్దిష్ట బిందువు వద్ద చేరింది.
4(డి) లో ప్రధానాక్షానికి దూరంగా జరిగింది.

iv) ఈ (4(సి), 4(డి) మధ్య తేడాకు కారణం ఏమై ఉంటుంది?
జవాబు:
దీనికి ముఖ్యకారణం కాంతికిరణం వేర్వేరు యానకాలలో వక్రీభవనం చెందుట.

v) నిమ్మకాయ పరిమాణంలో కనిపించే ఈ మార్పును ఎలా వివరిస్తారు?
జవాబు:
కాంతి సాంద్రతర యానకం నుండి విరళయానకంలోకి ప్రయాణించినపుడు లంబానికి దూరంగా వంగును.

vi) పెద్దగా కనిపించే నిమ్మకాయ అసలు నిమ్మకాయా? లేక దాని ప్రతిబింబమా?
జవాబు:
నిమ్మకాయ యొక్క ప్రతిబింబము.

10th Class Physical Science Textbook Page No. 72 ఉదాహరణ : 1)

ప్రశ్న 13.
ఆకాశంలో ఉన్న పక్షి సరస్సులోని నీటి ఉపరితలం దిశగా లంబంగా స్థిరవడితో కిందికి ప్రయాణిస్తుంది. పక్షికి లంబంగా నీటిలో ఒక చేప ఉంటే, ఆ చేపకు
a) పక్షి అసలు స్థానం కంటే దూరంలో కనబడుతుంది.
b) పక్షి అసలు స్థానం కంటే దగ్గరగా కనబడుతుంది.
c) పక్షి యొక్క వాస్తవ వేగం కంటే ఎక్కువ వేగంతో కదులుతున్నట్లు కనబడుతుంది.
d) పక్షి యొక్క వాస్తవ వేగం కంటే తక్కువ వేగంతో కదులుతున్నట్లు కనబడుతుంది.
పై అంశాలలో ఏవి సరియైనవి ? వాటిని మీరు ఎలా నిరూపిస్తారు? (AS7)

జవాబు:
సమతలం వద్ద వక్రీభవనానికి మనం ఉపయోగించే సూత్రం \(\frac{\mathrm{n}_{2}}{\mathrm{~V}}=\frac{\mathrm{n}_{1}}{\mathrm{u}}\) . ……. (1)

ఒకానొక సమయంలో నీటి ఉపరితలం నుండి X ఎత్తులో పక్షి ఉందనుకుందాం.
నీటి వక్రీభవన గుణకం n అనుకుందాం.
గాలి వక్రీభవన గుణకం (n₁) = 1; నీటి వక్రీభవన గుణకం (n₂) = n
పటం ప్రకారం, వస్తుదూరం (u) = – X; ప్రతిబింబదూరం (v) =-y

ఈ విలువలను సమీకరణం (1) లో ప్రతిక్షేపించగా
\(\frac{n}{(-y)}=\frac{1}{(-x)} \Rightarrow y=n x\)

నీటి వక్రీభవన గుణకం (1) విలువ 1 కన్నా ఎక్కువని మనకు తెలుసు. కాబట్టి పై సమీకరణం ప్రకారం y విలువ X కంటే ఎక్కువ. కాబట్టి చేపకు పక్షి దాని అసలు స్థానం కంటే దూరంగా కనబడుతుంది. పక్షి స్థిరవడితో లంబంగా కిందికి ప్రయాణిస్తుందని మనం భావించాం. భూమిపై నుండి చూసే పరిశీలకునికి నిర్దిష్ట సమయంలో పక్షి X దూరం ప్రయాణించినట్లు కనిపిస్తే, అదేకాలంలో పక్షి ల దూరం ప్రయాణించినట్లుగా చేపకు కనబడుతుంది. X కన్నా y విలువ ఎక్కువ కాబట్టి పక్షి వాస్తవ వేగం కంటే ఎక్కువ వేగంతో కదులుతున్నట్లుగా చేపకు కనబడుతుందని మనం చెప్పవచ్చు.
దీనినిబట్టి సమస్యలో ఇచ్చిన అంశాలలో (a) మరియు (c) సరియైనవి.

10th Class Physical Science Textbook Page No. 73 (ఉదాహరణ : 2)

ప్రశ్న 14.
R వ్యాసార్ధం గల పారదర్శక గోళం గాలిలో ఉంది. దాని వక్రీభవన గుణకం n. వస్తు దూరానికి సమాన దూరంలో గోళానికి రెండోవైపు నిజప్రతిబింబం ఏర్పడాలంటే, ప్రధానాక్షంపై గోళం ఉపరితలం నుండి ఎంత దూరంలో వస్తువును ఉంచాలి?

జవాబు:
పటంను పరిశీలిస్తే వస్తుదూరానికి సమానమైన దూరంలో ప్రతిబింబం ఏర్పడాలంటే గోళంలో ప్రయాణించే వక్రీభవన కిరణం ప్రధానాక్షానికి సమాంతరంగా ప్రయాణించాలని తెలుస్తుంది.
గాలి వక్రీభవన గుణకం n₁ = 1; గోళం వక్రీభవన గుణకం n₂ = n

పటం నుండి, వస్తుదూరం u = – X; ప్రతిబింబదూరం V = 0 (ఒకటో వక్రతలం వద్ద వక్రీభవనం పొందిన కిరణం ప్రధానాక్షానికి సమాంతరంగా ప్రయాణిస్తుంది.)

ఉదాహరణ : 3

ప్రశ్న 14.
ఒక పారదర్శక గోళకేంద్రం వద్ద ఒక చిన్న అపారదర్శక బిందువు ఉంది. గోళం బయటి నుండి చూసినపుడు ఆ బిందువు యథాస్థానంలో కనబడుతుందా?
జవాబు:

అంటే వస్తుదూరం, ప్రతిబింబదూరం సమానం. కనుక బిందువు ఏ స్థానంలో ఉందో, అదే స్థానంలో కనిపిస్తుంది. ఇది పదార్థం యొక్క వక్రీభవన గుణకంపై ఆధారపడదు.

10th Class Physical Science Textbook Page No. 76 (ఉదాహరణ : 4)

ప్రశ్న 15.
కుంభాకార కటకం యొక్క ప్రధానాక్షం (MN)పై నాభి (F)కి ఆవల ఒక బిందురూప వస్తువు (S)ను ఉంచినపుడు, ప్రతిబింబ స్థానాన్ని గుర్తించడానికి కిరణచిత్రాన్ని గీయండి.
జవాబు:
నాభి (F’) వద్ద ప్రధానాక్షానికి ఒక లంబరేఖ గీయండి.

బిందురూప వస్తువు (S) నుండి కటకంపై ఏదేని బిందువు (P’) ను చేరేటట్లు ఒక కిరణాన్ని గీయండి. వస్తువు (S) నుండి గీసిన కిరణానికి సమాంతరంగా కటక దృక కేంద్రం (P) గుండా పోయే మరో రేఖను గీయండి. ఈ రేఖ, నాభి వద్ద గీసిన లంబాన్ని F₀ వద్ద ఖండిస్తుంది.

– P’ బిందువు నుండి బయలుదేరి F₀ బిందువు గుండా పోతూ ప్రధానాక్షాన్ని I అనే బిందువు వద్ద ఖండించే విధంగా మరొక రేఖను గీయండి.

– S అనే బిందురూప వస్తువుకు ‘I’ బిందువు ప్రతిబింబం అవుతుంది.

10th Class Physical Science Textbook Page No. 80 (ఉదాహరణ : 5)

ప్రశ్న 16.
పటం (ఎ), (బి) లలో చూపిన కిరణాలు కటకం గుండా ప్రయాణించాక ఏర్పడే వక్రీభవన కిరణాల మార్గాలను గీయండి.

జవాబు:
కిరణచిత్రాలను గీయడానికి ఉదాహరణ 4లో తెలిపిన సూచనలను పాటించండి. ఆ కిరణాల మార్గాలు (సి), – (డి) పటాలలో చూపిన విధంగా ఉంటాయని మీరు గుర్తిస్తారు.

10th Class Physical Science Textbook Page No. 83 (ఉదాహరణ : 6)

ప్రశ్న 17.
ఒక టేబుల్ పై వెలుగుతున్న విద్యుత్ బల్బు, తెరను ఒకదానికి ఒకటి 1 మీ|| దూరంలో ఉంచాం. 21 సెం.మీ. నాభ్యంతరం గల కుంభాకార కటకాన్ని వీటి మధ్య ఏ స్థానంలో ఉంచితే స్పష్టమైన ప్రతిబింబం ఏర్పడుతుంది?

జవాబు:
వస్తువు (విద్యుత్ బల్బు) కు, తెరకు మధ్య దూరం d మరియు వస్తువుకు, కటకానికి మధ్య దూరం X అనుకుందాం. పటం ప్రకారం u = – X, V = d – x

ఈ విలువలను కటక సూత్రంలో ప్రతిక్షేపించగా
\(\frac{1}{f}=\frac{1}{(d-x)}+\frac{1}{x}\)
ఈ సమీకరణాన్ని సాధించి x² – dx + fd = 0 అని పొందవచ్చు.
ఇది ఒక వర్గసమీకరణం. దీనికి రెండు సాధనలుంటాయి. అవి

f = 21 సెం.మీ.; d= 1 మీ. 100 సెం.మీ. అని ఇవ్వబడింది.

ఈ విలువలను పై సమీకరణంలో ప్రతిక్షేపించి, x₁ = 70 సెం.మీ. మరియు x₂ = 30 సెం.మీ. అని పొందవచ్చు.

గమనిక : f విలువ 25 సెం.మీ. లేదా అంతకన్నా తక్కువ ఉన్నప్పుడు మాత్రమే బల్బ్ యొక్క ప్రతిబింబం స్పష్టంగా ఏర్పడుతుంది.

దీనికి గల కారణమేమిటో, సమీకరణం – (1) ఉపయోగించి చర్చించండి. ఉపాధ్యాయుని సహకారం తీసుకోండి.

10th Class Physical Science Textbook Page No. 89 (అనుబంధ ఉదాహరణ)

ప్రశ్న 18.
వక్రీభవన గుణకం n = 1.5 గల ఒక ద్విపుటాకార కటకం గాలిలో ఉంచబడింది. కటకం యొక్క రెండు వక్రతలాల వక్రతావ్యా సార్ధాలు R₁ = – 30 సెం.మీ., R₂ = 60 సెం.మీ. అయిన ఆ కటక నాభ్యంతరం ఎంత?
జవాబు:
పటం ప్రకారం సంజ్ఞా సంప్రదాయాన్ని ఉపయోగించి
R₁ = – 30 సెం.మీ. R₂ = 60 సెం.మీ. అని రాయవచ్చు. n = 1.5 అని ఇవ్వబడింది.
పై విలువలను \(\frac{1}{\mathrm{f}}=(\mathrm{n}-1)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\)

పై సమీకరణాన్ని సాధిస్తే f = – 40 సెం.మీ. అవుతుంది. ఇందులో ‘-‘ అనేది వికేంద్రీకరణ కటకాన్ని తెలియజేస్తుంది.

10th Class Physical Science 4th Lesson వక్రతలాల వద్ద కాంతి వక్రీభవనం Textbook Activities

కృత్యములు

కృత్యం – 1

ప్రశ్న 1.
వక్రతలాల ద్వారా కాంతి వక్రీభవనంను అవగాహన చేసుకోవడానికి ఒక కృత్యంను వ్రాయుము.
జవాబు:
ఉద్దేశ్యం : వక్రతలాలపై కాంతి వక్రీభవనంను అవగాహన చేసుకొనుట.

కావలసిన పరికరాలు :
మందపాటి కాగితం ముక్క నల్ల స్కెచ్ పెన్, గాజు స్థూపాకార పాత్ర, టేబుల్ మరియు నీరు.

పద్ధతి : సందర్భం – 1:

1. ఒక మందపాటి కాగితం ముక్కను తీసుకొనుము.
2. దానిపై నల్లని స్కెచ్ తో 4 సెం.మీ. బాణం గుర్తును గీయుము.
3. టేబుల్ పై గాజు గ్లాసు వంటి స్థూపాకారపు పాత్ర నుంచుము.
4. ఆ పాత్ర గుండా అవతల వైపునున్న బాణం గుర్తును పరిశీలించుము.
5. బాణం గుర్తు కంటే తక్కువ పరిమాణం గల ప్రతిబింబం ఏర్పడును.
6. దీనికి కారణం బాణం గుర్తునుండి వచ్చే కాంతి వక్రతలం ద్వారా వక్రీభవనం చెంది గాజు గుండా ప్రయాణించింది. మరల గాజు నుండి గాలిలోకి, మరొకసారి వక్రీభవనం చెందడం వలన చిన్న ప్రతిబింబం ఏర్పరుస్తుంది.

సందర్భం – 2 :

1. ఇప్పుడు గాజు పాత్రను నీటితో నింపుము.
2. అదే స్థానంలో ఉండి మరల బాణం గుర్తును పరిశీలించుము.
3. ప్రతిబింబం వ్యతిరేకదిశలో ఏర్పడుతుంది.
4. దీనికి కారణము కాంతి వక్రతలంలోకి ప్రవేశించి నీటిగుండా ప్రయాణించి, నీటి నుండి బయటకు వచ్చాక వ్యతిరేక ఆ దిశలో ఉన్న ప్రతిబింబాన్ని ఏర్పరుస్తుంది.

కృత్యం – 2

ప్రశ్న 2.
కటకం యొక్క నాభ్యంతరం ఏఏ అంశాలపై ఆధారపడుతుంది?
జవాబు:
ఉద్దేశ్యం : కటక నాభ్యంతరం పరిసర యానకంపై ఆధారపడుతుందని నిరూపించుట.

కావలసిన పరికరాలు :
కటకం, స్థూపాకార పాత్ర, నల్లటి రాయి, నీరు

ప్రయోగం :

1. నాభ్యాంతరం తెలిసిన కటకాన్ని తీసుకొంటిని.
2. కటక నాభ్యాంతరానికి 4 రెట్లు ఎత్తు ఉండే గాజు గ్లాసు వంటి ఒక ఇక స్థూపాకార పాత్రను తీసుకొంటిని.
3. పాత్ర అడుగుభాగాన నల్లటి రాయి నుంచితిని.
4. రాయిపై నుండి కటక నాభ్యాంతరం కన్నా ఎక్కువ ఎత్తు వరకు ఉండేటట్లు పాత్రలో నీరు నింపితిని.
5. పటంలో చూపినట్లు కటకాన్ని నీటి ఉపరితలానికి సమాంతరంగా నీటిలో యుంచితిని.
6. రాయి ఉపరితలం నుండి కటకానికి గల దూరం, కటక నాభ్యంతరానికి సమానంగా గానీ, లేదా తక్కువగా గానీ ఉండే విధంగా కటకాన్ని పట్టుకుంటిని.

పరిశీలనలు :

1. రాయి ప్రతిబింబాన్ని చూడగలిగాను.
2. గాలిలో రాయి, కటకానికి మధ్య దూరం కటక నాభ్యాంతరం కంటే తక్కువ ఉంటేనే రాయి ప్రతిబింబం కనబడుతుంది.
3. కానీ ప్రయోగంలో కటకం గాలిలో ఉన్నప్పుడు కనుగొన్న నాభ్యంతరం కంటే, రాయి-కటకం మధ్య దూరం ఎక్కువగా ఉండే విధంగా కటకాన్ని నీటిలో ముంచిన రాయి ప్రతిబింబం కనబడింది.
4. దీనిని బట్టి నీటిలో ఉన్నప్పుడు కటక నాభ్యంతరం పెరిగిందని తెలుస్తుంది.

నిర్ణయము :
కనుక కటక నాభ్యంతరం పరిసరయానకంపై ఆధారపడుతుంది.

SCERT AP 10th Class Physics Study Material Pdf 1st Lesson సమతల ఉపరితలాల వద్ద కాంతి వక్రీభవనం Textbook Questions and Answers.

AP State Syllabus 10th Class Physical Science 3rd Lesson Questions and Answers సమతల ఉపరితలాల వద్ద కాంతి వక్రీభవనం

10th Class Physical Science 3rd Lesson సమతల ఉపరితలాల వద్ద కాంతి వక్రీభవనం Textbook Questions and Answers

అభ్యసనాన్ని మెరుగుపరుచుకోండి

ప్రశ్న 1.
నీటిలో ఈదే చేపను తుపాకీతో కాల్చడం కష్టం. ఎందుకు? (AS1)
జవాబు:
నీటిలో ఈదే చేపను తుపాకీతో కాల్చడం కష్టం. దీనికి కారణం కాంతి యొక్క వక్రీభవన లక్షణమే.

వివరణ :

1. చేప, పరిశీలకుడు వేర్వేరు యానకాలలో ఉన్నారు. అనగా చేప నీరు అను సాంద్రతర యానకంలోనూ, పరిశీలకుడు గాలి అను విరళయానకంలోనూ కలరు.
2. గమనించగా – నీరు, గాలి అనే యానకాలను వేరుచేసే తలం వద్ద చేప ఉపరితలం వైపునకు పైకి వచ్చినట్లుగా కనపడుతుంది.
3. కావున తుపాకీని గురి పెట్టినపుడు దాని నిజమైన స్థానానికి బదులుగా స్థానభ్రంశం చెందిన స్థానం కనిపిస్తుంది. అందుకనే నీటిలో ఈదే చేపను తుపాకీతో కాల్చడం కష్టం.

ప్రశ్న 2.
శూన్యంలో కాంతివేగం 3,00,000 కి.మీ./సె., వజ్రంలో కాంతివేగం 1,24,000 కి.మీ./సె. అయిన, వజ్రం వక్రీభవన గుణకాన్ని కనుగొనండి. (AS1)
జవాబు:
వజ్రంలో కాంతివేగం (V) : 1,24,000 కి.మీ./సె.
శూన్యంలో కాంతివేగం (C) = 3,00,000 కి.మీ./సె.

ప్రశ్న 3.
నీటిపరంగా గాజు వక్రీభవన గుణకం 9/8. గాజుపరంగా నీటి వక్రీభవన గుణకం ఎంత? (AS1)
జవాబు:

ప్రశ్న 4.
బెంజీన్ యొక్క సందిగ్ధ కోణం 42°. అయిన బెంజీన్ వక్రీభవన గుణకం కనుగొనండి. (AS1)
(లేదా)
బెంజీన్ సందిగ్ధకోణం విలువ 42° అయిన దాని యొక్క వక్రీభవన గుణకం విలువ ఎంత?
జవాబు:
బెంజీన్ సందిగ్ధ కోణం (C) = 42°

ప్రశ్న 5.
ఎండమావులు ఏర్పడే విధానాన్ని వివరించండి. (AS1)
(లేదా)
ఎండమావులు ఏ విధముగా ఏర్పడతాయో వివరించుము.
(లేదా)
వేసవిలో రోడ్డుపై ఏర్పడే మానవుని యొక్క దృక్ భ్రమను వివరించుము.
(లేదా)
రాజు రోడ్డుపై ప్రయాణించుచున్నాడు. అతనికి కొంతదూరంలో రోడ్డుపై నీటిగుంట వున్నట్లు కన్పించినది. అక్కడకు వెళ్ళి చూడగా నీటిగుంట లేదు. ఈ దృగ్విషయాన్ని ఏమంటారు? అది ఎలా సాధ్యపడినది? వివరింపుము.
(లేదా)
ఎండ తీవ్రంగా ఉన్న మధ్యాహ్నం సమయంలో తారురోడ్డుపై కొన్ని సార్లు నీరు ఉన్నట్లు కన్పిస్తుంది. కాని అక్కడ నీరు ఉండదు ఆ దృగ్విషయం ఏమిటి? అది ఎందుకు ఆ విధంగా జరుగుతుందో వివరించండి.
జవాబు:
ఎండ తీవ్రంగా ఉన్న మధ్యాహ్న సమయంలో తారు రోడ్డుపై కొన్నిసార్లు నీరు ఉన్నట్లు కన్పించును, కానీ అక్కడ నీరుండదు. ఈ దృగ్విషయాన్ని “ఎండమావి” అంటారు.

1. ఎండమావులు దృఢమ వల్ల ఏర్పడు ఒక ఊహాత్మక చిత్రం.
2. ఎండమావులు యానకపు వక్రీభవన గుణకాలలోని తేడాల వలన మరియు కాంతి సంపూర్ణాంతర పరావర్తనం వలన ఏర్పడతాయి.
   ఏర్పడు విధానం :
   
3. వేసవికాలంలో రోడ్డు ఉపరితలానికి దగ్గరగా ఉన్న గాలి వేడిగానూ, రోడ్డు ఉపరితలానికి చాలా ఎత్తులో ఉన్న గాలి వక్రీభవన గుణకం తగ్గుతుంటుంది. చల్లగానూ ఉండును.
4. దీనినిబట్టి ఎత్తుపై ఉష్ణోగ్రత తగ్గుతుంది. దీనివలన గాలి సాంద్రత పెరుగుతుంది.
5. ఎత్తు పెరుగుతున్న కొలదీ గాలి వక్రీభవన గుణకం పెరుగును. కావున రోడ్డు ఉపరితలానికి దగ్గరగా ఉన్న వేడిగాలి కంటే పైన ఉన్న చల్లగాలి వక్రీభవన గుణకం ఎక్కువ.
   
6. కాబట్టి పైన ఉన్న చల్లని సాంద్రతర గాలికంటే, క్రింద ఉన్న వేడి విరళగాలిలో కాంతి వేగంగా ప్రయాణించును.
7. కాంతి పై నుండి కిందకు, సాంద్రత మారుతున్నటువంటి గాలిగుండా ప్రయాణిస్తూ రోడ్డుకు దగ్గరగా వచ్చినపుడు వక్రీభవనానికి లోనై సంపూర్ణాంతర పరావర్తనం వల్ల పటంలో చూపిన విధంగా ప్రయాణిస్తుంది.
8. ఈ విధంగా కాంతి నేలపై పరావర్తనం చెంది వస్తున్నట్లుగా మనకు కనిపిస్తుంది.
9. ఇలా జరగడం వల్లనే ఆకాశం యొక్క మిథ్యా ప్రతిబింబం పటంలో చూపినట్లు మనకు రోడ్డుపై నీళ్ళవలె కనబడుతుంది. దీనినే “ఎండమావి” అంటాం.

ప్రశ్న 6.
\(\frac{\sin i}{\sin r}\) విలువ స్థిరమని ప్రయోగపూర్వకంగా ఎలా సరిచూస్తారు? (ప్రయోగశాల కృత్యం – 1) (AS1)
(లేదా)
పతన కోణము మరియు వక్రీభవన కోణంలకు మధ్యనగల సంబంధంను ప్రయోగ పూర్వకముగా వ్రాయుము.
(లేదా)
పటం ద్వారా పతన మరియు పరావర్తన కోణంల మధ్య సంబంధంను ప్రయోగ పూర్వకముగా వివరించుము.
జవాబు:
ఉద్దేశ్యం :
పతనకోణానికి, వక్రీభవన కోణానికి మధ్య గల సంబంధాన్ని గుర్తించడం.

కావలసిన వస్తువులు :
ప్రొ సర్కిల్, తెల్ల డ్రాయింగ్ షీట్, స్కేలు, నలుపురంగు వేసిన చిన్న కార్డుబోర్డు ముక్క (10 సెం.మీ. X 10 సెం.మీ.), 2 సెం.మీ. మందం గల అర్ధవృత్తాకారపు గాజుపలక, పెన్సిల్ మరియు లేజర్ లైట్.

ప్రొ సర్కిల్ తయారీ :

1. కార్డుబోర్డు షీట్ పై తెల్ల డ్రాయింగ్ షీట్ ను అంటించుము.
2. డ్రాయింగ్ షీట్ మధ్యలో రెండు లంబరేఖలను పటంలో చూపిన విధంగా గీయుము.
3. ఆ లంబరేఖల ఖండన బిందువును ‘0’ గా గుర్తించుము.
4. లంబరేఖలకు MM, NN అని పేర్లు పెట్టుము.
5. ఈ రేఖలలో MM అనునది రెండు యానకాలను వేరుచేసే తలాన్ని సూచిస్తుంది.
6. NN అనునది MM రేఖకు ‘O’ బిందువు వద్ద గీసిన లంబాన్ని సూచిస్తుంది.
7. NN రేఖ వెంబడి ఒక కోణమానిని ఉంచి, దాని కేంద్రం బిందువు ‘O’ తో ఏకీభవించునట్లు చేయుము.
8. పటంలో చూపిన విధంగా NN యొక్క రెండు చివరల నుండి అనగా 0-90° కోణాలను గుర్తించుము.
9. ఈ విధంగా -NN కు రెండోవైపు కూడా కోణాలను గుర్తించుము.
10. పటంలో చూపిన విధముగా ఈ కోణరేఖలన్నింటినీ ఒక వృత్తం పై వచ్చునట్లుగా గుర్తించుము.

ప్రయోగ నిర్వహణ పద్ధతి :

1. క్రింది పటంలో చూపిన విధంగా అర్ధవృత్తాకారపు గాజు పలకను MM వెంబడి అమర్చుము.
2. గాజుపలక వ్యాసం MM తో ఏకీభవించాలి. దాని కేంద్రం (0) బిందువుతో ఏకీభవించాలి.
3. ఇప్పుడు లేజర్ లైట్ తో NN వెంబడి కాంతిని ప్రసరింపజేయుము.
   ఈ కాంతి మొదట గాలిలో ప్రయాణించి రెండు యానకాలను వేరుచేయు తలం అయిన MM గుండా ‘O’ బిందువు వద్ద గాజులోకి ప్రవేశిస్తుంది.
4. పటంలో చూపినట్లుగా గాజు నుండి బయటకు వచ్చు కాంతి యొక్క మార్గాన్ని గమనించుము.
5. ఇప్పుడు NN రేఖకు 15° కోణం (పతన కోణం) చేసే రేఖ వెంబడి లేజర్ కాంతిని ప్రసరింపజేసిన అది ‘O’ బిందువు గుండా పోయే విధంగా జాగ్రత్త తీసుకొనుము.
6. ఈ కాంతి గాజుపలక యొక్క వక్రతలం గుండా బయటకు వచ్చు కాంతిని పరిశీలించి, దాని వక్రీభవన కోణమును కొలువుము.
7. ఈ విధంగా వివిధ పతన కోణాలు 209, 30, 409, 50° మరియు 60° లతో ఈ ప్రయోగాన్ని చేసి, వాటి వక్రీభవన కోణాలను క్రింది పట్టికలో నమోదు చేయుము.
   
8. ప్రతీ i, r విలువలకు sini, sin r లను లెక్కించి, \(\frac{\sin i}{\sin r}\) విలువను గణించుము.
9. ప్రతీ సందర్భంలో sin i, sin r నిష్పత్తి విలువ స్థిరము.

ప్రశ్న 7.
సంపూర్ణాంతర పరావర్తనాన్ని ఏదేని కృత్యంతో వివరించండి. (కృత్యం – 5) (AS1)
జవాబు:
ఉద్దేశ్యం : కాంతి సంపూర్ణాంతర పరావర్తనాన్ని వివరించుట.

కావలసిన వస్తువులు :
ప్రొ సర్కిల్, తెల్ల డ్రాయింగ్ షీట్, స్కేలు, నలుపురంగు వేసిన చిన్న కార్డుబోర్డు ముక్క (10 సెం.మీ. X 10 సెం.మీ.), 2 సెం.మీ. మందం గల అర్ధవృత్తాకారపు గాజుపలక, పెన్సిల్ మరియు లేజర్ లైట్.

నిర్వహణ పద్ధతి :

1. ప్రయోగశాల కృత్యం – 1 లో ఉంచినట్లుగానే అర్ధవృత్తాకార గాజుదిమ్మె వ్యాసం యానకాలను వేరుచేసే రేఖ MM తో ఏకీభవించేటట్లుగా అమర్చండి.
2. MM మధ్య బిందువు ‘O’ తో గాజు దిమ్మె వ్యాసం యొక్క మధ్య – బిందువు ఏకీభవించాలి.
3. గాజు దిమ్మె వక్రతలం వైపు నుండి కాంతిని పంపండి.
4. మనం కాంతిని సాంద్రతర యానకం నుండి విరళయానకంలోకి పంపుతున్నాము.
5. మొదటగా 0° పతన కోణంతో ప్రారంభించి గాజు దిమ్మె రెండోవైపు వక్రీభవన కిరణంను పరిశీలించుము.
6. వక్రీభవన కిరణం తన మార్గాన్ని మార్చుకోలేదని మనము గమనించవచ్చును.
7. ఇదే విధంగా 59, 10, 15-9, ….. పతన కోణాలతో కాంతిని పంపి వక్రీభవన కోణాలను లెక్కించుము.
8. i, r విలువలను క్రింది పట్టికలో నమోదు చేయుము.
   
9. నిర్దిష్ట పతనకోణం వద్ద వక్రీభవన కిరణం గాజు, గాలి యానకాలను వేరుచేయు రేఖ వెంబడి ప్రయాణించడం గమనించవచ్చును.
10. ఈ సందర్భంలో ఏర్పడు పతనకోణం సందిగ్ధ కోణం అగును.
11. ఏదైనా పతన కోణం (i) కి పరావర్తన కోణం (r) అయినపుడు స్నెల్ నియమం ప్రకారం
    

15) సందిగ్ధ కోణం కన్నా పతనకోణం ఎక్కువైనపుడు యానకాలను వేరుచేయు తలం వద్ద కాంతికిరణం తిరిగి సాంద్రతర ఆ యానకంలోకే పరావర్తనం చెందును.
16) అనగా కాంతికిరణం విరళయానకంలోకి ప్రవేశించదు. ఈ దృగ్విషయాన్ని సంపూర్ణాంతర పరావర్తనం అంటాం.

ప్రశ్న 8.
సాంద్రతర యానకం నుండి విరళయానకంలోకి కాంతి ప్రయాణించినప్పుడు, పతనకోణం కన్నా వక్రీభవన కోణం విలువ ఎక్కువని ప్రయోగపూర్వకంగా ఎలా సరిచూస్తారు? (AS1)
(లేదా)
సాంద్రతర యానకం నుండి విరళయానకంలోకి కాంతి ప్రయాణించినపుడు లంబానికి దూరంగా వంగుతుందని r > i అని తెలిపే కృత్యాన్ని వ్రాయండి.
జవాబు:
ఉద్దేశ్యం :
సాంద్రతర యానకం నుండి విరళ యానకంలోకి కాంతి ప్రయాణించినప్పుడు లంబానికి దూరంగా వంగుతుందని లేదా r> i అగునని నిరూపించుట.

కావలసిన పరికరాలు :
కోణమాని, రెండు స్ట్రాలు, నీరు.

నిర్వహణ పద్ధతి :

1. ఒక వృత్తాకారపు కోణమానిని తీసుకొని దానిపై కేంద్రం వద్ద రెండు ‘స్ట్రా’లను, కేంద్రం చుట్టూ సులభంగా తిరిగేటట్లు అమర్చండి.
2. ఒక స్ట్రాను 10° కోణరేఖ వెంబడి అమర్చుము.
3. ఈ కోణమానిని పటం (బి) లో చూపినట్లు పారదర్శక పాత్రలో గల నీటిలో సగం వరకు ముంచుము.
4. కోణమానిని నీటిలో ముంచినపుడు 10° కోణరేఖ వద్ద ఉంచిన స్ట్రా నీటిలో మునిగి ఉండేటట్లు జాగ్రత్త వహించాలి.
5. పాత్ర పై భాగం నుండి నీటిలో మునిగి ఉన్న స్ట్రాను చూస్తూ, నీటి బయట – ఉన్న స్ట్రాను లోపల ఉన్న స్ట్రాతో సరళరేఖలో ఉండే విధంగా అమర్చుము.
6. తరువాత కోణమానిని నీటి నుండి బయటకు తీసి రెండు స్ట్రాలను పరిశీలించుము.
7. పరిశీలించగా రెండూ ఒకే సరళరేఖలో లేవని గుర్తించవచ్చును.
8. రెండవ ‘కు, లంబానికి మధ్య కోణాన్ని కొలవండి.
9. పట్టికలో i, r విలువలు నమోదు చేయండి.
   
10. ప్రయోగంలో పతనకోణం 48°లను మించకుండా i, r విలువలకు వక్రీభవన గుణకాలను కనుగొనుము.
11. నీటి నుండి గాలిలోకి కాంతి ప్రయాణించేటపుడు ప్రతి సందర్భంలోనూ r విలువ 1 విలువ కన్నా ఎక్కువ ఉంటుందని గమనించవచ్చును.
12. దీనినిబట్టి సాంద్రతర యానకం నుండి విరళయానకంలోకి కాంతి ప్రయాణించేటప్పుడు లంబానికి దూరంగా వంగుతుందని, r > i అని చెప్పవచ్చును.

ప్రశ్న 9.
ప్రకాశవంతమైన ఒక లోహపు గోళాన్ని తీసుకొని, కొవ్వొత్తి నుండి వచ్చే మసితో గోళాన్ని నల్లగా చేయండి. ఆ గోళాన్ని నీటిలో ముంచండి. ఆ గోళం ఎలా కనిపిస్తుంది? ఎందుకు? (AS2)
జవాబు:

1. ప్రకాశవంతమైన లోహపు గోళాన్ని కొవ్వొత్తి నుండి వచ్చు మసితో నల్లగా మార్చుము.
2. ఈ లోహపు గోళాన్ని నీటిలో ఉన్న పాత్రలో ముంచుము.
3. ఈ సందర్భంలో నీటికి, మసికి మధ్య ఒక ఖాళీ పటంలో చూపినట్లుగా, ఏర్పడును.
4. ఇక్కడ ఏర్పడిన ఖాళీ విరళయానకంగానూ, నీరు సాంద్రతర యానకంగానూ పనిచేయును.
5. కాంతికిరణం నీటి గుండా ఆ ఖాళీ వైపునకు ప్రయాణించును.
6. ఏ సందర్భంలోనైతే పతనకిరణము కన్నా సందిగ్ధ కోణము ఎక్కువ అగునో అప్పుడు సంపూర్ణాంతర పరావర్తనం జరుగును.
7. ఈ సంపూర్ణాంతర పరావర్తనం వలన కాంతిగోళం మెరయును.
8. అదే విధంగా కాంతి వక్రీభవనం వలన కూడా గోళం మిథ్యా ప్రతిబింబాన్ని ఏర్పరచి కొంత ఎత్తులో కనపడును. దాని అసలు పరిమాణం కన్నా ఎక్కువ పరిమాణంతో కూడా వక్రీభవనము కనపడును.

ప్రశ్న 10.
కృత్యం – 7ను మరలా చేయండి. నీటి సందిగ్ధ కోణాన్ని మీరు ఎలా కనుగొంటారు? కనుగొనే పద్ధతిని వివరించండి. (AS3)
జవాబు:

1. ఒక స్థూపాకార పారదర్శక పాత్రను తీసుకొనుము.
2. ఆ పాత్ర అడుగున ఒక నాణాన్ని ఉంచుము.
3. పటంలో చూపిన విధంగా ఆ నాణెం ప్రతిబింబం నీటి ఉపరితలంపై కనబడేంత వరకు ఆ పాత్రలో నీరు పోయుము.
4. బీకరు ప్రక్క భాగం నుండి నీటి ఉపరితలాన్ని చూడండి.
5. నీరు పోయకముందు నాణెం కనిపించదు. కాని నీరు పోసిన తరువాత నాణెం కనిపిస్తుంది.
6. దీనికి కారణము కాంతి సంపూర్ణాంతర పరావర్తనము.
7. నీటి వక్రీభవన గుణకం = 1.33
   

ప్రశ్న 11.
ఆప్టికల్ ఫైబర్స్ పనిచేసే విధానాన్ని వివరించే సమాచారాన్ని సేకరించండి. మన నిత్యజీవితంలో ఆప్టికల్ ఫైబర్స్ ఉపయోగాల గురించి ఒక నివేదిక తయారుచేయండి. (AS4)
(లేదా)
ఆప్టికల్ ఫైబర్స్ ఏ విధముగా పనిచేయునో, మనదైనందిన జీవితంలో వాటి ఉపయోగాలను తెలుపు సమాచారాన్ని సేకరించి, నివేదికను చూపుము.
(లేదా)
ఆప్టికల్ ఫైబర్స్ అంటే ఏమిటి ? దాని పనిచేయు విధానమును వర్ణించుము.
జవాబు:
పనిచేయు విధానము :
ఆప్టికల్ ఫైబర్స్ సంపూర్ణాంతర పరావర్తనంపై ఆధారపడి పనిచేస్తాయి.

1. ఆప్టికల్ ఫైబర్ అనునది గాజు లేదా ప్లాస్టిక్ తో తయారు చేయబడిన అతి సన్నని తీగ.
2. ఇటువంటి సన్నని తీగలు కొన్ని కలిసి లైట్ పైప్ గా ఏర్పడతాయి.

పనిచేయు విధానం :

1. ఆప్టికల్ ఫైబర్ లో కాంతి ప్రయాణించే విధానాన్ని పక్క పటం వివరిస్తుంది.
2. ఆప్టికల్ ఫైబర్ యొక్క అతి తక్కువ వ్యాసార్ధం వల్ల దానిలోకి ప్రవేశించు కాంతి, దాని లోపలి గోడలకు తగులుతూ పతనం చెందుతుంది.
3. పతనకోణం సందిగ్ధ కోణం కన్నా ఎక్కువ ఉండడం వల్ల సంపూర్ణాంతర పరావర్తనం జరుగుతుంది.
4. తద్వారా ఆప్టికల్ ఫైబర్ గుండా కాంతి ప్రయాణిస్తుంది.
5. ఆ కాంతి పొట్ట లోపలి భాగాన్ని ప్రకాశవంతంగా చేస్తుంది.
6. ఆ లోపలి కాంతి, లైట్ పైపులోని మరికొన్ని ఆప్టిక్ ఫైబర్స్ ద్వారా బయటకు వస్తుంది.
7. ఆ ఫైబర్స్ రెండవ చివర నుండి వచ్చు కాంతిని పరిశీలించడం ద్వారా పొట్ట లోపలి భాగాల చిత్రాన్ని పరిశీలకులు తెలుసుకుంటారు.

ఉపయోగాలు :

1. మానవ శరీరంలోని కంటితో చూడలేని లోపలి అవయవాలను లేపరోస్కోపీ, ఎండోస్కోపీల ద్వారా పరీక్ష చేస్తారు.
2. గుండెలోని రక్త ప్రసరణను కొలుచుటలో,
3. పీడనాన్ని మరియు ఉష్ణోగ్రతను కొలవడంలో వాడే “సెన్సార్స్”లలో,
4. వివిధ రకాల ద్రవాల యొక్క వక్రీభవన గుణకాలను కనుగొనుటలో,
5. సమాచార సంకేతాలను ప్రసారం చేయుటకు ఈ ఆప్టికల్ ఫైబర్ లను విరివిగా వాడతారు.

ప్రశ్న 12.
గాజు దిమ్మెలో కాంతి వక్రీభవనం చెందే విధానాన్ని పటం గీసి, వివరించండి. (ప్రయోగశాల కృత్యం – 2) (AS5)
(లేదా)
గాజు దిమ్మె గుండా కాంతి పార్శ్వ విస్థాపనం కనుగొనే ప్రయోగశాల కృత్య విధానాన్ని వ్రాయండి.
జవాబు:
ఉద్దేశ్యం :
గాజుదిమ్మెను ఉపయోగించి పార్శ్వవిస్థాపనం అవగాహన చేసికొనుట.

కావలసిన వస్తువులు :
డ్రాయింగ్ బోర్డు, డ్రాయింగ్ చార్టు, క్లాంట్లు, స్కేలు, పెన్సిల్, పలుచని గాజుదిమ్మె మరియు గుండుసూదులు.

నిర్వహణ పద్దతి :

1. డ్రాయింగ్ బోర్డుపై డ్రాయింగ్ చార్టును ఉంచి దానికి క్లాంట్లు పెట్టుము.
2. డ్రాయింగ్ చార్టు మధ్య భాగంలో గాజు దిమ్మెను ఉంచి, చార్టుపై దిమ్మె దాని అంచువెంబడి ‘పెన్సిల్ లో గీత , గీయుము. ఇది దీర్ఘచతురస్రంలో ఉంటుంది.
3. ఈ దీర్ఘచతురస్ర శీర్షాలకు A, B, C, D అని పేర్లు పెట్టుము.
   
4. దీర్ఘచతురస్రం పొడవులలో ఒక దానికి (AB) ఏదైనా బిందువు వద్ద ఒక లంబరేఖను గీయుము.
5. మరలా గాజు దిమ్మెను యథాస్థానంలో ఉంచుము.
6. రెండు గుండుసూదులను మీరు గీసిన లంబంపై నిలువుగా ఒకే ఎత్తులో గుచ్చుము.
7. మరో రెండు గుండుసూదులను తీసుకొని గాజు దిమ్మెకు రెండోవైపు నుండి చూస్తూ మొదటి రెండు గుండుసూదులతో ఒకే సరళరేఖలో ఉండు విధంగా గుచ్చుము.
8. గాజు దిమ్మెను, గుండుసూదులను తీసివేసి గుండుసూదుల వల్ల ఏర్పడిన గుర్తులను కలుపుతూ AB వరకు గీత గీయుము.
9. గాజు దిమ్మె ఉపరితలంపై లంబంగా పతనమైన కాంతి కిరణం ఎటువంటి విచలనం పొందకుండా గాజు దిమ్మె రెండోవైపు నుండి బయటకు వస్తుంది.
10. ఇప్పుడు మరొక డ్రాయింగ్ చార్టును కార్డుబోర్డు షీట్ పై ఉంచి అది కదలకుండా క్లాంట్లు పెట్టుము. పై విధంగానే గాజు దిమ్మె అంచును తెలిపే ABCD దీర్ఘచతురస్రాన్ని, AB లంబాన్ని గీయుము.
11. ఈ లంబంతో 30° కోణం చేస్తూ, లంబం మరియు AB రేఖలు కలిసే బిందువును చేరే విధంగా మరొక రేఖను గీయుము. ఇది పతన కిరణాన్ని సూచిస్తుంది. లంబంతో ఈ రేఖ చేసే కోణం పతనకోణం అగును.
12. ఇప్పుడు గాజు దిమ్మెను ABCD దీర్ఘచతురస్రంలో ఉంచుము. పతనకిరణంపై రెండు గుండుసూదులను నిలువుగా, ఒకే ఎత్తులో గుచ్చుము.
13. గాజు దిమ్మె యొక్క రెండోవైపు నుండి చూస్తూ మొదటి రెండు గుండుసూదులతో సరళరేఖలో ఉండే విధంగా మరో . రెండు గుండుసూదులను దిమ్మెకు రెండోవైపు గుచ్చుము.
14. ఈ గుండుసూదుల గుర్తులను కలుపుతూ CD వరకు రేఖను గీయుము. ఈ రేఖ బహిర్గత కాంతికిరణాన్ని తెలుపును.
15. ఈ బహిరత కిరణం CD ని తాకే బిందువు వద్ద, CD రేఖకు ఒక లంబంను గీయుము.
16. ఆ లంబానికి, బహిర్గత కిరణానికి మధ్య కోణాన్ని కొలువుము. దీనినే “బహిర్గత కోణం” అంటాము.
17. ఈ పతన, బహిరత కోణాలు సమానము. ఈ పతన, బహిరత రేఖలు సమాంతరాలు. ఈ రెండు సమాంతర రేఖల మధ్య దూరాన్ని “పార్శ్వ విస్థాపనం” అంటాం.

ప్రశ్న 13.
వజ్రం ప్రకాశించడానికి కారణమేమిటి? ఇందులో ఇమిడి ఉన్న అంశాన్ని మీరెలా అభినందిస్తారు? (AS6)
(లేదా)
ఏ కారణం చేత వజ్రము ప్రకాశించును? దీని తయారీకి కారణమైన పదార్థ స్వభావంను నీవు ఏ విధంగా అభినందిస్తావు?
జవాబు:

1. వజ్రం యొక్క సందిగ్ధ కోణము విలువ చాలా తక్కువ (24.49).
2. కావున వజ్రంలోనికి ప్రవేశించిన కాంతి సంపూర్ణాంతర పరావర్తనం చెందును.
3. ఈ లక్షణం వలన వజ్రం ప్రకాశించును.
4. వజ్రమును కోసినపుడు పతనకోణం, సందిగ్ధకోణం కన్నా ఎక్కువై సంపూర్ణాంతర పరావర్తనం పదేపదే జరుగును.
5. అనగా వజ్రంలోకి ప్రవేశించిన కాంతి సులభంగా సంపూర్ణాంతర పరావర్తనం చెంది వజ్రం మిరుమిట్లు గొలిపే కాంతిలో ప్రకాశవంతంగా మెరయును.

ప్రశ్న 14.
కిరణ చిత్రాలను గీయడంలో ‘ఫెర్మాట్ సూత్రం’ ప్రాముఖ్యతను మీరెలా అభినందిస్తారు? (AS6)
(లేదా)
“ఫెర్మాట్ సూత్రంను ఆధారంగా చేసుకొని కిరణ చిత్రాలను గీయగలము”, ఈ విధముగా ఉపయోగపడు ఫెర్మాట్ సూత్రం ప్రాముఖ్యతను అభినందించుము.
జవాబు:

1. కాంతి ఫెర్మాట్ సూత్రంపై ఆధారపడి ప్రసరించును.
2. కాంతి యొక్క ఫలితాలను, దాని ధర్మాలను క్లుప్తంగా వివరించుటకు కిరణ చిత్రాలు ఉపయోగపడతాయి.
3. కిరణ చిత్రాలను గీయడంలో ఫెర్మాట్ సూత్రం ఇమిడి ఉంటుంది.
4. ఈ విధముగా కొన్ని దృక్ సాధనాల పనితీరును పూర్తిగా తెలుసుకొనుటకు ఫెర్మాట్ సూత్రం ఎంతో ఉపయోగపడినందున ఇది అభినందనీయమైంది.

ప్రశ్న 15.
మనం చలిమంట కాచుకుంటున్నప్పుడు మంట వెనుక భాగాన ఉన్న వస్తువులు స్వల్పంగా ఊగుతున్నట్లుగా కనిపిస్తాయి. కారణం ఏమిటి? (AS7)
(లేదా)
ఏదైనా మంట వద్ద ఉన్నప్పుడు మనకు అభిముఖంగా (వ్యతిరేకంగా లేదా మంట వెనుక) ఉన్న వస్తువులు కదులుతున్నట్లు
(లేదా) ఊగుతున్నట్లుగా కనిపించుటకు గల కారణంను వివరించుము.
జవాబు:

1. చలిమంట కాచుకుంటున్నప్పుడు ఉష్ణం బహిర్గతమగును.
2. ఈ బహిర్గతమైన ఉష్ణము చుట్టుప్రక్కల గల పరిసరాలలోనికి ప్రసారమగును.
3. దీని ద్వారా గాలి యొక్క దృశ్య సాంద్రత పదేపదే మారుతూ ఉండును. కావున దాని యొక్క వక్రీభవన గుణకం కూడా మారును.
4. ఈ విధమైన సాంద్రత మరియు వక్రీభవన గుణకాల నిరంతర మార్పు వలన పరావర్తన కోణము మరియు విస్థాపన విలువలు మారును.
5. అందుకనే మంట వెనుక ఉన్న వస్తువులు స్వల్పంగా కదులుతున్నట్లు మన కంటికి కనిపించుచుండును.

ప్రశ్న 16.
నక్షత్రాలు ఎందుకు మిణుకుమిణుకుమంటాయి? (AS7)
(లేదా)
నక్షత్రాలు మిణుకు మిణుకుమనుటకు గల కారణంను వివరింపుము.
జవాబు:

1. వాతావరణం యొక్క వక్రీభవనం వలన నక్షత్రాలు మిణుకు మిణుకుమంటాయి.
2. వాతావరణం యొక్క వక్రీభవన గుణకపు మార్పుల వలన వక్రీభవనం జరుగును.
3. నక్షత్రం నుండి వచ్చిన కాంతి విరళ యానకం లేక శూన్యం నుండి సాంద్రతర యానకం (వాతావరణం) లోనికి ప్రయాణించుట వలన, లంబానికి దూరంగా ప్రయాణించుట వలన దాని స్థానం నుండి కొద్దిగా దూరంగా గాని, దగ్గరగా గాని కనిపించును.
4. అందువలన పరావర్తనం కొన్నిసార్లు సరిగా జరిగి, కొన్నిసార్లు సరిగా జరగక మిణుకుమిణుకుమని ప్రకాశిస్తాయి.

ప్రశ్న 17.
ఒకే ఆకారంలో తయారుచేయబడిన గాజుముక్క వజ్రాలలో వజ్రం ఎక్కువగా మెరుస్తుంది. ఎందుకు? (AS7)
(లేదా)
ఒకే ఆకృతిలో గల గాజు ముక్క వజ్రాలలో ఎక్కువగా వజ్రం మెరయుటకు గల కారణంను వివరింపుము.
జవాబు:

1. వజ్రం యొక్క సందిగ్ధ కోణము విలువ 24.4°. అనగా చాలా తక్కువ.
2. వజ్రంలోకి ప్రవేశించిన అన్ని కాంతి కిరణములు సంపూర్ణాంతర పరావర్తనం చెంది వజ్రం ప్రకాశవంతంగా మెరయును.
3. గాజు యొక్క సందిగ్ధ కోణం విలువ 42° అనగా వజ్రం విలువ కన్నా ఎక్కువ.
4. వజ్ర రూపంలో కత్తిరించబడిన గాజులోనికి ప్రవేశించిన కాంతి కిరణాలు చాలా తక్కువ సంఖ్యలో మాత్రమే సంపూర్ణాంతర పరావర్తనం చెందుట వలన వజ్రం కంటే గాజు తక్కువగా మెరయును.

ప్రశ్న 18.
నీటి పరమ వక్రీభవన గుణకం 4/8. అయిన నీటి సందిగ్ధ కోణం ఎంత?
జవాబు:
నీటి పరమ వక్రీభవన గుణకం = 4/3

ప్రశ్న 19.
ఒక గాజు పాత్రలో సగం వరకు గ్లిజరిన్ పోయండి. తరువాత దాని నిండుగా నీరు నింపండి. ఈ పాత్రలో క్వార్ట్ గాజుకడ్డీని ఉంచండి. పాత్ర ప్రక్కభాగం నుండి గాజుకడ్డీని పరిశీలించండి.
ఎ) మీరు ఏం మార్పులు గమనించారు?
బి) ఈ మార్పులకు కారణాలేమై ఉంటాయి?
జవాబు:

ఎ) ఈ కృత్యంలో పాత్ర ప్రక్క భాగం నుండి గాజుకడ్డీని పరిశీలించిన, గ్లిజరిన్ లో మునిగిన గాజుకడ్డీ యొక్క భాగం కనిపించదు. అందువలన గాజుకడ్డీ నీటి పై తేలుతున్నట్లుగా కనిపించును. నీటిలోని గాజుకడ్డీ భాగము కనిపించును.
బి) గాజుకడ్డీ యొక్క భాగం మనకు కనిపించదు. దీనికి కారణం గాజుకడ్డీ మరియు గ్లిజరిన్స్ యొక్క వక్రీభవన గుణకాలు సమానం మరియు వాటిలో కాంతి గ్లిజరిన్ వేగాలు కూడా సమానం కావున కాంతి పరావర్తన ప్రక్రియ జరగదు.

ప్రశ్న 20.
కింది యానకాల వక్రీభవన గుణకాల విలువలను సేకరించండి.
నీరు, కొబ్బరినూనె, ఫ్లింట్ గాజు, వజ్రం, బెంజీన్, హైడ్రోజన్ వాయువు.
జవాబు:

ప్రశ్న 21.
థర్మాకోల్ షీట్ తో 2 సెం.మీ., 3 సెం.మీ., 4 సెం.మీ.,. 4.5 సెం.మీ, 5 సెం.మీ. మొదలగు వ్యాసార్ధాలు కలిగిన వృత్తాకార ముక్కలను తయారు చేయండి. ప్రతిదానికి కేంద్రాన్ని గుర్తించండి. అన్ని వృత్తాలకు కేంద్రం వద్ద 6 సెం.మీ. పొడవు గల సూదిని గుచ్చండి. ఒక వెడల్పాటి అపారదర్శక పాత్రలో నీటిని తీసుకొని, 2 సెం.మీ. వ్యాసార్ధం గల థర్మాకోల్ ముక్కను పటంలో చూపిన విధంగా సూది నీటిలో ఉండేటట్లుగా అమర్చండి. ఆ సూది రెండవ చివరను పాత్ర పై నుండే చూడడానికి ప్రయత్నించండి.

1) సూది కొనను మీరు చూడగలిగారా? ఎందుకు?
వేర్వేరు వ్యాసార్ధాలను కలిగిన మిగతా థర్మాకోల్ వృత్తాలతో ఈ ప్రయోగాన్ని మళ్ళీ చేయండి. సూది కొనభాగాన్ని చూడడానికి ప్రయత్నించండి.
గమనిక : ప్రతి సందర్భంలోనూ థర్మాకోల్ వృత్తం యొక్క స్థానం, మీ కంటి స్థానం మారకుండా జాగ్రత్త వహించండి.
2) ఏయే వ్యాసార్ధాలు కలిగిన వృత్తాలకు ఉంచిన సూదుల కొనలను మీరు చూడలేకపోయారు? వాటిలో తక్కువ వ్యాసార్ధం విలువ ఎంత?
3) కొన్ని సూదుల కొనలను మీరు చూడలేకపోవడానికి కారణమేమిటి?
4) యానకం యొక్క సందిగ్ధ కోణాన్ని కనుగొనడానికి మీకు ఈ కృత్యం సహాయపడిందా?
5) వివిధ సందర్భాలలో సూది కొన నుండి కాంతి ప్రయాణాన్ని తెలిపే చిత్రాలను గీయండి.
జవాబు:
ఈ ప్రయోగంను సాధించుటకు కాంతి యొక్క సంపూర్ణాంతర పరావర్తన ధర్మం ఉపయోగపడును.

ఇచ్చిన వృత్తాకార ముక్కలనుపయోగించి సూది మొనను చూచుటకు ఆ ముక్కల వ్యాసార్ధంను కనుగొనవలెను.

1. అవును, సూదిమొనను చూడగలిగాను. ఎందుకనగా గరిష్ఠ వ్యాసార్ధం కన్నా ఇచ్చిన వ్యాసార్ధము తక్కువ కావటం చేత.
2. గరిష్ఠ వ్యాసార్ధానికి సమానమైన వ్యాసార్ధం గల వృత్తంకు ఉంచిన సూదిమొనను చూడలేకపోయాను.
3. కారణమేమనగా వస్తువు నుండి వచ్చు కాంతి కిరణాల పతనకోణం కన్నా సందిగ్ధకోణం విలువ ఎక్కువై సంపూర్ణాంతర పరావర్తనం చెందటం వలన సూదికొనను చూచుట సాధ్యపడలేదు.
4. అవును, సందిగ్ధకోణంను కల్గొనగలము.
   గాలి యొక్క వక్రీభవన గుణకం విలువ = 1.003 = n₂
   నీటి యొక్క వక్రీభవన గుణకం విలువ = 1.33 = n₁

ప్రశ్న 22.
టేబుల్ పై ఒక వస్తువును ఉంచండి. దానిని ఒక గాజు దిమ్మెగుండా చూస్తే ఆ వస్తువు మీకు చేరువుగా కనిపిస్తుంది. ఈ సందర్భంలో కాంతికిరణ ప్రయాణాన్ని వివరించే కిరణ చిత్రాన్ని గీయండి.
జవాబు:

పై పటంలో O – వస్తు స్థానం
O’ – ప్రతిబింబ స్థానం (లేదా) దృశ్యస్థానం
y- వస్తు, ప్రతిబింబ స్థానమార్పిడి

ప్రశ్న 23.
గాలి – ఒక ద్రవం వేరు చేయబడే తలం వద్ద కాంతి కిరణం 45° కోణంతో పతనమై 30° కోణంతో వక్రీభవనం పొందింది. ఆ ద్రవం వక్రీభవనగుణకం ఎంత? వక్రీభవన కిరణం, పరావర్తన కిరణం మధ్య కోణం 90° ఉండాలంటే కాంతి ఎంత కోణంతో పతనం చెందాలి?
జవాబు:

ప్రశ్న 24.
ఒక పాత్రలోని నీటిలో నిర్దిష్ట కోణంతో ముంచబడిన పరీక్ష నాళికను (పరీక్షనాళికలోకి నీరు చేరరాదు) ఒక ప్రత్యేక స్థానం నుండి చూసినప్పుడు, పరీక్షనాళిక గోడ అద్దం వలె కనిపిస్తుంది. దీనికి కారణమేమిటో వివరించగలరా?
జవాబు:

1. పరీక్షనాళిక యొక్క ఉపరితలం నీటిని మరియు గాలిని వేరుచేస్తుంది.
2. పరీక్షనాళికపై కాంతికిరణము పతనమైనపుడు అది సంపూర్ణాంతర పరావర్తనం చెంది వెనుదిరిగి అదే యానకంలోకి ప్రవేశించును.
3. ఒక ప్రత్యేక స్థానం నుండి చూసినప్పుడు పరీక్షనాళిక గోడ అద్దంవలె కనిపించుటకు సంపూర్ణాంతర పరావర్తనమే కారణము.

ప్రశ్న 25.
ఏ సందర్భాల్లో కాంతి కిరణం యానకాలను వేరుచేసే తలం వద్ద విచలనం పొందదు?
(లేదా)
రెండు యానకాలను వేరు చేయు తలం వద్ద ఏ సందర్భాల్లో కాంతి కిరణం విచలనం చెందదు?
జవాబు:
కాంతి కిరణం క్రింది సందర్భాలలో ఎటువంటి విచలనం పొందదు.

ఖాళీలను పూరించండి

1. సందిగ్ధ కోణం వద్ద వక్రీభవన కోణం విలువ ………… (90)
2. n₁ sin i = n₂ sin r ను ……………….. అంటాం. (స్నెల్ నియమం)
3. శూన్యంలో కాంతివడి విలువ ………… (3 × 10⁸ మీ/సె)
4. సంపూర్ణాంతర పరావర్తనం జరగాలంటే కాంతి కిరణం ……………….యానకం నుండి ……….. యానకంలోనికి ప్రయాణించాలి. (సాంద్రతర, విరళ)
5. ఒక పారదర్శక పదార్థ వక్రీభవన గుణకం 3/2. ఆ యానకంలో కాంతివడి ……………. (2 × 10⁸ మీ/సె)
6. ఎండమావులు ……………………… కు ఒక ఉదాహరణ. (సంపూర్ణాంతర పరావర్తనం)

సరైన సమాధానాన్ని ఎన్నుకోండి

1. కింది వాటిలో స్నెల్ నియమం …..
(లేదా)
స్నెల్ నియమాన్ని తెలుపు సమీకరణం

జవాబు:
C

2. గాలి పరంగా గాజు వక్రీభవన గుణకం 2. గాజు – గాలి కలిసే తలం యొక్క సందిగ్ధ కోణం …
A) 0°
B) 45°
C) 30°
D) 60°
జవాబు:
C) 30°

3. సంపూర్ణాంతర పరావర్తనం జరగాలంటే కాంతి …….. లోకి ప్రయాణించాలి.
A) విరళ యానకం నుండి సాంద్రతర యానకం
B) విరళ యానకం నుండి విరళ యానకం
C) సాంద్రతర యానకం నుండి విరళ యానకం
D) సాంద్రతర యానకం నుండి సాంద్రతర యానకం
జవాబు:
C) సాంద్రతర యానకం నుండి విరళ యానకం

4. గాజు దిమ్మె వల్ల కాంతి పొందే విచలన కోణం …….. .
A) 0°
B) 20°
C) 90°
D) గాజు దిమ్మెతలానికి గీసిన లంబంతో కాంతికిరణం చేసే కోణంపై ఆధారపడి ఉంటుంది.
జవాబు:
D) గాజు దిమ్మెతలానికి గీసిన లంబంతో కాంతికిరణం చేసే కోణంపై ఆధారపడి ఉంటుంది.

పరికరాల జాబితా

పింగాణీ పాత్ర, ఐదు రూపాయిల నాణెం, నీరు, తెల్లని డ్రాయింగ్ ‘షీట్, కార్డు బోర్డు షీట్, కోణమానిని, అర్ధవృత్త ఆకారపు గాజు పలక, రెండు స్ట్రాలు, వృత్తాకారపు కోణమానిని, నీరు, 1 లీ. గాజు బీకరు, క్లాంపు, స్కేలు, పలుచని గాజు దిమ్మె, గుండు సూదులు.

10th Class Physical Science 3rd Lesson సమతల ఉపరితలాల వద్ద కాంతి వక్రీభవనం Textbook InText Questions and Answers

10th Class Physical Science Textbook Page No. 60

ప్రశ్న 1.
ఎండమావి నిలిచి ఉన్న నీరులా ఎందుకు కనిపిస్తుంది?
జవాబు:

1. ఆకాశం నుండి లేదా ఎత్తైన చెట్టు నుండి వచ్చే కాంతి “పై నుండి క్రిందకు సాంద్రత మారుతున్నటువంటి గాలి” గుండా ప్రయాణిస్తూ రోడ్డుకు దగ్గరగా వచ్చినపుడు వక్రీభవనానికి లోనై సంపూర్ణాంతర పరావర్తనం వల్ల పటంలో చూపినట్లుగా వక్రమార్గంలో ప్రయాణిస్తుంది.
2. ఈ వక్రీభవన కాంతి పటంలో చూపిన మార్గంలో పరిశీలకున్ని చేరుతుంది.
3. ఆ కాంతి నేలపై పరావర్తనం చెంది వస్తున్నట్లుగా పరిశీలకునికి కనిపిస్తుంది.
4. ఇలా జరగడం వల్లనే ఆకాశం యొక్క మిథ్యా ప్రతిబింబం, రోడ్డుపై నీళ్ళవలె కనబడుతుంది.

ప్రశ్న 2.
ఎండమావిని మీరు ఫోటో తీయగలరా?
జవాబు:
ఎండమావి ఒక మిథ్యా ప్రతిబింబం కావున దీనిని ఫోటో తీయలేము.

10th Class Physical Science Textbook Page No. 47

ప్రశ్న 3.
ఒక పాత్రలోని నీటిలో పడవేసిన నాణెం ఆ పాత్ర అడుగు భాగం నుండి పైకి కొంత ఎత్తులో కనబడటం మీరు గుర్తించి ఉంటారు కదా! అదేవిధంగా ఒక గాజు గ్లాసులోని నీటిలో ఉంచిన నిమ్మకాయ పరిమాణం పెరిగినట్లు కనబడుతుంది. కాగితంపై రాసిన అక్షరాలపై ఒక మందపాటి గాజుపలకనుంచి చూస్తే ఆ అక్షరాలు కాగితంపై నుండి కొంత ఎత్తులో కనబడతాయి. ఈ విధమైన మార్పులకు కారణమేమై ఉంటుంది?
జవాబు:
ఈ విధమైన మార్పులకు కారణము కాంతి యొక్క వక్రీభవన లక్షణమే.

10th Class Physical Science Textbook Page No. 49

ప్రశ్న 4.
వక్రీభవన కిరణాల ప్రవర్తనకు, కాంతి వేగాలకు ఏదైనా సంబంధం ఉందా?
జవాబు:

1. వక్రీభవన కాంతి వేగము యానకము నుండి యానకమునకు మారును.
2. సాధారణ కాంతి వేగములో యానకము మారినప్పటికీ ఎట్టి మార్పుండదు.

10th Class Physical Science Textbook Page No. 51

ప్రశ్న 5.
వివిధ పదార్థ యానకాల వక్రీభవన గుణకాలు వేర్వేరుగా ఎందుకుంటాయి?
జవాబు:
వక్రీభవన గుణకము పదార్థ స్వభావంపై ఆధారపడును. అందుకనే వివిధ పదార్థాల యానకాల వక్రీభవన గుణకాలు వేర్వేరుగా ఉంటాయి.

ప్రశ్న 6.
ఒక యానకం యొక్క వక్రీభవన గుణకం ఏ అంశాలపై ఆధారపడుతుంది?
జవాబు:
వక్రీ. “కం పదార్థ స్వభావం, ఉపయోగించిన కాంతి తరంగదైర్ఘ్యంపై ఆధారపడి ఉంటుంది.

10th Class Physical Science Textbook Page No. 54

ప్రశ్న 7.
పతనకోణానికి, వక్రీభవన కోణానికి మధ్య సంబంధాన్ని తెలిపే సూత్రాన్ని మనం ఉత్పాదించగలమా?
జవాబు:
అవును ఉత్పాదించగలము. కాంతి పతన కోణానికి, వక్రీభవన కోణానికీ మధ్యగల సంబంధమును తెలుపు సూత్రము
n₁ sin i = n₂ sin r

10th Class Physical Science Textbook Page No. 56

ప్రశ్న 8.
వక్రీభవన కోణం 90° అయ్యే సందర్భం ఉంటుందా? అది ఎప్పుడు అవుతుంది?
జవాబు:
అవును, పతన కోణము, సందిగ్ధ కోణముకు సమానమైన సందర్భంలో వక్రీభవన కోణం 90° అగును.

10th Class Physical Science Textbook Page No. 57

ప్రశ్న 9.
సందిగ్ధకోణం కంటే పతనకోణం ఎక్కువైనప్పుడు కాంతి కిరణం ఏమవుతుంది?
జవాబు:
సందిగ్ధకోణం కన్నా పతన కోణం ఎక్కువైనపుడు యానకాలను వేరుచేసే తలం వద్ద కాంతి కిరణం తిరిగి సాంద్రతర యానకంలోకే పరావర్తనం చెందును.

10th Class Physical Science Textbook Page No. 61

ప్రశ్న 10.
కాంతి ప్రసార మార్గంలో ఒక గాజుదిమ్మెను అడ్డుగా ఉంచితే ఏం జరుగుతుంది?
జవాబు:
కాంతి ప్రసారమార్గంలో గాజు దిమ్మెనుంచిన కాంతి రెండుసార్లు వక్రీభవనం చెందును.

10th Class Physical Science Textbook Page No. 49

ప్రశ్న 11.
పటం (ఎ), (బి) పటాలలోని వక్రీభవన కిరణాలలో మీరు ఏం తేడా గమనించారు?

జవాబు:
పటం – (ఎ) లో కాంతి కిరణము లంబము వైపుగా వంగినది.
పటం – (బి) లో కాంతి కిరణము లంబము నుండి దూరముగా వంగినది.

10th Class Physical Science 3rd Lesson సమతల ఉపరితలాల వద్ద కాంతి వక్రీభవనం Textbook Activities

కృత్యములు

కృత్యం – 1

• ఒక గాజు గ్లాసులోని నీటిలో పెన్సిల్ ఉంచినపుడు నీ పరిశీలనలు వ్రాయుము.
జవాబు:

1. ఒక గాజు గ్లాసులో కొంత నీటిని తీసుకొనుము.
2. దీనిలో ఒక పెన్సిల్ ను ఉంచుము.
3. గ్లాసు పై భాగం నుండి, ప్రక్క భాగం నుండి పెన్సిల్ ను గమనించగా దాని స్థానంలో మార్పు ఉండును.
4. పెన్సిల్ ను పై భాగం నుండి గమనించగా అది వంగినట్లుగా కనబడును.

కృత్యం – 2

కాంతి వక్రీభవనాన్ని తెలిపే కృత్యాన్ని రాయండి.
జవాబు:

1. సూర్యుని ఎండపడుతున్న ఒక పొడవైన గోడ వద్దకు మీరు, మీ స్నేహితుడు వెళ్ళండి.
2. గోడ ఒక చివర వద్ద మీరు నిల్చొని, మరొక చివర వద్ద ప్రకాశవంతమైన ఒక లోహపు వస్తువును చేతిలో పట్టుకొనమని మీ స్నేహితునికి చెప్పండి.
3. గోడకు కొద్ది అంగుళాల దూరంలో ఆ లోహపు వస్తువున్నప్పుడు వస్తువు మసకబారినట్లుగా కనబడుతుంది.
4. గోడ అద్దం వలె ప్రవర్తిస్తున్నట్లుగా దానిపై లోహపు వస్తువు ప్రతిబింబము కనబడుతుంది.
5. కాంతి వక్రీభవనం చెందడం వలన గోడపై ఆ లోహపు వస్తువు యొక్క ప్రతిబింబం కనబడును.

కృత్యం – 3

కాంతి ఒక యానకం నుండి మరొక యానకంలోనికి ప్రయాణించునపుడు దాని దిశలో మార్పు ఏ రకంగా వస్తుందో కృత్యం ద్వారా వివరించుము.
(లేదా)
నీటి పాత్ర అడుగుభాగాన ఉన్న నాణెం పైకి కొంత ఎత్తులో కనబడుటను కిరణ చిత్రం ద్వారా చూపుము.
జవాబు:

1. అపారదర్శక పదార్థంతో తయారు చేయబడిన, తక్కువ లోతు కలిగిన పాత్రను తీసుకొనుము.
2. పాత్ర అడుగున నాణెమునుంచుము.
3. ఆ నాణెము మీకు కనపడకుండాపోయే వరకు పాత్ర నుండి వెనుకకు జరుగుము.
4. మీరు అక్కడే నిల్చుని మీ స్నేహితుడిని ఆ పాత్రను నీటితో నింపమనుము.
5. పాత్రను నీటితో నింపితే నాణెం కనబడుతుంది.

పరిశీలన :

1. కాంతి ఋజుమార్గంలో ప్రయాణిస్తుంది అనే అంశం ఆధారంగా నాణెం నుండి మీ కంటికి చేరే కాంతి కిరణ చిత్రం గీయుము.
2. కాంతి కిరణాన్ని పరిశీలిస్తే నీరు, గాలి అనే యానకాలను వేరు చేసే తలం వద్ద కాంతికిరణం తన దిశను మార్చుకుంటుంది.
3. నాణెం నుండి కంటిని చేరడానికి అతి తక్కువ కాలం పట్టేందుకుగాను కాంతి కిరణం ఈ మార్గాన్ని ఎన్నుకుంది.
4. అనగా వివిధ యానకాలలో కాంతి వేగం వేర్వేరుగా ఉంటుంది.
5. ఈ రకంగా కాంతి వక్రీభవనం చెందిందని చెప్పవచ్చును.

కృత్యం – 6

ఒక గాజు గ్లాసు అడుగున ఒక నాణెము నుంచి, గ్లాసు పక్క భాగం నుండి పరిశీలించినపుడు నాణెం కనుమరుగవుతుంది. కారణం తెలపండి.
జవాబు:

1. ఒక టేబుల్ పై నాణాన్ని ఉంచి దానిపై ఒక గాజు గ్లాసును పెట్టుము.
2. గాజు ప్రక్క భాగం నుండి పరిశీలించుము.
3. ఆ నాణెం యొక్క ప్రతిబింబం పూర్వంకన్నా పెద్దగా కనిపిస్తుంది.
4. ఇపుడు ఆ గ్లాసును నీటితో నింపుము.
5. మరల ఆ నాణాన్ని పరిశీలించుము.
6. నాణెం మనకు కనపడదు.
7. దీనికి గల కారణము సంపూర్ణాంతర పరావర్తనము.

కృత్యం – 7

గాజుగ్లాసులోని నీటిలో ఉన్న నాణెం కొంచెం పైకి లేచినట్లు కనబడుతుంది. ఎందుకు?
జవాబు:

1. ఒక స్థూపాకార పారదర్శక పాత్రను తీసుకొనుము.
2. ఆ పాత్ర అడుగున ఒక నాణాన్ని ఉంచుము.
3. ఆ నాణెం యొక్క ప్రతిబింబం నీటి ఉపరితలంపై కనబడేంత వరకు ఆ పాత్రలో నీరు పోయుము.
4. సంపూర్ణాంతర పరావర్తనం వలన నాణెం యొక్క ప్రతిబింబం ఏర్పడుతుంది.

కృత్యం – 8

గాజు దిమ్మె యొక్క వక్రీభవన గుణకాన్ని కనుగొనుటను కృత్యం ద్వారా చూపుము.
(లేదా)
కాంతి వక్రీభవననుపయోగించి ఒక గాజు దిమ్మె యొక్క వక్రీభవన గుణకంను ఏ విధంగా కనుగొనవచ్చునో ప్రయోగపూర్వకంగా తెల్పుము. గాజు దిమ్మె నిలువు విస్థాపనము ద్వారా వక్రీభవనంను కనుగొను ప్రయోగమును వివరింపుము.
జవాబు:

1. గాజు దిమ్మె మందాన్ని కొలిచి మీ నోట్ బుక్ లో రాసుకొనుము.
2. గాజు దిమ్మెను డ్రాయింగ్ చార్టుపై మధ్య భాగంలో ఉంచుము.
3. గాజు దిమ్మె అంచు ABCD దీర్ఘచతురస్రాన్ని గీయుము.
4. AB రేఖకు ఏదేని బిందువు వద్ద లంబాన్ని గీయుము.
5. గాజు దిమ్మెను ABCD దీర్ఘ చతురస్రంలో ఉంచుము.
6. ఒక గుండుసూదిని తీసుకొని, AB రేఖకు గీసిన లంబంపై గాజు దిమ్మె నుండి 15 సెం.మీ. దూరంలో P బిందువు వద్ద ఉంచుము.
7. ఆ గుండుసూదిని గాజు దిమ్మె యొక్క రెండోవైపు నుండి చూస్తూ మరొక గుండుసూదిని మొదటిదానితో ఒకే సరళరేఖలో ఉండునట్లు అమర్చుము.
8. గాజు దిమ్మెను తొలగించి గుండుసూదుల స్థానాన్ని పరిశీలించుము.
9. రెండవ గుండుసూది కొన నుండి మొదటి గుండుసూది ఉంచిన రేఖ పైకి ఒక లంబాన్ని గీయుము.
10. వాటి ఖండన బిందువు Q గా గుర్తించుము.
11. P, Q ల మధ్య దూరాన్ని కొలిచిన, ఇది లంబ విస్థాపనం అగును.
12. గాజు దిమ్మె నుండి గుండుసూది దూరాన్ని మార్చి ఈ ప్రయోగాన్ని మరలా చేయుము.
13. లంబవిస్థాపనం మారదని మనము గుర్తించవచ్చును.
14. గాజు వక్రీభవన గుణకాన్ని క్రింది సూత్రం ద్వారా కనుగొనవచ్చును.

SCERT AP 10th Class Physics Study Material Pdf 1st Lesson ఉష్ణం Textbook Questions and Answers.

AP State Syllabus 10th Class Physical Science 1st Lesson Questions and Answers ఉష్ణం

10th Class Physical Science 1st Lesson ఉష్ణం Textbook Questions and Answers

అభ్యసనాన్ని మెరుగుపరుచుకోండి

ప్రశ్న 1.
20°C ఉష్ణోగ్రత గల 50 గ్రాముల నీటిని, 40°C ఉష్ణోగ్రత గల 50 గ్రాముల నీటికి కలిపితే మిశ్రమం ఫలిత ఉష్ణోగ్రత ఎంత ఉంటుంది? (AS1)
జవాబు:
T₁ = 20°C ; m₁ = 50 గ్రా.
T₂ = 40°C ; m₂ = 50 గ్రా.

∴ మిశ్రమం ఫలిత ఉష్ణోగ్రత = 30°C.

ప్రశ్న 2.
వేసవి రోజుల్లో కుక్కలు నాలుకను బయటకు చాచి ఉంచటానికి (panting) గల కారణాన్ని ‘బాష్పీభవనం’ భావనతో వివరించండి. (AS1)
(లేదా)
కుక్కలు ఏ విధముగా వాటి శరీరమును చల్లబరుచుకుంటాయి? బాష్పీభవనం ప్రక్రియతో వివరించుము.
జవాబు:

1. కుక్కలకు శరీరంపై స్వేదరంధ్రాలు ఉండవు. శరీరం వెంట్రుకలతో నిండి ఉంటుంది. కేవలం పాదాలలో మాత్రమే స్వేద రంధ్రాలు ఉంటాయి.
2. మానవులకు శరీరంపై స్వేదరంధ్రాలు ఉండి, వాటి ద్వారా నీరు బాష్పీభవనం చెందుతుంది.
3. బాష్పీభవనం చెందుట వలన శరీరం ఉష్ణోగ్రత తగ్గి చల్లబడుతుంది.
4. కుక్కలు వేసవిలో నాలుక బయటకు చాచుట వలన నాలుకపై నీరు బాష్పీభవనం చెందుతుంది. తద్వారా శరీర ఉష్ణోగ్రత తగ్గుతుంది.
5. ఈ విధంగా కుక్కలు శరీరాన్ని చల్లబరుచుకుంటాయి.

ప్రశ్న 3.
“కూల్ డ్రింక్” సీసా బయట ఉపరితలంపై తుషారం ఎందుకు ఏర్పడుతుంది? (AS1)
(లేదా)
రాజు ఫ్రిజ్ నుంచి తీసిన కూల్ డ్రింక్ సీసా యొక్క పై భాగమున నీటి తుంపరలు ఏర్పడుటను గమనించెను. ఈ విధముగా ఏర్పడుటకు గల కారణములను వ్రాయుము.
జవాబు:

1. ఫ్రిజ్ నుండి తీసిన కూల్ డ్రింక్ సీసా లాంటి ఘనపదార్థాల ఉష్ణోగ్రతలు తక్కువగా ఉంటాయి.
2. ఈ చల్లటి సీసాలను తాకిన గాలిలోని నీటి ఆవిరి సాంద్రీకరణం చెంది చిన్నచిన్న నీటి బిందువులుగా మారి సీసా ఉపరితలంపై ఏర్పడుతుంది.
3. ఈ చిన్నచిన్న నీటి బిందువులను తుషారం అంటారు.

ప్రశ్న 4.
బాష్పీభవనం, మరగటం మధ్య భేదాలను తెల్పండి. (AS1)
(లేదా)
సీత, ఒక పాత్రలో ఆరుబయట ఉంచబడిన పెట్రోల్ పరిమాణం తగ్గుటను గమనించినది. అదే విధంగా రాము నీటిని వేడి చేస్తున్నపుడు బుడగలు ఏర్పడుటను గమనించినాడు. ఈ రెండు ప్రక్రియలు ఏమిటి? వీటి మధ్యన గల భేదాలను వ్రాయుము.
జవాబు:

ప్రశ్న 5.
నీటి ఆవిరి సాంద్రీకరణం చెందేటప్పుడు పరిసరాలలోని గాలి చల్లబడుతుందా? వేడిగా అవుతుందా? వివరించండి. (AS1)
జవాబు:

1. వాయువు ద్రవంగా స్థితి మార్పు చెందటమే సాంద్రీకరణం.
2. అధిక ఉష్ణోగ్రతలో నీటి ఆవిరి చల్లటి వస్తువులను తాకగానే ప్రతి గ్రాము ద్రవ్యరాశి 540 కేలరీల ఉష్ణశక్తిని విడుదల చేస్తుంది. ఇది ఉష్ణమోచక చర్య.
3. ఇందువల్లనే వేడినీటి కంటే నీటి ఆవిరి మనల్ని ఎక్కువగా గాయపరుస్తుంది.
4. కాబట్టి నీటి సాంద్రీకరణ ఒక ఉద్ధీయ ప్రక్రియ.
5. ఆవిరి సాంద్రీకరణం చెందినప్పుడు పరిసరాలలోని గాలి వేడెక్కుతుంది.

ప్రశ్న 6.
కింది ప్రశ్నలకు సమాధానాలివ్వండి. (AS1)
a) 100°C వద్ద గల 1 గ్రా. నీటి ఆవిరి 100°C గల నీరుగా సాంద్రీకరణం చెందడానికి ఎంత ఉష్ణం బదిలీ కావాలి?
జవాబు:
100°C వద్ద గల 1 గ్రా. నీటి ఆవిరి 100°C గల నీరుగా సాంద్రీకరణం చెందటానికి 540 కేలరీల ఉష్ణం పరిసరాలలోనికి బదిలీ కావాలి.

వివరణ :
మరిగే నీటి ఉష్ణోగ్రత = 1 గ్రా. ; నీటి బాష్పీభవన గుప్తోష్ణం = 540 కేలరీ/గ్రా.
మరిగే నీరు → నీరు
100°C → 100°C

స్థితి మారింది కావున గుప్తోష్ణం పరిగణనలోకి తీసుకుంటే L = \(\frac{Q}{m}\) ⇒ Q = mL =1 × 540 = 540 కేలరీలు.

b) 100°C వద్ద గల 1 గ్రా. నీటి ఆవిరి 0°C గల నీరుగా సాంద్రీకరణం చెందడానికి ఎంత ఉష్ణం బదిలీ కావాలి?
జవాబు:
నీటి ద్రవ్యరాశి = 1 గ్రా. ; . నీటి విశిష్టోష్ణం = 1 cal/g°C
మరిగే నీరు → నీరు 100°C → 0°C
బదిలీ కాబడిన ఉష్ణం Q = mS∆T = 1 × 1 × (100 – 0) = 100 కేలరీలు.

c) 0°C వద్ద గల 1 గ్రా. నీరు, 0°C వద్ద గల మంచుగా మారడానికి ఎంత ఉష్ణం గ్రహింపబడాలి లేదా విడుదలవ్వాలి?
జవాబు:
0°C వద్ద గల 1 గ్రా. నీరు, 0°C వద్ద మంచుగా మారటానికి 80 కేలరీల శక్తి బయటకు విడుదలవ్వాలి.
వివరణ :
నీరు → మంచు
0°C → 0°C
ఉష్ణోగ్రతలో మార్పు లేదు కావున, సాంద్రీకరణ గుప్తోష్ణం ప్రకారం
L = \(\frac{Q}{m}\) ⇒ Q = mL =1 × 80 = 80 కేలరీలు.

d) 100°C వద్ద గల 1 గ్రా. నీటి ఆవిరి, 0°C వద్ద గల మంచుగా మారడానికి ఎంత ఉష్ణం గ్రహింపబడాలి లేదా విడుదలవ్వాలి?
జవాబు:
100°C వద్ద గల 1 గ్రా. నీటి ఆవిరి, 0°C వద్ద మంచుగా మారటానికి 520 కేలరీల శక్తి విడుదల అవ్వాలి.
వివరణ : నీటి ఆవిరి ద్రవ్యరాశి = 1 గ్రా.
నీటి ఆవిరి → నీరు → నీరు → మంచు
100°C → 100°C → 0°C → 0°C

100°C వద్దనున్న నీటి ఆవిరి, 100°C లోనున్న నీరుగా మారడానికి కావలసిన ఉష్ణరాశి
Q₁ = mL = 1 × 540 = 540 కేలరీలు.

100°C వద్దనున్న నీరు, 0°C లోనున్న నీరుగా మారడానికి కావలసిన ఉష్ణరాశి
Q₂ = mS∆T = 1 × 1 × (100 – 0) = 100 కేలరీలు.

0°C వద్దనున్న నీరు, 0°C లోనున్న మంచుగా మారడానికి కావలసిన ఉష్ణరాశి
Q₃ = mL = 1 × 80 = 80 కేలరీలు,

మొత్తం వ్యవస్థలోని ఉష్ణరాశి
Q = Q₁ + Q₂ + Q₃
= 540 + (100) + 80
= 720 కేలరీలు.

ప్రశ్న 7.
ఘనపదార్థ విశిష్టోష్ణాన్ని ప్రయోగపూర్వకంగా కనుగొనే విధానాన్ని వివరించండి. (AS1)
(లేదా)
ఏదైనా ఘనపదార్ధపు విశిష్టోష్ణంను ఏ విధంగా కనుగొంటావో ప్రయోగపూర్వకముగా వివరించుము.
(లేదా)
వంటపాత్రలపై మూతగా ఉపయోగించుటకు ఎక్కువ విశిష్టోషం గల లోహముతో తయారుచేసిన మూతను ఉపయోగించాలని మనోభిరామ్ భావించాడు. దానికొరకు అల్యూమినియం, రాగి లోహాల విశిష్టోష్ణాలను ప్రయోగపూర్వకంగా కనుగొనాలంటే ఏ ఏ పరికరాలు కావాలి? ఆ ప్రయోగాన్ని ఎలా నిర్వహించాలి?
జవాబు:
ఉద్దేశ్యం : ఇచ్చిన ఘనపదార్థాల విశిష్టోష్ణం కనుగొనుట.

కృత్యం :
కావలసిన పరికరాలు :
కెలోరిమీటర్, ఉష్ణమాపకం, మిశ్రమాన్ని కలిపే కాడ, నీరు, నీటి ఆవిరి గది, చెక్కపెట్టె, సీసపు గుళ్లు.

1. కెలోరీ మీటరు ద్రవ్యరాశి = m, gr.
2. కెలోరీ మీటరు విశిష్టోష్ణం = S, కేలరీ/గ్రాం × °C
3. నీటితో సహా కెలోరీ మీటరు ద్రవ్యరాశి = m₂ gr.
4. నీటి ద్రవ్యరాశి = నీటితో సహా కెలోరీ మీటరు ద్రవ్యరాశి – కెలోరీ మీటరు ద్రవ్యరాశి
   నీటి ద్రవ్యరాశి = m₂ – m₁
5. నీటి విశిష్టోష్ణం = S_w కేలరీ/గ్రాం × °C .
6. నీటి తొలి ఉష్ణోగ్రత = T₁ °C
7. సీసపు గుళ్లను తీసుకొని వేడినీటిలో లేదా హిట్ చాంబర్ లో ఉంచి 100°C వరకు వేడి చెయ్యండి.
8. సీసపు గుళ్ల ఉష్ణోగ్రత = T₂°C
9. 
10. నీరు, సీసపు గుళ్లు, కెలోరీ మీటరు ద్రవ్యరాశి = m₃ గ్రా.
11. నీరు, సీసపు గుళ్లు, కెలోరీమీటరు ఉష్ణోగ్రత = T₃°C
12. సీసపు గుళ్ల ద్రవ్యరాశి = m₃ – m₂
13. సీసపు గుళ్లు కోల్పోయిన ఉష్ణరాశి
    Q = m × S× ∆T
    Q₁ = (m₃ – m₂) × S_l × (T₂ – T₃)
14. నీరు గ్రహించిన ఉష్ణరాశి Q₂ = (m₂ – m₁) × S_w × (T₃ – T₁)
15. కెలోరీ మీటరు గ్రహించిన ఉష్ణరాశి Q₃ = m₁ × S_c × (T₃ – T₁)
16. కానీ సీసపు గుళ్లు కోల్పోయిన ఉష్ణం = కెలోరీ మీటరు + నీరు గ్రహించిన ఉష్ణరాశి
    

ప్రశ్న 8.
20°C ను కెల్విన్ మానంలోకి మార్చండి. (AS1)
జవాబు:
కెల్విన్ K = 273 + °C. = 273 + 20 = 293 K

ప్రశ్న 9.
బాష్పీభవనానికి, మరగడానికి గల తేడాను మీ స్నేహితుడు గుర్తించలేకపోయాడు. అతను ఆ తేడాను గుర్తించడానికి కొన్ని ప్రశ్నలు అడగండి. (AS2)
(లేదా)
కుమార్ బాష్పీభవనం, మరగడంలకు తేడాలను గుర్తించలేకపోతున్నానని తన టీచర్ తో చెప్పాడు. అప్పుడు ఆ టీచర్ తనని కొన్ని ప్రశ్నలు అడిగి వాటికి సమాధానాలు రప్పించడం ద్వారా తేడాలను గ్రహించేటట్లు చేశాడు. ఆ టీచర్ కుమారిని అడిగిన ప్రశ్నలేమై ఉంటాయి?
జవాబు:

1. బాష్పీభవనం ఏ ఉష్ణోగ్రత వద్ద జరుగును?
2. నీరు మరగటం ఏ ఉష్ణోగ్రత వద్ద జరుగును?
3. నీటిని వేడిచేసినపుడు ఆవిరిగా మారును ఈ ప్రక్రియను ఏమంటారు?
4. రోడ్ల ప్రక్కన నిల్వ ఉన్న నీరు ఏ ప్రక్రియ వలన ఆవిరగును?
5. తడిబట్టలు ఆరడం ఏ ప్రక్రియ వలన జరుగును?
6. శరీరంపై చెమట ఆరడం ఏ ప్రక్రియ వలన జరుగును?
7. 100°C వద్ద నీరు ఆవిరిగా మారే ప్రక్రియను ఏమంటారు?

ప్రశ్న 10.
తడిబట్టలు పొడిగా మారినప్పుడు వాటిలోని నీరు ఏమవుతుంది? (AS3)
జవాబు:
తడిబట్టలు గాలిలో లేదా ఎండలో ఆరబెట్టినపుడు బట్టలలోని నీటి అణువులు నిరంతరం చలిస్తూ అభిఘాతాలు చెందుతాయి. ఈ సందర్భంలో అణువులు శక్తిని వేరొక అణువులకు బదిలీ చేస్తాయి.

బదిలీ చెందిన శక్తి ఉపరితలంలో ఉన్న అణువులకు అందితే ఉపరితలాన్ని వదిలి పైకిపోతాయి. ఈ విధంగా నీరు ఆవిరిగా బాష్పీభవనం చెందును. బట్టలు క్రమేణ పొడిగా మారతాయి. తడిబట్టలను గాలి తగిలే ప్రాంతంలో ఆరబెడితే బాష్పీభవన రేటు వేగంగా జరిగి బట్టలు త్వరగా ఆరిపోతాయి.

ప్రశ్న 11.
ఒక చిన్న మూత, ఒక పెద్ద పాత్రలో ఒకే పరిమాణం గల ద్రవాన్ని ఉంచితే, ఏది త్వరగా బాష్పీభవనం చెందుతుంది? (AS3)
(లేదా)
శ్రీను ఒక పాత్రనందు మరియు వెడల్పు మూతనందు సమాన పరిమాణం గల నీటిని పోసి ఆరుబయట ఉంచెను. అతను గమనించిన విషయమేమి? దీనిని ప్రయోగ పూర్వకంగా వివరింపుము.
జవాబు:

1. ఒక సెకను కాలంలో నీటి అణువులు ఆవిరిగా మారే సంఖ్యను బాష్పీభవన రేటు అంటారు.
2. బాష్పీభవనరేటు పాత్ర యొక్క ఉపరితల వైశాల్యానికి, ఉష్ణోగ్రతకు, అర్ధతకు అనులోమానుపాతంలో ఉండును.
3. కాబట్టి చిన్న మూతలో, పెద్ద పాత్రలో ఒకే పరిమాణం గల ద్రవాన్ని ఉంచినా పెద్ద పాత్రలోని ద్రవమే త్వరగా బాష్పీభవనం చెందును.

ప్రశ్న 12.
బాష్పీభవనం అనేది ద్రవ ఉపరితలం, పరిసరాలలో ఉన్న గాలిలోని ద్రవభాష్పం వంటి అంశాలపై ఆధారపడుతుందని నిరూపించడానికి ఒక ప్రయోగాన్ని సూచించండి. (AS3)
జవాబు:

1. ఒక పరీక్షనాళిక, పింగాణీ పాత్రలో విడివిడిగా 5 మి.లీ. నీటిని తీసుకోండి.
2. రెండింటిని తిరుగుతున్న ఫ్యాన్ క్రింద ఉంచండి.
3. మరొక పింగాణీ పాత్రలో 5 మి.లీ. నీటిని తీసుకొని దానిని బీరువాలో ఉంచండి.
4. గది ఉష్ణోగ్రతను నమోదు చెయ్యండి.
5. మూడు సందర్భాలలో నీరు బాష్పీభవనానికి పట్టిన కాలాన్ని నమోదు చెయ్యండి.
6. వర్షం కురిసిన రోజున కూడా ఇదే కృత్యం నిర్వహించండి. పరిశీలన నమోదు చెయ్యండి.
7. ఫ్యాన్ క్రింద ఉంచిన పింగాణీ పాత్రలో నీరు బాష్పీభవనం చెందటం మనం గమనిస్తాం.
8. కారణం పరీక్షనాళిక కంటే పింగాణీ పాత్ర యొక్క ఉపరితల వైశాల్యం ఎక్కువ.
9. బాష్పీభవనం ఉపరితల దృగ్విషయం. ఉపరితల వైశాల్యం పెరిగితే ఎక్కువ కణాలు బాష్పంగా మారే అవకాశం ఏర్పడుతుంది.
10. బాష్పీభవనం మరొక అంశం ఆర్థత.
11. గాలిలోని తేమశాతాన్ని అర్థత అంటారు.
12. పరిసరంలోని గాలి నిర్దిష్ట పరిమాణం మేరకు మాత్రమే నీటి బాష్పాన్ని నిలిపి ఉంచుకోగలుగుతుంది.
13. గాలిలో నీటి బాష్పం అనగా ఆర్ధత ఎక్కువ ఉంటే బాష్పీభవన వేగం తగ్గుతుంది.
14. ఇందువల్ల తడిబట్టలు వర్షాకాలంలో నెమ్మదిగానూ, గాలి వేగంగా వీచే రోజులలో వేగంగానూ ఆరతాయి.

ప్రశ్న 13.
అంచు కలిగిన ఒక పళ్లెంలో నీరు పోసి అందులో ఒక గరాటును బోర్లించండి. గరాటు అంచు పూర్తిగా పళ్లానికి ఆని ఉండకుండా, గరాటును ఒక వైపు నాణెంపై ఉంచండి. ఈ పళ్లాన్ని బర్నర్ పై ఉంచి నీరు మరగడం ప్రారంభించే వరకు వేడిచేయండి. మొదట ఎక్కడ బుడగలు ప్రారంభమయ్యాయి? ఎందుకు? ఈ ప్రయోగ పరిశీలన ఆధారంగా గీజర్ (వేడినీటి ఊట) పనిచేసే విధానాన్ని మీరు వివరించగలరా? (AS4)
జవాబు:

1. అంచు కలిగిన పళ్లెంలో నీరుపోసి అందులో ఒక గరాటును ఉంచండి.
2. గరాటు యొక్క అంచు పూర్తిగా పళ్లానికి ఆనకుండా ఒక నాణెంపై ఉంచండి.
3. పళ్లాన్ని బర్నర్‌పై ఉంచి నీరు మరిగే వరకు వేడి చెయ్యండి.
4. ఉషాన్ని మొదట పళ్ళెం గ్రహించి, నీటికి అందించును.
5. నీరు ఉష్ణరాశిని గ్రహించును. నీటిలో ఉష్ణప్రసారం సంవహన పద్ధతిలో జరుగును.
6. అనగా ఉష్ణాన్ని గ్రహించిన నీటి అణువులు తేలికై బుడగల రూపంలో నీటి పైకి చేరును. పైన చల్లగా ఉన్న నీటి అణువులు నీటి అడుగుకు చేరును. ఈ విధంగా అణువులు చక్రీయంగా తిరుగుతూ ఉష్ణాన్ని గ్రహిస్తాయి.
7. గరాటు-నాణెం విషయానికి వస్తే నాణెం దగ్గర నీటి బుడగలు తక్కువగా ఉంటాయి. నాణేనికి దూరంలో నీటి బుడగలు ప్రారంభమవుతాయి.
8. కారణం నీరు బాష్పీభవనం చెందటానికి కావలసిన ఉష్ణరాశి అందదు. ఎక్కువ ఉష్ణాన్ని లోహంతో తయారైన నాణెం గ్రహిస్తుంది.
9. గీజర్ లో హీటింగ్ కాయిల్ దగ్గర ఉన్న నీటి అణువులు ఉష్ణాన్ని గ్రహించి దూరంగా పోతాయి.
10. తక్కువ ఉష్ణోగ్రత ఉన్న నీటి అణువులు హీటింగ్ కాయిల్ దగ్గరకు చేరుతాయి.
11. హీటింగ్ కాయిల్ నుండి ఉష్ణప్రసారం సంవహన పద్ధతిలో జరుగును.

ప్రశ్న 14.
వేసవి, శీతాకాలాల్లో వాతావరణ ఉష్ణోగ్రత దాదాపు స్థిరంగా ఉండడంలో నీటి విశిష్టోష్ణం పాత్రను మీరెలా అభినందిస్తారు? (AS6)
జవాబు:
నీటికి విశిష్టోష్ణం విలువ ఎక్కువగా ఉండుట వలన వేసవిలో పగటిపూట నీటి ఉష్ణోగ్రత పెరగదు. కాని భూమి ఉష్ణోగ్రత అమాంతం పెరిగి భూమిపై గాలి వేడెక్కి వ్యాకోచం చెంది సాంద్రత తగ్గును. కావున సముద్రపు చల్లగాలులు భూమి వైపునకు వ్యాపించి వాతావరణాన్ని చల్లబరుచును.

1. శీతాకాలంలో రాత్రిళ్లు భూమి, నీటికంటే త్వరగా ఉష్ణాన్ని కోల్పోయి చల్లబడును. సముద్రంలో నీరు ఎక్కువ ఉష్ణోగ్రతతో ఉండి పరిసరాలలోని గాలి వేడెక్కి వ్యాకోచించి సాంద్రత తగ్గును. కావున భూమిపై శీతల పవనాలు సముద్రం వైపునకు ప్రయాణించును.
2. ఈ విధంగా భూమి యొక్క వాతావరణాన్ని నీరు సమతుల్యం చేస్తుంది.
3. నీటికి గల అధిక విశిష్టోష్ణం వలన నీరు త్వరగా ఉష్ణాన్ని కోల్పోదు. అందువలన చలి ప్రదేశాలలో రబ్బరు బాటిల్స్ లో నీటిని నింపి బెడ్ క్రింద ఉంచుతారు.
4. గదులు వెచ్చగా ఉంచటానికి పైపులలో వేడినీటిని సరఫరా చేస్తారు.
5. థర్మల్ పవర్ స్టేషన్లలో నీటి విశిష్టోష్ణం అధికంగా ఉండుటవలన శీతలీకరణిగా వాడతారు.

ఈ విధంగా అనేక రకాలుగా ఉపయోగపడుతూ వాతావరణాన్ని సమతుల్యం చేస్తుంది కాబట్టి మనం నీటిని తప్పక అభినందించవలసి యున్నది.

ప్రశ్న 15.
ఫ్రిజ్ నుండి బయటకు తీసిన ‘పుచ్చకాయ’ ఎక్కువ సమయం పాటు చల్లగా ఉండటంలో విశిష్టోష్ణం పాత్రను వివరించండి. (AS7)
జవాబు:

1. సాధారణంగా పుచ్చకాయలో అధికశాతం నీరు ఉండును.
2. పదార్థాలన్నింటిలో విశిష్టోష్ణం విలువ నీటికి గరిష్ఠంగా ఉండును.
3. అనగా ఎక్కువ విశిష్టోష్ణం ఉన్న పదార్థాలు ఉష్ణోగ్రత పెరుగుదలను వ్యతిరేకిస్తాయి. అనగా చల్లదనాన్ని కొనసాగిస్తాయి.
4. అందువల్ల పుచ్చకాయ ఎక్కువ సమయం పాటు చల్లదనాన్ని నిలిపి ఉంచుకుంటుంది.

ప్రశ్న 16.
మీరు చల్లని నీటితో స్నానం చేసినా, స్నానం తర్వాత స్నానాల గదిలో అలాగే ఉంటే వేడిగా అనిపిస్తుంది. ఎందుకు? (AS7)
జవాబు:

1. స్నానాల గదిలో ప్రమాణ ఘనపరిమాణంలోని నీటి ఆవిరి అణువుల సంఖ్య, స్నానాల గది బయట ప్రమాణ ఘన పరిమాణంలోని నీటిఆవిరి అణువుల సంఖ్య కంటే ఎక్కువ.
2. మనం కండువాతో శరీరాన్ని తుడుచుకున్నప్పుడు మన చుట్టూ ఉన్న నీటి ఆవిరి అణువులు చర్మంపై సాంద్రీకరణం చెందుతాయి.
3. సాంద్రీకరణం ఉష్ణాన్ని విడుదల చేసే ప్రక్రియ.
4. కనుక మన శరీరం వెచ్చగా అనిపిస్తుంది.

ప్రశ్న 17.
A అనే వస్తువు 30°C వద్ద, B అనే వస్తువు 303 K వద్ద, C అనే వస్తువు 420K వద్ద కలవు. ఈ మూడు వస్తువులు ఉయ స్పర్శలో ఉన్నట్లయితే,
1) A, B, C లలో ఏ రెండు వస్తువులు ఉష్ణ సమతాస్థితిలో కలవు?
2) A, B, C లలో ఏ రెండు వస్తువుల మధ్య ఉష్ణ ప్రసారం జరుగుతుంది?
జవాబు:
1) 303K = 273K + 30K = 0°C + 30°C = 30°C.
∴ A మరియు B వస్తువులు ఉష్ణ సమతాస్థితిలో కలవు.

2) A మరియు B వస్తువులకు, C వస్తువు నుండి ఉష్ణ ప్రసారం జరుగుతుంది.

ఖాళీలను పూరించండి

1. విశిష్టోష్ణానికి S.I. ప్రమాణం ………… (J/kg – K)
2. అధిక ఉష్ణోగ్రత వద్ద గల వస్తువు నుండి అల్ప ఉష్ణోగ్రత వద్ద గల వస్తువుకు ……………. ప్రవహిస్తుంది. (ఉష్ణం)
3. …………. అనేది ఒక శీతలీకరణ ప్రక్రియ. (బాష్పీభవనం)
4. 10°C వద్ద గల A అనే వస్తువును, 10K వద్ద గల B అనే వస్తువుతో ఉష్ట్రీయ స్పర్శలో ఉంచితే ఉష్ణం …………. నుండి ………… కు ప్రవహిస్తుంది. (10°C నుండి 100)
5. మంచు ద్రవీభవన గుప్తోష్ణం విలువ …………….. (80 కెలోరీలు/గ్రాం)
6. వస్తువు ఉష్ణోగ్రత ……………………… కు అనులోమానుపాతంలో ఉంటుంది. (కణాల సరాసరి గతిజశక్తికి)
7. మిశ్రమాల పద్ధతి సూత్రం ప్రకారం వేడివస్తువులు కోల్పోయిన ఉష్ణం = ……………… (చల్లని వస్తువులు గ్రహించిన ఉష్ణం)
8. వేసవి రోజుల్లో ఉక్కపోతకు కారణం ……….. (ఆర్ధత ఎక్కువ లేదా అధిక నీటి బాష్పం)
9. …………. ను శీతలీకరణిగా వాడతాం. (నీటిని)
10. నీటిపై మంచు తేలడానికి కారణం ……………………. (సాంద్రత తగ్గడం)

సరైన సమాధానాన్ని ఎన్నుకోండి

1. కింది వాటిలో ఏది ఉద్ధీకరణ ప్రక్రియ (warming process)?
A) బాష్పీభవనం
B) సాంద్రీకరణం
C) మరగడం
D) పైవన్నీ
జవాబు:
B) సాంద్రీకరణం

2. A, B మరియు C అనే వస్తువులు ఉష్ణ సమతాస్థితిలో ఉన్నాయి. B యొక్క ఉష్ణోగ్రత 45°C అయిన, C యొక్క ఉష్ణోగ్రత …………..
A) 45°C
B) 50°C
C) 40°C
D) 90°C
జవాబు:
A) 45°C

3. ఒక స్టీలు కడ్డీ ఉష్ణోగ్రత 330 K. దాని ఉష్ణోగ్రత °C పరంగా
A) 55°C
B) 57°C
C) 59°C
D) 53°C
జవాబు:
B) 57°C

4. విశిష్టోష్ణం S = ………..
A) Q/∆T
B) Q∆T
C) Q/m∆r
D) m∆T/Q
జవాబు:
C) Q/m∆r

5. సాధారణ వాతావరణ పీడనం వద్ద నీటి మరుగుస్థానం ……….
A) 0°C
B) 100°C
C) 110°C
D) -5°C
జవాబు:
B) 100°C

6. ద్రవీభవనం చెందేటప్పుడు మంచు ఉష్ణోగ్రత
A) స్థిరంగా ఉంటుంది
B) పెరుగుతుంది
C) తగ్గుతుంది
D) చెప్పలేము
జవాబు:
A) స్థిరంగా ఉంటుంది

పరికరాల జాబితా

చెక్కముక్క, లోహపు ముక్క గాజు గ్లాసులు, రెండు ఉష్ణ మాపకములు, వేడినీరు, కొబ్బరి నూనె, రెండు బీకర్లు, మూత, రెండు స్టాండులు, రెండు పరీక్ష నాళికలు, పెద్ద జాడీ, రబ్బరు బిరడా, సారాయి దీపం, కెలోరిమీటర్, మిశ్రమాన్ని కలిపే షర్రర్, నీటి ఆవిరి గది, చెక్కపెట్టె, సీసపు గుళ్ళు లేదా 50 గ్రా. ఇనుప బోల్ట్, డ్రాపర్, పేట్రిడిష్ లేదా వాచ్ గ్లాస్, స్పిరిట్, బున్సెన్ బర్నర్, ఫుడ్ కలర్ లేదా పొటాషియం పర్మాంగనేట్.

10th Class Physical Science 1st Lesson ఉష్ణం Textbook InText Questions and Answers

10th Class Physical Science Textbook Page No. 2

ప్రశ్న 1.
ఉష్ణోగ్రత అంటే ఏమిటి?
జవాబు:
చల్లదనం, వెచ్చదనం స్థాయిని ఉష్ణోగ్రత అంటారు. దీనిని T తో సూచిస్తారు.

10th Class Physical Science Textbook Page No. 2

ప్రశ్న 2.
ఉష్ణం, ఉష్ణోగ్రతకు తేడా ఏమిటి?
జవాబు:

ప్రశ్న 3.
గీజర్ (geiser) పనిచేసే విధానాన్ని తెలియచేసే సమాచారాన్ని సేకరించి, ఒక నివేదికను తయారుచేయండి.
జవాబు:

1. విద్యుచ్ఛక్తిని, యాంత్రిక శక్తిగా మార్చే పరికరాన్ని గీజర్ అంటారు.
2. దీనిలో హీటింగ్ కాయిల్ అమర్చబడి ఉండును. ఇది నీటికి కావలసిన ఉష్ణోగ్రతను అందించును.
3. దీనికి రెండు పైపు మార్గాలు ఉండును. మొదటి పైప్ లైన్ చల్లటి నీటిని గీజర్ లోనికి పంపించటానికి ఉపయోగపడును.
4. రెండవ పైప్ లైన్ వేడినీటిని బయటకు పంపించును.
5. గీజర్ లోని హీటింగ్ ఎలిమెంట్ కు థర్మోస్టాట్ ను అమర్చుతారు.
6. ఈ థర్మోస్టాట్ కొంతవరకు మాత్రమే ఉష్ణోగ్రత పెరిగేలా కంట్రోల్ చేయబడును.
7. గీజర్ ట్యాంక్ నుండి ఉష్ణం వికిరణ రూపంలో బయటకు పోకుండా ఉండటానికి ఉష్ణబంధక పదార్థమైన గాజు, ఉన్నితో సీల్ చేస్తారు.
8. గీజర్ ను లోహపు స్థూపాకార పాత్రలో ఉంచి గోడకు బిగించటానికి అనువుగా తయారుచేస్తారు.

ప్రశ్న 4.
-5°C వద్ద గల రెండు కి.గ్రా. మంచుకు నిరంతరంగా ఉష్ణాన్ని అందిస్తున్నామనుకోండి. 0°C వద్ద మంచు కరుగుతుందని, 100°C వద్ద నీరు మరుగుతుందని మీకు తెలుసు. మంచు నీరుగా మారి, మరగడం ప్రారంభించేవరకు వేడిచేస్తూనే ఉండండి. ప్రతి నిమిషానికి ఉష్ణోగ్రత నమోదు చేయండి. మీరు పొందిన సమాచారంతో ఉష్ణోగ్రత, కాలానికి మధ్య గ్రాఫ్ గీయండి. గ్రాఫ్ ద్వారా మీరు ఏం తెలుసుకున్నారు? మీ నిర్ధారణలు రాయండి.
జవాబు:

1. – 5°C ఉన్న మంచుగడ్డ 0°C వద్ద కరుగుట ప్రారంభమైంది.
2. A బిందువు అనగా 0°C వద్ద మంచు కరుగుట ప్రారంభమైంది. దీనిని ద్రవీభవన స్థానం అంటారు.
3. B, C బిందువుల మధ్య ఉష్ణోగ్రత స్థిరంగా ఉంది అనగా మంచు నీరుగా మారేవరకు ఉష్ణం ఎంత అందించిన ఉష్ణోగ్రతలో మార్పులేదు. దీనినే ద్రవీభవన గుప్తోష్ణం అంటారు.
4. B, C బిందువుల మధ్య అందించిన ఉష్ణం మంచు కరిగి నీరుగా మారడానికి అనగా స్థితి మార్చటానికి మాత్రమే ఉపయోగపడింది.
5. C, D ల మధ్య నీటి ఉష్ణోగ్రత క్రమేణ 100°C వరకు పెరిగింది. అంటే నీరు బాష్పీభవనం చెందుతుంది.
6. D బిందువు వద్ద నీరు 100°C కి చేరుకుంది.
7. దీనినే నీటి మరుగు ఉష్ణోగ్రత అంటారు.
8. D, E ల మధ్య అందించిన ఉష్ణం నీటి స్థితిని మార్చటానికి మాత్రమే ఉపయోగపడింది. కానీ ఉష్ణోగ్రత పెరగలేదు. దీనినే బాష్పీభవన గుప్తోష్ణం అంటారు.
9. F బిందువు వద్ద నీరు పూర్తిగా ఆవిరయింది. దీనినే నీటి ఆవిరి అంటారు.

ప్రశ్న 3.
1 లీ. నీటికి కొంతసేపు ఉష్ణాన్ని అందిస్తే దాని ఉష్ణోగ్రత 2°C పెరిగిందనుకుందాం. అంతే ఉష్ణాన్ని అంతే సమయం పాటు 2 లీ. నీటికి అందిస్తే ఆ నీటి ఉష్ణోగ్రతలో పెరుగుదల ఎంత ఉంటుంది?
జవాబు:

∴ నీటి ఉష్ణోగ్రత 1°C పెరుగును.

10th Class Physical Science 1st Lesson ఉష్ణం Textbook Activities

కృత్యములు

కృత్యం – 1

ప్రశ్న 1.
ఉష్ణసమతాస్థితిని ఒక కృత్యం ద్వారా వివరించుము.
(లేదా)
ఉష్ణోగ్రత అను పదంను ఉదాహరణతో వివరింపుము.
(లేదా)
వెచ్చదనం లేక చల్లదనం యొక్క తీవ్రతను దేనితో పిలుస్తారు? దీని పరిమాణంను ఉదాహరణతో వివరింపుము.
(లేదా)
ఉష్ణోగ్రత నిర్వచనాన్ని వివరించే కృత్యాన్ని రాయండి.
జవాబు:

1. ఒక చెక్కముక్కను, ఒక లోహపు ముక్కను తీసుకొని వాటిని ఫ్రిజ్ లేదా ఐస్ బాక్స్ లో 15 నిమిషాలు ఉంచి, బయటకు తీయవలెను.
2. ఇప్పుడు చెక్కముక్కను, లోహపు ముక్కను తాకి ఏది చల్లగా ఉందో గమనించవలెను.
3. ఫ్రిజ్ నుండి బయటకు తీసినప్పుడు చెక్కముక్క ఉష్ణోగ్రత కంటే లోహపు ముక్క ఉష్ణోగ్రత తక్కువగా ఉందని గమనిస్తాము.
4. ఒక వేడి వస్తువును, ఒక చల్లని వస్తువును ఒకదానికొకటి తాకే విధముగా ఉంచినప్పుడు ఏమి జరుగుతుందో గమనించవలెను.
5. వేడి వస్తువు నుండి చల్లని వస్తువుకు ఉష్ణశక్తి బదిలీ అవుతుందని గమనిస్తాము.
6. వేడి వస్తువు నుండి చల్లని వస్తువుకు ఉష్ణశక్తి ఎప్పటి వరకు బదిలీ అవుతుందో గమనించవలెను.
7. ఆ రెండు వస్తువులు ఒకే వెచ్చదనం తీవ్రత లేదా చల్లదనం తీవ్రత పొందే వరకు ఈ ఉష్ణశక్తి బదిలీ కొనసాగుతుందని గమనిస్తాము.
8. పై పరిశీలన నుండి పరిసరాల నుండి వెచ్చదనం లేదా చల్లదనం అనుభూతిని పొందకపోతే, శరీరం పరిసరాల వాతావరణంతో ఉష్ణ సమతాస్థితిలో ఉంటుందని తెలుస్తుంది.

కృత్యం – 2

ప్రశ్న 2.
ఉష్ణ నిర్వచనాన్ని వివరించే కృత్యాన్ని రాయండి.
జవాబు:

1. రెండు గాజు గ్లాసులను తీసుకొని ఒకదానిని వేడినీటితో, మరొక దానిని చల్లని నీటితో నింపవలెను.
2. ఒక ఉష్ణమాపకాన్ని తీసుకొని వేడి నీటిలో ఉంచినప్పుడు పాదరసమట్టము ఎలా ఉంటుందో గమనించవలెను.
3. పాదరసమట్టంలో పెరుగుదలను గమనిస్తాము.
4. చల్లని నీటిలో ఉంచినప్పుడు పాదరసమట్టము ఎలా ఉంటుందో గమనించవలెను.
5. పాదరసమట్టంలో తగ్గుదలను గమనిస్తాము.
6. ఉష్ణమాపకానికి, నీటికి మధ్య ఉష్ణ సమతాస్థితి ఏర్పడితే పాదరసమట్టము ఎలా ఉంటుందో గమనించవలెను.
7. పాదరసమట్టము నిలకడగా ఉంటుందని గమనిస్తాము.
8. ఈ కృత్యం ద్వారా ఉష్ణాన్ని క్రింది విధంగా నిర్వచించవచ్చు.
9. ఉష్ణం : అధిక ఉష్ణోగ్రత గల వస్తువు నుండి అల్ప ఉష్ణోగ్రత గల వస్తువుకు ప్రవహించే శక్తి స్వరూపాన్ని ‘ఉష్ణం’ అంటారు.

కృత్యం – 3 ఉష్ణం మరియు గతిజశక్తి

ప్రశ్న 3.
ఉష్ణం మరియు గతిజశక్తుల మధ్య గల సంబంధాన్ని వివరించే కృత్యాన్ని రాయండి.
(లేదా)
ఒక పదార్థం యొక్క అణువుల సగటు గతిశక్తి, దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉండునని చూపు కృత్యమును వ్రాయుము.
(లేదా)
ఒక వస్తువు యొక్క ఉష్ణోగ్రత, దాని సగటు గతిశక్తికి సూచన అని నిరూపించు కృత్యం వ్రాయుము.
జవాబు:

1. రెండు గాజు పాత్రలను తీసుకొని ఒకదానిని వేడినీటితో, మరొక దానిని చల్లని నీటితో నింపవలెను.
2. రెండు పాత్రల నీటి ఉపరితలాలపై ఫుడ్ కలర్ చల్లి, ఆ కణాల కదలికను గమనించవలెను.
3. చల్లని నీటిలోని కణాల కంటే వేడినీటిలోని కణాలు వేగంగా కదులుతున్నాయని గమనిస్తాము.
4. ఆ రెండు పాత్రలలోని నీటి గతిశక్తులు వేరువేరుగా ఉన్నందున కణాల కదిలికల వేగాలు కూడా వేరువేరుగా ఉన్నాయి.
5. పై పరిశీలన ద్వారా అణువుల సరాసరి గతిజశక్తి చల్లని వస్తువులో కంటే వేడి వస్తువులో ఎక్కువగా ఉంటుందని తెలుస్తుంది.
6. కనుక ఒక వస్తువు యొక్క ఉష్ణోగ్రత దానిలోని అణువుల సరాసరి గతిజశక్తిని సూచిస్తుంది.

∴ “ఒక వస్తువులోని అణువుల సరాసరి గతిజశక్తి దాని పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుంది”.

కృత్యం – 4

ప్రశ్న 4.
రెండు వేరువేరు ఉష్ణోగ్రతలు గల ద్రవాల మధ్య ప్రసరించే గతిజశక్తిని వివరించే కృత్యాన్ని రాయండి.
లేదా
వేడి వస్తువు నుండి చల్లని వస్తువుకు ఉష్ణ ప్రసారం జరుగుతుందని ప్రయోగ పూర్వకముగా తెలుపదానికి కావలసిన పరికరాల జాబితాను, ప్రయోగంను వ్రాయుము.
(లేదా)
ఉష్ణమాపకం ఉష్ణం ఏ దిశలో ప్రవహించును? దీనిని ప్రయోగ పూర్వకంగా వ్రాయుము.

జవాబు:

1. ఒక పాత్రలో నీటిని తీసుకొని 60°C వరకు వేడి చేయవలెను.
2. ఒక స్థూపాకార పారదర్శక గాజు జాడీని తీసుకొని దానిలో సగం వరకు నీటిని నింపవలెను.
3. గాజు జాడీ అంచుల వెంబడి జాగ్రత్తగా నీటి తలంపై కొబ్బరినూనేను పోయవలెను.
4. రెండు రంధ్రాలు గల మూతను ఉంచవలెను.
5. రెండు ఉష్ణమాపకాలను ఒకటి నీటిలో, మరొకటి నూనెలో మునిగి ఉండేటట్లుగా రంధ్రాలలో అమర్చవలెను.
6. ఉష్ణమాపకాల రీడింగులను గమనించగా నూనెలో ఉంచిన ఉష్ణమాపకం రీడింగ్ పెరుగుతూ, నీటిలో ఉంచిన ఉష్ణమాపకం. రీడింగు తగ్గుతూ ఉంటుంది.
7. దీనికి కారణం నీటి అణువుల సరాసరి గతిజశక్తి తగ్గుతుంటే, నూనె అణువుల సరాసరి గతిజశక్తి పెరుగుతుంది.
8. అంటే నీటి ఉష్ణోగ్రత తగ్గుతుండగా నూనె ఉష్ణోగ్రత పెరుగుతుంది.

కృత్యం – 5

ప్రశ్న 5.
ఉష్ణోగ్రత పెరుగుదల రేటు పదార్థ స్వభావంపై ఆధారపడి ఉంటుందనే కృత్యాన్ని వివరించండి.
జవాబు:

1. ఒక పెద్ద జాడీలో నీటిని తీసుకొని 80°C వరకు వేడి చేయవలెను.
2. ఒకే పరిమాణం గల రెండు పరీక్షనాళికలను తీసుకొని ఒక దానిలో 50 గ్రాముల నీటిని, మరొక దానిలో 50 గ్రాముల నూనెను పోయవలెను.
3. రబ్బరు బిరడాల సహాయంతో రెండు పరీక్షనాళికలలో రెండు ఉష్ణమాపకాలను అమర్చవలెను.
4. ప్రతి 3 నిమిషాలకు ఒకసారి ఉష్ణమాపకాల రీడింగులను గమనించవలెను.
5. రెండు పరీక్షనాళికలు ఒకే ఉష్ణోగ్రత గల నీటిలో సమాన కాలవ్యవధులలో ఉంచబడినవి.
6. కాబట్టి నీరు, నూనెలకు ఒకే పరిమాణం గల ఉష్ణం సమకూర్చబడి ఉండాలి.
7. కాని నూనె ఉష్ణోగ్రత పెరుగుదల రేటు, నీటి ఉష్ణోగ్రత పెరుగుదల రేటు కంటే ఎక్కువగా ఉంది.
8. కనుక ఉష్ణోగ్రత పెరుగుదల రేటు పదార్థ స్వభావంపై ఆధారపడి ఉంటుంది.

కృత్యం – 6

ప్రశ్న 6.
విశిష్టోష్ణం నిర్వచనాన్ని వివరించే కృత్యాన్ని రాయండి.
(లేదా)
ఒక పదార్థపు ఉష్ణోగ్రతలో పెరుగుదలకు, దాని స్వభావంకు మధ్య గల సంబంధంను తెలుపు కృత్యంను వ్రాయుము.
(లేదా)
పదార్థపు ఉష్ణోగ్రతలో పెరుగుదల రేటు, పదార్థ స్వభావంపై ఆధారపడునని సూచించు ప్రయోగంను వివరింపుము.
(లేదా)
శరీరముపై వేడినీటి కన్నా వేడి నూనె ఎక్కువ ప్రభావంను చూపుటకు గల కారణమును ప్రయోగపూర్వకముగా తెల్పుము.
జవాబు:

1. ఒకే పరిమాణం గల రెండు బీకర్లను తీసుకొని ఒకదానిలో 250 గ్రా. నీటిని, మరొకదానిలో ఒక కిలోగ్రాం నీటిని తీసుకొని ఉష్ణమాపకం సహాయంతో వాటి తొలి ఉష్ణోగ్రతలను గుర్తించండి.
2. వాటి తొలి ఉష్ణోగ్రతలు రెండునూ సమానంగా ఉన్నాయి.
3. బీకర్లలోని నీటి ఉష్ణోగ్రత వాటి తొలి ఉష్ణోగ్రత కంటే 60° పెరిగే వరకు రెండు బీకర్లను వేడిచేసి, రెండు బీకర్లలో నీటి ఉష్ణోగ్రత 60° పెరగడానికి అవసరమైన కాలవ్యవధులను గుర్తించవలెను.
4. ఉష్ణోగ్రత పెరగడానికి 250 గ్రా. నీటితో పోలిస్తే, 1 కి.గ్రా. నీటికి ఎక్కువ సమయం పట్టిందని గమనిస్తాము.
5. ఇప్పుడు ఒక బేకరులో 1 లీటరు నీటిని తీసుకుని వేడిచేసి ప్రతి 2 నిమిషాలకు ఉష్ణోగ్రతలోని మార్పును గుర్తించవలెను.
6. ఉష్ణాన్ని అందించే సమయానికి అనుగుణంగా ఉష్ణోగ్రతలో పెరుగుదల స్థిరంగా ఉంటుంది.
7. దీనిని బట్టి స్థిర ద్రవ్యరాశి గల నీటి ఉష్ణోగ్రతలోని మార్పు అది గ్రహించిన ఉష్ణానికి అనులోమానుపాతంలో ఉంటుంది.
8. విశిష్టోష్ణం : ప్రమాణ ద్రవ్యరాశి గల పదార్థ ఉష్ణోగ్రతను 1°C పెంచడానికి కావలసిన ఉష్ణాన్ని ఆ పదార్థ విశిష్టోష్ణం అంటారు.

కృత్యం – 7

ప్రశ్న 7.
ఒక మిశ్రమము యొక్క అంత్య ఉష్ణోగ్రతను ఏవిధంగా కనుగొనవచ్చును?
(లేదా)
“మిశ్రమముల నియమము” అంటే ఏమిటి? దీనిని ఒక కృత్యం ద్వారా వివరించుము.
జవాబు:
సందర్భం -1:

1. ఒకే పరిమాణంలో ఉండే రెండు బీకరులను తీసుకొని, ఒక్కొక్క దానిలో 200 మి.లీ. నీటిని పోయపలెను.
2. ఈ రెండు బీకర్లలో నీటిని ఒకే ఉష్ణోగ్రత వరకు వేడి చేయవలెను.
3. ఈ రెండు బీకర్లలోని నీటిని వేరొక పెద్ద బీకరులోకి మార్చవలెను.
4. ఈ మిశ్రమ నీటి ఉష్ణోగ్రతలో ఎలాంటి మార్పు ఉండదు.

సందర్భం – 2:

1. ఒక బీకరులోని నీటిని 90° C వరకు, రెండవ బీకరులోని నీటిని 60° C వరకు వేడిచేసి, ఈ నీటిని వేరొక పెద్ద బీకరులో కలపండి.
2. ఈ మిశ్రమ నీటి ఉష్ణోగ్రత 90°C మరియు 60° C ల మధ్య ఉంటుంది.
3. దీనికి కారణం ఉష్ణము 90° C ఉన్న వేడి నీటి నుండి 60° C ఉన్న వేడి నీటిలోనికి ప్రవహించడమే.

సందర్భం – 3:

1. 90°C వద్ద ఉన్న 100 మి.లీ. నీటిని, 60°C వద్ద ఉన్న 200 మి.లీ. నీటిని తీసుకొని వాటిని వేరొక బీకరులోకి కలపండి.
2. ఈ మిశ్రమం ఉష్ణోగ్రత 90°C మరియు 60°C ల మధ్య ఉంటుంది.
3. కాని రెండవ సందర్భంలోని మిశ్రమం ఉష్ణోగ్రత కంటె మూడవ సందర్భంలో మిశ్రమం ఉష్ణోగ్రత తక్కువగా ఉంటుంది.

ప్రశ్న 8.
ఒక ఘనపదార్థం యొక్క విశిష్టోష్ణాన్ని ఎలా కనుగొంటారు?
(లేదా)
ఘనపదార్థ విశిష్టోష్ణాన్ని ప్రయోగపూర్వకముగా కనుగొను విధానాన్ని వివరించుము.
జవాబు:
ఉద్దేశ్యం : ఇచ్చిన ఘనపదార్థ విశిష్టోష్ణాన్ని కనుగొనడం.

కావలసిన వస్తువులు :
కెలోరిమీటర్, ఉష్ణమాపకం, మిశ్రమాన్ని కలిపే కాడ లేదా స్టర్రర్, నీరు, నీటిఆవిరి గది, చెక్కపెట్టె మరియు సీసపుగుళ్ళు లేదా ఇనుపబోల్టు (కనీసం 50గ్రాII).

నిర్వహణ విధానం :

1. స్టర్రర్ తో సహా కెలోరిమీటర్ ద్రవ్యరాశి ‘m₁‘ ను కనుగొనండి.
2. ఇప్పుడు కెలోరిమీటర్ ను 1/3 వంతు వరకు నీటితో నింపవలెను.
3. నీటితో సహా కెలోరిమీటర్ ద్రవ్యరాశి m₂ ను కనుగొనవలెను.
   నీటితో సహా కెలోరిమీటరు ద్రవ్యరాశి m₂ = …………
4. నీటి ద్రవ్యరాశి m₁₂ – m₁ ను కనుగొనవలెను.
5. కెలోరిమీటర్ లోని నీటి ఉష్ణోగ్రత T₁ ను కనుగొనవలెను.
6. కెలోరిమీటర్ మరియు నీటి ఉష్ణోగ్రతలు సమానంగా ఉంటాయి.
7. కొన్ని సీసపు గుళ్ళను తీసుకొని, వేడినీటిలో లేదా స్టీమ్ చాంబర్ లో ఉంచి 100°C వరకు వేడిచేయండి. ఈ ఉష్ణోగ్రతను T₂ అనుకొనవలెను.
8. ఉష్ణనష్టం జరగకుండా, సీసపుగుళ్ళను త్వరగా కెలోరిమీటర్ లోకి మార్చవలెను.
9. కొద్దిసేపటి తర్వాత ఈ మిశ్రమం ఒక స్థిర ఉష్ణోగ్రతకు చేరుతుంది.
10. నీరు, సీసపు గుళ్ళతో సహా కెలోరిమీటర్ ద్రవ్యరాశి m₃ ను కనుగొనవలెను.
11. సీసపు గుళ్ళ ద్రవ్యరాశి m₃ – m₁ ను కనుగొనవలెను.
12. ఇప్పుడు ఫలిత ఉష్ణోగ్రత T₃ ను కనుగొనవలెను.
13. కెలోరీమీటర్, ఘనపదార్ధం, (సీసపుగుళ్ళు) మరియు నీటి విశిష్టోష్ణాలు వరుసగా S_1c, S_l మరియు S_w అనుకొనవలెను.
14. మిశ్రమాల పద్ధతి సూత్రం ప్రకారం …..
    ఘనపదార్థం (సీసపు గుళ్ళు) కోల్పోయిన ఉష్ణం = కెలోరిమీటర్ గ్రహించిన ఉష్ణం + నీరు గ్రహించిన ఉష్ణం
15. (m₃– m₂) S_l (T₂ – T₃) = m₁ S_c (T₃ – T₁) + (m₂ – m₁) S_w (T₃ – T₁)
    ∴ S_l = [m₁S_c + (m₂ – m₁) S_w] (T₃ – T₁)/ (m₃ – m₂) (T₂ – T₃)
16. కెలోరిమీటర్, నీటి విశిష్టోష్టాలు తెలిస్తే, పై సమీకరణంతో ఘనపదార్థం (సీసపుగుళ్ళు) విశిష్టోష్ణాన్ని లెక్కగట్టవచ్చును.

కృత్యం – 8

ప్రశ్న 9.
బాష్పీభవన ప్రక్రియను వివరించే కృత్యాన్ని రాయండి.
(లేదా)
రాజు ఒక పాత్రలో ఆరుబయట ఉంచిన స్పిరిట్ మాయమవుటను గమనించెను. దీనిని వివరించు ప్రయోగము తెలుపుము.
జవాబు:

1. ఒక కప్పులో కొద్దిగా స్పిరిట్ తీసుకొని రెండు లేదా మూడు చుక్కలను అరచేతిలో వేసుకొనవలెను.
2. స్పిరిట్ బాష్పీభవనం చెందడం వలన చర్మం చల్లగా అనిపిస్తుంది.
3. రెండు పెట్టాడిలో సుమారు 1 మి.లీ. స్పిరిట్ ను తీసుకొనవలెను.
4. ఒక పెట్రెడిషను గాలి తగిలే విధంగా, మరొకదానిని గాలి తగలకుండా మూతపెట్టి ఉంచవలెను.
5. 5 నిమిషాల తరువాత పరిశీలించిన గాలికి ఉంచిన పెట్రెడిష్ లోని స్పిరిట్ ఏమి లేకపోవడం, మూత పెట్టిన స్పిరిట్ అలాగే ఉండటం గమనిస్తాము.
6. గాలికి ఉంచిన స్పిరిట్ బాష్పీభవనం చెందడం వలన ఏమీ లేకుండా పోయినది.
7. బాష్పీభవనం : ద్రవ అణువులు ఏ ఉష్ణోగ్రత వద్దనైనా ద్రవ ఉపరితలాన్ని వీడిపోయే ప్రక్రియనే బాష్పీభవనం అంటారు.
8. బాష్పీభవన సమయంలో వ్యవస్థ ఉష్ణోగ్రత తగ్గుతుంది.

కృత్యం – 9 / సాంద్రీకరణం

ప్రశ్న 10.
సాంద్రీకరణాన్ని వివరించే కృత్యాన్ని రాయండి.
(లేదా)
మనోభిరామ్ తన స్నేహితునితో చల్లని రస్నాను గ్లాసులో పోసిన, కొంతసేపటికి దాని బయట వైపు నీటి తుంపరలు ఏర్పడుటను గమనించెనని చెప్పెను. ఈ దృగ్విషయంకు కారణమైన విషయంను ప్రయోగ పూర్వకముగా తెలుపుము.
జవాబు:

1. ఒక గాజుగ్లాసులో సగం వరకు చల్లని నీరు పోయవలెను.
2. గ్లాసు బయటి గోడలపై నీటి బిందువులు ఏర్పడటం గమనిస్తాము.
3. నీటి బిందువులు ఏర్పడటానికి గల కారణం :
   a) చల్లని నీటి ఉష్ణోగ్రత కన్నా, దాని పరిసరాలలోని గాలి. ఉష్ణోగ్రత ఎక్కువగా ఉంటుంది.
   b) గాలిలో ఆవిరి రూపంలో నీటి అణువులుంటాయి.
   c) గాలిలోని నీటి అణువులు చలనంలో ఉన్నప్పుడు, చల్లని నీరు గల గ్లాసు ఉపరితలాన్ని తాకితే అవి తమ గతిశక్తిని కోల్పోతాయి. అందువల్ల వాటి ఉష్ణోగ్రత తగ్గిపోయి నీటి బిందువులుగా మారతాయి.
   d) గాలిలోని నీటి అణువులు కోల్పోయిన శక్తి గాజుగ్లాసు అణువులకు అందజేయబడుతుంది. అందువల్ల గాజు అణువుల సరాసరి గతిజశక్తి పెరుగుతుంది.
   e) ఆ శక్తి గాజు గ్లాసులోని నీటి అణువులకు అందజేయబడుతుంది.
   f) తద్వారా గ్లాసులోని నీటి అణువుల సరాసరి గతిజశక్తి పెరుగుతుంది. కాబట్టి, గ్లాసులోని నీటి ఉష్ణోగ్రత పెరుగుతుంది.
   g) ఈ ప్రక్రియనే సాంద్రీకరణం అంటాం. ఇది ఒక ఉద్ధీకరణ ప్రక్రియ.
4. సాంద్రీకరణం : “వాయువు ద్రవంగా స్థితిమార్పు చెందడమే సాంద్రీకరణం”.

కృత్యం – 10 మరగడం

ప్రశ్న 11.
‘మరగడం’ అనే ప్రక్రియను వివరించే కృత్యాన్ని రాయండి.
(లేదా)
“మరుగుట” అను ప్రక్రియను ఉదాహరణతో వివరింపుము.
(లేదా)
రాజు నీటిని వేడి చేస్తున్నప్పుడు కొన్ని బుడగలు ఉపరితలంపై చేరుటను గమనించెను. ఈ దృగ్విషయంను కృత్యం ద్వారా వివరింపుము.
జవాబు:
1) ఒక బీకరులో నీరుపోసి బర్నరో వేడిచేయవలెను.

2) ప్రతి 2 నిమిషాలకు నీటి ఉష్ణోగ్రతను థర్మామీటర్ సహాయంతో పరిశీలించవలెను. ఇక్కడ మూడు విషయాలను గమనిస్తాము.
a) నీటి ఉష్ణోగ్రత 100°C ని చేరే వరకు నిరంతరం పెరుగుతుందని గమనిస్తాము.
b) 100°C తరువాత ఇంకా ఉష్ణాన్ని అందిస్తున్నా నీటి ఉష్ణోగ్రతలో పెరుగుదల ఉండదు.
c) 100°C వద్ద నీటి ఉపరితలంలో చాలా ఎక్కువ మొత్తంలో బుడగలు ఏర్పడటం గమనిస్తాము.

3) ఈ విధంగా జరగడానికి గల కారణము :
a) నీరు ఒక ద్రావణం. ఇందులో కొన్ని వాయువులతో సహా అనేక రకాల మలినాలు కరిగి ఉంటాయి.
b) నీటిని లేదా ఏదేని ద్రవాన్ని వేడిచేసినప్పుడు అందులోని వాయువుల ద్రావణీయత తగ్గుతుంది.
c) అందువల్ల ద్రవంలో పాత్ర అడుగున, గోడల వెంబడి వాయు బుడగలు ఏర్పడతాయి.
d) బుడగల చుట్టూ ఉన్న ద్రవంలోని నీటి అణువులు బాష్పీభవనం చెంది బుడగలలో చేరడం వల్ల, అవి పూర్తిగా నీటి ఆవిరితో నిండిపోతాయి.
e) ద్రవం ఉష్ణోగ్రత పెరుగుతున్న కొలదీ బుడగలలో పీడనం పెరుగుతుంది.
f) ఒక నిర్దిష్ట ఉష్ణోగ్రత వద్ద బుడగలలోని నీటి ఆవిరి పీడనం, బుడగలపై కలుగజేయబడే బయటి పీడనంతో సమానమవుతుంది.
g) అప్పుడు బుడగలు నెమ్మదిగా ఉపరితలం వైపు కదలడం ప్రారంభిస్తాయి.
h) ద్రవ ఉపరితలాన్ని చేరాక బుడగలు విచ్ఛిన్నమై వాటిలోని నీటి ఆవిరిని గాలిలోకి విడుదల చేస్తాయి.
i) మనం ఉష్ణాన్ని అందిస్తున్నంత వరకూ, ద్రవం వాయువుగా మారే ఈ ప్రక్రియ కొనసాగుతూనే ఉంటుంది. అందువల్ల నీరు మరుగుతున్నట్లు మనకు కనిపిస్తుంది.

4) మరగడం :
ఏదేని పీడనం, స్థిర ఉష్ణోగ్రత వద్ద ద్రవస్థితిలోని పదార్థం వాయుస్థితిలోకి మారడాన్ని మరగడం అంటారు.

కృత్యం – 11 / ద్రవీభవనం

ప్రశ్న 12.
ద్రవీభవనాన్ని వివరించే కృత్యాన్ని రాయండి.
(లేదా)
ద్రవీభవన ప్రక్రియను మరియు ద్రవీభవన గుప్తోష్ణంలను వివరించు ప్రక్రియను వ్రాయుము.
(లేదా)
0°C వద్ద మంచును వేడి చేసిన అది నీరుగా మారుట జరిగినది. కాని ఉష్ణోగ్రతలో కొంత సేపటి వరకు మార్పులేదు. ఈ దృగ్విషయంలో ఇమిడి ఉన్న పద్ధతి ఏమిటి? వివరింపుము.
జవాబు:
1) ఒక బీకరులో కొన్ని మంచుముక్కలు తీసుకొని, థర్మామీటరు సహాయంతో ఉష్ణోగ్రతను కొలవవలెను.

2) బీకరును బర్నర్ పై ఉంచి వేడిచేస్తూ ప్రతి నిమిషం ఉష్ణోగ్రతను నమోదు చేయవలెను.

3) మంచుముక్కలు కరిగేటప్పుడు మనం ఈ క్రింది విషయాలను గమనిస్తాము.
a) ప్రారంభంలో మంచు తక్కువ ఉష్ణోగ్రత 0°C లేదా అంతకంటే తక్కువగా ఉంటుందని గమనిస్తాము.
b) 0°C కంటే తక్కువగా ఉంటే 0°C ను చేరే వరకు ఉష్ణోగ్రత నిరంతరము పెరుగుతుంది.
c) మంచు కరగడం ప్రారంభం అవగానే ఎంత ఉష్ణాన్ని అందిస్తున్నా ఉష్ణోగ్రతలో మార్పు లేకపోవడం గమనిస్తాము.

4) ఈ విధముగా జరగడానికి గల కారణము :
a) మంచుముక్కలకు మనం అందించిన ఉష్ణం మంచు అణువుల అంతర్గత శక్తిని పెంచుతుంది.
b) ఇలా పెరిగిన అంతర్గత శక్తి మంచులోని అణువుల (H₂O) మధ్య గల బంధాలను బలహీనపరచి, తెంచుతుంది.
c) అందువల్ల మంచు (ఘన స్థితి) నీరుగా (ద్రవస్థితి) మారుతుంది.
d) ఈ ప్రక్రియ స్థిర ఉష్ణోగ్రత (0°C లేదా 273K) వద్ద జరుగుతుంది. ఈ ఉష్ణోగ్రతను ద్రవీభవన స్థానం (melting point) అంటాం.

5) ద్రవీభవన స్థానం :
స్థిర ఉష్ణోగ్రత వద్ద ఘనస్థితిలో ఉన్న పదార్థం ద్రవస్థితిలోకి మారే ప్రక్రియనే ద్రవీభవనం అంటారు.

6) ద్రవీభవనం చెందేటప్పుడు ఉష్ణోగ్రత మారదు.

7) ఎందుకనగా, మంచుకు అందించబడిన ఉష్ణం పూర్తిగా నీటి అణువుల మధ్య గల బంధాలను తెంచడానికే వినియోగపడుతుంది.

కృత్యం – 12

ప్రశ్న 13.
ఘనీభవించేటప్పుడు నీరు వ్యాకోచిస్తుందని నిరూపించే కృత్యాన్ని రాయండి.
(లేదా)
నీటితో నింపబడిన గాజు సీసాను అతిశీతలీకరణం చేసిన పగులుటకు గల కారణంను ప్రయోగ పూర్వకంగా వీవరించుము. మంచు సాంద్రత, నీటి కన్నా ఎక్కువగా ఉండుటకు గల కారణంను వివరించుము.
(లేదా)
నీటి కన్నా మంచు ఘనపరిమాణం ఎక్కువని ప్రయోగపూర్వకంగా వివరించుము.
జవాబు:

1. మూత కలిగిన గాజు సీసాను తీసుకొని, గాలి బుడగలు లేకుండా పూర్తిగా నీటితో నింపవలెను.
2. కొన్ని గంటల పాటు సీసాను ఫ్రిజ్ లో ఉంచవలెను.
3. సీసాను తరువాత బయటకు తీసి పరిశీలిస్తే సీసాకు పగుళ్ళు ఏర్పడటాన్ని గమనిస్తాము.
4. సీసాలో పోసిన నీటి ఘనపరిమాణం, సీసా ఘనపరిమాణానికి సమానము.
5. నీరు ఘనీభవించినప్పుడు సీసా పగిలింది. అనగా మంచు ఘనపరిమాణం, సీసాలో నింపిన నీటి ఘనపరిమాణం కంటే ఎక్కువై ఉండాలి.
6. దీనిని బట్టి, ఘనీభవించినప్పుడు నీరు వ్యాకోచిస్తుంది (ఘనపరిమాణం పెరుగుతుంది) అని చెప్పవచ్చు.
7. కనుక నీటి సాంద్రత కన్నా మంచు సాంద్రత తక్కువ. అందుకే నీటి పై మంచు తేలుతుంది.

SCERT AP 10th Class Maths Textbook Solutions Chapter 8 సరూప త్రిభుజాలు Exercise 8.1 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 8th Lesson సరూప త్రిభుజాలు Exercise 8.1

ప్రశ్న 1.
∆PQRS లో \(\frac{\mathbf{P S}}{\mathbf{S Q}}=\frac{\mathbf{P T}}{\mathbf{T R}}\) అగునట్లు ST ఒక సరళరేఖ, ఇంకనూ ∠PST = ∠PRQ అయిన ∆PQR ఒక సమద్విబాహు త్రిభుజమని చూపండి.

సాధన.
దత్తాంశము : ∆PQR లో \(\frac{\mathbf{P S}}{\mathbf{S Q}}=\frac{\mathbf{P T}}{\mathbf{T R}}\) మరియు
∠PST = ∠PRQ.
సారాంశము : ∆POR ఒక సమద్విబాహు త్రిభుజము.
ఉపపత్తి : \(\frac{\mathbf{P S}}{\mathbf{S Q}}=\frac{\mathbf{P T}}{\mathbf{T R}}\) కావున ST || QR
(థమిక సిద్ధాంతపు విపర్యయము నుండి)
∴ ∠PST = ∠POR ………… (1) (ST || QR కావున వాటి సదృశ్య కోణాలు)
మరియు, ∠PST = ∠PRQ……….. (2) (దత్తాంశము)
(1), (2) ల నుండి, ∠PQR = ∠PRQ
∴ PR = PQ [త్రిభుజంలో సమాన కోణాలకు ఎదురుగా ఉన్న భుజాలు సమానము)
కావున ∆PQR సమద్విబాహు త్రిభుజము.

ప్రశ్న 2.
ఇచ్చిన పటంలో, LM || CB మరియు LN || CD అయిన AM = AN అని చూపండి.

సాధన.
దత్తాంశము : LM || CB మరియు LN || CD
∆ABC లో, LM || BC కావున

ప్రశ్న 3.
ఇచ్చిన పటంలో, DE || AC మరియు DF || AE అయిన BF = BE అని చూపండి.

సాధన.
∆ABC లో, DE || AC కావున
\(\frac{\mathrm{BE}}{\mathrm{EC}}=\frac{\mathrm{BD}}{\mathrm{DA}}\) …………. (1)
(థమిక సిద్ధాంతం నుండి) మరలా ∆ABE లో, DF || AE కావున
\(\frac{\mathrm{BF}}{\mathrm{FE}}=\frac{\mathrm{BD}}{\mathrm{DA}}\) …………. (2)
(1) మరియు (2) ల నుండి
\frac{B E}{E C}=\frac{B F}{F E}\(\) అని నిరూపించబడినది.

ప్రశ్న 4.
ఒక త్రిభుజములో ఒక భుజము మధ్య బిందువు గుండా పోయేరేఖ, రెండవ భుజానికి సమాంతరంగా ఉంటే అది మూడవ భుజాన్ని సమద్విఖండన చేస్తుందని చూపండి. (ప్రాథమిక అనుపాత సిద్ధాంతము నుపయోగించి)
సాధన.

దత్తాంశము : AB మధ్య బిందువు D మరియు DE || BC
సారాంశము : AE = EC
నిరూపణ : ∆ABC లో DE || BC
∴ \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) (ప్రాథమిక అనుపాత సిద్ధాంతము)

\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) [AB మధ్య బిందువు D ∴ AD = DB]
1 = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)
∴ AE = EC
కావున DE, AC ని సమద్విఖండన చేస్తుంది.

ప్రశ్న5.
ఒక త్రిభుజములో రెండు భుజాల మధ్య బిందువులను కలిపే రేఖాఖండము మూడవ భుజానికి సమాంతరంగా ఉంటుందని చూపండి. (ప్రాథమిక అనుపాత సిద్ధాంత విపర్యయము నుపయోగించి)
సాధన.
దత్తాంశము : ∆ABC లో AB మధ్య బిందువు ‘D’
మరియు AC మధ్య బిందువు ‘E’.
సారాంశం : DE || BC.
ఉపపత్తి :

AB మధ్య బిందువు ‘D’,
AD = DB
⇒ \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = 1 ………. (1)
మరియు AC మధ్య బిందువు ‘E’ అయిన
AE = EC
⇒ \(\frac{\mathrm{AE}}{\mathrm{EC}}\) = 1 ………… (2)
(1), (2) ల నుండి
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
ఒక త్రిభుజంలో ఏవైనా రెండు భుజాలను ఒకే నిష్పత్తిలో విభజించు సరళరేఖ, మూడవ భుజానికి సమాంతరంగా నుండును.
∴ DE || BC [∴ ప్రాథమిక అనుపాత సిద్ధాంత విపర్యం నుండి నిరూపించబడినది].

ప్రశ్న 6.
ఇచ్చిన పటములో, DE || OQ మరియు DF || OR అయిన EF || QR అని చూపండి.

సాధన.
దత్తాంశము : ∆PQRలో DE || OQ; DF || OR
సారాంశము : EF || QR
ఉపపత్తి : ∆POQ లో DE || OQ, కావున ప్రాథమిక అనుపాత సిద్ధాంతమును అనుసరించి
\(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PD}}{\mathrm{DO}}\) ………………(1)
∆PQR లో DF || OR కావున ప్రాథమిక అనుపాత సిద్ధాంతమును అనుసరించి
\(\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{\mathrm{PD}}{\mathrm{DO}}\) ……….. (2)
(1), (2) ల నుండి, \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PF}}{\mathrm{FR}}\)
(1), (4) అంతు EQ , FR ఆ విధముగా APQR ను EF రేఖ PQ మరియు
PR లను ఒకే నిష్పత్తిలో విభజించుచున్నది.. కావున EF || QR. (ప్రాథమిక సిద్ధాంతపు విపర్యయం నుండి).

ప్రశ్న 7.
ఇచ్చిన పటంలో A, B, C లు వరుసగా OP, OQ మరియు OR లపై బిందువులు. AB || PQ మరియు AC || PR అయిన BC || QR అని చూపండి.

సాధన.
దత్తాంశము : ∆PQRలో AB || PQ; AC || PR.
సారాంశము : BC || QR
ఉపపత్తి : ∆POQలో AB || PQ కావున
\(\frac{\mathrm{OA}}{\mathrm{AP}}=\frac{\mathrm{OB}}{\mathrm{BQ}}\) ………… (1)
∆OPRలో AC || PR కావున
\(\frac{\mathrm{OA}}{\mathrm{AP}}=\frac{\mathrm{OC}}{\mathrm{CR}}\) ………… (2)
(1) మరియు (2) ల నుండి \(\frac{\mathrm{OB}}{\mathrm{BQ}}=\frac{\mathrm{OC}}{\mathrm{CR}}\)
ఆ విధముగా ∆OQR ను BC రేఖ OQ మరియు OR అను సమాన నిష్పత్తిలో విభజిస్తుంది.
∴ BC || QR.
[ప్రాథమిక సిద్ధాంత విపర్యయము నుండి)

ప్రశ్న 8.
ట్రెపీజియం ABCD లో AB||DC. దాని కర్ణములు పరస్పరం బిందువు ‘0’ వద్ద ఖండించుకొంటాయి. అయిన \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\) అని చూపండి.
సాధన.
దత్తాంశము : ట్రెపీజియము ABCD లో AB || CD మరియు AC, BD కర్ణాలు ‘O’ వద్ద ఖండించుచున్నవి.
సారాంశము : \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)

నిర్మాణము : EF అనురేఖను CD మరియు AB లకు సమాంతరంగా ఉంటూ ‘O’ గుండా పోవు విధంగా గీయుము.
ఉపపత్తి: ∆ACDలో EO // CD కావున AO _ AE
\(\frac{\mathrm{AO}}{\mathrm{CO}}=\frac{\mathrm{AE}}{\mathrm{DE}}\) …………… (1) [ప్రాథమిక అనుపాత సిద్ధాంతం నుండి]

∆ABD లో, EO || AB కావున
\(\frac{\mathrm{DE}}{\mathrm{AE}}=\frac{\mathrm{DO}}{\mathrm{BO}}\) [ప్రాథమిక అనుపాత సిద్ధాంతం నుండి)

\(\frac{\mathrm{BO}}{\mathrm{DO}}=\frac{\mathrm{AE}}{\mathrm{DE}}\) ……………… (2) [విలోమము చేయగా )
(1), (2) ల నుండి
\(\frac{\mathrm{AO}}{\mathrm{CO}}=\frac{\mathrm{BO}}{\mathrm{DO}}\)

⇒ \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\) నిరూపించబడినది.

ప్రశ్న 9.
7.2 సెం.మీ పొడవు గల ఒక రేఖాఖండమును గీసి దానిని 5 : 3 నిష్పత్తిలో విభజించండి. ఏర్పడిన రెండు భాగముల పొడవులను కొలిచి రాయండి.
సాధన.

నిర్మాణ సోపానాలు :
(1) \(\overline{\mathrm{AB}}\) = 7.2 సెం. మీతో ఒక రేఖాఖండంను గీయుము.
2) ‘A’ వద్ద ∠BAX అను అల్పకోణంను గీయుము.
3) \(\stackrel{\leftrightarrow}{\mathrm{AX}}\) పై సమాన వ్యాసార్ధ కొలతలతో 5 + 3 = 8కి సమాన చాపములు (A₁, A₂, A₃, …… A₈) లను గీయుము.
4) A₈ మరియు B ను కలుపుము.
5) A₅ బిందువు గుండా \(\stackrel{\leftrightarrow}{A_{8} B}\) కి సమాంతర రేఖను గీయుము.
6) AB రేఖాఖండంను ‘C’ రేఖ 5 : 3 నిష్పత్తిలో ఖండించుచున్నది.
7) AC మరియు BC లను కొలవగా AC = 4.5 సెం.మీ. మరియు BC = 2.7 సెం.మీ.

SCERT AP 10th Class Maths Textbook Solutions Chapter 7 నిరూపక రేఖాగణితం Intext Questions Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 7th Lesson నిరూపక రేఖాగణితం InText Questions

ఇవి చేయండి:

ప్రశ్న 1.
క్రింది పటం నుండి A, B, C, D, E, F, G, H బిందువుల నిరూపకాలు కనుగొనండి. (పేజీ నెం. 159)

సాధన.
గుర్రం యొక్క స్థానం మూల బిందువుగా ఉందనుకోవాలి.
A (- 1, 2), B (1, 2), C (2, 1), D (2, – 1), E (1, – 2), F (- 1, – 2), G (- 2, – 1), H (- 2, 1).

ప్రశ్న 2.
8 కదలికల తర్వాత గుఱ్ఱం కదిలిన దూరం కనుగొనండి. అనగా మూలబిందువు (0, 0) నుండి A, B, C, D, E, F, G, H బిందువుల మధ్య దూరంను కనుగొనండి. (పేజీ నెం. 159)
సాధన.
గుర్రం (0, 0) నుండి, A కి కదిలిన దూరం + B కి కదిలిన దూరం + ……… + H కి కదిలిన దూరం
= 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3
= 24 యూనిట్లు .

ప్రశ్న 3.
బిందువులు H మరియు C ల మధ్య దూరమెంత ? అలాగే బిందువులు A మరియు B ల మధ్య దూరమెంత? (పేజీ నెం. 159).
సాధన.
H మరియు C ల మధ్య దూరం = 4 యూనిట్లు
A మరియు B ల మధ్యదూరం = 2 యూనిట్లు

ప్రశ్న 4.
(- 4, 0), (2, 0), (6, 0), (-8, 0) బిందువులు నిరూపక తలంలో ఎక్కడ ఉంటాయి ? (పేజీ నెం. 160)
సాధన.
ఇచ్చిన అన్ని బిందువులు X – అక్షంపై ఉంటాయి.

ప్రశ్న 5.
(- 4, 0), (6, 0) బిందువుల మధ్య దూరమెంత ? (పేజీ నెం. 160)
సాధన.
(- 4, 0), 16, 0) బిందువులు X – అక్షంపై ఉంటాయి.
కావున వాని మధ్య దూరం = |x₂ – x₁|
= |6 – (- 4)| = |6 + 4| = 10 యూనిట్లు.

ప్రశ్న 6.
కింది బిందువుల మధ్య దూరం కనుగొనండి. (పేజీ నెం. 162)
(i) (3, 8), 16, 8)
సాధన.
బిందువుల మధ్య దూరం = |x₂ – x₁|
(∵ రెండు బిందువులలో Y నిరూపకాలు సమానం)
= | 6 -3 | = 3 యూనిట్లు..

(ii) (- 4, – 3), (- 8, – 3)
సాధన.
బిందువుల మధ్య దూరం = |x₂ – x₁| (∵ రెండు బిందువులలో Y నిరూపకాలు సమానం)
= | – 8 – (- 4) | = | – 8 + 4 |
= | – 4 | = 4 యూనిట్లు.

(iii) (3, 4), (3, 8)
సాధన.
బిందువుల మధ్య దూరం = |y₂ – y₁| (∵ రెండు బిందువులలో X నిరూపకాలు సమానం)
= | 8 – 4 | = 4 యూనిట్లు.

(iv) (- 5, – 8), (- 5, – 12)
సాధన.
బిందువుల మధ్య దూరం = |y₂ – y₁|
= |- 12 – (- 8)|
= |- 12 + 8| ( ∵ రెండు బిందువులలో X నిరూపకాలు సమానం)
= | – 4 | = 4 యూనిట్లు.

ప్రశ్న 7.
కింది బిందువుల మధ్య దూరం కనుగొనండి. (పేజీ నెం. 162)
(i) A (2, 0) మరియు B (0, 4)
సాధన.
A (2, 0) X – అక్షంపైన,
B (0, 4) Y – అక్షం పైన ఉంటాయి.

∆AOB లంబకోణ త్రిభుజము
OA = 2; OB = 4
AB² = OA² + OB²
AB² = (2)² + (4)²
AB = √(4 + 16) = √20 = 2√5
గమనిక : (x₁, 0), (0, y₁) బిందువుల మధ్య దూరం = √(x₁² + y₁²).

(ii) P(0, 5) మరియు Q (12, 0)
సాధన.
P (0, 5) మరియు Q (12, 0) .
P, Q ల మధ్య దూరం = \(\sqrt{(12)^{2}+(5)^{2}}\)
= \(\sqrt{144+25}=\sqrt{169}\) = 13
P, Q ల మధ్య దూరం = 13 యూనిట్లు.

ప్రశ్న 8.
కింద ఇవ్వబడిన బిందువుల మధ్య దూరం కనుగొనండి. (పేజీ నెం. 164)
(i) (7, 8) మరియు ( – 2, 3)
సాధన.
A (7, 8) మరియు B (- 2, 3)
A, B ల మధ్య దూరం = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(-2-7)^{2}+(3-8)^{2}}\)
= \(\sqrt{(-9)^{2}+(-5)^{2}}=\sqrt{81+25}=\sqrt{106}\)

(ii) (- 8, 6) మరియు (2,0)
సాధన.
A (- 8, 6) మరియు B (2, 0)
X = – 8, x, = 2, y = 6, y) = 0
A, B ల మధ్య దూరం = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(2-(-8))^{2}+(0-6)^{2}}\)
= \(\sqrt{10^{2}+(-6)^{2}}=\sqrt{100+36}\)
= √136.

ప్రయత్నించండి:

ప్రశ్న 1.
(0, – 3), (0, – 8), (0, 6), (0, 4) బిందువులు నిరూపక తలంలో ఎక్కడ ఉంటాయి ? (పేజీ నెం. 161)
సాధన.
అన్ని బిందువులు Y – అక్షంపై ఉంటాయి.

ప్రశ్న 2.
(0, – 3) మరియు (0, – 8) బిందువుల మధ్య దూరమెంత ? అలాగే Y – అక్షంపై ఉన్న బిందువుల మధ్యదూరం | y₂ – y₁| అవుతుందని చెప్పగలవా ? (పేజీ నెం. 161)
సాధన.
(0, – 3), (0, – 8) లు Y – అక్షంపై గల బిందువులు.
వీని మధ్యదూరం= |y₂ – y₁|
= |- 8 – (- 3)| = |- 8 + 3| = |- 5 | యూనిట్లు
Y – అక్షంపై గల బిందువుల మధ్య దూరం = |y₂ – y₁| అవుతుంది.

ప్రశ్న 3.
మూలబిందువు ‘0’ మరియు బిందువు A (7, 4) ల మధ్యదూరం కనుగొనండి. (పేజీ నెం. 162)
సాధన.

పై పటం నుండి AB = 4 యూనిట్లు, OB = 7 యూనిట్లు
∆ABO లంబకోణ త్రిభుజము
OA² = OB² + BA²
= 7² + 4² = 49 + 16
OA² = 65
OA = √65 యూనిట్లు.

గమనిక :
మూలబిందువు (0, 0) నుండి (x₁, y₁) బిందువుకు గల దూరము \(\sqrt{x_{1}^{2}+y_{1}^{2}}\).
మూలబిందువు నుండి A (7, 4) కు గల దూరం = \(\sqrt{7^{2}+4^{2}}=\sqrt{49+16}=\sqrt{65}\) యూనిట్లు.

ప్రశ్న 4.
ఒక రేఖాఖండం \(\overline{\mathrm{AB}}\) యొక్క తొలి, చివరి బిందువులు A(1, – 3) మరియు B(- 4, 4) అయిన AB మధ్య దూరాన్ని దగ్గరి దశాంశాలకు కనుగొనండి. (పేజీ నెం. 164)
సాధన.
A (1, – 3) మరియు B (- 4, 4) ..
x₁ = 1, x₂ = – 4, y₁ = – 3, y₂ = 4
AB ల మధ్య దూరం, d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(-4-1)^{2}+(4-(-3))^{2}}\)
= \(\sqrt{(-5)^{2}+(7)^{2}}\)
= \(\sqrt{25+49}=\sqrt{74}\)
AB ల మధ్య దూరం = 8.602

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
రెండు బిందువులలోని X లేదా 5 నిరూపకాలు సమానంగా (0 కాకుండా) ఉంటే వాటి మధ్యదూరం ఎలా కనుగొంటావు ? (పేజీ నెం, 161)
సాధన.
సందర్భం – 1:
రెండు బిందువులలోని x నిరూపకాలు సమానంగా ఉంటే ఆ రెండు బిందువులు Y- అక్షానికి సమాంతరంగా గల రేఖపై ఉంటాయి.
కావున రెండు బిందువులలోని y నిరూపకాల భేదం |Y₂ – Y₁| ఆ రెండు బిందువుల మధ్య దూరం అవుతుంది.
(x₁, y₁), (x₂, y₂) బిందువుల మధ్య దూరం = |y₂ – y₁|

సందర్భం – 2:
రెండు బిందువులలోని y నిరూపకాలు సమానం అయితే ఆ బిందువులు X – అక్షానికి సమాంతరంగా గల రేఖపై ఉంటాయి. కావున ఈ రెండు బిందువులలోని X నిరూపకాల భేదం |x₂ – x₁| ఆ రెండు బిందువుల మధ్య దూరం అవుతుంది.
(x₁, y₁), (x₂, y₂) బిందువుల మధ్య దూరం = |x₂ – x₁|

ప్రశ్న 2.
రెండు బింధువులు నిరూపకతలంలోని వేర్వేరు పాదాలలో ఉంటే వాటి మధ్య దూరం ఎలా కనుగొంటారు? (పేజీ నెం. 163)
సాధన.
A, B అనే రెండు బిందువులు వేర్వేరు తలాలలో ఉంటే A, Bల మధ్య దూరాన్ని కనుగొనడానికి, A, B బిందువుల గుండా అక్షాలకు లంబ రేఖలను గీచి, \(\overline{\mathrm{AB}}\) కర్ణంగా గల లంబకోణ త్రిభుజాన్ని ఏర్పరచాలి. అలా ఏర్పడిన లంబకోణ త్రిభుజం యొక్క కర్ణం పొడవును పైథాగరస్ సిద్ధాంతాన్ని ఉపయోగించి కనుగొంటాము. ఈ పొడవే A, B ల మధ్య దూరం అవుతుంది.
ఉదాహరణకు A(3, 4), B(- 2, – 5) లు వరుసగా 1వ, 3వ పాదాలలో కలవు. వీని మధ్యదూరం కనుగొందాము.
సాధన.
A (3, 2) గుండా Y – అక్షానికి లంబం AP, B (- 2, – 5) గుండా X – అక్షానికి లంబం BQ లను గీయాలి. వీటి ఖండన బిందువు C అవుతుంది.
ఇప్పుడు AC = 5 యూనిట్లు
BC = 7 యూనిట్లు .
లంబకోణ త్రిభుజం ∆ABCలో AB² = AC² + BC² (పైథాగరస్ సిద్ధాంతము)
= 5² + 7²

AB² = 25 + 49 = 74
AB = √74 యూనిట్లు

గమనిక : A (x₁, y₁), B (x₂, y₂) బిందువుల మధ్యదూరం సూత్రం రాబట్టిన తర్వాత అయితే రెండు బిందువుల మధ్య దూరం సూత్రం
d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) ను ఉపయోగించి ఒకే తలంలో గల ఏ రెండు బిందువుల మధ్య దూరాన్నైనా కనుగొనవచ్చును.

ప్రశ్న 3.
రాము, బిందువు P(x, y) మరియు మూలబిందువు O(0, 0)ల మధ్య దూరం \(\sqrt{x^{2}+y^{2}}\) అని తెలిపెను. నీవు రాము తెలిపిన దానితో ఏకీభవిస్తున్నావా? లేదా? ఎందుకు ? (పేజీ నెం. 163)
సాధన.
రాముతో ఏకీభవిస్తాను.
O(0, 0), P(x, y) ల మధ్య దూరం d = \(\sqrt{(x-0)^{2}+(y-0)^{2}}\)
= \(\sqrt{x^{2}+y^{2}}\)

ఈ విలువ రాము సమాధానంతో సరిపోతున్నది. కావున రాముతో ఏకీభవిస్తున్నాను.
(లేదా)

పై పటం నుండి, ∆PQO లంబకోణ త్రిభుజము.
PQ = y, QQ = x
OP² = OQ² + QP²
= x² + y²
OP = √(x² + y²⁾
ఈ విలువ, రాము సమాధానము ఒకటే. కావున ‘ రాము సమాధానంతో ఏకీభవిస్తాను.

ప్రశ్న 4.
రాము రెండు బిందువుల మధ్య దూరాన్ని ఈ విధంగా రాశాడు. AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) ఎందుకు ? (పేజీ నెం. 163)
సాధన.
A(x₁, y₁), B(x₂, y₂) బిందువుల మధ్య దూరం \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) కు సమానం.
A, B బిందువుల మధ్య దూరాన్ని AB గా రాస్తాము.
కావున AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) అని రాశాడు.

ప్రశ్న 5.
శ్రీధర్ రెండు బిందువులు T (5, 2) మరియు R (- 4, – 1) ల మధ్య దూరం 9.5 యూనిట్లుగా లెక్కించాడు. ఇపుడు మీరు రెండు బిందువులు P (4, 1) మరియు Q (-5, – 2) ల మధ్య దూరాన్ని కనుగొనండి. మీరు కూడా శ్రీధర్ పొందిన సమాధానాన్నే పొందారా ? ఎందుకు ? (పేజీ నెం. 164)
సాధన.
P(4, 1), Q (- 5, – 2) బిందువుల మధ్య దూరం
రెండు బిందువుల మధ్య దూరం PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(-5-4)^{2}+(-2-1)^{2}}\)
= \(\sqrt{(-9)^{2}+(-3)^{2}}\)
= \(\sqrt{81+9}=\sqrt{90}\)
= 3√10 = 3√2 × √5
= 3 × 1.414 × 2.236 [∵ √2 = 1.413, √5 = 2.236]
PQ = 9.4851 = 9.5
PQ = 9.4851ను ఒక దశాంశానికి సవరించినపుడు మనం కూడా శ్రీధర్ పొందిన సమాధానాన్నే పొందుతున్నాము.
T (5, 2), R (- 4, – 1) బిందువులలోని x, y నిరూపకాల యొక్క గుర్తులను మార్చగా P (4, 1) మరియు Q (- 5, – 2) వస్తున్నాయి.
కాబట్టి TR = PQ అవుతుంది.

గమనిక :
P (x₁, y₁), Q (x₂, y₂) మరియు R(- x₁, – y₁), S (- x₂, – y₂) అయిన PQ = RS అగును.

ఇవి చేయండి:

ప్రశ్న 1.
బిందువులు (3, 5) మరియు (8, 10) లచే ఏర్పడు రేఖాఖండమును 2:3 నిష్పత్తిలో అంతరంగా విభజించు బిందువును కనుగొనండి. (పేజీ నెం. 171)
సాధన.
ఇచ్చిన బిందువులు (3, 5), (8, 10) లను 2 : 3 నిష్పత్తిలో విభజించే బిందువు P (x, y) అనుకుందాం.
విభజించే సూత్రం – P(x, y) = \(=\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)

= \(\left(\frac{2(8)+3(3)}{2+3}, \frac{2(10)+1(5)}{2+3}\right)\)

= \(\left(\frac{16+9}{5}, \frac{20+5}{5}\right)\)

= (\(\frac{25}{5}\), \(\frac{25}{5}\)) = (5, 5)
∴ కావలసిన బిందువు P(x, y) = (5, 5)

ప్రశ్న 2.
బిందువులు (2, 7) మరియు (12, -7) లచే ఏర్పడు రేఖాఖండం యొక్క మధ్యబిందువును కనుగొనండి. (పేజీ నెం. 171)
సాధన.
(2, 7), (12, – 7) బిందువుల మధ్య బిందువు M (x, y) అనుకొనుము.
(x₁, y₁), (x₂, y₂) బిందువులతో ఏర్పడు రేఖ యొక్క మధ్యబిందువు నిరూపకాలు M(x,y) అనుకొనుము.
M(x, y) = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

= \(\left(\frac{2+12}{2}, \frac{7+(-7)}{2}\right)\)

= \(\left(\frac{14}{2}, \frac{0}{2}\right)\) = (7, 0)
కావలసిన బిందువు M(x, y) = (7,0) .

ప్రశ్న 3.
బిందువులు (- 4, 6), (2, -2 ) మరియు (2, 5)లు శీర్షాలుగా గల త్రిభుజం యొక్క గురుత్వ కేంద్రంను కనుగొనండి. (పేజీ నెం. 173)
సాధన.
గురుత్వ కేంద్ర నిరూపకాలు = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)
= \(\left(\frac{-4+2+2}{3}, \frac{6+(-2)+5}{3}\right)\)
= \(\left(\frac{-4+4}{3}, \frac{11-2}{3}\right)\)
= (0, \(\frac{9}{3}\)) = (0, 3)
∴ గురుత్వ కేంద్రం (0, 3)

ప్రశ్న 4.
బిందువులు (2, – 6) మరియు ( 4, 8) లను కలుపు రేఖాఖండం యొక్క త్రిథాకరణ బిందువులను కనుగొనండి. (పేజీ నెం. 175)
సాధన.
ఇచ్చిన బిందువులు A (2, – 6), B (- 4, 8).
A(2, – 6), B(- 4, 8) లను కలుపు రేఖాఖండము యొక్క త్రిథాకరణ బిందువులు P, Q అనుకుందాం.

\(\overline{\mathrm{AB}}\) రేఖాఖండాన్ని P 1 : 2 నిష్పత్తిలో విభజిస్తుంది.
∴ P(x, y) = \(\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)

= \(\left(\frac{1(-4)+2(2)}{1+2}, \frac{1(8)+2(-6)}{1+2}\right)\)

= \(\left(\frac{-4+4}{3}, \frac{8-12}{3}\right)=\left(\frac{0}{3}, \frac{-4}{3}\right)\)

= (1-4+2[2] 18 +2-))
∴ P = (0, \(\frac{-4}{3}\))
ఇపుడు \(\overline{\mathrm{AB}}\) రేఖాఖండాన్ని Q 2 : 1 నిష్పత్తిలో విభజిస్తుంది.
Q (x, y) = \(\left(\frac{2(-4)+1(2)}{2+1}, \frac{2(8)+1(-6)}{2+1}\right)\)

= \(\left(\frac{-8+2}{3}, \frac{16-6}{3}\right)\)

= \(\left(\frac{-6}{3}, \frac{10}{3}\right)=\left(-2, \frac{10}{3}\right)\)
∴ Q = (- 2, \(\frac{10}{3}\)) కావున (2, – 6) మరియు (- 4, 8) లను కలిపే రేఖాఖండం యొక్క త్రిథాకరణ బిందువులు (0, \(-\frac{4}{3}\)) మరియు (- 2, \(\frac{10}{3}\)).

సరిచూచుకోవడం :
(i) \(\overline{\mathrm{AB}}\) యొక్క త్రిథాకరణ బిందువులు P, Q అయిన A, Bల మధ్యబిందువు, P, Qల మధ్యబిందువు ఒకటే అవుతుంది.
A, B ల మధ్య బిందువు = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

= \(\left(\frac{2+(-4)}{2}, \frac{-6+8}{2}\right)=\left(\frac{-2}{2}, \frac{2}{2}\right)\) = (-1.1)

P, Qల మధ్య బిందువు = \(\left(\frac{0+(-2)}{2}, \frac{\frac{-4}{3}+\frac{10}{3}}{2}\right)\)

= \(\left(\frac{-2}{2}, \frac{\frac{6}{3}}{2}\right)=\left(-1, \frac{2}{2}\right)\) = (- 1, 1)

(ii) AP, PQ, QB పొడవులను కనుగొని కూడా సరిచూచుకోవచ్చును.
AP = PQ = QB అవుతాయి.

ప్రశ్న 5.
బిందువులు (- 3, – 5), (- 6, – 8) లను కలుపు రేఖండము యొక్క త్రిథాకరణ బిందువులను కనుగొనుము. (పేజీ నెం. 175)
సాధన.
బిందువులు A (- 3, – 5), B (- 6, – 8) లను కలుపు రేఖాఖండము యొక్క ప్రాథాకరణ బిందువులు P, Q అనుకొంటే \(\overline{\mathrm{AB}}\) ను P 1 : 2 నిష్పత్తిలో అంతరంగా విభజిస్తుంది.
P(x, y) = \(\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)

= \(\left(\frac{1(-6)+2(-3)}{1+2}, \frac{1(-8)+2(-5)}{1+2}\right)\)

= \(\left(\frac{-6-6}{3}, \frac{-8-10}{3}\right)=\left(\frac{-12}{3}, \frac{-18}{3}\right)\)

= (- 4, – 6)
∴ P = (- 4, – 6)
ఇప్పుడు \(\overline{\mathrm{AB}}\) ని Q 2 : 1 నిష్పత్తిలో అంతరంగా విభజిస్తుంది.
Q(x, y) = \(\left(\frac{2(-6)+1(-3)}{2+1}, \frac{2(-8)+1(-5)}{2+1}\right)\)

= \(\left(\frac{-12-3}{3}, \frac{-16-5}{3}\right)=\left(\frac{-15}{3}, \frac{-21}{3}\right)\)
= (- 5 – 7)
Q = (- 5, – 7)
కావున బిందువులు (- 3, – 5), (- 6, – 8) లను కలుపు రేఖాఖండం యొక్క త్రిథాకరణ బిందువులు (- 4, – 6) మరియు Q (- 5, – 7)

సరిచూచుకొనుట :
A, B మధ్యబిందువు = \(\left(\frac{(-3)+(-6)}{2}, \frac{(-5)+(-8)}{2}\right)\)
= \(\left(\frac{-9}{2}, \frac{-13}{2}\right)\)

P, Q మధ్యబిందువు = \(\left(\frac{(-4)+(-5)}{2}, \frac{(-6)+(-7)}{2}\right)\)
= \(\left(\frac{-9}{2}, \frac{-13}{2}\right)\)

కృత్యము:

బిందువులు A(4, 2), B(6, 5) మరియు C(1, 4) లు ∆ABC యొక్క శీర్షాలు.

ప్రశ్న 1.
A నుండి BC పైకి గీసిన మధ్యగతరేఖ D వద్ద కలుస్తుంది. అయిన D బిందువు నిరూపకాలు కనుగొనండి. (పేజీ నెం. 172)
సాధన.
B (6, 5) మరియు C(1, 4) ల మధ్యబిందువు
D(x, y) = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

= \(\left(\frac{6+1}{2}, \frac{5+4}{2}\right)=\left(\frac{7}{2}, \frac{9}{2}\right)\).

ప్రశ్న 2.
AP : PD = 2 : 1 అయ్యే విధంగా AD రేఖపై P బిందువు నిరూపకాలను కనుగొనండి. (పేజీ నెం. 172)
సాధన.
A(4, 2), D\(\left(\frac{7}{2}, \frac{9}{2}\right)\) లను 2 : 1 నిష్పత్తిలో -విభజించే బిందువు
∴ P = \(\left(\frac{\mathrm{m}_{1} \mathrm{x}_{2}+\mathrm{m}_{2} \mathrm{x}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1} \mathrm{y}_{2}+\mathrm{m}_{2} \mathrm{y}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\right)\)

= \(\left(\frac{2\left(\frac{7}{2}\right)+1(4)}{2+1}, \frac{2\left(\frac{9}{2}\right)+1(2)}{2+1}\right)\)

= \(\left(\frac{7+4}{3}, \frac{9+2}{3}\right)\)

⇒ P = \(\left(\frac{11}{3}, \frac{11}{3}\right)\)

ప్రశ్న 3.
BE రేఖను 2 : 1 నిష్పత్తిలో విభజించు బిందువును మరియు CF రేఖను 2 : 1 నిష్పత్తిలో విభజించు బిందువును కనుగొనండి. (పేజీ నెం. 172)
సాధన.
A(4, 2), C (1, 4) ల మధ్య బిందువు E = \(\left(\frac{4+1}{2}, \frac{2+4}{2}\right)=\left(\frac{5}{2}, 3\right)\)

A(4, 2), B (6, 5) ల మధ్య బిందువు F = \(\left(\frac{4+6}{2}, \frac{2+5}{2}\right)=\left(5, \frac{7}{2}\right)\)

(i) B(6, 5), E(\(\frac{5}{2}\). 3) లను 2 : 1 నిష్పత్తిలో విభజించే బిందువు
Q = \(\left(\frac{\mathrm{m}_{1} \mathrm{x}_{2}+\mathrm{m}_{2} \mathrm{x}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1} \mathrm{y}_{2}+\mathrm{m}_{2} \mathrm{y}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\right)\)

= \(\left(\frac{2\left(\frac{5}{2}\right)+1(6)}{2+1}, \frac{2(3)+1(5)}{2+1}\right)\)

= \(\left(\frac{5+6}{3}, \frac{6+5}{3}\right)\)

⇒ Q = \(\left(\frac{11}{3}, \frac{11}{3}\right)\)

(ii) C(1, 4), F(5,7) లను 2 : 1 నిష్పత్తిలో విభజించే బిందువు
R = \(\left(\frac{2(5)+1(1)}{2+1}, \frac{2\left(\frac{7}{2}\right)+1(4)}{2+1}\right)\)
= \(\left(\frac{10+1}{3}, \frac{7+4}{3}\right)\)
⇒ R = (11 11)

ప్రశ్న 4.
మీరేమి గమనించారు ? “ఒక త్రిభుజంలోని ప్రతి మధ్యగతరేఖను 2 : 1 నిష్పత్తిలో విభజించు బిందువు ఆ త్రిభుజం యొక్క గురుత్వకేంద్రం అవుతుంది”. (పేజీ నెం. 172)
సాధన.
మధ్యగతాలను 2 : 1 నిష్పత్తిలో విభజించే బిందువులు P, Q, Rలు ఏకీభవిస్తున్నాయి. మధ్యగతరేఖల మిళిత బిందువును గురుత్వ కేంద్రము అంటామని మనకు తెలుసు. P, Q, R లు ఈ గురుత్వ కేంద్రంతో ఏకీభవిస్తున్నాయి.

“అనగా “ఒక. త్రిభుజంలోని ప్రతి మధ్యగత రేఖను 2 : 1 నిష్పత్తిలో విభజించు బిందువు ఆ త్రిభుజం యొక్క గురుత్వ కేంద్రము అవుతుంది”.

ప్రయత్నించండి:

బిందువులు (2, 3), (x, y), (3, -2 ) లు శీర్షాలుగా గల త్రిభుజం యొక్క గురుత్వ కేంద్రం మూలబిందువు అయిన (x, y) లను కనుగొనండి.(పేజీ నెం. 173)
సాధన.
ఇచ్చినది (2, 3), (x, y), (3, -2) లు త్రిభుజ శీర్షాలు గురుత్వ కేంద్రం = (0,0)
అనగా
\(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\) = (0, 0)

\(\left(\frac{2+x+3}{3}, \frac{3+y+(-2)}{3}\right)\) = (0, 0)

\(\left(\frac{5+x}{3}, \frac{y+1}{3}\right)\) = 0
⇒ 5 + x = 0
⇒ x = – 5
⇒ y + 1 = 0
⇒ y = – 1
∴ (x, y) = (- 5, – 1).

అలోచించి, చర్చించి, రాయండి:

బిందువులు A(6, 9) మరియు B(- 6, – 9) లను కలుపు రేఖాఖందమును. (పేజీ నెం. 174)

(a) మూలబిందువు ఏ నిష్పత్తిలో విభజిస్తుంది ? ఆ రేఖా ఖండమునకు మూలబిందువును ఏమంటారు ?
సాధన.
ఇచ్చిన బిందువులు : A (6, 9), B (- 6, – 9) లను మూలబిందువు m₁ : m₂ నిష్పత్తిలో విభిజిస్తుందని అనుకొందాం.

(0, 0) = \(\left(\frac{\mathrm{m}_{1}(-6)+\mathrm{m}_{2}(6)}{\mathrm{m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1}(-9)+\mathrm{m}_{2}(9)}{\mathrm{m}_{1}+\mathrm{m}_{2}}\right)\)

(0, 0) = \(\left(\frac{-6 m_{1}+6 m_{2}}{m_{1}+m_{2}}, \frac{-9 m_{1}+9 m_{2}}{m_{1}+m_{2}}\right)\)

∴ \(\frac{-6 m_{1}+6 m_{2}}{m_{1}+m_{2}}\) = 0
– 6m₁ + 6m₂ = 0
– 6m₁ = – 6m₂
⇒ 6m₁ = 6m₂

⇒ \(\frac{m_{1}}{m_{2}}=\frac{6}{6}=\frac{1}{1}\)
m₁ : m₂ = 1 : 1
∴ కావలసిన నిష్పత్తి = 1 : 1.
A, B బిందువులను మూలబిందువు 1 : 1 నిష్పత్తిలో విభజిస్తుంది.
కావున మూలబిందువును AB రేఖాఖండానికి మధ్యబిందువు అంటారు.

(b) బిందువు P(2, 3) ఏ నిష్పత్తిలో విభజిస్తుంది ?
సాధన.
A (6, 9), B (- 6, – 9) ను P (2, 3) m₁ : m₂ నిష్పత్తిలో విభజిస్తుంది అనుకొందాం. 1) 1 ( m (-6) + ma(6) ma (-9) + ma(9)]
(2, 3) = \(\left(\frac{\mathrm{m}_{1}(-6)+\mathrm{m}_{2}(6)}{\mathrm{m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1}(-9)+\mathrm{m}_{2}(9)}{\mathrm{m}_{1}+\mathrm{m}_{2}}\right)\)

(2, 3) = \(\left(\frac{-6 m_{1}+6 m_{2}}{m_{1}+m_{2}}, \frac{-9 m_{1}+9 m_{2}}{m_{1}+m_{2}}\right)\)

∴ 2 = \(\frac{-6 m_{1}+6 m_{2}}{m_{1}+m_{2}}\)
⇒ 2m₁ + 2m₂ = – 6m₁ + 6m₂
⇒ 8m₁ = 4m₂
\(\frac{m_{1}}{m_{2}}=\frac{4}{8}=\frac{1}{2}\)
m₁ : m₂ = 1 : 2

(c) బిందువు Q(- 2, – 3) ఏ నిష్పత్తిలో విభజిస్తుంది ?
సాధన.
A (6, 9), B (- 6, – 9) లను Q (- 2, – 3) విభజించే నిష్పత్తి m₁ : m₂ అనుకొనుము.
(- 2, – 3) = \(\left(\frac{-6 m_{1}+6 m_{2}}{m_{1}+m_{2}}, \frac{-9 m_{1}+9 m_{2}}{m_{1}+m_{2}}\right)\)

∴ – 2 = \(\frac{-6 m_{1}+6 m_{2}}{m_{1}+m_{2}}\)
⇒ – 2m₁ – 2m₂ = – 6m₁ + 6m₂
4m₁ = 8m₂
\(\frac{\mathrm{m}_{1}}{\mathrm{~m}_{2}}=\frac{8}{4}=\frac{2}{1}\)
∴ m₁ : m₂ = 2 : 1

(d) బిందువులు P, Qలు AB ని ఎన్ని సమాన భాగాలుగా విభజిస్తాయి ?
సాధన.

బిందువులు P, Q \(\overline{\mathrm{AB}}\) ని 3 సమాన భాగాలుగా విభజిస్తాయి.

(e) P, Q లను ఏమంటారు ?
సాధన.
P, Q లను AB యొక్క సమత్రిఖండన బిందువులని అంటారు. ఈ సమత్రిఖండన బిందువులను త్రిథాకరణ బిందువులని పిలుస్తాము.

ఇవి చేయండి:

కింద ఇవ్వబడిన శీర్షాలు గల త్రిభుజ వైశాల్యం కనుగొనండి. (పేజీ నెం. 180)
ప్రశ్న 1.
(5, 2) (3, – 5) మరియు (- 5, -1 )
సాధన.
బిందువులు: (5, 2), (3, – 5), మరియు (- 5, – 1) లు శీర్షాలుగా గల త్రిభుజ వైశాల్యం ∆ = \(\frac{1}{2}\) |x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₂ – y₁)|
= \(\frac{1}{2}\) |5(- 5 – (- 1) + 3((- 1) – 2) + (- 5) (2 – (- 5))|
= \(\frac{1}{2}\) |(- 5 + 1) + 3(- 3) + – 5(2 + 5)|
= \(\frac{1}{2}\) |- 20 – 9 – 35|
= \(\frac{1}{2}\) |- 64|
= \(\frac{1}{2}\) × 64 = 32 చ.యూ.

ప్రశ్న 2.
(6, – 6), (3, – 7) మరియు (3, 3) (పేజీ నెం. 180)
సాధన.
(6, – 6), (3, – 7) మరియు (3, 3) లు శీర్షాలుగా గల త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) |6(- 7 – 3) +3(3 – (- 6)) + 3(- 6 – (- 7))|
= \(\frac{1}{2}\) | 6(- 10) + 3(9) + 3(1)|
= \(\frac{1}{2}\) |- 60 + 27 + 3|
= \(\frac{1}{2}\) |- 30|
= \(\frac{1}{2}\) × 30 = 15 చ.యూ.

ప్రశ్న 3.
కింద ఇవ్వబడిన బిందువులు సరేఖీయాలు అవుతాయా? కావా ? సరి చూడండి. (పేజీ నెం. 182)
(i) (1, – 1), (4, 1), (- 2, – 3)
సాధన.
ఇచ్చిన బిందువులు = (1, – 1), (4, 1), (- 2, – 3) లతో ఏర్పడే త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) |x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₂ – y₁)|
= \(\frac{1}{2}\) |1[1 – (- 3)] + 4[- 3 – (- 1) + (- 2)[- 1 – 1]|
= \(\frac{1}{2}\) |1(4) + 4 (- 2) – 2 (- 2)|
= \(\frac{1}{2}\) |4 – 8 + 4|
= \(\frac{1}{2}\) |0| = 0
∴ త్రిభుజ వైశాల్యము సున్న ‘0’ కావున ఇచ్చిన బిందువులు సరేఖీయాలు.

(ii) (1, -1), (2, 3), (2, 0)
సాధన.
(1, – 1), (2, 3), (2, 0) బిందువులతో ఏర్పడే త్రిభుజ వైశాల్యం
= \(\frac{1}{2}\) | 1(3 – 0) + 2[0 – (- 1)] +2(- 1 – 3)|
= \(\frac{1}{2}\) |3 + 2 – 8|
= \(\frac{1}{2}\) |5 – 8|
= \(\frac{1}{2}\) |- 3|
= \(\frac{1}{2}\) × 3
= \(\frac{3}{2}\) చ.యూ.
∴ త్రిభుజ వైశాల్యము \(\frac{3}{2}\) చ.యూ. కావున ఇచ్చిన మూడు బిందువులు సరేఖీయాలు కావు.

(iii) (1, – 6), (3, – 4), (4, – 3)
సాధన.
(1, – 6), (3, – 4), (4, – 3) లతో ఏర్పడే త్రిభుజ వైశాల్యం
= \(\frac{1}{2}\) |1[- 4 – (- 3)] + 3[- 3 – (- 6)] + [- 6 – (- 4)]|
= \(\frac{1}{2}\) |1[- 4 + 3] + 3[- 3 + 6] + 4(- 6 – 4)|
= \(\frac{1}{2}\) |1 (- 1) + 3 (3) + 4 (- 2)|
= \(\frac{1}{2}\) |- 1 + 9 – 8|
= \(\frac{1}{2}\) |9 – 9| = 0
∴ త్రిభుజ వైశాల్యము సున్న’ ‘0’ కావున ఇచ్చిన మూడు బిందువులు సరేఖీయాలు.

ప్రశ్న 4.
15 మీ, 17 మీ, 21 మీ భుజాలుగా గల త్రిభుజం వైశాల్యం (హెరాన్ సూత్రం ద్వారా) కనుగొనండి. (పేజీ నెం. 189)
సాధన.
ఇచ్చిన త్రిభుజ భుజాలు
a = 15 మీ b = 17 మీ. మరియు c = 21 మీ.
∴ s =\(\frac{a+b+c}{2}=\frac{15+17+21}{2}=\frac{53}{2}\)

s – a = \(\frac{53}{2}\) – 15 = \(\frac{53-30}{2}=\frac{23}{2}\)

s- b = \(\frac{53}{3}\) – 17 = \(\frac{53-34}{2}=\frac{19}{2}\)

s – c = \(\frac{53}{3}\) – 21 = \(\frac{53-42}{2}=\frac{11}{2}\)

త్రిభుజ వైశాల్యం (హెరాన్ సూత్రం) A = \(\sqrt{S(S-a)(S-b)(S-c)}\)
∴ A = \(\sqrt{\frac{53}{2}\left(\frac{23}{2}\right)\left(\frac{19}{2}\right)\left(\frac{11}{2}\right)}\)
A = \(\sqrt{\frac{53 \times 23 \times 19 \times 11}{16}}\)
A = \(\frac{1}{4} \sqrt{254771}\) చ.మీటర్లు.

ప్రశ్న 5.
బిందువులు (0, 0), (4, 0) మరియు (4, 3) లతో ఏర్పడు త్రిభుజ వైశాల్యంను హెరాన్ సూత్రం ద్వారా కనుగొనండి. (పేజీ నెం. 183)
సాధన.
A (0, 0), B (4, 0), C(4, 3)
a = BC = |y₂ – y₁| = |3 – 0| = 3 యూనిట్లు

b = AC = \(\sqrt{x^{2}+y^{2}}\)
= \(\sqrt{4^{2}+(-3)^{2}}=\sqrt{16+9}\)
= √25 = 5 యూనిట్లు

C = AB = |x₂ – x₁| = |4| = 4 యూ.
S = \(\frac{a+b+c}{2}=\frac{3+4+5}{2}\) = 6
∴ త్రిభుజ వైశాల్యం (హెరాన్ సూత్రం)
A = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{6(6-3)(6-5)(6-4)}\)
= \(\sqrt{6 \times 3 \times 1 \times 2}=\sqrt{36}\) = 6 చ.యూ.
∴ త్రిభుజ వైశాల్యం = 6 చ. యూనిట్లు.

సరిచూచుకొవడం :
3, 4, 5 భుజాలుగా గల త్రిభుజం లంబకోణ త్రిభుజం అవుతుంది.
∴ లంబకోణ త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) × 3 × 4 = 6 చ. యూనిట్లు.

ప్రయత్నించండి:

ప్రశ్న 1.
ఏదేని ఒక బిందువు Aను X-అక్షంపై, మరొక బిందువు Bను Y- అక్షంపై తీసుకొని AOB త్రిభుజ వైశాల్యం కనుగొనండి. మీ మిత్రులు చేసిన వాటిని గమనించండి. మీరేం గమనించారు ? (పేజీ నెం. 178)
సాధన.

A(- 6, 0), B(0, 5) బిందువులు తీసుకొందాం.
∆AOB ఒక లంబకోణ త్రిభుజం అవుతుంది.
∆AOB యొక్క భూమి OA = 6 యూనిట్లు
ఎత్తు OA = 5 యూనిట్లు
∆AOB వైశాల్యం = \(\frac{1}{2}\) × భూమి × ఎత్తు
= \(\frac{1}{2}\) × 6 × 5 = 15 చ.యూ.

గమనించిన అంశాలు :
(i) X – అక్షంపై ఒక బిందువు, Y – అక్షంపై మరొకmబిందువు గల త్రిభుజం లంబకోణ – త్రిభుజం అవుతుంది.
(ii) బిందువులలోని x, y నిరూపకాలు ఒకటి భూమి, మరొకటి ఎత్తు అవుతుంది.
(iii) ఏర్పడు త్రిభుజం’ యొక్క వైశాల్యము x, y ల లబ్దంలో సగం ఉంటుంది.
(x₁ , 0) మరియు (0, y₁) మరియు నిరూపక అక్షాలతో ఏర్పడే త్రిభుజ వైశాల్యం
A = \(\frac{1}{2}\) |x₁ y₁| చ.యూనిట్లు.

ప్రశ్న 2.
బిందువులు (0, – 1), (2, 1) (0, 3) మరియు (- 2, 1) లు శీర్షాలుగా గల చతురస్రము యొక్క వైశాల్యము కనుగొనండి. (పేజీ నెం. 181)
సాధన.

ABCD చతురస్రాన్ని కర్ణం AC, ∆ABC మరియు ∆ADC అనే త్రిభుజాలుగా విభజిస్తుంది.
∴ ∆ABCవైశాల్యం = \(\frac{1}{2}\) |x₁(y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)|
= \(\frac{1}{2}\) |0 (1 – 3) + 2 [3 – (- 1)] + 0(- 1 – 1)|
= \(\frac{1}{2}\) |0 + 8 + 0|
= \(\frac{1}{2}\) |8| = 4 చ. యూనిట్లు,
∴ ∆ABC వైశాల్యం = 4 చ. యూనిట్లు.
∆ADC వైశాల్యం = \(\frac{1}{2}\) |0(1 – 3) + (- 2) [ 3 – (- 1)] +0 (- 1 – 1)|
= \(\frac{1}{2}\) × 8 = 4 చ.యూ.
∆ADC వైశాల్యం = 4 చ.యూ.
చతురస్రం ABCD వైశాల్యం = 2 ∆ABC వైశాల్యం + ∆ADC వైశాల్యం
= 4 + 4 = 8 చ. యూనిట్లు

రెండవ పద్ధతి :
ABCD చతురస్రాన్ని కర్ణం AC రెండు సర్వసమాన త్రిభుజాలు ∆ABC మరియు ∆ADCలుగా విభజిస్తుంది.

∆ABC వైశాల్యం = ∆ADC వైశాల్యం
చతురస్రం ABCD వైశాల్యం = 2 × ∆ABC వైశాల్యం
= 2 × \(\frac{1}{2}\) |0(1 – 3) +2[3 – (- 1)] + 0(- 1 – 1)|
= \(\frac{1}{2}\) |0 + 2 (4) + 0|
= | 8| = 8 చ. యూనిట్లు
∴ ABCD చతుర్భుజ వైశాల్యం = 8 చ. యూనిట్లు

మూడవ పద్ధతి :
చతురస్రం ABCD యొక్క ఒక భుజం AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(2-0)^{2}+\left[(1-(-1))^{2}\right]}\)
= \(\sqrt{2^{2}+2^{2}}=\sqrt{4+4}\)
భుజం AB = √8 యూనిట్లు.
చతురస్ర వైశాల్యం = భుజం × భుజం
= √ 8 × √8 = 8 చ.యూనిట్లు.

నాలుగవ పద్ధతి :
కర్ణం AC పొడవు d = |y₂ – y₁|
= |3 – (- 1)| = |4| = 4 యూ.
చతురస్ర వైశాల్యం A = \(\frac{\mathrm{d}^{2}}{2}=\frac{4^{2}}{2}\)
= \(\frac{16}{2}\) = 8 చ.యూనిట్లు.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
బిందువులు A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) నిరూపకతలంపై ఉన్నవనుకొనుము. అయిన కింది త్రిభుజాల యొక్క వైశాల్యమును కనుగొనండి. మరియు వాటి వైశాల్యముల గురించి గ్రూపులలో మీ స్నేహితులతో చర్చించండి. (పేజీ నెం. 178)

సాధన.
(i) 1వ పటం నుండి : –

A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) = (0, 0)
ABC ఒక లంబకోణ త్రిభుజము,
∴ ∆ABC వైశాల్యం = \(\frac{1}{2}\) భూమి × ఎత్తు
= \(\frac{1}{2}\) BC × AB
= \(\frac{1}{2}\) |x₂ (y₁ – y₂) | చ.యూ.
గమనిక : వైశాల్యము ధనాత్మకము కావున పరమ మూల్యం | | ను తీసుకొంటాము. ..

(ii) 2వ పటం నుండి :

భూమి BC = ya
ఎత్తు AB = x₁ – x₂
∆ABC వైశాల్యం = \(\frac{1}{2}\) BC × AB
= \(\frac{1}{2}\) |y₂ (x₂ – x₁)| చ.యూ.

(iii) 3వ పటం నుండి :

∆ABC వైశాల్యం = \(\frac{1}{2}\) AB × BC
= \(\frac{1}{2}\) |(x₂ – x₁) (y₂ – y₃) చ.యూ.

(iv) 4 వ పటం నుండి :

∴ ∆ABC వైశాల్యం – – BC X AB
= \(\frac{1}{2}\) |(x₂ – x₃) (y₁ – y₂)|

గమనిక :
X, Y అక్షాలకు సమాంతరంగా భుజాలు గల త్రిభుజం యొక్క వైశాల్యము X నిరూపకాల భేదం మరియు y నిరూపకాల భేదాల లబ్దానికి సమానము. మరియు ఏర్పడే త్రిభుజము ‘ లంబకోణ త్రిభుజము అవుతుంది.

ప్రశ్న 2.
కింది. బిందువులతో ఏర్పడే త్రిభుజ వైశాల్యాన్ని కనుగొనండి. (పేజీ నెం. 181)
(i) (2, 0), (1, 2), (1, 6)
(ii) (3, 1), (5, 0), (1, 2)
(iii) (- 1.5, 3), (6, 2), (- 3, 4)
(a) మీరేం గమనించారు ?
(b) ఈ బిందువులను మూడు వేర్వేరు గ్రాఫులలో గుర్తించండి. మీరేం గమనించారు ? మీ మిత్రునితో చర్చించండి.
(c) వైశాల్యం ‘0’ (సున్నా) చ.యూనిట్లు గల త్రిభుజమును గీయగలమా ? మరి దీని అర్థమేమిటి ?
(i) (2, 0), (1, 2), (1, 6)
సాధన.
మూడవ బిందువు (- 1, 6) గా తీసుకొందాం.
(2, 0), (1, 2), (-1, 6) బిందువులు శీర్షాలుగా గల త్రిభుజ వైశాల్యం A = \(\frac{1}{2}\) |x₁ (y₂ – y₃3) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)|
= \(\frac{1}{2}\) |2(2 – 6) + 1(6 – 0) + (- 1)(0 – 2)|
= \(\frac{1}{2}\) (2(- 4) + 6 – 1(- 2)|
= \(\frac{1}{2}\) |- 8 + 6 + 2|
= \(\frac{1}{2}\) |0| = 0.
త్రిభుజ వైశాల్యం = 0 చ. యూనిట్లు.

(ii) (3, 1), (5, 0), (1, 2)
సాధన.
∆ = \(\frac{1}{2}\) |3(0 – 2) + 5(2 – 1) + 1(1 – 0)|
= \(\frac{1}{2}\) |- 6 + 5 + 1| = 0
త్రిభుజ వైశాల్యం = 0 చ. యూనిట్లు.

(iii) (- 1.5, 3), (6, 2), (- 3, 4)
సాధన.
రెండవ బిందువు (6, – 2) గా తీసుకొందాం.
(- 1.5, 3), (6, – 2) మరియు (- 3, 4)
బిందువులు శీర్షాలుగా గల త్రిభుజ వైశాల్యం, = \(\frac{1}{2}\) |(- 1.5) [- 2 – 4] + 6 (4 – 3) + (- 3) [3 – (- 2)]|
= \(\frac{1}{2}\) |(- 1.5) (- 6) + 6 (1) – 3 (5)|
= \(\frac{1}{2}\) |9 + 6 – 15|
= \(\frac{1}{2}\) |15 – 15| = \(\frac{1}{2}\) |0| = 0

(a) పై మూడు సందర్భాలలోనూ త్రిభుజం యొక్క వైశాల్యము శూన్యము అనగా ఇచ్చిన బిందువులు శీర్షాలుగా గల త్రిభుజం ఏర్పడదు అని తెలుస్తున్నది. కావున మూడు సందర్భాలలోను ఇచ్చిన మూడు బిందువులు ఒకే రేఖపై ఉంటాయి. అనగా ఆ మూడు బిందువులు సరేఖీయాలు అవుతాయి. కాబట్టి వైశాల్యము ‘0’ (సున్నా) చ.యూనిట్లు గల త్రిభుజాన్ని గీయలేము. త్రిభుజ వైశాల్య సూత్రం = 0 చ. యూనిట్లు.
∆ ABC వైశాల్యం సున్న ⇒ A, B, C లు సరేఖీయాలు.

(b) ఈ బిందువులను మూడు వేర్వేరు గ్రాఫులలో గుర్తించండి. మీరేం గమనించారు? మీ మిత్రులతో చర్చించండి. (పేజీ నెం. 181)
సాధన.
(2, 0), (1, 2), (- 1, 6), (3, 1), (5, 0), (1, 2), (- 1.5, 3), (6, – 2), (- 3, 4) లను గ్రాఫ్ పై గుర్తించుట.

కావున ఇచ్చిన బిందువులు సరేఖీయాలు.

(c) వైశాల్యం )(సున్నా). చ.యూనిట్లు గల త్రిభుజమును గీయగలమా ? మరి దీని అర్థమేమిటి ? (పేజీ నెం. 181)
సాధన.
వైశాల్యం 0 చ.యూ, గల త్రిభుజాన్ని నిర్మించలేము. దీని అర్థం ఇచ్చిన బిందువులు సరేఖీయాలు అనగా ఒకే సరళరేఖ పై గల బిందువులు

ఇవి చేయండి:

కిందనీయబడిన బిందువులను నిరూపకతలంపై గుర్తించి వాటిని కలుపుము.
(పేజీ నెం. 185)
(i) A(1, 2), B(- 3, 4) మరియు C(7,- 1)
(ii) P(3, – 5), Q(5, – 1), R(2, 1) మరియు S(1, 2) ఇందులో ఏది సరళరేఖను సూచిస్తుంది ? ఏది సూచించదు ? ఎందుకు?
సాధన.

(i) వ సమస్యలోని బిందువులు A, B, C లు – శేఖను సూచిస్తాయి.
(ii) వ సమస్యలోని బిందువులు P, Q, R, S లు సరళరేఖను సూచించవు.
ఎందుకనగా A, B, C లు సరేఖీయ బిందువులు. కాబట్టి ఒకే సరళరేఖపై ఉంటాయి. P, Q, R, S లు సరేఖీయాలు కావు. కావున ఒకే సరళరేఖపై ఉండవు.

కింది బిందువులతో ఏర్పడు రేఖాఖండము \(\overline{\mathbf{A B}}\) వాలును కనుగొనండి. (పేజీ నెం. 188)
(i) A(4, -6) మరియు B (7, 2)
సాధన.
\(\overline{\mathbf{A B}}\) వాలు, m =\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

= \(\frac{2-(-6)}{7-4}\)

= \(\frac{2+6}{3}\) = \(\frac{8}{3}\).

(ii) A(8, – 4) మరియు B (-4, 8)
సాధన.
AB వాలు, m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

= \(\frac{8-(-6)}{-4-8}\)

= \(\frac{12}{-12}\) = – 1

(iii) A(- 2, – 5) మరియు B(1, – 7) .
సాధన.
AB వాలు, m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

= \(\frac{-7-(-5)}{1-(-2)}=\frac{-7+5}{1+2}=\frac{-2}{3}\)

ప్రయత్నించండి:

కింద ఇవ్వబడిన బిందువులు \(\overline{\mathbf{A B}}\) రేఖపై ఉన్నవి. \(\overline{\mathbf{A B}}\) రేఖ వాలు. కనుగొనండి. (పేజీ నెం. 188)
ప్రశ్న 1.
A(2, 1) మరియు B(2, 6)
సాధన.
\(\overline{\mathbf{A B}}\) వాలు, m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

= \(\frac{6-1}{2-2}=\frac{6}{0}\) నిర్వచించబడదు.

ప్రశ్న 2.
A(- 4, 2) మరియు B (- 4, – 2)
\(\overline{\mathbf{A B}}\) వాలు, m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{-2-2}{-4-(-4)}\)
= \(\frac{-4}{-4+4}=\frac{4}{0}\) నిర్వచించబడదు.

ప్రశ్న 3.
A(- 2, 8) మరియు B (- 2, – 2)
సాధన.
\(\overline{\mathbf{A B}}\) వాలు, m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

= \(=\frac{-2-8}{-2+2}\)

= \(\frac{-10}{0}\) నిర్వచించబడదు.

∴ వాలు నిర్వచింపబడదు.

ప్రశ్న 4.
“ఇచ్చిన బిందువులతో ఏర్పడు \(\overline{\mathbf{A B}}\) రేఖాఖండం Y-అక్షానికి సమాంతరంగా ఉంటుంది”. ఈ వాక్యము సరైనదేనా ? ఎందుకు ? అయితే వాలు ఏ విధంగా ఉంటుంది? (పేజీ నెం. 188)
సాధన.
“ఇచ్చిన బిందువులతో ఏర్పడు \(\overline{\mathbf{A B}}\) రేఖండము Y – అక్షానికి సమాంతరంగా ఉంటుంది” అనే ఈ వాక్యము సరైనదే. ఎందుకనగా ఇచ్చిన రెండు బిందువులలోని X నిరూపకాలు సమానంగా కలవు. అనగా ఇచ్చిన రెండు బిందువులు (x₁, y₁) మరియు (x₂, y₂) రూపంలో ఉన్నాయి. Y – అక్షానికి సమాంతరంగా గల రేఖల యొక్క వాలు నిర్వహించబడదు.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
y = x + 7 సమీకరణం ఒక సరళరేఖను సూచిస్తుందా? నిరూపకతలంలో గీసి చూడండి. ఈ సరళరేఖ X – అక్షాన్ని ఏ బిందువు వద్ద ఖండిస్తుంది? అదే విధంగా ఈ సరళరేఖ Y – అక్షంతో ఎంత కోణం చేస్తుంది ? మీ మిత్రులతో … చర్చించండి. : (పేజీ నెం. 185)
సాధన.
y = x + 7

y = x + 7 సూచించు సరళరేఖ X – అక్షాన్ని (0, – 7) బిందువు వద్ద ఖండిస్తుంది. మరియు ఈ సరళరేఖ 1 0 | y = 0 + 7 = 7 | (0, 7) .
Y- అక్షంతో ధనదిశలో 135° కోణాన్ని, రుణదిశలో 45° కోణాన్ని చేస్తుంది.
y= x + 7 గ్రాఫ్ :

ప్రశ్న 2.
బిందువులు A(3, 2), B (- 8, 2) లు \(\overline{\mathbf{A B}}\) రేఖపై ఉన్నచో ఆ రేఖ వాలును కనుగొనండి. \(\overline{\mathbf{A B}}\) రేఖ ఎప్పుడు X-అక్షమునకు సమాంతరంగా ఉంటుంది ? ఎందుకు ? మీ స్నేహితులతో గ్రూపులలో చర్చించండి. (పేజీ నెం. 188)
సాధన.
బిందువులు = A (3, 2), B (- 8, 2) అయిన \(\overline{\mathbf{A B}}\) రేఖవాలు (m) = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{2-2}{-8-3}=\frac{0}{-11}\) = 0
A, B బిందువులలో Y నిరూపకాలు సమానంగా ఉన్నప్పుడు \(\overline{\mathbf{A B}}\) రేఖ X – అక్షానికి సమాంతరంగా ఉంటుంది. ఈ సందర్భంలో \(\overline{\mathbf{A B}}\) రేఖ వాలు ‘0’, అనగా ఒక రేఖ వాలు ‘0’ (సున్న) అయితే ఆ రేఖ X – అక్షానికి సమాంతరంగా ఉంటుంది.

ఉదాహరణలు:

ప్రశ్న 1.
A (4, 0) మరియు B (8, 0) బిందువుల మధ్య దూరం ఎంత ? (పేజీ నెం. 162)
సాధన.
A, B లలో y – నిరూపకాలు సమానం.
A, B ల మధ్య దూరం = |x₂ – x₁|
= |8 – 4| = 4 యూనిట్లు.

ప్రశ్న 2.
A మరియు B బిందువులు వరుసగా (8, 3), ( – 4, 3), అయిన వాటి మధ్యదూరాన్ని కనుక్కోండి. (పేజీ నెం. 162)
సాధన.
A (8, 3), B (- 4, 3), బిందువులలో y నిరూపకాలు సమానం.
A, B ల మధ్య దూరం = |x₂ – x₁|
. = |- 4 – 8|
= |- 12| = 12 యూనిట్లు.

ప్రశ్న 3.
బిందువులు A(4, 3) మరియు B(8, 6)ల మధ్యదూరాన్ని కనుగొనండి. (పేజీ నెం. 164)
సాధన.
A (4, 3), B (8, 6) (x₁, y₁), (x₂, y₂) లతో పోల్చగా x₁ = 4, x₂ = 8, y₁ = 3, y₂ = 6
∴ AB ల మధ్య దూరం = d = \(\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}\)
= \(\sqrt{(8-4)^{2}+(6-3)^{2}}=\sqrt{4^{2}+3^{2}}\)
= \(\sqrt{16+9}=\sqrt{25}\) = 5 యూనిట్లు.

ప్రశ్న 4.
బిందువులు A (4, 2), B (7, 5) మరియు C(9, 7) లు ఒకే సరళరేఖపై ఉన్నాయని చూపండి. (పేజీ నెం. 164)
సాధన.
ఇచ్చిన బిందువులు A (4, 2), B (7, 5), C (9, 7) AB, BC, AC లను కనుగొందాము.
బిందువుల మధ్య దూరం = \(\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}\)
AB = d = \(\sqrt{(7-4)^{2}+(5-2)^{2}}\)
= \(\sqrt{3^{2}+3^{2}}=\sqrt{9+9}=\sqrt{18}\)
= \(\sqrt{9 \times 2}=3 \sqrt{2}\)

BC = \(\sqrt{(9-7)^{2}+(7-5)^{2}}\)
= \(\sqrt{2^{2}+2^{2}}=\sqrt{4+4}=\sqrt{4 \times 2}=2 \sqrt{2}\)

AC = \(\sqrt{(9-4)^{2}+(7-2)^{2}}\)
= \(\sqrt{5^{2}+5^{2}}=\sqrt{25+25}=\sqrt{50}\)
= \(\sqrt{25 \times 2}\) = 5√2
AB + BC = 3√2 + 2√2 = 5√2 = AC.
∴ AB + BC = AC.
కావున A(4, 2), B(7, 5) మరియు C(9, 7)లు ఒకే సరళరేఖపై ఉన్నాయి.

ప్రశ్న 5.
బిందువులు (3, 2), (- 2, – 3) మరియు (2, 3)లు త్రిభుజాన్ని ఏర్పరుస్తాయా ? (పేజీ నెం. 165)
సాధన.
ఇచ్చిన బిందువులు A(3, 2), B(- 2, – 3), C(2, 3) AB, BC, AC లను కనుగొందాము.
AB = \(\sqrt{(-2-3)^{2}+(-3-2)^{2}}\)
= \(\sqrt{(-5)^{2}+(-5)^{2}}\)
= \(\sqrt{25+25}=\sqrt{50}\)
= 7.07 యూనిట్లు (సుమారుగా)

BC = \(\sqrt{[2-(-2)]^{2}+[3-(-3)]^{2}}\)
= \(\sqrt{4^{2}+6^{2}}=\sqrt{16+36}\)
= √52 = 7.21 యూనిట్లు (సుమారుగా)

AC = \(\sqrt{(2-3)^{2}+(3-2)^{2}}\)
= \(\sqrt{(-1)^{2}+(1)^{2}}=\sqrt{2}\)` `
= 1.41 యూనిట్లు (సుమారుగా)
పై విలువలను బట్టి ఏ రెండు విలువల మొత్తమైనా మూడవ దాని కంటే ఎక్కువ. (త్రిభుజ అసమానత్వ నియమం ప్రకారం త్రిభుజంలో ఏవైనా రెండు భుజాల పొడవుల మొత్తం మూడవదాని కంటే ఎక్కువ) కావున బిందువులు A, B మరియు C లు ఒక విషమబాహు త్రిభుజాన్ని ఏర్పరుస్తాయి.
`(లేదా)
AB, BC, ACలలో ఏ రెండు రేఖాఖండాల మొత్తమైనా మూడవ దానికి సమానం కాలేదు. అనగా A, B, C లు సరేఖీయాలు కావు. కావున A, B, Cలు త్రిభుజాన్ని ఏర్పరుస్తాయి.

ప్రశ్న 6.
బిందువులు (1, 7), (4, 2), (- 1, – 1) మరియు (- 4, 4) లు ఒక చతురస్రం యొక్క శీర్షాలు అవుతాయని చూపండి. (పేజీ నెం. 165)
సాధన.
ఇచ్చిన బిందువులు A (1, 7), B (4, 2), C (-1, -1)
రెండు బిందువుల మధ్య దూరం d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

AB = d = \(\sqrt{(4-1)^{2}+(2-4)^{2}}\)
= \(\sqrt{9+25}=\sqrt{34}\) యూనిట్లు

BC = \(\sqrt{(-1-4)^{2}+(-1-2)^{2}}\)
= \(\sqrt{25+9}=\sqrt{34}\) యూనిట్లు

CD = \(\sqrt{(-4-(-1))^{2}+(-4-(-1))^{2}}\)
= \(\sqrt{9+25}=\sqrt{34}\) యూనిట్లు

DA = \(\sqrt{(-4-1)^{2}+(4-7)^{2}}\)
= \(\sqrt{25+9}=\sqrt{34}\) యూనిట్లు
మరియు కర్ణాలు
AC = \(\sqrt{(-1-1)^{2}+(-1-7)^{2}}\)
= \(\sqrt{4+64}=\sqrt{68}\) యూనిట్లు

BD = \(\sqrt{(-4-4)^{2}+(4-2)^{2}}\)
= \(\sqrt{64+4}=\sqrt{68}\) యూనిట్లు
AB = BC = CD = DA మరియు AC = BD. నాలుగు భుజాలు సమానము మరియు కర్ణాలు సమానం.
∴ ABCD ఒక చతురస్రం అవుతుంది.

ప్రశ్న 7.
ప్రక్క పటం ఒక తరగతి గదిలోని డెస్క్ల యొక్క అమరికను చూపిస్తుంది. మాధురి, మీన, పల్లవిలు వరుసగా A (3, 1), B(6, 4) మరియు C(8, 6) స్థానాలలో కూర్చున్నారు. వారు ముగ్గురూ ఒకే సరళరేఖలో కూర్చున్నారని మీరు భావిస్తున్నారా ? మీ సమాధానానికి సరైన కారణం తెలపండి. (పేజీ నెం. 166)

సాధన.
A(3, 1), B(6, 4), C (8, 6)
రెండు బిందువుల మధ్య దూరం \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
AB = \(\sqrt{(6-3)^{2}+(4-1)^{2}}\)
= \(\sqrt{9+9}=\sqrt{9 \times 2}=3 \sqrt{2}\) యూనిట్లు

BC = \(\sqrt{(8-6)^{2}+(6-4)^{2}}\)
= \(\sqrt{4+4}=\sqrt{4 \times 2}=2 \sqrt{2}\) యూనిట్లు

AC = \(\sqrt{(8-3)^{2}+(6-1)^{2}}\)
= \(\sqrt{25+25}=\sqrt{25 \times 2}=\dot{5} \sqrt{2}\) యూనిట్లు

దీని నుండి ∴ AB + BC = 3√2 + 2√2 = 5√2 = AC
కాబట్టి A, B, C బిందువులు సరేఖీయాలు. కాబట్టి వారు ముగ్గురూ ఒకే సరళరేఖలో కూర్చున్నారు.

ప్రశ్న 8.
బిందువు (x, y) అనునది బిందువులు (7, 1) మరియు (3, 5) లకు – సమాన దూరంలో ఉన్నది. అయిన X మరియు y ల మధ్య సంబంధమును కనుగొనండి. (పేజీ నెం. 166).
సాధన.
P(x, y) బిందువు, A (7, 1) మరియు B (3, 5) లకు సమానదూరంలో ఉన్నది.
∴ AP = BP
⇒ AP² = BP²
AP = \(\sqrt{(7-x)^{2}+(1-y)^{2}}\)
⇒ AP² = (7 – x)² + (1 – y)²

BP = \(\sqrt{(3-x)^{2}+(5-y)^{2}}\)
⇒ BP² = (3 – x)² + (5 – y)²

(7 – x)² + (1 – y)² = (3 – x)² + (5 –²y)²
= 49 – 14x + x² + 1 – 2y + y²
= 9 – 6x + x² + 25 – 10y + y²
x² + y² – 14x – 2y + 50 – x² – y² + 6x + 10y – 34 = 0
– 8x + 8y + 16 = 0
– 8 [x – y – 2] = 0
∴ x – y – 2 = 0
కావలసిన సంబంధము x – y = 2.

ప్రశ్న 9.
A(6, 5) మరియు B(- 4, 3) లకు సమానదూరంలో Y-అక్షంపై ఉన్న బిందువు నిరూపకాలు కనుగొనండి. (పేజీ నెం. 167)
సాధన.
Y-అక్షంపై గల బిందువు (0, y) రూపంలో ఉంటుంది.
∴ A (6, 5) మరియు B (- 4, 3) బిందువులకు సమాన దూరంలో Y-అక్షంపై నున్న బిందువు P(0, y) అనుకొందాము.
PA = \(\sqrt{(6-0)^{2}+(5-y)^{2}}\)
= \(\sqrt{36+25-10 y+y^{2}}\)
= \(\sqrt{y^{2}-10 y+61}\)

PA² = y² – 10y + 61

PB = \(\sqrt{(-4-0)^{2}+(3-y)^{2}}\)
= \(\sqrt{16+9-6 y+y^{2}}\)
= \(\sqrt{y^{2}-6 y+25}\)

PB² = y² – 6y + 25
PA = PB
⇒ PA² = PB²
y² – 10y + 61 = y² – 6y + 25
y² – 10y + 61 – y² + 6y – 25 = 0
– 4y + 36 = 0
4y = 36
∴ y = \(\frac{36}{4}\) = 9
∴ కావలసిన బిందువు P (0, y) = (0, 9).

సరిచూచుట :
AP = \(\sqrt{(6-0)^{2}+.(5-9)^{2}}\)
= \(\sqrt{36+16}=\sqrt{52}\)

BP = \(\sqrt{(-4-0)^{2}+(3-9)^{2}}\)
= \(\sqrt{16+36}=\sqrt{52}\)

ప్రశ్న 10.
బిందువులు (4, – 3) మరియు (8, 5) లచే ఏర్పడు. రేఖాఖండమును 3 : 1 నిష్పత్తిలో అంతరంగా విభజించు బిందువు నిరూపకాలను కనుగొనండి. (పేజీ నెం. 171)
సాధన.
ఇచ్చిన బిందువులు (4, -3) మరియు (8, 5) లను P (x, y) 3 : 1 నిష్పత్తిలో విభిజిస్తుంది అనుకొనుము.
విభజన సూత్రం P(x, y) = \(\left(\frac{\mathrm{m}_{1} \mathrm{x}_{2}+\mathrm{m}_{2} \mathrm{x}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1} \mathrm{y}_{2}+\mathrm{m}_{2} \mathrm{y}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\right)\)

= \(\left(\frac{3(8)+1(4)}{3+1}, \frac{3(5)+1(-3)}{3+1}\right)\)

= \(\left(\frac{24+4}{4}, \frac{15-3}{4}\right)=\left(\frac{28}{4}, \frac{12}{4}\right)\)

∴ కావలసిన బిందువు P(x, y) = (7, 3).

ప్రశ్న 11.
బిందువులు (3, 0) మరియు (-1, 4) లచే ఏర్పడు – రేఖాఖండం యొక్క మధ్యబిందువును కనుగొనండి. (పేజీ నెం. 171)
సాధన.
బిందువులు (3, 0) మరియు (- 1, 4) లచే ఏర్పడు రేఖాఖండం యొక్క మధ్యబిందువు M(x, y) అనుకొనిన,
మధ్యబిందువు M(x, y) = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
M(x, y) = \(\left(\frac{3+(-1)}{2}, \frac{0+4}{2}\right)\)
= \(\left(\frac{2}{2}, \frac{4}{2}\right)\) = (1, 2).

ప్రశ్న 12.
బిందువులు (3, – 5), (- 7, 4), (10, – 2) లు శీర్షాలుగా గల త్రిభుజం యొక్క గురుత్వ కేంద్రంను కనుగొనండి. (పేజీ నెం. 173) .
సాధన.
ఇచ్చిన బిందువులు (3, – 5), (- 7, 4), (10, – 2).
గురుత్వ కేంద్రం నిరూపకాలు = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)
= \(\left(\frac{3+(-7)+10}{3}, \frac{(-5)+4+(-2)}{3}\right)\)
= \(\left(\frac{6}{3}, \frac{-3}{3}\right)\) = (2, – 1)
∴ గురుత్వ కేంద్రం = (2, – 1).

ప్రశ్న 13.
బిందువులు AC- 6, 10) మరియు B (3, – 8) లచే ఏర్పడు రేఖాఖండమును బిందువు (-4, 6) ఏ నిష్పత్తిలో విభజిస్తుంది ? (పేజీ నెం. 173)
సాధన.
A(- 6, 10), B(3, – 8) రేఖాఖండాన్ని (- 4, 6) అంతరంగా m₁ : m₂ నిష్పత్తిలో విభజిస్తుందనుకొనిన
(- 4, 6) = \(\left(\frac{3 m_{1}-6 m_{2}}{m_{1}+m_{2}}, \frac{-8 m_{1}+10 m_{2}}{m_{1}+m_{2}}\right)\)
(x, y) = (a, b) ⇒ x = a మరియు y = b అని మనకు తెలుసు.
∴ – 4 = \(\frac{3 m_{1}-6 m_{2}}{m_{1}+m_{2}}\) ………. (1) మరియు

6 = \(\frac{-8 m_{1}+10 m_{2}}{m_{1}+m_{2}}\) ……….. (2)

(1) ⇒ – 4m₁ – 4m₂ = 3m₁ – 6m₂
– 4m₁ – 3m₁ = – m₂ + 4m₂
– 7m₁ = – 2m₂
7m₁ = 2m₂
∴ \(\frac{\mathrm{m}_{1}}{\mathrm{~m}_{2}}=\frac{2}{7}\)
అనగా m₁ : m₂ = 2 : 7
ఈ నిష్పత్తి (2) సమీకరణాన్ని కూడా సంతృప్తిపరుస్తుందని చూపవచ్చును.
(2) ⇒ 6 =
∴ 6 = 6 కావున బిందువులు A (-6, 10) మరియు B (3, – 8) లచే ఏర్పడు రేఖాఖండమును (- 4, 6) బిందువు 2 : 7 నిష్పత్తిలో విభజిస్తుంది.

ప్రశ్న 14.
బిందువులు A(2, – 2) మరియు B(- 7, 4) లచే, ఏర్పడు రేఖాఖండము యొక్క ప్రాథాకరణ బిందువులు కనుగొనండి. (పేజీ నెం. 175)
సాధన.
AB రేఖాఖండం యొక్క త్రిథాకరణ బిందువులు P మరియు Q లు అనుకొనిన AP = PQ = QB (పటంలో చూపినట్లు).

అందువల్ల AB రేఖాఖండాన్ని బిందువు P అంతరంగా 1 : 2 నిష్పత్తిలో విభజిస్తుంది. కావున విభజన సూత్రం నుండి.
P (x, y) = \(\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)

= \(\left(\frac{1(-7)+2(2)}{1+2}, \frac{1(4)+2(-2)}{1+2}\right)\)

= \(\left(\frac{-7+4}{3}, \frac{4-4}{3}\right)=\left(\frac{-3}{3}, \frac{0}{3}\right)\) = (- 1, 0)
ఇపుడు బిందువు Q కూడా AB రేఖాఖండాన్ని అంతరంగా 2 : 1 నిష్పత్తిలో విభజిస్తుంది.
అందువల్ల బిందువు Q యొక్క నిరూపకాలు = \(\left(\frac{2(-7)+1(2)}{2+1}, \frac{2(4)+1(-2)}{2+1}\right)\)
అనగా \(\left(\frac{-14+2}{3}, \frac{8-2}{3}\right)\)
= \(\left(\frac{-12}{3}, \frac{6}{3}\right)\) = (- 4, 2)
కాబట్టి, AB రేఖాఖండము యొక్క ప్రాథాకరణ బిందువులు P(- 1, 0) మరియు Q(- 4, 2).

ప్రశ్న 15.
బిందువులు (5, – 6) మరియు (- 1, – 4) లచే ఏర్పడు రేఖాఖండమును Y- అక్షము ఏ నిష్పత్తిలో విభజిస్తుంది? ఆ ఖండన బిందువును కనుగొనండి. (పేజీ నెం. 176)
సాధన.
బిందువులు A(5, – 6) మరియు B(- 1, – 4) లచే ఏర్పడు రేఖాఖండము AB ని Y – అక్షంపైనున్న బిందువు
P(0, y), m₁ : m₂ నిష్పత్తిలో విభజిస్తుందనుకొంటే
P(o, y) = \(\left(\frac{\mathrm{m}_{1}(-1)+\mathrm{m}_{2}(5)}{\mathrm{m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1}(-4)+\mathrm{m}_{2}(-6)}{\mathrm{m}_{1}+\mathrm{m}_{2}}\right)\)

(0, y) = \(\left(\frac{-m_{1}+5 m_{2}}{m_{1}+m_{2}}, \frac{-4 m_{1}-6 m_{2}}{m_{1}+m_{2}}\right)\)

⇒ \(\frac{-\mathrm{m}_{1}+5 \mathrm{~m}_{2}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\) = 0
⇒ – m₁ + 5m₂ = 0
⇒ – m₁ = – 5m₂
⇒ m₁ = 5m₂
\(\frac{\mathrm{m}_{1}}{\mathrm{~m}_{2}}=\frac{5}{1}\)
Y- అక్షం విభజించే నిష్పత్తి = m₁ : m₂ = 5 : 1
ఇప్పుడు y = \(\frac{-4 m_{1}-6 m_{2}}{m_{1}+m_{2}}\)

⇒ \(\frac{-4 \frac{m_{1}}{m_{2}}-6}{\frac{m_{1}}{m_{2}}+1}=\frac{-4\left(\frac{5}{1}\right)-6}{\frac{5}{1}+1}=\frac{-20-6}{6}\)

⇒ y = \(\frac{-26}{6}\) = \(\frac{-13}{3}\)
∴ ఖండన బిందువు P = ( 0, \(\frac{-13}{3}\))

2వ పద్ధతి :
A(x₁, y₁), B (x₂, y₂) బిందువులను Y- అక్షం విభజించే నిష్పత్తి m₁ : m₂ = – x₁ : x₂
∴ (5, – 6) మరియు (-1, – 4) లను Y – అక్షం విభజించే నిష్పత్తి = – x₁ : x₂ = – 5 : – 1
= 5 : 1
(5, – 6) మరియు (- 1, – 4) లను 5 : 1 నిష్పత్తిలో విభజించే బిందువే ఖండన బిందువు అవుతుంది.
∴ ఖండన బిందువు =
∴ ఖండన బిందువు P = (0, \(\frac{-13}{3}\))
3వ పద్ధతి :
పాఠ్యపుస్తకంలో కలదు చూడగలరు.

ప్రశ్న 16.
బిందువులు A(7, 3), B(6, 1), C(8, 2) మరియు D(9, 4)లు వరుసగా సమాంతర చతుర్భుజం యొక్క శీర్షాలని చూపండి. (పేజీ నెం. 176)
సాధన.
బిందువులు A(7, 3), B(6, 1), C(8, 2) మరియు D(9, 4) లు వరుసగా ఒక సమాంతర చతుర్భుజం శీర్షాలు అనుకొనిన, సమాంతర చతుర్భుజంలో కర్ణాలు పరస్పరం సమద్విఖండన చేసుకుంటాయని తెలుసు.
∴ అందువల్ల కర్ణాలు AC మరియు BD ల మధ్య బిందువులు సమానం కావాలి.
A (7, 3), C (8, 2) ల మధ్యబిందువు = \(\left(\frac{7+8}{2}, \frac{3+2}{2}\right)=\left(\frac{15}{2}, \frac{5}{2}\right)\)
B(6, 1), D(9, 4) ల మధ్య బిందువు = \(\left(\frac{6+9}{2}, \frac{1+4}{2}\right)=\left(\frac{15}{2}, \frac{5}{2}\right)\)
∴ AC మధ్య బిందువు = DB మధ్య బిందువు.
కాబట్టి బిందువులు A, B, C, D లు సమాంతర చతుర్భుజం యొక్క శీర్షాలు అవుతాయి.

ప్రశ్న 17.
బిందువులు A(6, 1), B (8, 2), C(9, 4) మరియు D(p, 3) లు వరుసగా సమాంతర చతుర్భుజం యొక్క శీర్షాలయిన p యొక్క విలువను కనుగొనండి. (పేజీ నెం. 177)
సాధన.
ఇచ్చిన బిందువులు A(6, 1), B(8, 2), C(9, 4) D(p, 3) సమాంతర చతుర్భుజంలో కర్ణాలు పరస్పరం సమద్విఖండన చేసుకుంటాయని మనకు తెలుసు.
కాబట్టి AC మధ్య బిందువు = BD మధ్య బిందువు
\(\left(\frac{6+9}{2}, \frac{1+4}{2}\right)=\left(\frac{8+\mathrm{p}}{2}, \frac{5}{2}\right)\)

⇒ \(\left(\frac{15}{2}, \frac{5}{2}\right)=\left(\frac{8+\mathrm{p}}{2}, \frac{5}{2}\right)\)

⇒ \(\frac{15}{2}=\frac{8+p}{2}\)
⇒ 15 = 8 + p
⇒ P = 15 – 8 =7
∴ p = 7.

ప్రశ్న 18.
బిందువులు A(1, – 1), B (- 4, 6), C(- 3, – 5)లు శీర్షాలుగా గల త్రిభుజ యొక్క వైశాల్యం కనుగొనండి..
సాధన.
A(1, – 1), B (- 4, 6), C(- 3, – 5) లు శీర్షాలుగా గల త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) |x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)|
= \(\frac{1}{2}\) |1(16 – (- 5) )+ (- 4) (- 5 _ (- 1)) + (- 3) (- 1 – 6)|
= \(\frac{1}{2}\) |11 + 16 + 21|
= \(\frac{1}{2}\) |48| = 24
∴ ∆ ABC వైశాల్యం = 24 చదరపు యూనిట్లు.

ప్రశ్న 19.
బిందువులు A(5, 2), B(4, 7) C(7, – 4)లు శీర్షాలుగా గల త్రిభుజ యొక్క వైశాల్యం కనుగొనండి.
సాధన.
A(1, – 1), B (- 4, 6), C(- 3, – 5) లు శీర్షాలుగా గల త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) |x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)|
= \(\frac{1}{2}\) |5(7 – (- 4)) + 4(- 4 – 2) + 7(2 – 7)|
= \(\frac{1}{2}\) |5(11) + 4(- 6) + 7(- 5)|
= \(\frac{1}{2}\)|55 – 24 – 35|
= \(\frac{1}{2}\) |- 4|
= \(\frac{1}{2}\) × 4 = 2
∴ త్రిభుజ వైశాల్యం = 24 చదరపు యూనిట్లు.

ప్రశ్న 20.
బిందువులు A(- 5, 7), B (- 4, – 5), C(- 1, – 6) మరియు D(4, 5) లు ఒక చతుర్భుజం యొక్క శీర్షాలు అయిన , ABCD చతుర్భుజ. వైశాల్యం కనుగొనండి. (పేజీ నెం. 181)
సాధన.

A, B, C, D లు చతుర్భుజం యొక్క శీర్షాలు.
కర్ణము BD, □ABCDA, ∆ABD మరియు ABCD అనే రెండు త్రిభుజాలుగా విభజిస్తుంది.
∆ABD వైశాల్యం = \(\frac{1}{2}\) |- 5 (- 5 – 5) + (- 4) (5 – 7) + 4 (7 – (-5))|
= \(\frac{1}{2}\) |50 + 8 + 48|
= \(\frac{1}{2}\) |106| = 53
చదరపు యూనిట్లు ∆BCD వైశాల్యం = \(\frac{1}{2}\)|- 4(- 6 – 5) + (- 1)(5 + 5) +4(- 5 – (- 6))|
= \(\frac{1}{2}\) |44 – 10 + 4|
= \(\frac{1}{2}\) |38| = 19 చ.యూ.
□ ABCD చతుర్భుజ వైశాల్యం = ∆ABD వైశాల్యం + ∆BCD వైశాల్యం
= 53 + 19 = 72 చదరపు యూనిట్లు

ప్రశ్న 21.
ఒక తలంలో ఉన్న బిందువులు (3, – 2), (- 2, 8) మరియు (0, 4)లు సరేఖీయ బిందువులు అని చూపండి. (పేజీ నెం. 182)
సాధన.
(3, – 2), (- 2, 8) మరియు (0, 4) లతో ఏర్పడే త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) |x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₂ – y₁)|
= \(\frac{1}{2}\) |3(8 – 4) + (- 2) (4 – (- 2)) + 0 ((- 2) – 8)|
= \(\frac{1}{2}\) |12 – 12| = 0
∴ త్రిభుజ వైశాల్యం సున్నా ‘0’. కావున పై ఇచ్చిన మూడు బిందువులు సరేఖీయ బిందువులు.

ప్రశ్న 22.
బిందువులు (1, 2), (- 1, b), (- 3, – 4) సరేఖీయాలైతే ‘b’ విలువను కనుగొనండి. (పేజీ నెం. 183)
సాధన.
ఇచ్చిన బిందువులు
A(1, 2), B(- 1, b), C(- 3, – 4) అనుకొనుము.
∆ABC వైశాల్యం = \(\frac{1}{2}\) |x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₂ – y₁)|
= \(\frac{1}{2}\) |1(b – (- 4)) + (- 1) (- 4 – 2) + (- 3)(2 – b)|
= \(\frac{1}{2}\) |(b + 4) – 1(- 6) – 3(2 – b)|
= \(\frac{1}{2}\) |1(b + 4) + 6 – 6 + 3b|
= \(\frac{1}{2}\) |b + 4 + 6 – 6 + 36|
= \(\frac{1}{2}\) |4b + 4|
= \(\frac{1}{2}\) × 2| 2b + 2 | = |2b + 2| = 0 (∵ ఇచ్చిన బిందువులు సరేఖీయాలు త్రిభుజ వైశాల్యం సున్న)
⇒ 2b + 2 = 0 ⇒ 2b = – 2
∴ b = \(\frac{-2}{2}\) = -1.

ప్రశ్న 23.
12మీ, 9మీ, 15మీ పొడవులు గల భుజాలతో ఏర్పడిన త్రిభుజ వైశాల్యంను “హెరాన్ సూత్రం”ను ఉపయోగించి కనుక్కొందాం. (పేజీ నెం. 183)
సాధన.
A = \(\sqrt{S(S-a)(S-b)(S-c)}\) (∵ S = \(\frac{a+b+c}{2}\))
S = \(\frac{12+9+15}{2}=\frac{36}{2}\) = 18 మీ.

అపుడు
S – a = 18 – 12 = 6 మీ.
S – b = 18 – 9 = 9 మీ.
S – C = 18 – 15 = 3 మీ.
A = \(\sqrt{18(6)(9)(3)}=\sqrt{2916}\) = 54 చదరపు మీటర్లు.

ప్రశ్న 24.
ఒక రేఖాఖండం యొక్క తొలి, చినరి బిందువుల వరుసగా (2, 3), (4, 5). ఆ రేఖాఖండం యొక్క వాలును కనుగొనండి. (పేజీ నెం. 188)
సాధన.
రేఖాఖండం యొక్క తొలి, చివరి బిందువులు (2, 3), (4, 5) అయిన ఆ రేఖాఖండం వాలు,
m = \(\frac{\mathrm{y}_{2}-\mathrm{y}_{1}}{\mathrm{x}_{2}-\mathrm{x}_{1}}=\frac{5-3}{4-2}=\frac{2}{2}\) = 1
∴ ఇచ్చిన రేఖాఖండం యొక్క వాలు = 1

ప్రశ్న 25.
బిందువులు P(2, 5) మరియు Q(x, 3) ల గుండా పోయే రేఖవాలు 2 అయిన x విలువను కనుగొనుము (పేజీ నెం. 186).
సాధన.
ఇచ్చిన బిందువులు P(2, 5) మరియు Q(x, 3) గుండా పోయే రేఖవాలు 2.
pQ రేఖాఖండం వాలు m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\) = 2
⇒ \(\frac{3-5}{x-2}\) = 2
⇒ \(\frac{-2}{x-2}\) = – 2
⇒2x – 4 = 2
⇒ x = \(\frac{2}{2}\) = 1
∴ x =1

SCERT AP 10th Class Maths Textbook Solutions Chapter 7 నిరూపక రేఖాగణితం Optional Exercise Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 7th Lesson నిరూపక రేఖాగణితం Optional Exercise

ప్రశ్న 1.
వృత్తం ‘Q’ యొక్క కేంద్రం -అక్షంపై ఉన్నది. మరియు 2. (0, 7) మరియు (0, -1) లు ఆ వృత్తం పై బిందువులు. వృత్తం ‘Q’ ధన X-అక్షాన్ని బిందువు (P, 0) వద్ద ఖండించిన ‘P’ విలువ ఎంత ?
సాధన.

పై పటం నుండి వృత్తంపై బిందువులు A (0, 7), B (0, – 1) అనుకుంటే A, B లు వ్యాసాగ్రాలు.
వృత్తకేంద్రం ‘O’ = A, B ల మధ్య బిందువు = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
= \(\left(\frac{0+0}{2}, \frac{7-1}{2}\right)\) = (0, 3)
∴ వృత్తకేంద్రం = (0, 3)
వృత్త వ్యాసార్ధం r = OA = |7 – 3| = 4 యూనిట్లు
వృత్తం Q ధన X – అక్షాన్ని (P, 0) వద్ద ఖండించును.
O(0, 3), P(P, 0)
∴ OP = r = 4
\(\sqrt{\mathrm{P}^{2}+3^{2}}\) = 4
\(\sqrt{\mathrm{P}^{2}+9}\) = 4
⇒ P² + 9 = 16
⇒ P² = 16 – 9 = 7
⇒ P = √7,

2వ పద్ధతి :
పై పటం నుండి వృత్త కేంద్రం O = A, B ల మధ్య బిందువు = \(\left(\frac{0+0}{2}, \frac{7-1}{2}\right)\) = (0, 3)
A (0, 7), (P, 0) బిందువులు వృత్తం పై కలవు.
∴ OA = OP
\(\sqrt{(0-0)^{2}+(7-3)^{2}}=\sqrt{(P-0)^{2}+(0-3)^{2}}\)
\(\sqrt{4^{2}}=\sqrt{\mathrm{P}^{2}+9}\)
⇒ 4² = P² + 9
16 – 9 = P²
7 = P²
√7 = P.

ప్రశ్న 2.
బిందువులు A(2, 3), B(- 2, – 3) మరియు C(4, 3) శీర్చాలతో త్రిభుజం ∆ABC ఏర్పడినది. భుజం BC మరియు. శీర్షం A యొక్క కోణ సమద్విఖండన రేఖల ఖండన బిందువును కనుగొనండి.
సాధన.

A (2, 3), B (- 2, – 3), C (4, 3) లు శీర్షాలుగా గల త్రిభుజం ∆ ABC
BC ని A యొక్క కోణ సమద్విఖండన రేఖ D వద్ద ఖండిస్తున్నది అనుకొనుము.
అప్పుడు \(\) ……….. (1) (∵ కోణ సమద్విఖండన సిద్ధాంతము)
AB = \(\sqrt{(-2-2)^{2}+(-3-3)^{2}}\)
= \(\sqrt{16+36}=\sqrt{52}\)
= 2√13

AC = \(\sqrt{(4-2)^{2}+(3-3)^{2}}\)
= \(\sqrt{2^{2}+0^{2}}\) = 2

∴ \(\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{2 \sqrt{13}}{2}\) = √13 : 1
(∵ AB, AC లను (1) లో రాయగా)
అనగా BCని D అంతరంగా√13 : 1 నిష్పత్తిలో ఖండిస్తుంది.
∴ D = \(\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)

D = \(\left(\frac{\sqrt{13} \times 4+1(-2)}{\sqrt{13}+1}, \frac{\sqrt{13} \times 3+1(-3)}{\sqrt{13}+1}\right)\)

D = \(\left[\frac{4 \sqrt{13}-2}{\sqrt{13}+1}, \frac{3 \sqrt{13}-3}{\sqrt{13}+1}\right]\)
BC ని A యొక్క కోణ సమద్విఖండన రేఖ ఖండించే బిందువు D = \(\left[\frac{4 \sqrt{13}-2}{\sqrt{13}+1}, \frac{3 \sqrt{13}-3}{\sqrt{13}+1}\right]\).

సరిచూచుట :
B, D, C లు సరేఖీయాలు అవుతాయని చూపి సరిచూసుకోవచ్చును.

ప్రశ్న 3.
సమబాహు త్రిభుజం ∆ABC యొక్క భుజం BC X – అక్షానికి సమాంతరంగా ఉంది. దాని భుజాలు BC, CA, AB ల గుండా పోయే సరళరేఖల వాలులు కనుగొనుము.
సాధన.

∆ABC సమబాహు త్రిభుజం AB = BC = AC = a యూనిట్లు మరియు B(x₁, y₁) అనుకొందాం.
BC మధ్య బిందువు D మరియు AD; ∆ABC యొక్క ఎత్తు = \(\frac{\sqrt{3}}{2}\)a యూనిట్లు అవుతుంది.
D = AC ల మధ్యబిందువు = \(\left(\frac{x_{1}+x_{1}+a}{2}, \frac{y_{1}+y_{1}}{2}\right)=\left(\frac{2 x_{1}+a}{2}, y_{1}\right)\) మరియు C = (x₁ + a,y₁),
A \(\left(\frac{2 x_{1}+a}{2}, y_{1}+\frac{\sqrt{3}}{2} a\right)\)
ఇప్పుడు, AB పాలు = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

∴ AB వాలు = √3
BC వాలు = \(\frac{y_{1}-y_{1}}{x_{1}+a-x_{1}}=\frac{0}{a}\) = 0
లేదా BC, X – అక్షానికి సమాంతరం. కావున BC వాలు = 0
AC వాలు = \(\frac{y_{1}-\left(y_{1}+\frac{\sqrt{3}}{2} a\right)}{x_{1}+a-\left(\frac{2 x_{1}+a}{2}\right)}\)

= \(\frac{y_{1}-y_{1}-\frac{\sqrt{3}}{2} a}{x_{1}+a-x_{1}-\frac{a}{2}}\)

= \(\frac{-\frac{\sqrt{3}}{2} a}{\frac{a}{2}}=-\frac{\sqrt{3}}{2} a \times \frac{2}{a}\) = – √3

AC వాలు = – √3.

2వ పద్ధతి :

∆ABC సమబాహు త్రిభుజం AB = BC = AC = a యూనిట్లు
X – అక్షంపై BC భుజం కలదు అనుకుందాం. (ప్రతిరేఖ దానికదే సమాంతరము కాబట్టి BC X – అక్షం)
B (0, 0) అయిన C(a, 0) అవుతుంది. BC ల మధ్యబిందువు
D = \(\left(\frac{0+a}{2}, \frac{0+0}{2}\right)\) = (\(\frac{a}{2}\), 0)
AD = \(\frac{\sqrt{3}}{2}\) a
[సమబాహు త్రిభుజ ఉన్నతి = \(\frac{\sqrt{3}}{2}\) × భుజం]
∴ A = (\(\frac{a}{2}\), \(\frac{\sqrt{3}}{2}\) a)
∴ త్రిభుజ శీర్షాలు A(\(\frac{a}{2}\), \(\frac{\sqrt{3}}{2}\) a), B(0, 0), C(a, 0)

∴ AB రేఖ వాలు = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{0-\frac{\sqrt{3}}{2} a}{0-\frac{a}{2}}\)
= \(-\frac{\sqrt{3}}{2} a \times-\frac{2}{a}=\sqrt{3}\)

BC-రేఖ వాలు = \(\frac{0-0}{a-0}=\frac{0}{a}=0\)

AC రేఖ వాలు = \(\frac{0-\frac{\sqrt{3}}{2} a}{0-\frac{a}{2}}=\frac{-\frac{\sqrt{3}}{2} a}{\frac{a}{2}}\)
= \(\frac{-\sqrt{3}}{2} a \times \frac{2}{a}=-\sqrt{3}\).

3వ పద్ధతి :

∆ABC సమబాహు త్రిభుజము మరియు BC, X – అక్షానికి సమాంతరము. \(\overleftrightarrow{A B}\) రేఖ X – అక్షం ధనదిశలో చేసే కోణము θ₁, అనుకొనుము.
θ₁, = ∠ABC = 60° (∵ BC // X – అక్షం, θ₁, మరియు ∠ABC లు సదృశ్యకోణాలు)
\(\overleftrightarrow{A C}\) X – అక్షం ధనదిశలో చేసే కోణం θ₂, అనుకొనుము. ర
θ₂ = ∠ACD = 120° [∵ BC // X – అక్షం, మరియు θ₂, ∠ACD లు సదృశ్యకోణాలు] కాని వాలు నిర్వచనం ఒక రేఖ X – అక్షం యొక్క ధనదిశలో చేసే కోణం θ అయితే ఆ రేఖవాలు ,
m = tan θ.
∴ A, B రేఖవాలు = tan θ₁ = tan 60° = √3
A, C రేఖవాలు = tan θ₂ = tan 120° .
= tan (90 + 30)
= – cot 30° = – √3 B
BC రేఖవాలు = tan 0° = 0 [∵ BC // X -అక్షం కాబట్టి X -అక్షంతో BC చేసే కోణం 0°].

ప్రశ్న 4.
a > b అయ్యేటట్లు భుజాలు ‘a’, ‘b’లు కలిగిన ఒక లంబకోణ త్రిభుజం ∆ABC ఉంది. దానిలో లంబకోణం యొక్క సమద్విఖండన రేఖ ద్వారా ఏర్పడిన రెండు చిన్న త్రిభుజాల లంబకేంద్రాల మధ్య దూరాన్ని కనుగొనుము.
సాధన.
పటంలో చూపినట్లు ∆ABC ఒక లంబకోణ త్రిభుజం
AC – కర్ణం ; ∠B = 90° అనుకుందాం
\(\overline{\mathrm{BG}}\) కోణ సమద్విఖండన రేఖ వలన ఏర్పడే చిన్న త్రిభుజాలు వరుసగా ∆ABG, ∆BCG అనుకుందాం.
A, B, C శీర్షాల నిరూపకాలు వరుసగా A(0, a), B(0,0), C(b, 0) అనుకుందాం .

∴ \(\overline{\mathrm{BG}}\) వాలు = m = tan 45° = 1 (∵ BG, ∠B యొక్క కోణ సమద్విఖండన రేఖ)
మరియు \(\overline{\mathrm{AC}}\) వాలు = 0 = \(\frac{0-a}{b-0}=\frac{-a}{b}\),
అదే విధంగా \(\overline{\mathrm{BC}}\) అనునది X – అక్షంపై గలదు కావున \(\overline{\mathrm{BC}}\) వాలు = 0

(I) \(\overline{\mathrm{BD}}\) అనునది \(\overline{\mathrm{AC}}\) పైకి గీయబడిన ‘ఉన్నతి’ అనుకుందాం.
∴ \(\overline{\mathrm{BD}}\) వాలు = \(\frac{b}{a}\)
(∵ m₁, m₂ = – 1, m, = 6)
∴ \(\overline{\mathrm{BD}}\) సమీకరణం = (y – 0) = \(\frac{b}{a}\) (x – 0)
⇒ bx = ay లేదా bx – ay = 0 – (1) అదే విధంగా.

(II) \(\overline{\mathrm{AE}}\) అనునది ∆ABG నందలి. \(\overline{\mathrm{BD}}\) పైకి గీయబడిన ‘ఉన్నతి’ అనుకుందాం = \(\overline{\mathrm{AE}}\) వాలు = – 1
(∵ m₁, m₂ = – 1) అయిన
ఉన్నతి \(\overline{\mathrm{AE}}\) సమీకరణం = (y – a) = 1(x – 0)
⇒ x – y = – a లేదా x – y + a = 0 – (2)
ఇపుడు (1), (2) సమీకరణాల ఖండన బిందువు అనునది రెండు ఉన్నతుల (\(\overline{\mathrm{AE}}\), \(\overline{\mathrm{BD}}\)) ఖండన బిందువు అనగా AABG యొక్క లంబకేంద్రం అగును.
∴ by – ay = 0 ______ (1) ⇒ bx – ay = 0
x – y = – a _________ (2) ⇒ ax – dy = – a²

x = \(\frac{a^{2}}{b-a}\) మరియు y = x + a .
⇒ y = \(\frac{a^{2}}{b-a}\) + a
= \(\frac{a^{2}+a b-a^{2}}{b-a}=\frac{a b}{b-a}\)
∴ ∆ABG యొక్క లంబ కేంద్రం ‘F’ యొక్క నిరూపకాలు = F|\(\left(\frac{a^{2}}{b-a}, \frac{a b}{b-a}\right)\)
అదే విధంగా ∆BCG నందు,
\(\overline{\mathrm{GC}}\) వాలు = \(\overline{\mathrm{AC}}\) వాలు = – \(\frac{a}{b}\)

‘B’ నుండి \(\overline{\mathrm{GC}}\) మీదకు గీయబడు లంబం \(\overline{\mathrm{BD}}\) గుండా పోవును.
(∵ ఒక రేఖకు ఒక బిందువు గుండా ఒకే ఒక లంబం గీయగలం)
∴ \(\overline{\mathrm{BH}}\) అనునది \(\overline{\mathrm{CG}}\) పైకి గల ఉన్నతి అనుకుందాం
[Note : a > b కావున ∆ABC నందు. ∠A ≠ ∠C ≠ 45 కావున ∆ABG, ∆BGC లలో ఒకటి తప్పనిసరిగా అధిక కోణ త్రిభుజం అగును)
\(\overline{\mathrm{BH}}\) వాలు = \(\overline{\mathrm{BD}}\) వాలు = \(\frac{b}{a}\)

∴ \(\overline{\mathrm{BH}}\) సమీకరణం = \(\overline{\mathrm{BH}}\) సమీకరణం = bx – ay = 0 ((1) నుండి)
మరియు \(\overline{\mathrm{CJ}}\) అనునది \(\overline{\mathrm{BG}}\) పైకి లంబం
∴ \(\overline{\mathrm{CJ}}\) వాలు = – 1 (∵ \(\overline{\mathrm{BG}}\) వాలు = 1)
∴ \(\overline{\mathrm{CJ}}\) సమీకరణం = (y – 0) = – 1(x – b)
⇒ x + y = b – (3)
∴ ABCG యొక్క ఉన్నతులు (\(\overline{\mathrm{CJ}}\), \(\overline{\mathrm{BH}}\)) ఖండన బిందువు,
దాని యొక్క లంబ కేంద్రం అగును.

⇒ x = \(\frac{a b}{b+a}\) అయిన y = – x + b = – \(\frac{a b}{b+a}\) + b
= \(\frac{-\not ab+\not ab+b^{2}}{b+a}=\frac{b^{2}}{b+a}\)
∴ K (\(\frac{a b}{b+a}\), \(\frac{b^{2}}{b+a}\) అనునది ∆BGC యొక్క లంబకేంద్రం నిరూపకాలు.
∴ రెండు లంబకేంద్రాల మధ్య దూరం \(\overline{\mathrm{KF}}\) =

ప్రశ్న 5.
2x + 3y – 6 = 0 అను సరళరేఖ నిరూపకాక్షాలతో చేసే త్రిభుజం యొక్క గురుత్వ కేంద్రంను కనుగొనుము.
సాధన.

ఇచ్చిన సరళరేఖ 2x + 3y – 6 = 0
X – అక్షాన్ని ఖండించే బిందువు B వద్ద y నిరూపకం సున్న అనగా y = 0
y = 0 ⇒ 2x + 3(0) – 6 =.0
⇒ 2x – 6 = 0 ⇒ 2x = 6,
x = \(\frac{6}{2}\) = 3
∴ B(3, 0) ఇదే విధంగా
x = 0 ⇒ 2(0) + 3y – 6 = 0
⇒ y = 2
∴ A(0, 2)
∴ 2x + 3y – 6 = 0 మరియు నిరూపకాక్షాలతో ఏర్పరిచే త్రిభుజ శీర్షాలు A(0, 2), 000, 0), B(3, 0)
∆ABC గురుత్వ కేంద్రం = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)
= \(\left(\frac{0+0+3}{3}, \frac{2+0+0}{3}\right)\)
= \(\left(\frac{3}{3}, \frac{2}{3}\right)\)
∆ABC గురుత్వకేంద్రం = (1, \(\frac{2}{3}\))

SCERT AP 10th Class Maths Textbook Solutions Chapter 7 నిరూపక రేఖాగణితం Exercise 7.4 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 7th Lesson నిరూపక రేఖాగణితం Exercise 7.4

ప్రశ్న 1.
రెండు బిందువులను కలుపుచూ గీయబడిన రేఖవాలు కనుగొనండి.
(i) (4, – 8) మరియు (5, – 2)
సాధన.
(4, – 8) మరియు (5, – 2) కలుపు రేఖావాలు
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-2-(-8)}{5-4}\)
m = \(\frac{-2+8}{1}\) = 6

(ii) (0, 0) మరియు (13,3)
సాధన.
(0, 0) మరియు (√3, 3) కలుపు రేఖావాలు
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-0}{\sqrt{3}-0}=\frac{3}{\sqrt{3}}\) = √3.

(iii) (2a, 3b) మరియు (a, – b)
సాధన.
(2a, 3b) మరియు (a, – b) కలుపు రేఖావాలు
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-b-3 b}{a-2 a}\)
= \(\frac{-4b}{-a}\)
= \(\frac{4b}{a}\)

(iv) (a, 0) మరియు (0, b)
సాధన.
(a, 0) మరియు (0, b) కలుపు రేఖావాలు
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{b-0}{0-a}=\frac{-b}{a}\).

(v) A(- 1.4, -3.7), B(- 2.4, 1.3)
సాధన.
A(- 1.4, – 3.7) మరియు B(- 2.4, 1.3) అయిన
\(\overleftrightarrow{A B}\) రేఖావాలు,
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

= \(\frac{1.3-(-3.7)}{-2.4-(-1.4)}\)

= \(\frac{1.3+3.7}{-2.4+1.4}=\frac{5}{-1}\) = – 5

(vi) A(3, – 2), B(- 6, – 2)
సాధన.
A(3, – 2) మరియు B(- 6, – 2) అయిన \(\overleftrightarrow{A B}\) రేఖావాలు,
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{\Gamma}}=\frac{-2-(-2)}{-6-3}\)
= \(\frac{-2+2}{-9}=\frac{0}{-9}\)
వాలు m = 0 కావున \(\overleftrightarrow{A B}\) X-అక్షానికి సమాంతరము.

(vii) A(- 3\(\frac{1}{2}\), 3), B(- 7, 2\(\frac{1}{2}\))
సాధన.
A (- 3\(\frac{1}{2}\) – 3) మరియు B (- 7, 2\(\frac{1}{2}\)) అయిన \(\overleftrightarrow{A B}\)
రేఖావాలు; m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

∴ AB రేఖావాలు, m = \(\frac{1}{7}\).

(viii) A(0, 4), B(4, 0)
సాధన.
A(0, 4) మరియు B(4, 0) అయిన \(\overleftrightarrow{A B}\) రేఖావాలు,
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

= \(\frac{0-4}{4-0}=\frac{-4}{4}\) = – 1

SCERT AP 10th Class Maths Textbook Solutions Chapter 7 నిరూపక రేఖాగణితం Exercise 7.3 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 7th Lesson నిరూపక రేఖాగణితం Exercise 7.3

ప్రశ్న 1.
కింద ఇవ్వబడిన బిందువులు శీర్షాలుగా కలిగిన త్రిభుజ – వైశాల్యం కనుక్కోండి. .
(i) (2, 3), (-1, 0), (2, – 4)
సాధన.
A (2, 3), B (- 1, 0),C (2, – 4) ,
∆ABC వైశాల్యం = \(\frac{1}{2}\) |x₁(y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)|

= \(\frac{1}{2}\) |2[0 – (- 4)] + (- 1)(- 4 – 3) + 2 (3 – 0)|
= \(\frac{1}{2}\) |2 (4) – 1 (- 7) + 2 (3)|
= \(\frac{1}{2}\) |8 + 7 + 6|
= \(\frac{1}{2}\) × 21
= \(\frac{21}{2}\)
∴ ∆ABC వైశాల్యం = \(\frac{21}{2}\) చ.యూ.

మరొక పద్ధతి :

= \(\frac{1}{2}\)

త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) |(x₁y₂ + x₂y₃ + x₃y₁) – (y₁x₂ + y₂x₃ + y₃x₁)|

=

త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) |(2 × 0 + (- 1) × (- 4) + 2 × 3) – (3 × (- 1) + 0 × 2 + (- 4) ×2) |
= \(\frac{1}{2}\) (0 + 4 + 6) – (- 3 + 0 – 8)|
= \(\frac{1}{2}\) |10 – (- 11)|
= \(\frac{1}{2}\) |21|
= \(\frac{1}{2}\) × 21 = \(\frac{21}{2}\)
త్రిభుజ వైశాల్యం = \(\frac{21}{2}\) చయూ.

(ii) (- 5, – 1), (3, – 5) మరియు (5, 2)
సాధన.
A (- 5, – 1), B (3, – 5), C (5, 2) అనుకొనుము.
∆ABC వైశాల్యం = \(\frac{1}{2}\) |x₁ (y₂ – y₃) + x₂ (y₃ – y₂) + x₃ (y₁ – y₂)|
= \(\frac{1}{2}\) |(- 5) (- 5 – 2) + 3[2 – (- 1)] + 5[- 1 – (- 5)]|
= \(\frac{1}{2}\) |(- 5) (- 7) + 3 (3) + 5 (4)|
= \(\frac{1}{2}\) |35 + 9 + 20|
= \(\frac{1}{2}\) |64|
= \(\frac{1}{2}\) × 64 = 32 చ.యూ.
∆ABC వైశాల్యం = 32 చ.యూ.

మరొక పద్ధతి :

=

∆ABC వైశాల్యం = \(\frac{1}{2}\) |(- 5) × (- 5) + 3 × 2 + 5 × (- 1)| – [(- 1) (3) + (- 5) × (5) + 2 × (- 5)]
= \(\frac{1}{2}\) |(25 + 6 – 5) – (- 3 – 25 – 10)|
= \(\frac{1}{2}\) |26 – (- 38)|
= \(\frac{1}{2}\) |26 + 38|
= \(\frac{1}{2}\) |64| = \(\frac{1}{2}\) × 64 = 32 చ.యూ.
∴ త్రిభుజ వైశాల్యం = 32 చ.యూ.

(iii) (0,0), (3, 0) మరియు (0, 2)
సాధన.
A (0, 0), B (3, 0), C (0, 2) అనుకుందాం.
∆ABC వైశాల్యం = \(\frac{1}{2}\) |x₁ (y₂ – y₃) + x₂ (y₃ – y₂) + x₃ (y₁ – y₂)|
= \(\frac{1}{2}\) |0(0 – 2) + 3(2 +0) + 0(0 – 0)|
= \(\frac{1}{2}\) |6|
= \(\frac{1}{2}\) × 6 = 3 చ.యూ.

మరొక పద్ధతి :

=

త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) |(0 × 0 + 3 × 2 + 0 × 0) – (0 × 3 + 0 × 0 + 2 × 0)|
= \(\frac{1}{2}\) |6 – 0|
= \(\frac{1}{2}\) |6|
= \(\frac{1}{2}\) × 6 = 3 చ.యూ.

ప్రశ్న 2.
కింద ఇవ్వబడిన బిందువులు సరేఖీయాలైతే ‘k’ విలువను కనుగొనండి.
(i) (7, – 2), (5, 1) మరియు (3, k)
సాధన.
A (7, – 2), B (5, 1),C (3, k) అనుకొనుము.
∆ABC వైశాల్యం : = \(\frac{1}{2}\) |x₁ (y₂ – y₃) + x₂ (y₃ – y₂) + x₃ (y₁ – y₂)|
= \(\frac{1}{2}\) |7(1 – k) + 5[k – (- 2)] + 3(- 2 – 1)|
= \(\frac{1}{2}\) |7 – 7k + 5k + 10 – 9|
= |8 – 2k|
సరేఖీయాలు కావున ∆ABC వైశాల్యం సున్న
∴ |8 – 2k| = 0
8 – 2k = 0
8 = 2k
⇒ \(\frac{8}{2}\) = k
∴ k = 4.

(ii) (8, 1), (k, – 4) మరియు (2, – 5)
సాధన.
ఇచ్చిన బిందువులు A (8, 1), B (k, – 4), C (2, – 5) లు సరేఖీయాలు..
∴ ∆ABC = 0
⇒ \(\frac{1}{2}\) |x₁ (y₂ – y₃) + x₂ (y₃ – y₂) + x₃ (y₁ – y₂)| = 0
= \(\frac{1}{2}\) |8(- 4 – (- 5)) + k(- 5 – 1) +2[1 – (- 4)] = 0
= \(\frac{1}{2}\) |8 (1) + k (- 6) + 2 (5)| = 0
= \(\frac{1}{2}\) |8 – 6k + 10| = 0
∴ 18 – 6k = 0
⇒ 18 = 6k
⇒ \(\frac{18}{6}\) = k.
∴ k = 3.

సరిచూచుకోవడం :
k = 3 అయిన A(8, 1), B (3, – 4), C(2, – 5)
∆ABC వైశాల్యం = \(\frac{1}{2}\) |8 (- 4 + 5) + 3(- 5 – 1) + 2 (1 + 4)|
\(\frac{1}{2}\) |8 – 18 + 10| = 0

(iii) (k, k), (2, 3) మరియు (4, – 1)
సాధన..
A (k, k), B (2, 3) మరియు C (4, – 1) లు సరేఖీయాలు అయితే ∆ABC వైశాల్యం సున్న.
\(\frac{1}{2}\) |k[(3 – (- 1)) + 2(- 1 – k) +4(k – 3)]| = 0
= \(\frac{1}{2}\) |4k – 2 – 2k + 4k – 12| = 0
= \(\frac{1}{2}\) |6k -14| = 0
6k – 14 = 0
⇒ 6k = 14
⇒ k = \(\frac{14}{6}=\frac{7}{3}\)
∴ k = \(\frac{7}{3}\)

ప్రశ్న 3.
బిందువులు (0, – 1), (2, 1) మరియు (0, 3) శీర్షాలుగా కలిగిన త్రిభుజ వైశాల్యం, మరియు దాని భుజాల మధ్యబిందువులను కలుపగా ఏర్పడిన త్రిభుజ వైశాల్యాల నిష్పత్తిని కనుగొనండి.
సాధన.

ఇచ్చిన బిందువులు A (0, – 1), B (2, 1), C (0, 3) అనుకొందాం.
AB, BC, ACల మధ్య బిందువులు వరుసగా D, E, F లు అనుకొనుము.
AB మధ్యబిందువు D = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

= \(\left(\frac{0+2}{2}, \frac{-1+1}{2}\right)\) = (1, 0)

BC మధ్యబిందువు E = \(\left(\frac{2+0}{2}, \frac{1+3}{2}\right)\) =(1, 2)

AC మధ్యబిందువు F = \(\left(\frac{0+0}{2}, \frac{-1+3}{2}\right)\) = (0, 1)
A(0, – 1), B(2, 1), C(0, 3)
x₁ = 0, x₂ = 2, x₃ = 0,
y₁ = – 1, y₂ = 1, y₃ = 3
∆ABC వైశాల్యం = \(\frac{1}{2}\) |x₁ (y₂ – y₃) + x₂ (y₃ – y₂) + x₃ (y₁ – y₂)|
= \(\frac{1}{2}\) |0(1 – 3) + 2[3 – (- 1)] + 0 (- 1 – 1)|
= \(\frac{1}{2}\) |0 + 2 (4) + 0|
= \(\frac{1}{2}\) |8| = \(\frac{1}{2}\) × 8 = 4 చ.యూ.
∆ABCవైశాలం = 4 చ.యూనిట్లు
భుజాల మధ్యబిందువులు D(1, 0), E (1, 2), F (0, 1) లతో ఏర్పడే త్రిభుజం ∆DEF వైశాల్యం
= \(\frac{1}{2}\) |1(2 – 1) + 1(1 – 0) + 0 (1 – 0)|
= \(\frac{1}{2}\) |1 (1) + 1(1)|
∴ ∆DEF వైశాల్యం = 1 చ.యూనిట్
∆ABC మరియు ∆DEF ల వైశాల్యాల నిష్పత్తి = 4 : 1.

ప్రశ్న 4.
బిందువులు (- 4, – 2), (-3, – 5),(3, – 2) మరియు . (2, 3)లు శీర్షాలుగా గల చతుర్భుజం యొక్క వైశాల్యం కనుగొనండి.
సాధన.

ఇచ్చిన బిందువులు A (- 4, – 2), B (- 3, – 5), C (3, – 2) మరియు D (2, 3) అనుకుంటే □ABCDని AC రెండు త్రిభుజాలు ∆ABC మరియు ∆ADC గా విభజిస్తుంది. .
∆ABC వైశాల్యం = \(\frac{1}{2}\) |x₁ (y₂ – y₃) + x₂ (y₃ – y₂) + x₃ (y₁ – y₂)|
= \(\frac{1}{2}\) |- 4(- 5 – (- 2)] + (- 3)(- 2 – (- 2)] + 3[- 2 – (- 5)]|
= \(\frac{1}{2}\) |(- 4) [- 5 + 2] – 3(- 2 + 2) + 3 [- 2 + 5]|
= \(\frac{1}{2}\) |(- 4) (- 3) – 3(0) + 3 (3)|
= \(\frac{1}{2}\) |12 – 0 + 9|
= \(\frac{1}{2}\) |21| = 11 చ.యూ.

∆ADC వైశాల్యం = \(\frac{1}{2}\) |(- 4) [3 – (- 2)] + (- 2) – (- 2)] + 3(- 2) – 3]
= \(\frac{1}{2}\) |(- 4) (5) + 2 (0) + 3 (- 5)|
= \(\frac{1}{2}\) |- 20 + 0 – 15|
= \(\frac{1}{2}\) |- 35]
= \(\frac{1}{2}\) × 35 = \(\frac{35}{2}\) చ.యూ, ”

□ABCD వైశాల్యము = ∆ABC వైశాల్యం + ∆ADC వైశాల్యం
= \(\frac{21}{2}\) + \(\frac{35}{2}\)
= \(\frac{56}{2}\) = 28 చ.యూనిట్లు

రెండవ పద్ధతి : .

A (- 4, – 2), B (- 3, – 5),C (3, – 2)మరియు D (2, 3) అనుకొనుము.
□ABCD వైశాల్యం = ∆ABD వైశాల్యం + ∆BDC వైశాల్యం

=

= \(\frac{1}{2}\) |(20 – 9 – 4) – (6 – 10 – 12)| + \(\frac{1}{2}\) |(- 9 – 4 – 15) – (- 10 + 9 +6)|
= \(\frac{1}{2}\) |7 + 16| + \(\frac{1}{2}\) |- 28 – 5|
= \(\frac{1}{2}\) |23| + \(\frac{1}{2}\) |33|
= \(\frac{1}{2}\) (23 + 33)
= \(\frac{1}{2}\) × 56 = 28 చ.యూనిట్లు
□ABCD వైశాల్యం = 28 చ.యూనిట్లు.

ప్రశ్న 5.
క్రింది బిందువులచే ఏర్పడు త్రిభుజ వైశాల్యమును హెరాస్ సూత్రాన్ని ఉపయోగించి కనుగొనుము.
(i) (1, 1), (1, 4) మరియు (5, 1).
(ii) (2, 3), (- 1, 3) మరియు (2, – 1)
సాధన.
(i) A (1, 1), B (1, 4) మరియు C (5, 1)
c = AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(1-1)^{2}+(4-1)^{2}}\)
= \(\sqrt{0+3^{2}}\) = 3 యూనిట్లు

a = BC = \(\sqrt{(5-1)^{2}+(1-4)^{2}}\)
= \(\sqrt{16+9}=\sqrt{25}\) = 5 యూనిట్లు

b = AC = \(\sqrt{(5-1)^{2}+(1-1)^{2}}\)
= \(\sqrt{4^{2}+0}\) = 4 యూనిట్లు

s = \(\frac{a+b+c}{2}=\frac{3+4+5}{2}=\frac{12}{2}\) = 6

త్రిభుజ వైశాల్యం హెరాన్ సూత్రం = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{6(6-5)(6-4)(6-3)}\)
= \(\sqrt{6 \times 1 \times 2 \times 3}\)
= √36 = 6 చ.యూ.

(ii) (2, 3), (- 1, 3) మరియు (2, -1)
(2, 3) (- 1, 3) మరియు (2, – 1) బిందువులచే ఏర్పడు త్రిభుజ వైశాల్యంను హెరాన్ సూత్రంను ఉపయోగించి కనుగొనుట.
పటంలో చూపినట్లు AABC యొక్క శీర్షాల నిరూపకాలు A(2, 3), B(- 1, 3) మరియు C(2, – 1) అనుకుందాం.

∴ ఆ త్రిభుజ భుజాల పొడవులు, AB = c, BC = a, CA = b తో సూచిస్తాం.
హెరాన్ సూత్ర పద్ధతిన త్రిభుజ వైశాల్యము = \(\sqrt{s(s-a)(s-b)(s-c)}\)
ఇక్కడ s = \(\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}\) కావున మనం భుజాల పొడవులు కనుగొందాం.
భుజాల పొడవులను \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) సూత్ర సహాయాన కనుగొందాం.
∴ AB = c = (2, 3) మరియు (- 1, 3) బిందువుల మధ్య దూరం.
c = \(\sqrt{(2-(-1))^{2}+(3-3)^{2}}\)
= \(\sqrt{(2+1)^{2}+0^{2}}=\sqrt{3^{2}+0}=\sqrt{3^{2}}\) = 3 మరియు

BC = a = (-1, 3) మరియు (2, – 1)ల మధ్య దూరం
a = \(\sqrt{(-1-2)^{2}+[3-(-1)]^{2}}\)
= \(\sqrt{(-3)^{2}+(3+1)^{2}}\)
= \(\sqrt{9+16}=\sqrt{25}\) = 5

మరియు CA = b = (2, – 1) మరియు (2, 3) బిందువుల మధ్య దూరం
b = \(\sqrt{(2-2)^{2}+(-1-3)^{2}}\)
= \(\sqrt{0^{2}+4^{2}}=\sqrt{16}\) = 4

∴ a = 5, b = 4, c = 3.
⇒ s = \(\frac{a+b+c}{2}=\frac{5+4+3}{2}=\frac{12}{2}\)
∴ ∆ABC వైశాల్యము = \(\sqrt{s(s-a)(s-b)(s-c)}\)
=\(\sqrt{6(6-5)(6-4)(6-3)}\)
= \(\sqrt{6(1)(2)(3)}\)
= \(\sqrt{6 \times 6}\) = 6 చllయూనిట్లు
∴ ఇచ్చిన త్రిభుజ వైశాల్యము = 6 చ|| యూనిట్లు.

SCERT AP 10th Class Maths Textbook Solutions Chapter 7 నిరూపక రేఖాగణితం Exercise 7.2 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 7th Lesson నిరూపక రేఖాగణితం Exercise 7.2

ప్రశ్న 1.
బిందువులు (- 1, 7) మరియు (4, – 3). లచే ఏర్పడు రేఖాఖండమును 2 : 3 నిష్పత్తిలో విభజించు బిందువు నిరూపకాలను కనుగొనండి.
సాధన.
బిందువులు P (- 1, 7), Q (4, – 3) లచే ఏర్పడు రేఖాఖండమును 2 : 3 నిష్పత్తిలో విభజించు బిందువు
(x, y) = \(\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)

(x, y) = \(\left(\frac{2(4)+3(-1)}{2+3}, \frac{2(-3)+3(7)}{2+3}\right)\)

= \(\left(\frac{8-3}{5}, \frac{-6+21}{5}\right)=\left(\frac{5}{5}, \frac{15}{5}\right)\) = (1, 3).

ప్రశ్న 2.
బిందువులు (4, – 1) మరియు (- 2, – 3) లచే ఏర్పడు రేఖాండము యొక్క త్రిథాకరణ బిందువుల నిరూపకాలను కనుగొనండి.
సాధన.
బిందువులు (4, – 1) మరియు (-2, – 3) లచే ఏర్పడు రేఖాఖండమును P, Q లు త్రిథాకరణ బిందువులు అనుకొందాం.

(4, – 1) మరియు (- 2, – 3) లచే ఏర్పడు రేఖాఖండాన్ని P 1 : 2 నిష్పత్తిలో అంతరంగా విభజిస్తుంది.
P(x, y) = \(\left(\frac{\mathrm{m}_{1} \mathrm{x}_{2}+\mathrm{m}_{2} \mathrm{x}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1} \mathrm{y}_{2}+\mathrm{m}_{2} \mathrm{y}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\right)\)

= \(\left(\frac{1(-2)+2(4)}{1+2}, \frac{1(-3)+2(-1)}{1+2}\right)\)

= \(\left(\frac{-2+8}{3}, \frac{-3-2}{3}\right)\)

= \(\left(\frac{6}{3}, \frac{-5}{3}\right)\)

= (2, \(\frac{-5}{3}\))
∴ P = (2, \(\frac{-5}{3}\))
ఇప్పుడు (4 – 1) మరియు (- 2, – 3) లచే ఏర్పడు రేఖాఖండాన్ని Q 2 : 1 నిష్పత్తిలో విభజిస్తుంది.
Q(x, y) = \(\left(\frac{2(-2)+1(4)}{2+1}, \frac{2(-3)+1(-1)}{2+1}\right)\)

= \(\left(\frac{-4+4}{3}, \frac{-6-1}{3}\right)\)

= \(\left(\frac{0}{3}, \frac{-7}{3}\right)\)

= (0, \(\frac{-7}{3}\))
∴ Q = (0, \(\frac{-7}{3}\))
కావున (4, – 1) మరియు (- 2, – 3) లచే ఏర్పడే రేఖాఖండం యొక్క త్రిథాకరణ బిందువులు (2, \(\frac{-5}{3}\)), (0, \(\frac{-7}{3}\))

సరిచూచుకొనుట :
(4, – 1) మరియు. (- 2, – 3) ల మధ్యబిందువు
= \(\left(\frac{4+(-2)}{2}, \frac{(-1)+(-3)}{2}\right)\)
= (1, – 2)
P(2, \(\frac{-5}{3}\)), Q(0, \(\frac{-7}{3}\)) ల మధ్యబిందువు
= \(\left(\frac{2+0}{2}, \frac{\left(\frac{-5}{3}\right)+\left(\frac{-7}{3}\right)}{2}\right)\)

= \(\left(\frac{2}{2}, \frac{\frac{-12}{3}}{2}\right)\) = (1, – 2).

ప్రశ్న 3.
బిందువులు (- 3, 10) మరియు (6, – 8) లచే ఏర్పడు రేఖాఖండమును బిందువు (- 1, 6) ఏ నిష్పత్తిలో విభజిస్తుందో కనుగొనండి.
సాధన.
బిందువులు (- 3, 10) మరియు (6, – 8) లచే ఏర్పడు రేఖాఖండమును (- 1, 6), m₁ : m₂.
నిష్పత్తిలో అంతరంగా విభజిస్తుంది అనుకుందాం.
విభజన సూత్రం
P (x, y) = \(\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)

(- 1, 6) = \(\left(\frac{m_{1}(6)+m_{1}(-3)}{m_{1}+m_{2}}, \frac{m_{1}(-8)+m_{2}(10)}{m_{1}+m_{2}}\right)\)

(- 1, 6) = \(\left(\frac{6 m_{1}-3 m_{2}}{m_{1}+m_{2}}, \frac{-8 m_{1}+10 m_{2}}{m_{1}+m_{2}}\right)\)

∴ \(\frac{6 m_{1}-3 m_{2}}{m_{1}+m_{2}}\) = – 1

∴ 6m₁ – 3m₂ = – m₁ – m₂
6m₁ + m₁ = – m₂ + 3m₂
7m₁ = 3m₂
⇒ \(\frac{\mathrm{m}_{1}}{\mathrm{~m}_{2}}=\frac{2}{7}\)
విభజన నిష్పత్తి m₁ : m₁ = 2 : 7.

2వ పద్దతి :
ఇచ్చిన బిందువులు (- 3, 10) మరియు (6, – 8) యొక్క రేఖాఖండాన్ని బిందువు (- 1, 6) λ : 1 నిష్పత్తిలో విభజిస్తుంది అనుకొందాం.
∴ (- 1, 6) = \(\left(\frac{\lambda(6)+1(-3)}{\lambda+1}, \frac{\lambda(-8)+1(10)}{\lambda+1}\right)\)

(- 1, 6) = \(\left(\frac{6 \lambda-3}{\lambda+1}, \frac{-8 \lambda+10}{\lambda+1}\right)\)

∴ \(\frac{6 \lambda-3}{\lambda+1}\) = – 1

⇒ 6λ – 3 = – λ – 1
⇒ 6λ + λ = – 1 + 3
7λ = 2
λ = \(\frac{2}{7}\)
విభజన నిష్పత్తి λ : 1 = \(\frac{2}{7}\) : 1 = 2 : 7

ప్రశ్న 4.
బిందువులు (1, 2), (4, y), (x, 6) మరియు (3, 5) లు వరుసగా ఒక సమాంతర చతుర్భుజం యొక్క ఆశీర్షాలయిన x, y ల విలువలు కనుగొనండి.
సాధన.

ఇచ్చిన బిందువులు . A (1, 2), B (4, y), C (x, 6) మరియు D (3, 5) లు ఒక సమాంతర చతుర్భుజం యొక్క శీర్షాలు.
∴ కర్ణం AC యొక్క మధ్యబిందువు = కర్ణం BD మధ్యబిందువు
\(\left(\frac{1+x}{2}, \frac{2+6}{2}\right)=\left(\frac{4+3}{2}, \frac{y+5}{2}\right)\)

∴ \(\frac{1+x}{2}=\frac{7}{2}\)
⇒ 2 + 2x = 14
⇒ 2x = 14 – 2
⇒ 2x = 12
∴ x = \(\frac{12}{2}\) = 6
\(\frac{y+5}{2}\) = 4
⇒ y + 5 = 8
⇒ y = 8 – 5
⇒ y = 3
x = 6, y = 3.

ప్రశ్న 5.
AB వ్యాసంగా గల వృత్తం యొక్క కేంద్రము (2, – 3) మరియు వృత్తం పైనున్న ఒక బిందువు B(1, 4) అయిన A బిందువు యొక్క నిరూపకాలు కనుగొనండి.
సాధన.

AB వ్యాసంగా గల వృత్తానికి AB యొక్క మధ్య బిందువు వృత్తకేంద్రం అవుతుంది.
∴ A(x, y), B (1, 4)ల మధ్య బిందువు = కేంద్రము (2, – 3)
\(\left(\frac{x+1}{2}, \frac{y+4}{2}\right)\) = (2, 3)
∴ \(\frac{x+1}{2}\) = 2
⇒ x + 1 = 4
⇒ x = 4 – 1 = 3
∴ \(\frac{y+4}{2}\) = – 3
⇒ y + 4 = – 6
⇒ y = – 4 – 6 = – 10
∴ A బిందువు యొక్క నిరూపకాలు (3, – 10).

ప్రశ్న 6.
బిందువులు A, B లు వరుసగా (- 2, – 2) మరియు (2, – 4). AB రేఖాఖండంపై AP = \(\frac{3}{7}\) AB అయ్యే విధంగా P బిందువు నిరూపకాలను కనుగొనండి.
సాధన.
A (- 2, – 2), B (2, – 4) రేఖాఖండముపై AP = \(\frac{3}{7}\) AB అయ్యే విధంగా P బిందువు కలదు.

AP = \(\frac{3}{7}\) AB
⇒ \(\frac{\mathrm{AP}}{\mathrm{AB}}=\frac{3}{7}\)
⇒ AP : AB = 3:7
కావున PB = AB – AP = 7 – 3 = 4
∴ AP : PB = 3 : 4
A (- 2, – 2), B (2, – 4) ను P 3 : 4 నిష్పత్తిలో అంతరంగా విభజిస్తుంది.

విభజన సూత్రం P(x, y) = \(\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)

= \(\left(\frac{3(2)+4(-2)}{3+4}, \frac{3(-4)+4(-2)}{3+4}\right)\)

= \(\left(\frac{6-8}{7}, \frac{-12-8}{7}\right)\)

= \(\left(\frac{-2}{7}, \frac{-20}{7}\right)\)
కావలసిన బిందువు P(x, y) = \(\left(\frac{-2}{7}, \frac{-20}{7}\right)\).

ప్రశ్న 7.
బిందువులు A(- 4, 0) మరియు B(0, 6) లచే ఏర్పడు రేఖాఖండమును నాలుగు సమభాగాలుగా విభజించు బిందువుల నిరూపకాలను కనుగొనండి.
సాధన.
A (- 4, 0), B (0, 6) లచే ఏర్పడు రేఖాఖండము \(\overline{\mathrm{AB}}\) ను నాలుగు సమభాగాలుగా విభజించే బిందువులు P, Q, R అనుకొందాం.

\(\overline{\mathrm{AB}}\) ని P 1 : 3 నిష్పత్తిలో విభజిస్తుంది. విభజన సూత్రం
P(x, y) = \(\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)

P = \(\left(\frac{1(0)+3(-4)}{1+3}, \frac{1(6)+3(0)}{1+3}\right)\)

= \(\left(\frac{-12}{4}, \frac{6}{4}\right)\)

= (- 3, \(\frac{3}{2}\))
\(\overline{\mathrm{AB}}\) ను Q 2 : 2 = 1 : 1 నిష్పత్తిలో విభజిస్తుంది. అనగా A, B ల మధ్య బిందువు
Q = \(\left(\frac{\mathrm{x}_{1}+\mathrm{x}_{2}}{2}, \frac{\mathrm{y}_{1}+\mathrm{y}_{2}}{2}\right)\)

= \(\left(\frac{-4+0}{.2}, \frac{0+6}{2}\right)\)

= \(\left(\frac{-4}{2}, \frac{6}{2}\right)\) = (- 2, 3)
AB ని R 3 : 1 నిష్పత్తిలో విభజిస్తుంది.
∴ R = \(\left(\frac{3(0)+1(-4)}{3+1}, \frac{3(6)+1(0)}{3+1}\right)\)

= \(\left(\frac{-4}{4}, \frac{18}{4}\right)=\left(-1, \frac{9}{2}\right)\)

A (- 4, 0), B (0, 6) లచే ఏర్పడే రేఖాఖండాన్ని నాలుగు సమానభాగాలుగా విభజించు బిందువులు (- 3, \(\frac{3}{2}\)), (- 2, 3) మరియు (- 1, \(\frac{9}{2}\)).

రెండవ పద్ధతి :
A (- 4, 0), B (0, 6) ల యొక్క రేఖాఖండమును P, Q, R లు వరుసగా నాలుగు సమభాగాలుగా విభజిస్తాయి అనుకుందాం.

A, B ల మధ్య బిందువు Q
A, Q ల మధ్య బిందువు P
Q, B ల మధ్య బిందువు R అవుతాయి.
కావున A, B ల మధ్య బిందువు
Q = \(\left(\frac{\mathrm{x}_{1}+\mathrm{x}_{2}}{2}, \frac{\mathrm{y}_{1}+\mathrm{y}_{2}}{2}\right)\)

= \([\left(\frac{-4+0}{2}, \frac{0+6}{2}\right)/latex] = (- 2, 3)
A (- 4, 0), Q(- 2, 3) ల మధ్య బిందువు
P = [latex]\left(\frac{-4+(-2)}{2}, \frac{0+3}{2}\right)\)

= \(\left(\frac{-6}{2}, \frac{3}{2}\right)=\left(-3, \frac{3}{2}\right)\)

Q (- 2, 3), B (0, 6) ల మధ్య బిందువు R
R = \(\left(\frac{-2+0}{2}, \frac{3+6}{2}\right)\)

= \(\left(\frac{-2}{2}, \frac{9}{2}\right)=\left(-1, \frac{9}{2}\right)\)
A, B లను నాలుగు సమ భాగాలుగా విభజించే బిందువులు P = (- 3, \(\frac{3}{2}\)), Q = (- 2, 3) , R = (- 1, \(\frac{9}{2}\)).

ప్రశ్న 8.
బిందువులు A(- 2, 2) మరియు B(2, 8)లచే ఏర్పడు రేఖాఖండమును నాలుగు సమాన భాగాలుగా విభజించు బిందువుల నిరూపకాలను కనుగొనండి.
పాదన.

A (- 2, 2), B (2, 8) లచే ఏర్పడే రేఖాఖండాన్ని P, Q, R లు నాలుగు సమభాగాలుగా విభజిస్తాయి అనుకొనుము.
A (- 2, 2), B (2, 8) రేఖాఖండాన్ని P 1 : 3 నిష్పత్తిలో అంతరంగా విభజిస్తుంది.
P(x, y) = \(=\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)

= \(\left(\frac{2-6}{4}, \frac{8+6}{4}\right)\)

= \(\left(\frac{-4}{4}, \frac{14}{4}\right)=\left(-1, \frac{7}{2}\right)\)

P= (- 1, \(\frac{7}{2}\))
A (- 2, 2), B (2, 8) రేఖాఖండాన్ని Q 2 : 2 = 1 : 1 నిష్పత్తిలో విభజిస్తుంది. అనగా Q, AB కి మధ్యబిందువు
∴ Q = \(\left(\frac{\mathrm{x}_{1}+\mathrm{x}_{2}}{2}, \frac{\mathrm{y}_{1}+\mathrm{y}_{2}}{2}\right)\)

= \(\left(\frac{-2+2}{2}, \frac{2+8}{2}\right)\)

= \(\left(\frac{0}{2}, \frac{10}{2}\right)\) = (0, 5)

A (- 2, 2), B (2, 8) రేఖాఖండాన్ని R 3:1 = 1 : 1 నిష్పత్తిలో విభజిస్తుంది.
R = \(\left(\frac{3(2)+1(-2)}{3+1}, \frac{3(8)+1(2)}{3+1}\right)\)

= \(\left(\frac{6-2}{4}, \frac{24+2}{4}\right)\)

= \(\left(\frac{4}{4}, \frac{26}{4}\right)=\left(1, \frac{13}{2}\right)\)

A, B లను నాలుగు సమ భాగాలుగా విభజించే బిందువులు (- 1, \(\frac{7}{2}\)), (0, 5) మరియు (1, \(\frac{13}{2}\)).

రెండవ పద్ధతి :
A, B కి మధ్య బిందువు Q
A, Q కి మధ్య బిందువు P
Q, R కి మధ్య బిందువు R అవుతాయి.
Q = \(\left(\frac{\mathrm{x}_{1}+\mathrm{x}_{2}}{2}, \frac{\mathrm{y}_{1}+\mathrm{y}_{2}}{2}\right)\)

= \(\left(\frac{-2+2}{2}, \frac{2+8}{2}\right)=\left(\frac{0}{2}, \frac{10}{2}\right)\) = (0, 5)

P = A(- 2, 2), Q (0, 5) ల మధ్య బిందువు = \(\left(\frac{-2+0}{2}, \frac{2+5}{2}\right)=\left(-1, \frac{7}{2}\right)\)

R= Q(0, 5); B(2, 8) ల మధ్య బిందువు = \(\left(\frac{0+2}{2}, \frac{5+8}{2}\right)=\left(\frac{2}{2}, \frac{13}{2}\right)=\left(1, \frac{13}{2}\right)\)
∴ కావలసిన బిందువులు (-1, \(\frac{7}{2}\)), (0, 5), (1, \(\frac{13}{2}\)).

ప్రశ్న 9.
బిందువులు (a + b, a – b) మరియు (a – b, a + b)లచే ఏర్పడు రేఖాఖండమును అంతరంగా 3 : 2 నిష్పత్తిలో విభజించు బిందువు నిరూపకాలను కనుగొనండి.
సాధన.
ఇచ్చిన బిందువులు
(a + b, a – b) మరియు (a – b, a + b) ల రేఖాఖండాన్ని అంతరంగా P (x, y) 3 : 2 నిష్పత్తిలో విభజిస్తుంది అనుకొనుము.

∴ P (x, y) = \(\left(\frac{\mathrm{m}_{1} \mathrm{x}_{2}+\mathrm{m}_{2} \mathrm{x}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1} \mathrm{y}_{2}+\mathrm{m}_{2} \mathrm{y}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\right)\)

P = \(\left(\frac{3(a-b)+2(a+b)}{3+2} ; \frac{3(a+b)+2(a-b)}{3+2}\right)\)

= \(\left(\frac{3 a-3 b+2 a+2 b}{5}, \frac{3 a+3 b+2 a-2 b}{5}\right)\)

= \(\left(\frac{5 a-b}{5}, \frac{5 a+b}{5}\right)\)
∴ కావలసిన బిందువులు = \(\left(\frac{5 a-b}{5}, \frac{5 a+b}{5}\right)\).

ప్రశ్న 10.
కింద ఇవ్వబడిన బిందువులతో ఏర్పడు త్రిభుజం యొక్క గురుత్వ కేంద్రమును కనుగొనండి.
(i) (- 1, 3), (6, – 3) మరియు (- 3, 6)
సాధన.
(- 1, 3), (6, – 3) మరియు (- 3, 6) బిందువులచే ఏర్పడే త్రిభుజ గురుత్వ కేంద్రం
= \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)

= \(\left(\frac{-1+6+(-3)}{3}, \frac{3+(-3)+6}{3}\right)\)

= \(\left(\frac{2}{3}, \frac{6}{3}\right)=\left(\frac{2}{3}, 2\right)\)
∴ గురుత్వ కేంద్రం = \(\left(\frac{2}{3}, 2\right)\)

(ii) (6, 2), (0,0) మరియు (4, – 7) .
సాధన.
(6, 2), (0, 0) మరియు (4, – 7) లతో ఏర్పడు త్రిభుజం యొక్క గురుత్వ కేంద్రం
= \(\left(\frac{\mathrm{x}_{1}+\mathrm{x}_{2}+\mathrm{x}_{3}}{3}, \frac{\mathrm{y}_{1}+\mathrm{y}_{2}+\mathrm{y}_{3}}{3}\right)\)

= \(\left(\frac{6+0+4}{3} ; \frac{2+0+(-7)}{3}\right)\)

= \(\left(\frac{10}{3}, \frac{-5}{3}\right)\)
∴ గురుత్వ కేంద్రం = \(\left(\frac{10}{3}, \frac{-5}{3}\right)\)

(iii) (1, – 1), (0, 6) మరియు (- 3, 0)
సాధన.
(1, – 1), (0, 6) మరియు (-3, 0) లతో ఏర్పడు త్రిభుజం యొక్క గురుత్వ కేంద్రం
= = \(\left(\frac{\mathrm{x}_{1}+\mathrm{x}_{2}+\mathrm{x}_{3}}{3}, \frac{\mathrm{y}_{1}+\mathrm{y}_{2}+\mathrm{y}_{3}}{3}\right)\)

= \(\left(\frac{1+0+(-3)}{3}, \frac{-1+6+0}{3}\right)\)

= \(\left(\frac{-2}{3}, \frac{5}{3}\right)\)

∴ గురుత్వకేంద్రం = \(\left(\frac{-2}{3}, \frac{5}{3}\right)\)

SCERT AP 10th Class Maths Textbook Solutions Chapter 7 నిరూపక రేఖాగణితం Exercise 7.1 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 7th Lesson నిరూపక రేఖాగణితం Exercise 7.1

ప్రశ్న 1.
కింద ఇవ్వబడిన బిందువుల మధ్య దూరంను కనుగొనండి.
(i) (2, 3) మరియు (4, 1)
సాధన.
A (2, 3) మరియు B (4, 1)
రెండు బిందువుల మధ్య దూరం
d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
A, B ల మధ్య దూరం
d = \(\sqrt{(4-2)^{2}+(1-3)^{2}}\)
= \(\sqrt{2^{2}+(-2)^{2}}=\sqrt{4+4}=\sqrt{8}\)
∴ AB = 2√2 యూనిట్లు.

(ii) (- 5, 7) మరియు (- 1, 3)
సాధన.
A (- 5, 7) మరియు B (- 1, 3)
AB = d = \(\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}\)
= \(\sqrt{(-1+5)^{2}+(3-7)^{2}}\)
= \(\sqrt{(-1+5)^{2}+(-4)^{2}}\)
= \(\sqrt{16+16}=\sqrt{32}=4 \sqrt{2}\)
∴ AB = 4√2 యూనిట్లు.

(iii) (- 2, – 3) మరియు (3, 2)
సాధన.
A (- 2, – 3) మరియు B (3, 2)
AB = d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{[3-(-2)]^{2}+[2-(-3)]^{2}}\)
= \(\sqrt{(3+2)^{2}+(2+3)^{2}}\)
= \(\sqrt{25+25}=\sqrt{50}=5 \sqrt{2}\)
∴ AB = 5√2 యూనిట్లు.

(iv) (a, b) మరియు (-a, -b) . సాధన. A (a, b) మరియు B (-a, – b)
AB = d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(-a-a)^{2}+(-b-b)^{2}}\)
= \(\sqrt{(-2 a)^{2}+(-2 b)^{2}}=\sqrt{4\left(a^{2}+b^{2}\right)}\)
= \(2 \sqrt{a^{2}+b^{2}}\)
∴ AB = 2\(2 \sqrt{a^{2}+b^{2}}\) యూనిట్లు.

ప్రశ్న 2.
బిందువులు (0, 0) మరియు (36, 15) ల : మధ్య దూరాన్ని కనుగొనండి.
సాధన.
మూల బిందువు: (0, 0) నుండి (x, y ) బిందువు దూరం = \(\sqrt{x^{2}+y^{2}}\)
(0, 0), (36, 15) బిందువుల మధ్య దూరం = \(\sqrt{36^{2}+15^{2}}=\sqrt{1296+225}\)
= \(\sqrt{1521}\) = 39
(0, 0), (36, 15) బిందువుల మధ్య దూరం = 39 యూనిట్లు.

ప్రశ్న 3.
బిందువులు (1, 5), (2, 3) మరియు (- 2, – 1) లు సరేఖీయాలో, కాదో సరిచూడండి.
సాధన.
ఇచ్చిన బిందువులు
A (1, 5), B (2, 3), C (- 2, – 1) అనుకుందాం.
AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(2-1)^{2}+(3-5)^{2}}\)
= \(\sqrt{1^{2}+(-2)^{2}}=\sqrt{1+4}=\sqrt{5}\)

BC = \(\sqrt{(-2-2)^{2}+(-1-3)^{2}}\)
= \(\sqrt{(-4)^{2}+(-4)^{2}}\)
= \(\sqrt{16+16}=\sqrt{32}=4 \sqrt{2}\)

AC = \(\sqrt{(-2-1)^{2}+(-1-5)^{2}}\)
= \(\sqrt{(-3)^{2}+(-6)^{2}}\)
= \(\sqrt{9+36}=\sqrt{45}=3 \sqrt{5}\)
ఏ రెండు కొలతలైనా (రేఖాఖండాల పొడవులు) మూడవ కొలతకు సమానం కాదు. కావున పై మూడు బిందువులు సరేఖీయాలు కావు.

ప్రశ్న 4.
బిందువులు (5, -2), (6,4) మరియు (7, -2)లు ఒక సమద్విబాహు త్రిభుజం యొక్క శీర్షాలు అవుతాయో? కావో ? చూడండి.
సాధన.
ఇచ్చిన బిందువులు A = (5, – 2), B = (6, 4), C = (7, – 2) లు ∆ABC శీర్షాలు అనుకొందాం.

AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(6-5)^{2}+(4-(-2))^{2}}\)
= \(\sqrt{1+36}=\sqrt{37}\)

BC = \(\sqrt{(7-6)^{2}+(-2-4)^{2}}\)
= \(\sqrt{1+36}=\sqrt{37}\)
∴ ∆ABC లో AB = BC
కావున ఇచ్చిన బిందువులు ఒక సమద్విబాహు త్రిభుజ శీర్షాలు అవుతాయి.

ప్రశ్న 5.
పటంలో చూపినట్లు, ఒక తరగతిలో నలుగురు స్నేహితురాళ్ళు A, B, C, D స్థానాల్లో తరగతిలో అటూ ఇటూ తిరుగుతూ కొన్ని నిమిషాలు పరిశీలించిన తర్వాత, జరీనా ఫణిని ఇలా అడిగింది. “ABCD ఒక చతురస్రం అవుతుందని నీవు భావించడం లేదా ?” అందుకు ఫణి ఒప్పుకోలేదు. ” బిందువుల మధ్య దూరంనకు సూత్రాన్నుపయోగించి – ఎవరి సమాధానం సరైనది ? ఎందుకు ? తెలపండి.

సాధన.
పై పటం నుండి A, B, C, D నిరూపకాలు A (3, 4), B (6, 7), C (9, 4), D (6, 1)
లు
AB = \(\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}\)
= \(\sqrt{(6-3)^{2}+(7-4)^{2}}=\sqrt{3^{2}+3^{2}}\)
= \(\sqrt{9+9}=\sqrt{18}=3 \sqrt{2}\)

BC = \(\sqrt{(9-6)^{2}+(4-7)^{2}}\)
= \(\sqrt{3^{2}+(-3)^{2}}=\sqrt{9+9}=\sqrt{18}=3 \sqrt{2}\)

CD = \(\sqrt{(6-9)^{2}+(1-4)^{2}}\)
= \(\sqrt{(-3)^{2}+(-3)^{2}}\)
= \(\sqrt{9+9}=\sqrt{18}=3 \sqrt{2}\)

DA = \(\sqrt{(6-3)^{2}+(1-4)^{2}}\)
= \(\sqrt{3^{2}+(-3)^{2}}\)
= \(\sqrt{9+9}=\sqrt{18}=3 \sqrt{2}\)

AB = BC = CD = DA

కర్ణాలు AC = \(\sqrt{(9-3)^{2}+(4-4)^{2}}\)
= \(\sqrt{6^{2}+0}=\sqrt{36}\) = 6 యూనిట్లు.

BD = \(\sqrt{(6-6)^{2}+(1-7)^{2}}\)
= \(\sqrt{0+(-6)^{2}}=\sqrt{36}\) = 6 యూనిట్లు.
AC = BD
□ ABCD యొక్క నాలుగు భుజాలు సమానం మరియు కర్ణాలు కూడా సమానాలు. కావున ABCD ఒక చతురస్రం అవుతుంది. కాబట్టి జరీనా సమాధానము సరైనది.
(లేదా)
AB² + BC² = 18 + 18 = 36 = AC²
పైథాగరస్ సిద్దాంత విషర్యము నుండి ∠B = 90° అవుతుంది. AB = BC = CD = DA మరియు ∠B = 90°.
కావున □ ABCD ఒక చతురస్రము.

ప్రశ్న 6.
బిందువులు A(a, 0), B(- a, 0), C(0, a√3) అనునవి ఒక సమబాహు త్రిభుజాన్ని ఏర్పరచగలవని చూపండి.
సాధన.

త్రిభుజ శీర్షాలు A (a, 0), B (- a, 0), C (o, a√3).
AB = | – a – a| = |- 2a| = 2a యూనిట్లు
BC = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{[0-(-a)]^{2}+(a \sqrt{3}-0)^{2}}\)
= \(\sqrt{a^{2}+3 a^{2}}=\sqrt{4 a^{2}}\) = 2a యూనిట్లు.

AC = \(\sqrt{(0-a)^{2}+(a \sqrt{3}-0)^{2}}\)
= \(\sqrt{a^{2}+3 a^{2}}=\sqrt{4 a^{2}}\) = 2a యూనిట్లు.
∴ AB = BC = CA = 2a
∴ ∆ABC ఒక సమబాహు త్రిభుజం.
(∵ సమబాహు త్రిభుజంలో అన్ని భుజాలు సమానాలు).

ప్రశ్న 7.
బిందువులు (- 7, – 3), (5, 10), (15, 8) మరియు (3, – 5) లు వరుసగా ఒక సమాంతర చతుర్భుజానికి శీర్షాలు అవుతాయని చూపండి.
సాధన.

ఇచ్చిన బిందువులు A (- 1, – 3), B (5, 10), C (15, 8), D (3, – 5)
రెండు బిందువుల మధ్య దూరం = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
AB = \(\sqrt{[5-(-7)]^{2}+[10-(-3)]^{2}}\)
= \(\sqrt{12^{2}+13^{2}}=\sqrt{144+169}\)
= √313 యూనిట్లు

BC = \(\sqrt{(15-5)^{2}+(8-10)^{2}}\)
= \(\sqrt{(10)^{2}+(-2)^{2}}=\sqrt{100+4}\)
= \(\sqrt{100+4}=\sqrt{104}\) యూనిట్లు.

CD = \(\sqrt{(3-15)^{2}+[8-(-5)]^{2}}\)
= \(\sqrt{(-12)^{2}+13^{2}}=\sqrt{144+169}\)
= √313 యూనిట్లు

DA = \(\sqrt{(-7-3)^{2}+[-3-(-5)]^{2}}\)
= \(\sqrt{(-10)^{2}+2^{2}}\)
= \(\sqrt{100+4}=\sqrt{104}\) యూనిట్లు

పై కొలతల నుండి □ABCD చతుర్భుజంలో AB = CD మరియు BC = DA.
∴ □ABCD ఒక సమాంతర చతుర్భుజం అవుతుంది.

ప్రశ్న 8.
బిందువులు (- 4, – 7), (- 1, 2), (8, 5) మరియు (5, 4) లు వరుసగా ఒక సమచతుర్భుజం (రాంబస్) యొక్క శీర్షాలు అవుతాయని చూపండి. దాని వైశాల్యం కనుగొనండి. (సూచన : రాంబస్ వైశాల్యం = \(\frac{1}{2}\) × కర్ణముల లబ్ధం)
సాధన.
ఇచ్చిన బిందువులు AC(- 4, – 7), B (- 1, 2), C (8, 5), D (5, – 4)

రెండు బిందువుల మధ్య దూరం = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
AB = \(\sqrt{[-1-(-4)]^{2}+[2-(-7)]^{2}}\)
= \(\sqrt{(3)^{2}+9^{2}}=\sqrt{9+81}\)
= √90 యూనిట్లు,

BC = \(\sqrt{[8-(-1)]^{2}+(5-2)^{2}}\)
= \(\sqrt{9^{2}+3^{2}}=\sqrt{81+9}\)
= √90 యూనిట్లు,

CD = \(\sqrt{(5-8)^{2}+(-4-5)^{2}}\)
= \(\sqrt{(-3)^{2}+(-9)^{2}}\)
= \(\sqrt{9+81}=\sqrt{90}\) యూనిట్లు.

DA = \(\sqrt{[5-(-4)]^{2}+[-7-(-4)]^{2}}\)
= \(\sqrt{9^{2}+(-3)^{2}}\)
= \(\sqrt{9+81}=\sqrt{90}\) యూనిట్లు.

పై కొలతల నుండి AB = BC = CD = DA.
కావున ఇచ్చిన నాలుగు బిందువులు వరుసగా ఒక సమచతుర్భుజం (రాంబస్)ను ఏర్పరుస్తాయి.
d₁ = BD = \(\sqrt{5-(-1)^{2}+(-4-2)^{2}}\)
= \(\sqrt{6^{2}+(-6)^{2}}=\sqrt{36 \times 2}\)
= 6√2

d₂ = AC = \(\sqrt{[8-(-4)]^{2}+[5-(-7)]^{2}}\)
= \(\sqrt{12^{2}+12^{2}}=\sqrt{144+144}\)
= \(\sqrt{2 \times 144}\) = 12√2

రాంబస్ వైశాల్యము = \(\frac{1}{2}\) × కర్ణాల లబ్ధం
= \(\frac{1}{2}\) d₁d₂
= \(\frac{1}{2}\) × 6√2 × 12√2
= 36 × 2 = 72 చ.యూ.

ప్రశ్న 9.
క్రింద ఇవ్వబడిన బిందువులతో ఏర్పడే చతుర్భుజం ఏ రకమైనది ? దాని పేరును తెలపండి. మీ సమాధానానికి సరైన కారణం తెలపండి.
(i) (- 1, – 2), (1, 0), (- 1, 2), (- 3, 0)
సాధన.
ఇచ్చిన బిందువులు A (- 1, – 2), B (1, 0), C (- 1, 2), D (- 3, 0)
రెండు బిందువుల మధ్య దూరం , d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
AB = \(\sqrt{[1-(-1)]^{2}+[0-(-2)]^{2}}\)
= \(\sqrt{2^{2}+2^{2}}=\sqrt{4+4}=\sqrt{8}=2 \sqrt{2}\)

BC = \(\sqrt{(-1-1)^{2}+(2-0)^{2}}\)
= \(\sqrt{2^{2}+2^{2}}=\sqrt{4+4}=\sqrt{8}=2 \sqrt{2}\)

CD = \(\sqrt{[-3-(-1)]^{2}+(0-2)^{2}}\)
= \(\sqrt{2^{2}+2^{2}}=\sqrt{4+4}=\sqrt{8}=2 \sqrt{2}\)

DA = \(\sqrt{[-1-(-3)]^{2}+[0-(-2)]^{2}}\)
= \(\sqrt{2^{2}+2^{2}}=\sqrt{4+4}=\sqrt{8}=2 \sqrt{2}\)

∴ AB = BC = CD = DA.
ఇప్పుడు AC = \(\sqrt{[-1-(-1)]^{2}+[2-(-2)]^{2}}\)
= \(\sqrt{0^{2}+4^{2}}=\sqrt{16}\) = 4 యూనిట్లు

BD = \(\sqrt{(-3-1)^{2}+(0-0)^{2}}\)
= \(\sqrt{(-4)^{2}}=\sqrt{16}\) = 4 యూనిట్లు
∴ AC = BD.
ABCD బిందువులు ఏర్పరిచే చతుర్భుజంలో నాలుగు భుజాలు సమానం మరియు కర్ణాలు కూడా సమానము.
కావున ABCD ఒక చతురస్రం అవుతుంది.

(ii) (- 3, 5), (1, 10), (3, 1), (- 1, – 4)
సాధన.
ఇచ్చిన బిందువులు
A(- 3, 5), B(1, 10), C(3, 1), D(- 1, – 4)
\(\overline{\mathrm{AB}}=\sqrt{(1+3)^{2}+(10-5)^{2}}\)
= \(\sqrt{16+25}=\sqrt{41}\)

\(\overline{\mathrm{BC}}=\sqrt{(3-1)^{2}+(1-10)^{2}}\)
= \(\sqrt{4+81}=\sqrt{85}\)

\(\overline{C D}=\sqrt{(-1-3)^{2}+(-4-1)^{2}}\)
= \(\sqrt{16+25}=\sqrt{41}\)

\(\overline{\mathrm{AD}}=\sqrt{(-1+3)^{2}+(-4-5)^{2}}\)
= \(\sqrt{4+81}=\sqrt{85}\)

\(\overline{\mathrm{AC}}=\sqrt{(3+3)^{2}+(1-5)^{2}}\)
= \(\sqrt{36+16}=\sqrt{52}\)

\(\overline{\mathrm{BD}}=\sqrt{(-1-1)^{2}+(-4-10)^{2}}\)
= \(\sqrt{4+196}=\sqrt{200}=10 \sqrt{2}\)

□ABCD లో \(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{CD}}\) మరియు \(\overline{\mathrm{BC}}\) = \(\overline{\mathrm{AD}}\) (∵ ఎదురెదురు భుజాలు సమానం) మరియు \(\overline{\mathrm{AC}}\) ≠ \(\overline{\mathrm{BD}}\).
కావున, □ABCD ఒక సమాంతర చతుర్భుజం. ఇచ్చిన బిందువులతో సమాంతర చతుర్భుజం ఏర్పడుతుంది.
□ABCD లో AB = CD, BC = AD మరియు AC ≠ BD.

(iii) (4, 5), (7, 6), (4, 3), (1, 2)
సాధన.
ఇచ్చిన బిందువులు
A (4, 5), B (7, 6), C (4, 3), D (1, 2)
d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
AB = \(\sqrt{(7-4)^{2}+(6-5)^{2}}\)
= \(\sqrt{3^{2}+1^{2}}\)
= \(\sqrt{9+1}=\sqrt{10}\) యూనిట్లు

BC = \(\sqrt{(4-7)^{2}+(3-6)^{2}}\)
= \(\sqrt{(-3)^{2}+(-3)^{2}}\)
= \(\sqrt{9+9}=\sqrt{18}\)
= 3√2 యూనిట్లు

CD = \(\sqrt{(1-4)^{2}+(2-3)^{2}}\)
= \(\sqrt{(-3)^{2}+(-1)^{2}}\)
= \(\sqrt{9+9}\)
= √10 యూనిట్లు

DA = \(\sqrt{(4-1)^{2}+(5-2)^{2}}\)
= \(\sqrt{9+9}=\sqrt{18}=3 \sqrt{2}\) = 3√2 యూనిట్లు
AB = CD మరియు BC = DA

ఇప్పుడు కర్ణాలు AC = \(\sqrt{(4-4)^{2}+(3-5)^{2}}\)
= \(\sqrt{0+(-2)^{2}}=\sqrt{4}\) = 2 యూనిట్లు

BD = \(\sqrt{(1-7)^{2}+(2-6)^{2}}\)
= \(\sqrt{(-6)^{2}+(-4)^{2}}\)
= \(\sqrt{36+16}=\sqrt{52}\) యూనిట్లు
AC ≠ BD
∴ ABCD బిందువులతో ఏర్పడే చతర్భుజం యొక్క ఎదురెదురు భుజాలు సమానం మరియు కర్ణాలు అసమానాలు. కావున □ ABCD దీర్ఘచతురస్రం కానటువంటి సమాంతర చతుర్భుజాన్ని ఏర్పరుస్తుంది.

ప్రశ్న 10.
x-అక్షంపై ఉంటూ బిందువులు (2, – 5) మరియు (- 2, 9) లకు సమాన దూరంలోనున్న బిందువును కనుగొనండి.
సాధన.
x-అక్షంపై గల బిందువు (x, 0) రూపంలో ఉంటుంది.
P (x, 0) బిందువు A (2, – 5) మరియు B (- 2, 9) లకు సమాన దూరంలో కలదు అనుకొనుము.
∴ AP = BP ⇒ AP² = BP²
AP = \(\sqrt{(2-x)^{2}+(-5-0)^{2}}\)
= \(\sqrt{4-4 x+x^{2}+25}\)
= \(\sqrt{x^{2}-4 x+29}\)

AP² = x² – 4x + 29

BP = \(\sqrt{(-2-x)^{2}+(9-0)^{2}}\)
= \(\sqrt{4+4 x+x^{2}+81}\)
= \(\sqrt{x^{2}+4 x+85}\)

BP² = x² + 4x + 85
AP² = BP².
x² – 4x + 29 = x² + 4x + 85
x² – 4x – x² – 4x = 85 – 29
– 8x = 56
8x = – 56 ⇒ x = \(\frac{-56}{8}\) = – 7
∴ కావలసిన బిందువు P= (- 7, 0)

సరిచూచుకోవడం :
AP = \(\sqrt{[2-(-7)]^{2}+(-5-0)^{2}}\)
= \(\sqrt{9^{2}+(-5)^{2}}=\sqrt{81+25}\)
= √107 యూనిట్లు

BP = \(\sqrt{[-2-(-7)]^{2}+(9-0)^{2}}\)
= \(\sqrt{5^{2}+9^{2}}=\sqrt{25+81}\)
= √107 యూనిట్లు.

ప్రశ్న 11.
బిందువులు (x, 7) మరియు (1, 15) ల మధ్య దూరం 10 యూనిట్లు, అయిన x విలువ ఎంత ?
సాధన.
ఇచ్చిన బిందువులు A (x, 7), B (1, 15)
AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(1-x)^{2}+(15-7)^{2}}\)
= \(\sqrt{1-2 x+x^{2}+64}\)

AB = \(\sqrt{x^{2}-2 x+65}\)

లెక్క ప్రకారం AB = 10 యూనిట్లు
= \(\sqrt{x^{2}-2 x+65}\) = 10
ఇరువైపులా వర్గం చేయగా,
∴ x² – 2x + 65 = 100
x² – 2x + 65 – 100 = 0
x² – 2x – 35 = 0
x² – 7x + 5x – 35 = 0
x (x -7) + 5 (x – 7) = 0
(x – 7) (x + 5) = 0
x – 7 = 0 లేదా x + 5 = 0
x = 7 లేదా x = – 5
∴ x = 7 లేదా – 5.

ప్రశ్న12.
బిందువులు P(2, – 3) మరియు Q(10, y) ల మధ్య దూరం 10 యూనిట్లు, అయిన y విలువ ఎంత?
సాధన.
ఇచ్చిన బిందువులు P (2, – 3) మరియు Q (10, y)
PQ = \(\sqrt{(10-2)^{2}+[y-(-3)]^{2}}\)
= \(\sqrt{8^{2}+(y+3)^{2}}\)
= \(\sqrt{64+y^{2}+6 y+9}\)
= \(\sqrt{y^{2}+6 y+73}\)
లెక్క ప్రకారం PQ = 10 యూనిట్లు
\(\sqrt{y^{2}+6 y+73}\) = 10
y² + 6y + 73 = 100 (∵ ఇరువైపులా వర్గం చేయగా)
y² + 6y – 27 = 0
y² + 9y – 3y – 27 = 0
y (y + 9) – 3 (y + 9) = 0
(y + 9) (y – 3) = 0 .
y + 9 = 0 లేదా y – 3 = 0
y = – 9 లేదా y = 3
∴ y = – 9 లేదా 3.

ప్రశ్న 13.
బిందువు, (- 5, 6) గుండా పోవు వృత్తం యొక్క కేంద్రం (3, 2) అయిన దాని వ్యాసార్ధంను కనుగొనండి.
సాధన.

వృత్తకేంద్రం O = (3, 2)
వృత్తంపై ఒక బిందువు A = (- 5, 6)
వృత్త వ్యాసార్థం OA = \(\sqrt{(-5-3)^{2}+(6-2)^{2}}\)
= \(\sqrt{(-8)^{2}+4^{2}}=\sqrt{64+16}\) = √80
= \(\sqrt{16 \times 5}=\sqrt{4 \times 4 \times 5}\) = 4√5
వృత్త వ్యాసార్థం r = 4√5 యూనిట్లు.

ప్రశ్న 14.
బిందువులు (1, 5), (5, 8) మరియు (13, 14)లతో త్రిభుజమును గీయగలమా ? కారణం తెల్పండి.
సాధన.
ఇచ్చిన బిందువులు
A (1, 5), B (5, 8), C (13, 14)
∴ రెండు బిందువుల మధ్య దూరం
d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
∴ AB = \(\sqrt{(5-1)^{2}+(8-5)^{2}}\)
= \(\sqrt{4^{2}+3^{2}}=\sqrt{16+9}\)
= √25 = 5

BC = \(\sqrt{(13-5)^{2}+(14-8)^{2}}\)
= \(\sqrt{8^{2}+6^{2}}=\sqrt{64+36}\)
= √100 = 10

AC = \(\sqrt{(13-1)^{2}+(14-5)^{2}}\)
= \(\sqrt{12^{2}+9^{2}}=\sqrt{144+81}\)
= √225 = 15
పై కొలతల నుండి, AB + BC = AC కావున A, B, C లు సరేఖీయాలు.
కాబట్టి A, B, C బిందువులగుండా త్రిభుజాన్ని గీయలేము.

ప్రశ్న 15.
బిందువు (x, y), (- 2, 8) మరియు (- 3, – 5) లకు సమాన దూరంలో ఉన్నది. అయిన x మరియు y ల
మధ్య సంబంధమును కనుక్కోండి.
సాధన.
ఇచ్చిన బిందువులు
P (x, y), A (- 2, 8), B (- 3, – 5) అనుకొనుము.
లెక్క ప్రకారం,
∴ AP = BP = AP² = BP² ……… (1)
∴ AP = \(\sqrt{[(-2-x)]^{2}+(8-y)^{2}}\)
= \(\sqrt{x^{2}+4 x+4+y^{2}-16 y+64}\)

AP² = x² + y² + 4x – 16y + 68

BP = \(\sqrt{[x-(-3)]^{2}+[y-(-5)]^{2}}\)
= \(\sqrt{(x+3)^{2}+(y+5)^{2}}\)
= \(\sqrt{x^{2}+6 x+9+y^{2}+10 y+25}\)

BP = x² + y² + 6x + 10y + 34
AP = BP
∴ x² + y² + 4x – 16y + 68 = x² + y² + 6x + 10y + 34
x² + y² + 4x – 16y + 68 – x² – y² – 6x – 10y – 34 = 0
– 25 – 26y + 34 = 0
∴ – 2[x + 13y – 17] = 0
X + 13y = 17.

గమనిక : (- 3, – 5) మరియు (- 2, 8) లకు సమానదూరంలో గల బిందువులు C, D, E, F, G, H, I, J, ……. x + 13y – 17 = 0 సరళరేఖపై ఉంటాయి.
ఈ సరళరేఖ AB రేఖాఖండాన్ని లంబ సమద్విఖండన చేస్తుంది. ఒక రేఖండం యొక్క లంబ సమద్విఖండన రేఖపై గల బిందువులు ఆ రేఖాఖండం యొక్క చివరి బిందువులకు సమాన దూరంలో ఉంటాయి.