Class 7

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 13 Area and Perimeter Ex 5 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 13th Lesson Area and Perimeter Exercise 5

Question 1
Find the circumference of a circle whose radius is
(i) 35cm (ii) 4.2cm (iii) 15.4 cm
Solution:
i) Given: r= 35 cm
Circumference of the circle = 2πr = 2 × \(\frac{22}{7}\) × 35 = 220 cms.

ii) Given : r = 4.2 cm
Circumference of the circle = 2πr = 2 × \(\frac{22}{7}\) × 4.2 26.4 cms

iii) Given: r = 15.4cm
Circumference of the circle = 2πr = 2 × \(\frac{22}{7}\) × 15.4 = 96.8 cms

Question 2.
Find the circumference of circle whose diameter is
(i) 17.5 cm (ii) 5.6 cm (iii) 4.9 cm
Note : take π = \(\frac{22}{7}\) in the above two questions.
Solution:
i) Given : d = 17.5 cm
Circumference of the circle = πd = \(\frac{22}{7}\) × 17.5 = 55 cm
ii) Given d = 5.6 cm
Circumference of the circle = πd = \(\frac{22}{7}\) × 5.6 = 17.6 cm
iii) Given d = 4.9 cm
Circumstances of the circle = πd = \(\frac{22}{7}\) × 4.9 = 15.4 cm

Question 3.
(i) Taking π = 3.14, find the circumference of a circle whose radius is
(a) 8 cm (b) 15 cm (c) 20cm
(ii) Calculate the radius of a circle whose circumference is 44cm?
Solution:
i) a) Given r = 8 cm π = 3.14
Circumference of circle = 2πr
= 2 × 3.14 × 8 = 50.24cm

b) Given r = 15cm
Circumference of circle = 2πr
= 2 × 3.14 × 15 = 942cm

c) Given r 20cm
Circumference of circle = 2πr
= 2 × 3.14 × 20 = 125.6cm

ii) Given,
Circumference = 44cm
Circumference of a circle = 2πr
2 × \(\frac{22}{7}\) x r =
2 × 22 × r = 44 x 7
r = \(\frac{44 \times 7}{2 \times 22}\) = 7cm
∴ radius of the circle = 7cm.

Question 4.
If the circumference of a circle is 264 cm, find its radius. Take π = \(\frac{22}{7}\)
Solution:
Given : Circumference = 264 cm
Circumference of a circle = 2πr = 2 × \(\frac{22}{7}\) x r = 264
2 × 22 × r = 264 × 7
r = \(\frac{264 \times 7}{2 \times 22}\) = 42
∴ radius of the circle = 42 cm.

Question 5.
If the circumference of a circle is 33 cm, fmd its diameter.m
Solution:
Given circumference = 33cm
Circumference of a circle = πd
\(\frac{22}{7}\) × d = 33
22d = 33 × 7
d = \(\frac{33 \times 7}{22}=\frac{21}{2}\) = 10.5cm
∴ diameter of the circle = 10.5 cm

Question 6.
How many times will a wheel of radius 35cm be rotated to travel 660 m?
(Take π = \(\frac{22}{7}\)).
Solution:
Given radius = 35cm.
Circumference of the circle = 2πr
= 2 × \(\frac{22}{7}\) × 35
= 220cm.
∴ The number of times the wheel will he rotated = \(\frac{660}{220}\) = 3 times.

Question 7.
The ratio of the diameters of two circles is 3 :4. Find the ratio of their circumferences.
Solution:
Given: Ratio of diameter = d₁ : d₂ = 3 : 4
Ratio of their circumferences C₁ : C₂ = πd₁ : πd₁
= \(\frac{22}{7}\) × 3: \(\frac{22}{7}\) : 4 = 3 : 4

Question 8.
A road roller makes 200 rotations in covering 2200 m.
Find the radius of the roller.
Solution:
Given : Road roller makes 200 rotations covering a distance = 2200m
(i.e.,) 200 × circumference = 2200
200 × 2 × π × r = 2200
200 × 2 \(\frac{22}{7}\) × r = 2200
r = 2200 × \(\frac{7}{22} \times \frac{1}{200} \times \frac{1}{2}=\frac{7}{4}\) = 1.75m

Question 9.
The minute hand of a circular clock is 15 cm.
How far does the tip of the minute hand move in 1 hour?
(Take π = 3.14)
Solution:
Given : The length of minute hand = 15cm
In one hour it completes a rotation.
i.e. distance covered by its tip = circumference of the circle with a radius 15cm
22 660
= 2 × \(\frac{22}{7}\) × 15 = \(\frac{660}{7}\) cm = 94.28cm

Question 10.
A wire is bent in the form of a circle with radius 25 cm. It is straightened and made ¡rito a square. What is the length of the side of the square?
Solution:
Given: Radius of the circle 25 cm .
Circumference of the circle = Perimeter of the square
2πr = 4 × side
4 × side=2 × \(\frac{22}{7}\) × 25
Side = 2 × \(\frac{22}{7}\) × 25 × \(\frac{1}{4}\) = \(\frac{275}{7}\) = 39.28
∴ Side of square = 39.28 cm

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 13 Area and Perimeter Ex 4 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 13th Lesson Area and Perimeter Exercise 4

Question 1.
Find the area of the following rhombuses.

Solution:
Area = \(\frac { 1 }{ 2 }\)d₁d₂
d₁ = 5 + 5 = 10cm
d₂ = 2 + 2 = 4cm
A = \(\frac { 1 }{ 2 }\) × 10 × 4 = 20 cm²

d₁ = 3 + 3 = 6 cm
d₂ = 4 + 4 = 8cm
Area = \(\frac { 1 }{ 2 }\)d₁d₂
= \(\frac { 1 }{ 2 }\) × 6 × 8
= 24 cm²

Question 2.
Find the missing values.

Solution:

Question 3.
If length of diagonal of a rhombus whose area 216 sq. cm. is 24 cm. when find the length of second diagonal.
Solution:
Given: Length of one diagonal d₁ = 24cm, d₂ =?
Area = \(\frac { 1 }{ 2 }\)d₁d₂ = 216
\(\frac { 1 }{ 2 }\) × d₁ × d₂ = 216
\(\frac { 1 }{ 2 }\) × 24 × d₂ = 216
d₂ = \(\frac{216}{12}\) = 18

Question 4.
The floor of a building consists of3 000 tiles which are rhombus shaped. The diagonals of each of the tiles are 45 cm and 30 cm. Find the total cost of polishing the floor, if cost per m² is Rs.2.50.
Solution:
Diagonals of each (shape / rhombus) tiles
d₁ = 45cm, d₂ = 30cm
Total tiles = 3000
Total area = 3000 × Area of each tile = 3000 × \(\frac { 1 }{ 2 }\) × d₁ × d₂
= 3000 x \(\frac { 1 }{ 2 }\) × 45 × 30 = 2025000 cm²
= \(\frac{2025000}{100 \times 100}\) m² = 202.5m²
∴ Cost of polishing the floor at the rate of Rs. 2.50 per a square metre 202.5 × 2.50 = Rs. 506.25

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 13 Area and Perimeter Ex 3 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 13th Lesson Area and Perimeter Exercise 3

Question 1.
Find the area of each of the following triangles.

Solution:
î) Area = \(\frac{1}{2}\) = \(\frac{1}{2}\) x 5 x 8 = 20 cm²
ii) Area = \(\frac{1}{2}\) = \(\frac{1}{2}\) x 6 x 4 = 12 cm²
iii) Area = \(\frac{1}{2}\) = \(\frac{1}{2}\) x 5.4 x 7.5 = 20.25 cm²
iv)Area = \(\frac{1}{2}\) = \(\frac{1}{2}\) x 6 x 4 = 12 cm²

Question 2.
In ΔPQR, PQ = 4 cm, PR =8 cm and RT = 6cm. Find (i) the area of ΔPQR (ii) the length of QS.

Solution:
Given PQ 4cm, PR = 8cm, RT = 6cm
1) Area of ΔPQR = \(\frac { 1 }{ 2 }\) × base × height = \(\frac { 1 }{ 2 }\) × PQ × RT
= \(\frac { 1 }{ 2 }\) × 4 × 6 = 12cm²

ii) Also area of ΔPQR = \(\frac { 1 }{ 2 }\) × base x height = \(\frac { 1 }{ 2 }\) × PR × QS
12 = \(\frac { 1 }{ 2 }\) × 8 × QS
QR = \(\frac{12 \times 2}{8}\) = 3cm

Question 3.
ΔABC is right-angled at A. AD is perpendicular to BC, AB =5 cm, BC = 13 cm and AC = 12 cm. Find the area of ΔABC. Also, find the length of AD.

Solution:
Given.
In ΔABC, ∠A = 90°
AB = 5cm; AC = 12cm; AD ⊥ BC; BC = 13cm.
Now area of ΔABC = \(\frac { 1 }{ 2 }\) × base × height
= \(\frac { 1 }{ 2 }\) x AB x AC = \(\frac { 1 }{ 2 }\) × 5 × 12 = 30cm²
Also area of MBC = \(\frac { 1 }{ 2 }\) × BC × AD
30 = \(\frac { 1 }{ 2 }\) × 13 × AD
∴ \(\frac{30 \times 2}{13}=\frac{60}{13}=4 \frac{8}{13}\) cm

Question 4.
ΔPQR is isosceles with PQ = PR = 7.5 cm and QR = 9 cm. The height PS from P to QR, is 6 cm. Find the area of ΔPQR. What will be the height from R to PQ i.e. RT?

Solution:
Given: PQ = PR = 7.5cm, QR = 9cm PS = 6cm
Area of ΔPQR = \(\frac { 1 }{ 2 }\) bh = latex]\frac { 1 }{ 2 }[/latex] x 9 x 6 = 27cm²
Also area of ΔPQR = \(\frac { 1 }{ 2 }\) × PQ × RT
27 = \(\frac { 1 }{ 2 }\) × 7.5 × RT [PQ = PR]
∴ RT = \(\frac{2 \times 27}{7.5}=\frac{2 \times 27 \times 2}{15}=\frac{36}{5}\) = 7.2 cm

Question 5.
ABCD rectangle with AB =8 cm, BC = 16 cm and AE = 4 cm. Find the area of ABCE. Is the area of ΔBEC equal to the sum of the area of ΔBAE and ΔCDE. Why?

Solution:
Given : In rectangle ABCD,
AB = 8cm, BC = 16 cm, AE = 4cm
Now Area of ΔBAE = \(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) × \(\overline{\mathrm{BC}} \times \overline{\mathrm{AB}}\)
= \(\frac { 1 }{ 2 }\) × 16 x 8 = 64cm²

Area of ΔCDE = \(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) × \(\overline{\mathrm{ED}} \times \overline{\mathrm{DC}}\)
= \(\frac { 1 }{ 2 }\) × 12 × 8 = 48cm²
(∵ \(\overline{\mathrm{ED}}\) = AD – AE = 16 – 4 = 12cm and \(\overline{\mathrm{DC}}=\overline{\mathrm{AB}}\))
Now ΔBAE + ΔCDE = 16 + 48 = 64 = ΔBCE.

Question 6.
Ramu says that the area of ΔPQR is, A = \(\frac{1}{2}\) × 7 × 5 cm².
Gopi says that it is, A = \(\frac{1}{2}\) × 8 × 5 cm². Who is correct’? Why?

Solution:
Ramu is correct.
Since area of a triangle = \(\frac { 1 }{ 2 }\) × base × corresponding height
= \(\frac { 1 }{ 2 }\) × 7 × 5cm²
But height 5cm is not corresponding to side &m.
∴ Gopi is not correct.

Question 7.
Find the base of a triangle whose area is 220 cm² and height is 11cm.
Solution:
Given Area = 220 cm², h = 11 cm
Area of a triangle = \(\frac { 1 }{ 2 }\)b.h
= \(\frac { 1 }{ 2 }\) × b × 11 = 220cm² (given)
b × 11 = 220 × 2
b = \(\frac{220 \times 2}{11}\) = 40
∴ base of the triangle = 40 cm.

Question 8.
In a triangle the height is double the base and the area is 400 cm². Find the length of the base and height.
Solution:
Area = 400 cm²
Let the base of the triangle be x.
height = 2x
Area of the triangle = \(\frac { 1 }{ 2 }\)b.h
\(\frac { 1 }{ 2 }\) × x × 2x = 400 (given)
x² = 400
x = \(\sqrt{400}\) = 20
∴ base of the triangle = 20 cm
height = 2(base)= 2(20) = 40 cm.

Question 9.
The area of triangle is equal to the area of a rectangle whose length and breadth are 20 cm and 15 cm respectively. Calculate the height of the triangle if its base measures 30 cm.
Solution:
Given :Length of the rectangle = 20 cm
Breadth of the rectangle = 15 cm
Base of the triangle = 30 cm
Area of the rectangle = Area of the triangle
Length x breadth = \(\frac { 1 }{ 2 }\) × base × height
20 × 15 = \(\frac { 1 }{ 2 }\) × 30 × height
∴ height = \(\frac{20 \times 15}{15}\) = 20cm

Question 10.
In Figure ABCD find the area of the shaded region.

Solution:
Given : Side of the square ABCD = 40cm
Area of the shaded rgion = (Area of the square) — (Area of the unshaded region)
= (side × side) – \(\frac { 1 }{ 2 }\) × base × height
= 40 × 40 – \(\frac { 1 }{ 2 }\) × 40 × 40
= 1600 – 800 = 800cm²

Question 11.
In Figure ABCD, find the area of the shaded region.

Solution:
Given: Side of the square = 20 cm
Area of the shade region
= (Area of the square) – (Area of unshaded region)
= (Square ABCD) – (ΔEAF + ΔFBC + ΔEDC)
= side × side – (\(\frac { 1 }{ 2 }\)AF × AE + \(\frac { 1 }{ 2 }\) FB × BC + \(\frac { 1 }{ 2 }\) DE × DC)
= 20 × 20 – (\(\frac { 1 }{ 2 }\) × 10 × 12 + \(\frac { 1 }{ 2 }\) × 10 × 20 + \(\frac { 1 }{ 2 }\) × 8 × 20)
= 400 – [60 + 100 + 80] = 400 – 240 = 160cm²

Question 12.
Find the area of a parallelogram PQRS, if PR =24 cm and QU = ST =8 cm.

Solution:
Given : In PQRS, PR = 24cm, ST = 8cm, QU =8cm
Area of PQRS = ΔPQR + ΔPRS
= \(\frac { 1 }{ 2 }\) × \(\frac { 1 }{ 2 }\)base x height + x base x height
= \(\frac { 1 }{ 2 }\) × 24 x 8 + \(\frac { 1 }{ 2 }\) × 24 × 8 = 96 + 96 = 192 cm²

Question 13.
The base and height of the triangle are in the ratio 3:2 and its area is 108 cm². Find its base
and height.
Solution:
Given : Area = 108 cm2
Let the base of the triangle be 3x and height of the triangle be 2x.
Area of the triangle = \(\frac { 1 }{ 2 }\) × base × height = \(\frac { 1 }{ 2 }\) x (3x) (2x) = 108 cm² (given)
3x² = 108
x² = 108/3 = 36
x = \(\sqrt{36}\) = 6
∴ base 3x = 3(6) = 18 cm
height = 2x = 2(6) = 12cm

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 13 Area and Perimeter Ex 2 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 13th Lesson Area and Perimeter Exercise 2

Question 1.
Find the area of the each of the following parallelograms.

Solution:

Question 2.
PQRS is a parallelogram. PM is the height from P to \(\overline{\mathrm{SR}}\) and PN is the height from P to \(\overline{\mathrm{QR}}\). If SR = 12cm and PM = 7.6 cm.
(i) Find the area of the parallelogram PQRS
(ii) Find PN, if QR = 8 cm.
Solution:

i) Given:SR = 12cm
PM = 7.6cm
∴ Area = base × height
= 12 × 7.6 = 91.2 cm²

ii) Also area = base × height
91.2 = QR × PN
91.2 = 8 × PN
∴ PN = \(\frac{91.2}{8}\) = 11.4cm

Question 3.
DF and BE are the height on sides AB and AD respectively in parallelogram ABCD. Ifthe area of the parallelogram is 1470 cm², AB = 35 cm and AD = 49 cm, find the length of BE and DF.

Solution:
Given : AB = 35 cm, AD = 49 cm
area of ????ABCD = 1470 cm²
Area of a parallelogram = base × height
AB × DF = area of ????ABCD
35 × DF = 1470
DF = \(\frac{1470}{35}\) = 42cm
Also AD × BE = 1470
49 × BE = 1470
∴ BE= \(\frac{1470}{49}\) = 30cm

Question 4.
The height of a parallelogram is one third of its base. If the area of the parallelogram is 192cm², find its height and base.
Solution:
Area of the parallelogram = 192 cm²
Area of parallelogram = base × height = 192 cm² (given)
Let the base of the parallelogram be x.
height = \(\frac{x}{3}\)
Area = base × height = x x \(\frac{x}{3}=\frac{x^{2}}{3}\) = 192
⇒ x² = 192 × 3 = 576
x = \(\sqrt{576}\) = 24
∴ base = 24 cm
height = \(\frac{x}{3}=\frac{24}{3}\) = 8cm.

Question 5.
In a parallelogram the base and height are is in the ratio of 5:2. If the area of the parallelogram is 360m², find its base and height.
Solution:
Let the base of the parallelogram be 5x and height of the parallelogram be 2x.
Area = height x base = 5x × 2x = 10x² = 360 cm² (given)
10x² = 360
x² = \(\frac{360}{10}\) = 36
x = √36 = 6
base = 5x = 5(6) = 30 cm
height = 2x = 2(6) = 12 cm

Question 6.
A square and a parallelogram have the same area. If a side of the square is 40m and the height of the parallelogram is 20m, find the base of the parallelogram.
Solution:
Given: Side of a square = 40m
Height of a parallelogram = 20m
Area of parallelogram = Area of the square
base × height side × side
base × 20 40 × 40
∴ base = \(\frac{40 \times 40}{20}\) = 80 m.

SCERT AP 7th Class Science Study Material Pdf 11th Lesson దారాలు – దుస్తులు Textbook Questions and Answers.

AP State Syllabus 7th Class Science 11th Lesson Questions and Answers దారాలు – దుస్తులు

7th Class Science 11th Lesson దారాలు – దుస్తులు Textbook Questions and Answers

Improve Your Learning (అభ్యసనాన్ని మెరుగుపరచుకుందాం)

I. ఖాళీలను పూరింపుము.

1. పొట్టిగా ఉన్న ఉన్ని వెంట్రుకలను తొలగించడం కోసం దువ్వెన వంటి యంత్రం దంతాల మధ్య నుండి వాటిని లాగడాన్ని ……………. అంటారు . (కూంబింగ్)
2. పట్టు దారాల కోసం పట్టుపురుగులను పెంచే ప్రక్రియను …………………… అంటారు. (పట్టు సంవర్ధనం)
3. పట్టువలె కనిపించే కృత్రిమ దారం …………. (రేయాన్)
4. పట్టులో ఉండే ప్రోటీన్ ……………….. (ఫైబ్రాయిన్)
5. ఊలుని ఇచ్చే జంతువుల మృదువైన పొట్టి శ్రేష్ఠమైన వెంట్రుకలు గల లోపలి పొరను ………….. అంటారు. (ఉన్ని)

II. సరైన జవాబు సూచించు అక్షరమును బ్రాకెట్లో రాయండి.

1. ఈ క్రింది వానిలో ఊలుని ఇచ్చే జంతువు కానిది ఏది?
a) జడల బర్రె
b) మేక
c) మోత్
d) ఒంటె
జవాబు:
c) మోత్

2. పట్టు పురుగు ………………..
a) ప్యూపా
b) కకూన్
c) డింభకము
d) ప్రౌఢ దశ
జవాబు:
c) డింభకము

3. షీరింగ్ అనగా………………
a) నాణ్యత ఆధారంగా ఉన్నిని ఎంపిక చేయడం
b) ఉన్నికి రంగు వేయడం
c) సన్నని చర్మపు పొరతో పాటుగా ఉన్నిని కత్తిరించడం
d) వేడి నీటిలో ఫైబర్లను శుభ్రపరచడం
జవాబు:
c) సన్నని చర్మపు పొరతో పాటుగా ఉన్నిని కత్తిరించడం

4. పట్టుదారం తయారీ ఈ మొక్కల సాగుతో ముడిపడి ఉన్నది ……………
a) ఓక్ చెట్లు
b) సాల్ చెట్లు
c) తెల్ల మద్ది వృక్షం
d) మల్బరీ చెట్టు
జవాబు:
d) మల్బరీ చెట్టు

5. భారతదేశంలో ఎక్కువగా తయారయ్యే పట్టు రకము ……….
a) ఈరీ
b) టసర్
c) మల్బరీ
d) మూగా
జవాబు:
c) మల్బరీ

III. జతపరచండి.

జవాబు:

IV. ఈ క్రింది ప్రశ్నలకు జవాబులు రాయండి.

ప్రశ్న 1.
స్టిప్లింగ్ ఎలా చేస్తారో తెలపండి. కకూన్లను సిప్లింగ్ చేయడం వలన కలిగే ప్రయోజనం ఏమిటి?
జవాబు:
స్టింగ్ : కకూన్ లోపలి గొంగళి పురుగును చంపే ప్రక్రియను స్టిప్లింగ్ అంటారు.

ఆవశ్యకతలు :

1. 1. కకూన్లను స్టిఫ్టింగ్ చేయకపోతే, కకూన్ లోపలి మోత్, కకూనను పగలగొట్టుకొని వెలుపలికి వస్తుంది. పగిలిపోయిన కకూన్ల నుండి పొడవాటి దారాలను ఉత్పత్తి చేయలేము. ఇది పట్టువస్త్రాల నాణ్యతను తగ్గిస్తుంది.
2. స్టిఫ్టింగ్ చేసిన కకూన్లను ఎక్కువకాలం పాటు నిలువచేసి అవసరమైనప్పుడు సరైన ధరకు మార్కెట్లో అమ్ముకోవచ్చు.

ప్రశ్న 2.
జంతు దారాలకు, మొక్కల నుండి లభించే దారాలకు భేదాలను తెలపండి.
జవాబు:

ప్రశ్న 3.
కృత్రిమ దారాల వినియోగంలో ఉండే ప్రయోజనాలను, నష్టాలను విశ్లేషించండి. ఏ రకమైన దుస్తులను ధరించేందుకు నీవు ఇష్టపడతావు?
జవాబు:
కృత్రిమ దారాల ప్రయోజనాలు:

1. తక్కువ ధరకు లభిస్తాయి.
2. తేలికగా ఉంటాయి.
3. ఎక్కువ కాలం మన్నుతాయి.
4. దృఢంగా ఉంటాయి.
5. తక్కువ నీటిని పీల్చుకుంటాయి.
6. త్వరగా ఆరిపోతాయి.
7. శుభ్రం చేయటం సులభం.

కృత్రిమ దారాల నషాలు:

1. ఇవన్ని పూర్తిగా రసాయనాలతో తయారౌతాయి.
2. వీటి ఉత్పత్తి పర్యావరణ కాలుష్యానికి దారి తీస్తుంది.
3. కొన్ని సంవత్సరాల పాటు నేలలో కలవవు.
4. విచ్ఛిన్నం అయినపుడు విషపదార్థాలను విడుదల చేస్తాయి.
5. చర్మానికి ఎలర్జీ కలిగించవచ్చు.

కావున నేను సహజ దారాలతో తయారైన దుస్తులు ధరించటానికి ప్రాధాన్యత ఇస్తాను. ఇది వ్యవసాయరంగానికి, కుటీర పరిశ్రమలకు చేయూతనివ్వటంతోపాటు పర్యావరణానికి హాని చేయదు.

ప్రశ్న 4.
కకూన్లను స్టిప్లింగ్ చేయకపోతే ఏమి జరుగుతుంది?
జవాబు:

1. కకూన్ లోపలి గొంగళి పురుగును చంపే ప్రక్రియను స్టిఫ్లింగ్ అంటారు.
2. కకూన్లను స్టింగ్ చేయకపోతే, లోపలి మోతా, కకూనను పగలగొట్టుకొని వెలుపలికి వస్తుంది.
3. పగిలిపోయిన కకూన్ల నుండి పొడవైన పట్టుదారాలను తీయలేము.
4. ఇది పట్టువస్త్రాల నాణ్యత తగ్గటానికి కారణమౌతుంది.

ప్రశ్న 5.
పట్టు పురుగు జీవిత చక్రము పటము గీసి, భాగములను గుర్తించండి. జీవిత చక్రంలో ఏ దశ పట్టు ఉత్పత్తిలో ముఖ్యమైనది? ఎందువలన?
జవాబు:

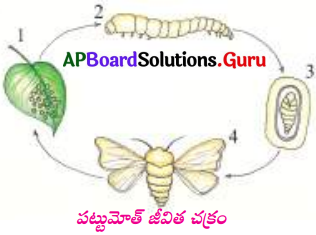
1. పట్టుపురుగు జీవిత చక్రంలో కకూన్ లేదా పట్టుకాయ అనేది కీలకమైనది. దీని నుండి పట్టు తీస్తారు.
2. కకూన్ దశలో గొంగళి పురుగు తన చుట్టు ఒక గుళికను -ఏర్పర్చుకొంటుంది. ఈ నిర్మాణాన్నే పట్టుకాయ అంటారు.
3. పట్టుకాయనే సిప్లింగ్ చేసి, రీలింగ్ యూనిట్ కి పంపుతారు.
4. రీలింగ్ యూనిట్‌లో పట్టుకాయ నుండి పట్టుదారము తీస్తారు.

ప్రశ్న 6.
జంతువుల ఉన్ని కోసం షీరింగ్ చేసే సమయంలో జంతువును బాధించకుండా ఉండటం కోసం షీరింగ్ చేసే వారు ఎటువంటి జాగ్రత్తలు తీసుకోవాలో సూచించండి.
జవాబు:

1. జంతువుల చర్మంపై రెండు రకాల రోమాలు ఉంటాయి. మొదటి రకం బిరుసుగా, గట్టిగా ఉండగా రెండవ రకం మెత్తగా, మృదువుగా ఉంటుంది. దీనినే ఉన్ని లేదా ప్లీస్ అంటారు.
2. జంతు చర్మం నుండి ఉన్ని లేదా ప్లీస్ ను తొలగించడాన్ని షీరింగ్ అంటారు.
3. పదునైన కత్తెర వంటి సాధనాన్ని షీరింగ్ కి వాడతారు.
4. ప్రస్తుత కాలంలో గన్ వంటి పరికరాలు వాడుతున్నారు.

జాగ్రత్తలు:

1. షీరింగ్ సమయంలో చర్మం దెబ్బతినకుండా నూనె లేదా గ్రీజు వంటి పదార్థం పూస్తారు.
2. శీతాకాలంలో జీవులకు ఉన్ని అవసరం. కావున, ఈ నెలలో షీరింగ్ చేయరు.
3. వేసవికాలంలో జంతువులకు ఉన్ని అవసరం ఉండదు. కావున, వేసవికి ముందు వచ్చే వసంత కాలంలో సీరింగ్ చేస్తారు.
4. షీరింగ్ తరువాత గొర్రెలకు ఆహారం బాగా అందించటం వలన అవి త్వరగా కోలుకొని ఉన్నిని ఉత్పత్తి చేసుకుంటాయి.

ప్రశ్న 7.
పట్టు దారాలు కోసం కకూన్లలోని డింభకాలను చంపటంపై మీ అభిప్రాయాలను తెలియజేయండి. పట్టు మోత్ పట్ల ఇటువంటి నిర్ధయాపూరితమైన చర్యలను నివారించటం కోసం నీవు ఎటువంటి చర్యలను సూచిస్తావు?
జవాబు:

1. పట్టుదారాల కోసం కకూన్లను చంపటం నాకు చాలా బాధగా అనిపించింది.
2. నిజంగా ఇది నిర్దయకరమైన చర్య.
3. దీనికి ప్రత్యామ్నాయంగా మోతలు జీవించగలిగే ప్రక్రియకు ప్రాధాన్యత ఇవ్వాలి.
4. అహింసా పట్టు అహింసా మార్గంలో పట్టు సంవర్ధనం ద్వారా ఉత్పత్తి చేసే పట్టు.
5. ఈ పద్దతిలో పట్టుపురుగును కకూన్ నుండి వెలుపలికి రానిచ్చి తరువాత మిగిలిన పట్టుకాయల నుండి పట్టు దారం తీస్తారు.
6. ఈ పద్ధతిని, ఆంధ్రప్రదేశ్ చేనేత పరిశ్రమ శాఖలో పని చేసిన చేనేత నిపుణులు శ్రీ కుసుమ రాజయ్య పరిచయం చేశారు.
7. అయితే ఈ విధానంలో పట్టు ఉత్పత్తి ఎక్కువ ఖర్చుతో కూడుకున్నది.

7th Class Science 11th Lesson దారాలు – దుస్తులు InText Questions and Answers

7th Class Science Textbook Page No. 137

ప్రశ్న 1.
ప్రజలు చలి ప్రదేశములలో నివసిస్తున్నప్పుడు ఏఏ దుస్తులను ధరిస్తారు?
జవాబు:
చలి ప్రదేశాలలో నివసించే ప్రజలు ఉన్ని దుస్తులు ధరిస్తారు.

ప్రశ్న 2.
ఈ దుస్తులు ఏ వస్త్రంతో తయారవుతాయి?
జవాబు:
ఉన్ని దుస్తులు జంతువుల నుండి తీసిన రోమాలతో తయారవుతాయి.

ప్రశ్న 3.
సంక్రాంతి వంటి ముఖ్య వేడుకలలో ఏ వస్త్రంతో తయారయిన దుస్తులను నీవు ధరిస్తావు?
జవాబు:
సంక్రాంతి వంటి ప్రత్యేక సందర్భములలో నేను పట్టు దుస్తులు ధరిస్తాను.

7th Class Science Textbook Page No. 139

ప్రశ్న 4.
మన పరిసరాలలో గొర్రెలు, మేకలను ఎందుకని ఎక్కువ మొత్తంలో పెంచుతారు?
జవాబు:
ఉన్ని మరియు మాంసం కోసం గొర్రెలను, మేకలను పెంచుతారు.

7th Class Science Textbook Page, No. 143

ప్రశ్న 5.
మనకు రంగు రంగుల ఉన్ని దుస్తులు ఎలా లభిస్తున్నాయి?
జవాబు:
గొర్రెల ఉన్ని నలుపు, గోధుమ, తెలుపు రంగులలో ఉంటుంది. రంగు వేయటం ద్వారా, ప్లీస్ మొదట దానిలోని రంగు తొలగించబడటం కోసం బ్లీచింగ్ చేయబడి, తరువాత వేరు వేరు రంగులలో ముంచబడుతుంది.

7th Class Science Textbook Page No. 157

ప్రశ్న 6.
మనం దుస్తులు ఎందుకు శుభ్రపరుస్తాము?
జవాబు:
చర్మ వ్యాధులు రాకుండా ఉండటం కోసం మనం ధరించిన దుస్తులు శుభ్రం చేయటం అవసరం.

ఆలోచించండి – ప్రతిస్పందించండి

7th Class Science Textbook Page No. 157

ప్రశ్న 1.
పూర్వం పారాచూట్ తాళ్ళను పట్టుతో తయారుచేసేవారు. దీనికి ఉన్న బలం, సాగే గుణము, గాలిలో ఎగురుతున్నప్పుడు వ్యక్తి బరువును తట్టుకునే విధంగా ఉంటుంది. పట్టుకి ఉన్న ఈ సద్గుణాలతో పాటుగా నీటిని నిరోధించే గుణం కారణంగా పారాచూట్ తాళ్ళ తయారీదారులు నైలాన్ వైపుకు మొగ్గు చూపడం జరిగింది. నూలు లేదా ఊలును ఈ అవసరం కోసం ఉపయోగిస్తే ఏమి జరుగుతుంది?
జవాబు:

1. పారాచూట్ తయారీకి పట్టు లేదా నైలాన్ దారాలు వాడటం మంచిది.
2. వాటి స్థానంలో నూలు లేదా ఉన్ని ఉపయోగిస్తే గట్టిదనం తగ్గిపోతుంది.
3. మనిషి బరువు మోయటంలో పారాచూట్ సామర్థ్యం తగ్గిపోతుంది.
4. నూలు లేదా ఉన్నికి నీటిని పీల్చుకొనే స్వభావం వలన తేమ వాతావరణంలో ఉపయోగించలేము.
5. ఈ దారాలు నీటిని పీల్చుకోవటం వలన పారాచూట్ బరువు పెరుగుతుంది.
6. వాటిని వాడటం ప్రమాదకరం.

ప్రాజెక్ట్ పనులు

7th Class Science Textbook Page No. 165

ప్రశ్న 1.
భారతదేశ పటమును తీసుకుని, దేశంలోని వివిధ ప్రదేశాలలో ఉన్నిని ఇచ్చే జంతువులు జీవించే ప్రదేశాలను గుర్తించి, ఆయా ప్రదేశాలలో లభ్యమయ్యే ఆ జంతువుల పేర్లను నమోదు చేయండి.
జవాబు:

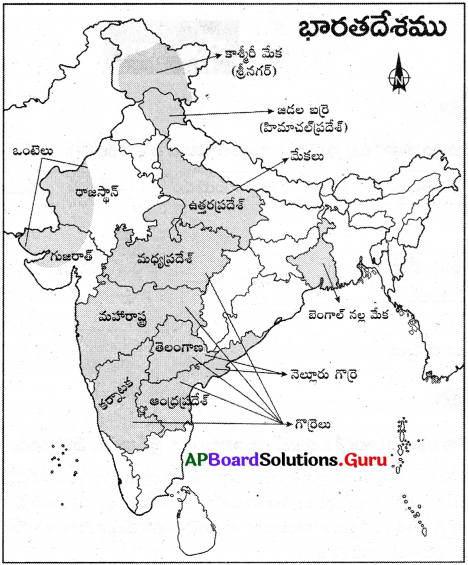
ప్రశ్న 2.
వివిధ రకములైన ఊలుని ఇచ్చే జంతువుల బొమ్మలతో ఒక స్క్రాప్‌బుక్‌ తయారు చేయండి.
జవాబు:

కృత్యాలు

కృత్యం – 1

ప్రశ్న 1.
“ఉన్ని నుండి వస్త్రం దాకా” ఉన్ని దుస్తుల తయారీలో ఇమిడి ఉన్న దశలతో ఒక ఫ్లో చార్ట్ ను తయారు చేయండి.
జవాబు:

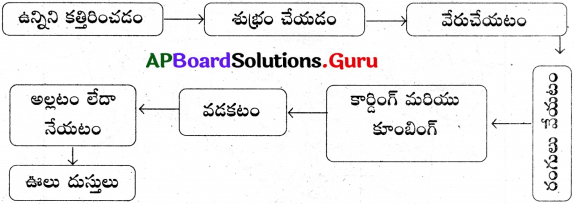
కృత్యం – 2

ప్రశ్న 2.
ఆంధ్రప్రదేశ్ లోని వివిధ జిల్లాలలో సెరికల్చర్ యూనిట్లు ఉన్న ప్రదేశాలను పేర్కొనండి.
జవాబు:
ఆంధ్రప్రదేశ్ లోని అనంతపురం జిల్లా ధర్మవరం, కర్ణాటకలోని రామనగర, గుజరాత్ లోని సూరత్, మధ్యప్రదేశ్ లోని చందేరీ, తమిళనాడులోని కాంచీపురం, తెలంగాణలోని పోచంపల్లి, ఉత్తరప్రదేశ్ లోని వారణాసిలు అధిక నాణ్యత గల పట్టు ఉత్పత్తి, నేత పరిశ్రమల కారణంగా భారతదేశంలో పట్టునగరాలుగా పేరుగాంచాయి. ఆంధ్రప్రదేశ్ అంతటా పట్టు పరిశ్రమ నెలకొని ఉంది.

ప్రశ్న 3.
టైలర్ లేదా బట్టల దుకాణం నుండి ఊలు, పట్టు, నూలు మరియు మరికొన్ని దారాలను సేకరించండి. ఒకదాని తరువాత ఒకటి క్రొవ్వొత్తి మంటలో మండించండి..అవి ఎలా మండుతున్నాయో మరియు ఎటువంటి పొగలను ఉత్పత్తి చేస్తున్నాయో పరిశీలించండి. పట్టికలో నమోదు చేయండి.
జవాబు:

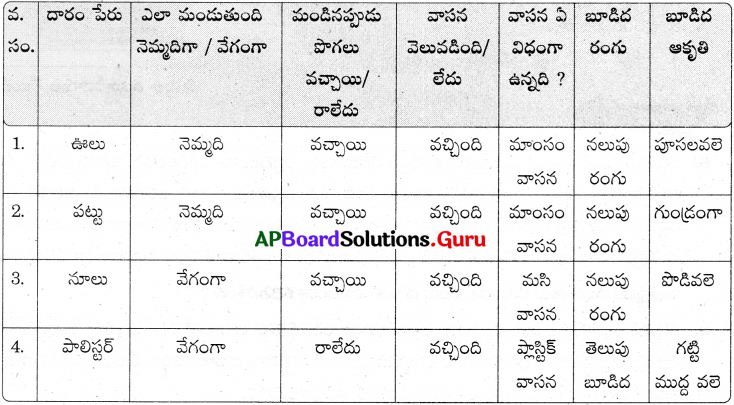
కృత్యం – 4

ప్రశ్న 4.
జంతు దారాల స్వచ్ఛతను ఎలా పరీక్షిస్తావు?
జవాబు:
ఉద్దేశం : జంతు దారాల స్వచ్ఛతను పరీక్షించుట.

పరికరాలు : రెండు బీకర్లు, సోడియం హైపోక్లోరైట్.

విధానం :
టాయిలెట్ క్లీనర్ లో ఉంచిన పట్టు దారాలు

1. రెండు బీకర్లు తీసుకొని, వాటిలో కొంచెం సోడియం హైపోక్లోరైట్ ద్రావణం తీసుకోవాలి.
2. రెండు బీకరులలో ఒకదానిలో ఉన్ని దారాన్ని మరొకదానిలో పట్టు దారాన్ని ఉంచాలి.
3. 20 నిముషాలు ఆగి మార్పులు పరిశీలించాలి.

పరిశీలన :
రెండు దారాలు హైపోక్లోరైట్ ద్రావణంలో కరిగిపోయాయి.

వివరణ :
జంతు దారాలు ప్రోటీన్లతో తయారవుతాయి. ఇవి హైపోక్లోరైట్ వంటి బ్లీచింగ్ ద్రావణాలలో కరుగుతాయి.

నిర్ధారణ :
మంచి జంతు దారాలు, హైపోక్లోరైట్ ద్రావణాలలో కరుగుతాయి.

కృత్యం – 5

ప్రశ్న 5.
ఇవ్వబడిన పటంలోని దుస్తుల తయారీదారుల లేబుల్ ని పరిశీలించి క్రింది ప్రశ్నలకు సమాధానాలు రాయండి.
1) ఈ దుస్తులు ఏ వస్త్రంతో తయారయ్యాయి?
జవాబు:
ఈ దుస్తులు పాలిస్టర్ మరియు కాటన్లతో తయారైనవి.

2) ఈ దుస్తులను ఏ రకంగా ఉతకవచ్చు?
జవాబు:
ముదురు రంగు ఉన్న దుస్తులను వేరుచేసి ఉతకాలి.

3) దుస్తుల దీర్ఘకాల మన్నిక కొరకు ఎటువంటి జాగ్రత్తలు తీసుకోవాలి?
జవాబు:

1. డిటర్జంట్ ను తక్కువగా వాడాలి.
2. తక్కువ ఉష్ణోగ్రతలో ఆరవేయాలి.
3. బ్లీచింగ్ వాడరాదు.
4. తక్కువ వేడితో ఇస్త్రీ చేయాలి.

కృత్యం – 6

ప్రశ్న 6.
దర్జీ వద్ద నుండి రిబ్బను వెడల్పుతో, పొడవైన రెండు పట్టు వస్త్రములను సేకరించండి. వాటిని నీటిలో ముంచి తీసి, వాటిపై ఏర్పడిన ముడుతలను పరిశీలించండి. ఒక వస్త్రమును అలాగే ఆరవేయండి మరియు రెండవ వస్త్రమును ఒక కర్ర బొంగుకు కానీ, లోహపు కడ్డీకి కానీ బిగుతుగా, ముడుతలు లేకుండా లాగి, చుట్టివేయండి. ఈ వస్త్రమును అలాగే గాలికి ఆరనివ్వండి. రెండు మూడు గంటల తరువాత రెండు వస్త్రములను పరిశీలించండి.
ఏ వస్త్రము ముడుతలు లేకుండా, ముడుచుకుని పోకుండా కనిపిస్తోంది?
జవాబు:
చుట్టబడి ఆరబెట్టిన వస్త్రము ముడుతలు లేకుండా ఉంటుంది. కృత్రిమ దారాలతో చేసిన వస్త్రములను నిర్వహించడం సులభం కాబట్టి వాటిని ధరించేందుకు ఎక్కువ ఇష్టపడతాము. సహజ దారాలు జీవుల నుండి లభించే పదార్థాలతో తయారవుతాయి. అందువలన అవి మన చర్మానికి అనుకూలమైనవి.

Students can go through AP Board 7th Class Maths Notes Chapter 11 Exponents to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 11 Exponents

→ Very large numbers are easier to read, write and understand when expressed in exponential form.
Eg : 10000 = 10⁴
8 × 8 × 8 × 8 × 8 × ….. × 8 (16 times) = 8¹⁶.

→ When a number is multiplied by itself for many number of times (repeated multiplication) then we write it in exponential form.
Eg : 2 × 2 × 2 × 2 = 2⁴ Here 2 is base 4 is exponent.
3 × 3 × 3 × 3 × 3 = 3⁵ Here 3 is base 5 is exponent.

→ a . a . a . a ….. a (m times) = a^m.

→ Here ‘a’ is called the base and ‘m’ is called the exponent.

→ Laws of exponents

i) a^m × aⁿ = a^m+n

ii)  (a^m)ⁿ = a^mn

iii) (ab)^m = a^m . b^m

iv) a^m = aⁿ ⇒ m = n

v) a^-n = \(\frac{1}{a^{n}}\)

vi) \(\frac{\mathrm{a}^{\mathrm{m}}}{\mathrm{a}^{\mathrm{n}}}\) = a^m-n  if (m > n)
= \(\frac{1}{a^{n-m}}\)  if (m < n)
= 1 if (m = n)

vii) \(\left(\frac{a}{b}\right)^{m}\) = \(\frac{a^{m}}{b^{m}}\)

viii) a⁰ = 1 where a ≠ 0

Students can go through AP Board 7th Class Maths Notes Chapter 10 Algebraic Expressions to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 10 Algebraic Expressions

→ Variable: It takes different values.
Ex: x, y, z, a, b, c, m etc.
Constant: The value of constant is fixed.
Ex: 1, 2, \(\frac{-2}{3}\), \(\frac{4}{5}\) etc.

→ Algebraic Expression: An algebraic expression is a single term or a combination of terms connected by the symbols ‘+’ (plus) or(minus).
Ex: 2x + 3, \(\frac{2}{5}\)p, 3x – 1 etc.

→ Numerical Expression : If every term of an expression is a constant term, then the expression is called a Numerical expression.
Ex: 2 + 1, -5 × 3, (12 + 4) ÷ 3.
Note: In the expression 2x + 9, ‘2x’ is an algebraic term. ‘9’ is called numeric term.

→ Like terms are terms which contain the same variables with the same exponents.
Ex: 12x, 25x, -7x are like terms.
2xy², 3xy², 7xy² are like terms.

→ Coefficient: In a.xⁿ, ‘a’ is called the numerical coefficient and ‘x’ is called the literal coefficient.
Types of algebraic expressions.

→ Degree of a monomial: The sum of all exponents of the variables present in a monomial is called the degree of the term or degree of the monomial.
Ex: The degree of 9x²y² is 4 [∵ 2 + 2 = 4]
Note: Degree of constant term is zero.
The highest of the degrees of all the terms of an expression is called the degree of the expression.
Ex: The degree of the expression ax + bx² + cx³ + dx⁴ + ex⁵ is 5.

→ The difference between two like terms is a like term with a numerical coefficient equal to the difference between the numerical coefficients of the two like terms.
Note:

1. If no two terms of an expression are alike then it is said to be in the simplified form.
2. In an expression, if the terms are arranged in such a way that the degrees of the terms are in descending order then the expression is said to be in standard form.
3. Addition (or) subtraction of expressions should be done in two methods, they are
   i) Column or Vertical method.
   ii) Row or Horizontal method.

Students can go through AP Board 7th Class Maths Notes Chapter 9 Construction of Triangles to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 9 Construction of Triangles

→ A triangle can be drawn of any three of its elements are known.

→ To construct a triangle, we need

1. Three sides
2. Any two sides and the angle included between them.
3. Two angles and the side included between them.
4. Hypotenuse and one adjacent side of a right angled triangle.
5. Two sides and a non-included angle.

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 11 Exponents Ex 1 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 11th Lesson Exponents Exercise 1

Question 1.
Write the base and the exponent in each case. Also, write the term in the expanded form.
(i) 34
(ii) (7x)²
(iii) (5ab)³
(iv) (4y)⁵
Solution:

Question 2.
Write the exponential form of each expression.
(i) 7 × 7 × 7 × 7 × 7
(ii) 3 × 3 × 3 × 5 × 5 × 5 × 5
(iii) 2 × 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5 × 5
Solution:
(i) 7 × 7 × 7 × 7 × 7 = 7⁵
(ii) 3 × 3 × 3 × 5 × 5 × 5 × 5 = 3³ × 5⁴
(iii) 2 × 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5 × 5 = 2³ × 3⁴ × 5³

Question 3.
Express the following as the product of exponents through prime factorization.
(i) 288
(ii) 1250
(iii) 2250
(iv) 3600
(v) 2400
Solution:
(i) 288
1) 288 = 2 × 144
= 2 × 2 × 72
= 2 × 2 × 2 × 36
= 2 × 2 × 2 × 2 × 18
= 2 × 2 × 2 × 2 × 2 × 9
= (2 × 2 × 2 × 2× 2) × (3 × 3)
= 2⁵ × 3²

(ii) 1250 = 2 × 625
= 2 × 5 × 125
= 2 × 5 × 5 × 25
= 2 × 5 × 5 × 5 × 5
= 2 × 5⁴

(iii) 2250 = 2 × 1125
= 2 × 3 × 375
= 2 × 3 × 3 × 125
= 2 × 3 × 3 × 5 × 25
= 2 × 3 × 3 × 5 × 5 × 5
= 2¹ × 3² × 5³

(iv) 3600 = 2 × 1800
= 2 × 2 × 900
=2 × 2 × 2 × 450
=2 × 2 × 2 × 2 × 225
= ( 2 × 2 × 2 × 2 ) × 3 × 75
= (2 × 2 × 2 × 2) × (3 × 3) × 25
= (2 × 2 × 2 × 2) × (3 × 3) × (5 × 5)
= 2⁴ × 3² × 5²

(v) 2400
2400 = 2 × 1200
= 2 × 2 × 600
= 2 × 2 × 2 × 300
= 2 × 2 × 2 × 2 × 150
= 2 × 2 × 2 × 2 × 2 × 75
= (2 × 2 × 2 × 2 × 2) × 3 × 25
= (2 × 2 × 2 × 2 × 2) × 3 × (5 × 5)
= 2⁵ × 3¹

Question 4.
Identify the greater number in each of the following pairs.
(i) 2³ or 3²
(ii) 5³ or 3⁵
(iii) 2⁸ or 8²
Solution:
(i) 2³ or 3² = 2³ = 2 × 2 × 2 = 8 and 3² = 3 × 3 = 9
∴ 2³ < 3² or 3² > 2³

(ii) 5³ or 3⁵ = 5³ = 5 × 5 × 5 = 125 and 3⁵ = 3 × 3 × 3 × 3 × 3 = 243
∴ 3⁵ > 5³

(iii) 2⁸ or 8² = 2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
8² = 8 × 8 = 64
∴ 2⁸ > 8²

Question 5.
If a = 3, b = 2 find the value of
(i) a^b + b^a
(ii) a^a + b^b
(iii) (a + b)a^b
(iv)(a – b)^a
Solution:
(i) a^b + b^a = 3² + 2³ = 3 × 3 + 2 × 2 × 2 = 9 + 8 =17
(ii) a^a + b^b = 3³ + 2² = 3 × 3 × 3 + 2 × 2 = 27 + 4 = 31
(iii) (a + b)^b = (3 + 2)² = 5² = 5 × 5 = 25
(iv)(a – b)^a = (3 – 2)²= 1² = 1 × 1 = 1 .

Students can go through AP Board 7th Class Maths Notes Chapter 8 Congruency of Triangles to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 8 Congruency of Triangles

→ Two figures are said to be identical if their shapes are same.
Eg: Any two squares, circles or equilateral triangles.

→ Two figures are said to be congruent if they are identical in shape and equal in size.

→ Two line segments are congruent if they have same lengths.

→ Two triangles are congruent if the corresponding angles are equal.

→ We establish the congruency of the triangles by following criteria.

→ S.S.S. criterion: If three sides of a triangle are equal to the corresponding three sides of another triangle, then the triangles are congruent.

FA = TI; AN = IN; FN = TN then △FAN ≅ △TIN

→ S.A.S. criterion: If two sides and the angle included between the two sides of a triangle are equal to the corresponding two sides and the included angle of another triangle, then the two triangles are congruent.

CA = PI; ∠C = ∠P; CT = PG
then, △CAT ≅ △PIG

→ A.S.A. criterion : If two angles and the included side of a triangle are equal to the corresponding two angles and included side of another triangle then the triangles are congruent.

∠A = ∠I; AT = IM; ∠T = ∠M then △MAT ≅ △DIM.

→ R.H.S. criterion: In two right angled triangles, if the hypotenuse and one corresponding side are equal then they are congruent.

∠B = ∠E = 90°
BC = EF
AC = DF
then △ABC ≅ △DEF

→ If by any criterion two triangles are congruent then all the corresponding parts are equal.

Students can go through AP Board 7th Class Maths Notes Chapter 7 Data Handling to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 7 Data Handling

→ Data: Information which is in the form of numbers or words and helps in taking decisions or drawing conclusions is called data. Tables and graphs are the ways in which data is presented.
The numerical entries in the data are called ‘observations’.

→ The average or Arithmetic Mean or Mean
A.M = \(\frac{\text { Sum of all observations }}{\text { Number of observations }}\)

→ (i.e.,) A.M. is equal to sum of all the observations of a data set divided by the number of observations. It lies between the lowest and highest values of the data.

→ Mode: An observation of data that occurs most frequently is called the mode of the data. A data may have one or more modes and sometimes none.

→ Median: Median is simply the middle observation, when all observations are arranged in ascending or descending order. In case of even number of observations median is the average of middle observations.

→ Mean, mode, median are representative values for a data set.

→ When all values of data set are increased or decreased by a certain number, the mean also increases or decreases by the same number.

→ Data can be presented in bar graphs / double bar graphs or pie chart.

→ Bar graph: Bar graph are made up of bars of uniform width which can be drawn horizontally or vertically with equal spacing between them. The length of each bar tells us the frequency of the particular item. We take convenient scale for the length of bar graph.

→ Double bar graph: It presents two observations side by side.

→ Pie chart: A circle is divided into sectors to represent the given data.
Angle subtended by the sector at the centre of the circle is directly proportional to each observation.

Students can go through AP Board 7th Class Maths Notes Chapter 6 Ratio – Applications to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 6 Ratio – Applications

→ Ratio: A ratio is an ordered comparison of quantities of the same units.
We use the symbol ‘:’ to represent a ratio. The ratio of two quantities ‘a’ and ‘b’ is a : b and we read it as “a is to b”. The two quantities ‘a’ and ‘b’ are called the terms of the ratio. The first quantity ‘a’ is called first term or antecedent and the second quantity ‘b’ is called consequent.

→ Proportion: If two ratios are equal, then the four terms of the ratios are said to be in proportion. We use the symbol : : (is as)
If two ratios a : b and c : d are equal, we write a : b :: c : d or a : b = c : d
Here ‘a’, ‘d’ are called extremes and b, c are called means.

→ Unitary Method: The method in which we first find the value of one unit and then the value of the required number of units is known as unitary method.
Eg: If the cost of 5 pens is Rs. 85; then the cost of 12 pens is ……… ?
Solution. Cost of 5 pens = Rs. 85
Cost of 1 pen = \(\frac{85}{5}\) = Rs. 17
∴ Cost of 12 pens = 12 × 17 = Rs. 204

→ Direct proportion: If in two quantities, when one quantity increases, the other also increase or vice-versa then the two quantities are said to be in direct proportion.
Eg: The number of books and their cost are in direct proportion.
As the number of books increases, the cost also increases.

→ Ratios also appear in the form of percentages.

→ The word percent means “per every hundred” or for a hundred. The symbol % is used to denote percentage.

→ To convert a quantity into its equivalent percentage

• express it as a fraction.
• multiply it with 100.
• assign % symbol.

Eg: A man purchased an article for Rs. 80 and sells it for Rs. 100. Find his gain percent.
Solution. Cost price = Rs. 80
Selling price = Rs. 100
gain = Rs. 20
gain as a fraction = \(\frac{20}{80}\)
gain as percent = \(\frac{20}{80}\) × 100 = 25%

→ When C.P > S.P there incurs loss.

→ When C.P < S.P there is gain.

→ When C.P = S.P neither loss nor gain.

→ Loss = C.P – S.P gain = S.P – C.P

→ Discount is always expressed as some percentage of marked price.

→ In general when P is principle; R% is rate of interest per annum and I is the interest, then
I = R% of P
I = R% of P for T years