Class 7

Students can go through AP Board 7th Class Maths Notes Chapter 5 Triangle and Its Properties to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 5 Triangle and Its Properties

→ Triangles can be classified according to properties of their sides and angles. Based on sides, triangles are of three types.

→ Equilateral triangle: A triangle in which all the three sides are equal is called an equilateral triangle. In △ABC
AB = BC = CA, also ∠A = ∠B = ∠C In an equilateral triangle each angle is equal to 60°.

→ Isosceles triangle: A triangle in which two sides are equal is called an isosceles triangle.
In △PQR
PQ = PR also ∠Q = ∠R

The non-equal side in an isosceles triangle may be taken as base of the triangle.

→ Scalene triangle: A triangle in which no two sides are equal is called a scalene triangle.

In △BAT
BA ≠ AT ≠ BT also ∠B ≠ ∠A ≠ ∠T.

→ Based on angles, triangles can be classified into three types.

→ Acute angled triangle: A triangle in which all the three angles are acute is called an acute-angled triangle.

In △TAP,
∠T, ∠A, ∠P are acute angles.

→ Obtuse angled triangle: A triangle in which one angle is obtuse is called an obtuse angled triangle.

In △FAN,
∠A is obtuse angle.
A triangle cannot have more than one obtuse angle,

→ Right angled triangle: A triangle in which one angle is a right angle is called a right angled triangle.

In △COT
ZO is right angle (i.e) 90°.
A triangle cannot have more than one right angle,

→ Right angled isosceles triangle: A triangle in which one angle is right angle and two sides are equal is called a right angled isosceles triangle.

In △POT,
PO = OT and ∠O = 90° also
∠P = ∠T = 45°

→ Family of triangles – Flow chart

→ Relation between sides of a triangle
In any triangle the sum of the lengths of any two sides is greater than the length of the third side.

In △TIN,
TI + IN > TN; TN + NI > TI; TI + TN > IN
Also the difference between lengths of any two sides of the triangle is less than the length of the third side.
In △TIN, TI > TN – NI; IN > TI – TN; TN > IN – TI

→ Altitutes of a triangle
The length of a line segment drawn from a vertex to its opposite side and is perpendicular to it is called an altitude or height of the triangle. An altitude can be drawn from each vertex.

Altitude of a triangle may be in its interior or exterior.

→ Medians of a triangle
A line segment joining a vertex and the mid-point of its opposite side is called a median.

A triangle has three medians.
The medians of a triangle are concurrent.
The point of concurrence of medians of a triangle is called the centroid of the triangle.
In △ABC, D, E and F are mid-points of the sides AB, BC and AC.
AE, CD and BF are mid-points.
G is the centroid.

→ Angle – sum property of a triangle: The sum of interior angles of a triangle is equal to 180° or two right angles.

In △BET,
∠B + ∠E + ∠T = 180°

→ Exterior angle of a triangle

→ When one side of a triangle is produced, the angle thus formed is called an exterior angle.

In △COL; the side OL is produced to D.
∠CLD is an exterior angle.
The exterior angle of a triangle is equal to the sum of the interior opposite angles.
∠COL + ∠OCL = ∠CLD

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 10 Algebraic Expressions Ex 4 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 10th Lesson Algebraic Expressions Exercise 4

Question 1.
Add the following algebraic expressions using both horizontal and vertical methods. Did
you get the same answer with both methods.
(i) x² – 2xy + 3y²; 5y² + 3xy – 6x²
(ii) 4a² + 5b² + 6ab 3ab ; 6a² – 2b² ; 4b² – 5ab
(iii) 2x + 9y – 7z ; 3y + z + 3x ;2x – 4y – z
(iv) 2x² – 6x + 3 ; – 3x² – x – 4 ; 1 + 2x – 3x²
Solution:
(i) x² – 2xy + 3y²; 5y² + 3xy – 6x²
Addition by Horizontal method
(x² – 2xy + 3y²) + ( – 6x² + 3xy + 5y²)
= (x² – 6x²) + ( – 2xy + 3xy) + (3y² + 5y²)
= – 5x² + xy + 8y² .

ii) 4a² + 5b² + 6ab;3ab; 6a² – 2b²; 4a² – 5ab
Horizontal Method
(4a² + 5b² + 6ab) + 3ab + (6a² – 2b²) (4a² – 5ab)
= (4a² + 6a² + 4a²) + (5b² – 2b²) + (6ab + 3ab – 5ab)
= 14a² + 3b² + 4ab

iii) 2x² + 9y – 7z ; 3y + z + 3x; 2x4y – z
Horizontal Method
= (2x + – 7z) + (3y + z + 3x) + (2x – 4y – z)
= (2x + 3x + 2x) + (9y + 3y_4y) + ( – 7z + z – z)
= 7x + 8y – 7z

iv) 2x² – 6x – 3; – 3x² – x – 4; 1 + 2x – 3x²
Horizontal Method
(2x² – 6x + 3) + ( – 3x² – x – 4) + (1 + 2x – 3x²)
(2x² – 3x² – 3x²) + (- 6x – x + 2x) + (3 – 4 + 1)
= – 4x² – 5x + 0
= – 4x² – 5x

In all the above sums
(i), (ii), (iii), (iv) we got same answer in both horizontal and vertical methods.

Question 2.
Simpli1’: 2x² + 5x – 1 + 8x + x² + 7 – 6x + 3 – 3x²
Solution:
Given algebraic expression is
2x² + 5x – 1 + 8x + x² + 7 – 6x + 3 – 3x²
= (2x² + x² – 3x²) + (5x + 8x – 6x) . ( – 1 + 7 + 3)
= 0 + 7x + 9 = 7x + 9

Question 3.
Find the perimeter of the following rectangle?

Solution:
The perimeter of a rectangle = 2 (length + breadth)
= 2 (6x + y + 3x – 2y)
= 2 (9x – y)
∴ P = (18x – 2y) units

Question 4.
Find the perimeter of a triangle whose sides are 2a + 3b, b – a, 4a – 2b.

Solution:
Perimeter of the triangle ABC = \(\overline{\mathrm{AB}}+\overline{\mathrm{BC}}+\overline{\mathrm{CA}}\)
= (b – a) + (3a + 2b) + (4a – 2b)
=( – a + 3a + 4a) +(b + 2b – 2b)
= (6a + b) units

Question 5.
Subtract the second expression from the first expression
(i) 2a + b, a – b
(ii) x + 2y + z , – x – y – 3z
(iii) 3a² – 8ab – 2b², 3a² – 4ab+6b²
(iv) 4pq – 6p² – 2q², 9p²
(v) 7 – 2x – 3x², 2x² – 5 x – 3
(vi) 5x² – 3xy – 7y² , 3x² – xy – 2y²
(vii) 6m³ + 4m² + 7m – 3 , 3m³ + 4
Solution:
(i) 2a + b, a – b = 2a + b – a + b
= (2a – a) + (b + b)
= a + 2b

ii) (x + 2y + z) – ( – x – y – 3z) = x + + z + x + y + 3z
=(x + x) + (2y + y) +(z + 3z)
= 2x + 3y + 4z

iii) (3a² – 8ab – 2b²) – (3a² – 4ab + 6b²) = 3a² – 8ab – 2b² – 3a² +4ab – 6b²
= (3a² – 3a²) + ( – 8ab + 4ab) + (2b² – 6b²)
= 0 – 4ab – 8b²
= – 4ab – 8b²

iv) (4pq – 6p² – 2q²) – (9p²) = 4pq – 6p² – 2q² – 9p²
= 4pq – 15p² – 2q²

v) (7 – 2x – 3x²) – (2x² – 5x – 3)=7 – 2x – 3x² – 2x² + 5x + 3
= ( – 3x² – 2x²) + ( – 2x + 5x) + (7 + 3)
= – 5x² + 3x + 10

vi) (5x² – 3xy – 7y²) – (3x² – xy – 2y²) = 5x²– 3xy – 7y² – 3x² + xy + 2y²
= (5x² – 3x²) + ( – 3xy + xy) + ( – 7y² + 2y²)
= 2x² – 2xy – 5y²

viii) (6m³ + 4m² + 7m – 3) – (3m³ + 4)= 6m³ + 4m² + 7m – 3 – 3m3 – 4
= (6m³ – 3m³) + 4m² + 7m + (- 3 – 4)
= 3m³ + 4m² + 7m – 7

Question 6.
Subtract the sum of x² – 5xy + 2y² and y² – 2xy – 3x² from the sum of 6x² – 8xy – y² and 2xy – 2y² – x².
Solution:
The sum of x² – 5xy + 2y² and y² – 2xy – 3x² = (x² – 5xy + 2y²) (y – 2xy – 3x²)
= (x² – 3x²) + ( – 5xy – 2xy) + (2y² + y²)
= – 2x² – 7xy + 3y² ………………….(1)

The sum of 6x² – 8xy – y² and
2xy – 2y² – x² = (6x² – 8xy – y²) + (2xy – 2y² – x²)
= (6x² – x²) + ( – 8xy + 2xy) + (-y² – 2y²)
= 5x² – 6xy – 3y² ………………. (2)

From (1) and (2)
(2) – (1)= (5x² – 6xy – 3y²) – ( – 2x² – 7xy + 3y²)
= 5x² – 6xy – 3y² + 2x² + 7xy – 3y²
= (5x² + 2x²) + ( – 6xy + 7xy) + ( – 3y² – 3y²)
= 7x² + xy – 6y²

Question 7.
What should be added to 1 + 2x – 3x² to get x² – x – 1?
Solution:
Let the added algebraic expression may be ‘A say
(1 + 2x – 3x²) + A = x² – x – 1
=A =(x² – x – 1) – (1 + 2x – 3x²)
= x² – x – 1 – 1 – 2x + 3x²
= (x² + 3x²) + ( – x – 2x) +( – 1 – 1)
∴ A = 4x² – 3x – 2
∴ The required added expression (A) = 4x² – 3x – 2

Question 8.
What should be taken away from 3x² – 4y² + 5xy +20 to get – x² – y² + 6xy + 20.
Solution:
Let the subtracted algebraic expression may be B’ say
3x² – 4y² + 5xy – B = – x² – y² + 6xy + 20
B = (3x² – 4y² + 5xy) – (- x² – y² + 6xy + 20)
= 3x² – 4y² + 5xy + x² +y² – 6xy – 20
= (3x² + x²) ( – 4y² + y²) + (5xy – 6xy) – 20
∴ B = 4x² – 3y² – xy – 20
∴ The required subtracted expression is B = 4x² – 3y² – xy – 20

Question 9.
The sum of 3 expressions is 8 + 13a + 7a². Two of them are 2a² + 3a + 2 and 3a2 – 4a + 1. Find the third expression.
Solution:
Given that f he sum of 3 expressions is 8 + 13a + 7a² ……………..(1)
Two of them are 2a² + 3a + 2 and 3a² – 4a + 1.
∴ The sum of above two expressions (2a² + 3a + 2) + (3a² – 4a + 1)
= 2a² + 3a + 2 + 3a² – 4a + 1.
= (2a² + 3a²) + (3a – 4a) + (2 + 1)
= 5a² – a + 3
∴ The required 3rd expression (1) – (2)
(1) – (2) =(7a² + 13a + 8) – (5a² – a + 3) = 7a² + 13a + 8 – – 5a² – a – 3
=(7a² – 5a²) +(13a + a)+ (8 – 3)
= 2a² + 14a + 5

Question 10.
If A = 4x² + y² – 6xy;
B = 3y²+ 12x² + 8xy;
C = 6x² + 8y² + 6xy
Find (i) A + B + C (ii) (A – B) – C
Solution:
(i) im 7
(ii) (A – B) – C
(A – B) = (4x² + y² – 6xy) – (3y² + 12x² + 8xy)
= (4x² – 12x²) + (y² – 3y²) + ( – 6xy – 8xy)
A – B = – 8x² – 2y² – 14xy
∴ (A – B) – C = ( – 8x² – 2y² – 14xy) – (6x² + 8y² + 6xy)
= ( – 8x² – 6x²) + -2y² – 8y²) + ( – 14xy – 6xy)
= – 14x² – 10y² – 20xy
∴ (A – B) – C = – (14x² + 10y² + 20xy)

iii) 2A + B
2A = 2(4x² + y² – 6xy) = 8x² + 2y² – 12xy
∴ 2A + B = (8x² + 2y² – 12xy) + (3y² + 12x² + 8xy)
= (8x² + 12x²) + (2y² + 3y²) + ( – 12xy + 8xy)
∴ 2A + B = 20x² + 5y² – 4xy

iv) A – 3B
38 = 3(3y² + 12x² + 8xy) = 9y² + 36x² + 24xy
∴ A – 3B = (4x² + y² – 6xy) – (9y² + 36x² + 24xy)
= (4x² – 36x²) (y² – 9y²) ( 6xy – 24 xy)
= 32x² – 8y² – 30xy
∴ A – 3B = – 32x² – 8y² – 30xy (or)
= – [32x² + 8y + 30xy]

Students can go through AP Board 7th Class Maths Notes Chapter 4 Lines and Angles to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 4 Lines and Angles

→ Complementary angles: If the sum of two angles is 90°, the angles are called complementary angles.
Eg: 55°, 35° are complementary angles.

→ Linear pair of angles: When a ray stands on a line, the pair of angles thus formed are called linear pair of angles and their sum is 180°. In the figure ∠x and ∠y are called linear pair of angles.

→ Adjacent angles: Two angles with a common vertex and a common arm are called adjacent angles. Here the non-common arms lie on either sides of the common arm.
Eg: ∠AOB and ∠BOC are adjacent angles.

→ Supplementary angles : Two angles are said to be supplementary if their sum is 180°. Eg : (100°, 80°), (110°, 70°), (60°, 120°)

→ Vertically opposite angles: Two angles are said to be vertically opposite angles if they are formed by two intersecting lines and are not adjacent.
Eg: ∠AOC and ∠BOD are vertically opposite angles.

→ A line which intersects two or more lines at distinct points is called a transversal. In the figures ‘t’ is a transversal.

In the figure (i) t is not a transversal as it doesn’t intersect other two lines at two distinct points.

→ When a transversal intersects a pair of lines, 8 angles are formed.
Here l, m are two lines and ‘t’ is a transversal.

The angles are ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8.
∠3, ∠4, ∠5, ∠6 are called interior angles and ∠1, ∠2, ∠7 and ∠8 are called exterior angles.

→ When a transversal intersects a pair of lines the following pairs of angles are called corresponding angles.

i) One angle is interior and the other is exterior.
ii) Not adjacent angles.
iii) Two angles are on the same side of the transversal.

→ The following pairs are called alternate interior angles
i) both are interior
ii) not-adjacent
iii) either sides of the transversal

→ The following pairs are called alternate exterior angles
i) both are exterior
ii) not-adjacent
iii) on the either sides of the transversal

→ The following pairs are called interior angles on the same side of the transversal.

→ When a pair of parallel lines intersected by a transversal the pairs of corresponding angles are equal.
∠1 = ∠5
∠2 = ∠6
∠3 = ∠7
∠4 = ∠8

The pairs of alternate interior angles are equal.
∠3 = ∠5
∠4 = ∠6
The pairs of alternate exterior angles are equal.
∠1 = ∠7
∠2 = ∠8
The interior angles on the same side of the transversal are supplementary.
∠3 + ∠6 = 180°
∠4 + ∠5 = 180°
The exterior angles on the same side of the transversal are supplementary.
∠1 + ∠8 = ∠2 + ∠7 = 180°

→ Conversely when a transversal intersects a pair of lines in such way
i) making pairs of corresponding angles equal
(or)
ii) making alternate interior angles equal.
(or)
iii) making alternate exterior angles equal.
(or)
iv) making angles on the same side of the transversal interior/exterior supplementary then the lines are parallel.

Students can go through AP Board 7th Class Maths Notes Chapter 3 Simple Equations to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 3 Simple Equations

→ Simple equations help in solving various problems in daily life.
Eg: After 5 years Ramesh’s age is 15 years. What is his present age?
Solution. Let Ramesh’s present age be x years
After 5 years Ramesh’s age = x + 5
By problem, x + 5 = 15
x = 15 – 5 = 10 years
∴ Ramesh’s present age = 10 years

→ To balance an equation
a) Same number can be added on both sides.
b) Same number can be subtracted from both sides.
c) Multiply both sides with same number.
d) Divide both sides with same number.
So that the equality remains unaltered.

→ An equation remains same if the L.H.S and R.H.S are interchanged.

→ To solve a simple equation we transform term from one side to another.
While transforming term from one side to another
‘+’ quantity becomes ‘-‘ quantity
‘-‘ quantity becomes ‘+’ quantity
‘×’ quantity becomes ‘÷’ quantity
‘÷’ quantity becomes ‘×’ quantity
(i.e.) when the terms are transposed they get opposite signs and the term which multiplies one side, divides the other side.

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 10 Algebraic Expressions Ex 3 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 10th Lesson Algebraic Expressions Exercise 3

Question 1.
Find the length of the line segment PR in the following figure in terms of ’a’.

Solution:
The length of PR = \(\overline{\mathrm{PQ}}+\overline{\mathrm{QR}}\)
= 3a + 2a
= 5a units

Question 2.
(i) Find the perimeter of the following triangle.

(ii) Find the perimeter of the following rectangle.

Solution:
i) The perimeter of the triangle = \(\overline{\mathrm{AB}}+\overline{\mathrm{BC}}+\overline{\mathrm{CA}}\)
= 2x + 6x + 5x
= 13x units
ii) The perimeter of the rectangle ABCD = \(\overline{\mathrm{AB}}+\overline{\mathrm{BC}}+\overline{\mathrm{CD}}+\overline{\mathrm{DA}}\)
or
= 2 (l + b)
= 2 (3x + 2x)
= 2 × 5x
= 10x units

Question 3.
Subtract the second terni from first term.
(i) 8x, 5x
(ii) 5p, 11p
(iii) 13m², 2m²
Solution:
i) 8x – 5x = 3x
ii) 5p – 11p = -6p
iii) 13m² – 2m² = 11m²

Question 4.
Find the value of following monomials, if x =1.
(i) -x
(ii) 4x
(iii) -2x²
Solution:
1) If x = 1 ⇒ – x = – (1)= – 1
ii) If x = 1 ⇒ 4x = 4 x 1 = 4
iii) If x= 1 ⇒ – 2x² = – 2(1)² = – 2 × 1= – 2

Question 5.
Simplify and find the value of 4x + x – 2x² + x – 1 when x = -1.
Solution:
Given expression = 4x + x – 2x² + x – 1
= 4x + x + x – 2x² – 1
= – 2x² + 6x – 1
If x = – 1 then, the value of – 2x² + 6x – 1 = – 2 (-1)2 + 6( – 1) – 1
= – 2(1) – 6 – 1
= – 2 – 6 – 1
= – 9

Question 6.
Write the expression 5x² – 4 – 3x² + 6x + 8 + 5x – 13 in its simplified form. Find its value when x = -2
Solution:
The given algebraic expression = 5x² – 4 – 3x² + 6x + 8 + 5x – 13.
= (5x² – 3x²) (6x + 5x) + (-4 – 13)
= 2x² + 11x – 17
When x = – 2. then the value of 2x²+ 11x – 17 = 2(- 2)² + 11(-2) – 17
= 2 × 4 – 22 – 17
= 8 – 39
= – 31

Question 7.
If x = 1; y = 2 find the values of the following expressions
(i) 4x – 3y + 5
(ii) x² + y²
(iii) xy + 3y – 9
Solution:
i) 4x – 3y+5
If x = 1, y = 2 then the value of 4x – 3y + 5 = 4(1) – 3(2) + 5
= 4 – 6 + 5
= 9 – 6 = 3

ii) x² + y²
If x = 1, y = 2, the value of x² + y²= (1)² + (2)²
=(1 × 1) + (2 × 2)
= 5

iii) xy + 3y – 9
If x = 1; y = 2,the value of xy + 3y – 9 = 1 × 2 + 3(2) – 9
= 2 + 6 – 9
= 8 – 9

Question 8.
Area of a rectangle is given by A = l × b . If l = 9cm, b = 6cm, find its area?
Solution:
Formula for area of a rectangle (A) = l × b
If l = 9cm, b = 6cm
then the area of the rectangle = l × b
= 9 × 6
= 54 cm²

Question 9.
Simple interest is given by I = \(\frac{P T R}{100}\) . If P = ₹ 900, T =2 years; and R =5%, find the simple interest.
Solution:
Given that the formula for simple interest (I) = \(\frac{P T R}{100}\)
P = Rs.900, T = 2years, R = 5%
∴ The required simple interest (I) = \(\frac{\mathrm{PTR}}{100}=\frac{900 \times 2 \times 5}{100}\) = 9 x 2 x 5 = Rs. 90

Question 10.
The relationship between speed (s), distance (d) and time (t) is given by S = – . Find the
value of s, if d = 135 meters and t = 10 seconds.
Solution:
Given that s = \(\frac{\mathrm{d}}{\mathrm{t}}\) and d = 135 meters, t = 10 seconds
∴ The value of s = \(\frac{\mathrm{d}}{\mathrm{t}}=\frac{135}{10}\)
∴ speed (s) = 13.5 m/sec.

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 11 Exponents Ex 3 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 11th Lesson Exponents Exercise 3

Question 1.
Express the number appearing in the following statements in standard form.
(i) The distance between the Earth and the Moon is approximately 384,000,000m.
(ii) The universe is estimated to be about 12,000,000,000 years old.
(iii) The distance of the sun from the center of the Milky Way Galaxy is estimated to be 300,000,000,000,000,000.,000 m.
(iv) The earth has approximately 1,353,000,000 cubic km of sea water.
Solution:
(i) 3.84 × 10⁸ m
(ii) 1.2 × 10¹⁰ years
(iii) 3 × 10²⁰ m
(iv) 1.353 × 10⁹cubic km

Students can go through AP Board 7th Class Maths Notes Chapter 2 Fractions, Decimals and Rational numbers to understand and remember the concepts easily.

AP State Board Syllabus 7th Class Maths Notes Chapter 2 Fractions, Decimals and Rational numbers

→ A proper fraction is a fraction that represents a part of a whole i.e., a fraction in which numerator is less than the denominator is called a proper fraction.
Eg: \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{2}{3}\), \(\frac{5}{6}\), \(\frac{8}{13}\),….. etc

→ An improper fraction is a fraction that represents a whole or more than a whole i.e., a fraction in which the numerator is more than or equal to the denominator is called an improper fraction.
Eg: \(\frac{5}{3}\), \(\frac{4}{3}\), \(\frac{8}{7}\), \(\frac{11}{5}\), ….. etc

→ Fractions can be represented pictorially.
Eg:

→ Like fractions can be compared by their numerators.

→ Unlike fractions can be compared by converting them into like fractions.

→ An equivalent fraction of a given fraction can be obtained by multiplying its numerator and denominator by same number.
Eg: Equivalent fraction for \(\frac{3}{5}\) is

→ To multiply a fraction with a whole number; we take the product of the numerator and the whole number as the new numerator, keeping the denominator the same.
Eg:

→ Product of the fractions = \(\frac{\text { Product of Numerators }}{\text { Product of Denominators }}\)
Eg: \(\frac{5}{3}\) × \(\frac{4}{7}\) = \(\frac{20}{21}\)

→ In mathematical computation ‘of’ means multiplication.
Eg: \(\frac{1}{3}\) of 24 = \(\frac{1}{3}\) × 24 = 8

→ The product of two proper fractions is less than each of the fraction in multiplication.
Eg:

→ The product of a proper and improper fraction is less than the improper fraction and greater than the proper fraction.
Eg: \(\frac{3}{4}\) × \(\frac{7}{5}\) = \(\frac{21}{20}\)
Here \(\frac{3}{4}\) < \(\frac{21}{20}\) and \(\frac{7}{5}\) > \(\frac{21}{20}\)

→ The product of two improper fractions is greater than each of the fractions.
Eg: \(\frac{7}{5}\) × \(\frac{3}{2}\) = \(\frac{21}{20}\)
Here \(\frac{7}{5}\) < \(\frac{21}{10}\) and \(\frac{3}{2}\) < \(\frac{21}{20}\)

→ To divide a whole number with a fraction; multiply the whole number by the reciprocal of the given fraction and vice versa.
Eg:

→ To divide one fraction by another, multiply the first fraction with the reciprocal of 2nd fraction.
Eg: \(\frac{3}{5}\) ÷ \(\frac{5}{8}\) = \(\frac{3}{5}\) × \(\frac{8}{5}\)

→ To multiply a decimal by 10,100,1000,, we move the decimal point in the number to the right side as many places as there are zeros in the numbers 10, 100, 1000 ……
Eg:
1.125 × 10 = 11.25
1.125 × 100 = 112.5
1.125 × 1000 = 1125
1.255 × 10,000 = 12,550

→ To multiply two decimal numbers.
i) multiply them as whole numbers.
ii) count the total number of digits in decimal places and add them.
iii) place the decimal point in the product by counting the sum of digits from its right most place.
Eg: 6.25 × 3.14
i) 625 × 314 = 196250
ii) sum of the number of digits in decimal places = 2 + 2 = 4
iii) 19.6250

→ To divide a decimal number by numbers like 10,100,1000, …… etc. we shift the decimal point in the decimal number to the left by as many places as there are zeros in 10, 100,1000 etc.
Eg: 435.873 ÷ 10 = 43.5873
4551.3 ÷ 100 = 45.513
8374.2 ÷ 1000 = 8.3742
24.82 ÷ 1000 = 0.02482

→ To divide a decimal number by a whole number
i) divide them as whole numbers
ii) place the decimal point in the quotient as in the decimal number.
Eg: 86.5 ÷ 5
i) 865 ÷ 5 = 173
ii) 17.3
To divide a decimal number by another,
i) shift the decimal to the right by equal number of places in both to convert the denominator to a whole number.
ii) divide them as in above
Eg: 6.25 ÷ 2.5

→ The numbers in the form \(\frac{p}{q}\) where p, q are integers and q ≠ 0 are called rational numbers.

→ The set of rational numbers is represented by Q.

→ Q includes all integers, positive fractional numbers and negative fractional numbers.

→ All rational numbers can be represented on a number line.

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 11 Exponents Ex 2 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 11th Lesson Exponents Exercise 2

Question 1.
Simplify the following using laws of exponents.
(i) 2¹⁰ × 2⁴
(ii) (3²) × (3²)⁴
(iii) \(\frac{5^{7}}{5^{2}}\)
(iv) 9² × 9¹⁸ × 9¹⁰
(v) \(\left(\frac{3}{5}\right)^{4} \times\left(\frac{3}{5}\right)^{3} \times\left(\frac{3}{5}\right)^{8}\)
(vi) (-3)³ × (-3)¹⁰ × (-3)⁷
(vii) 3(²)²
(viii) 2⁴ × 3⁴
(ix) 2^4a × 2^5a
(x) (10²)³
(xi) \(\left[\left(\frac{-5}{6}\right)^{2}\right]^{5}\)
(xii) 2^3a+7 × 2^7a+3
(xiii) \(\left(\frac{2}{3}\right)^{5}\)
(xiv) (-3)³ × (-5)³
(xv) \(\frac{(-4)^{6}}{(-4)^{3}}\)
(xvi) \(\left(\frac{2}{3}\right)^{5}\)
(xvii) \(\frac{(-6)^{5}}{(-6)^{9}}\)
(xviii) (-7)⁷ × (-7)⁸
(xix) (-6⁴)⁴
(xx) a^x × a^y × a ^x
Solution:
(i) 2¹⁰ × 2⁴ = 2¹⁰⁺⁴ = 2¹⁴
[∵ a^m × aⁿ = a^m+n]

(ii) (3²) × (3²)⁴ = (3²)¹⁺⁴ = (3²)⁵
= 3^2×5
= 3¹⁰
[∵ a^m × aⁿ = a^m+n]
[∵ (a^m)ⁿ = (a)^mn]

(iii) \(\frac{5^{7}}{5^{2}}\) = 5^{7 – 2} = 5⁵
= 5 × 5 × 5 × 5 × 5 = 5⁵
[∵ \(\frac{a^{m}}{a^{n}}\) = a^m-n, m > n]

(iv) 9² × 9¹⁸ × 9¹⁰ = 9^2+18+10 = 9³⁰
[∵ a^m × aⁿ = a^m+n]

(v) \(\left(\frac{3}{5}\right)^{4} \times\left(\frac{3}{5}\right)^{3} \times\left(\frac{3}{5}\right)^{8}\) = \(\left(\frac{3}{5}\right)^{4+3+8}\) = \(\left(\frac{3}{5}\right)^{15}\)
[∵ a^m × aⁿ = a^m+n]

(vi) (-3)³ × (-3)¹⁰ × (-3)⁷ = (-3)^{3 + 10 + 7} = (-3)²⁰
[∵ a^m × aⁿ = a^m+n]

(vii) 3(²)² = 3^2×2 = 3⁴
[∵ (a^m)ⁿ = a^mn])

(viii) 2⁴ × 3⁴ = (2 × 3 )⁴ = 6⁴
[∵ a^m × b^m = (ab)^m]

(ix) 2^4a × 2^5a = 2^4a+5a = 2^9a
[∵ a^m × aⁿ = a^m+n]

(x) (10²)³ = 10^2×3 = 10⁶
[∵ (a^m)ⁿ = a^m×n ]

(xi) \(\left[\left(\frac{-5}{6}\right)^{2}\right]^{5}\)
\(\left[\left(\frac{-5}{6}\right)^{2}\right]^{5}=\left[\frac{-5}{6}\right]^{2 \times 5}\) = \(\left(\frac{-5}{6}\right)^{10}=\left(\frac{5}{6}\right)^{10}\) [∵ 10 even number]
[∵ (a^m)ⁿ = an]

(xii) 2^3a+7 × 2^7a+3
2^3a+7+7a+3 = = 2^10a+10 = 2^10(a+1)
[∵ a^m × aⁿ = (a)^m+n]

(xiii) \(\left(\frac{2}{3}\right)^{5}\) = \(\frac{2^{5}}{3^{5}}\)
[∵ \(\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}\) ]

(xiv) (-3)³ × (-5)³ = [(-3) × (-5)]³ = (15)³
[∵ a^m × b^m = (ab)^m]

(xv) \(\frac{(-4)^{6}}{(-4)^{3}}\) = (-4)³
[∵ \(\frac{a^{m}}{a^{n}}\) = a^m-n, m > n]

(xvi) \(\left(\frac{2}{3}\right)^{5}\) = \(\frac{1}{9^{15-7}}\) = \(\frac{1}{9^{8}}\) [∵ \(\frac{a^{m}}{a^{n}}=\frac{1}{a^{n-m}}\), n > m]

(xvii) \(\frac{(-6)^{5}}{(-6)^{9}}\) = \(\frac{1}{(-6)^{9-5}}\) [∵ \(\frac{a^{m}}{a^{n}}=\frac{1}{a^{n-m}}\), n > m]
\(\frac{1}{(-6)^{4}}=\frac{1}{6^{4}}\) [∵4 is even number ]

(xviii) (-7)⁷ × (-7)⁸ = (-7)⁷⁺⁸ [∵ a^m × aⁿ = a ^m+n]
= (-7)¹⁵ = -(7)¹⁵ [∵ 15 is odd number ]

(xix) (-6⁴)⁴ [∵ (a^m)ⁿ = a^mn]
= (-6)^4×4 = (-6)¹⁶ = 6¹⁶
[∵ 16 is even number ]

(xx) a^x × a^y × a ^x = a^x+y+z
[a^m × aⁿ × a^p = a^m+n+p]

Question 2.
By what number should 3 be multiplied so that the product is 729’?
Solution:
Given number = 3^-4
Given product = 729 [∵ 3⁶ = 729]
Let the number to be multiplied be x then
⇒ (3^-4) . (x) = 3⁶ ⇒ \(\frac{x}{3^{4}}\) =3⁶
[∵ a^m × nⁿ = a^m+n]
⇒ x = 3⁶ × 3⁴ = 3¹⁰

Question 3.
1f 5⁶ × 5^2x = 5¹⁰ then find x.
Solution:
Given that 5⁶ × 5^2x = 5¹⁰
⇒ 5^6+2x = 5¹⁰ [∵ a^m × aⁿ = a^m+n]
Since bases are equal, we equate the exponents
6 + 2x = 10
2x = 10 – 6 = 4
x = \(\frac{4}{2}\) = 2

Question 4.
Evaluate 2⁰ + 3⁰
Solution:
2⁰ + 3⁰ = 1 + 1 = 2 [∵ a⁰ = 1]

Question 5.
Simplify \(\left(\frac{x^{a}}{x^{b}}\right)^{a} \times\left(\frac{x^{b}}{x^{a}}\right)^{a} \times\left(\frac{x^{a}}{x^{a}}\right)^{b}\)
Solution:
Given \(\left(\frac{x^{\mathrm{a}}}{\mathrm{x}^{\mathrm{b}}}\right)^{\mathrm{a}} \times\left(\frac{\mathrm{x}^{\mathrm{b}}}{\mathrm{x}^{\mathrm{a}}}\right)^{\mathrm{a}} \times\left(\frac{\mathrm{x}^{\mathrm{a}}}{\mathrm{x}^{\mathrm{a}}}\right)^{\mathrm{b}}=\left(\frac{\mathrm{x}^{\mathrm{a}}}{\mathrm{x}^{\mathrm{b}}} \times \frac{\mathrm{x}^{\mathrm{b}}}{\mathrm{x}^{\mathrm{a}}}\right)^{\mathrm{a}} \times(1)^{\mathrm{b}}\)
[∵ a^m × b^m = (ab)^m]
= 1^a x 1^b = 1^a+b = 1

Question 6.
State true or false and justify your answer.
(i) 100 × 10¹¹ = 10¹³
(ii) 3² × 4³ = 12⁵
(iii)) 5° = (100000)°
(iv) 4³ = 8²
(v) 2³ > 3²
(vi) (-2)⁴ > (-3)⁴
(vii) (-2)⁵ > (-3)⁵
Solution:
(i) 100 × 10¹¹ = 10¹³ – True
as 100 × 10¹¹ = 10² × 10¹¹ = 10²⁺¹¹ = 10¹³

(ii) 3² × 4³ = 12⁵ – False
as 3² × 4³ ≠ 12⁵

(iii)) 5° = (100000)° – True as 5° = 1 and 100000° = 1

(iv) 4³ = 8² – True, as 4³ = 4 × 4 × 4 = 64 and 8² = 8 × 8 = 64

(v) 2³ > 3² – False as 2³ = 8 and 3² = 9 and 8 < 9

(vi) (-2)⁴ > (-3)⁴ – False, as (-2)⁴ = (-2) × (-2) × (-2) × (-2) = 16
(-3)⁴ = (-3) × (-3) × (-3) × (-3) = 81

(vii) (-2)⁵ > (-3)⁵ – True, as (-2)5 = (-2) × (-2) × (-2) × (-2) × (-2) = -32
(-3)⁵ = (-3) × (-3) × (-3) × (-3) × (-3) = -243

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 10 Algebraic Expressions Ex 2 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 10th Lesson Algebraic Expressions Exercise 2

Question 1.
Identify and write the like terms in each of the following groups.
(i) a², b², -2a², c², 4a
(ii) 3a, 4x, – yz, 2z
(iii) -2xy², x²y, 5y²x, x²z
(iv) 7p, 8pq, -5pq, -2p, 3p
Solution:
i) Group of like terms : [a², -2a²]
ii) Group of like terms: {-yz, 2zy}
iii) Group of like terms: {-2xy², 5y²x}
iv) Group of like terms: {7p, -2p, 3p} , : {8pq,-5pq}

Question 2.
State whether the expression is a numerical expression or an algebraic expression.
(i) x + 1
(ii) 3m²
(iii) -30 + 16
(iv) 4p² – 5q²
(v) 96
(vi) x² – 5yz
(vii) 215x²yz
(viii) 95 ÷ 5 x 2
(ix) 2 + m + n
(x) 310 + 15 + 62
(xi) 11 a² + 6b² – 5
Solution:
Algebraic expression
(i) x + 1
(ii) 3m²
(iv) 4p² – 5q²
(vi) x² – 5yz
(vii) 215x²yz
(ix) 2 + m + n
(x) 310 + 15 + 62
(xi) 11 a² + 6b² – 5

Numerical expression
(iii) -30 + 16
(v) 96
(viii) 95 ÷ 5 x 2
(x) 310 + 15 + 62

Question 3.
State whether the algebraic expression given below is monomial, binomial, trinomial or multinornial.
(i) y²
(ii) 4y — 7z
(iii) 1 + x + x²
(iv) 7mn
(v) a² + b²
(vi) 100 xyz
(vii) ax + 9
(viii) p² – 3pq + r
(ix) 3y² – x²y² + 4x
(x) 7x² – 2xy + 9y² – 11
Solution:

Question 4.
What is the degree of each of the monomials.
(i) 7y
(ii) -xy²
(iii) xy²z²
(iv) -11y²z²
(v) 3mn
(vi) -5pq²
Solution:

Question 5.
Find the degree of each algebraic expression.
(i) 3x – 15
(ii) xy + yz
(iii) 2y²z + 9yz – 7z – 11x²y²
(iv) 2y²z + 10yz
(v) pq + p²q – p²q²
(vi) ax² + bx + c
Solution:

Question 6.
Write any two Algebraic expressions with the same degree.
Solution:
Algebraic expression, with the same degree are
i) ax² + bx + c .
ii) 4x² – 5x – 1

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 10 Algebraic Expressions Ex 1 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 10th Lesson Algebraic Expressions Exercise 1

Question 1.
Find the rule which gives the number of matchsticks required to make the following patterns
(i) A pattern of letter ‘H’
(ii) A pattern of letter ‘V’
Solution:
i) A pattern of letter ‘H’
The letter ‘H’ is formed with 3 matchsticks.
∴ Its pattern should be 3, 6, 9, 12 (or)
3 × 1, 3 × 2, 3 × 3, 3 × 4 ……………….. 3 x n
∴ The required pattern is 3 × n = 3n

ii) A pattern of letter ‘V’
The letter ‘V’ is formed with 2 matchsticks.
∴ Its pattern should be 2, 4. 6. 8 (or)
2 × 1, 2 × 2, 2 × 3 …………………2 × n
∴ The required pattern is 2 × n = 2n

Question 2.
Given below is a pattern made from coloured tiles and white tiles.

(i) Draw the next two figures in the pattern above.
(ii) Fill the table given below and express the pattern in the form of an algebraic expression.

(iii) Fill the table given below and express the pattern in the form of an algebraic expression.

Solution:



∴ The required algebraic expression is “4”

∴ The required algebraic expression is “4+1”
If n = 1 ⇒ 4n + 1 = 4(1) + 1 = 5
n = 2 ⇒ 4 × 2 + 1 = 8 + 1 = 9
n = 3 ⇒ 4 × 3 + 1 = 12 + 1 =13 ……………….. soon.

Question 3.
Write the following statements using variables, constants and arithmetic operations.
(i) 6 more than p
(ii) ‘x’ is reduced by 4
(iii) 8 subtracted from y
(iv) q multiplied by ‘-5’
(v) y divided by 4
(vi) One-fourth of the product of ’p’ and ‘q’
(vii) 5 added to the three times of ’z’
(viii) x multiplied by 5 and added to ‘10’
(ix) 5 subtracted from two times of ‘y’
(x) y multiplied by 10 and added to 13
Solution:

Question 4.
Write the following expressions in Statements.
(i) x + 3
(ii) y – 7
(iii) 10l
(iv) \(\frac{x}{5}\)
(v) 3m + 11
(vi) 2y – 5
Solution:
Expression Statements

Question 5.
Some situations are given below. State the number in situations is a variable or constant?
Example: Our age – its value keeps on changing so it is an example of a variable quantity.
(i) The number of days in the month of January
(ii) The temperature of a day
(iii) Length of your classroom
(iv) Height of the growing plant
Solution:
i) No. of days ¡n the month of January are fixed in every year. So, “Number of days” is a constant.
ii) The temperature of a day changes every minute. So (temperature) it ¡s a variable.
iii) The length of the classroom is fixed. So it is a constant.
iv) The height of a growing plant changes in every month. So it is a variable.

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 9 Construction of Triangles Ex 4 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 9th Lesson Construction of Triangles Exercise 4

Question 1.
Construct a right-angled ΔABC such that ∠B = 90°, AB = 8 cm and AC = 10 cm.
Solution:
∠B = 90°, AB = 8cm, AC = 10 cm.

Step -1: Draw a rough sketch of the right angled triangle and label it with the given measurements.
Step -2: Draw a line segment AB of length 8 cm.
Step -3: Draw a ray \(\overrightarrow{\mathrm{BX}}\) perpendicular to AB to B.
Step -4 : Draw an arc from A with radius 10 cm to intersect \(\overrightarrow{\mathrm{BX}}\) at C.
Step -5: Join A, C to get the required ΔABC.

Question 2.
Construct a ΔPQR, right-angled at R, hypotenuse is 5 cm and one of its adjacent sides is 4cm.
Solution:
∠R=90D,QR=4cm,PQ=5cm.

Step -1: Draw a rough sketch of the right angled triangle and label it with the given measurements.
Step -2: Draw a line segment QR of length 4cm.
Step -3: Draw a ray \(\overrightarrow{\mathrm{RY}}\) perpendicular to QR at R.
Step -4: Draw an arc from Q with radius 5 cm to intersect \(\overrightarrow{\mathrm{RY}}\) at P.
Step -5: Join P, Q to get the required ΔPQR.

Question 3.
Construct an isosceles right-angled ΔXYZ in which ∠Y = 90° and the two sides are 5 cm each.
Solution:
∠Y = 90°,XY = YZ = 5cm.

Step- 1: Draw a rough sketch of a right angled triangle and label it with given measurements.
Step -2: Draw a line segment XY of length 5cm.
Step -3: Draw a ray \(\overrightarrow{\mathrm{YK}}\) perpendicular to XY at Y.
Step -4: Draw an arc from Y with radius 5 cm to intersect \(\overrightarrow{\mathrm{YK}}\) at Z.
Step -5: Join Z, X to get the required ΔXYZ.

SCERT AP State 7th Class Telugu Textbook Solutions 5th Lesson తెలుగు వెలుగు Questions and Answers.

AP State Syllabus 7th Class Telugu Solutions 5th Lesson తెలుగు వెలుగు

7th Class Telugu 5th Lesson తెలుగు వెలుగు Textbook Questions and Answers

ఆలోచించండి – మాట్లాడండి

ప్రశ్నలు జవాబులు

ప్రశ్న 1.
చిత్రంలో ఎవరెవరు ఉన్నారని మీరనుకుంటున్నారు?
జవాబు:
చిత్రంలో తాతగారూ, ఆయన మనుమరాండ్రు ఇద్దరూ ఉన్నారు.

ప్రశ్న 2.
చిత్రంలో ఏ భాష గురించి చెబుతున్నారు?
జవాబు:
చిత్రంలో తెలుగుభాషను గురించి చెబుతున్నారు.

ప్రశ్న 3.
తాతయ్య చెప్పిన మాటలకు అర్థం ఏమిటి?
జవాబు:
“తెనుగుభాష తేనె కంటె తియ్యగా ఉంటుంది. ఆ తెలుగుభాష మన కన్నులకు వెలుగును ఇస్తుంది” అని అర్థం.

ప్రశ్న 4.
తెలుగుభాష ఎటువంటి భాష?
జవాబు:
తెలుగుభాష చాలా అందమైన భాష. తెలుగు అన్ని భావాలను తెలిపే సామర్థ్యము గల భాష. తెలుగుభాషలో గొప్పదనం, సామెతలు, శబ్దపల్లవాలు, జాతీయాలు మొదలైన వాటిలోనూ, హరికథలు, సంకీర్తనలు మొదలయిన ప్రక్రియల్లోనూ ఉంది.

ఇవి చేయండి

I. వినడం – మాట్లాడడం

ప్రశ్న 1.
పాఠ్యభాగంలో మీకు బాగా నచ్చిన అంశం ఏమిటి?
జవాబు:
“అడిగెదనని కడు వడిఁ జను” అన్న పోతన గారి భాగవతంలోని పద్యం, నాకు బాగా నచ్చింది. ఆ చిన్న కంద పద్యంలో ‘డ’ అనే హల్లు, 23 సార్లు తిరిగి తిరిగి వచ్చింది. ఇది పోతన గారి చమత్కారం.

ప్రశ్న 2.
మనకు ఏ భాషా లేకపోతే ఏమౌతుంది? మన భాష గొప్పతనాన్ని గురించి మీరు ఏం తెలుసుకున్నారు?
జవాబు:
మనకు ఏ భాషా లేకపోతే, మన అభిప్రాయం ఇతరులకు తెలపడానికి వీలు కాదు. భాష వల్లనే ఒకరి అభిప్రాయం మరొకరికి చెప్పడానికి, ఇతరులతో మాట్లాడడానికి వీలు అవుతోంది. మనకు భాషలేకపోతే మనం జంతువులతో సమానం అవుతాం.

మన భాష తెలుగుభాష. అది. తేనె కన్న తీపిదనం కలది. ఈ భాషలో ఎన్నో చమత్కారాలున్నాయి. “దేశ భాషలలో తెలుగు లెస్స” అని, శ్రీ కృష్ణదేవరాయలు చెప్పాడు. ఈ తెలుగుభాషలో పొడుపుకథలు, సామెతలు, జాతీయాలు, శబ్దపల్లవాలు ఉన్నాయి. జోలపాటలు, సంకీర్తనలు ఉన్నాయి. జానపద గేయాలు, స్త్రీల పాటలు, హరికథలు, బుర్రకథలు ఉన్నాయి. అవధాన ప్రక్రియ ఉంది. ఆశుకవిత్వం ఉంది. తెలుగు అజంత భాష. తరగని భాష తెలుగు. మన మాతృభాష తెలుగు, మన కన్నతల్లి లాంటిది.

ప్రశ్న 3.
‘ఎన్ని భాషలు నేర్చుకున్నా మనం మన మాతృభాషను మరవగూడదు’ అనడానికి కారణం ఏమిటి?
జవాబు:
ఎవరి మాతృభాష వారికి కన్నతల్లి వంటిది. అందులో మన మాతృభాష మనకు అమృతం వంటిది. మాతృభాష నేర్చుకోవడం తల్లిపాలు త్రాగడం లాంటిది. అందుకే మనం మాతృభాషను ఎన్నడూ మరచిపోరాదు.

II. చదవడం -రాయడం

1. ఈ కింది వాక్యాలు ఎవరు ఎవరితో అన్నారు?

అ) తెలుగుభాష అంటే పద్యాలేనా తాతయ్యా?
జవాబు:
ఈ వాక్యం, ‘సురభి’, తాతగారితో అన్న వాక్యం.

ఆ) లేదమ్మా ! ఒక్కొక్క కథావిధానం ఒక్కొక్క రకంగా ఉంటుంది.
జవాబు:
ఈ వాక్యం, ‘తాతయ్య’ సురభితో అన్న వాక్యం.

ఇ) ఎప్పుడో పుట్టిన గోదావరి ఇప్పటికీ ప్రవహిస్తూనే ఉంది కదా !
జవాబు:
ఈ వాక్యం, తాతగారు సురభితో చెప్పిన వాక్యం.

ఈ) అజంత భాష అనీ పేరు వచ్చింది.
జవాబు:
ఈ వాక్యం, తాతగారు శ్రీనిధికి చెప్పిన వాక్యం.

2. కింది పేరాలోని సామెతలను గుర్తించి రాయండి.

అ) “అప్పుచేసి పప్పుకూడు తినకుండా, కోటి విద్యలు కూటి కొరకే కాబట్టి, ఏదో ఒక విద్యను నేర్చుకొని, తిన్న ఇంటి వాసాలు లెక్కపెట్టడం మాని, మూడు పువ్వులు ఆరు కాయలుగా జీవితంలో వృద్ధి చెందాలి”.
జవాబు:
పై పేరాలోని సామెతలు ఇవి :
1) అప్పుచేసి పప్పుకూడు
2) కోటి విద్యలు కూటి కొరకే
3) తిన్న ఇంటి వాసాలు లెక్కపెట్టడం
4) మూడు పువ్వులు ఆరుకాయలు

3. కింది ప్రశ్నలకు పాఠాన్ని చదివి, జవాబులు రాయండి.

అ) జాతీయాలు, శబ్దపల్లవాలు అంటే ఏమిటి? వాటికి ఉదాహరణలు ఇవ్వండి.
జవాబు:
జాతీయాలు :
ఒక విశేష అర్థాన్ని ఇచ్చే పదబంధమును జాతీయం అంటాం. ‘పలుకుబడి’ అనే పేరుతో కూడా జాతీయాన్ని పిలుస్తాం.
ఉదా :

1. నెమరువేయటం,
2. అడవిగాచిన వెన్నెల,
3. అరికాళ్ళ మంట నెత్తికెక్కడం మొదలయినవి.

శబ్దపల్లవం :
రెండు వేరు వేరు అర్థాలున్న పదాలు కలిసి, ఇంకో అర్థం వచ్చే కొత్త పదాన్ని శబ్దపల్లవం అంటారు. నామవాచకానికి క్రియచేరిన పదాలనే, శబ్ద పల్లవాలంటారు.
ఉదా : మేలుకొను

ఆ) నెమరువేయడం అంటే భాషాపరంగా అర్థం ఏమిటి?
జవాబు:
నెమరువేయడం అంటే, జ్ఞప్తికి తెచ్చుకోవటం అని భాషా విషయకంగా అర్థం చెప్పాలి.

ఇ) జానపద గేయాలు అంటే ఏమిటి?
జవాబు:
మన పల్లెల్లో ఉన్న జానపదులు, ఆనందంగా పాడుకొనే పాటలను “జానపద గేయాలు” అంటారు. ఈ గేయాలు మౌఖికంగా, ఆశువుగా చెప్పినవి. అంటే అప్పటికప్పుడు ఊహించుకొని పాడినవి. జానపదగేయం ఫలానావాడు రాశాడు అని చెప్పలేము.

ఈ) ఇటలీ భాషను, తెలుగు భాషతో పోల్చవచ్చా? ఎందువల్ల?
జవాబు:
ఇటలీ భాష తెలుగు భాషలాగే, అజంత భాష. అందువల్ల ఇటలీ భాషను తెలుగుభాషతో పోల్చవచ్చు. తెలుగుభాష ఇటలీ భాషలాగా అజంతంగా ఉంటుంది కాబట్టే పాశ్చాత్యులు మన తెలుగును, “ఇటాలియన్ ఆఫ్ ది ఈస్ట్” అని మెచ్చుకున్నారు.

ఉ) తెలుగు సాహిత్యంలోని కొన్ని రకాల ప్రక్రియల పేర్లను తెలపండి.
జవాబు:
తెలుగులో పద్యం, గద్యం, పొడుపు కథలు, సంకీర్తనలు, జోలపాటలు, జానపద గేయాలు, హరికథ, బుర్రకథ, ఒగ్గుకథ, డప్పు కథ, పజిల్స్, సమస్యాపూరణలు, అవధానాలు, గేయాలు, పాటలు, స్త్రీల పాటలు మొదలయిన ప్రక్రియలు ఉన్నాయి.

III. స్వీయరచన

1. కింది ప్రశ్నలకు ఐదేసి వాక్యాలలో ఆలోచించి జవాబులు రాయండి.

అ) మీ ప్రాంతంలోని ప్రజలు మాట్లాడే తెలుగు తీరుకూ, మీ పాఠ్యపుస్తకంలోని తెలుగు తీరుకూ తేడాలు కనిపిస్తున్నాయా? వాటిని గుర్తించి రాయండి.
జవాబు:
మా ప్రాంతంలోని ప్రజలు మాట్లాడే తెలుగు తీరుకూ, మా పాఠ్యపుస్తకంలోని తెలుగు తీరుకూ కొద్దిగా భేదం ఉంది. పాఠ్యపుస్తకాన్ని విద్యావంతులైన ఉపాధ్యాయులు తయారుచేస్తారు. అందువల్ల పాఠ్యపుస్తకంలోని తెలుగు శుద్ధ వ్యావహరికంలో ఉంటుంది. మా ప్రాంతంలోని ప్రజలు మాట్లాడే తెలుగు ఇండ్లలో మాట్లాడే వాడుకభాషకు దగ్గరగా ఉంటుంది.

ఆ) మన భాషలో మీకు తెలిసిన కవుల పేర్లు రాయండి.
జవాబు:
నన్నయభట్టు తెలుగులో ఆదికవి. తిక్కన, ఎఱ్ఱ ప్రగడ, శ్రీనాథుడు, పోతన, అనంతామాత్యుడు, బాలగంగాధర్ తిలక్, గురజాడ, రాయప్రోలు సుబ్బారావు, శ్రీశ్రీ, దాశరథి, జాషువ – నారాయణరెడ్డి వంటి తెలుగుకవుల పేర్లు నాకు తెలుసు.

ఇ) టీ.వీ, రేడియో, మీ ఇల్లు, తరగతి గది – వీటిలో ఏ ప్రదేశంలో మీకు భాష బాగా అర్థమవుతున్నదో, రాయండి. ఏ ప్రదేశంలో ఎందుకు అర్థంకావడం లేదో రాయండి.
జవాబు:
మా ఇంటిలో మాట్లాడే భాష మాకు బాగా అర్థం అవుతుంది. మా తరగతి గదిలో భాష కూడా చాలా వరకు అర్థం అవుతుంది. కాని టీవీ, రేడియోల ‘భాష పూర్తిగా అర్థం కాదు.

మా ఇంటిలో భాష మేము పుట్టినప్పటి నుండి వింటాము. కాబట్టి ఆ భాష మాకు పూర్తిగా అర్థం అవుతుంది. ఇక తరగతిలో మాట్లాడే భాష, మేము బడిలో చేరినప్పటి నుండి వింటున్నాము. అయితే ఒక్కొక్క టీచరు ఒక్కొక్క రకంగా మాట్లాడుతారు. అయినా చాలావరకు అది అలవాటై, అర్థం అవుతుంది.

కాని టీవీ, రేడియోలలో మాట్లాడేవారిలో అనేక రకాల గొంతుకలు, శైలి కలవారు ఉంటారు. ఒక్కొక్కరి ఉచ్ఛారణ వేగం, మాటతీరు ఒక్కొక్క తీరుగా ఉంటుంది. వారి భాషలో ఒక రకం భాషాశైలి ఉంటుంది. కాబట్టి దాన్ని మేము పూర్తిగా అర్థం చేసుకోలేము.

2. కింది ప్రశ్నలకు పదేసీ పంక్తుల్లో జవాబులు రాయండి.

అ) భాష వల్ల కలిగే ప్రయోజనాలను వివరిస్తూ తెలుగు భాష గొప్పతనాన్ని గురించి రాయండి.
జవాబు:
భాషాప్రయోజనాలు :
మనలోని భావాన్ని, ఇతరులకు తెలపడానికి మానవులు రూపొందించుకున్న ప్రధాన సాధనం “భాష”. భాష లేకపోతే, మనిషికీ, పశువుకు తేడా ఉండదు. జంతువులు తమ అభిప్రాయాన్ని ఇతరులకు చెప్పలేవు. మనిషికి భాష ఉంది కాబట్టి తన అభిప్రాయాన్ని ఇతరులకు అర్థం అయ్యేలా చెపుతున్నాడు. ప్రపంచంలో భాషలేని మనుషులు లేరు.

తెలుగుభాష గొప్పతనం :
తెలుగుభాష తేనెవలె తియ్యని భాష, అమృతం వంటిది. దీన్ని పాశ్చాత్యులు ‘ఇటాలియన్ ఆఫ్ ది ఈస్ట్’ అని మెచ్చుకున్నారు. తెలుగు అజంత భాష. సంగీతానికి అనువయినది. శ్రీకృష్ణదేవరాయలు ‘దేశ భాషలందు తెలుగు లెస్స’ అని కీర్తించాడు.

తెలుగులో పద్యగద్యాల వంటి ఎన్నో ప్రక్రియలు ఉన్నాయి. తెలుగులో అష్టావధానం, శతావధానం వంటి ప్రక్రియలు ఉన్నాయి. తెలుగులో ఆశుకవిత, సమస్యా పూరణలు, పొడుపుకథలు, జాతీయాలు, జానపదగేయాలు ఉన్నాయి.

తెలుగులో త్యాగయ్య, రామదాసు, అన్నమయ్య వంటి సంకీర్తనాచార్యులు ఉన్నారు. జోల, లాలిపాటలు ఉన్నాయి. కవిత్రయము, శ్రీనాథ ,పోతనల వంటి కవులు ఉన్నారు. కాబట్టి తెలుగు భాష గొప్పది.

ఆ) తెలుగు భాషను కాపాడడానికి మీరు ఏం చేస్తారో రాయండి.
జవాబు:
అంతర్జాతీయ సంస్థ “యునెస్కో” తెలుగుభాష మృతభాష కాబోతోందని ప్రకటించింది. మన తెలుగును మనం కాపాడాలి.

1. నేను తెలుగువాడిని అనే భావంతో మెలగుతాను.
2. ఇంటా, బయటా, చుట్టాలతో, స్నేహితులతో చక్కగా తెలుగులోనే మాట్లాడతాను.
3. తెలుగు భాషకు ప్రాధాన్యం ఇచ్చే పాఠశాలలోనే చేరతాను.
4. ఉన్నత పాఠశాల చదువు వరకైనా, అన్ని సబ్జక్టులూ తెలుగులోనే నేర్చుకుంటాను.
5. డిగ్రీ చదివే వరకూ నేను రెండవ భాషగా తెలుగునే చదువుతాను.
6. తెలుగులోని శతకములు, పోతన గారి పద్యాలు బాగా చదువుతాను.
7. ప్రభుత్వం కూడా పరిపాలనలో తెలుగునే ప్రోత్సహించేలా మిత్రులతో కలసి పోరాడతాను.
8. సమావేశాల్లో తెలుగులోనే మాట్లాడతాను. మిత్రులకు, బంధువులకు తెలుగులోనే ఉత్తరాలు రాస్తాను.
9. పోటీ పరీక్షలను తెలుగు మీడియంలోనే రాస్తాను.
10. తెలుగు సాహిత్య సమావేశాలకు తప్పక వెడతాను. తెలుగులో వచ్చే దినపత్రికలు, వారపత్రికలు, దానిలో కథలు చదువుతాను.
11. తెలుగు వచ్చిన స్నేహితులతో తెలుగులోనే మాట్లాడతాను.

IV. పదజాలం

1. కింది పట్టికలోని పదబంధాల్లో గల జాతీయాలను గుర్తించండి. వాటితో వాక్యాలు రాయండి.

ఉదా :
తలపండిన :
రామయ్య వ్యవసాయం చేయడంలో తలపండినవాడు, కాబట్టి ప్రతి ఏటా మంచి పంట పండిస్తున్నాడు.
జవాబు:
1) భగీరథ ప్రయత్నం ( అమోఘమైన కార్యదీక్ష) :
మా తమ్ముడు “భగీరథ ప్రయత్నం ” చేసి, ఐ.ఎ.ఎస్ పరీక్షలో ఉత్తీర్ణత సాధించాడు.

2) కొట్టిన పిండి (తన వశములోనే ఉన్నది) :
“ఇంద్రజాల విద్య” అంతా, నా స్నేహితుడికి “కొట్టిన పిండి”.

3) తలలో నాలుక (ఎక్కువ అణకువ గలిగియుండుట) :
నా మిత్రుడు గురువులందరికీ “తలలో నాలుకగా” మసలుకొనేవాడు.

4) కలగాపులగం (అన్నీ కలిపేయడం) :
అన్నం తినేటప్పుడు ..మా అబ్బాయి కూరలూ, పచ్చళ్ళూ అన్ని “కలగాపులగం” చేసి పారవేస్తాడు.

5) కాలికి బుద్ధి చెప్పటం (పారిపోవడం) :
పోలీసులను చూసి, దొంగలు కాలికి బుద్ధి చెప్పారు.

6) కళ్ళు కాయలు కాయడం (ఎంతో ఓపికగా ఎదురుచూడడం) :
మా అబ్బాయి రాక కోసం, మేము “కళ్ళు కాయలు కాచేలా” ఎదురుచూశాము.

7) పుక్కిటి పురాణం (విలువలేని మాటలు) :
నేను పుక్కిటి పురాణాలను పట్టించుకోను.

8) వీనుల విందు (చెవులకు ఇంపు) :
మల్లీశ్వరి సినిమాలో, పాటలు “వీనుల విందుగా” ఉంటాయి.

9) చెవిలో పోరు (ఎంతగానో శ్రద్ధగా చెప్పు) :
పెళ్ళి చేసుకోమని నేను “చెవిలో పోరి” చెప్పినా, నా తమ్ముడు వినలేదు.

10) చెప్పులరగడం (ఎక్కువ శ్రమ) :
“చెప్పులరిగిపోయేలా” తిరిగినా, నా చెల్లెలు పెళ్ళి ఇంకా చేయలేకపోయాను.

11) తలపండిన (పెద్దయైన) :
వ్యవసాయం చేయడంలో నా “తలపండిపోయింది.”

12) గుండె కరిగింది (జాలి పడింది) :
మా కష్టగాథ వింటే, ఎవరికైనా “గుండె కరుగుతుంది.”

13) కాయలు కాయటం (బిడ్డలు పుట్టడం) :
మా కోడలు కడుపున, “నాలుగు కాయలు కాస్తే,” చూసి సంతోషిస్తాను.

14) తుమ్మితే ఊడే ముక్కు (తేలికగా తప్పుకొను) :
“తుమ్మితే ఊడే ముక్కు” వంటి వాడి స్నేహం విషయం గూర్చి అంతగా పట్టించుకోవలసిన పనిలేదు.

2. కింది వృత్తంలోని పదాల ఆధారంగా శబ్దపల్లవాల్ని రాయండి. సొంతవాక్యాల్లో ఉపయోగించండి.
ఉదా : బయటపడు : కిషన్ కష్టపడి సమస్యల నుండి బయటపడ్డాడు.

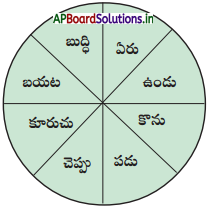
శబ్దపల్లవాలు :

1. బుద్ధిచెప్పు
2. ఏరుకొను
3. బయటపడు
4. కూరుచుండు

వాక్య ప్రయోగాలు :

1. ఉపాధ్యాయుడు పిల్లలకు బాగా బుద్ధి చెప్పాడు.
2. పారు సముద్రతీరాన గులకరాళ్ళను ఏరుకొన్నారు.
3. నేను ఎలాగో ఆ చిక్కుల నుండి బయటపడ్డాను.
4. నేను బల్లపై కూర్చోడానికి ఇష్టపడతాను.

3. కింది వాక్యాలను చదవండి. వీటిని పట్టికలోనున్న తెలుగు భాషాప్రక్రియలలో సరైన వాటితో జతపరచి వాటిని వాక్యాలుగా రాయండి.

ఉదా : ‘ఉప్పు కప్పురంబు నొక్కపోలికనుండు’ అనేది పద్యప్రక్రియ
జవాబు:
అ) ఉప్పు కప్పురంబు ఒక్క పోలికనుండు : పద్యం

ఆ) అదిగో అల్లదిగో శ్రీహరి వాసము : సంకీర్తన

ఇ) నేను అన్నం తిని బడికి వెళతాను : వచనం

ఈ) బొబ్బిలిపులిని నేనురా – సై
దేశరక్షణ చేసెదరా – సై : బుర్రకథ

ఉ) శ్రీమద్రమారమణ గోవిందో హరి : హరికథ

4. కింది వాటిని ఉదాహరణలో చూపిన విధంగా ఒకే పదంగా కూర్చండి.
ఉదా : తెలుగు అనే పేరు గల భాష = తెలుగుభాష

అ) కోపము, అనెడి అగ్ని = కోపాగ్ని
ఆ) హరి యొక్క కథ = హరికథ
ఇ) దేశము నందలి భాషలు = దేశభాషలు

V. సృజనాత్మకత

* కింది జాతీయాలను ఉపయోగించి, ఓక కథ రాయండి.
1) చెవిలో ఇల్లు కట్టుకొని, 2) కంటికి కాపలా, 3) తల పండిన, 4) వీనుల విందు, 5) తలలో నాలుక, 6) కాలికి . బుద్ధి చెప్పు, 7) చేతులు ముడుచుకోవడం, 8) కొట్టినపిండి.
జవాబు:
రామాపురంలో మా తాతగారు ఉండేవారు. ఆయన వ్యవసాయం చేయడంలో (3) తలపండినవాడు. ఆయనకు వేద విద్య అంతా (8) కొట్టిన పిండి. ఆయన శిష్యుడు రామావధాన్లు ఆయన దగ్గర (5) తలలో నాలుకలా మసలేవాడు. మా తాతగారు శిష్యుడికి వేదమంత్రాలు (1) చెవిలో ఇల్లు కట్టుకొని పోరి చెప్పేవారు. ఆ శిష్యుడు మా తాతగారికి (2)కంటికి కాపలాగా ఉండేవాడు. ఎప్పుడూ మా తాతగారి ఇంటిలో వేదమంత్రాలు (4) వీనుల విందుగా వినబడేవి. శిష్యుడు మాత్రం ఏ పనీ చేయకుండా (7) చేతులు ముడుచుకోవడం తాతగారికి ఇష్టం లేదు. ఒక రోజు ఆ శిష్యుడు గురువుగారి వద్ద 10 రూపాయలు దొంగిలించి, (6) కాలికి బుద్ధి చెప్పాడు.

(లేదా)
* ‘తెలుగు భాష’ గొప్పదనాన్ని గురించి, కాపాడడాన్ని గురించి నినాదాలు రాయండి.
జవాబు:

1. తెలుగుభాష మాట్లాడడం – తల్లి దండ్రులను గౌరవించడంతో, సమానం
2. తెలుగు తల్లి – మన చల్లని తల్లి
3. తెలుగు మాట్లాడు – కన్నతల్లిని చల్లగా చూడు
4. తెలుగును మాట్లాడదాం – తల్లిని రక్షిద్దాం
5. తేనెలాంటి భాష – మన తెలుగుభాష
6. దేశభాషల్లో – తెలుగు భాష గొప్పది
7. తెలుగు నేలలో – తెలుగువాడుగా పుట్టడం మన అదృష్టం
8. తెలుగు భాషాతల్లిని – రక్షించుకుందాం
9. తెలుగును విడిస్తే – తెల్ల మొహం వేస్తావు.

VI. ప్రశంస

* కింది సామెతల్ని మీకు తెలిసిన ఇతర భాషల్లో ఏమంటారో తెలుసుకోండి.

అ) మనసుంటే మార్గముంటుంది.
జవాబు:
Where there is a will, there is a way.

ఆ) సాధనమున పనులు సమకూరు ధరలోన
జవాబు:
‘Practice makes the men perfect. .

ఇ) మెరిసేదంతా బంగారం కాదు.
జవాబు:
All glitters is not gold.

ఈ) నోరు మంచిదైతే ఊరు మంచిదౌతుంది.
జవాబు:
Pleasant words please all.
(or)
A good tongue is a good weapon.

VII. ప్రాజెక్టు పని

* తెలుగుభాష/మాతృభాష గొప్పదనాన్ని గురించి తెలిపే పద్యాలు, పాటలు, గేయాలు సేకరించండి. వాటిని పాడి
వినిపించండి.
జవాబు:
విద్యార్థి కృత్యం

VIII. భాషను గురించి తెలుసుకుందాం

1. కింది పదాలను విడదీయండి. సంధి పేరు తెల్పండి.

అ) అయ్యయ్యో = అయ్యో + అయ్యో = ఆమ్రేడిత సంధి
ఆ) కుట్టుసురు = కుఱు + ఉసురు = ద్విరుక్తటకార సంధి
ఇ) కొట్టకొన = కొన + కొన = ఆమ్రేడిత సంధి
ఈ) పట్టపగలు = పగలు + పగలు = ఆమ్రేడిత సంధి
ఉ) అన్నన్న = అన్న + అన్న = ఆమ్రేడిత సంధి
ఊ) చిట్టెలుక = చిఱు + ఎలుక = ద్విరుక్తటకార సంధి
ఋ) ఎట్లెట్లు = ఎట్లు + ఎట్లు = ఆమ్రేడిత సంధి
ఋ) అహాహా = అహా + అహా = ఆమ్రేడిత సంధి.

2. కింది పదాలు ఏ సంధి సూత్రానికి వర్తిస్తాయో గుర్తించి, ఆ సంధి పేరు రాసి సూత్రం రాయండి.

అ) అచ్చు ………………… ఆమ్రేడితం …………………….. తరచు.
‘సంధిపేరు : ఆమ్రేడిత సంధి
సూత్రం : అచ్చునకు ఆమ్రేడితము పరమగునపుడు సంధి తరచుగానగు.

ఆ) బి, డ లు ………….. అచ్చు …………………. ద్విరుక్తటకారం …………………. ఆదేశం …………. కు ఱు, చిఱు, కడు, నిడు, నడు.
సంధి పేరు : ద్విరుక్తటకార సంధి.
సూత్రం : కుటు, చిఱు, కడు, నడు, నిడు శబ్దములందలి అడలకు అచ్చు పరమగునపుడు, ద్విరుక్తటకారంబు ఆదేశంబగు.

1. కింది పదాలను విడదీసి సంధి నామములను రాయండి.

1. తాతయ్య = తాత + అయ్య = (అ + అ = అ) – అత్వసంధి
2. అదేమిటి = అది + ఏమిటి = (ఇ + ఏ = ఏ) – ఇకారసంధి
3. ఏమిటది = ఏమిటి + అది = (ఇ + అ = అ) – ఇకారసంధి
4. పచ్చిదొకటి = పచ్చిది + ఒకటి = (ఇ + ఒ = ఒ) – ఇకార సంధి
5. అచ్చుతానంద = అచ్యుత + ఆనంద = (అ + ఆ = ఆ) – సవర్ణదీర్ఘ సంధి
6. పల్లెటూళ్ళు = పల్లె + ఊళ్ళు = (పల్లె + టు + ఊళ్ళు) – టుగాగమ సంధి
7. ప్రత్యేక = ప్రతి + ఏక = (ఇ + ఏ = యే) – యణాదేశ సంధి
8. ఏకాగ్రత = ఏక + అగ్రత = (అ + అ = ఆ) – సవర్ణదీర్ఘ సంధి
9. అష్టావధానం = అష్ట + అవధానం = (అ + అ = ఆ) – సవర్ణదీర్ఘ సంధి
10. శతావధానం = శత + అవధానం = (అ + అ = ఆ) – సవర్ణదీర్ఘ సంధి
11. సహస్రావధానం = సహస్ర + అవధానం = (అ + అ = ఆ) – సవర్ణదీర్ఘ సంధి
12. మహానుభావులు = మహా + అనుభావులు = (ఆ + అ = ఆ) – సవర్ణదీర్ఘ సంధి

2. కింది సమాసాలకు విగ్రహం తెలిపి సమాసాల పేర్లు రాయండి.

3. ఈ కింది ప్రకృతులకు వికృతులు, వికృతులకు ప్రకృతులు రాయండి.

1. ఆహారము (ప్రకృతి) – ఓగిరము (వికృతి)
2. సొంతము (వికృతి) – స్వతంత్రము (ప్రకృతి)
3. పద్యము , (ప్రకృతి) – పద్దెము (వికృతి)
4. . బంగారము (వికృతి) – భృంగారము (ప్రకృతి)
5. అమ్మ (వికృతి) – అంబ (ప్రకృతి)
6. రాత్రి (ప్రకృతి) – రాతిరి, రే, రేయి (వికృతి)
7. కథ (ప్రకృతి) – కత (వికృతి)
8. పుస్తకము (ప్రకృతి) – పొత్తము (వికృతి)
9. ధర్మము (ప్రకృతి) – దమ్మము (వికృతి)
10. బరువు (వికృతి) – భారము (ప్రకృతి)
11. భాష (ప్రకృతి) – బాస (వికృతి)
12. బువి (వికృతి) – భూమి, భువి (ప్రకృతి)

4. కింది పదాలను ఉపయోగించి సొంతవాక్యాలు రాయండి.

1. నెమరువేయు : గురువులు బోధించిన పద్యాలను పిల్లలు నెమరువేయాలి.
2. పలుకుబడి : తెలుగుభాష పలుకుబడిలో కమ్మదనం ఉంది.
3. ఫిర్యాదు చేయు : తన సైకిలు పోయిందని, పోలీసు స్టేషనులో రామయ్య ఫిర్యాదు చేశాడు.
4. మేలుకొను : తెలుగు జాతి త్వరగా మేలుకొనకపోతే తెలుగు మృతభాషలలో చేరుతుంది.
5. మౌఖికంగా : పరీక్షలలో ప్రశ్నలను మౌఖికంగా అడుగుతారు.
6. ఆశువు : తిరుపతి వెంకటకవులు గంటకు నూరు పద్యాలు ఆశువుగా చెప్పేవారు
7. ఆబాలగోపాలము : మా గ్రామంలో ఆబాల గోపాలమూ దేవుని పెండ్లి వేడుకల్లో పాల్గొన్నారు.
8. ఏకాగ్రత : అవధాన ప్రక్రియలో ఏకాగ్రతకు, ధారణకు ప్రాధాన్యం.
9. ఆధునికము : ఆధునికంగా వస్తున్న మార్పులను పాతతరం వారు అంగీకరించాలి.
10. ప్రాచీనము : సంస్కృత భాష, ప్రాచీనమయిన భాష.

కొత్త పదాలు-అర్థాలు

చిట్టి = చిన్నది
తాతయ్య చదివిన పద్యం :
“అడిగెదనని కడు వడిఁ జను …… నడుగిడు నెడలన్ ” అనేది

గమనిక :
ఈ పద్యం, పోతన మహాకవి రచించిన ‘ఆంధ్ర మహాభాగవతములో గజేంద్రమోక్షములోనిది. విష్ణుమూర్తి తన భార్య లక్ష్మీదేవికి కూడా చెప్పకుండా, తొందరగా గజేంద్రుణ్ణి రక్షించడానికి, తన చేతితో పట్టుకున్న లక్ష్మీదేవి కొంగును కూడా విడిచిపెట్టకుండా, ముందుకు వెడుతున్నాడు. అప్పుడు లక్ష్మీదేవి విష్ణువు వెనకాలే వెడుతూ ఉంది. అప్పటి లక్ష్మీదేవి స్థితిని పోతనగారు ఈ పద్యంలో వర్ణించారు.

పద్యభావం :
ఎక్కడకు వెడుతున్నారని భర్తను అడుగుతానని లక్ష్మీదేవి మిక్కిలి వేగంగా ముందుకు నడుస్తూ వెళ్ళింది. అడిగినా విష్ణువు జవాబు చెప్పడని తలచి, నడవడం మానింది. ఇంతలో విషయం తెలిసికోవాలనే తొందరతో, తిరిగి ముందుకు అడుగులు వేస్తోంది. ఇంతలో మ్రాన్పాటు కలిగి, ముందడుగు వేయడం మానింది.

గమనిక :
ఈ పద్యంలో ‘వృత్త్యనుప్రాస’ అనే శబ్దాలంకారం ఉంది. ఈ చిన్న కందపద్యంలో ‘డ’ అనే హల్లు 23 సార్లు తిరిగి తిరిగి వచ్చింది. అదే ఈ పద్యంలోని చమత్కారం.

నెమరువేయు = తిన్న పదార్థాన్ని తిరిగి నోట్లోకి తెచ్చుకొని మళ్ళీ నమలు
జాతీయము = ఒక జాతికి సంబంధించిన పదబంధము లేక పలుకుబడి
లెస్స = మంచిది
ఫిర్యాదు = కంప్లైస్ట్ (Complaint)
చర్య = యాక్షన్ (Action)

పొడుపుకథ పద్యం

పండిన వెండిన దొక్కటి : షండినది, ఎండినది అంటే ‘వక్క’ అనగా పోకచెక్క. (పోక కాయ పండి, అది ఎండిన తర్వాత, దాన్ని వక్కలుగా చేస్తారు.

ఖండించిన పచ్చిదొకటి : చెట్టునుండి కోసిన పచ్చిది ‘తమలపాకు’.

కాలినదొకటై : ఆల్చిప్పలను కాలిస్తే ‘సున్నం’ వస్తుంది.

తిండికి రుచిగానుండును : వక్క తమలపాకు, సున్నం కలిపిన తాంబూలము, తినడానికి రుచికరం.

తోకలేని పిట్ట తొంభై ఆమడలు పోయింది : ఈ పొడుపు కథకు సమాధానం, ‘ఉత్తరం’.

మొక్కె వంగనిది మానై వంగుతుందా? : చిన్న మొక్కగా ఉన్నపుడే అది వంగుతుంది. చెట్టు మానుగా అయిన తరువాత అది వంగదు.

జాగృతము + అవడం = మేల్కోవడం
జో జో అచ్యుత + ఆనంద = అచ్యుతా ! ఆనందా ! నీకు జోల
జోజో ముకుంద = ముకుందా ! విష్ణుమూర్తీ ! నీకు జోల
‘పలుకే బంగారమాయెనా?’ = ఈ పాటను రామదాసు అనే కంచెర్ల గోపన్న రాశాడు. (ఒక మాట మాట్లాడడం నీకు బంగారం లాంటిదా?) (తనతో మాట్లాడుమని ప్రార్థన)
మౌఖికం = ముఖం నుండి వచ్చేది
ఆశువు = అప్పటికప్పుడు, ఏ ప్రయత్నము లేకుండా చెప్పే పద్యం
ఆబాలగోపాలం = పిల్లల నుండి పెద్దల వరకూ అందరూ
ఫణివరుండు = పెద్దపాము
సమస్యాపూరణం = సమస్యను పూర్తిచేయుట
ధారణ = జ్ఞాపకము చేసికోవడం
అవధానం = ఏకాగ్రత
అష్టావధానం (అష్ట + అవధానం) = ఎనిమిది విషయాలలో ఏకాగ్రత చూపడం
శతావధానం (శత + అవధానం) = నూరు మంది అడిగిన ప్రశ్నలకు జవాబులు చెప్పడం
సహస్రావధానం (సహస్ర + అవధానం) = వేయి మంది ప్రశ్నించిన ప్రశ్నలకు జవాబులు చెప్పడం
ప్రతిభ = తెలివి
“మా నిజాం రాజు తరతరాల బూజు” = ఈ పద్యం చెప్పిన కవి “దాశరథి” నైజాం నవాబును గూర్చి ఆయన అలా చెప్పాడు.
“వట్టి మాటలు కట్టి పెట్టోయ్ గట్టి మేల్ తలపెట్టవోయ్ = ఈ గేయం పంక్తులు, గురజాడ అప్పారావు గారి ‘దేశభక్తి’ గేయం లోనివి.
మాతృభాష = తల్లి భాష
ఆరాధ్య భాష = పూజింపదగిన భాష
మహానుభావులు = గొప్పవారు
ఆధునికము = నవీనము
భువి = భూమి