Inter 1st Year Maths 1A Hyperbolic Functions Formulas

Use these Inter 1st Year Maths 1A Formulas PDF Chapter 9 Hyperbolic Functions to solve questions creatively.

Intermediate 1st Year Maths 1A Hyperbolic Functions Formulas

→ e^x = 1 + \(\frac{x}{1 !}+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+\ldots+\frac{x^{n}}{n !}\)+ … ∞

→ sinhx = \(\frac{e^{x}-e^{-x}}{2}\)
and coshx = \(\frac{e^{x}+e^{-x}}{2}\)

→ tanh x = \(\frac{\sinh x}{\cosh x}\),

→ coth x = \(\frac{1}{\tanh x}\),

→ sech x = \(\frac{1}{\cosh x}\)

→ cosech x = \(\frac{1}{\sinh x}\), if x ≠ 0

→ cosh²x – sinh²x – 1, sech²x – 1 – tanh²x, cosech²x = coth²x – 1

Function y = f(x)	Domain (x)	Range (y)
sinh x	R	R
cosh x	R	(1, ∞)
tanh x	R	(1, 1)
coth x	R- {0}	(-∞, -1) ∪ (1, ∞)
sech x	R	(0, 1]
cosech x	R – {0}	R – {0}

→ sinh^-1x = loge [x + \(\sqrt{x^{2}+1}\) ] for all x ∈ R

→ cosh^-1x = loge [x + \(\sqrt{x^{2}-1}\)] for all x ∈ (1, ∞)

→ tanh^-1x = \(\frac{1}{2}\)log_e\(\left(\frac{1+x}{1-x}\right)\), |x| < 1 (i.e) for all x ∈ (-1, -1)

→ coth^-1x = \(\frac{1}{2}\)log_e\(\left(\frac{1+x}{1-x}\right)\), |x| > 1 (i.e) for all x ∈ (-∞, -1) (1, ∞)

→ sech^-1x = log_e\(\left(\frac{1+\sqrt{1+x^{2}}}{x}\right)\) for all x ∈ (0, 1)

→ cosech^-1x = log_e\(\left(\frac{1-\sqrt{1+x^{2}}}{x}\right)\), if x < 0 (i.e,) x ∈ (-∞, 0) and
= log_e\(\left(\frac{1+\sqrt{1+x^{2}}}{x}\right)\), if x > 0 (i.e,) x ∈ (0, ∞)

→ sinh (x + y) = sinh x cosh y + cosh x sinh y

→ cosh (x + y)= cosh x cosh y + sinh x sinh y

→ sinh (x – y) = sinh x cosh y – cosh x sinh y

→ cosh (x – y) = cosh x cosh y – sinh x sinh y

→ tanh (x + y) = \(\frac{\tanh x+\tanh y}{1+\tanh x \tanh y}\)

→ tanh (x – y) = \(\frac{\tanh x-\tanh y}{1-\tanh x \tanh y}\)

→ sinh 2x = 2 sinh x cosh x = \(\frac{2 \tanh x}{1-\tanh ^{2} x}\)

→ cosh 2x = cosh²x + sinh²x
= 2 cosh²x – 1 = 1 + 2 sinh² x = \(\frac{1+\tanh ^{2} x}{1-\tanh ^{2} x}\)

→ tanh 2x = \(\frac{2 \tanh x}{1+\tanh ^{2} x}\)

→ sinh 3x = 3sinh x + 4sinh³ x

→ cosh 3x = 4cosh³ x – 3cosh x

→ tanh 3x = \frac{3 \tanh x+\tanh ^{3} x}{1+3 \tanh ^{2} x}

→ Inverse hyperbolic functions:

Function y = f(x)	Domain (x)	Range (y)
(i) sinh-1(x)	IR	IR
(ii) cosh-1(x)	[1, ∞)	[0, ∞)
(iii) tanh-1(x)	(-1, 1)	IR
(iv) coth-1(x)	R –[-1, 1]	R- {0}
(v) sech-1(x)	(0, 1]	[0, ∞)
(vi) cosech-1(x)	R- {0}	R – {0}

→ sin hx = \(\frac{e^{x}-e^{-x}}{2}\)

→ cos hx = \(\frac{e^{x}+e^{-x}}{2}\)

→ tan hx = \(\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\)

→ cosec hx = \(\frac{2}{e^{x}-e^{-x}}\)

→ sec hx = \(\frac{2}{e^{x}+e^{-x}}\)

→ cot hx = \(\frac{e^{x}+e^{-x}}{e^{x}-e^{-x}}\)

→ cos h²x – sinh²x = 1

→ 1 – tanh²x = sech²x

→ cot h²x – 1 = cosech²x

→ Prove that sinh^-1x = log{x + \(\sqrt{x^{2}+1}\)}
Proof:
Let sinh^-1x = y ⇒ x = sinh y

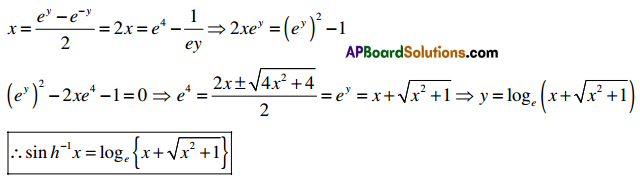
→ Prove that cosh^-1x = log_e(x – \(\sqrt{x^{2}-1}\)
proof:
Let cosh^-1x = y ⇒ x = cosh y

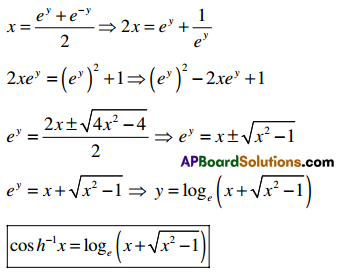
→ Prove that Tan^-1x = \(\frac{1}{2}\)log_e\(\left(\frac{4 x}{1-x}\right)\)
proof:
Let tanh^-1x = y ⇒ x = tanh y

→ sech^-1x = log\(\left\{\frac{1+\sqrt{1-x^{2}}}{x}\right\}\)

→ cosech^-1x = log\(\left(\frac{1-\sqrt{1+x^{2}}}{x}\right)\) x < 0 = log\(\left\{\frac{1-\sqrt{1+x^{2}}}{x}\right\}\) x > 0

→ sin h(x + y) = sin hx cos hy + cos hx sin hy

→ sinh(x – y) = sin hx cos hy + cos hx sin hy

→ cosh(x + y) = cos hx cos hy + sin hx sin hv

→ cosh(x – y) = cos hx cos hy – sin hx sin hy

→ sin h2x = 2 sin hx cos hx = \(\)

→ cos h2x = cosh²x + sinh²x = 2cosh²x – 1 = 1 + 2sinh²x = \(\frac{1+{Tanh}^{2} x}{1-{Tanh}^{2} x}\)

→ Tanh(x + y) = \(\frac{\text { Tanhx+Tanhy }}{1-\text { TanhxTanhy }}\)

→ Tanh(x – y) = \(\frac{\text { Tanhx-Tanhy }}{1+\text { TanhxTanhy }}\)

→ coth(x + y) = \(\frac{\cot h x \cot h y+1}{\cot h y+\cot h x}\)

→ coth(x – y) = \(\frac{\cot h x \cot h y-1}{\cot h y-\cot h x}\)

→ Tanh2x = \(\frac{2 \tan h x}{1+\tanh ^{2} x}\)

→ cot h2x = \(\frac{\operatorname{coth}^{2} x+1}{2 \cot h x}\)