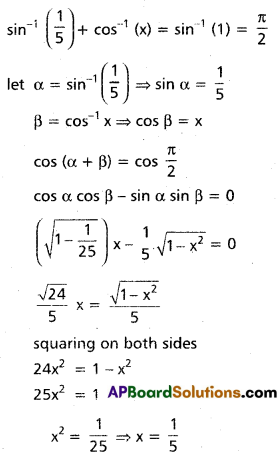Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Inverse Trigonometric Functions Solutions Exercise 8(a) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1A Inverse Trigonometric Functions Solutions Exercise 8(a)
I.
Question 1.
Evaluate the following.
(i) \(\sin ^{-1}\left(\frac{-\sqrt{3}}{2}\right)\)
Solution:
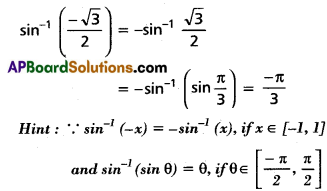
(ii) \(\cos ^{-1}\left(\frac{1}{\sqrt{2}}\right)\)
Solution:
\(\cos ^{-1}\left(\frac{1}{\sqrt{2}}\right)=\cos ^{-1}\left(\cos \frac{\pi}{4}\right)=\frac{\pi}{4}\)
![]()
(iii) sec-1(-√2)
Solution:

(iv) cot-1(-√3)
Solution:

(v) \(\sin \left(\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)\right)\)
Solution:

(vi) \(\sin ^{-1}\left(\sin \frac{5 \pi}{6}\right)\)
Solution:
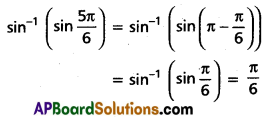
(vii) \(\cos ^{-1}\left(\cos \frac{5 \pi}{4}\right)\)
Solution:

Question 2.
Find the values of
(i) \(\sin \left(\cos ^{-1} \frac{3}{5}\right)\)
Solution:
\(\sin \left(\cos ^{-1} \frac{3}{5}\right)=\sin \left(\sin ^{-1} \frac{4}{5}\right)=\frac{4}{5}\)
(ii) \(\tan \left({cosec}^{-1} \frac{65}{63}\right)\)
Solution:
\(\tan \left({cosec}^{-1} \frac{65}{63}\right)=\tan \left(\tan ^{-1} \frac{63}{16}\right)\) = \(\frac{63}{16}\)
(iii) \(\sin \left(2 \sin ^{-1} \frac{4}{5}\right)\)
Solution:
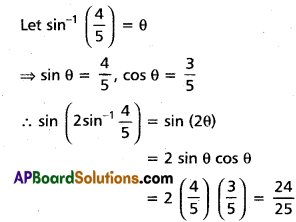
(iv) \(\sin ^{-1}\left(\sin \frac{33 \pi}{7}\right)\)
Solution:
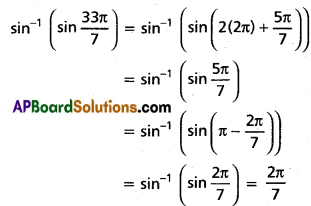
(v) \(\cos ^{-1}\left(\cos \frac{17 \pi}{6}\right)\)
Solution:

![]()
Question 3.
Simplify each of the following.
(i) \(\tan ^{-1}\left[\frac{\sin x}{1+\cos x}\right]\)
Solution:
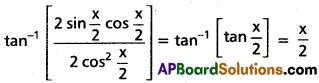
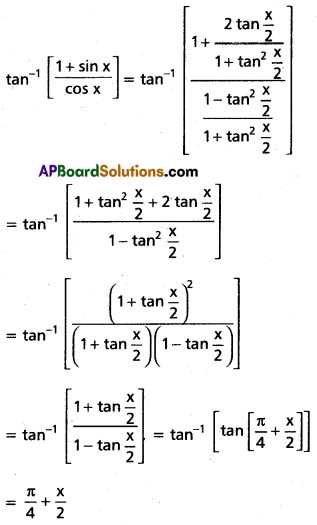
(ii) tan-1(sec x + tan x)
Solution:
(iii) \(\tan ^{-1} \sqrt{\frac{1-\cos x}{1+\cos x}}\)
Solution:
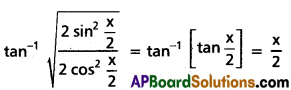
(iv) sin-1(2 cos2θ – 1) + cos-1(1 – 2 sin2θ)
Solution:
sin-1(cos 2θ) + cos-1(cos 2θ)
= sin-1[sin (90° – 2θ)] + cos-1(cos 2θ)
= 90° – 2θ + 2θ
= 90°
(v) \(\tan ^{-1}\left(x+\sqrt{1+x^{2}}\right)\); x ∈ R
Solution:

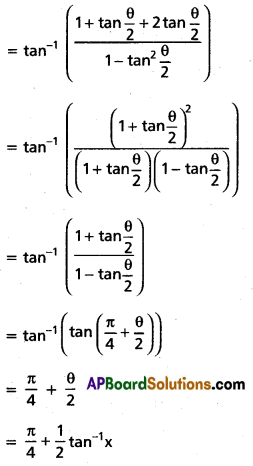
II.
Question 1.
Prove that
(i) \(\sin ^{-1} \frac{3}{5}+\sin ^{-1} \frac{8}{17}=\cos ^{-1} \frac{36}{85}\)
Solution:


(ii) \(\sin ^{-1} \frac{3}{5}+\cos ^{-1} \frac{12}{13}=\cos ^{-1} \frac{33}{65}\)
Solution:
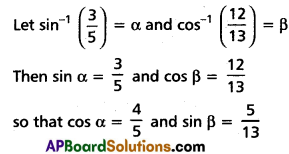
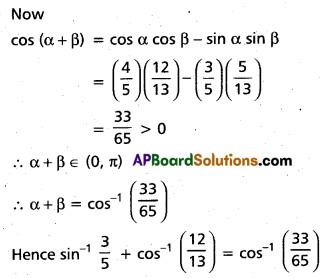
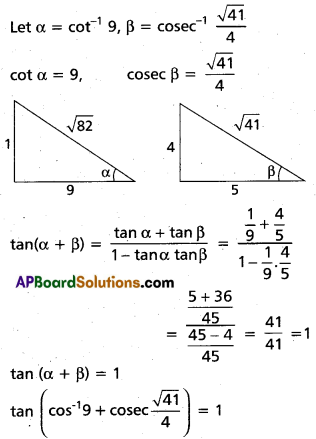
(iii) \(\tan \left[\cot ^{-1} 9+{cosec}^{-1} \frac{\sqrt{41}}{4}\right]=1\)
Solution:
(iv) \(\cos ^{-1} \frac{4}{5}+\sin ^{-1} \frac{3}{\sqrt{34}}=\tan ^{-1} \frac{27}{11}\)
Solution:
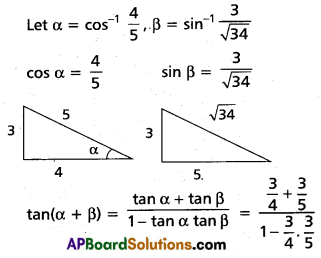

![]()
Question 2.
Find the values of
(i) \(\sin \left(\cos ^{-1} \frac{3}{5}+\cos ^{-1} \frac{12}{13}\right)\)
Solution:

(ii) \(\tan \left(\sin ^{-1} \frac{3}{5}+\cos ^{-1} \frac{5}{\sqrt{34}}\right)\)
Solution:
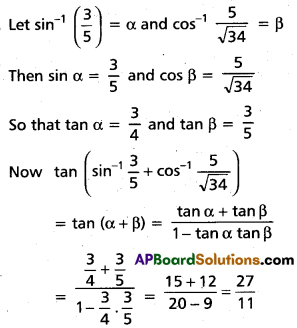
(iii) \(\cos \left(\sin ^{-1} \frac{3}{5}+\sin ^{-1} \frac{5}{13}\right)\)
Solution:
Let \(\sin ^{-1} \frac{3}{5}\) = α and \(\sin ^{-1} \frac{5}{13}\) = β
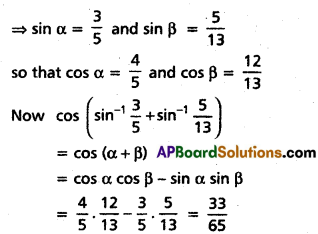
Question 3.
Prove that
(i) \(\cos \left[2 \tan ^{-1} \frac{1}{7}\right]=\sin \left[2 \tan ^{-1} \frac{3}{4}\right]\)
Solution:

(ii) \(\tan \left[2 \tan ^{-1}\left(\frac{\sqrt{5}-1}{2}\right)\right]=2\)
Solution:

(iii) \(\cos \left\{2\left[\tan ^{-1}\left(\frac{1}{4}\right)+\tan ^{-1}\left(\frac{2}{9}\right)\right]\right\}=\frac{3}{5}\)
Solution:

Question 4.
Prove that
(i) \(\tan ^{-1} \frac{1}{7}+\tan ^{-1} \frac{1}{13}-\tan ^{-1} \frac{2}{9}=0\)
Solution:
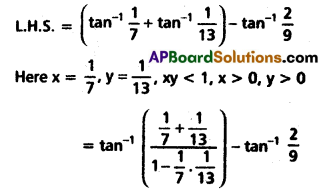

(ii) \(\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{5}+\tan ^{-1} \frac{1}{8}=\frac{\pi}{4}\)
Solution:

(iii) \(\tan ^{-1} \frac{3}{4}+\tan ^{-1} \frac{3}{5}-\tan ^{-1} \frac{8}{19}=\frac{\pi}{4}\)
Solution:
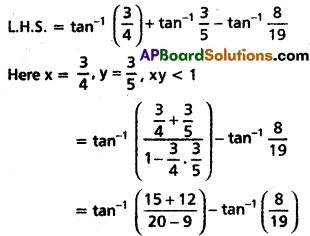

(iv) \(\tan ^{-1} \frac{1}{7}+\tan ^{-1} \frac{1}{8}\) = \(\cot ^{-1} \frac{201}{43}+\cot ^{-1} 18\)
Solution:

![]()
Question 5.
Show that
(i) sec2 (tan-1 2) + cosec2 (cot-1 2) = 10
Solution:
Let a = tan-1 2 ⇒ tan α = 2
sec2 α = 1 + tan-1 α = 1 + 4 = 5
Let β = cot-1 2 ⇒ cot β = 2
cosec2 β = 1 + cot2 β = 1 + 4 = 5
LHS = sec2 (tan-1 2) + cosec2 (cot-1 2)
= 5 + 5
= 10
= RHS
(ii) Find the value of \(\left(\cos ^{-1} \frac{4}{5}+\tan ^{-1} \frac{2}{3}\right)\)
Solution:

(iii) If sin-1 x – cos-1 x = \(\frac{\pi}{6}\) then find x.
Solution:

III.
Question 1.
Prove that
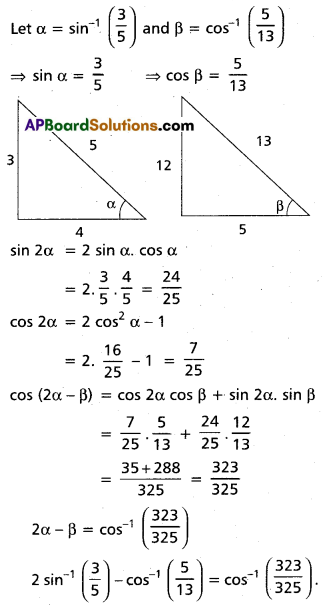
(i) \(2 \sin ^{-1} \frac{3}{5}-\cos ^{-1} \frac{5}{13}=\cos ^{-1} \frac{323}{325}\)
Solution:
(ii) \(\sin ^{-1} \frac{4}{5}+2 \tan ^{-1} \frac{1}{3}=\frac{\pi}{2}\)
Solution:


(iii) \(4 \tan ^{-1} \frac{1}{5}+\tan ^{-1} \frac{1}{99}-\tan ^{-1} \frac{1}{70}=\frac{\pi}{4}\)
Solution:
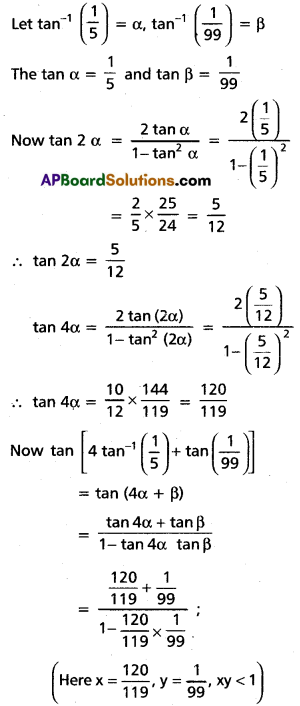
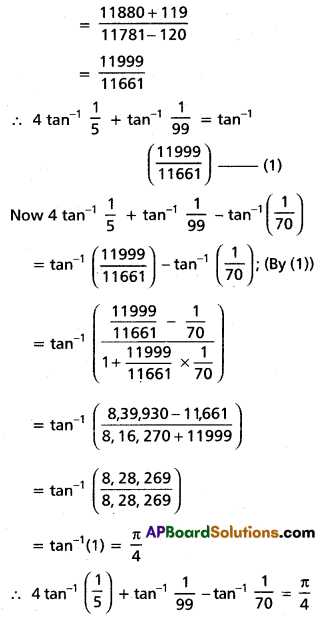
Question 2.
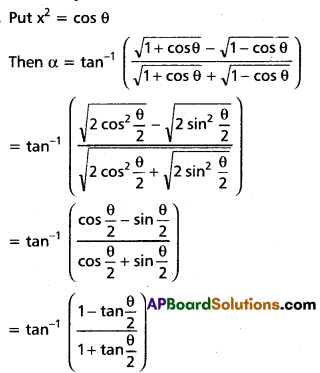
(i) If α = \({tan}^{-1}\left(\frac{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}\right)\) then prove that x2 = sin 2α.
Solution:

(ii) Prove that tan\(\left\{2-\tan ^{-1}\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\right\}=\mathbf{x}\)
Solution:

(iii) Prove that \(\sin \left[\cot ^{-1} \frac{2 x}{1-x^{2}}+\cos ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right)\right]\) = 1
Solution:

(iv) Prove that \(\left\{\frac{\pi}{4}+\frac{1}{2} \cos ^{-1}\left(\frac{a}{b}\right)\right\}\)
Solution:

Question 3.
(i) If cos-1 p + cos-1 q + cos-1 r = π, then prove that p2 + q2 + r2 + 2pqr = 1
Solution:
Let cos-1 p = A, cos-1 q = B and cos-1 r = C
then A + B + C = π ………(1)
and p = cos A, q = cos B and r cos C
Now p2 + q2 + r2 = cos2 A + cos2 B + cos2 C
= cos2 A + (1 – sin2 B + cos2 C)
= 1 + (cos2 A – sin2 B) + cos2 C
= 1 + cos (A + B) . cos (A – B) + cos2 C
= 1 + cos (π – C) cos (A – B) + cos2 C (By (1))
= 1 – cos C cos (A – B) + cos2 C
= 1 – cos C [cos (A – B) – cos C]
= 1 – cos C [cos (A – B) – cos(180° – \(\overline{A+B}\)]
= 1 – cos C [cos (A – B) + cos (A + B)]
= 1 – cos C [2 cos A cos B]
= 1 – 2 pqr
∴ p2 + q2 + r2 + 2pqr = 1
![]()
(ii) If \(\sin ^{-1}\left(\frac{2 p}{1+p^{2}}\right)-\cos ^{-1}\left(\frac{1-q^{2}}{1+q^{2}}\right)\) = \(\tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right)\), then prove that x = \(\frac{p-q}{1+p q}\)
Solution:

(iii) If a, b, c are distinct non-zero real numbers having the same sign, prove that \(\cot ^{-1}\left(\frac{a b+1}{a-b}\right)+\cot ^{-1}\left(\frac{b c+1}{b-c}\right)\) + \(\cot ^{-1}\left(\frac{c a+1}{c-a}\right)\) = π or 2π
Solution:
Since (a – b) + (b – c) + (c – a) = 0.
(a – b), (b – c), (c – a) all cannot have the same sign.
Now two cases arise, namely, either two of these numbers are positive and one negative (or) two of these numbers are negative and one is positive.
Case (i): Without loss of generality, we assume that (a – b), (b – c) are both positive and (c – a) is negative

Case (ii): Without loss of generality, we assume that (a – b) and (b – c) are both negative and (c – a) is positive.

(iv) If sin-1 (x) + sin-1 (y) + sin-1 (z) = π, then prove that \(x \sqrt{1-x^{2}}+y \sqrt{1-y^{2}}+z \sqrt{1-z^{2}}=2 x y z\)
Solution:
Let sin-1 (x) = A, sin-1 (y) = B and sin-1 (z) = C
Then A + B + C = π …………(1)
and x = sin A, y = sin B and z = sin C
Now LHS = \(x \sqrt{1-x^{2}}+y \sqrt{1-y^{2}}+z \sqrt{1-z^{2}}\)
= sin A \(\sqrt{1-\sin ^{2} A}\) + sin B \(\sqrt{1-\sin ^{2} B}\) + sin C \(\sqrt{1-\sin ^{2} C}\)
= sin A cos A + sin B cos B + sin C cos C
= \(\frac{1}{2}\) [sin 2A + sin 2B + sin 2C]
= \(\frac{1}{2}\) [2 . sin (A + B) cos (A – B) + sin 2C]
= \(\frac{1}{2}\) [2 sin (π – c). cos (A – B) + sin 2C]
= \(\frac{1}{2}\) [2 sin C cos (A – B) + 2 sin C cos C]
= \(\frac{1}{2}\) (2 sin C) [cos (A – B) + cos C]
= sin C [cos (A – B) + cos (180° – \(\overline{A+B}\)]
= sin C [cos (A – B) – cos (A + B)]
= sin C [2 sin A sin B]
= 2 xyz
∴ \(x \sqrt{1-x^{2}}+y \sqrt{1-y^{2}}+z \sqrt{1-z^{2}}=2 x y z\)
(v) (a) If tan-1 x + tan-1 y + tan-1 z = π, then prove that x + y + z = xyz.
Solution:
Let A = tan-1 x, B = tan-1 y, C = tan-1 z
tan A = x, tan B = y, tan C = z
Given A + B + C = π ……….(1)
A + B = π – C
tan (A + B) = tan (π – C)
\(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = -tan C
\(\frac{x+y}{1-x y}\) = -z
x + y = -z + xyz
∴ x + y + z = xyz
(b) If tan-1 x + tan-1 y + tan-1 z = \(\frac{\pi}{2}\), then prove that xy + yz + zx = 1.
Solution:
Let tan-1 x = A, tan-1 y = B and tan-1 z = C
Then A + B + C = \(\frac{\pi}{2}\) …….(1)
and x = tan A, y = tan B and z = tan C
∵ A + B + C = \(\frac{\pi}{2}\)
A + B = \(\frac{\pi}{2}\) – C
⇒ tan (A + B) = tan(\(\frac{\pi}{2}\) – C)
⇒ \(\frac{\tan A+\tan B}{1-\tan A \cdot \tan B}\) = cot C
⇒ \(\frac{x+y}{1-x y}=\frac{1}{z}\)
⇒ zx + yz = 1 – xy (or) xy + yz + zx = 1
![]()
Question 4.
Solve the following equations for x:
(i) \({Tan}^{-1}\left(\frac{x-1}{x-2}\right)+{Tan}^{-1}\left(\frac{x+1}{x+2}\right)=\frac{\pi}{4}\)
Solution:

(ii) \(\tan ^{-1}\left(\frac{1}{2 x+1}\right)+\tan ^{-1}\left(\frac{1}{4 x+1}\right)\) = \(\tan ^{-1} \frac{2}{x^{2}}\)
Solution:
Given that

⇒ x2(3x + 1) = 2x(4x + 3)
⇒ x [x(3x + 1) – 2(4x + 3)] = 0
⇒ x = 0 (or) 3x2 – 7x – 6 = 0
⇒ x = 0 (or) 3x2 – 9x + 2x – 6 = 0
⇒ x = 0 (or) 3x(x – 3) + 2(x – 3) = 0
⇒ x = 0 (or) (3x + 2) (x – 3) = 0
⇒ x = 0 (or) 3 (or) \(\frac{-2}{3}\)
(iii) \(3 \sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right)-4 \cos ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right)\) + \(2 \tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right)=\frac{\pi}{3}\)
Solution:
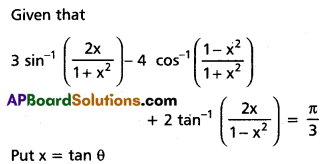
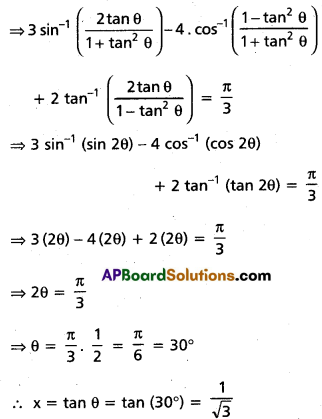
(iv) sin-1(1 – x) – 2 sin-1 x = \(\frac{\pi}{2}\)
Solution:
Given sin-1(1 – x) – 2 sin-1x = \(\frac{\pi}{2}\)
Let sin-1(1 – x) = α and sin-1(x) = β
Then sin α = 1 – x and sin β = x
cos α = \(\sqrt{1-(1-x)^{2}}\) and cos β = \(\sqrt{1-x^{2}}\)
Now sin-1(1 – x) – 2 sin-1(x) = \(\frac{\pi}{2}\)
⇒ α – 2β = \(\frac{\pi}{2}\)
⇒ α = \(\frac{\pi}{2}\) + 2β
⇒ sin α = sin (\(\frac{\pi}{2}\) + 2β)
⇒ sin α = cos 2β
⇒ 1 – x = 1 – 2 sin2β
⇒ 1 – x = 1 – 2x2
⇒ 2x2 – x = 0
⇒ x(2x – 1) = 0
⇒ x = 0 (or) x = \(\frac{1}{2}\)
But when x = \(\frac{1}{2}\)
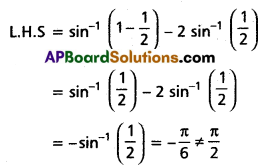
Hence x = 0 is the only solution for the given equation.
![]()
Question 5.
Solve the following equations.
(i) \(\cot ^{-1}\left(\frac{1+x}{1-x}\right)=\frac{1}{2} \cot ^{-1}\left(\frac{1}{x}\right)\), x > 0 and x ≠ 1
Solution:

(ii) \(\tan \left[\cos ^{-1} \frac{1}{x}\right]=\sin \left[\cot ^{-1} \frac{1}{2}\right]\); x ≠ 0
Solution:
Let \(\cos ^{-1}\left(\frac{1}{x}\right)=\alpha, \cot ^{-1} \frac{1}{2}=\beta\)

(iii) \(\cos ^{-1} x+\sin ^{-1} \frac{x}{2}=\frac{\pi}{6}\)
Solution:
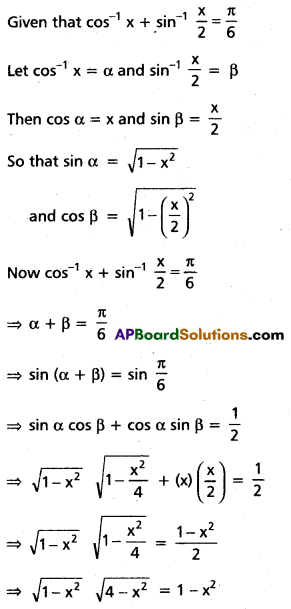

(iv) \(\cos ^{-1}(\sqrt{3} \cdot x)+\cos ^{-1} x=\frac{\pi}{2}\)
Solution:
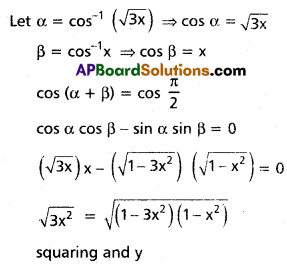
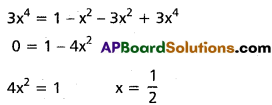
(v) \(\sin \left[\sin ^{-1}\left(\frac{1}{5}\right)+\cos ^{-1} x\right]=1\)
Solution: