Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B The Plane Solutions Exercise 7(a) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B The Plane Solutions Exercise 7(a)
I.
Question 1.
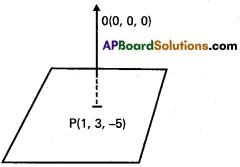
Find the equation of the plane if the foot of the perpendicular from origin to the plane is (1, 3, -5).
Solution:
OP is the normal to the plane D. Rs of op are 1, 3, -5
The plane passes through P( 1, 3, -5) equation of the plane is
1(x – 1) + 3(y – 3) – 5(z + 5) = 0
x – 1 + 3y – 9 – 5z – 25 = 0
x + 3y – 5z – 35 = 0
Question 2.
Reduce the equation x + 2y – 3z – 6 = 0 of the plane to the normal form.
Solution:
Equation of the plane is x + 2y – 3z – 6 = 0
i.e., x + 2y – 3z = 6
Dividing in the
\(\sqrt{1^{2}+2^{2}+(-3)^{2}}=\sqrt{1+4+9}=\sqrt{14}\)
The equation of the plane in the normal form is
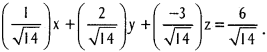
Question 3.
Find the equation of the plane. Whose intercepts on X, Y, Z – axis are 1, 2, 4 respectively.
Solution:
Equation of the plane in the intercept form is
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1
Given a = 1, b = 2, c = 4.
Equation of the required plane in the intercept form is
\(\frac{x}{1}+\frac{y}{2}+\frac{z}{4}\) = 1
Multiplying with 4, we get
4x + 2y + z = 4
![]()
Question 4.
Find the intercepts of the plane 4x + 3y – 2z + 2 = 0 on the co-ordinate axes.
Solution:
Equation of the plane is 4x + 3y – 2z + 2 = 0
– 4x – 3y + 2z = 2
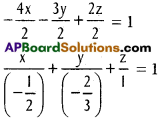
x – intercept = -1/2, y – intercept = -2/3, z intercept =1.
Question 5.
Find the d.c.’s of the normal to the plane x + 2y + 2z – 4 = 0.
Solution:
Equation of the plane is x + 2y + z- 4 = 0
d.r.’s of the normal are (1, 2, 2)
Dividing with \(\sqrt{1+4+4}\) = 3,
d.c.’s of the normal to the plane are (\(\frac{1}{3}, \frac{2}{3}, \frac{2}{3}\))
Question 6.
Find the equation of the plane passing through the point (-2, 1, 3) and having (3, -5, 4) as d.r.’s of its normal.
Solution:
d.r.’s of the normal are (3, -5, 4) and the plane passes through (-2, 1, 3).
Equation of the plane is 3(x + 2) – 5(y – 1) + 4(z – 3) = 0
3x + 6 – 5y + 5 + 4z – 12 = 0
3x -5y+ 4z – 1 = 0.
Question 7.
Write the equation of the plane 4x – 4y + 2z + 5 = 0 in the intercept form.
Solution:
Equation of the plane is
4x – 4y + 2z + 5 = 0
– 4x + 4y – 2z = 5
\(-\frac{4x}{5}, \frac{4y}{5}, \frac{2z}{5}\)
Intercept form is
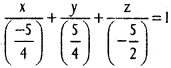
x – intercept = \(\frac{5}{4}\), y – intercept = \(\frac{5}{4}\), z – intercept = –\(\frac{5}{2}\)
Question 8.
Find the angle between the planes x + 2y + 2z-5 = 0 and 3x + 3y + 2z – 8 = 0.
Solution:
Equation of the planes are
x + 2y + 2z – 5 = 0
3x + 3y + 2z – 8 = 0
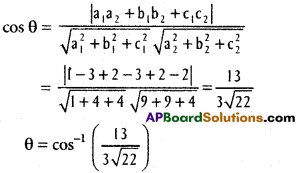
II.
Question 1.
Find the equation of the plane passing through the point (1,1,1) and parallel to the plane x +.2y + 3z – 7 = 0.
Solution:
Equation of the given plane is x + 2y + 3z – 7 = 0.
Equation of the parallel plane is x + 2y + 3z = k.
This plane passes through the point P (1, 1, 1)
1 + 2 + 3 = k ⇒ k = -6
Equation of the required plane is x + 2y + 3z = 6
Question 2.
Find the equation of the plane passing through (2, 3, 4) and perpendicular to x – axis.
Solution:
The plane is perpendicular to x – axis
∴ x – axis is the normal to the plane
d.c.’s of x -axis are 1, 0, 0
Equation of the required plane is x = k
This plane passes through the point P(2, 3, 4)
∴ 2 = k
Equation of the required plane is x = 2.
![]()
Question 3.
Show that 2x + 3y + 7 = 0 represents a plane perpendicular to XY – plane.
Solution:
Equation of the given plane is 2x + 3y + 7 = 0
Equation of xy – plane is z = 0
a1a2 + b1b2 + c1c2 = 2.0 + 3.0 + 0.1 = 0
+0+0=0
The plane 2x + 3y + 7 = 0 is perpendicular to XY – plane.
Question 4.
Find the constant k so that the planes x – 2y + kz = 0 and 2x + 5y – z = 0 are at right angles. Find the equation of the plane through (1, -1, -1) and perpen-dicular to these planes.
Solution:
Equations of the given planes are x – 2y + kz = 0 and 2x + 5y – z = 0
These the planes are perpendicular
1.2 – 2.5 + k (-1) = 0
2 – 10 = k ⇒ k = -8
Equation of the planes
x – 2y – 8z = 0 ………. (1)
2x + 5y – z = 0 ……….. (2)
The required plane passes through (1, -1, -1)
∴ Equation of the plane can be taken as
a(x – 1) + b(y + 1) + c(z + 1) = 0 ………… (3)
This plane is perpendicular to the planes (1) and (2)
a – 2b – 8c = 0
2a + 5b – c = 0
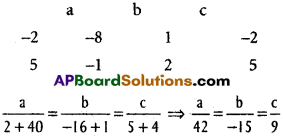
Substituting in (3), equation of the required planes
42 (x – 1) – 15(y + 1) + 9(z + 1) = 0
42x – 42 – 15y – 15 + 9z + 9 = 0
42x – 15y + 9z – 48 = 0.
Question 5.
Find the equation of the plane through (-1, 6, 2) and perpendicular to the join of (1, 2, 3) and (-2, 3, 4).
Solution:
The plane is perpendicular to the line joining A(1, 2, 3) and B(-2, 3, 4).
d.r.’s of AB are 1 + 2, 2 – 3, 3 – 4
i.e., 3, -1, -1
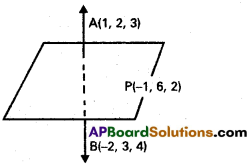
AB is normal to the plane and the plane passes through the point P(-1, 6, 2)
Equation of the required plane is 3(x + 1) – 1(y – 6) -1(z – 2) = 0
3x + 3 – y + 6- z + 2 = 0
3x – y – z + 11 = 0
Question 6.
Find the equation of the plane bisecting the line segment joining (2, 0, 6) and (-6, 2, 4) and perpendicular to it.
Solution:
A (2, 0, 1), B(-6, 2, 4) are the given points ‘o’ is the mid point of AB
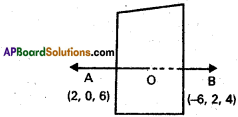
Co-ordinates of O are
\(\left(\frac{2-6}{2}, \frac{0+2}{2}, \frac{6+4}{2}\right)\) = (-2, 1, 5)
The plane is perpendicular to AB
d.r.’s of the normal to the plane are
2 + 6, 0 – 2, 6 – 4
8, -2, 2
Equation of the required plane is
+8 (x + 2) – 2(y – 1) + 2 (z – 5) = 0
8x + 16 – 2y + 2 + 2z – 10 = 0
8x – 2y + 2z + 8 = 0
Question 7.
Find the equation of the plane passing through (0, 0, -4) and perpendicular to the line joining the points (1, -2, 2) and (-3, 1, -2).
Solution:
A(1, -2, 2), B(-3, 1, -2) are the given points
d.r.’s of AB are 1 + 3, -2 -1, 2 + 2 i.e., 4, -3, 4
AB is normal to the plane and the plane passes through the point P(0, 0, -4).
Equation of the required plane is
4(x – 0) – 3(y – 0) + 4(z + 4) = 0
4x – 3y + 4z + 16 = 0
![]()
Question 8.
Find the equation of the plane through (4, 4, 0) and perpendicular to the planes 2x + y + 2 z + 3 = 0 and 3x + 3y + 2z – 8 = 0.
Solution:
Equation of the plane passing through P(4, 4, 0) is
a(x – 4) + b(y – 4) + c(z – 0) = 0 ………. (1)
This plane is perpendicular to
2x + y + 2z – 3 = 0
3x + 3y + 2z – 8 = 0
∴ 2a + b + 2c = 0 ………… (2)
3a + 3b + 2c = 0 ………….(3)
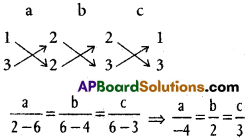
Substituting in (1), equation of the required plane is
-4 (x – 4) + 2(y – 4) + 3(z – 0) = 0
-4x + 16 + 2y – 8 + 3z = 0
-4x + 2y + 3z + 8 = 0
III.
Question 1.
Find the equation of the plane through the points (2, 2, -1), (3, 4, 2), (7, 0, 6).
Solution:
A(2, 2, -1), B(3, 4, 2), C(7, 0, 6) are the given points.
Equation of the plane passing through A(2, 2, -1) is
a(x – 2) + b(y – 2) + c(z + 1) = 0
This plane passes through B(3, 4, 2) and C(7, 0, 6)
a(3 – 2) + b(4 – 2) +c(2 + 1) = 0
a + 2b + 3c = 0 ……….. (2)
a(7 – 2) + b(0 – 2) + c(6 + 1) = 0
5a – 2b + 7c = 0 ……….. (3)
From (2) and (3)
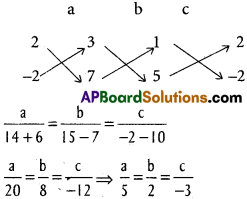
Substituting in (1) equation of the required plane is
5(x- 2) + 2(y- 2) – 3(z +1) = 0
5x – 10 + 2y – 4 – 3z – 3 = 0
5x + 2y – 3z -17 = 0 or 5x + 2y- 3z = 17
Question 2.
Show that the points (0, -1, 0), (2, 1, -1), (1, 1, 1), (3, 3, 0) are coplanar.
Solution:
Equation of the plane through A(0, -1, 0) is
ax + b(y + 1) + cz = 0 …….. (1)
This plane passes through B(2, 1, -1) and C(1, 1, 1)
2a + 2b – c = 0 …………. (2)
a + 2b + c = 0 ………….. (3)
(2) – (3) gives a – 2c = 0 ⇒ a = 2c ⇒ \(\frac{a}{2}=\frac{c}{1}\)
(2) + (3) gives 3a + 4b = 0 ⇒ 3a = – 4b
⇒ \(\frac{a}{4}=\frac{b}{-3}\)
∴ \(\frac{a}{4}=\frac{b}{-3}=\frac{c}{2}\)
Substitutes in (1) equation of the plane ABC is
4x – 3(y + 1) + 2(z – 0) = 0
4x – 3y + 2z – 3 = 0
4x – 3y + 2z – 3 = 4.3 – 3.3. + 0.3
= 12 – 9 – 3 = 0
The given points A, B, C, D are coplanar.
![]()
Question 3.
Find the equation of the plane through (6, – 4, 3), (0, 4, -3) and cutting of inter-cepts whose sum is zero.
Solution:
Suppose a, b, c are the intercepts of the plane.
Equation of the plane is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1
Given a + b + c = 0
c = – (a + b)
The plane passes through
P(6, -4, 3), Q(0, 4, -3)

c = -a – b = -3 – b
4(-3 – b) – 3b = b(-3 – b)
-12 – 4b – 3b = – 3b – b²
b² – 4b – 12 = 0
(b – 6) (b + 2) = 0 ⇒ b = 6 – 2
Case i) b = 6
c = -3 – b = -3 – 6 = -9
Equation of the plane is
\(\frac{x}{3}+\frac{y}{6}+\frac{z}{9}\) = 1
6x + 3y – 2z = 18
Case ii) b = -2
c = -3 – b = -3 + 2 = -1
Equation of the plane is
\(\frac{x}{3}+\frac{y}{-2}+\frac{z}{-1}\) = 1
Question 4.
A plane meets the co-ordinate axes in A, B, C. If the centroid of ∆ABC is (a, b, c). Show that the equation of the plane is
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1
Solution:
Suppose α, β, γ are the intercepts of the plane ABC.
Equation of the plane is the intercept form is
\(\frac{x}{\alpha}+\frac{y}{\beta}+\frac{z}{\gamma}=1\) ………… (1)
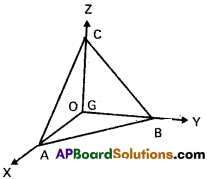
Co-ordinates of A are (α, 0, 0), B are (0, β, 0) and C are (0, 0, γ)
G is the centroid of ∆ABC
Co-ordinates of Gare =
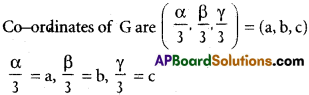
α = 3a, β = 3b, γ = 3c
Substituting in (1), equation of the plane ABC is
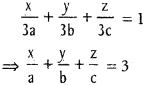
Question 5.
Show that the plane through (1, 1, 1) , (1, -1, 1) and (-7, -3, -5) is parallel . to Y-axis.
Solution:
Equation of the plane through A (1, 1, 1) can be taken as
a(x – 1) +b(y – 1) + c(z – 1) = 0 ……….. (1)
This plane passes through B(1, -1, 1) and C(-7, -3, -5)
0 – 2b + 0 = 0 ⇒ b – 0
Equation of zy – plane is y = 0
0.x + 1.y + 0.z = 0
a.0 + 0.1 + c.0 = 0
The required plane is perpendicular to zx – plane hence it is parallel to Y – axis.
![]()
Question 6.
Show that the equations ax + by + r =0, by + cz + p = 0, cz + ax + q = 0 represent planes perpendicular to xy,yz, zx planes respectively.
Solution:
Equation of the given plane is
ax + by + c = Q
d.rs of the normal are (a, b, c)
Equation of XY – plane is z = 0
d.rs of the normal are (0, 0, 1)
a.0 + b.0 + 0.1 = 0
∴ ax + by + r = 0 is perpendicular to xy – plane.
Similarly we can show that by + cz + p = 0 is perpendicular to yz – plane and cz + ax + q – 0 is perpendicular to zx – plane.