Inter 2nd Year Maths 2A Complex Numbers Important Questions

Students get through Maths 2A Important Questions Inter 2nd Year Maths 2A Complex Numbers Important Questions which are most likely to be asked in the exam.

Intermediate 2nd Year Maths 2A Complex Numbers Important Questions

Question 1.
If z₁ = -1, z₂ = i then find Arg \(\left(\frac{z_{1}}{z_{2}}\right)\) (AP Mar. 17) (TS Mar.’ 16; May ‘11)
Solution:
Z₁ = -1 = cos π + i sin π
⇒ Arg z₁ = π
z₂ = i = cos \(\frac{\pi}{2}\) + i sin \(\frac{\pi}{2}\)
⇒ Arg z₂ = \(\frac{\pi}{2}\)
⇒ Arg \(\left(\frac{z_{1}}{z_{2}}\right)\) = Arg z₁ – Arg z₂ = π – \(\frac{\pi}{2}\).
= \(\frac{\pi}{2}\)

Question 2.
If z = 2 – 3i, show that z² – 4z + 13 = 0. (Mar. ‘08)
Solution:
∴ z = 2 – 3i
⇒ z – 2 = -3i
⇒ (z – 2)² = (-3i)²
⇒ z² – 4z + 4 = 9i²
⇒ z² – 4z + 4 = 9(-1)
⇒ z² – 4z + 13 = 0

Question 3.
Find the multiplicative inverse of 7 + 24i. (TS Mar. 16)
Solution:
Since (x + iy)\(\left[\frac{x-i y}{x^{2}+y^{2}}\right]\) = 1, it follows that the multiplicative inverse of (x + iy) is \(\frac{x-i y}{x^{2}+y^{2}}\)
Hence the multiplicative inverse of 7 + 24i is

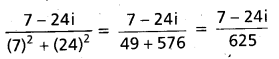
Question 4.
Write the following complex numbers in the form A + iB. (2 – 3i) (3 + 4i)  (AP Mar. ’17)
Solution:
(2 – 3i) (3 + 4i) = 6 + 8i – 9i – 12i²
= 6 – i + 12
= 18 – i = 18 + i(-1)

Question 5.
Write the following complex numbers in the form A + iB. (1 + 2i)³ (TS Mar. ’17)
Solution:
(1 + 2i)³ = 1 + 3.i².2i + 3.1. 4i² + 8i³
= 1 + 6i – 12 – 8i
= -11 – 2i = (-11) + i(-2)

Question 6.
Write the conjugate of the following complex number \(\frac{5 i}{7+i}\) (AP Mar. ’15)
Solution:

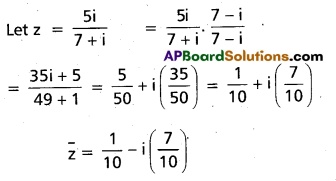
Question 7.
Find a square root for the complex number 7 + 24i. (Mar. ‘14)
Solution:
7 + 24i

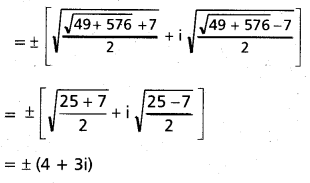
Question 8.
Find a square root for the complex number 3 + 4i  (Mar. ’13)
Solution:

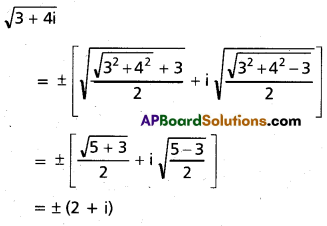
Question 9.
Express the following complex numbers in modulus amplitude form. 1 – i (AP Mar. 15)
Solution:
1 – i
Let 1 – i = r (cos θ + i sin θ)
Equating real and imaginary parts
r cos θ = 1
r sin θ = -1
⇒ θ lies in IV quadrant .
Squaring and adding
r² (cos² θ + sin² θ) = 1 + 1 = 2
r² = 2 ⇒ r = \(\sqrt{2}\)
tan θ = -1
⇒ θ = -π/4

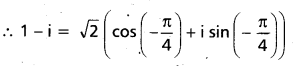
Question 10.
Express the complex numbers in modulus — amplitude form 1 + i\(\sqrt{3}\) (TS Mar. ’17)
Solution:
1 + i\(\sqrt{3}\) = r (cos θ + i sin θ)
Equating real and imaginary parts
r cos θ = 1 —– (1)
r sin θ = \(\sqrt{3}\) —– (2)
θ lies in I quadrant
Squaring and adding (1) and (2)
r² (cos² θ – sin² θ) = 1 + 3
r² = 4 ⇒ r = 2
Dividing (2) by (1)

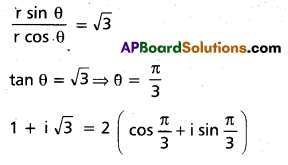
Question 11.
If the Arg \(\overline{\mathbf{z}}_{1}\) and Arg \(z_{2}\) are \(\frac{\pi}{5}\) and \(\frac{\pi}{3}\) respectively, find (Arg z₁ + Arg z₂) (AP Mar. ’16)
Solution:
Arg \(\overline{\mathbf{z}}_{1}\) = \(\frac{\pi}{5}\) ⇒ Arg z₁ = – Arg z₁ = – \(\frac{\pi}{5}\)
Arg z₂ = \(\frac{\pi}{3}\)
∴ Arg z₁ + Arg z₂ = – \(\frac{\pi}{5}\) + \(\frac{\pi}{3}\)
= \(\frac{-3 \pi+5 \pi}{15}\) = \(\frac{2 \pi}{15}\)

Question 12.
If |z – 3 + i| = 4 determine the locus of z. (May. ’14)
Solution:
Let z = x + iy
Given |z – 3 + i| = 4
|x + iy – 3 + i| = 4
⇒ (x – 3) + i(y + 1) = 4
⇒ \(\sqrt{(x-3)^{2}+(y+1)^{2}}\) = 4
⇒ (x – 3)² + (y + 1)² = 16
⇒ x² – 6x + 9 + y² + 2y + 1 = 16
⇒ x² + y² – 6x + 2y – 6 = 0
∴ The locus õf z is x² + y² – 6x + 2y – 6 = 0

Question 13.
The points P, Q denote the complex numbers z₁, z₂ in the Argand diagram. O is the origin. If z₁z₂ + z₂z₁ = 0, show that POQ = 90°. (Mar. ‘07)
Solution:
Let z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂

Question 14.
Find the real and imaginary parts of the complex number \(\frac{a+i b}{a-i b}\). (TS Mar. 15)
Solution:

Question 15.
Write z = –\(\sqrt{7}\) + i\(\sqrt{21}\) in the polar form. (Mar. ’11)
Solution:

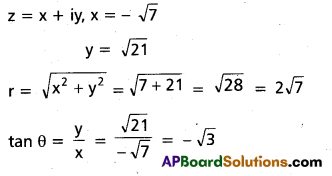
Since the given point lies in the second quadrant we look for a solution of tan θ = –\(\sqrt{3}\) that lies in \(\left[\frac{\pi}{2}, \pi\right]\), we find that θ = \(\frac{2 \pi}{3}\) is such a solution.

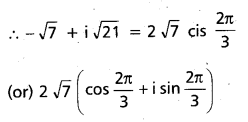
Question 16.
z = x + iy and the point P represents z in the Argand plane and \(\left|\frac{z-a}{z+\bar{a}}\right|\) = 1, Re (a) ≠ 0, then find the locus of P. (TS Mar. ’17)
Solution:
Let z = x + iy and a = α + iβ

Locus of P is x = 0 i.e., Y – axis

Question 17.
If x + iy = \(\frac{1}{1+\cos \theta+i \sin \theta}\), show that 4x² – 1 = 0 (AP Mar. ’16, TS Mar. ’17, ’15, ’06 )
Solution:

Equating real parts on both sides, we have
x = \(\frac{1}{2}\)
2x = 1
⇒ 4x² = 1
4x² – 1 = 0

Question 18.
If (\(\sqrt{3}\) + 1)¹⁰⁰ = 2⁹⁹ (a + ib), then show that a² + b² = 4. (AP Mar. ‘16)
Solution:

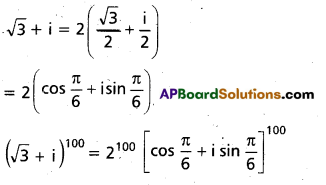
Question 19.
Show that the points in the Argand diagram represented by the complex numbers 2 + 2i, -2 – 2i, 2\(\sqrt{3}\) + 2\(\sqrt{3}\)i are the vertices of an equilateral triangle. (Mar ‘07)
Solution:
A (2, 2), B (-2, -2), C (-2\(\sqrt{3}\), 2\(\sqrt{3}\)) represents the given complex number in the Argand diagram.

Question 20.
Show that the points in the Argand plane represented by the complex numbers -2 + 7i, –\(\frac{3}{2}\), +\(\frac{1}{2}\)i, 4 – 3i, \(\frac{7}{2}\)(1 + i) are the vertices of a rhombus. (June 04) (TS Mar. ’16; AP Mar.’15 ’05; May ’05)
Solution:
A(-2, 7), B(-\(\frac{3}{2}\), \(\frac{1}{2}\)), C(4, -3), D(\(\frac{7}{2}\), \(\frac{7}{2}\)) represents the given complex numbers in the Argand diagram.


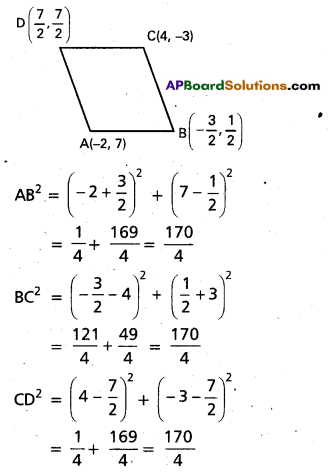
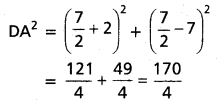
∴ AB² = BC² = CD² = DA²
⇒ AB = BC = CD = DA
AC² = (-2 – 4)² + (7 + 3)²
= 36 +100 = 136
(BD)² = (-\(\frac{3}{2}\) – \(\frac{7}{2}\))² + (\(\frac{1}{2}\) – \(\frac{7}{2}\))²
= 25 + 9 = 34
AC ≠ BD
A, B, C, D are the vertices of a Rhombus.

Question 21.
Show that the points in the Argand diagram represented by the complex numbers z₁, z₂, z₃ are collinear, if and only if there exists three real numbers p, q, r not all zero, satisfying pz₁ + qz₂ + rz₃ = 0 and p + q + r = 0. (Mar. ‘07)
Solution:
pz₁ + qz₂ + rz₃ = 0
⇔ rz₃ = -pz₁ – qz₂
⇔ z₃ = \(\frac{-p z_{1}-q z_{2}}{r}\) ∵ r ≠ 0
∵ p + q + r = 0
⇔ r = -p – q
⇔ z₃ = \(-\frac{\left(p z_{1}+q z_{2}\right)}{-(p+q)}\)
⇔ z₃ = \(\frac{p z_{1}+q z_{2}}{p+q}\)
⇔ z₃ = \(\frac{p z_{1}+q z_{2}}{p+q}\)
⇔ z₃ divides line segment joining z₁, z₂ in the ratio q : p
⇔ z₁, z₂, z₃ are collinear

Question 22.
If the amplitude of \(\left(\frac{z-2}{z-6 i}\right) \frac{\pi}{2}\), find its locus. (Mar. ’06)
Solution:
Let z = (x + iy)

Hence a = 0 and b > 0
∴ x(x – 2) + y(y – 6) = 0
or x² + y² – 2x – 6y = 0.

Question 23.
If x + iy = \(\frac{3}{2+\cos \theta+i \sin \theta}\) then show that x² + y² = 4x – 3 (TS Mar ’17)
Solution:

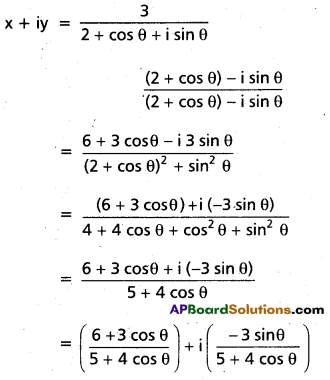
Equating real and imaginary parts on both sides, we have

Question 24.
Express \(\frac{4+2 i}{1-2 i}\) + \(\frac{3+4 i}{2+3 i}\) in the form a + ib, a ∈ R, b ∈ R.
Solution:

Question 25.
Find the real and imaginary parts of the complex number \(\frac{a+i b}{a-i b}\) (TS Mar ’15)
Solution:

Question 26.
Express (1 – 3)³ (1 + i) in the form of a + ib.
Solution:
(1 – i)³ (1 + j) = (1 – j)² (1 – i) (1 + j)
= (1 + i² – 2i) (1² – i²)
= (1 – 1 – 2i) (1 + 1)
= 0 – 4i = 0 + i (-4)

Question 27.
Find the multiplicative inverse of 7 + 24i.  (TS. Mar. ’16 )
Solution:
Since (x + iy)\(\left[\frac{x-i y}{x^{2}+y^{2}}\right]\) = 1, it follows that the multiplicative inverse of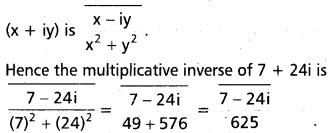

Question 28.
Determine the locus of z, z ≠ 2i, such that Re\(\left(\frac{z-4}{z-2 i}\right)\) = 0
Solution:
Let z = x + iy

Hence the locus of the given point representing the complex number is the circle with (2, 1) as centre and \(\sqrt{5}\) units as radius, excluding the point (0, 2).

Question 29.
If 4x + i (3x – y) = 3 -6i where x and y are real numbers, then find the values of x and y.
Solution:
∵ 4x + i(3x – y) = 3 – 6i
Equating real and imaginary parts, we get 4x = 3 and 3x – y = -6
4x = 3 and 3x – y = -6
⇒ x = 3/4 and 3\(\left(\frac{3}{4}\right)\) – y = -6
\(\frac{9}{4}\) + 6 = y
⇒ y = \(\frac{33}{4}\)
∴ x = \(\frac{3}{4}\) and y = \(\frac{33}{4}\)

Question 30.
If z = 2 – 3i, show that z² – 4z + 13 = 0. (Mar. ’08)
Solution:
∴ z = 2 – 3i
⇒ z – 2 = – 3i
⇒ (z – 2)² = (-3i)²
⇒ z² – 4z + 4 = 9i²
⇒ z² – 4z + 13 = 0
⇒ z² – 4z + 4 = 9

Question 31.
Find the complex conjugate of (3 + 4i) (2 – 3i).
Solution:
The given complex number is
(3 + 4i) (2 – 3i) = 6 + 8i – 9i – 12i²
= 6 – i – 12(-1) = 18 + i
Its complex conjugate is 18 + i

Question 32.
Show that z₁ = \(\frac{2+11 i}{25}\), z₂ = \(\frac{-2+i}{(1-2 i)^{2}}\), are conjugate to each other.
Solution:

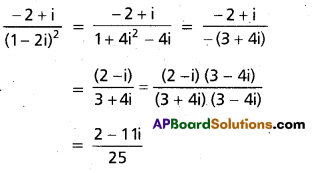
Since, this complex number is the conjugate of \(\frac{2+11 i}{25}\), the two given complex numbers
are conjugate to each other.

Question 33.
Find the square root of (-5 + 12i).
Solution:
We have \(\sqrt{a+i b}\) =

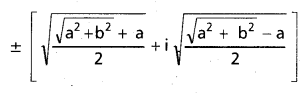
In this example a = -5, b = 12

Question 34.
Write z = –\(\sqrt{7}\) + i\(\sqrt{21}\) in the polar form. (Mar ’11)
Solution:

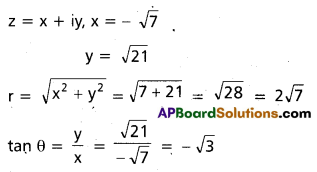
Since the given point lies in the second quadrant we look for a solution of
tan θ = – \(\sqrt{3}\) that lies in [\(\frac{\pi}{2}\), π] we find that θ = \(\frac{2 \pi}{3}\) is such a solution.
∴ –\(\sqrt{7}\) + i\(\sqrt{21}\) = 2\(\sqrt{7}\) cis \(\frac{2 \pi}{3}\)
(or) 2\(\sqrt{7}\)(cos \(\frac{2 \pi}{3}\) + i sin \(\frac{2 \pi}{3}\))

Question 35.
Express -1 – i in polar form with principle value of the amplitude.
Solution:
Let -1 – i = r (cos θ + i sin θ), then
-1 = r cos θ, -1 = r sin θ, tan θ = 1 ——— (1)
∴ r² = 2
⇒ r = ±\(\sqrt{2}\)
Since θ is positive, -π < θ < π, the value θ satisfying the equation (1) is
θ = -135° = \(\frac{-3 \pi}{4}\)

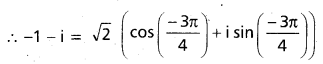
Question 36.
If the amplitude of \(\left(\frac{z-2}{z-6 i}\right) \frac{\pi}{2}\), find its locus.  (Mar. ’06)
Solution:

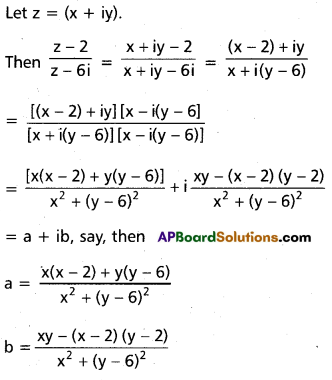
By hypothesis, amplitude of a + ib = \(\frac{\pi}{2}\)
So \(\frac{\pi}{2}\) = tan^-1 \(\frac{b}{a}\)
Hence a = 0 and b > 0
∴ x(x – 2) + y(y – 6) = 0
or x² + y² – 2x – 6y = 0.

Question 37.
Show that the equation of any circle in the complex plane is of the form z\(\overline{\mathbf{z}}\) + b\(\overline{\mathbf{z}}\) + b\(\overline{\mathbf{z}}\) + c = 0, 1(b ∈ C, c ∈ R).
Solution:
Assume the general form of the equation of a circle in cartesian co-ordinates as
x² + y² + 2gx + 2fy + c = 0, (g, f ∈ R) —— (1)
To write this equation in the complex variable form, let (x, y) = z.
Then \(\frac{z+\bar{z}}{2}\) = x, \(\frac{z-\bar{z}}{2 i}\)
= y = \(\frac{-i(z-\bar{z})}{2}\)
∴ x² + y² = |z|² = z\(\overline{\mathbf{z}}\)
Substituting these results in equation (1), we obtain
z\(\overline{\mathbf{z}}\) + g(z + \(\overline{\mathbf{z}}\)) + f(z – \(\overline{\mathbf{z}}\))(-i) + c = 0
i.e., z\(\overline{\mathbf{z}}\) + (g – if)z + (g + if)\(\overline{\mathbf{z}}\) + c = 0 ——-(2)
If (g + if) = b, then equation (2) can be written as z\(\overline{\mathbf{z}}\) + \(\overline{\mathbf{b}}\)z + b\(\overline{\mathbf{z}}\) + c = 0

Question 38.
Show that the complex numbers z satisfying z² + \((\overline{\mathbf{z}})^{2}\) = 2 constitute a hyperbola.
Solution:
Substituting z = x + iy in the given equation
z² + (\(\overline{\mathbf{z}}\))² = 2, we obtain the cartesian form of the given equation.
∴ (x + iy)² + (x – iy)² = 2
i.e., x² – y² + 2ixy + x² – y² – 2ixy = 2
i.e., x² – y² = 1.
Since, this equation denotes a hyperbola, all the complex numbers satisfying

lie on the hyperbola x² – y² = 1.

Question 39.
Show that the points in the Argand diagram represented by the complex numbers 1 + 3i, 4 – 3i, 5 – 5i are collinear.
Solution:
Let the three complex numbers be represented in the Argand plane by the points P, Q, R respectively. Then P = (1, 3), Q = (4, -3), R = (5, -5). The slope of the line segment joining P,Q is \(\frac{3+3}{1-4}\) = \(\frac{6}{-3}\) = -2.
Similarly the slope of the line segment joining Q, R is \(\frac{-3+5}{4-5}\) = \(\frac{2}{-1}\) = -2.
Since the slope of PQ is the slope of QR, the points P, Q and R are collinear.

Question 40.
Find the equation of the straight line joining the points represented by (- 4 + 3i), (2 – 3i) in the Argand plane.
Solution:
Take the given points as
A = -4 + 3i = (-4, 3)
B = 2 – 3i = (2, -3)
Then equation of the straight line \(\overleftrightarrow{\mathrm{AB}}\) is
y – 3 = \(\frac{3+3}{-4-2}\)(x + 4)
i.e., x + y + 1 = 0.

Question 41.
z = x + iy represents a point in the Argand plane, find the locus of z. Such that |z| = 2.
Solution:
|z| = 2, z = x + iy
if \(\sqrt{x^{2}+y^{2}}\) = 2
if \(\sqrt{x^{2}+y^{2}}\) = 2
if and only if x² + y² = 4
The equation x² + y² = 4 represents the circle with centre at the origin (0, 0) and radius 2 units.
∴ The locus of |z| = 2 is the circle
x² + y² = 4

Question 42.
The point P represents a complex number z in the Argand plane. If the amplitude of z is \(\frac{\pi}{4}\), determine the locus of P.
Solution:
Let z = x + iy.
By hypothesis, amplitude of z = \(\frac{\pi}{4}\)
Hence tan^-1 \(\left(\frac{y}{x}\right)\) = \(\frac{\pi}{4}\) and \(\frac{y}{x}\) = tan \(\frac{\pi}{4}\)
Hence x = y
∴ The locus of P is x = y.

Question 43.
If the point P denotes the complex number z = x + iy in the Argand plane and if \(\frac{z-i}{z-1}\) is a purely imaginary number, find the locus of P.
Solution:
We note that the quotient \(\frac{z-i}{z-1}\) is not defined if z = 1.

∴ The locus of P is the circle
x² + y² – x – y = 0
excluding the point (1, 0).

Question 44.
Describe geometrically the following subsets of C.
i) {z ∈ C| |z – 1 + i| = 1}
ii) {z ∈ C| |z + i| ≤ 3|
Solution:
i) Let S = {z ∈ C| z – 1 + i| = 1}
If we write z = (x, y), then
S = {(x, y) ∈ R²||x + iy – 1 + i| = 1}
= {x, y) ∈ R² || x + i(y – 1)| ≤ 3}
= {(x, y) ∈ R² || (x – 1)² + (y + 1)² = i}
Hence S is a circle with centre (1, -1) and radius 1 unit.

ii) Let S’ = {z ∈ C || z + i| ≤ 3}
Then S = {(x, y ∈ R² || x + iy + i| ≤ 3}
= {(x, y) ∈ R² || x² + i(y + 1) ≤ 3}
= {(x, y) ∈ R² || x² + (y + 1)² ≤ 9}
Hence S’ is the closed circular disc with centre at (0, -1) and radius 3 units.