Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Complex Numbers Solutions Exercise 1(d) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A Complex Numbers Solutions Exercise 1(d)
I.
Question 1.
(i) Find the equation of the perpendicular bisector of the line segment joining the points 7 + 7i, 7 – 7i in the Argand diagram.
Solution:
A(7, 7); B(7, -7) represents the given complex numbers in the Argand diagram.
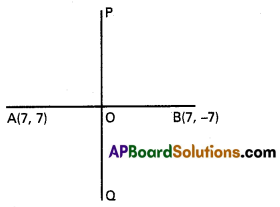
O is the mid-point of AB.
Co-ordinates of O are \(\left(\frac{7+7}{2}, \frac{7-7}{2}\right)\) = (7, 0)
Slope of \(\overleftrightarrow{\mathrm{AB}}=\frac{7+7}{7-7}=\frac{14}{0}\) = ∞
AB is parallel to Y-axis
PQ is perpendicular to AB
PQ is parallel to X-axis
Slope of PQ = 0
Equation of PQ is y – 0 = 0(x – 7)
i.e., y = 0
(ii) Find the equation of the straight line joining the point -9 + 6i, 11 – 4i in the Argand plane.
Solution:
Given points are -9 + 6i, 11 – 4i
Let A = (-9, 6); B = (11, -4)
Equation of the straight line AB is y – 6 = \(\frac{-4-6}{11+9}\) (x + 9)
⇒ y – 6 = \(\frac{-1}{2}\) (x + 9)
⇒ 2y – 12 = -x – 9
⇒ x + 2y – 3 = 0
![]()
Question 2.
If Z = x + iy and if the point P in the Argand plane represents Z, then describe geometrically the locus of z satisfying the equation.
(i) |z – 2 – 3i| = 5
(ii) 2|z – 2| = |z – 1|
(iii) Img z2 = 4
(iv) \({Arg}\left(\frac{z-1}{z+1}\right)=\frac{\pi}{4}\)
Solution:
(i) z = x + iy and |z – 2 – 3i| = 5
|z – 2 – 3i| = 5
⇒ |x + iy – 2 – 3i| = 5
⇒ |(x – 2) + i(y – 3)| = 5
⇒ \(\sqrt{(x-2)^{2}+(y-3)^{2}}\) = 5
⇒ (x – 2)2 + (y – 3)2 = 25
⇒ x2 – 4x + 4 + y2 – 6y + 9 = 25
∴ Locus of P is x2 + y2 – 4x – 6y – 12 = 0
(ii) 2|z – 2| = |z – 1|
2|x + iy – 2| = |x + iy – 1|
⇒ 2|(x – 2) + iy| = |(x – 1) + iy|
⇒ \(2 \sqrt{(x-2)^{2}+y^{2}}=\sqrt{(x-1)^{2}+y^{2}}\)
Squaring both sides
⇒ 4[(x – 2)2 + y2] = (x – 1)2 + y2
⇒ 4(x2 – 4x + 4 + y2) = x2 – 2x + 1 + y2
⇒ 4x2 + 4y2 – 16x + 16 = x2 + y2 – 2x + 1
∴ Locus of P is 3x2 + 3y2 – 14x + 15 = 0
(iii) Img z2 = 4
∵ z = x + iy
⇒ z2 = (x + iy)2
⇒ z2 = x2 + i2y2 + 2ixy
⇒ z2 = (x2 – y2) + i(2xy)
∴ Img (z2) = 2xy = 4
∴ The locus of P is xy = 2
(iv) \({Arg}\left(\frac{z-1}{z+1}\right)=\frac{\pi}{4}\)

Since \({Arg}\left(\frac{z-1}{z+1}\right)=\frac{\pi}{4}\)
∴ \(\frac{2 y}{x^{2}+y^{2}-1}=\tan \frac{\pi}{4}\)
⇒ 2y = x2 + y2 – 1
⇒ x2 + y2 – 2y – 1 = 0
∴ The locus of z is x2 + y2 – 2y – 1 = 0.
![]()
Question 3.
Show that the points in the Argand diagram represented by the complex numbers 2 + 2i, -2 – 2i, 2√3 + 2√3 i are the vertices of an equilateral triangle.
Solution:
A(2, 2), B(-2, -2), C(-2√3, 2√3) represent the given complex number in the Argand diagram.
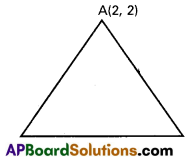
AB2 = (2 + 2)2 + (2 + 2)2
= 16 + 16
= 32
BC2 = (-2 + 2√3)2 + (-2 – 2√3)2
= 4 + 12 – 8√3 + 4 + 12 + 8√3
= 32
AC2 = (-2√3 – 2)2 + (2√3 – 2)2
= 12 + 4 + 8√3 + 12 + 4 – 8√3
= 32
AB2 = BC2 = AC2
⇒ AB = BC = CA
∴ ∆ABC is an Equilateral triangle.
![]()
Question 4.
Find the eccentricity of the ellipse whose equation is |z – 4| + |z – \(\frac{12}{5}\)| = 10
Solution:
SP + S’P = 2a
S = (4, 0), S’ = (\(\frac{12}{5}\), 0)
2a = 10 ⇒ a = 5
SS’ = 2ae
⇒ 4 – \(\frac{12}{5}\) = 2 × 5e
⇒ \(\frac{8}{5}\) = 10e
⇒ e = \(\frac{4}{25}\)
II.
Question 1.
If \(\frac{z_{3}-z_{1}}{z_{2}-z_{1}}\) is a real number, show that the points represented by the complex numbers z1, z2, z3 are collinear.
Solution:
Let z1 = x1 + iy1; z2 = x2 + iy2; z3 = x3 + iy3
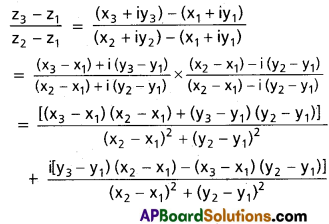
Given \(\frac{z_{3}-z_{1}}{z_{2}-z_{1}}\) is a real number.
Imaginary part = 0
⇒ (y3 – y1) (x2 – x1) – (x3 – x1) (y2 – y1) = 0
⇒ (y3 – y1) (x2 – x1) = (x3 – x1) (y2 – y1)
⇒ \(\frac{y_{3}-y_{1}}{x_{3}-x_{1}}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
The points A(x1, y1), B(x2, y2), C(x3, y3) represents the complex numbers z1, z2, z3 respectively.
Slope of \(\stackrel{\leftrightarrow}{\mathrm{AC}}\) = Slope of \(\stackrel{\leftrightarrow}{\mathrm{AB}}\)
∴ A, B, C are collinear.
Question 2.
Show that the points in the Argand plane represented by the complex numbers 2 + i, 4 + 3i, 2 + 5i, 3i are the vertices of a square.
Solution:
A(2, 1), B(4, 3) C(2, 5), D(0, 3) represent the given complex number in the Argand plane

AB2 = (2 – 4)2 + (1 – 3)2 = 4 + 4 = 8
BC2 = (4 – 2)2 + (3 – 5)2 = 4 + 4 = 8
CD2 = (2 – 0)2 + (5 – 3)2 = 4 + 4 = 8
DA2 = (0 – 2)2 + (3 – 1)2 = 4 + 4 = 8
AB2 = BC2 = CD2 = DA2
⇒ AB = BC = CD = DA ………(1)
AC2 = (2 – 2)2 + (1 – 5)2 = 0 + 16 = 16
BD2 = (4 – 0)2 + (3 – 3)2 = 16 + 0 = 16
AC2 = BD2
⇒ AC = BD …….(2)
By (1), (2)
A, B, C, D are the vertices of a square.
![]()
Question 3.
Show that the points in the Argand plane represented by the complex numbers -2 + 7i, \(-\frac{3}{2}+\frac{1}{2} i\), 4 – 3i, \(\frac{7}{2}\)(1 + i) are the vertices of a rhombus.
Solution:
A(-2, 7), B(\(-\frac{3}{2}\), \(\frac{1}{2}\)), C(4, -3), D(\(\frac{7}{2}\), \(\frac{7}{2}\)) represents the given complex numbers in the Argand diagram.
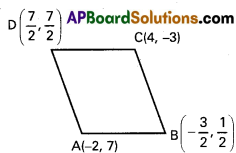
∴ AB2 = BC2 = CD2 = DA2
⇒ AB = BC = CD = DA ……….(1)
AC2 = (-2 – 4)2 + (7 + 3)2
= 36 + 100
= 136
BD2 = \(\left(-\frac{3}{2}-\frac{7}{2}\right)^{2}+\left(\frac{1}{2}-\frac{7}{2}\right)^{2}\)
= 25 + 9
= 34
AC ≠ BD ……..(2)
∴ A, B, C, D are the vertices of a Rhombus.
Question 4.
Show that the points in the Argand diagram represented by the complex numbers z1, z2, z3 are collinear, if and only if there exist three real numbers p, q, r not all zero, satisfying pz1 + qz2 + rz3 = 0 and p + q + r = 0.
Solution:
pz1 + qz2 + rz3 = 0
⇔ rz3 = -pz1 – qz2
⇔ z3 = \(\frac{-p z_{1}-q z_{2}}{r}\) [∵ r ≠ 0]
∵ p + q + r = 0
⇔ r = -p – q
⇔ z3 = \(-\frac{\left(p z_{1}+q z_{2}\right)}{-(p+q)}\)
⇔ z3 = \(\frac{p z_{1}+q z_{2}}{p+q}\)
⇔ z3 divides the line segment joining z1, z2 in the ratio q : p
⇔ z1, z2, z3 are collinear
![]()
Question 5.
The points P, Q denotes the complex numbers z1, z2 in the Argand diagram. O is the origin. If \(\bar{z}_{1} \bar{z}_{2}+\bar{z}_{2} \bar{z}_{1}=0\), show that POQ = 90°.
Solution:
Let z1 = x1 + iy1 and z2 = x2 + iy2
Then P(x1, y1), Q(x2, y2), O(0, 0)
\(\overline{\mathbf{z}}_{1}\) = x1 – iy1, \(\overline{\mathbf{z}}_{2}\) = x2 – iy2
\(\bar{z}_{1} \bar{z}_{2}+\bar{z}_{2} \bar{z}_{1}\) = (x1 + iy1) (x2 – iy2) + (x2 + iy2) (x1 – iy1) = 0
⇒ x1x2 + y1y2 – ix1y2 + ix2y1 + x1x2 + y1y2 – ix2y1 + ix1y2 = 0
⇒ 2(x1x2 + y1y2) = 0
⇒ x1x2 + y1y2 = 0
⇒ x1x2 = -y1y2
⇒ \(\left(\frac{-x_{1}}{y_{1}}\right)\left(-\frac{x_{2}}{y_{2}}\right)=-1\)
Slope of OP × Slope of OQ = -1
∴ OP, OQ are perpendicular
⇒ ∠POQ = 90°
Question 6.
The complex number z has argument θ, 0 < θ < \(\frac{\pi}{2}\) and satisfy the equation |z – 3i| = 3. Then prove that (cot θ – \(\frac{6}{z}\)) = i
Solution:
Let z = cos θ + i sin θ
Given |z – 3i| = 3.
⇒ |(cos θ + i sin θ) – 3i| = 3
⇒ |cos θ + i(sin θ – 3)| = 3
⇒ \(\sqrt{\cos ^{2} \theta+(\sin \theta-3)^{2}}\) = 3
⇒ cos2θ + sin2θ – 6 sin θ + 9 = 9
⇒ 1 – 6 sin θ = 0
⇒ 6 sin θ = 1
⇒ sin θ = \(\frac{1}{6}\)
since 0 < θ < \(\frac{\pi}{2}\)
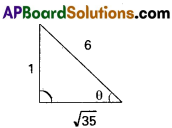
∴ cos θ = \(\frac{\sqrt{35}}{6}\)
cot θ = √35
∴ cot θ – \(\frac{6}{z}\) = cot θ – \(\frac{6}{\cos \theta+i \sin \theta}\)
= cot θ – 6(cos θ – i sin θ)
= √35 – 6\(\left[\frac{\sqrt{35}}{6}-i \cdot \frac{1}{6}\right]\)
= √35 – √35 + i
= i
Hence cot θ – \(\frac{6}{z}\) = i