Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Permutations and Combinations Solutions Exercise 5(b) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A Permutations and Combinations Solutions Exercise 5(b)
I.
Question 1.
Find the number of 4-digited numbers that can be formed using the digits 1, 2, 4, 5, 7, 8 when repetition is allowed.
Solution:
The number of 4 digited numbers that can be formed using the digits 1, 2, 4, 5, 7, 8 when repetition is allowed = 64 = 1296
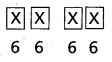
Question 2.
Find the number of 5-letter words that can be formed using the letters of the word RHYME if each letter can be used any number of times.
Solution:
The number of 5 letter words that can be formed using the letters of the word RHYME if each letter can be used any number of times = 55 = 3125
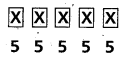
![]()
Question 3.
Find the number of functions from a set A containing 5 elements into a set B containing 4 elements.
Solution:
Set A contains 5 elements.
Set 8 contains 4 elements.
Hint: The total number of functions from set A containing m elements to set B containing n elements is nm.
For the image of each of the 5 elements of the set, A has 4 choices.
∴ The number of functions from set A containing 5 elements into a set B containing 4 elements = 4 × 4 × 4 × 4 × 4 (5 times)
= 45
= 1024
II.
Question 1.
Find the number of palindromes with 6 digits that can be formed using the digits
(i) 0, 2, 4, 6, 8
(iii) 1, 3, 5, 7, 9
Solution:
Palindromes mean first digit, sixth digit and second digit, fifth digit and third digit, and the fourth digit are the same numbers.
That is we have filled the first three digits only and then the remaining digits are the same.
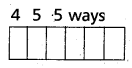
(i) Given numbers are 0, 2, 4, 6, 8
For the required 6-digit palindromes first digit can be filled 4 ways except ‘0’.
The second digit can be filled in 5 ways and the third can be filled in 5 ways.
∴ The number of 6-digit palindromes using the digits 0, 2, 4, 6, 8 are 4 × 52 = 100
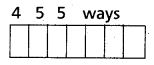
(ii) Given numbers are 1, 3, 5, 7, 9
For the required 6-digit palindromes first digit can be filled in 5 ways, the second digit can be filled in 5 ways and the third digit can be filled in 5 ways.
∴ The number of 6-digit palindromes using the digits 1, 3, 5, 7, 9 are 53 = 125
Question 2.
Find the number of 4-digit telephone numbers that can be formed using the digits 1, 2, 3, 4, 5, 6 with atleast one digit repeated.
Solution:
The number of 4 digited numbers formed using the digits 1, 2, 3, 4, 5, 6 when repetition is allowed = 64
The number of 4 digited numbers formed using the digits 1, 2, 3, 4, 5, 6 when repetition is not allowed = 6P4
The number of 4 digited telephone numbers in which atleast one digit is repeated = 64 – 6P4
= 64 – 6 × 5 × 4 × 3
= 1296 – 360
= 936
![]()
Question 3.
Find the number of bijections from a set A containing 7 elements onto itself.
Solution:
Hint: The number of bijections from set A with n elements to set B with the same number of elements in A is n!
Let A = [a1, a2, a3, a4, a5, a6, a7]
For a bijection, the element a1 has 7 choices
for its image, the element a2 has 6 choices
for its image, the element a3 has 5 choices
for its image, the element a4 has 4 choices
for its image, the element a5 has 3 choices
for its image, the element a6 has 2 choices
for its image and the element, a7 has 1 choice for its image.
∴ The number of bijections from set A with 7 elements onto itself = 7!
= 7 × 6 × 5 × 4 × 3 × 2 × 1
= 5040
Question 4.
Find the number of ways of arranging ‘r’ things in a line using the given ‘n’ different things in which atleast one thing is repeated.
Solution:
The number of ways of arranging, r things in a line using the given n different things
(i) when repetition is allowed is nr
(ii) when repetition is not allowed is nPr
∴ The number of ways of arranging ‘r’ things in a line using the ‘n1 different things in which atleast one thing is repeated = nr – nPr
Question 5.
Find the number of 5-letter words that can be formed using the letters of the word NATURE that begin with N when repetition is allowed.
Solution:
First, we can fill up the first place with N in one way.
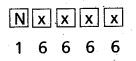
The remaining 4 places can be filled with any one of the 6 letters in 6 × 6 × 6 × 6 = 64 ways.
∴ The number of 5 letter words that can be formed using the letters of the word NATURE that begin with N when repetition is allowed = 1 × 64 = 1296
![]()
Question 6.
Find the number of 5-digit numbers divisible by 5 that can be formed using the digits 0, 1, 2, 3, 4, 5 when repetition is allowed.
Solution:
The unit place of 5 digited numbers which can be divisible by 5 using the given digits can be filled by either 0 or 5 in two ways.
The first place can be filled in any one of the given digits except ‘0’ in 5 ways.
The remaining 3 places can be filled by any one of the given digits in 6 × 6 × 6 ways (∵ repetition is allowed)
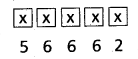
∴ The number of 5 digited numbers divisible by 5 that can be formed using the given digits when repetition is allowed = 2 × 5 × 6 × 6 × 6 = 2160 ways.
Question 7.
Find the number of numbers less than 2000 that can be formed using the digits, 1, 2, 3, 4 if repetition is allowed.
Solution:
All the single digited numbers, two digited numbers, three digited numbers and the four digited numbers started with 1 are the numbers less than 2000 using the digits 1, 2, 3, 4.
The number of single digited numbers formed using the given digits = 4
![]()
The number of two digited numbers formed using the given digits when repetition is allowed = 4 × 4 = 16
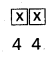
The number of three digited numbers formed using the given digits = 4 × 4 × 4 = 64
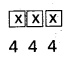
The number of 4 digited numbers started with 1 formed using the given digits = 4 × 4 × 4 = 64
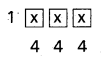
∴ The total number of numbers less than 2000 that can be formed using the digits 1, 2, 3, 4 if repetition is allowed = 4 + 16 + 64 + 64 = 148
III.
Question 1.
9 different letters of an alphabet are given. Find the number of 4 letter words that can be formed using these 9 letters which have
(i) no letter is repeated
(ii) At atleast one letter is repeated
Solution:
The number of 4 letter words can be formed using the 9 different letters of an alphabet when repetition is allowed = 94
(i) The number of 4 letter words can be formed using the 9 different letters of an alphabet in which no letter is repeated = 9P4
= 9 × 8 × 7 × 6
= 3024
(ii) The number of 4 letter words can be formed using the 9 different letters of an alphabet in which atleast one letter is repeated = 94 – 9P4
= 6561 – 3024
= 3537
![]()
Question 2.
Find the number of 4-digit numbers which can be formed using the digits 0, 2, 5, 7, 8 that are divisible by (i) 2 (ii) 4 when repetition is allowed.
Solution:
(i) First place can be filled by either 2 or 5 or 7 or 8 in 4 ways.
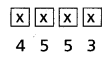
Second place can be filled by any one of the given digits in 5 ways.
Third place can be filled by any one of the given digits in 5 ways.
Last place (or units place) can be filled by either 0 or 2 or 8 in 3 ways.
∴ The number of 4 digited divisible by 2 numbers that can be formed using the digits 0, 2, 5, 7, 8 when repetition is allowed = 4 × 5 × 5 × 3 = 300
(ii) Since a number is divisible by 4, the last two places should be filled with one of the 00, 08, 20, 28, 52, 72, 80, 88 in 8 ways.
The first place can be filled 4 ways except 0. Second place can be filled in 5 ways.
Question 3.
Find the number of 4-digit numbers that can be formed using the digits 0, 1, 2, 3, 4, 5 which are divisible by 6 when repetition of the digits is allowed.
Solution:
Since a number is divisible by 4, the last two places should be filled with one of the 00, 04, 12, 20, 24, 32, 40, 44 = 8 ways
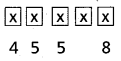
The first place can be filled in any one of the given digits except ‘0’ in 4 ways. The remaining 2 places can be filled by anyone the given digits in 5 × 5 ways.
∴ The number of 5 digited numbers that can be formed using the digits 0, 1, 2, 3, 4 that are divisible by 4 when repetition is allowed = 4 × 52 × 8 = 800