Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(a) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(a)
I.
Question 1.
Find the roots of the following equations.
(i) x2 – 7x + 12 = 0
Solution:
a = 1, b = -7, c = 12
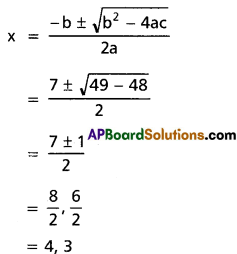
∴ The roots are 4, 3
(ii) -x2 + x + 2 = 0
Solution:
a = -1, b = 1, c = 2

∴ The roots are 2, -1
![]()
(iii) 2x2 + 3x + 2 = 0
Solution:
a = 2, b = 3, c = 2
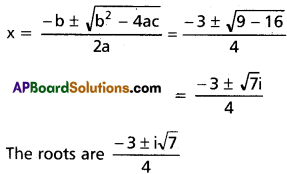
(iv) √3x2 + 10x – 8√3 = 0
Solution:
a = √3 , b = 10, c = -8√3

∴ The roots are \(\frac{2}{\sqrt{3}}\), -4√3
(v) 6√5x2 – 9x – 3√5 = 0
Solution:
a = 6√5 , b = -9, c = -3√5

∴ The roots are \(\frac{\sqrt{5}}{2},-\frac{1}{\sqrt{5}}\)
Question 2.
Form a quadratic equation whose roots are:
(i) 2, 5
Solution:
α + β = 2 + 5 = 7
αβ = 2 × 5 = 10
The required equation is x2 – (α + β)x + αβ = 0
⇒ x2 – 7x + 10 = 0
(ii) \(\frac{m}{n},-\frac{n}{m}\), (m ≠ 0, n ≠ 0)
Solution:
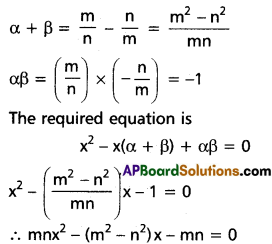
(iii) \(\frac{p-q}{p+q}, \frac{-p+q}{p-q}\), (p ≠ ±q)
Solution:

(iv) 7 ± 2√5
Solution:
α + β = 7 + 2√5 + 7 – 2√5 = 14
αβ = (7 + 2√5) (7 – 2√5)
= 49 – 20
= 29
The required equation is x2 – (α + β)x + αβ = 0
⇒ x2 – 14x + 29 = 0
(v) -3 ± 5i
Solution:
α + β = -3 + 5i – 3 – 5i = -6
αβ = (-3 + 5i) (-3 – 5i)
= 9 + 25
= 34
The required equation is x2 – (α + β)x + αβ = 0
⇒ x2 + 6x + 34 = 0
![]()
Question 3.
Find the nature of the roots of the following equation, without finding the roots.
(i) 2x2 – 8x + 3 = 0
Solution:
a = 2, b = -8, c = 3
b2 – 4ac = 64 – 24 = 40 > 0
∴ The roots are real and distinct.
(ii) 9x2 – 30x + 25 = 0
Solution:
a = 9, b = -30, c = 25
b2 – 4ac = 900 – 900 = 0
∴ The roots are rational and equal.
(iii) x2 – 12x + 32 = 0
Solution:
a = 1, b = -12, c = 32
b2 – 4ac = 144 – 128
= 16
= (4)2
= perfect square
∴ The roots are rational and distinct.
(iv) 2x2 – 7x + 10 = 0
Solution:
a = 2, b = -7, c = 10
b2 – 4ac = 49 – 80 = -31 < 0
∴ The roots are complex conjugate numbers.
Question 4.
If α, β are the roots of the equation ax2 + bx + c = 0, find the values of the following expressions in terms of a, b, c.
(i) \(\frac{1}{\alpha}+\frac{1}{\beta}\)
(ii) \(\frac{1}{\alpha^{2}}+\frac{1}{\beta^{2}}\)
(iii) α4β7 + α7β4
(iv) \(\left(\frac{\alpha}{\beta}-\frac{\beta}{\alpha}\right)^{2}\), if c ≠ 0
(v) \(\frac{\alpha^{2}+\beta^{2}}{\alpha^{-2}+\beta^{-2}}\)
Solution:
α, β are the roots of the equation ax2 + bx + c = 0
α + β = \(\frac{-b}{a}\), αβ = \(\frac{c}{a}\)




Question 5.
Find the values of m for which the following equations have equal roots.
(i) x2 – 15 – m(2x – 8) = 0
Solution:
Given equation is x2 – 15 – m(2x – 8) = 0
⇒ x2 – 2mx + 8m – 15 = 0
a = 1, b = -2m, c = 8m – 15
b2 – 4ac = (-2m)2 – 4(1) (8m – 15)
= 4m2 – 32m + 60
= 4(m2 – 8m + 15)
= 4(m – 3) (m – 5)
If the equation ax2 + bx + c = 0 has equal roots then its discriminant is zero.
∴ The roots are equal
⇒ b2 – 4ac = 0
⇒ 4(m – 3) (m – 5) = 0
⇒ m – 3 = 0 or m – 5 = 0
⇒ m = 3 or 5
(ii) (m + 1)x2 + 2(m + 3)x + (m + 8) = 0
Solution:
Given equation is (m + 1 )x2 + 2(m + 3)x + (m + 8) = 0
a = m + 1, b = 2(m + 3), c = m + 8
b2 – 4ac = [2(m + 3)]2 – 4(m + 1) (m + 8)
= 4(m2 + 6m + 9) – 4(m2 + 8m + m + 8)
= 4m2 + 24m + 36 – 4m2 – 36m – 32
= -12m + 4
= -4(3m – 1)
∴ The roots are equal
⇒ b2 – 4ac = 0
⇒ -4(3m – 1) = 0
⇒ 3m – 1 = 0
⇒ 3m = 1
⇒ m = \(\frac{1}{3}\)
![]()
(iii) x2 + (m + 3)x + m + 6 = 0
Solution:
Given equation is x2 + (m + 3)x + m + 6 = 0
a = 1, b = m + 3, c = m + 6
∴ The roots are equal
⇒ b2 – 4ac = 0
⇒ (m + 3)2 – 4(1) (m + 6) = 0
⇒ m2 + 6m + 9 – 4m – 24 = 0
⇒ m2 + 2m – 15 – 0
⇒ m2 + 5m – 3m – 15 = 0
⇒ m(m + 5) – 3(m + 5) = 0
⇒ (m + 5) (m – 3) = 0
⇒ m = -5, 3
(iv) (3m + 1)x2 + 2(m + 1)x + m = 0
Solution:
Given equation is (3m + 1)x2 + 2(m + 1)x + m = 0
a = 3m + 1, b = 2(m + 1), c = m
b2 – 4ac = 4(m + 1)2 – 4m(3m + 1)
= 4[(m + 1)2 – m(3m + 1)]
= 4(m2 + 2m + 1 – 3m2 – m)
= 4(-2m2 + m + 1)
= -4(2m2 – m – 1)
= -4(m – 1) (2m + 1)
∴ The roots are equal
⇒ discriminant = 0
⇒ b2 – 4ac = 0
⇒ -4(m – 1) (2m + 1) = 0
⇒ m – 1 = 0 or 2m + 1 = 0
⇒ m = 1 or m = \(\frac{-1}{2}\)
(v) (2m + 1)x2 + 2(m + 3)x + (m + 5) = 0
Solution:
Given equation is (2m + 1)x2 + 2(m + 3)x + m + 5 = 0
a = 2m + 1, b = 2(m + 3), c = m + 5
∴ The roots are equal
⇒ b2 – 4ac = 0
⇒ 4(m + 3)2 – 4(2m + 1) (m + 5) = 0
⇒ 4(m2 + 6m + 9 – 2m2 – 10m – m – 5) = 0
⇒ -m2 – 5m + 4 = 0
⇒ m2 + 5m – 4 = 0
⇒ m = \(\frac{-5 \pm \sqrt{25+16}}{2}\)
⇒ m = \(\frac{-5 \pm \sqrt{41}}{2}\)
![]()
Question 6.
If α and β are the roots of x2 + px + q = 0, form a quadratic equation whose roots are (α – β)2 and (α + β)2.
Solution:
∵ α, β are the roots of the equation x2 + px + q = 0
α + β = -p, αβ = q
(α – β)2 + (α + β)2 = 2(α2 + β2)
= 2[(α + β)2 – 2αβ]
= 2[p2 – 2q]
(α – β)2 (α + β)2 = [(α + β)2 – 4αβ)] (α + β)2
= (p2 – 4q) (p2)
∴ The required equation is x2 – (sum of the roots) x + product of the roots = 0
∴ x2 – 2(p2 – 2q)x + p2(p2 – 4q) = 0
Question 7.
If x2 + bx + c = 0, x2 + cx + b = 0 (b ≠ c) have a common root, then show that b + c + 1 = 0.
Solution:
If α is a common root of x2 + bx + c = 0, x2 + cx + b = 0 then
α2 + bα + c = 0 ………..(1)
α2 + cα + b = 0 ……….(2)
(1) – (2) ⇒ (b – c)α + (c – b) = 0
⇒ α – 1 = 0
⇒ α = 1
From (1), 1 + b + c = 0
Hence b + c + 1 = 0
Question 8.
Prove that the roots of (x – a) (x – b) = h2 are always real.
Solution:
Given equation is (x – a) (x – b) = h2
x2 – (a + b)x + (ab – h2) = 0
Discriminant = (a + b)2 – 4(ab – h2)
= (a + b)2 – 4ab + 4h2
= (a – b)2 + (2h)2 > 0
∴ The roots are real.
Question 9.
Find the condition that one root of the quadratic equation ax2 + bx + c = 0 shall be n times the other, where n is a positive integer.
Solution:
Let the roots of the equation ax2 + bx + c = 0 be α, nα
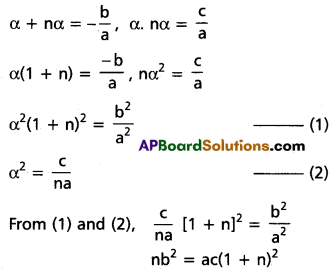
Question 10.
Find two consecutive positive even integers, the sum of whose squares is 340.
Solution:
Let the two consecutive positive even integers be 2λ, 2λ + 2
Sum of squares = 340
⇒ (2λ)2 + (2λ + 2)2 = 340
⇒ λ2 + (λ + 1)2 = 85
⇒ λ2 + λ2 + 2λ + 1 – 85 = 0
⇒ 2λ2 + 2λ – 84 = 0
⇒ λ2 + λ – 42 = 0
⇒ (λ + 7) (λ – 6) = 0
⇒ λ = 6, λ = -7
∵ Given numbers are positive λ = 6
∴ The two consecutive positive even integers are
2λ = 2(6) = 12 and 2λ + 2 = 12 + 2 = 14
![]()
II.
Question 1.
If x1, x2 are the roots of the quadratic equation ax2 + bx + c = 0 and c ≠ 0, find the value of (ax1 + b)-2 + (ax2 + b)-2 terms of a, b, c.
Solution:
x1, x2 are the roots of the equation ax2 + bx + c = 0
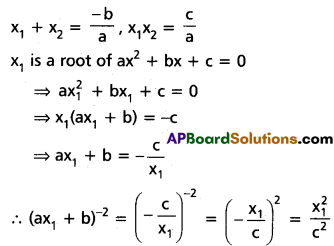

Question 2.
If α, β are the roots of the quadratic equation ax2 + bx + c = 0, form a quadratic equation whose roots are α2 + β2 and α-2 + β-2.
Solution:
α, β are the roots of ax2 + bx + c = 0, then


Question 3.
Solve the following equation:
2x4 + x3 – 11x2 + x + 2 = 0
Solution:
2x4 + x3 – 11x2 + x + 2 = 0
Dividing by x2

Substituting in (1)
2(a2 – 2) + a – 11 = 0
⇒ 2a2 – 4 + a – 11 = 0
⇒ 2a2 + a – 15 = 0
⇒ (a + 3) (2a – 5) = 0
⇒ a + 3 = 0 or 2a – 5 = 0
⇒ a = -3 or 2a = 5
⇒ a = -3 or a = \(\frac{5}{2}\)

⇒ 2x2 + 2 = 5x
⇒ 2x2 – 5x + 2 = 0
⇒ (2x – 1) (x – 2) = 0
⇒ 2x – 1 = 0 or x – 2 = 0
⇒ x = \(\frac{1}{2}\), 2
∴ The roots are \(\frac{1}{2}\), 2, \(\frac{-3 \pm \sqrt{5}}{2}\)
![]()
Question 4.
Solve 31+x + 31-x = 10
Solution:
31+x + 31-x = 10
\(\text { 3. } 3^{x}+\frac{3}{3^{x}}=10\)
Put a = 3x so that 3a + \(\frac{3}{a}\) = 10
⇒ 3a2 + 3 = 10a
⇒ 3a2 – 10a + 3 = 0
⇒ (a – 3) (3a – 1) = 0
⇒ a – 3 = 0 or 3a – 1 = 0
⇒ a = 3 or a = \(\frac{1}{3}\)
Case (i): a = 3
⇒ 3x = 31
⇒ x = 1
Case (ii): a = \(\frac{1}{3}\)
⇒ 3x = 3-1
⇒ x = -1
∴ The roots are 1, -1
Question 5.
Solve 4x-1 – 3 . 2x-1 + 2 = 0
Solution:
4x-1 – 3 . 2x-1 + 2 = 0
Put a = 2x-1 so that a2 = (2x-1)2 = 4x-1
∴ a2 – 3a + 2 = 0
⇒ (a – 2) (a – 1) = 0
⇒ a – 2 = 0 or a – 1 = 0
⇒ a = 2 or 1
Case (i): a = 2
2x-1 = 21
⇒ x – 1 = 1
⇒ x = 2
Case (ii): a = 1
2x-1 = 20
⇒ x – 1 = 0
⇒ x = 1
∴ The roots are 1, 2
![]()
Question 6.
\(\sqrt{\frac{x}{x-3}}+\sqrt{\frac{x-3}{x}}=\frac{5}{2}\), when x ≠ 0 and x ≠ 3
Solution:
\(\sqrt{\frac{x}{x-3}}+\sqrt{\frac{x-3}{x}}=\frac{5}{2}\)
Put a = \(\sqrt{\frac{x}{x-3}}\)
\(a+\frac{1}{a}=\frac{5}{2}\)
⇒ \(\frac{a^{2}+1}{a}=\frac{5}{2}\)
⇒ 2a2 + 2 = 5a
⇒ 2a2 – 5a + 2 = 0
⇒ (2a – 1) (a – 2) = 0
⇒ 2a – 1 = 0 or a – 2 = 0
⇒ a = \(\frac{1}{2}\) or 2
Case (i): a = 2
\(\sqrt{\frac{x}{x-3}}\) = 2
⇒ \(\frac{x}{x-3}\) = 4
⇒ x = 4x – 12
⇒ 3x = 12
⇒ x = 4
Case (ii): a = \(\frac{1}{2}\)
\(\sqrt{\frac{x}{x-3}}=\frac{1}{2}\)
⇒ \(\frac{x}{x-3}=\frac{1}{4}\)
⇒ 4x = x – 3
⇒ 3x = -3
⇒ x = -1
∴ The roots are -1, 4.
Question 7.
\(\sqrt{\frac{3 x}{x+1}}+\sqrt{\frac{x+1}{3 x}}=2\), when x ≠ 0 and x ≠ -1
Solution:
Put a = \(\sqrt{\frac{3 x}{x+1}}\)
\(a+\frac{1}{a}=2\)
⇒ \(\frac{a^{2}+1}{a}\) = 2
⇒ a2 + 1 = 2a
⇒ a2 – 2a + 1 = 0
⇒ (a – 1)2 = 0
⇒ a – 1 = 0
⇒ a = 1, 1
∴ \(\sqrt{\frac{3 x}{x+1}}\) = 1
⇒ \(\frac{3 x}{x+1}\)
⇒ 3x = x + 1
⇒ 2x = 1
⇒ x = \(\frac{1}{2}\)
∴ The root is \(\frac{1}{2}\)
![]()
Question 8.
Solve \(2\left(x+\frac{1}{x}\right)^{2}-7\left(x+\frac{1}{x}\right)+5=0\), when x ≠ 0.
Solution:
\(2\left(x+\frac{1}{x}\right)^{2}-7\left(x+\frac{1}{x}\right)+5=0\)
Put a = x + \(\frac{1}{x}\)
⇒ 2a2 – 7a + 5 = 0
⇒ (2a – 5)(a – 1) = 0
⇒ 2a – 5 = 0 or a -1 = 0
⇒ a = \(\frac{5}{2}\) or 1
Case (i): a = \(\frac{5}{2}\)
x + \(\frac{1}{x}\) = \(\frac{5}{2}\)
⇒ \(\frac{x^{2}+1}{x}=\frac{5}{2}\)
⇒ 2x2 + 2 = 5x
⇒ 2x2 – 5x + 2 = 0
⇒ (2x – 1) (x – 2) = 0
⇒ 2x – 1 = 0 or x – 2 = 0
⇒ x = \(\frac{1}{2}\) or 2
Case (ii): a = 1
\(x+\frac{1}{x}=1\)
⇒ \(\frac{x^{2}+1}{x}\)
⇒ x2 + 1 = x
⇒ x2 – x + 1 = 0
⇒ x = \(\frac{1 \pm \sqrt{1-4}}{2}=\frac{1 \pm \sqrt{3 i}}{2}\)
∴ The roots are \(\frac{1 \pm \sqrt{3 i}}{2}, \frac{1}{2}\), 2
Question 9.
Solve \(\left(x^{2}+\frac{1}{x^{2}}\right)-5\left(x+\frac{1}{x}\right)+6=0\), when x ≠ 0
Solution:
Put a = x + \(\frac{1}{x}\)
⇒ a2 = \(\left(x+\frac{1}{x}\right)^{2}\)
⇒ a2 = \(x^{2}+\frac{1}{x^{2}}+2\)
⇒ \(x^{2}+\frac{1}{x^{2}}\) = a2 – 2
∴ a2 – 2 – 5a + 6 = 0
⇒ a2 – 5a + 4 = 0
⇒ (a – 1) (a – 4) = 0
⇒ a = 1 or 4
Case (i): a = 1
x + \(\frac{1}{x}\) = 1
⇒ \(\frac{x^{2}+1}{x}\) = 1
⇒ x2 + 1 = x
⇒ x2 – x + 1 = 0
⇒ x = \(\frac{1 \pm \sqrt{1-4}}{2}=\frac{1 \pm \sqrt{3 i}}{2}\)
Case (ii): a = 4
x + \(\frac{1}{x}\) = 4
⇒ \(\frac{x^{2}+1}{x}\) = 4
⇒ x2 + 1 = 4x
⇒ x2 – 4x + 1 = 0
⇒ x = \(\frac{4 \pm \sqrt{16-4}}{2}\)
⇒ x = \(\frac{4 \pm 2 \sqrt{3}}{2}\)
⇒ x = 2 ± √3
∴ The roots are 2 ± √3, \(\frac{1 \pm \sqrt{3 i}}{2}\)
![]()
Question 10.
Find a quadratic equation for which the sum of the roots is 7 and the sum of the squares of the roots is 25.
Solution:
Let α, β be the roots of quadratic equation
α + β = 7, α2 + β2 = 25
⇒ (α + β)2 – 2αβ = 25
⇒ 49 – 25 = 2αβ
⇒ αβ = 12
The required equation is x2 – (α + β)x + αβ = 0
⇒ x2 – 7x + 12 = 0