Inter 2nd Year Maths 2B Circle Solutions Ex 1(b)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Circle Solutions Exercise 1(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Circle Solutions Exercise 1(b)

I.

Question 1.
Locate the position of the point P with respect to the circle S = 0 when
i) P(3, 4) and S ≡ x² + y² – 4x – 6y – 12 = 0
Solution:
S ≡ x² + y² – 4x – 6y – 12
P(3, 4) = (x₁, y₁)
S₁₁ = 3² + 4² – 4.3 – 6.4 – 12
= 9 + 16 – 12 – 24 – 12
= – 23 < 0
P (3, 4) lies inside the circle

ii) P(1, 5) and S ≡ x² + y² – 2x – 4y + 3 = 0
Solution:
S₁₁ = (1)² + (5)² – 2(-1) – 4(5) + 3 = 7
S₁₁ > 0 [∴ P is outside the circle]

iii) P (4, 2) and S ≡ 2x² + 2y² – 5x – 4y – 3 = 0
Solution:
S₁₁ = 2(4)² + 2(2)² – 5(4) – 4(2) – 3 = 9
S₁₁ > 0 (P lies outside the circle)

iv) P(2, -1) and S ≡ x² + y² – 2x – 4y + 3 = 0
Solution:
S₁₁ = (2)² + (-1)² – 2(2) – 4 (-1) + 3 = 8
S₁₁ > 0 [P is outside the circle]

Question 2.
Find the power of the point P with respect to the circle S = 0 when
i) P = (5, -6), and S ≡ x² + y² + 8x + 12y + 15
Solution:
S₁₁ = power of the point
= 25 + 36 + 40 – 72 + 15
= 116 – 72 = 44

ii) P = (-1, 1) and S ≡ x² + y² -6x + 4y – 12
Power of the point = S₁₁
= 1+1+6 + 4-12 = 0

iii) P = (2, 3) and S ≡ x² + y² – 2x + 8y – 23
Power of the point = S₁₁
= 4 + 9-4 + 24-23 = 10

iv) P = (2, 4) and S ≡ x² + y² – 4x – 6y – 12
Power of the point = 4 + 16 – 8 – 24 – 12
= -24.

Question 3.
Find the length of tangent from P to the circle S = 0 when
i) P = (-2, 5) and S = x² + y² – 25
Solution:
Length of tangent = \(\sqrt{s_{11}}\)
= \(\sqrt{(-2)^{2}+(5)^{2}-25}\) = 2 units

ii) P = (0, 0), S = x² + y² – 14x + 2y + 25
Solution:
Length of the tangent = \(\sqrt{s_{11}}\)
= \(\sqrt{0+0-0+0+25}\) = 5 units

iii) P = (2, 5) and S ≡ x² + y² – 5x + 4y – 5
Solution:
Length of the tangent = \(\sqrt{s_{11}}\)
= \(\sqrt{4+25-10+20-5}\)
= \(\sqrt{34}\) units

II.

Question 1.
If the length of the tangent from (5, 4) to the circle x² + y² + 2ky = 0 is 1 then find k.
Solution:
Length of tangent
\(\sqrt{s_{11}}=\sqrt{(5)^{2}+(4)^{2}+8k}\)
But length of tangent = 1
∴ 1 = \(\sqrt{25+16+8k}\)
Squaring both sides we get 1 = 41 + 8k
k = – 5 units.

Question 2.
If the length of the tangent from (2, 5) to the circle x² + y² – 5x + 4y + k = 0 is √37 then find k.
Solution:
Length of tangent = \(\sqrt{s_{11}}\)
= \(\sqrt{(2)^2+(5)^2-5 \times 2+4 \times 5+k}\)
= 37 = 39 + k
k = -2 units.

III.

Question 1.
If a point P is moving such that the lengths of tangents drawn from P to the circles x² + y² – 4x – 6y – 12 = 0 and x² + y² + 6x + 18y + 26 = 0 are in the ratio 2 : 3, then find the equation of the locus of P.
Solution:
P(x, y) is any point on the locus
S ≡ x² + y² – 4x – 6y – 12

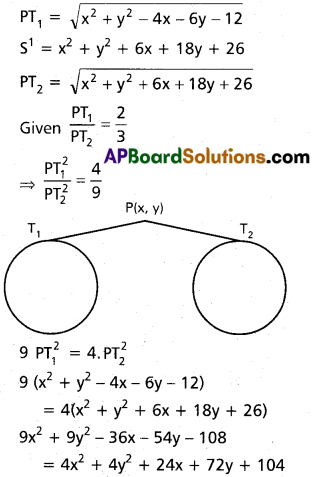
Locus of P is
5x² + 5y² – 60x – 126y – 212 = 0

Question 2.
If a point P is moving such that the lengths of the tangents drawn from P to the circles x² + y² + 8x + 12y + 15 = 0 and x² + y² – 4x – 6y – 12 = 0 are equal then find the equation of the locus of P.

Solution:
Equations of the circles are
S ≡ x² + y² + 8x + 12y + 15 = 0
S¹ ≡ x² + y² – 4x – 6y – 12 = 0
P (x₁, y₁) is any point on the locus and PT₁ PT₂ are the tangents from P to the two circles.
Given condition is PT₁ = PT₂ ⇒ P₁T₁² = PT₂²
x²₁ + y²₁ + 8x₁ + 12y₁ + 15
= x²₁ + y²₁ – 4x₁ – 6y₁ – 12
12x₁ + 18y₁ + 27 = 0
(or) 4x₁ + 6y₁ + 9 = 0
Locus of P(x₁, y₁) is 4x + 6y + 9 = 0