Students can go through AP Board 7th Class Maths Notes 4th Lesson Lines and Angles to understand and remember the concept easily.
AP Board 7th Class Maths Notes 4th Lesson Lines and Angles
→ Euclid (323 – 283 BC) was a Greek mathematician. He is well known as ‘Father of Geometry.’ He wrote a book named ‘Elements’ which was a collection of 13 volumes, dealing with geometry. ‘Elements’ was most influenced work in the history of mathematics. In his books he deduced many theorems using axioms. These theorems are being used in the study of Euclidean geometry.
→ If the sum of two angles is 90°, then the angles are called as complementary angles to each other.
→ If the sum of two angles is 180°, then the angles are called as supplementary angles to each other.
→ If the sum of the two angles is 360°, then the angles are called as conjugate angles to each other.
→ Two angles are said to be adjacent angles, if they have a common vertex, common arm and lie on either side of the common arm.
→ A pair of adjacent angles whose sum is 180° are called as linear pair of angles.
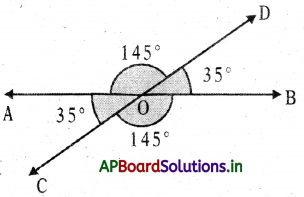
→ When two straight lines intersect, the opposite angles at the point of intersection are called as vertically opposite angles.
![]()
→ Vertically opposite angles are equal.
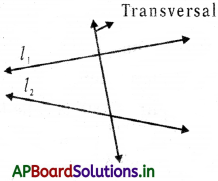
→ A transversal is a straight line that intersects two or more straight lines at distinct points.
→ When a transversal intersects a pair of parallel lines p and q, let the angles formed be ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8.

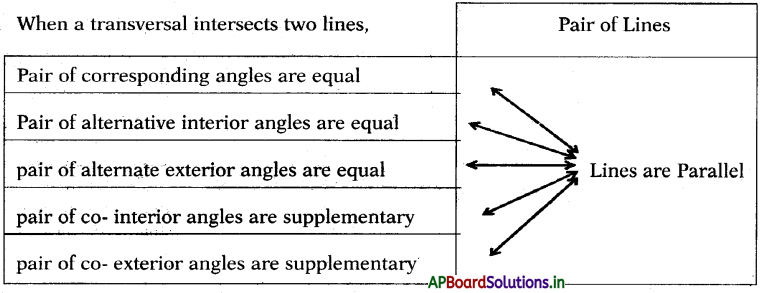
→ When a transversal intersects two lines,
![]()
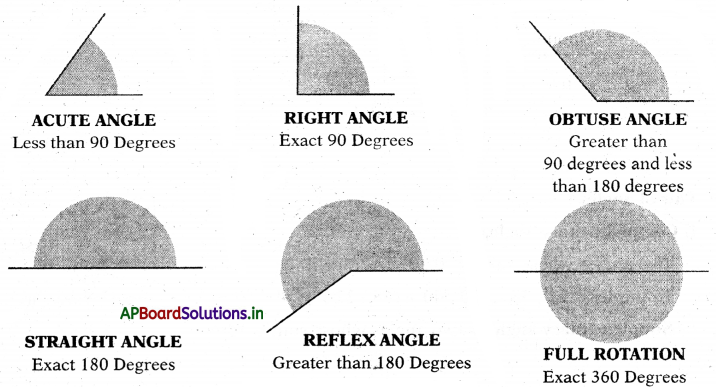
→ Types of angles:
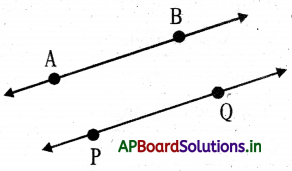
→ Parallel lines: Two or more lines are said to be parallel if they never meet each other however long they are produced.

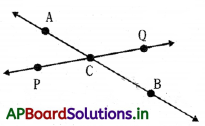
→ Intersecting lines: Two lines are said to be intersecting if they meet at a point or meet at a point if they are produced.
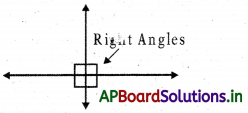
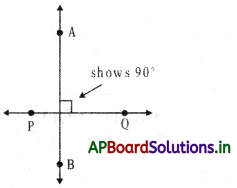
→ Perpendicular lines: Two lines are said to be perpendicular if they meet at right angles. In other words the angle between them is 900.
→ Pairs of Lines in a Plane:
Intersecting Lines: Lines that cross each other \(\overleftrightarrow{\mathrm{AB}}\) intersects \(\overleftrightarrow{\mathrm{PQ}}\) at C.
→ Parallel Lines: Lines that do not touch. They are always the same distance apart. \(\overrightarrow{\mathrm{AB}} \| \overleftrightarrow{\mathrm{PQ}}\)
→ Perpendicular Lines: Lines that cross a right angles. \(\overrightarrow{\mathrm{AB}} \perp \overleftrightarrow{\mathrm{PQ}}\)
→ Pair of angles:
(i) Complementary angles:
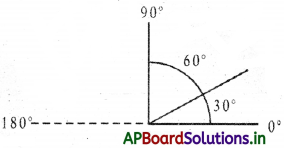
Two angles whose sum is 90°.
Examples: (52°, 38°), (50°, 406), (68°, 22°) 180°
(ii) Supplementary angles: Two angles whose sum is 180°
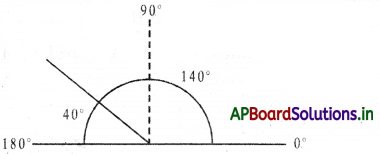
Examples: (52°, 128°), (50°, 130°), (68°, 112°)
(iii) Explementary or Conjugate angles: Two angles whose sum is 360°.
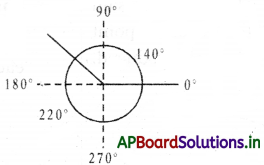
Examples: (132°, 228°), (150°, 210°), (168°, 192°)
- Complementary angles are always acute.
- In a pair of complementary angles no angle is obtuse.
- Two acute angles can’t be supplementary.
- Two obtuse angles can’t be supplementary.
![]()
→ In a pair of supplementary angles one angle must be obtuse or both are right angles.
| Type of angle | First Angle | Second angle in the pair |
| Complementary angles | x | (90 – x) |
| Supplementary angles | x | (180 – x) |
| Conjugate angles | x | (360 – x) |
→ Adjacent angles: Two angles are said to be adjacent if they have
- a common vertex
- a common arm
- and the two angles lie on either side of the common arm.
Example:
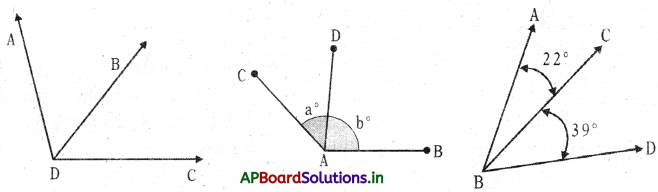
Angle ADB and Angle BDC share a common vertex of D and have a common side of DB.
- The interior of adjacent angles must have no common points.
- The adjacent angles need not be complementary or supplementary.
→ Linear pair of angles: A pair of adjacent angles whose sum is 180° is called a pair of linear angles.
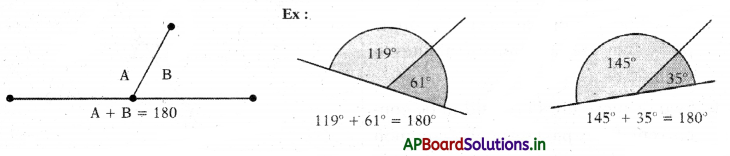
- A linear pair of angles must be supplementary.
- A pair of supplementary angles need not necessarily be a linear pair.
→ Vertically opposite angles: When a pair of straight lines intersect each other, the pairs of opposite angles thus formed at the point of intersection are called vertically opposite angles.
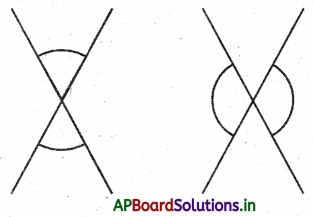
→ When a pair of lines intersects each other, the pairs of vertically opposite angles thus formed are equal.
→ Transversal: A transversal is a straight line that intersects two or more straight lines at distinct points. Here are two lines l1 and l2 is a transversal.
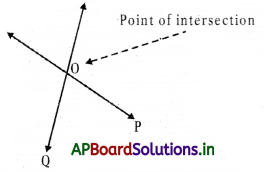
→ Two or more lines are said to be con current if they pass through a common point i.e., they intersect at a point.
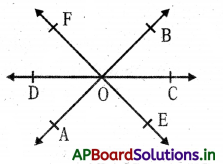
- Here the lines AB, CD and EF are concurrent lines since they intersect at a common point O.
- If two or more lines do not intersect at a common point, then they are non-concurrent.
→ Angles made by a transversal: When a transversal t intersects a pair of lilies ‘l’ and ‘m’, there form eight angles.
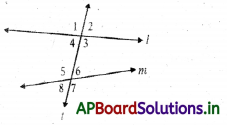
→ Interior angles: Angles lying between the two lines are called interior angles. Here, ∠3, ∠4, ∠5 and ∠6 are interior angles.
→ Exterior angles: Angles lying outside the two lines are called exterior angles. Here ∠1, ∠2, ∠7 and ∠8 are exterior angles.
![]()
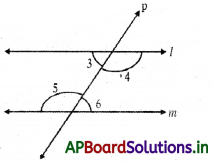
→ Corresponding angles: Two angles are said to form a pair of corresponding angles if
- One is interior and other is exterior
- They are not adjacent
- They lie on the same side of the transversal.
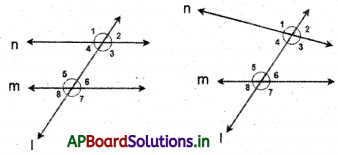
Here the pairs are (∠1 and ∠5), (∠2 and ∠6), (∠3 and ∠7), (∠4 and ∠8).
→ If lines are parallel then the pairs of corresponding angles become equal. (∠1 = ∠5), (∠2 = ∠6), (∠3 = ∠7), (∠4 = ∠8)
Conversely if a transversal intersects a pair of straight lines making corresponding angles equal, then the lines are parallel.
→ Alternate interior angles: Two angles are said to form a pair of alternate interior angle, if
- both are interior
- they are not adjacent
- they lie on the either side of the transversal.
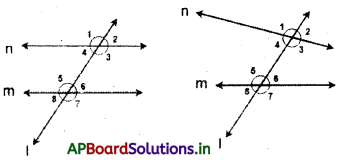
Here the pairs are (∠1 and ∠7), (∠2 and ∠8).
If lines are parallel, then the pairs of alternate interior angles become equal.
(∠1 = ∠7), (∠2 = ∠8).
Conversely, if a transversal intersects a pair of straight lines making alternate exterior angles equal, then the lines are parallel.
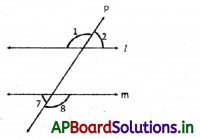
→ Alternate exterior angles: Two angles are said to form a pair of alternate exterior angle if
- both are exterior
- they are not adjacent
- they lie on the either side of the transversal.
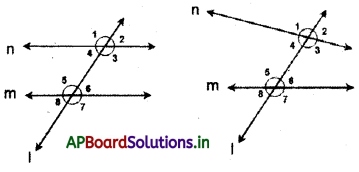
Here the pairs are (∠3 and ∠4), (∠5 and ∠6).
If lines are parallel, then the pairs of co-interior angles become supplementary.
(∠3 + ∠4 = 180°), (∠5 + ∠6 = 180°). Conversely if a transversal intersects a pair of straight lines making co-interior angles supplementary, then the lines are parallel.
→ Co-interior angles: Interior angles on same side of transversal are co-interior angles.
- both are interior
- they are adjacent
- they lie on the either side of the transversal.
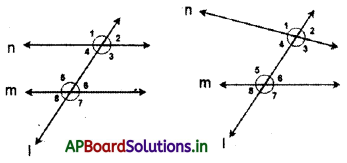
Here the pairs are (∠3 and ∠5), (∠4 and ∠6).
If lines are parallel, then the pairs of alternate interior angles become equal.
(∠3 = ∠5), (∠4 = ∠6).
Conversely, if a transversal intersects a pair of straight lines making alternate interior angles equal, then the lines are parallel.