Students can go through AP Board 7th Class Maths Notes 5th Lesson Triangles to understand and remember the concept easily.
AP Board 7th Class Maths Notes 5th Lesson Triangles
→ A triangle is a simple closed plane figure made up of three line segments. .
→ Based on the sides triangles are of three types.
- Equilateral triangle
- Isosceles triangle
- Scalene triangle
→ Based on the angles, triangles are of three types.
- Acute angled triangle
- Obtuse angled triangle
- Right angled triangle
→ The sum of the three interior angles in a triangle is 180°.
→ The exterior angle of a triangle is equal to the sum of it’s opposite interior angles.
![]()
→ Properties of the lengths of the sides of a triangle:
- The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
- The difference between the lengths of any two sides of a triangle is smaller than the length of the third side.
→ Triangle: A simple closed figure formed by three line segments is called a triangle. In the figure ABC is a triangle.
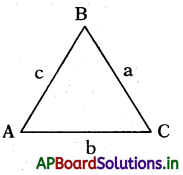
- A, B, C are its corners known as vertices.
- ∠A, ∠B & ∠C are called its interior angles,
- AB, BC & CA are called its sides.
- Side opposite to ∠A is BC, also denoted by a.
- Side opposite to ∠B is AC, also denoted by b,
- Side opposite to ∠C is AB, also denoted by c.
→ Types of Triangles:
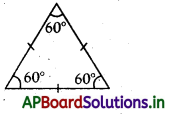
(i) Equilateral triangle: All 3 sides and angles are equal.
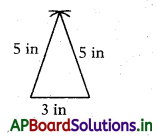
(ii) Isosceles triangle: 2 equal sides and 2 equal angles.
(iii) Scalene triangle: Has no equal sides or angles.
(iv) Acute angled triangle: All 3 angles re acute.
(v) Right angled triangle: Has 1 right angle.
(vi) Obtuse angled triangle: Has 1 Abtuse angle.
Note: The sides with equal lengthifBfS! denoted by same number of strokes (/), similarly for equal angles also.
- In an equilateral triangle all the three sides and each angle is equal to 60°.
- In an isosceles triangle two sides are equal.
- In an isosceles triangle angles opposite to equal sides are equal.
- Conversely in an isosceles triangle sides opposite to equal angles are equal.
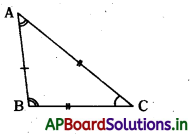
- In a right angled triangle the side opposite to right angle is called hypotenuse.
- Hypotenuse is the longest side of a right triangle.
![]()
→ Angle sum property of a triangle:
The sum of three interior angles of a triangle is equal to 180°
∠A + ∠B + ∠C = 180°
→ Exterior angle property of a triangle:
If in a triangle any side is produced angle, then formed is called its exterior angle.
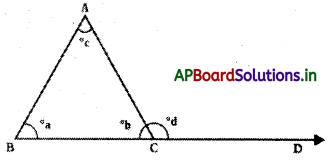
In ∆ABC, BC is produced to D, then ∠ACD is called exterior angle.
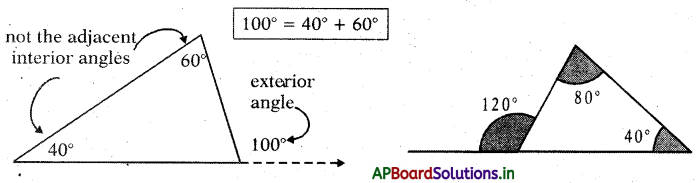
→ Exterior Angle Theorem: The exterior angle of a triangle is equal to the sum of the two opposite interior angles.
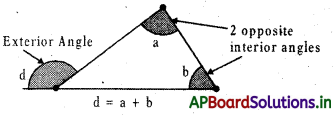
Example:
→ Inequality properties of a triangle:
→ In any ∆ABC, sum of any two sides is always greater than the third side. If AB, BC & CA are the sides of the triangle, then
- AB + BC > CA c + a > b
- BC + CA > AB a + b > c
- CA + AB > BC b + c > a
→ Also the difference between any two sides of a triangle is always less than the third side.
- AB – BC < CA c – a < b
- BC – CA < AB a – b < c
- CA – AB < BC b – c < a
→ In a triangle, if two sides are given, then the side opposite to greater angle is greater than the other.
→ In a triangle, if two sides are given, then the side opposite to smaller angle is smaller than the other.
![]()
→ Also in a triangle, if two angles are given,.then the angle opposite to greater side is greater than the other.
→ In a triangle, if two angles are given, then the angle opposite to smaller side is smaller than the other.
→ The perpendicular line segment from any vertex to its opposite side is called altitude.
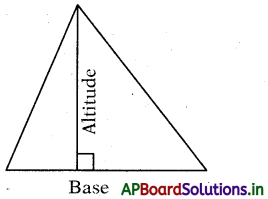
Height = length of the altitude
Area = space inside the triangle