AP Board 10th Class Maths Solutions Chapter 6 శ్రేఢులు Optional Exercise

SCERT AP 10th Class Maths Textbook Solutions Chapter 6 శ్రేఢులు Optional Exercise Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 6th Lesson శ్రేఢులు Optional Exercise

ప్రశ్న 1.
121, 117, 113, ……….., అంకశ్రేణిలో ఎన్నవ పదము మొదటి ఋణపదము అవుతుంది?
[సూచన : a_n < 0 అయ్యే విధంగా n విలువ కనుగొనుము]
సాధన.
ఇచ్చిన అంకశ్రేఢి 121, 117, 113,
a = 121, d = a₂ – a₁ = 117 – 121 = – 4
a_n మొదటి రుణపదం అనుకొంటే a_n < 0 అయ్యేటట్లు కనిష్ఠ సహజసంఖ్య n ను కనుగొనాలి.
a_n < 0 = a + (n – 1) d < 0
⇒ 121 + (in – 1) (- 4) < 0
⇒ 121 – 4n + 4 < 0
⇒ 125 – 4n < 0
⇒ 125 < 4n
⇒ \(\frac{125}{4}\) < n
31.25 < n అయ్యేటట్లుంటే కనిష్ఠ సహజసంఖ్య n = 32 అవుతుంది. కావున 32వ పదము.
ఇచ్చిన అంకశ్రేణిలో మొదటి రుణపదం అవుతుంది.

సరిచూచుకోవడం :
a₃₁ = a + 30d
= 121 + 30 (- 4)
= 121 – 120 = 1
a₃₂ = a + 31d
= 121 + 31 (- 4)
= 121 – 124 = – 3.

ప్రశ్న 2.
ఒక అంకశ్రేణిలో 3వ, 7వ పదాల మొత్తము 6 . మరియు వాని లబ్ధము 8 అయిన మొదటి 16 పదాల మొత్తము కనుగొనుము.
సాధన.
మొదటి పద్దతి :
ఒక అంకశ్రేణిలో 3వ పదం, 7వ పదముల మొత్తం = 6
a₃ + a₇ = 6
⇒ a + 2d + a + 6d = 6
⇒ 2a + 8d = 6
⇒ 2 (a + 4d) = 3
⇒ a + 4d = 3
∴ a = 3 – 4d ………… (1)
మరియు వాని లబ్దం = 8
a₃ . a₇ = 8
⇒ (a + 2d) (a.+ 6d) = 9
⇒ (3 – 4d + 2d) (3 – 4d + 6d) = 8 (1) నుండి)
⇒ (3 – 2d) (3 + 2d) = 8
⇒ 9 – 4d² = 8
⇒ 4d² = 8 – 9 = 1
⇒ 4d² = 1
⇒ d² = \(\frac{1}{4}\)
d = \(\sqrt{\frac{1}{4}}=\pm \frac{1}{2}\)
d = \(\frac{1}{2}\) అయిన
d = \(\frac{1}{2}\) ను (1) లో రాయగా
a = 3 4(\(\frac{1}{2}\)) = 3 . 2 = 1
a = 1, d = \(\frac{1}{2}\), n = 16
S_n = \(\frac{n}{2}\)[2a + {n – d]
S_n = \(\frac{16}{2}\) [2(1) + (16 – 1) (\(\frac{1}{2}\))]
= 8 [2 + \(\frac{15}{2}\)]
= 8 × [latex]\frac{19}{2}[/latex]
S₁₆ = 76
d = – \(\frac{1}{2}\) అయిన
d = – \(\frac{1}{2}\) ను (1) లో రాయగా
a = 3 . 4(- \(\frac{1}{2}\)) = 3 + 2 = 5
a = 5, d = – \(\frac{1}{2}\) n = 16
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₁₆ = \(\frac{16}{2}\) [2(5) + (16 – 1) (\(\frac{-1}{2}\))]
= 8 [10 – \(\frac{15}{2}\)]
S₁₆ = 20
S₁₆ = 76, 20
16 పదాల మొత్తం S₁₆ = 76, 20.

రెండవ పద్ధతి :
ఒక A.P. లో 3వ పదం = a + 2d = x;
7వ పదం = a + 6d = y
లెక్క ప్రకారం,
x + y = 6 ………. (1);
x + y = 8 ……….. (2)
(2) ⇒ y = \(\frac{8}{x}\) ని (1) లో రాయగా, x + \(\frac{8}{x}\) = 6 –
⇒ x² + 8 = 6x
⇒ x² – 6x + 8 = 0
⇒ x² – 4x – 2x + 8 = 0
⇒ (x – 4) (x – 2) = 0
x = 4 లేదా x = 2
x = 4 అయిన
(1) నుండి
4 + y = 6 ⇒ y = 2

d = \(\frac{1}{2}\) ను a + 2d = 4 లో రాయగా,
a + 2(- \(\frac{1}{2}\)) = 4
⇒ a – 1 = 4
⇒ a = 4 + 1 = 5
a = 5, d = – \(\frac{1}{2}\), n = 16

x = 2 అయిన
(1) నుండి 2 + y = 6 ⇒ y = 6 – 2 = 4

d = \(\frac{1}{2}\) ను a + 2d = 2 లో రాయగా
a + 2(\(\frac{1}{2}\)) = 2
⇒ a + 1 = 2
⇒ a = 2 – 1 = 1
a = 1, d = \(-\frac{1}{2}\), n = 16
S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
S₁₆ = \(\frac{16}{2}\) [2(5) + (16 – 1) (- 1)]
= 8 [10 – \(\frac{15}{2}\)]
= 8 × [latex]\frac{20-15}{2}[/latex]
= 8 × \(\frac{5}{2}\)
= 4 × 5 = 20
S₁₆ = 20
∴ 16 పదాల మొత్తం 20 లేదా 76.

ప్రశ్న 3.
ఒక నిచ్చెనకు 25 మెట్లు కలవు. మెట్ల యొక్క పొడవు క్రింది నుంచి పైకి ఏకరీతిగా తగ్గుతూవుంచి, క్రింది నుంచి మొదటి మెట్టు పొడవు 45 సెం.మీ. మరియు పై నుంచి మొదటి మెట్టు పొడవు 25 సెం.మీ. ఈ రెండింటి మధ్య దూరం 21/2 మీ. అయిన అన్ని మెట్ల తయారీకి కావలసిన చెక్క పొడవు ఎంత? [సూచన : మెట్ల సంఖ్య = \(\frac{250}{25}\) +1]

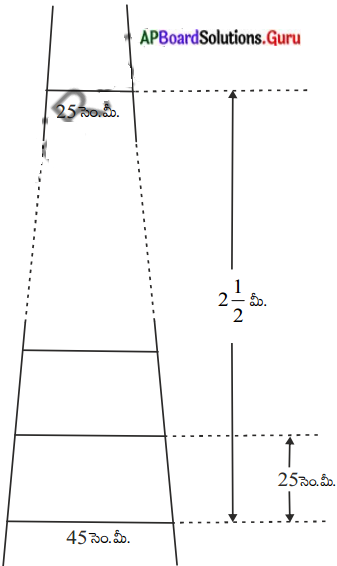
సాధన.
నిచ్చెన యొక్క రెండు వరుస మెట్ల మధ్య దూరం = 25 సెం.మీ.
క్రింది నుండి మొదటి మెట్టు పొడవు a₁ = 45 సెం.మీ.
పై నుండి మొదటి మెట్టు పొడవు a₁₁ = 25 సెం.మీ.
నిచ్చెన మొదటి మెట్టుకు, చివరి మెట్టుకు మధ్య దూరం = 2\(\frac{1}{2}\) మీ. = 250 సెం.మీ.
S₁₆ = \(\frac{16}{2}\) [2(1) + (16 – 1) (\(\frac{1}{2}\))]
= \(\frac{16}{2}\) [2 + \(\frac{15}{2}\)]
= 8 \(\left[\frac{4+15}{2}\right]\)
= 4 × 19 = 76
S₁₆ = 76
∴. నిచ్చెన యొక్క మెట్ల సంఖ్య = \(\frac{250}{25}\) + 1 = 10 + 1 = 11
మెట్ల యొక్క పొడవు క్రింది నుండి పైకి ఏకరీతిన తగ్గుతూ ఉంది.
కావున మెట్ల పొడవుల జాబితా అంకశ్రేణి అవుతుంది. మెట్ల తయారీకి కావలసిన చెక్క పొడవు = A.P లోని 11 పదాల మొత్తం
S_n = \(\frac{11}{2}\) [45 + 25]
= \(\frac{11}{2}\) × 70
= 385 సెం.మీ.
S₁₁ = 3.85 మీ.

ప్రశ్న 4.
కొన్ని ఇండ్లు ఒక వరుసలో కలవు. దీనికి 1 నుంచి 49 వరకూ సంఖ్యలను కేటాయించటం జరిగింది. ఏదైనా ఒక ఇంటికి కేటాయించిన సంఖ్య X అనుకుంటే ; ఈ ఇంటికి ముందు – (Preceeding) ఉన్న ఇండ్ల సంఖ్యల మొత్తము, తరువాత ఉన్న ఇండ్ల సంఖ్యల మొత్తము సమానం అయ్యే విధంగా ఆ ఇంటి సంఖ్య X వ్యవస్థితమని చూపండి. మరియు x విలువను
కనుగొనుము. (సూచన : S_{x – 1} = S₄₉ – S_x]
సాధన.
మొదటి పద్ధతి : –
ఇంటి సంఖ్య x గల ఇళ్ళు దానికి ముందున్న ఇండ్ల సంఖ్య మొత్తం, తరువాత గల ఇండ్ల సంఖ్యలు సమానం అయ్యే విధంగా ఉంది అనుకొందాం.

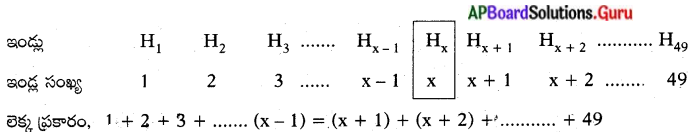
⇒ \(\frac{x-1}{2}\) [1 + (x – 1)] = \(\frac{49-x}{2}\) [(x + 1) + 49]
[∵ (x + 1), (x + 2), …. , 49 వరకు గల పదాల సంఖ్య = 49 – x]
⇒ \(\left(\frac{x-1}{2}\right)[x]=\left(\frac{49-x}{2}\right)[x+50]\)

⇒ \(\frac{x^{2}-x}{2}=\frac{49 x+2450-x^{2}-50 x}{2}\)

⇒ x² – x = – x² – x + 2450
⇒ x² – x + x² + x = 2450
⇒ 2x² = 2450
⇒ x² = \(\frac{2450}{2}\) = 1225
x = √1225 = 35
x ఒక సహజసంఖ్య అవుతున్నది. కావున ఇచ్చిన నియమాలను పాటించేటట్లు x వ్యవస్థితము మరియు x = 35.

రెండవ పద్దతి :
x ఇంటి సంఖ్యల ఇళ్ళు దాని ముందున్న ఇండ్ల సంఖ్యల మొత్తం తరువాత గల ఇళ్ళ సంఖ్యల మొత్తం సమానం అయ్యేటట్లు కలదు అనుకుందాం.
ఇండ్ల సంఖ్య S₄₉ = {1 + 2 + 3 + ……………. } S₁ + {(x – 1) + x + (x + 1) + (x + 2) + ………….. + 49} S₂
S₁ + x + S₂ = S₄₉ ……….. (1)
S₁ = x సంఖ్య ఇంటికి ముందున్న ఇండ్ల సంఖ్యల మొత్తం.
S₂ = x సంఖ్య ఇంటికి తరువాత గల ఇండ్ల సంఖ్యల మొత్తం.
లెక్క ప్రకారం, S₁ = S₂ ……….. (2) మరియు
S₁ = 1 + 2 + 3 + ……… + x – 1
= \(\frac{x-1}{2}\)[1 + (x – 1)]
= ……………..(3)
S₄₉ = 1 + 2 + 3 + …… + 49
= \(\frac{49}{2}\) [1 + 49]
= \(\frac{49}{2}\) × 50
S₄₉ = 1225
∴ S₁ + x + S₂ = S₄₉ = 1225 [∵ S₁ = S₂]
2S₁ + x = 1225
2(\(\frac{x(x-1)}{2}\)) + x = 1225 [(3) నుండి)
x² – x + x = 1225
x² = 1225
x = √1225 = 35
x ఒక సహజ సంఖ్య కావున నియమాలను పాటించేటట్లు x వ్యవస్థతము.

ప్రశ్న 5.
క్రింది పటములో చూపిన విధంగా ఒక ఫుట్ బాల్ గ్రౌండ్ లో 16 మెట్లు కల ఒక మెట్ల సోపానము . కలదు. దీనిలో ప్రతి మెట్టు పొడవు 50 మీ. మరియు వెడల్పు \(\frac{1}{2}\) మీ. మొదటి మెట్టు భూమి నుంచి \(\frac{1}{4}\) మీ. ఎత్తులో మరియు ప్రతి మెట్టు దాని ముందున్న మెట్టుకు \(\frac{1}{4}\) మీ. ఎత్తులో ఉన్న ఆ మెట్ల సోపానాన్ని నిర్మించ డానికి కావలసిన కాంక్రీట్ యొక్క ఘనపరిమాణమును కనుగొనుము.
[సూచన : మొదటి సోపానము నిర్మించుటకు కావల్సిన కాంక్రీటు ఘనపరిమాణం = \(\frac{1}{4}\) × \(\frac{1}{2}\) × 50 మీ.]

సాధన.
ప్రతి మెట్టు పొడవు l = 50 మీ.
వెడల్పు b = \(\frac{1}{2}\) మీ.
ఎత్తు h = మొదటి మెట్టు \(\frac{1}{4}\) మీ. తరువాతి ప్రతి మెట్టు దాని ముందున్న మెట్టుకు \(\frac{1}{4}\) మీ. పెరుగును.
l = 50.మీ., b = \(\frac{1}{2}\) మీ.

దిమ్మె ఘనపరిమాణం V = V₁ + V₂ + V₃ + V₄ + ………. + V₁₅
= 25 × \(\frac{1}{4}\) + 25 × \(\frac{2}{4}\) + 25 × \(\frac{3}{4}\) + 25 × \(\frac{4}{4}\) …………… + 25 × \(\frac{15}{4}\)
= \(\frac{25}{4}\) [1 + 2 + 3 + 4 ………. + 15] [∵ S_n = \(\frac{n}{2}\) (a+ a_n)]
= \(\frac{25}{4}\) × [ \(\frac{15}{2}\) (1 + 15)]
= \(\frac{25}{4}\) × \(\frac{15}{2}\) x× 16
= 25 × 15 × 2
V = 750 ఘ.మీ.

V= 750 ఘ.మీ.

ప్రశ్న 6.
ఒక పనిని పూర్తి చేయుటకు 150 మంది కూలీలను నియమించారు. అయితే రెండవ రోజు వారిలో నలుగురు పనిలోకి రావటం మానుకున్నారు. మూడవ రోజు, మరి నలుగురు మానుకున్నారు. ప్రతిరోజూ ఈ విధంగా జరగటం వల్ల ఆ పని పూర్తి కావడానికి అనుకున్న రోజుల కంటే 8 రోజులు ఎక్కువ అవసరం పట్టింది. అయిన ఆ పని పూర్తి కావడానికి పట్టిన మొత్తం రోజులు ఎన్ని ? .. [సూచన : ప్రారంభంలో పని పూర్తి కావడానికి అవసరమయ్యే రోజుల సంఖ్యను ‘x’ అనుకొంటే
150x = \(\frac{x+8}{2}\) [2 × 150 + (x + 8 = 1) (- 4)]
సాధన.
ప్రారంభంలోని 150 మంది కూలీలతో పని పూర్తి కావడానికి కావలసిన రోజుల సంఖ్య x అనుకొనుము.
∴ ఆ పని పూర్తి కావడానికి కావలసిన మనుష్యుల సంఖ్య = 150x
రెండవ రోజు నుండి ప్రతిరోజు 4గురు చొప్పున పని మానివేస్తుంటే ప్రతి రోజు పనిచేసే మనుష్యుల జాబితా 150, 146, 142, 138, ……., (x + 8) పదాలు .
(లెక్క ప్రకారం పని పూర్తికావడానికి అనుకొన్న రోజులు కన్నా 8 రోజులు ఎక్కువ)
పనిచేసిన మొత్తం మనుష్యులు S_x+8
a = 150, d = a₂ – a₁ = 146 – 150 = – 4,
n = x +8
S_n = \(\frac{n}{2}\) [2a + (n – 1]d]
S_{x + 8} = \(\frac{x+8}{2}\) [2(150) + (x + 8 – 1) (- 4)]
= \(\frac{x+8}{2}\) [300 – 4x – 28]
= \(\frac{x+8}{2}\) [272 – 4x]
= \(\frac{x+8}{2}\) × 2 (136 – 2x)
= (x + 8) (136 – 2x)
= 136x – 2x² + 1088 – 16x
∴ S_{x + 8} = – 2x² + 120x + 1088
ఈ విలువ పని పూర్తికావడానికి కావలసిన మనుష్యులకు సమానం.
∴ 150x = S_{x + 8}
150x = – 2x² + 120x + 1088
2x² + 150x – 120x – 1088 = 0
2x² + 30x – 1088 = 0
2 [x² + 15x – 544] = 0
x² + 15x – 544 = 0
x² – 17x + 32x – 544 = 0
x (x – 17) + 32 (x – 17) = 0
(x – 17) (x + 32) = 0
x – 17 = 0 లేదా x + 32 = 0
x = 17 లేదా x = – 32
రోజుల సంఖ్య రుణాత్మకం కాదు.
కావున x = 17.
∴ పని పూర్తికావడానికి పట్టిన మొత్తం రోజులు x + 8 = 17 + 8 = 25.

ప్రశ్న 7.
ఒక యంత్రము వెల రూ. 5,00,600/-. మొదటి సంవత్సరము దీని వెలలో తగ్గుదల 15%, రెండవ సంవత్సరము 13\(\frac{1}{2}\)% మూడవ సం||ము ,12%….. ఈ విధానము కొనసాగించబడిన 10 సంవత్సరముల అనంతరము దాని వెల ఎంత ? ఇవ్వబడిన శాతాలన్నీ ప్రారంభ వెల పైననే పేర్కొనడం జరిగింది.
[సూచన : మొత్తం తగ్గుదల = 15 + 13\(\frac{1}{2}\) + 12 + ……. + 10 పదాలు S_n = \(\frac{10}{2}\) [30 – 13.5] = 82.5 %
∴ 10 సంవత్సరముల అనంతరము దాని వెల = 100 – 82.5 = 17.5 (అనగా 5,00,000 లో 17.5%)]
సాధన.
మొదటి పద్దతి : మొదట యంత్రం వెల = ₹ 5,00,000
యంత్రం యొక్క వెల తగ్గుదల ప్రారంభవెలపై ఇవ్వడం జరిగింది.

యంత్రం యొక్క ప్రారంభవెలలో 10 సం||ల తరువాత మొత్తం తగ్గుదల
15 + 13 \(\frac{1}{2}\) + 12 + …. 10 పదాలు.
a = 15, d = a₂ – a₁ = – 1\(\frac{1}{2}\)
= – \(\frac{3}{2}\), n = 10
S_n = \(\frac{n}{2}\) [2a + (n -1) d]
S₁₀ = \(\frac{10}{2}\) [2(15) + 9 (\(\frac{-3}{2}\))]
= 5[30 – \(\frac{27}{2}\)] = 5 [30 – 13.5]
= 5 [ 16.5] = 82.5 %
10 సం||ల తరువాత యంత్రం ధర ప్రారంభ ధరలో 100 – 82.5 = 17.5%
∴ 10 సం||ల తరువాత’ యంత్రం ధర = 500000 × \(\frac{17.5}{100}\) = ₹ 87500.

2వ పద్దతి :
యంత్రం ప్రారంభ ధర = ₹ 5,00,000

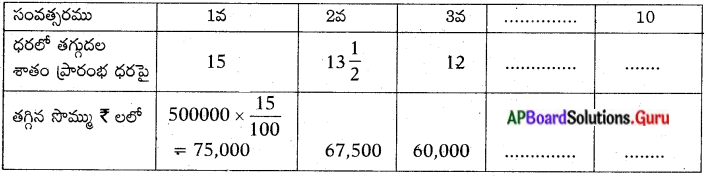
10సంవత్సరాల తరువాత యంత్రంలో మొత్తం తగ్గుదల 75000 + 67500 + 60000 + ….. + 10 పదాలు
ఇది A.P. లో కలదు.
∴ a = 75000, d = – 7500, n = 10
∴ S₁₀ = \(\frac{10}{2}\) [2(75000) + (10 – 1) (- 7500)]
= 5[150000 – 9 × 7500]
= 5[150000 – 67500]
= 5[82500] = 412500
∴ 10 సంవత్సరాల తరువాత యంత్రము వెల = 500000 – 412500 = ₹ 87500.