SCERT AP 7th Class Maths Solutions Pdf Chapter 4 Lines and Angles Ex 4.3 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 4th Lesson Lines and Angles Exercise 4.3
Question 1.
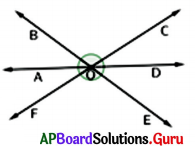
Name three pairs of vertically opposite angles in the figure. If ∠AOB = 45°, then find ∠DOE.
Answer:
Vertically opposite angles :
∠AOB, ∠DOE; ∠BOC, ∠EOF; ∠COD, ∠AOF
Given ∠AOB = 45°
In the given figure, ∠AOB is the vertically opposite angle to ∠DOE.
So, ∠DOE = ∠AOB = 45°
∴ ∠DOE = 45°
Question 2.
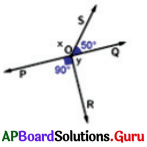
In the given figure \(\overrightarrow{\mathbf{PQ}}\) is a straight line. Check whether x and y are vertically opposite angles or not. Give reason.
Answer:
\(\overrightarrow{\mathbf{PQ}}\) is a straight line. But \(\overrightarrow{\mathbf{SR}}\) is not a straight line.
If \(\overrightarrow{\mathbf{PQ}}\) and \(\overrightarrow{\mathbf{SR}}\) are intersecting lines the x and y become vertically opposite angles.
So, x and y are not vertically opposite angles.
![]()
Question 3.
Write any three examples for vertically opposite angles in your surroundings.
Answer:
Scissors, window grills, cross roads, rail cross junctions, etc.
Question 4.
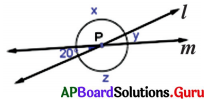
In the given figure, the lines l and m intersect at point P. Observe the figure and find the values of x, y and z.
Answer:
Given l and m are intersecting lines at P.
∠y = 20° (vertically opposite angles)
∠x = ∠z (vertically opposite angles)
∠y + ∠x = 180° (linear pair)
⇒ 20° + ∠x = 180°
⇒ 20° + ∠x – 20° = 180°- 20
⇒ ∠x = 160°
∴ ∠x = ∠z = 160°
∠x = 160°, ∠y = 20° and ∠z = 160°.
Question 5.
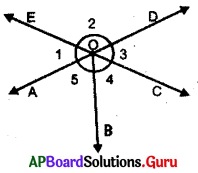
In the given figure, two lines \(\overleftrightarrow{\mathbf{A D}}\) and \(\overleftrightarrow{\mathbf{E C}}\) intersects at O. Name two pairs of vertically opposite angles in the given figure.
Answer:
In the given figure \(\overleftrightarrow{\mathbf{A D}}\) and \(\overleftrightarrow{\mathbf{E C}}\) are intersecting at O.
∠AOE = ∠COD (Vertically opposite angles)
∠1 = ∠3
∠EOD = ∠AOC (Vertically opposite angles)
∠EOD = ∠AOB + ∠BOC (we know ∠AOC = ∠AOB + ∠BOC)
∠2 = ∠5 + ∠4
![]()
Question 6.
Two lines \(\overleftrightarrow{\mathbf{P S}}\) and \(\overleftrightarrow{\mathbf{Q T}}\) intersect at M. Observe the figure and find x.
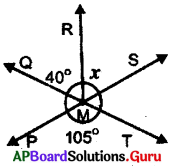
Answer:
In the given figure \(\overleftrightarrow{\mathbf{P S}}\) and \(\overleftrightarrow{\mathbf{Q T}}\) are intersecting at M.
∠PMQ = ∠TMS (Vertically opposite angles)
∠QMS = ∠PMT (Vertically opposite angles)
∠QMR + ∠RMS = ∠PMT (we know ∠QMS = ∠QMR + ∠RMS)
But, given, ∠QMR = 40°, ∠RMS = x° and ∠PMT = 105°
⇒ 40° + x° – 40° = 105° – 40°
∴ x° = 65°