SCERT AP 7th Class Maths Solutions Pdf Chapter 4 రేఖలు మరియు కోణాలు Unit Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 4th Lesson రేఖలు మరియు కోణాలు Unit Exercise
ప్రశ్న 1.
36° యొక్క పూరక, సంపూరక మరియు సంయుగ్మ కోణాలను కనుగొనండి.
సాధన.
36°ల యొక్క పూరక కోణం = 90° – 36° = 54°
36° ల యొక్క సంపూరక కోణం = 180° – 36° = 1440
36°ల యొక్క సంయుగ్మ కోణం = 360° – 36° = 324°
![]()
ప్రశ్న 2.
క్రింది పటాన్ని పరిశీలించండి. పటంలో ఏవైనా 4 జతల ఆసన్న కోణాలను రాయండి.
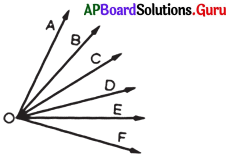
సాధన.
(i) ∠AOB, ∠BOC.
(ii) ∠BOC, ∠COD.
(iii) ∠COD, ∠DOE.
(iv) ∠DOE, ∠EOF.
ప్రశ్న 3.
ఇచ్చిన పటంలో సరళరేఖలుl మరియు mలు 0 అనే బిందువు వద్ద ఖండించిన X విలువను కనుగొనండి.
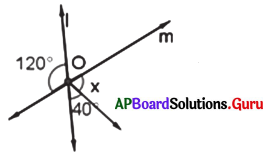
సాధన.
పటంలో l, m లు ‘O’ వద్ద ఖండించుకొంటున్నాయి.
x° + 40° = 120° (శీర్షాభిముఖ కోణాలు)
x = 120° – 40°
∴ x = 80°
![]()
ప్రశ్న 4.
ఇచ్చిన పటంలో \(\overleftrightarrow{A E}\) ఒక సరళరేఖ. కోణాలు ∠1, ∠2, ∠3, ∠4 ల నిష్పత్తి 1 : 2 : 3 : 4 అయిన ఆ కోణాలను కనుగొనండి.
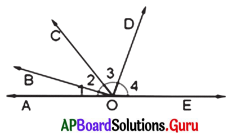
సాధన.
ఇచ్చిన పటంలో \(\overleftrightarrow{A E}\) ఒక సరళరేఖ.
∠1, ∠2, ∠3, ∠4 ల నిష్పత్తి 1 : 2 : 3 : 4.
∴ ∠1 = x°, ∠2 = 2x°, ∠3 = 3x°, ∠4 = 4x° అనుకొందాం.
∠1 + ∠2 + ∠3 + ∠4 = 180° (సరళరేఖపై ఒక బిందువు వద్ద సరళరేఖకు ఒకేవైపు గల కోణాల మొత్తం 180°).
∴ x° + 2x° + 3x° + 4x° = 180°
⇒ 10x° = 180°
⇒ x° = \(\frac{180^{\circ}}{10}\) = 18°
∴ x = 18°
2x° = 2 × 18° = 36°
3x° = 3 × 18° = 54
4x° = 4 × 18° = 720
∴ ∠1 = x° = 18°, ∠2 = 2x° = 36°
∠3 = 3x° = 54°, ∠4 = 4x° = 72°
(లేదా)
నిష్పత్తుల మొత్తం = 1 + 2 + 3 + 4 = 10

ప్రశ్న 5.
రేఖీయ కోణాల జతకు మీ పరిసరాల నుండి రెండు ఉదాహరణలు రాయండి.
సాధన.
- కిటికి నిలువు అడ్డు కమ్మీల మధ్య ఏర్పడు కోణాలు.
- కిటికీ తలుపు తెరచినపుడు తలుపు రెండు వైపులా ఏర్పడే కోణాలు.
![]()
ప్రశ్న 6.
“రెండు అధిక కోణాలు ఒక జత సంయుగ్మ కోణాలను ఏర్పరుస్తాయి” అని మణి చెప్పెను. దీనిని మీరు అంగీ కరిస్తారా ? మీ సమాధానాన్ని సమర్థించుము.
సాధన.
అంగీకరించను.
కారణం: అధిక కోణం విలువ 90° కన్నా ఎక్కువ 180° కన్నా తక్కువ ఉంటుంది. 180° కన్నా తక్కువ ఉన్న ఏ రెండు కోణాల మొత్తమైనా 360° కన్నా తక్కువ ఉంటుంది. కావున, ఆ రెండు కోణాలు సంయుగ్మ కోణాలు కావు.
ప్రశ్న 7.
ఒకదానికొకటి సంపూరకాలు కాని ఒక జత ఆసన్న కోణాలకు పటాన్ని గీయండి.
సాధన.
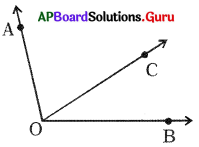
∠AOC, ∠COB లు ఆసన్న కోణాలు మరియు
∠AOC + ∠COB ≠ 180°
ప్రశ్న 8.
ఇచ్చిన పటంలో l || m మరియు t ఒక తిర్యగ్రేఖ. ∠1 మరియు ∠2 లను కనుగొనండి.
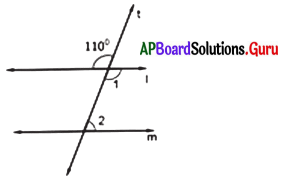
సాధన.
ఇచ్చిన పటంలో l|| m మరియు t ఒక తిర్యగ్రేఖ.
∠1 = 110° (శీర్షాభిముఖ కోణాలు)
∠1 + ∠2 = 180°
(తిర్యగ్రేఖకు అంతరంగా ఒకేవైపు గల కోణాలు)
110° + ∠2 = 180°
∠2 = 180° – 110°
∴ ∠2 = 70°
∴ ∠1 = 110° మరియు ∠2 = 70°
![]()
ప్రశ్న 9.
రెండు సరళరేఖలు l మరియు mలను మరో సరళరేఖ p రెండు విభిన్న బిందువుల వద్ద ఖండించినది. పటాన్ని పరిశీలించి, ఖాళీలను పూరించండి.
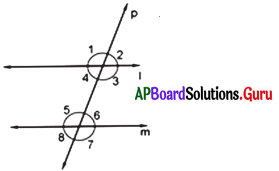
(i) సరళరేఖ ‘p’ ని ………………… అని అంటారు.
(ii) ∠1 మరియు ∠5 లు ………… కోణాల జత.
(iii) ∠4 మరియు ∠6 లు …………. కోణాల జత.
(iv) ∠3 మరియు ∠6 లు ……….. కోణాల జత.
సాధన.
(i) తిర్యక్ రేఖ
(ii) సదృశ కోణాల
(iii) ఏకాంతర కోణాల
(iv) తిర్యగేఖకు ఒకేవైపు అంతరంగా గల
ప్రశ్న 10.
ఇచ్చిన పటంలో \(\overleftrightarrow{C F}\) || \(\overrightarrow{\mathrm{BD}}\) మరియు \(\overrightarrow{\mathrm{BE}}\) ఒక తిర్యగ్రేఖ, ∠CAE = 135° అయిన ∠ABD విలువ కనుగొనండి.
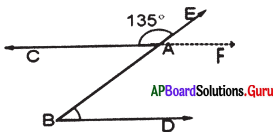
సాధన.
ఇచ్చిన పటంలో \(\overleftrightarrow{C F}\) || \(\overrightarrow{\mathrm{BD}}\) మరియు \(\overrightarrow{\mathrm{BE}}\) తిర్యగ్రేఖ.
∠CAE = 135°
∠BAF = ∠CAE (శీర్షాభిముఖ కోణాలు)
∴∠BAF = 1350
∠BAF + ∠ABD = 180° (తిర్యగ్రేఖకు అంతరంగా ఒకేవైపు గల కోణాలు)
⇒ 135° + ∠ABD = 180°
⇒ ∠ABD = 180° – 135°
∴ ∠ABD = 45°