SCERT AP 7th Class Maths Solutions Pdf Chapter 5 త్రిభుజాలు Ex 5.4 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 5th Lesson త్రిభుజాలు Exercise 5.4
ప్రశ్న 1.
త్రిభుజములోని రెండు భుజాలు 5 సెం.మీ. మరియు 4 సెం.మీ. అయిన మూడవ భుజమునకు సాధ్యమయ్యే మూడు కొలతలు రాయండి.
సాధన.
త్రిభుజంలోని రెండు భుజాలు 5 సెం.మీ. మరియు 4 సెం.మీ.
(మూడవ భుజమునకు సాధ్యమయ్యే కొలత 1 సెం.మీ. కన్నా ఎక్కువ, 9 సెం.మీ. కన్నా తక్కువగా ఉండాలి. 5 + 4 = 9, 5 – 4 = 1)
∴ మూడవ భుజమునకు సాధ్యమవు మూడు కొలతలు.
2 సెం.మీ., 3 సెం.మీ., 4 సెం.మీ.
ప్రశ్న 2.
రేఖా ఖండముల పొడవులు 3 సెం.మీ., 5 సెం.మీ., 6 సెం.మీ. మరియు 9 సెం.మీ.
(i) పై కొలతల నుండి ఏ మూడు కొలతలు త్రిభుజమును ఏర్పరుచునో చెప్పండి.
సాధన.
3 సెం.మీ., 5 సెం.మీ., 6 సెం.మీ. మరియు 5 సెం.మీ., 6 సెం.మీ., 9 సెం.మీ. పొడవు గల రేఖాఖండాలు త్రిభుజాలను ఏర్పరుస్తాయి.
(∵ ఏ రెండు భుజాల మొత్తమైనా మూడవ భుజం కన్నా ఎక్కువ).
![]()
(ii) ఏ కొలతలు త్రిభుజమును ఏర్పరచవు ? కారణం చెప్పండి.
సాధన.
3 సెం.మీ., 6 సెం.మీ., 9 సెం.మీ. పొడవు గల రేఖాఖండాలు త్రిభుజాన్ని ఏర్పరచవు.
కారణం: 3 సెం.మీ + 6 సెం.మీ. = 9 సెం.మీ.
రెండు భుజాల మొత్తం మూడవ భుజం కన్నా ఎక్కువ కావడం లేదు.
ప్రశ్న 3.
కింది త్రిభుజాలలో ‘x’ విలువను కనుగొనండి.
(i)
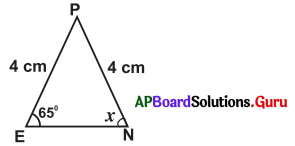
సాధన.
ఇచ్చిన త్రిభుజం PEN లో, PE = PN = 4 సెం.మీ.
కావున, ∠N = ∠E (∵ త్రిభుజంలో సమాన భుజాలకు ఎదురుగా గల కోణాలు సమానాలు)
∴ x = 65°
(ii)
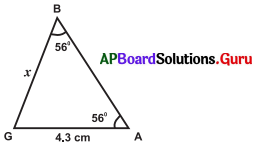
సాధన.
ఇచ్చిన త్రిభుజంలో ∠A = ∠B = 56°
కావున, \(\overline{\mathrm{GB}}\) = \(\overline{\mathrm{GA}}\) (∵ సమాన కోణాలకు ఎదురుగా గల భుజాలు సమానాలు)
∴ x = 4.3 సెం.మీ.
ఒక త్రిభుజంలో మూడు కోణాల మొత్తం 180°.
∆BGA లో, ∠B + ∠G + ∠A = 180°
⇒ 56° + x + 56° = 180°
⇒ 112° + x = 180°
⇒ x = 180° – 112°
∴ x = 68°
ప్రశ్న 4.
∆ABC ఒక సమద్విబాహు త్రిభుజం, AB = AC. ∠A = 80° అయిన ∠B మరియు ∠C లను కనుగొనండి.
సాధన.
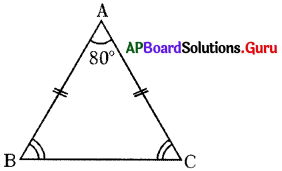
సమద్విబాహు త్రిభుజం ∆ABC లో AB = AC
కావున, ∠C = ∠B (∵ త్రిభుజంలో సమాన భుజాలకు ఎదురుగా గల కోణాలు సమానం)
ఇంకా ∠A + ∠B + ∠C = 180°
(∵ త్రిభుజంలోని మూడు కోణాల మొత్తం 180°)
⇒ 80° + ∠B + ∠B = 180° (∠B = ∠C)
⇒ 80° + 2∠B = 180°
⇒ 2∠B = 180° – 80°
⇒ 2∠B = 100°
⇒ ∠B = \(\frac{100^{\circ}}{2}\) = 50°
∴ ∠C = 50°
![]()
ప్రశ్న 5.
క్రింద ఇవ్వబడిన త్రిభుజాలలోని ‘X’ విలువలు కనుక్కోండి.
(i)
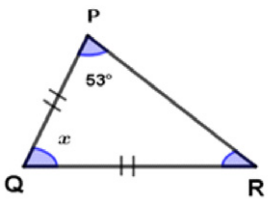
సాధన.
ఇచ్చిన త్రిభుజం POR లో, ∠P = 53°
PQ = QR కావున ∠R = ∠P
(∴ త్రిభుజంలో సమాన భుజాలకు ఎదురుగా గల కోణాలు సమానం)
∴ ∠R = 53°
ఇంకా ∠P + ∠Q + ∠R = 180°
⇒ 53° + x + 53° = 180°
⇒ 106° + x = 180°
⇒ x = 180° – 106
∴ x = 74°
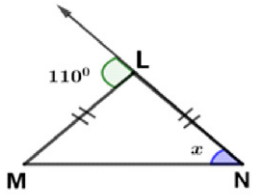
(ii)
సాధన.
ఇచ్చిన త్రిభుజం ∆LMN లో,
బాహ్యకోణం ∠L = 110° మరియు ∠M = ∠N
కావున, ∠N = ∠M = x
∴ ∠M + ∠N = 110° (∵ త్రిభుజ బాహ్యకోణం, దాని అంతరాభిముఖ కోణాల మొత్తానికి సమానం)
⇒ x + x = 110°
⇒ 2x = 110°
∴ x = \(\frac{110^{\circ}}{2}\) = 55°
![]()
ప్రశ్న 6.
క్రింద ఇవ్వబడిన పటము నుండి ఈ క్రింద ఇవ్వబడిన వాక్యములు ఏవి సత్యములు ?
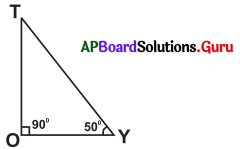
(i) OY < OT
సాధన.
సత్యము.
[కారణం: ∠T = 40° మరియు ∠Y = 50°
∠T మిగిలిన రెండు కోణాల కన్నా చిన్నది.
కావున, ∠T కి ఎదరుగా గల భుజం OY మిగిలిన రెండు భుజాల కన్నా చిన్నది.]
= ∠T + ∠Y = 90°
= ∠T = 90° – 50°
∴ ∠T = 40
(ii) TY < TO
సాధన.
అసత్యము.
[కారణం: 20 మిగిలిన రెండు కోణాల కన్నా పెద్దది. కావున, 20 కు ఎదురుగా గల భుజం మిగిలిన రెండు భుజాల కన్నా పెద్దది.]
(iii) ∠Y < ∠T
సాధన.
అసత్యము.
[కారణం: ∠Y = 50°, ∠T = 40°]
![]()
(iv) TY < OY
సాధన.
అసత్యము.
[కారణం: ∠O మిగిలిన రెండు కోణాల కన్నా పెద్దది. కావున, ∠O కు ఎదురుగా గల భుజం మిగిలిన రెండు భుజాల కన్నా పెద్దది.]