AP State Syllabus AP Board 9th Class Maths Solutions Chapter 10 Surface Areas and Volumes InText Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 10th Lesson Surface Areas and Volumes InText Questions
![]()
Try This
Take a cube of edge T cm and cut it as we did in the previous activity and find total surface area and lateral surface area of cube. [Page No. 216]
Solution:
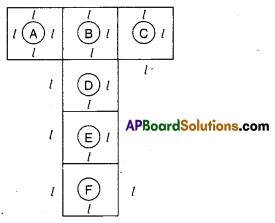
If we cut and open a cube of edgewe obtain a figure as shown above.
In the figure, A, B, C, D, E, F are squares of side
The faces A, C, D, F forms the lateral surfaces of the cube.
∴ Lateral surface area of the cube = 4l2
And all six faces form the cube.
∴ Total surface area of the cube = 6l2
![]()
Do This
Question 1.
Find the total surface area and lateral surface area of the cube with side 4 cm. By using the formulae deduced in above. Try this. [Page No. 216]1. Find the total surface area and lateral surface area of the cube with side 4 cm. By using the formulae deduced in above. Try this. [Page No. 216]
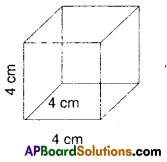
Solution:
Total surface area of a cube = 6l2
Given l = 4crn
∴ T.S.A. = 6 × 42 = 6 × 16 = 96 cm2
∴ L.S.A. = 4l2 = 4 × 42 = 64cm2
Question 2.
Each edge of a cube is increased by 50%. Find the percentage increase in the surface area. [Page No. 216]
Solution:
Let the edge of a cube x units
Its surface area = 6l2 = 6x2 sq. units
If its edge is increased by 50%, then
new edge = x + 50% of x


Where x = increase/decrease
![]()
Try These
Question
a) Find the volume of a cube whose edge is ‘a’ units. [Page No. 217]
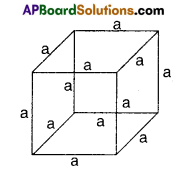
Solution:
V = edge3 = a3 cubic units.
b) Find the edge of a cube whose volume is 1000 cm3. [Page No. 217]
Solution:
V = edge3 = 1000 = 10 × 10 × 10 = 103
∴ Edge =10 cm
![]()
Do These
Question 1.
Find the volume of a cuboid if l = 12 cm, b = 10 cm, h = 8 cm. [Page No. 218]
Solution:
Volume V = lbh = 12 × 10 × 8 = 960cm3
Question 2.
Find the volume of cube, if its edge is 10 cm [Page No. 218]
Solution:
Volume V = l3 = 10 × 10 × 10 = 1000cm3
![]()
Question 3.
Find the volume of isosceles right angled triangular prism. [Page No. 218]
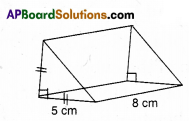
Solution:
Volume = Area of base × height
= Area of isosceles triangle × height

Activity
Question
Take the square pyramid and cube containers of same base and with equal heights. [Page No. 218]
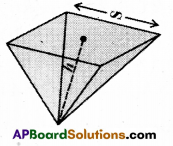
Fill the pyramid with a liquid and pour into the cube (prism) completely. How many times it takes to fill the cube? From this, what inference can you make?
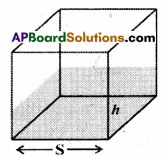
Thus volume of pyramid = \(\frac { 1 }{ 3 }\) × of the volume of right prism
= \(\frac { 1 }{ 3 }\) × Area of the base × height.
Note : A right prism has bases perpendicu¬lar to the lateral edges and all lateral faces are rectangles.
![]()
Do These
Question 1.
Find the volume of a pyramid whose square base is 10 cm and height is 8 cm. (Page No. 219)
Solution:
Volume of a pyramid
= \(\frac { 1 }{ 3 }\) × Area of the base × height
= \(\frac { 1 }{ 3 }\) × 10 x 10 × 8 = \(\frac { 800 }{ 3 }\) cm3
Question 2.
The volume of a cube is 1200 cubic cm. Find the volume of square pyra¬mid of the same height. (Page No. 219)
Solution:
Volume of the square pyramid
= \(\frac { 1 }{ 3 }\) × volume of the square prism
= \(\frac { 1 }{ 3 }\) × 1200 = 400 cm3
![]()
Activity
Cut out a rectangular sheet of paper. Paste a thick string along the line as shown in the figure. Hold the string with your hands on either sides of the rectangle and rotate the rectangle sheet about the string as fast as you can.
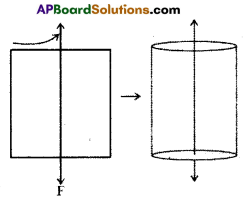
Do you recognize the shape that the rotating rectangle is forming ?
Does it remind you the shape of a cylinder ? [Page No. 220]
Do This
Question 1.
Find C.S.A. of each of the following cylinders. [Page No. 221]
i) r = x cm; h = y cm
Solution:
CSA = 2πrh = 2πxy cm2
ii) d = 7 cm; h = 10 cm
Solution:
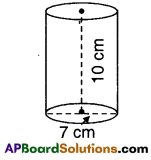
CSA = 2πrh
= 2 × \(\frac{22}{7} \times \frac{7}{2}\) × 10
= 220 cm2
iii) r = 3 cm; h = 14 cm
Solution:
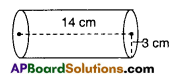
CSA = 2πrh
= 2 × \(\frac{22}{7} \times \frac{7}{2}\) × 3 × 14
= 264 cm2
![]()
Question 2.
Find the total surface area of each of the following cylinder. [Page No. 222]
i)
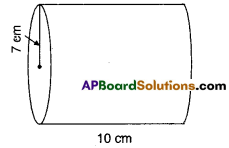
Solution:
r = 7 cm; h = 10 cm
T.S.A. = 2πr (r + h)
=2 × \(\frac{22}{7}\) × 10 (7 + 10)
= 2 × \(\frac{22}{7}\) × 10 × 17
= 1068.5 cm2
ii)
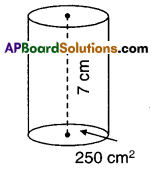
h = 7cm; πr2 = 250
πr2 = 250 = 250
\(\frac{22}{7}\) × r2 = 250 = 250
r2 = 125 x \(\frac{7}{11}\)

![]()
Try These
Question 1.
If the radius of a cylinder is doubled keeping Its lateral surface area the same, then what is its height? [Page No. 225]
Solution:
Let the initial radius and height of the
cylinder be r and h.
Then L.S.A. = 2πrh
When r is doubled and the L.S.A. remains the same, then the height be hr By problem new L.S.A. = 2πrh
= 2π (2r) (h1)
⇒ 2πrh = 4πrh1
∴ \(\frac{2 \pi \mathrm{rh}}{4 \pi \mathrm{r}}=\frac{1}{2} \mathrm{~h}\)
Height becomes its half.
Question 2.
A hot water system (Geyser) consists of a cylindrical pipe of length 14 m and diameter 5 cm. Find the total radiating surface of hot water system. [Page No. 225]
Solution:
Radius (r) = \(\frac{\text { diameter }}{2}=\frac{5}{2}\) = 2.5 cm
Length of the pipe = height = 14 m Radiating surface = 2πrh
= 2 × \(\frac{22}{7}\) × 2.5 × 1400
= 22000 cm3
Activity
Question
Making a cone from a sector. [Page No. 227] Follow the instructions and do as shown in the figure.
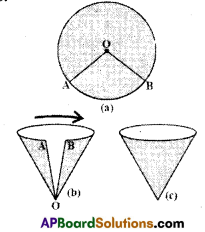
i) Draw a circle on a thick paper Fig (a).
ii) Cut a sector AOB from it Fig (b).
iii) Fold the ends A, B nearer to each other slowly and join AB. Remember A, B should not overlap on each other. After joining A, B attach them with cello tape Fig (c).
iv) What kind of shape you have obtained? Is it a right cone?
While making a cone observe what hap-pened to the edges ‘OA’ and ‘OB’ and length of arc AB of the sector?
![]()
Try This
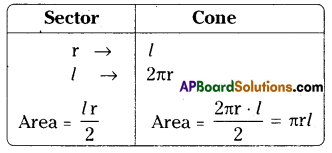
A sector with radius r and length of its arc / is cut from a circular sheet of paper. Fold it as a cone. How can you derive the formula of its curved surface area A = πrl. [Page No. 228]
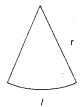
C.S.A = πrl
Solution:
When a sector of radius ‘r’ and whose length of arc l is folded to form a cone. Radius ‘r’ becomes slant height ‘l’ and arc ‘l’ becomes perimeter of the base 2πr.
∴ Area of the sector = \(\frac{l r}{2}\) = Area of the cone
\(\frac{2 \pi \mathrm{r} l}{2}\) = Surface area of the cone
C.S.A = πrl
![]()
Do This
Question 1.
Cut a right angled triangle. Stick a string along its perpendicular side, as shown in fig. (T) hold both the sides of a string with your hands and rotate it with constant speed. What do you observe ? [Page No. 229]
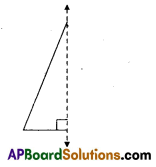
Solution:
A right circular cone is observed.
Question 2.
Find the curved surface area and total surface area of the each following right circular cones.[Page No. 229]
Solution:
OP = 2 cm; OB = 3.5 cm
OP = h = 2 cm
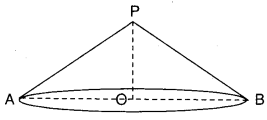
OP = 3.5 cm; AB = 10 cm
r = \(\frac{\mathrm{AB}}{2}\) = 5cm; h = 3.5cm
r = OB = 3.5 cm
C.S.A. = πrl
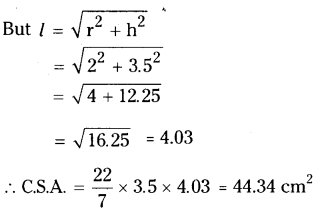
T.S.A. = πr (r + l)
= \(\frac{22}{7}\) × 3.5(3.5 + 4.03)
= \(\frac{22}{7}\) × 3.5 × 7.53 = 82.83cm2
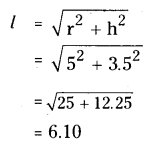
C.S.A. = πrl
\(\frac{22}{7}\) × 5 × 6.10
= 95.90cm2
T.S.A. = πr (r + l)
= \(\frac{22}{7}\) × 5 × (5 + 6.10)
= 174.42 cm2
![]()
Activity
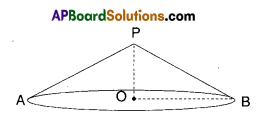
Draw a circle on a thick paper and cut it neatly. Stick a string along its diam¬eter. Hold the both the ends of the string with hands and rotate with con¬stant speed and observe the figure so formed. [Paper 235]
Try This
Question 1.
Can you find the surface area of sphere in any other way ? (Page No. 235)
Solution:
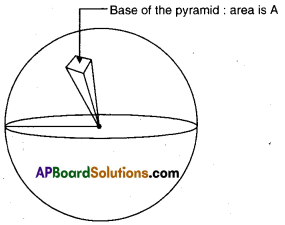
Height of the pyramid is equal to r.
To derive the formula of the surface area of a sphere, we imagine a sphere with many pyramids inside of it until the base of all the pyramids cover the entire surface area of the sphere. In the figure below, only one of such pyra¬mid is shown.
Then, do a ratio of the area of the pyramid to the volume of the pyramid.
The area of the.pyramid is A.
The volume of the pyramid is V = (1/3) × A × r = (A × r)/3
So, the ratio of area to volume is A/V = A + (A × r) / 3 = (3 × A) / (A × r) = 3 / r
For a large number of pyramids, let say that n is such large number, the ratio of the surface area of the sphere to the volume of the sphere is the same as 3/r.
For n pyramids, the total area is n × A- Also for n pyramids, the total volume is n × V.
Therefore, ratio of total area to total volume is n × A/n × V = A/ V and we already saw before that A / V = 3 / r
Further more, n × Apyramid = Asphere (The total area of the bases of all pyramids or n pyramids is approximately equal to the surface area of the sphere).
n × Vpyramid = Vsphere (The total Volume of all pyramids or n pyramids is approximately equal to the volume of the sphere.
Putting observation # 1 and # 2 together, we get

Therefore, the total surface area of a sphere, call it S.A. is 4πr 2
![]()
Do These
Question 1.
A right circular cylinder just encloses a sphere of radius r (see figure). Find i) surface area of the sphere
ii) curved surface area of the cylinder
iii) ratio of the areas obtained in (i) and (ii) [Page No. 236]
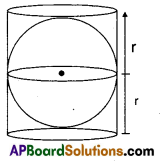
[Page No. 236]
Solution:
i) Radius of the sphere = radius of the cylinder = r
∴Surface area of the sphere = 4πr2
ii) C.S.A. of cylinder = 2πr (2r) [∵ h = 2r]
= 4πr2
iii) Ratio of (i) and (ii) = 4πr2 : 4πr2 = 1:1
Question 2.
Find the surface area of each of the following figure.
i)
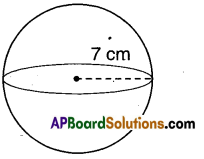
Surface area = 4πr2
C.S.A = 4 × \(\frac{22}{7}\) × 7 × 7
= 616cm2
ii)
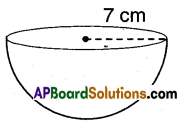
C.S.A = 2πr2 = 2 × \(\frac{22}{7}\) × 7 × 7 = 308cm2
Total Surface area = 3πr2
= 3 × \(\frac{22}{7}\) × 7 × 7 = = 462cm2
![]()
Do This
Question 1.
Find the volume of the sphere given below[Page No. 238]
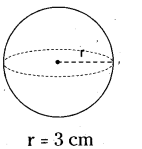
Solution:
r = 3 cm
V = \(\frac{4}{3} \pi r^{3}=\frac{4}{3} \times \frac{22}{7}\) × 3 × 3 × 3
= 113.14cm3
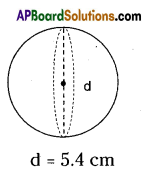
d = 5.4 cm
r = \(\frac{\mathrm{d}}{2}=\frac{5.4}{2}\) = 2.7 cm
V = \(\frac{4}{3} \pi r^{3}=\frac{4}{3} \times \frac{22}{7}\) × 2.7 × 2.7 × 2.7 = 82.48cm3
![]()
Question 2.
Find the volume of sphere of radius 6.3 cm. [Page No. 238]
Solution:
r = 6.3 cm
V = \(\frac{4}{3} \pi r^{3}\)
= \(\frac{4}{3} \times \frac{22}{7}\) × 6.3 × 6.3 × 6.3 = 1047.81cm3