AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2

by

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 13th Lesson Geometrical Constructions Exercise 13.2

AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2

Question 1.
Construct AABC in which BC = 7 cm,∠B = 75° and AB + AC =12 cm.
Solution:
A.
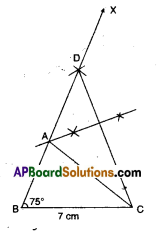
AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2 1
Steps:

  • Draw a line segment BC = 7 cm.
  • Erect ∠B = 75°
  • MarkapointDon \(\overrightarrow{\mathrm{BX}}\) suchthat BD = AB + AC.
  • Join D, C and draw the perpendicular bisector of \(\overline{\mathrm{CD}}\) meeting BD at A.
  • Join A to C to form the ΔABC.

AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2

Question 2.
Construct ΔPQR in which QR = 8 cm, ∠B = 60° and AB – AC = 3.5 cm.
Read ∠Q = 60°and PQ – PR = 3.5 cm
Solution:
A.
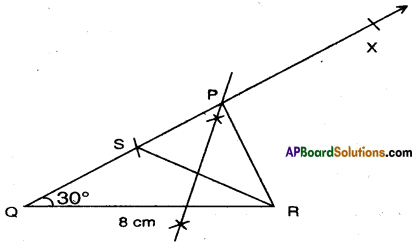
AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2 2
Steps: I

  • Draw QR = 8 cm.
  • Construct ∠RQX = 300 at Q.
  • Mark a point S on \(\overrightarrow{\mathrm{QX}}\) such that QS = PQ  –  PR = 3.5 cm.
  • Join S, R and draw the perpendicular bisector to \(\overline{\mathrm{QR}}\) meeting \(\overrightarrow{\mathrm{QX}}\) at P.
  • Join P, R to form the ΔPQR.

AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2

Question 3.
Construct ΔXYZ in which ∠Y = 30 °; ∠Z = 60 ° and XY + YZ + ZX = 10 cm.
Solution:
A.
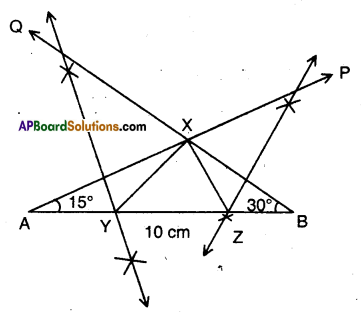
AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2 3
Steps:

  • Draw a line segment AB = XY + YZ + ZX = 10 cm.
  • Construct ∠BAP = \(\frac { 1 }{ 2 }\) ∠Y at A and ∠ABQ = \(\frac { 1 }{ 2 }\) ∠Z at B meeting at X.
  • Draw the perpendicular bisectors to XA and XB meeting \(\overline{\mathrm{AB}}\) at Y and Z respectively.
  • Join X to Y and Z to form the ΔXYZ.

AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2

Question 4.
Construct a right triangle whose base is 7.5 cm and sum of its hypotenuse and otherside is 15 cm.
Solution:
A.
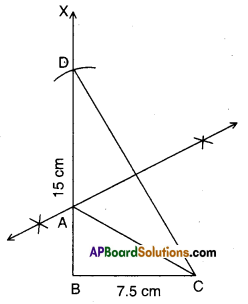
AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2 4
Steps:

  • Draw BC = 7.5 cm.
  • Construct ∠CBX = 90°
  • Mark a point D on \(\overrightarrow{\mathrm{BX}}\) such that BD = 15 cm.
  • Join C, D. ‘
  • Draw the perpendicular bisectors of \(\overline{\mathrm{CD}}\) meeting BD at A.
  • Join A, C to form the ΔABC.

AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2

Question 5.
Construct a segment of a circle on a chord of length 5 cm containing the following angles i) 90° ii) 45° iii) 120°
Solution:
i) 90°
A.
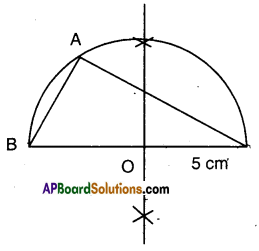
AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2 5
AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2 6

Steps:

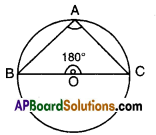
  • Draw a rough sketch of ∠BAC = 90° and ∠BOC = 180°.
  • Draw a line segment BC = 5 cm.
  • Draw the perpendicular bisector of BC meeting \(\overline{\mathrm{BC}}\) at O
  • Draw an arc of radius OB or OC with centre O.
  • Mark any point A on the arc and join it with B and C.
  • ∠BAC = 90°

ii) 45°
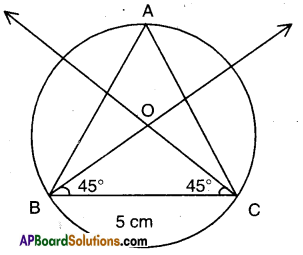
AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2 7
AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2 8

Steps:

  • Draw a line segment BC = 5 cm.
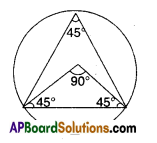
  • Construct ABOC such that BC = 5 cm, ∠B = 45° = ∠C.
  • Draw a circle segment of radius OB or OC with centre ’O’.
  • Mark any point A on the segment and join it with B and C.
  • ∠BAC = 45°

AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2

iii) 120°
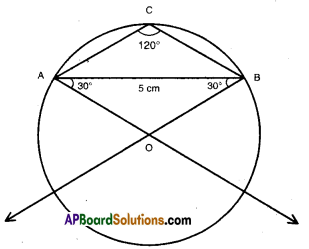
AP Board 9th Class Maths Solutions Chapter 13 Geometrical Constructions Ex 13.2 9

Steps:

  • Draw a line segment AB = 5 cm. ,
  • Construct ΔAOB in which ∠A = 30°; ∠B = 30°; AB = 5 cm.
  • With ‘O’ as centre draw a circle segment.
  • On the opposite side make any point C and join it with B and C.
  • ∠ACB = 120°