AP Inter 1st Year Maths 1A Important Questions Chapter 9 అతిపరావలయ ప్రమేయాలు

Students get through AP Inter 1st Year Maths 1A Important Questions Chapter 9 అతిపరావలయ ప్రమేయాలు which are most likely to be asked in the exam.

AP Inter 1st Year Maths 1A Important Questions Chapter 9 అతిపరావలయ ప్రమేయాలు

సాధించిన సమస్యలు
(Solved Problems)

ప్రశ్న 1.
ప్రతి x ∈ R sinh (3x) = 3 sinh x + 4sinh³ x అని నిరూపించండి.
సాధన:
LHS = sinh (3x)
= sinh (2x + x)
= sinh (2x) . cosh (x) + cosh (2x) . sinh (x)
= (2 sinh x cosh x) cosh x + (1 + 2 sinh² x) sinh x
= 2 sinh x (cosh² x) + (1 + 2 sinh² x) sinh x
= 2 sinh x (1 + sinh² x) + (1 + 2 sinh² x) sinh x
∵ cosh² x – sinh² x = 1
= 3 sinh x + 4 sinh³ x
∵ sinh (3x) = 3 sinh x + 4 sinh³ x

ప్రశ్న 2.
ప్రతి x ∈ R కు tanh 3x = \(\frac{3 \tanh x+\tanh ^3 x}{1+3 \tanh ^2 x}\) అని నిరూపించండి.
సాధన:
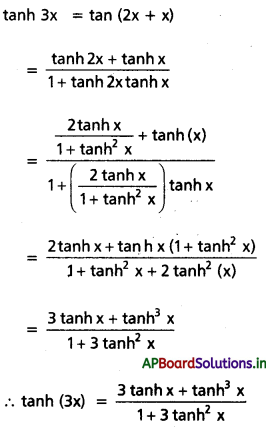
AP Inter 1st Year Maths 1A Important Questions Chapter 9 అతిపరావలయ ప్రమేయాలు 5

ప్రశ్న 3.
cosh x = \(\frac{5}{2}\) అయితే,
i) cosh (2x)
ii) sinh (2x) లువలు కనుక్కోండి (May ’11, ’06)
సాధన:
i) cosh (2x) = 2 cosh² (x) – 1
= 2\(\left(\frac{5}{2}\right)^2\) – 1 = \(\frac{25}{2}\) – 1 = \(\frac{23}{2}\)

ii) sinh² (2x) = cosh² (2x) – 1
= \(\left(\frac{23}{2}\right)^2\) – 1 = \(\frac{529-4}{4}\) = \(\frac{525}{4}\)
∴ sinh (2x) = ± \(\sqrt{\frac{525}{4}}\) = ± \(\frac{5 \sqrt{21}}{2}\)

ప్రశ్న 4.
cosh x = sec θ అయితే tanh² \(\frac{x}{2}\) = tan² \(\frac{\theta}{2}\) అని నిరూపించండి.
సాధన:
tan²\(\frac{x}{2}\) =
\(\frac{\cosh x-1}{\cosh x+1}\) = \(\frac{\sec \theta-1}{\sec \theta+1}\) = \(\frac{1-\cos \theta}{1+\cos \theta}\) = tan^-1 \(\frac{\theta}{2}\)

ప్రశ్న 5.
θ ∈ \(\left(-\frac{p}{4}, \frac{p}{4}\right)\), x = log_e\(\left(\cot \left(\frac{p}{4}+q\right)\right)\)
అయినప్పుడు
(i) cosh x = sec 2θ,
(ii) sinh x = tan 2θ అని నిరూపించండి.
సాధన:
AP Inter 1st Year Maths 1A Important Questions Chapter 9 అతిపరావలయ ప్రమేయాలు 1

i) cosh (x) = \(\frac{e^x+e^{-x}}{2}\)
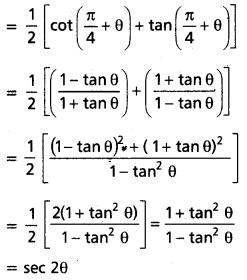
AP Inter 1st Year Maths 1A Important Questions Chapter 9 అతిపరావలయ ప్రమేయాలు 2
∴ cosh x = sec 2θ

ii) sinh x = \(\frac{\mathrm{e}^{\mathrm{x}}-\mathrm{e}^{-\mathrm{x}}}{2}\)
AP Inter 1st Year Maths 1A Important Questions Chapter 9 అతిపరావలయ ప్రమేయాలు 3
∴ sinh x = tan 2θ

ప్రశ్న 6.
sinh x = 5 soma x = log_e (5 + \(\sqrt{26}\)) అని చూపండి.
సాధన:
∴ sinh (x) = 5
⇒ x = sinh^-1 (5)
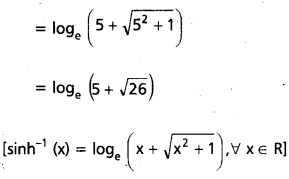
AP Inter 1st Year Maths 1A Important Questions Chapter 9 అతిపరావలయ ప్రమేయాలు 4

ప్రశ్న 7.
tanh^-1 \(\left(\frac{1}{2}\right)\) = \(\frac{1}{2} \log _e 3\) అని చూపండి. (Mar. ’15, ’08, 05; May ’07, ’05)
సాధన:
∵ tanh^-1(x) = \(\frac{1}{2}\)log_e \(\left(\frac{1+x}{1-x}\right)\), ∀ x ∈ (-1, 1)
∵ tanh^-1(x) \(\frac{1}{2}\) = \(\frac{1}{2}\)log_e\(\left(\frac{1+\frac{1}{2}}{1-\frac{1}{2}}\right)\)
= \(\frac{1}{2}\)log_e (3)