Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 3 మాత్రికలు Exercise 3(g) will help students to clear their doubts quickly.
AP Inter 1st Year Maths 1A Solutions Chapter 3 మాత్రికలు Exercise 3(g)
క్రింది సమీకరణ వ్యవస్థలు సంగతమో, కాదో పరీక్షించండి. సంగతమైతే పూర్తిగా సాధించండి.
Question 1.
x + y + z = 4
2x + 5y – 2z = 3
x + 7y – 7z = 5
Solutions:

ρ(A) = 2, ρ(AD) = 3
ρ(A) ≠ ρ(AD)
∴ దత్త సమీకరణ వ్యవస్థ అసంగతం.
సాధన లేదు.
![]()
Question 2.
x + y + z = 6
x – y + z = 2
2x – y + 3z = 9 [Mar. ’11]
Solution:
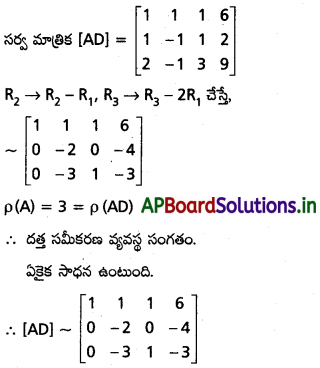

Question 3.
x + y + z = 1
2x + y + z = 2
x + 2y + 2z = 1 [(T.S) Mar. ’15]
Solution:

ρ(A) = 2 = ρ(AB) < 3
దత్త వ్యవస్థ సంగతం. అనేక సాధనాలు ఉంటాయి.
సాధన సమితి [(x, y, z) 1x = 1, y + z = 0].
Question 4.
x + y + z = 9
2x + 5y + 7z = 52
2x + y – z = 0
Solution:


∴ ρ(A) = ρ(AB) = 3
దత్త వ్యవస్థ సంగీతం ఏకైక సాధన ఉంటుంది.
∴ సాధన x = 1, y = 3, z = 5.
![]()
Question 5.
x + y + z = 6
x + 2y + 3z = 10
x + 2y + 4z = 1
Solution:

∴ ρ(A) = ρ(AB) = 3
దత్త వ్యవస్థ సంగతం.
ఏకైక సాధన ఉంటుంది.
∴ సాధన x = -7, y = 22, z = -9.
Question 6.
x – 3y – 8z = -10
3x + y – 4z = 0
2x + 5y + 6z = 13
Solution:
సర్వ మాత్రిక


ρ(A) = ρ(AB) = 2 < 3
∴ దత్త వ్యవస్థ సంగతము అనేక సాధనాలు ఉంటాయి.
x + y = 2, y + 2z = 3
z = k అయిన y = 3 – 2z = 3 – 2k
x = 2 – y
= 2 – (3 – 2k)
= 2 – 3 + 2k
= 2k – 1
∴ సాధన x = -1 + 2k, y = 3 – 2k, z = k, ‘k’ ఒక సంఖ్య.
Question 7.
2x + 3y + z = 9
x + 2y + 3z = 6
3x + y + 2z = 8
Solution:


ρ(A) = ρ(AB) = 3
దత్త వ్యవస్థ సంగతము ఏకైక సాధన ఉంటుంది.
∴ సాధన x = \(\frac{35}{18}\), y = \(\frac{29}{18}\), z = \(\frac{5}{18}\)
![]()
Question 8.
x + y + 4z = 6
3x + 2y – 2z = 9
5x + y + 2z = 13
Solution:

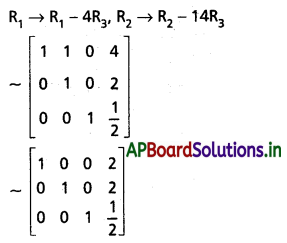
ρ(A) = ρ(AB) = 3
∴ దత్త వ్యవస్థ సంగతము ఏకైక సాధనం ఉంటుంది.
∴ సాధన x = 2, y = 2, z = \(\frac{1}{2}\)