AP Inter 1st Year Physics Study Material Chapter 14 అణుచలన సిద్ధాంతం

Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 14th Lesson అణుచలన సిద్ధాంతం Textbook Questions and Answers.

AP Inter 1st Year Physics Study Material 14th Lesson అణుచలన సిద్ధాంతం

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
స్వేచ్ఛా పథమథ్యమాన్ని నిర్వచించండి.
జవాబు:
రెండు వరుస అభిఘాతాల మధ్య అణువు ప్రయాణం చేసిన సరాసరి దూరంను స్వేచ్ఛా పథమధ్యమము అంటారు.

ప్రశ్న 2.
అణుచలనానికి నిర్ణయాత్మక రుజువును ఇచ్చే రెండు ప్రధాన దృగ్విషయాలను తెలపండి.
జవాబు:

1. డాల్టన్ నియమము
2. అవగాడ్రో నియమము.

ప్రశ్న 3.
అణుచలన సిద్ధాంతం అవగాడ్రో పరికల్పనను ఏవిధంగా సమర్ధిస్తుంది? వివిధ వాయువులకు ఉండే అవగాడ్రో సంఖ్య ఒకటే అయి ఉంటుందని చూపండి.
జవాబు:
రెండు వేర్వేరు వాయువులకు, \(\frac{P_1V_1}{T_1}=\frac{P_2V_2}{T_2}\) = K_B (స్థిరాంకం)
P, V, Tలు సమానం అయిన, రెండు వాయువులకు N కూడా సమానం.

N ను అవగాడ్రో సంఖ్య అంటారు. అవగాడ్రో భావన ప్రకారము, ప్రమాణ ఘనపరిమాణంలోని అణువుల సంఖ్య, అన్ని వాయువులకు స్థిర ఉష్ణోగ్రత మరియు పీడనాల వద్ద సమానము.

ఈ విధంగా గతిజ సిద్ధాంతం అవగాడ్రో భావనకు న్యాయం చేకూర్చుతుంది.

ప్రశ్న 4.
నిజ వాయువు ఆదర్శ వాయువులాగా ఎప్పుడు ప్రవర్తిస్తుంది? [Mar. ’14]
జవాబు:
అల్ప పీడనము మరియు అధిక ఉష్ణోగ్రతల వద్ద నిజ వాయువులు ఆదర్శ వాయువుల వలె ప్రవర్తించును.

ప్రశ్న 5.
బాయిల్, చార్లెస్ నియమాలను పేర్కొనండి.
జవాబు:
బాయిల్ నియమము :
స్థిర ఉష్ణోగ్రత వద్ద, నియమిత ద్రవ్యరాశి గల వాయువు ఘనపరిమాణం, పీడనానికి విలోమానుపాతంలో ఉండును.

చార్లెస్ నియమము :
స్థిర పీడనం వద్ద, నియమిత ద్రవ్యరాశి గల వాయువు ఘనపరిమాణం, వాయు పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉండును.

ప్రశ్న 6.
డాల్టన్ పాక్షిక పీడనాల నియమాన్ని తెలపండి. [Mar. ’14]
జవాబు:
“ఆదర్శ వాయువుల మిశ్రమం మొత్తం పీడనం, ఆ మిశ్రమంలోని వివిధ వాయువులు కలుగజేసే పాక్షిక పీడనాల మొత్తానికి సమానం”. దీనినే డాల్టన్ పాక్షిక పీడనాల నియమం అంటారు.

ప్రశ్న 7.
పాత్రలోని ఆదర్శ వాయువు పీడనం ‘పాత్ర ఆకారంపై ఆధారపడదు – వివరించండి.
జవాబు:
ఒక పాత్రలోని నిర్ణీత ద్రవ్యరాశి గల ఆదర్శ వాయువు పీడనంనకు, గతిజ సిద్ధాంత సమాసము P = \(\frac{1}{3}\) nm V^-2, ఇక్కడ V² సగటు వర్గ వడి, n అణువుల సంఖ్య, m అణు ద్రవ్యరాశి. కావున ఆదర్శ వాయు పీడనం, పాత్ర ఆకారంపై ఆధారపడదు.

ప్రశ్న 8.
వాయువులోని అణువుల స్వతంత్ర పరిమితులనే భావనను వివరించండి.
జవాబు:
అంతరాళంలో స్వేచ్ఛగా చలిస్తున్న అణువు స్థానాన్ని నిర్దేశించు నిరూపకాలను స్వతంత్ర పరిమితులు అంటారు. ఏకపరమాణుక అణువు (He) మూడు స్వేచ్ఛా కంపనరీతులను, ద్విపరమాణుక అణువు (H₂, O₂) ఐదు స్వేచ్ఛా కంపనరీతులను, త్రిపరమాణుక అణువు (H₂O) ఆరు స్వేచ్ఛా కంపనరీతులను కల్గి ఉండును.

ప్రశ్న 9.
వాయు అణువు గతిజశక్తికీ, వాయు పీడనానికి మధ్య సంబంధాన్ని తెలిపే సమాసం ఏమిటి?
జవాబు:

ప్రశ్న 10.
వాయువు పరమ ఉష్ణోగ్రతను 3 రెట్లు పెంచితే, ఆ వాయు అణువు rms వేగంలో పెరుగుదల ఎంత ఉంటుంది?
జవాబు:

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
ఉష్ణోగ్రతకు గతిక అర్థ వివరణను వివరించండి.
జవాబు:
ఉష్ణోగ్రతకు గతిక అర్థ వివరణ :
వాయువు యొక్క పీడనము P = \(\frac{1}{3} \mathrm{mn} \overline{\mathrm{V}}^2\)
ఇక్కడ m = వాయువు ద్రవ్యరాశి, n = \(\frac{N}{V}\) = ప్రమాణ ఘనపరిమాణంలో అణువుల సంఖ్య \(\overline{\mathrm{V}}\) = వాయు r.m.s వేగం

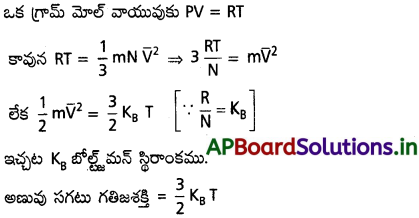
ఇది ఉష్ణోగ్రతపై ఆధారపడును. ఉష్ణోగ్రత పెరిగిన అణువుల గతిజశక్తి కూడ పెరుగును.

ప్రశ్న 2.
ఏకపరమాణక, ద్విపరమాణుక, బహు పరమాణుక వాయువుల విశిష్టోష్ణ సామర్థ్యాన్ని శక్తి సమవిభజన నియమం ఆధారంగా ఏ విధంగా వివరించవచ్చు? [Mar. ’13]
జవాబు:
విశిష్ట ఉష్ణధారణ సామర్థ్యం :
1) ఏకపరమాణుక వాయువులు :
సమశక్తి తుల్యతా నియమము ప్రకారము, ఏకపరమాణుక వాయువులు 3(స్థానాంతరణ) స్వతంత్ర పరిమితులు కలిగి ఉండును. i.e., f = 3.

స్థిర ఘనపరిమాణం వద్ద వాయు మోలార్ విశిష్టోష్ణము, C_V = \(\frac{f}{2}\)R
ఇక్కడ f స్వతంత్ర పరిమితులను తెల్పును.

2) ద్విపరమాణుక వాయువులు :
ఒక ద్విపరమాణుక వాయువుకు 3 స్థానాంతరణ మరియు 2 భ్రమణ, మొత్తం 5 స్వతంత్ర పరిమితులు కలిగి ఉండును. i. e., f = 5

3) బహుపరమాణుక వాయువులు :
బహుపరమాణుక అణువు 3 స్థానాంతరణ, 3 భ్రమణ, మొత్తం 6 స్వతంత్ర పరిమితులు కలిగి ఉండును. i.e., f = 6

ప్రశ్న 3.
అణుచలన సిద్ధాంతం ఆధారంగా పరమశూన్య ఉష్ణోగ్రత భావనను వివరించండి.
జవాబు:
అణుచలన సిద్ధాంతం ఆధారంగా పరమశూన్య ఉష్ణోగ్రత భావన :

పై సమీకరణంలో T = 0 ప్రతిక్షేపించితే, \(\overline{\mathrm{V}}\) = 0.

కావున పీడనం శూన్యమగును. అప్పుడు వాయువు ద్రవంలోనికి మారును. ఈ ఉష్ణోగ్రతను పరమశూన్యం అంటారు.

ప్రశ్న 4.
ఆదర్శ వాయువులోని అణువు సగటు గతిజశక్తి, వాయువు పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉంటుందని రుజువు చేయండి.
జవాబు:
వాయువు యొక్క పీడనము P = \(\frac{1}{3} \mathrm{mn} \overline{\mathrm{V}}^2\)
ఇక్కడ m = వాయు ద్రవ్యరాశి, n = \(\frac{N}{V}\) = ప్రమాణ ఘనపరిమాణంలోని అణువుల సంఖ్య,
\(\overline{\mathrm{V}}\) = వాయు r.m.s వేగము.

అణువు సగటు గతిజశక్తి, వాయు పరమ ఉష్ణోగ్రతకు అనులోమానుపాతంలో ఉండును.

ప్రశ్న 5.
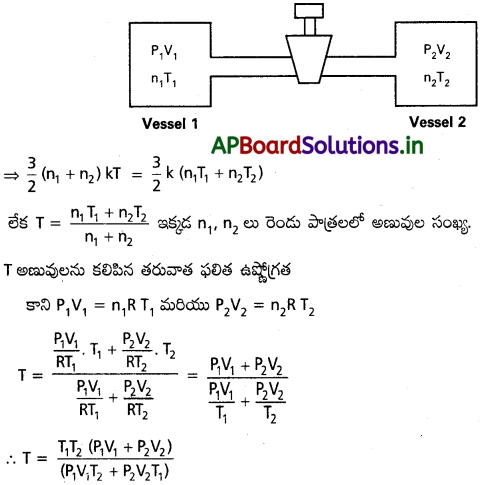
V₁, V₂ ఘనపరిమాణాలు కలిగిన రెండు ఉష్ణ బంధక పాత్రలు 1,2 లను ఒక వాల్వుతో కలిపి వాటిలో ఉష్ణోగ్రతలు (T₁, T₂) పీడనాలు (P₁, P₂) వరుసగా ఉండేటట్లుగా గాలిని నింపారు. ఈ రెండు పాత్రలను కలిపే ఆ వాల్వ్ు ఇప్పుడు తెరిస్తే, సమతాస్థితి వద్ద ఆ పాత్రల్లో ఉష్ణోగ్రత ఎంత ఉంటుంది?
జవాబు:
స్థిరోష్ణక ప్రక్రియలో, శక్తిలో నష్టం ఉండదు. i.e. అణువులను కలుపక ముందు K.E_T = అణువులను కల్పిన తరువాత K.E_T

ప్రశ్న 6.
ఒకే ఉష్ణోగ్రత వద్ద ఉన్న ఆక్సిజన్, హైడ్రోజన్ అణువులు rms వడుల నిష్పత్తి ఎంత?
జవాబు:

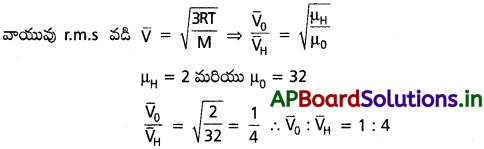
ప్రశ్న 7.
ఒక వాయువులోని నాలుగు అణువుల 1,2, 3, 4 km/s. ల వడులు కలిగి ఉన్నాయి. ఆ వాయు అణువు rms వడిని కనుక్కోండి.
జవాబు:

ప్రశ్న 8.
ఒక వాయువుకు f స్వతంత్ర పరిమితులు ఉంటే, Cp, C. ల నిష్పత్తిని కనుక్కోండి.
జవాబు:
ఒక వాయువు f స్వతంత్ర పరిమితులను కలిగి ఉంటే,

ప్రశ్న 9.
127°C వద్ద ఉన్న 1 గ్రాము హీలియం (అణుభారం 4)కు అణు గతిజశక్తిని లెక్కించండి.
R = 8.31 J mol^-1 K^-1.
జవాబు:
ఇచ్చినవి t = 127°C, T = 273 + 127 = 400; R = 8.31 J mol^-1 K^-1
K.E. = \(\frac{3}{2}\)K_ВТ = \(\frac{3}{2}\) × 1.38 × 10^-23 × 400 = 8.28 × 10^-21 J

ప్రశ్న 10.
ఒక వాయువుకు పీడనం 2% పెరిగితే, దాని ఘనపరిమాణంలో తగ్గుదల శాతం ఎంత ఉంటుంది ? వాయువు బాయిల్ నియమం పాటిస్తుందని ఊహించండి.
జవాబు:
వాయువు బాయిల్ నియమాన్ని పాటిస్తే, PV = స్థిరాంకం.
అవకలనం చేయగా, PdV + VdP = 0

% ఘనపరిమాణంలో మార్పు = – % పీడనంలో మార్పు
% ఘనపరిమాణంలో మార్పు = – 2%
ఇచ్చట రుణగుర్తు. ఘనపరిమాణంలో తగ్గుదలను సూచిస్తుంది.

దీర్ఘ సమాధాన ప్రశ్న

ప్రశ్న 1.
అణుచలన సిద్ధాంతం నుంచి ఒక పాత్రలోని ఆదర్శ వాయువు పీడనానికి సమాసం రాబట్టి, తద్వారా ఉష్ణోగ్రతకు గతిక అర్థ వివరణను ఇవ్వండి.
జవాబు:
a) భుజం l ఉన్న, పరిపూర్ణ స్థితిస్థాపక గోడలున్న ఘనాకార పాత్ర ఆదర్శ వాయు అణువులు కలిగి ఉన్నట్లు భావిద్దాము. ఘనాకార మూడు భుజాలకు సమాంతరంగా నిరూపక అక్షాలు x,y మరియు Z లను తీసుకుందాము. ఏక్షణానైన ఏదిశలోనైన అణువు V వేగంతో చలిస్తుందని భావిద్దాం. మూడు అక్షాల వెంట V అంశాలు వరుసగా V_x, V_y, మరియు V_z.
అప్పుడు V²₁ = V²_x + V²_y + V²_z → (1)

m ద్రవ్యరాశిగల అణువు, ఘనం ABCD ముఖం (గోడ)ను తాకితే, అణువు బదిలీ చేయు ద్రవ్యవేగం mV_x గోడ పరిపూర్ణ స్థితిస్థాపకత కలిగి ఉండుటవల్ల, అణువు – V_x వేగంతో మరియు – mV_x ద్రవ్యవేగంతో పరావర్తనం చెందును.
ద్రవ్యవేగంలోని మార్పు = mV_x – (- mV_x) = 2 mV_x

ఈ అణువు ఎదురుగా ఉన్న గోడ (ముఖం)వైపు ప్రయాణించి అభిఘాతం జరిపి మరలా ABCD ముఖం వైపు ప్రయాణించును. రెండు వరుస అభిఘాతాల మధ్య అణువు ప్రయాణించిన దూరం 2l. రెండు వరుస అభిఘాతాలకు పట్టిన కాలము \(\frac{2l}{V_x}\).

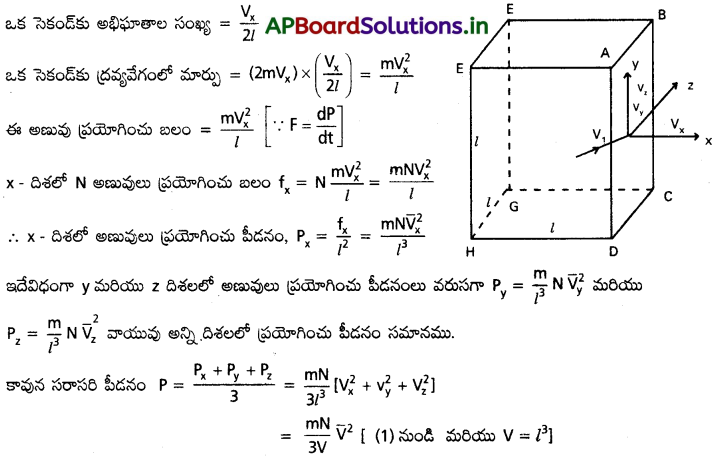
ఇచ్చట K_B బోల్ట్స్ మన్ స్థిరాంకం. అణువు సగటు గతిజశక్తి \(\frac{3}{2}\)K_B T. గతిజశక్తి ఉష్ణోగ్రతపై ఆధారపడును. ఉష్ణోగ్రత పెరిగిన, అణువుల సగటు గతిజశక్తి కూడ పెరుగును.

లెక్కలు (Problems)

ప్రశ్న 1.
STP వద్ద ఆక్సిజన్ వాయువు ఆక్రమించే ఘనపరిమాణంలో, ఆక్సిజన్ అణు ఘన పరిమాణ భాగాన్ని అంచనా వేయండి. ఆక్సిజన్ అణు వ్యాసాన్ని 3 గా తీసుకోండి.
సాధన:

ప్రశ్న 2.
ప్రామాణిక ఉష్ణోగ్రతా పీడనాల వద్ద (STP : 1 వాతావరణ పీడనం, 0°C) ఏదైనా ఒక మోల్ (ఆదర్శ) వాయువు ఆక్రమించే ఘనపరిమాణాన్ని మోలార్ ఘనపరిమాణం అంటారు. ఇది 22.4 లీటర్లు అని చూపండి.
సాధన:
ఒక మోల్ ఆదర్శవాయువుకు,

ప్రశ్న 3.
రెండు వేరు వేరు ఉష్ణోగ్రతల వద్ద 1.00 × 10^-3 kg ఆక్సిజన్ వాయువుకు PVT కి Pకీ మధ్య గ్రాఫ్ వక్రాన్ని పటం సూచిస్తుంది.

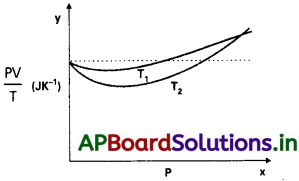
a) చుక్కల గీత వక్రం ఏ ప్రాధాన్యతను సూచిస్తుంది?
b) వీటిలో ఏది నిజం : T₁ > T₂ లేదా T₁ < T₂?
c) y – అక్షంపై వక్రాలు కలిసిన చోట PVT విలువ ఎంత?
d) 1.00 × 10^-3 kg హైడ్రోజన్ కు ఇటువంటి వక్రాలే వస్తే, y – అక్షంపై వక్రాలు కలిగిన చోట PVT కి ఇదే విలువ వస్తుందా ? ఒకవేళ రాకుంటే, ఎంత ద్రవ్యరాశి ఉన్న హైడ్రోజన్, అదే PVT విలువను ఇస్తుంది. (గ్రాఫ్లో అల్పపీడనం, అధిక ఉష్ణోగ్రత ఉన్న ప్రాంతానికి) ? (H₂ అణు ద్రవ్యరాశి = 2.02 u, O₂ అణు ద్రవ్యరాశి = 32.0 u, R = 8.31 J mol^-1 K^-1)
సాధన:
a) చుక్కల గీత, పీడనంపై ఆధారపడని \(\frac{PV}{T}\)(= μR) స్థిరాంకంను చూపిస్తుంది. ఇది ఆదర్శవాయు ప్రవర్తనను ఇస్తుంది.

b) T₂ వద్ద ఉష్ణోగ్రత వద్ద ఉన్న వక్రము కన్నా T₁ వద్ద ఉన్న వక్రము, చుక్కల గీతకు దగ్గరగా ఉంది. ఉష్ణోగ్రతను పెంచిన నిజవాయు, ఆదర్శవాయు ప్రవర్తనను సమీపిస్తుంది.
∴ T₁ > T₂.

c) y అక్షంపై రెండు వక్రాలు కలిసిన, \(\frac{PV}{T}\) విలువ μR కు సమానము.
ఆక్సిజన్ వాయువు ద్రవ్యరాశి
= 1.00 × 10^-3 kg = 1g·

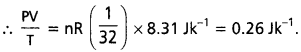
d) y అక్షంపై వక్రాలు కలిసిన, 1.00 × 10^-3 kg హైడ్రోజన్కు సాదృశ్యమైన వక్రాలు పొందిన, అదే బిందువు వద్ద \(\frac{PV}{T}\) సమానమైన విలువను పొందలేము.

ప్రశ్న 4.
30 లీటర్ల ఘనపరిమాణం ఉన్న ఆక్సిజన్ సిలిండర్ తొలి గేజ్ పీడనం 15 atm, ఉష్ణోగ్రత 27 °C. ఆ సిలిండర్ నుంచి కొంత ఆక్సిజన్ వాయువును తొలగించిన తరువాత గేజ్ పీడనం 11 atm కు, ఉష్ణోగ్రత 17 °C కు పడిపోయాయి. అయితే, సిలిండరు నుంచి తొలగించిన ఆక్సిజన్ వాయువు ద్రవ్యరాశిని అంచనా కట్టండి. (R : 8.31 J mol^-1 K^-1, O₂ అణు ద్రవ్యరాశి = 32 u).
సాధన:
మొదట ఆక్సిజన్ స్థూపంలో
v₁ = 30 lit = 30 × 10^-3m³
P₁ = 15 atm = 15 × 1.01 × 10⁵ Pa;
T₁ = 27 + 273 = 300k.
స్థూపం n₁ మోల్ ఆక్సిజన్ వాయువు కలిగి ఉంటే, అప్పుడు

ఆక్సిజన్ అణుభారం M = 32 g
స్థూపం ద్రవ్యరాశి
M₁ = n₁ M = 18.253 × 32 = 584.1 g
ఆక్సిజన్ స్థూపంలో తుదిగా, n₂ మోలుల ఆక్సిజన్ మిగిలితే
v₂ 30 × 10^-3 m³, P₂ = 11 × 1.01 × 10⁵
Pa, T₂ = 17 + 273 = 29K
ఇప్పుడు

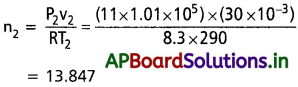
∴ స్థూపంలో ఆక్సిజన్ తుది ద్రవ్యరాశి,
m₂ = 13.847 × 32 = 453.1 g
∴ బయటకు వచ్చిన ఆక్సిజన్ వాయువు ద్రవ్యరాశి,
= m₁ – m₂ = 631.0 g.

ప్రశ్న 5.
40 m లోతు, 12°C ఉష్ణోగ్రత ఉన్న సరస్సు అడుగు నుంచి 1.0 cm³ ఘనపరిమాణం ఉన్న గాలి బుడగ పైకి లేస్తుంది. ఉష్ణోగ్రత 35°C ఉన్న సరస్సు ఉపరితలాన్ని చేరుకోగానే అది ఎంత ఘనపరిమాణానికి పెరుగుతుంది?
సాధన:
v₁ = 1.0 cm³ = 1.0 × 10^-6 m³,
T₁ = 12 °C = 12 + 273 = 285 k
P₁ 1 atm + h₁ ρg = 1.01 × 10⁵ + 40 × 10³ × 9.8 = 493000 Pa.
సరస్సు అడుగునకు గాలి బుడగ చేరితే, అప్పుడు
v₂ = 2, T₂ = 35°C 35 + 273 = 308 K,
P₂ = 10 atm = 1.01 × 10⁵ pa.

ప్రశ్న 6.
27 °C ఉష్ణోగ్రత, 1 atm పీడనం వద్ద 25.0 m³ ఘనపరిమాణం (capacity) ఉన్న గదిలోని మొత్తం గాలి (ఆక్సిజన్, నైట్రోజన్, నీటి ఆవిరి, ఇతర అంతర్భాగాలను కలుపుకొని) అణువుల సంఖ్యను అంచనా కట్టండి.
సాధన:
ఇక్కడ, V = 25.0 m³, T = 27 + 273 = 300 k,
k = 1.38 × 10^-23 Jk^-1
Pv = nRT = n(NK) T = (nN) kT = N’kT
nN = N’ = ఇచ్చిన వాయువులో గాలి అణువుల సంఖ్య.

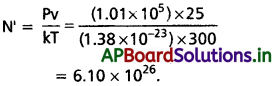
ప్రశ్న 7.

హీలియం పరమాణువు సగటు ఉష్ణశక్తిని, (i) గది ఉష్ణోగ్రత (27 °C), (ii) సూర్యుని ఉపరి తల ఉష్ణోగ్రత (6000 K), (iii) 10 మిలియన్ కెల్విన్ ఉష్ణోగ్రత (ఒక నక్షత్రం యొక్క మాదిరి అంతర్భాగ ఉష్ణోగ్రత)ల వద్ద అంచనా కట్టండి.
సాధన:
i) ఇచ్చినవి, T = 27 °C = 27 + 273 సరాసరి ఉష్ణశక్తి

ప్రశ్న 8.
సమాన ఘనపరిమాణాలు ఉన్న మూడు పాత్రలలోని వాయువులు ఒకే ఉష్ణోగ్రతా పీడనాల వద్ద ఉన్నాయి. మొదటి పాత్రలో నియాన్ (ఏకపరమాణుక), రెండో దానిలో క్లోరిన్ (ద్విపరమాణుక), మూడో దానిలో యురేనియం హెక్సాఫ్లోరైడ్ (బహు పరమాణుక) వాయువులు ఉన్నాయి. ఈ పాత్రలలో ఉన్న సంబంధిత వాయు అణువుల సంఖ్యలు సమానంగా ఉంటాయా? ఈ అణువులు rms (వడి వర్గమధ్యమ వర్గమూల) వడి మూడు సందర్భాలలో సమానంగా ఉంటుందా ? అలా ఉండకపోతే, ఏ సందర్భానికి Ums అత్యధికమై ఉంటుంది?
సాధన:
మూడు పాత్రలు (ఒకే ఉష్ణోగ్రత మరియు పీడనం వద్ద) ఒకే ఘనపరిమాణం కలిగియుండును. అవగాడ్రో నియమము ప్రకారం, మూడు పాత్రలు సమాన సంఖ్యలో అణువులు కల్గి, అవగాడ్రో సంఖ్య
N = 6.023 × 10²³ కు సమానం.

rms వడి మూడు సందర్భాలలో సమానం కాదు. నియాన్ స్వల్ప ద్రవ్యరాశి కలిగి ఉంటే, rms అణువుల వడి నియాన్ సందర్భంలో హెచ్చుగా ఉండును.

ప్రశ్న 9.
ఏ ఉష్ణోగ్రత వద్ద ఆర్గాన్ వాయువు సిలిండర్ ని ఒక పరమాణువు rms వడి – 20 °C వద్ద ఉన్న హీలియం పరమాణువు rms వడికి సమానంగా ఉంటుంది? (Ar పరమాణు ద్రవ్యరాశి = 39.9 u, He పరమాణు ద్రవ్యరాశి = 4.0u).
సాధన:
TK మరియు TK ఉష్ణోగ్రతల వద్ద ఆర్గాన్ మరియు హీలియం వాయు పరమాణువుల rms వడి వరుసగా C మరియు C’.
ఇచ్చినవి, µ = 39.9, µ = 4.0,
T = 2, T’ = -20 + 273
= 253 K.

ప్రశ్న 10.
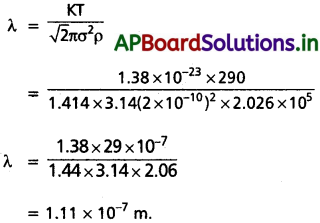
ఒక సిలిండర్లో 2.0 atm పీడనం, 17 °C ఉష్ణోగ్రత వద్ద ఉన్న నైట్రోజన్ వాయు అణువు స్వేచ్ఛా పథమధ్యమాన్ని, అభిఘాత పౌనః పున్యాన్ని లెక్కించండి. నైట్రోజన్ అణువు వ్యాసార్థాన్ని సుమారు 1.0 Å గా తీసుకోండి. దాని అభిఘాత కాలాన్ని రెండు వరుస అభిఘాతాల మధ్య అణువు స్వేచ్ఛగా తిరగడానికి పట్టే కాలంతో పోల్చండి. (N₂ అణువు ద్రవ్యరాశి = 28.0 u).
సాధన:
ఇచ్చినవి λ = 2, f = 2
P = 2 atm = 2 × 1.013 × 10⁵ Nm^-2
T = 17°C = (17 + 273) K = 290 k
σ = 2 × 1 = 2A° = 2 × 10^-10 m,
K = 1.38 × 10^-23 J molecule^-1 k^-1,
µ = 28 × 10^-3 kg

ప్రశ్న 11.
ఒక మీటరు పొడవు కలిగి, ఇరుకైన బోలు రంధ్రం (bore) ఉన్న (ఒకవైపు మూసిన) గొట్టాన్ని క్షితిజ సమాంతరంగా ఉంచినప్పుడు, అందులో 76 cm పొడవైన పాదరస దారం (thread) ఉంటే, అది 15 cm (పొడవైన) ల గాలి స్తంభాన్ని పట్టుకోగలుగుతుంది. ఇప్పుడు గొట్టాన్ని, తెరిచిన కొన కిందివైపు ఉండేటట్లు నిలువుగా ఉంచితే ఏం జరుగుతుంది?
సాధన:
నాళికను క్షితిజ సమాంతరంగా ఉంచినపుడు, 76 cm పొడవు గల పాదరసం, బంధించి ఉంచు గాలి పొడవు= 15 cm. పటం(a)లో తెరిచిన వైపు 9 cm పొడవు మిగిలి ఉంది. నాళికలో బంధించి ఉన్న గాలి పీడనము, వాతావరణ పీడనంనకు సమానము. నాళిక మధ్యచ్ఛేద వైశాల్యం 1 sq.cm.
∴ P₁ = 76 cm మరియు v₁ = 15 cm³.

నాళికను నిలువుగా ఉంచితే, 15 cm గాలి మరో 9 cm గాలిని కల్గి ఉంది(కుడిచేతివైపు స్థానంలో నింపితే). పటం (b)లో చూపినట్లు h cm పాదరసంను బయటకు పంపితే, వాతావరణ పీడనంతో సమానమగును. అప్పుడు గాలిస్థంభం మరియు పాదరసం స్థంభం ఎత్తులు (24 + h) cm మరియు (76 – h) cm గాలిపీడనం 76-(76-h) = h cm of Hg.

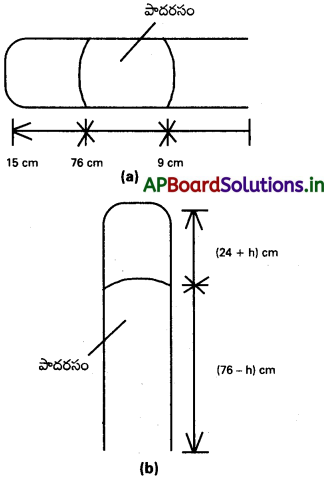
∴ v₂ = (24 + h) cm³ మరియు P₂ = hcm
ఉష్ణోగ్రతను స్థిరంగా ఉంచితే, అప్పుడు
P₁v₁ = P₂v₂ లేక 76 × 15 = h × (24 + h)
లేక h² + 24h – 1140 = 0

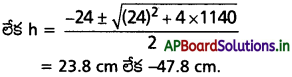
h ఎప్పుడు రుణాత్మకం కాదు.
∴ h = 23.8 cm.
నిలువు స్థానంలో 23.8 cm బయటకు వచ్చును.

ప్రశ్న 12.
ఒక నిర్దిష్టమైన పరికరం నుంచి హైడ్రోజన్ సగటు విసరణ రేటు విలువ 28.7 cm³s^-1 గా ఉంది. అదే పరిస్థితులలో ఉన్న మరొక వాయువు సగటు విసరణ రేటు 7.2 cm³s^-1 గా కొలవడమైంది. ఆ వాయువు ఏదో గుర్తించండి. సూచన: గ్రాహమ్ విసరణ నియమాన్ని ఉపయోగించండి : R₁/R₂ = (M₂/M₁)^1/2 ఇందులో R₁, R₂ లు వరుసగా 1, 2 వాయువుల విసరణ రేట్లు M₁, M₂ లు వాటి (అనురూప) అణు ద్రవ్యరాశులు. అణుచలన సిద్ధాంతం యొక్క సరళమైన పర్యవసానమే ఈ నియమం.]
సాధన:
గ్రాహం విసరణ నియమము ప్రకారము

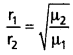
ఇచ్చట
r₁ = హైడ్రోజన్ విసరణ రేటు = 28.7 cm³ s^-1
r₂ = తెలియని వాయు విసరణ రేటు = 7.2 cm³ s^-1
M₁ = హైడ్రోజన్ అణుభారం = 2u
M₂ = ?

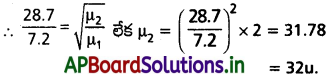
ప్రశ్న 13.
సమతాస్థితిలో ఉన్న వాయువు, దాని ఘన పరిమాణమంతటా ఏకరీతి సాంద్రత, పీడనాలను కలిగి ఉంది. ఇది తప్పనిసరిగా బాహ్య ప్రభావాలు లేనపుడే యదార్థం. ఉదాహరణకు, గురుత్వ ప్రభావంలో ఉన్న ఒక వాయు స్థంభం ఏకరీతి సాంద్రత (పీడనం) కలిగి ఉండదు. ఎత్తుతో దాని సాంద్రత తగ్గుతుందని మీరు ఊహించవచ్చు. ఎత్తుపై వాయు సాంద్రత కచ్చితంగా ఎలా ఆధారపడుతుందో మనం చెప్పుకొనే వాతావరణాల నియమం ఇవ్వగలుగుతుంది, అది, n₂ = n₁ exp [-mg(h₂ – h₁)/k_BT] దీనిలోని n₂, n₁ లు ఎత్తులు h₂, h₁ ల వద్ద గల సంఖ్యా సాంద్రతను వరుసగా సూచిస్తాయి. ద్రవ స్తంభంలోని వ్యాక్షేపం suspension) యొక్క అపసారం (మద్ది) (sedimentation) కు ఉండే కింది సమీకరణాన్ని ఉత్పాదించటానికి పై సంబంధాన్ని ఉపయోగించండి:
n₂ = n₁ exp (-mg N_B (ρ – ρ’) (h₂ – h₁)(ρRT)

ఇందులో ρ ద్రవంలో వేలాడే కణం సాంద్రత, ρ’ అనేది ఆ కణం చుట్టూ ఉన్న యానకం సాంద్రత [N_A అవగాడ్రో సంఖ్య, R సార్వత్రిక వాయు స్థిరాంకం)
[సూచన:వేలాడే కణం దృశ్యభారాన్ని కనుక్కోవడానికి ఆర్కెమిడిస్ సూత్రాన్ని ఉపయోగించండి.]
సాధన:
వాతావరణాల నియమము ప్రకారము

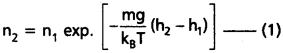
ఇచ్చట n₂ మరియు n₁ లు h₂ మరియు h₁ ఎత్తుల వద్ద కణాల సాంద్రత సంఖ్యలు. ద్రవంలో అవక్షేప కణాలు సమతాస్థితిలో, .mg బదులుగా, వ్రేలాడుతున్న కణాల ప్రభావ భారంను తీసుకుందాము.
v = వ్రేలాడే కణాల సరాసరి ఘనపరిమాణం
ρ = వ్రేలాడే కణాల సాంద్రత
ρ’ = ద్రవ సాంద్రత
m = వ్రేలాడే ఒక కణం ద్రవ్యరాశి
m’ = స్థానభ్రంశం చెందిన ద్రవఘనపరిమాణంనకు తుల్యమైన ద్రవ్యరాశి,

ఆర్కిమెడిస్ సూత్రం ప్రకారము, వ్రేలాడే ఒక కణం ప్రభావ భారం = వాస్తవభారం – స్థానభ్రంశం చెందిన వరం
= mg – m’g
= mg – m,g = mg – v ρ’g
mg – (m/ρ)

ఇదియే కావల్సిన సంబంధము.

ప్రశ్న 14.
కొన్ని ఘనపదార్థాలకు, ద్రవాలకు సాంద్రతలను కింద ఇచ్చాం. వాటి పరమాణువుల పరిమాణా లకు (size) ఉజ్జాయింపు అంచనాలను ఇవ్వండి.

పదార్థం	పరమాణు ద్రవ్యరాశి (u)	సాంద్రత (103 Kg m-3)
కార్బన్ (వజ్రం)	12.01	2.22
బంగారం	197.00	19.32
నైట్రోజన్ (ద్రవం)	14.01	1.00
లీథియం	6.94	0.53
ఫ్లోరిన్ (ద్రవం)	19.00	1.14

[సూచన: ఘన (పదార్థం) రూప, ద్రవరూప ప్రావస్థ (phase) లో అణువులు దగ్గర దగ్గరగా బంధితమై ఉంటాయని ఊహించుకొంటూ, మీకు తెలిసిన అవొగాడ్రో సంఖ్య విలువను ఉపయోగించండి. అయితే, వివిధ పరమాణు పరిమాణాలకు, ఈ విధంగా మీరు పొందే వాస్తవిక విలువలను నిజంగానే వాటికుంటాయని మాత్రం భావించకండి. దగ్గర దగ్గరగా అణువులు బంధితమై ఉంటాయనే ఉజ్జాయింపుకుండే ముడితత్వ భావన (crudeness of the tight packing approximation) వల్ల, ఈ ఫలితాలు కొన్ని Å ల వ్యాప్తిలో పరమాణు పరిమాణాలు ఉంటాయని మాత్రమే సూచిస్తాయి].
సాధన:
పరమాణు వ్యాసార్థం అయితే, ప్రతి పరమాణువు
ఘనపరిమాణం = \(\frac{4}{3}\)πr³
ఒక మోల్ పదార్థంలో అన్ని పరమాణువులు ఘనపరిమాణం

బంగారంనకు, r = 1.59Å
ద్రవ నైట్రోజన్కు, r = 1.77 Å
లీథియం r = 1.73Å
ద్రవ ఫ్లోరిన్్కు, r = 1.88Å

సాధించిన సమస్యలు (Solved Problems)

ప్రశ్న 1.
నీటి సాంద్రత 1000 kg m^-3. 100° C ఉష్ణోగ్రత, 1 atm పీడనం వద్ద నీటి బాష్పం సాంద్రత 0.6 kg m^-3. ఒక అణువు (molecule) ఘనపరిమాణాన్ని మొత్తం (అణువుల) సంఖ్యతో గుణిస్తే అణు (molecular) ఘన పరిమాణం వస్తుంది. ఈ ఉష్ణోగ్రతా పీడనాల వద్ద, అణు ఘనపరిమాణానికి, నీటి బాష్పం ఆక్రమించే మొత్తం ఘనపరిమాణానికి ఉండే నిష్పత్తి (లేదా భిన్నం) అంచనా కట్టండి.
సాధన:
ఇచ్చిన నీటి అణువుల ద్రవ్యరాశికి ఘనపరిమాణం ఎక్కువగా ఉంటే, సాంద్రత తక్కువగా ఉంటుంది. కాబట్టి బాష్పం ఘనపరిమాణం, 1000/0.6 = 1/(6 × 10^-4) రెట్లు ఎక్కువ. స్థూలమైన నీరు, నీటి అణువుల సాంద్రతలు సమానం అయితే, అణు ఘనపరిమాణానికి, ద్రవస్థితిలోని మొత్తం ఘనపరిమాణానికి ఉండే భిన్నం 1 అవుతుంది. బాష్ప స్థితిలో ఉన్నప్పుడు ఘనపరిమాణం పెరుగుతుంది కాబట్టి, ఘనపరిమాణ భిన్నం కూడా అంతే పరిమాణంలో తగ్గుతుంది. అంటే 6 × 10^-4.

ప్రశ్న 2.
ఇచ్చిన దత్తాంశాలను ఉపయోగించి ఒక నీటి అణువుకు ఉండే ఘనపరిమాణాన్ని అంచనా కట్టండి.
సాధన:
ద్రవ లేదా ఘన ప్రావస్థలో, నీటి అణువులు బాగా దగ్గరగా పేర్చబడి (సంపుటీకరించబడి) ఉంటాయి. కాబట్టి ఒక నీటి అణువు సాంద్రత పెద్ద పరిమాణంలోని (స్థూల) నీటి సాంద్రతకు దాదాపు సమానంగా పరిగణించవచ్చు. దీని విలువ 1000 kgm 3. ఒక నీటి అణువు ఘన పరిమాణాన్ని అంచనా కట్టడానికి మనకు ఒక నీటి అణువు ద్రవ్యరాశి తెలిసి ఉండాలి. 1 మోల్ నీటి ద్రవ్యరాశి, సుమారుగా ·
(2 + 16) g = 18 g = 0.018 kg
ఉంటుందని మనకు తెలుసు.
ఒక మోల్లోని అణువుల సంఖ్య 6 × 10²³ (అవగాడ్రో సంఖ్య) కాబట్టి, ఒక నీటి అణువు ద్రవ్యరాశి
(0.018) / (6 × 10²³) kg 3 × 10^-26 kg.

కాబట్టి కింది విధంగా నీటి అణువు ఘనపరిమాణాన్ని సుమారుగా అంచనా వేయవచ్చు.
నీటి అణువు ఘనపరిమాణం
= (3 × 10^-26 kg) (1000 kg m^-3)
= 3 × 10^-26 m³
= (4/3)π (వ్యాసార్థం)³
అందువల్ల, వ్యాసార్థం = 2 × 10^-10 m = = 2Å

ప్రశ్న 3.
నీటిలో పరమాణువుల మధ్య సగటు దూరం (అంతర్ పరమాణు దూరం) ఎంత? 1, 2 ఉదాహరణలలో ఇచ్చిన దత్తాంశాలను వాడండి.
సాధన:
బాష్పస్థితిలో ఇచ్చిన నీటి ద్రవ్యరాశి ఘనపరిమాణం, ద్రవస్థితిలో అంతే ద్రవ్యరాశి గల నీటి ఘనపరిమాణానికి 1.67 × 10³ రెట్లు ఎక్కువ. (ఉదాహరణ 1). ఒక్కొక్క నీటి అణువుకు అందుబాటులో ఉండే ఘనపరిమాణంలో కలిగే పెరుగుదల కూడా ఇదే. ఘనపరిమాణం 103 రెట్లు పెరిగితే, వ్యాసార్థం 13 లేదా 10 రెట్లు పెరుగుతుంది. అంటే 10 × 2Å = 20Å. అందువల్ల సగటు దూరం (నీటిలోని పరమాణువుల మధ్య) 2 × 20 40 Å.

ప్రశ్న 4.
ఒక పాత్రలో పరస్పరం చర్య జరపని రెండు వాయువులు: నియాన్ (ఏకపరమాణుక), ఆక్సిజన్ (ద్విపరమాణుక) ఉన్నాయి. వాటి పాక్షిక పీడనాల నిష్పత్తి 3 : 2 పాత్రలోని నియాన్, ఆక్సిజన్ల (i) అణువుల సంఖ్య (ii) ద్రవ్యరాశి సాంద్రతల నిష్పత్తిని అంచనా కట్టండి. Ne పరమాణు ద్రవ్యరాశి = 20.2 u, O₂ అణు ద్రవ్యరాశి 32.0 u.
సాధన:
మిశ్రమంలోని వాయువు పాక్షిక పీడనం, అంటే అంతే ఘనపరిమాణం, ఉష్ణోగ్రతల వద్ద పాత్రలో ఆ వాయువు ఒక్కటే ఉన్నప్పుడు కలిగించే వాయు పీడనానికి సమానంగా ఉంటుంది. (రసాయనికంగా చర్య జరపని వాయువుల మిశ్రమం మొత్తం పీడనం దానిలోని వివిధ వాయువుల పాక్షిక పీడనాల మొత్తానికి సమానం).
ఒక్కొక్క వాయువు (ఆదర్శ వాయువుగా ఊహించడమైంది) వాయు నియమాన్ని పాటిస్తుంది. రెండు వాయువులకు V, T లు ఒకే విలువ కలిగి ఉంటాయి కాబట్టి, మనకు P₁V = µ₁ RT, P₂V = µ₂ RT వస్తుంది. అంటే (P₁/P₂) = (µ₁/µ₂). ఇక్కడ 1, 2 లు వరుసగా నియాన్, ఆక్సిజన్లను సూచిస్తాయి. (P₁ / P₂) = (3/2) అని ఇవ్వడమైంది కాబట్టి, (µ₁/µ₂) = 3/2.

i) నిర్వచనం ప్రకారం µ₁ = (N₁/N_A), µ₂ = (N₂/N_A) ఇక్కడ N₁, N₂ లు 1, 2 వాయువుల అణువుల సంఖ్యలు, N_A అవగాడ్రో సంఖ్య. కాబట్టి (N₁/ N₂) = (µ₁/µ₂) = 3/2.

ii) µ₁ = (m₁/ M₁), µ₂ = (m₂/ M₂) అని కూడా రాయవచ్చు. m₁ m₂ లు 1, 2 ల ద్రవ్యరాశులు. M₁, M₂ లు వాటి అణు ద్రవ్యరాశులు (molecular masses), (m₁, M₁; అదే విధంగా m₂, M₂ లు అన్నింటినీ ఒకే ప్రమాణాలలో వ్యక్తపరచాలి). ρ₁, ρ₂ లు వరుసగా 1, 2 ల ద్రవ్యరాశి సాంద్రతలు అయితే,

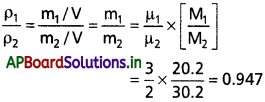
ప్రశ్న 5.
ఒక ఫ్లాస్క్ లోని ఆర్గాన్, క్లోరిన్ ద్రవ్యరాశుల నిష్పత్తి 2 : 1. ఈ మిశ్రమం ఉష్ణోగ్రత 27° C. (i) ఒక అణువుకు సగటు గతిజశక్తి, (ii) రెండు వాయువుల అణువులకు ఉండే rms వడి υ_rms ల విలువలను కనుక్కోండి. ఆర్గాన్’ పరమాణు ద్రవ్యరాశి = 39.9 u; క్లోరిన్ అణు (molecular) ద్రవ్యరాశి = 70:9 u.
సాధన:
ఏదైనా (ఆదర్శ) వాయువులోని (ఆర్గాన్ వంటి ఏక పరమాణుక లేదా క్లోరిన్ వంటి ద్విపరమాణుక లేదా బహు పరమాణుక వాయువుకైనా) ఒక అణువుకుండే సగటు గతిజశక్తి ఎప్పుడూ (3/2) k_BT కి సమానంగా ఉంటుందనే ముఖ్యమైన అంశాన్ని గుర్తుంచుకోవాలి. ఇది వాయు స్వభావంపై ఆధారపడక, ఎప్పుడూ ఉష్ణోగ్రతపై మాత్రమే ఆధారపడి ఉంటుంది.

i) ఫ్లాస్క్ లోని ఆర్గాన్, క్లోరిన్ల ఉష్ణోగ్రతలు సమానం కాబట్టి, ఈ రెండు వాయువుల సగటు గతిజశక్తుల (ఒక అణువుకు (per molecule))ల నిష్పత్తి 1 : 1.
ii) ఇప్పుడు 1/2 mυ_rms² = ఒక అణువుకు సగటు
గతిజశక్తి = (3/2) k_B T; ఇక్కడ m వాయువులోని ఒక అణువు ద్రవ్యరాశి కాబట్టి,

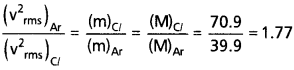
ఇక్కడ M వాయు అణు ద్రవ్యరాశిని సూచిస్తుంది.
(ఆర్గాన్క, అణువు అంటే పరమాణువే).
రెండు వైపులా వర్గమూలం తీసుకుంటే,

ప్రశ్న 6.
యురేనియమ్కు రెండు ఐసోటోపులు ఉన్నాయి. వాటి ద్రవ్యరాశులు 235, 238 ప్రమాణాలు. యురేనియం హెక్సాఫ్లోరైడ్ వాయువులో ఈ రెండు ఐసోటోపులు ఉన్నాయనుకుంటే, దేనికి అధిక సగటు వడి ఉంటుంది. ఫ్లోరిన్ పరమాణు ద్రవ్యరాశి 19 ప్రమాణాలు అయితే, ఏ ఉష్ణోగ్రత వద్ద అయినా వాటి వడులలోని తేడా శాతాన్ని లెక్కించండి.
సాధన:
స్థిర ఉష్ణోగ్రత వద్ద సగటు శక్తి = 1/2 m < υ² >, స్థిరాంకం కాబట్టి అణు ద్రవ్యరాశి తక్కువ అవుతున్న కొద్దీ, దాని వడి పెరుగుతూ ఉంటుంది. వడుల నిష్పత్తి, ద్రవ్యరాశుల నిష్పత్తి యొక్క వర్గమూలానికి విలోమానుపాతంలో ఉంటుంది. ద్రవ్యరాశులు 349, 352 ప్రమాణాలుగా ఉంటాయి. కాబట్టి,

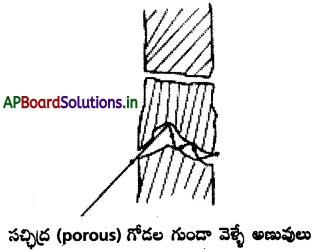
[కేంద్రక విచ్ఛిత్తికి ²³⁵U ఐసోటోపు అవసరమవుతుంది. అధిక సమృద్ధి (abundant) ఉన్న ²³⁸U ఐసోటోపు నుంచి దీన్ని వేరుచేయడానికి ఈ మిశ్రమం చుట్టూ సచ్ఛిద్ర స్తూపాన్ని ఉంచుతారు. ఈ సచ్ఛిద్ర స్తూపం మందం గానూ, సన్నగా (narrow) ఉండాలి; ఆ కారణంగా, అణువు ఛిద్రాల గుండా వైయక్తికంగా (individually) అటూ, ఇటూ తిరగగలుగుతుంది. అంతేకాక, అణువు పొడవుగా ఉండే ఛిద్రపు గోడలతో అభిఘాతం చేస్తూ ఉంటుంది; ఎక్కువ వడి ఉన్న అణువు, నెమ్మది అణువు కంటే, ఎక్కువ బయటకు వస్తూ ఉంటుంది. అంటే సచ్ఛిద్ర స్తూపం బయట తేలిక అణువు ఎక్కువగా ఉండటం సాధ్యమవుతుంది. ఈ పద్ధతి గొప్ప దక్షత కలిగిందేమీ కాదు; కాబట్టి తగినంత (U²³⁵ ఐసోటోపు) సంవృద్ధి (enrichment) సాధించడానికి ప్రక్రియను అనేకసార్లు పునరావృతం చేయవలసి ఉంటుంది.]

వాయువులు విసరణమైనప్పుడు, వాటి విసరణ రేటు ద్రవ్యరాశుల వర్గమూలానికి విలోమానుపాతంలో
ఉంటుంది.

ప్రశ్న 7.
a) ఒక అణువు (లేదా ఒక స్థితిస్థాపక బంతి) ఒక పెద్ద (massive) గోడను ఢీకొన్నప్పుడు, అది అంతే వడితో వెనుకకు మరలుతుంది. గట్టిగా పట్టుకొన్న బ్యాట్ (bat) ను బంతి ఢీకొన్నప్పుడు కూడా అదే జరుగుతుంది. కాని బ్యాట్ బంతివైపు కదులుతున్నప్పుడు, బంతి వేరే వడితో వెనుకకు మరలుతుంది. బంతి వేగంగా చలిస్తుందా లేదా నెమ్మదిగా చలిస్తుందా? (స్థితిస్థాపక అభిఘాతాలపై మీ జ్ఞాపకాలకు అధ్యాయం 6 పునర్వికాసం కలిగిస్తుంది).
b) స్తూపంలోని వాయువును, ముషలకాన్ని లోపలికి తోయడం ద్వారా సంపీడనానికి లోనుచేసినప్పుడు, దాని ఉష్ణోగ్రత పెరుగుతుంది. అణుచలన సిద్ధాంతం నేపథ్యంలో, పై (a) ను ఉపయోగిస్తూ, ఒక వివరణను ఊహించండి.
c) ఒక సంపీడిత వాయువు, ముషలకాన్ని వెలుపలికి తోసి, వ్యాకోచించినప్పుడు ఏమి జరుగుతుంది? నీవు ఏమి గమనిస్తావు?
d) సచిన్ టెండూల్కర్ ఆట ఆడుతున్నప్పుడు, బరువైన క్రికెట్ బ్యాట్ను ఉపయోగిస్తాడు. ఇది అతనికి ఏ విధంగానైనా సహాయ పడుతుందా?
సాధన:
a) బ్యాట్కు వెనక ఉన్న వికెట్ పరంగా బంతి వడి u అనుకొందాం. వికెట్కు సాపేక్షంగా బ్యాట్, బంతివైపు V వడితో చలిస్తుందనుకుంటే, బ్యాట్ పరంగా బంతి సాపేక్ష వడి V + u. ఇది బ్యాట్ వైపు ఉంటుంది. బంతి వెనుకకు మరలినపుడు (బరువైన బ్యాట్ను అది ఢీకొన్న తరువాత) దాని వడి, బ్యాట్పరంగా V + u ఉండి, బ్యాట్ నుంచి దూరంగా చలిస్తుంది. వికెట్ పరంగా వెనుకకు మరలుతున్న బంతి వడి, V + (V + u) = 2V + u గా ఉండి వికెట్ నుంచి దూరంగా చలిస్తుంది. కాబట్టి బ్యాట్ను ఢీకొన్న తరువాత బంతి వడి పెరుగుతుంది. బ్యాట్ అంత బరువైనది (massive) కాకపోతే, వెనుకకు మరలినపుడు దాని వడి, తొలి వడి uకంటే తక్కువగా ఉంటుంది. ఇక అణువు సందర్భంలో ఇది ఉష్ణోగ్రతలో పెరుగుదలను సూచిస్తుంది.

(a) కు పైన ఇచ్చిన సమాధానం ఆధారంగా (b), (c), (d) లకు సమాధానాలను మీరు చెప్పగలిగి ఉండాలి.
(సూచన: అనురూపకతను గమనించండి. ముషలకం → బ్యాట్, స్తూపం → వికెట్, అణువు → బంతి.)

ప్రశ్న 8.
373 K వద్ద నీటి బాష్పంలో ఉన్న నీటి అణువుకు స్వేచ్ఛా పథమధ్యమాన్ని అంచనా కట్టండి. అభ్యాసం.1 లో L = 2.9 × 10⁷ m = 1500 d ఉన్న సమాచారాన్ని ఉపయోగించుకోండి.
సాధన:
నీటి బాష్పం d (అణు వ్యాసం) గాలి అణు వ్యాసానికి సమానం. సంఖ్యా సాంద్రత పరమ ఉష్ణోగ్రతకు విలోమానుపాతంలో ఉంటుంది. అందువల్ల,

కాబట్టి స్వేచ్ఛా పథమధ్యమం, 1 = 4 × 10^-7 m.