AP Inter 1st Year Physics Study Material Chapter 8 డోలనాలు

Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 8th Lesson డోలనాలు Textbook Questions and Answers.

AP Inter 1st Year Physics Study Material 8th Lesson డోలనాలు

అతిస్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
డోలనాత్మకం కాని ఆవర్తన చలనాలకు రెండు ఉదాహరణలు ఇవ్వండి.
జవాబు:

1. సూర్యుడి చుట్టూ గ్రహాల చలనం
2. కేంద్రకం చుట్టూ ఎలక్ట్రాన్ల చలనం

ప్రశ్న 2.
సరళ హరాత్మక చలన స్థానభ్రంశాన్ని y = a sin (20t + 4) తో సూచించారు. కాలాన్ని 210/ఱ పెంచితే దాని స్థానభ్రంశం ఎంత
జవాబు:
స.హ.చ. లో స్థానభ్రంశము y = a sin (20t + 4)
ఆవర్తన కాలం T = \(\frac{2 \pi}{\omega}\) పెరిగినా, కణం యొక్క స్థానభ్రంశం మారదు.

ప్రశ్న 3.
ఒక బాలిక ఊయలలో కూర్చొని ఊగుతుంది. బాలిక ఊయలలో నిలబడితే దాని డోలన పౌనఃపున్యం ఏవిధంగా మారుతుంది?
జవాబు:

బాలిక నిలబడి ఊయల ఊగుతుంటే, ద్రవ్యరాశి కేంద్రం స్థానం పైకి మారి, పొడవు (1) తగ్గుతుంది. కాబట్టి డోలన పౌనః పున్యము పెరుగుతుంది.

ప్రశ్న 4.
లఘులోలకం గుండు నీటితో నిండిన ఒక బోలు గోళం. గోళం నుంచి నీరు కారిపోతుంటే దాని డోలనావర్తన కాలం ఏవిధంగా మారుతుంది?
జవాబు:
గోళం బోలుగా ఉన్నా (లేదా) పూర్తిగా నీటితో నింపినా ఆవర్తనకాలం ఒకే విధంగా ఉంటుంది. గోళం నుండి నీరు బయటకు పోతుంటే గోళం గరిమనాభి క్రిందకు మారుతుంది. లోలకం పొడవు పెరిగి, ఆవర్తన కాలం కూడా పెరుగుతుంది. గోళం పూర్తిగా ఖాళీ అయితే, గరిమనాభిపైకి మారుతుంది. అప్పుడు లోలకం పొడవు తగ్గి, ఆవర్తన కాలం కూడా తగ్గుతుంది.

ప్రశ్న 5.
లఘులోలకానికి కట్టిన చెక్క గుండుకు బదులు దాన్ని పోలి ఉండే అల్యూమినియం గుండును ఉపయోగిస్తే దాని ఆవర్తన కాలం ఏవిధంగా మారుతుంది?
జవాబు:
ఆవర్తన కాలం (T) = 2π \(\sqrt{\frac{1}{g}}\)
ఆవర్తన కాలం గోళం యొక్క ద్రవ్యరాశిపై ఆధారపడదు.
చెక్కగుండును తొలగించి, అదేవిధమైన అల్యూమినియమ్ గుండును ఉంచినా ఆవర్తన కాలం మారదు.

ప్రశ్న 6.
లోలక గడియారాన్ని పర్వతం పైకి తీసుకొని వెళితే అది సమయాన్ని పొందుతుందా? కోల్పోతుందా?
జవాబు:
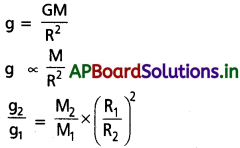
T ∝ \(\frac{1}{\sqrt{g}}\) పర్వతం పైన g విలువ తక్కువగా ఉండును. కాబట్టి ఆవర్తన కాలం పెరుగుతుంది. అనగా లోలకం ఒకపూర్తి

డోలనం చేయడానికి ఎక్కువ సమయం పడతుంది. అందువల్ల పర్వతం మీద లోలక గడియారం కాలాన్ని కోల్పోతుంది.

ప్రశ్న 7.
భూమధ్య రేఖ వద్ద సరైన సమయాన్ని చూపే లోలక గడియారాన్ని ధ్రువాల వద్దకు తీసుకొనిపోతే అది సమయాన్ని పొందుతుందా? కోల్పోతుందా? అయితే ఎందుకు?
జవాబు:
ఆవర్తన కాలం (T) = 2π \(\sqrt{\frac{1}{g}}\)
g విలువ భూమధ్యరేఖ వద్ద కన్నా ధృవాల వద్ద ఎక్కువ లోలక గడియారంను ధృవాల వద్దకు తీసుకుపోతే g విలువ పెరిగి ఆవర్తనకాలం తగ్గుతుంది. కాబట్టి లోలక గడియారం కాలాన్ని పొందుతుంది.

ప్రశ్న 8.
సరళ హరాత్మక చలనం చేసే కణం స్థానభ్రంశం కంపన పరిమితిలో సగానికి సమానమైనప్పుడు, దానిమొత్తం శక్తిలో KE. వంతు ఎంత?
జవాబు:

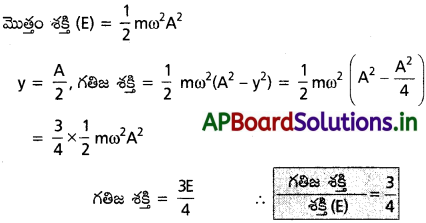
ప్రశ్న 9.
సరల హరాత్మక డోలకం కంపన పరిమితిని రెట్టింపు చేస్తే దాని శక్తి ఏవిధంగా మారుతుంది ?
జవాబు:
మొత్తం శక్తి (E) = \(\frac{1}{2}\)mω²A²
కంపన పరిమితి రెట్టింపైతే
E’ = \(\frac{1}{2}\)mω²(2A)²
E’ = 4 × \(\frac{1}{2}\)mω²A²
E’ = 4E
∴ శక్తి నాలుగు రెట్లు పెరుగుతుంది.

ప్రశ్న 10.
కృత్రిమ ఉపగ్రహంలో లఘులోలకాన్ని ఉపయోగించవచ్చా?
జవాబు:
లేదు. కృత్రిమ ఉపగ్రహంలో గురుత్వత్వరణం శూన్యం కాబట్టి కృత్రిమ ఉపగ్రహంలో లఘులోలకాన్ని ఉపయోగించలేము.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.
సరళ హరాత్మక చలనాన్ని నిర్వచించండి. రెండు ఉదాహరణలు ఇవ్వండి.
జవాబు:
సరళ హరాత్మక చలనం :
ఏదైనా ఒక వస్తువు ఒక స్థిర మాధ్యమిక బిందువు పరంగా రేఖాగమనం చేస్తున్నప్పుడు, దాని త్వరణం మాధ్యమిక బిందువు నుంచి ఆ వస్తువు స్థానభ్రంశానికి అనులోమానుపాతంలో ఉండి, ఎప్పుడూ ఆ మాధ్యమిక బిందువువైపే ఉంటే ఆ చలనాన్ని సరళహరాత్మక చలనం అంటారు.
a ∝ – x
వస్తువు స.హ.చ. లో ఉన్నప్పుడు మాధ్యమిక స్థానం నుండి x స్థానభ్రంశంలో ఉన్నప్పుడు వస్తువు యొక్క త్వరణం a. స.హ.చ. లో ఉన్నకణం యొక్క స్థానభ్రంశం x(t) = A cos (ωt + Φ)

ఉదాహరణలు :

1. లఘులోలకం యొక్క చలనం.
2. స్ప్రింగ్కు వ్రేలాడదీసిన ద్రవ్యరాశి యొక్క చలనం.
3. ఘన పదార్థాలలో పరమాణువుల యొక్క చలనం.
4. నీటిమీద తేలే బెండు.

ప్రశ్న 2.
సరళ హరాత్మక చలనం చేసే కణం స్థానభ్రంశం, వేగం, త్వరణాలు కాలం దృష్ట్యా మారే విధానాన్ని గ్రాఫ్ ద్వారా సూచించండి.
జవాబు:

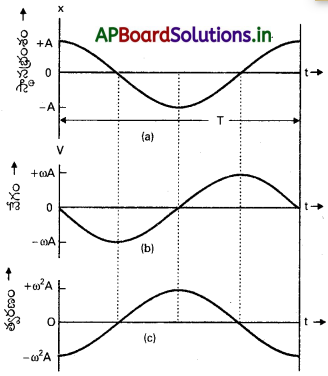
Φ = 0 తీసుకుంటే x(t), υ(t) మరియు a(t) లను ఈ విధంగా వ్రాయవచ్చు.
x(t) = A cos ωt, υ(t) = -Aωsinωt
a(t) = – ω²A cos ωt.
వీటికి సంబంధించిన గ్రాఫ్లను పటంలో చూడండి. అన్ని రాశులు కాలంతోపాటు సైను వక్రీయంగా (sinusoidally) మారుతూ ఉంటాయని తెలుస్తుంది.

x(t) విలువ – A నుండి A మధ్యమారుతుంది; υ(t) విలువ – ωA నుండి ωA వరకు మారుతుంది మరియు a(t) విలువ – ω²A నుండి ω²A మధ్య మారుతూ స్థానభ్రంశం, వేగం మధ్య దశాభేదం \(\frac{2 \pi}{2}\) మరియు స్థానభ్రంశం,
త్వరణం మధ్య దశాభేదం π.

ప్రశ్న 3.
దశ అంటే ఏమిటి? సరళ హరాత్మక చలనంలో స్థానభ్రంశం, వేగం, త్వరణాల మధ్య దశా సంబంధాన్ని చర్చించండి.
జవాబు:
దశ :
సరళ హరాత్మక చలనంలో ఉన్న కణం తత్కాల స్థానము, దిశాపరంగా దాని కంపనస్థితిని దశ అని నిర్వచిస్తారు.
i) స్థానభ్రంశం : x = A cos (ωt – Φ), (ωt – Φ) అనునది దశ. ఇక్కడ Φ తొలిదశ.
ii) వేగం : V = -Aω sin (ωt – Φ), ఇక్కడ (ωt – Φ) దశా కోణం
iii) త్వరణం : a = -ω²A cos (ωt – Φ), ఇక్కడ కూడా (ωt – Φ) దశాకోణం
స్థానభ్రంశం మరియు వేగం మధ్య దశాభేదం \(\frac{2 \pi}{2}\)
వేగం మరియు త్వరణం మధ్య దశాభేదం \(\frac{2 \pi}{2}\)
స్థానభ్రంశం మరియు త్వరణం మధ్య దశాభేదం = π

ప్రశ్న 4.
k బల స్థిరాంకం గల స్ప్రింగుకు m ద్రవ్యరాశిని తగిలించారు. స్ప్రింగ్ వ్యవస్థ చేసే డోలన పౌనః పున్యానికి సమీకరణం రాబట్టండి.
జవాబు:

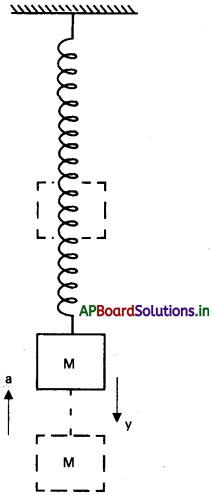
దృఢమైన ఆధారం నుండి నిలువుగా వేలాడే స్ప్రింగ్ కొనకు m ద్రవ్యరాశి గల వస్తువును వేలాడదీశామనుకోండి దానిని కొద్దిగా కిందికి లాగి వదిలితే, మాధ్యమిక బిందువుపరంగా నిలువు తలంలో డోలనాలు చేస్తుంది.

పునఃస్థాపకబలం, స్థానభ్రంశానికి అనులోమానుపాతంలోను మరియు వ్యతిరేకదిశలోను ఉంటుంది.
F ∝ – y F = – ky ——— (1)
ఇక్కడ k అనుపాత స్థిరాంకం
Ma = – ky (∵ F = Ma)
a = – (\(\frac{K}{M}\))y …………….. (2)

అనగా త్వరణం, స్థానభ్రంశానికి అనులోమానుపాతంలోను మరియు వ్యతిరేక దిశలోను ఉండును.
K మరియు M స్థిరాంకాలు కావున a c – y గా వ్రాయవచ్చు.
(2) వ సమీకరణంను a = – ω²yతో పోల్చగా

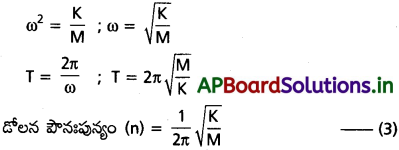
ప్రశ్న 5.
సరళ హరాత్మక డోలకానికి గతిజ, స్థితిజ శక్తులకు సమీకరణాలను రాబట్టండి.
జవాబు:
సరళ హరాత్మక డోలకం యొక్క గతిజ శక్తి :
స.హ.చ.లోవున్న కణం యొక్క వేగం v = ω\(\sqrt{{A^2}-{y^2}}\)
∴ గతిజశక్తి = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\)mω²(A² – y²)
У = 0 అయినప్పుడు, (గతిజశక్తి)_{గరిష్ఠం} = \(\frac{1}{2}\)mω²A² (మాధ్యమిక స్థానం)
y = A అయినప్పుడు, (గతిజశక్తి)_{కనిష్టం} = 0 (అంత్యస్థానం)
∴ మాధ్యమిక స్థానం వద్ద గతిజశక్తి గరిష్ఠంగాను, అంత్యస్థానాల వద్ద కనిష్ఠంగాను ఉంటుంది.

సరళహరాత్మక డోలకం యొక్క స్థితిజశక్తి :
సరళహరాత్మక డోలనాలు చేయుచున్న కణం యొక్క స్థానభ్రంశం పెరిగితే, పునః స్థాపకబలం కూడా పెరుగుతుంది. పునః స్థాపక బలం స్థానభ్రంశానికి వ్యతిరేక దిశలో ఉంటుంది. కాబట్టి పునఃస్థాపక బలానికి వ్యతిరేకంగా స్థానభ్రంశం చెందాలంటే కొంత పని జరగాలి.
y స్థానభ్రంశం వద్ద పునఃస్థాపకబలం F అయితే
సగటు నిరోధక బలం = \(\frac{O+F}{2}\) = \(\frac{F}{2}\)
∴ y స్థానభ్రంశాన్ని పొందేందుకు జరిగే పని = సగటు బలం × స్థానభ్రంశం
ω = \(\frac{F}{2}\) × y
ω = \(\frac{ma y}{2}\) ……….. (1) (∵ F=ma)
స.హ.చలో ఉన్న కణం త్వరణం
a = ω²y ……………. (2)
(1) మరియు (2) సమీకరణాలను ఉపయోగించి
జరిగినపని (ω) = \(\frac{1}{2}\)mω²y²
ఈ పని ఆ కణంలో స్థితిజశక్తి రూపంలో నిల్వయుండును.
∴ స్థితిజశక్తి = \(\frac{1}{2}\)mω²y²
y = 0 అయితే(స్థితిజ శక్తి)_{కనిష్ఠం} = 0 (మాధ్యమిక స్థానం వద్ద)
y = A అయితే (స్థితిజశక్తి)_{గరిష్ఠం} = \(\frac{1}{2}\)mω²A² (అంత్యస్థానం వద్ద)
∴ స్థితిజశక్తి మాధ్యమిక స్థానం వద్ద కనిష్ఠంగాను మరియు అంత్యస్థానాల వద్ద గరిష్ఠంగాను ఉంటుంది.

ప్రశ్న 6.
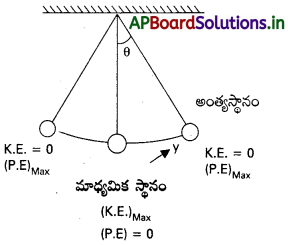
డోలనాలు చేసే లఘులోలకం ఒక అంత్యస్థానం నుంచి మరో అంత్యస్థానానికి చలించే సమయంలో శక్తి ఏవిధంగా మారుతుంది?
జవాబు:
కణం స.హ.చలోవున్నప్పుడు ఏదైనా బిందువువద్ద దాని మొత్తం శక్తి, స్థితిజ శక్తి, గతిజ శక్తుల మొత్తానికి సమానం.
మొత్తం శక్తి (E) = గతిజశక్తి + స్థితిజశక్తి
గతిజశక్తి = \(\frac{1}{2}\)mω²(A² – y²)

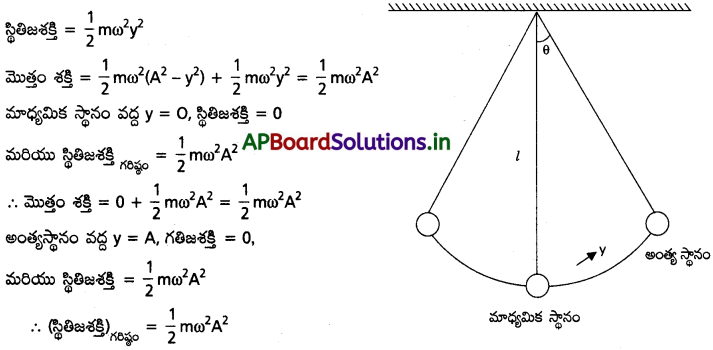
మాధ్యమిక స్థానం నుండి, అంత్యస్థానానికి పోయేసరికి గతిజశక్తి, స్థితిజశక్తిగా మారుతుంది.

ప్రశ్న 7.
సరళ హరాత్మక చలనం చేసే కణం స్థానభ్రంశం, వేగం, త్వరణాలకు సమాసాలను ఉత్పాదించండి.
జవాబు:
A వ్యాసార్థంగల వృత్తి పరిధిపై సమకోణీయ వేగం ω తో గమనంలో ఉన్న కణం Pని తీసుకుందాం. P నుండి yy’కు PN లంబాన్ని గీశామనుకోండి.
P వృత్త పరిధి వెంట చలిస్తే, N మాధ్యమిక స్థానం 0 పరంగా yy’ వ్యాసంపై అటూ, ఇటూ చలిస్తుంది.

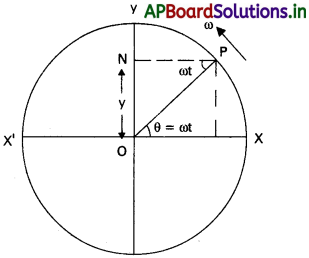
∠POX = = θ, OP = A, ON = y అనుకొనుము.
ONP త్రిభుజం నుండి sin ωt = \(\frac{ON}{OP}\)
ON = OP sin ωt
y = A sin ωt ……………. (1)

వేగము : స.హ.చ.లో ఉన్న కణం యొక్క వేగం

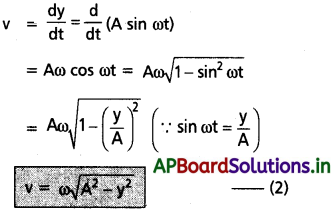
త్వరణం : వేగంలో మార్పురేటు స.హ.చ. లోవున్న కణం యొక్క త్వరణాన్ని ఇస్తుంది.
a = \(\frac{dv}{dt}=\frac{d}{dt}\)(Aω cos ωt) = -Aω² sin ωt
∴ a = – ω²y ……………. (3)

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.
సరళ హరాత్మక చలనాన్ని నిర్వచించండి. ఏకరీతి వృత్తాకార చలనం చేసే కణం విక్షేపం (ఏదైనా) వ్యాసం పై సరళ హరాత్మక చలనం చేస్తుందని చూపండి.
జవాబు:
సరళహరాత్మక చలనం :
ఏదైనా ఒక వస్తువు ఒక స్థిర మాధ్యమిక బిందువు పరంగా రేఖాగమనం చేస్తున్నప్పుడు, దాని త్వరణం మాధ్యమిక బిందువు నుంచి ఆ వస్తువు స్థానభ్రంశానికి అనులోమానుపాతంలో ఉండి, ఎప్పుడూ ఆ మాధ్యమిక బిందువువైపే ఉంటే ఆ చలనాన్ని సరళ హరాత్మక చలనం అంటారు.
a ∝ -y

వృత్తవ్యాసంపై ఏకరీతి వృత్తాకార చలనం ఆచ్ఛాదన సరళ హరాత్మక చలనం అని చూపుట :
A వ్యాసార్థం గల వృత్త పరిధిపై సమకోణీయ వేగం ω తో చలనంలో ఉన్న కణం P ని తీసుకుందాం. పటంలో చూపినట్లు ‘O’ వృత్తకేంద్రం XX’, YY’ లు రెండు పరస్పరం లంబంగా ఉన్న వృత్త వ్యాసాలని అనుకుందాం. PN అనునది P నుండి Y కు లంబంగా గీయబడిందనుకుందాం. వృత్త పరిధిపై గమనంలో ఉన్నప్పుడు N వ్యాసం YY మీద ‘O’ కు అటూ, ఇటూ చలనంలో ఉంటుంది. అంటే YY’ వ్యాసంపై P గమనం ఆచ్ఛాదనే N చలనం అన్నమాట. ‘O’ ను దాటిన తర్వాత ఏదైనా తత్కాల సమయం t వద్ద N స్థితిని గమనిద్దాం. ఈ స్థితిలో P కోణీయ స్థానభ్రంశం ∠XOP = θ
= ωt అనుకుందాం.

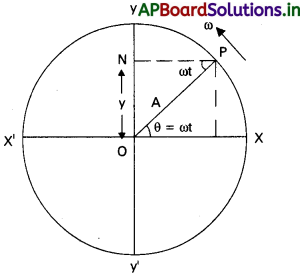
ONP త్రిభుజం నుండి, sin ωt = \(\frac{ON}{OP}\)
ON = OP sin ωt (∵ ON = y, OP = A)
y = A sin ωt ………….. (1)
(1) వ సమీకరణంను ‘t’ తో అవకలనం చేయగా

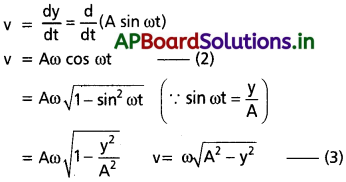
(2) వ సమీకరణంను ‘t’ తో అవకలనం చేయగా, త్వరణం వస్తుంది.
a = \(\frac{dv}{dt}=\frac{d}{dt}\)(Aω cos ωt)
a = -(Aω cos ωt) (∵ y = A sin ωt)
a = -ω²y ………….. (4)
(4) వ సమీకరణం నుండి a ∝ – y …………. (5)

కాబట్టి త్వరణము, స్థానభ్రంశానికి అనులోమానుపాతంలోను మరియు వ్యతిరేకదిశలోను ఉంది. కాబట్టి N యొక్క చలనం కూడా సరళ హరాత్మకం అవుతుంది.

ప్రశ్న 2.
లఘులోలకం చలనం సరళ హరాత్మకం అని చూపి, దాని డోలనావర్తన కాలానికి సమీకరణం ఉత్పాదించండి. సెకండ్ల లోలకం అంటే ఏమిటి? [Mar. ’14, ’13; May ’13]
జవాబు:
i) ఒక లఘులోలకం m ద్రవ్యరాశి గల లోహపు గోళం కలిగి ఉందనుకుందాం. ఈ గోళాన్ని దృఢమైన ఆధారం నుండి సాగుటకు వీలులేని దారంతో L పొడవు దారంతో వ్రేలాడదీశామనుకుందాం.

ii) గోళాన్ని కొద్దిగా ప్రక్కకు లాగివదిలితే, అది మాధ్యమిక స్థానానికి అటూ, ఇటూ డోలనాలు చేస్తుంది.

iii) θ అనునది కోణీయ స్థానభ్రంశం మరియు T అనునది దారంలో తన్యత.

iv) గోళంపై పనిచేసే బలాలు (a) దారంలో తన్యత T (b) భారం mg నిట్టనిలువుగా కిందకు పనిచేస్తుంది.

v) లోలకం భారం mg ని రెండు అంశాలుగా విభజించవచ్చు.
(1) mg cos θ PA దిశలో మరియు (2) mg sin θ PB దిశలో పనిచేస్తుంది.

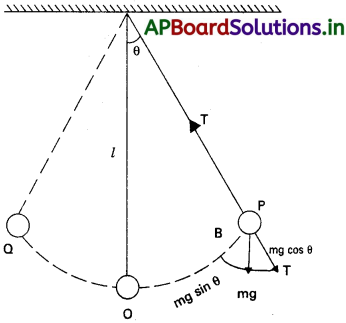
vi) పటంలో P బిందువు వద్ద T = mg cos θ ………….. (1)

vii) బలం mg sin θ పునః స్థాపక టార్క్ను కలిగించి, గోళంను మాధ్యమిక స్థానం వైపు తీసుకు వస్తుంది.

vii) పునఃస్థాపక టార్క్ (7 ) = పునఃస్థాపక బలం × లంబదూరం
τ = – mg sin θ × L ………….. (2)
ఇక్కడ ఋణగుర్తు టార్క్ పనిచేయుటవల్ల θ క్షీణిస్తుందని తెలుపుతుంది.
sin θ కు బదులుగా 6 ను తీసుకుంటే, అనగా sin θ ≈ θ

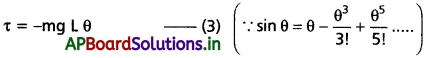
ix) సమీకరణం (3) ప్రకారం, τ ∝ θ మరియు ఈ టార్క్ గోళాన్ని తిరిగి సమతాస్థితికి చేరుస్తుంది.
గోళాన్ని స్వేచ్ఛగా వదిలితే, అది కోణీయ సరళహరాత్మక చలనం చేస్తుంది.
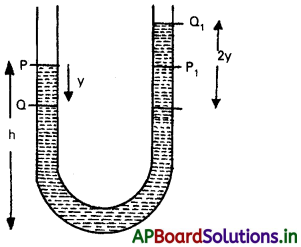
τ = kθ, సమీకరణాన్ని 3 వ సమీకరణంతోపోల్చగా, స్ప్రింగ్ కారకం k = mgL

x) ఇక్కడ జఢత్వ కారకం వ్రేలాడ దీసిన బిందువుపరంగా గోళం జడత్వ భ్రామకం = mL²


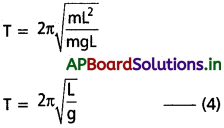
సెకన్ల లోలకం : ఆవర్తనకాలం 2 సెకండ్లు గల లోలకాన్ని సెకన్ల లోలకం అంటారు.
T = 2 సెకన్లు

ప్రశ్న 3.
సరళహరాత్మక డోలకం గతిజ, స్థితిజ శక్తులకు సమీకరణాలను ఉత్పాదించండి. సరళ హరాత్మక చలనంలోని కణం పథంపై అన్ని బిందువుల వద్ద మొత్తం శక్తి స్థిరం అని చూపండి.
జవాబు:
గతిజశక్తి :
స.హ.చ. లోవున్న కణం యొక్క వేగం (v) = ω\(\sqrt{{A^2}-{y^2}}\)
∴ గతిజ శక్తి = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) mω²(A² – y²) ……….. (1)
y = A sin ωt అని మనకు తెలుసు
గతిజశక్తి = \(\frac{1}{2}\)mω²A²(1 – sin²ωt) ………….. (2)
y = 0, అయినప్పుడు (గతిజశక్తి)_{గరిష్ఠం} = \(\frac{1}{2}\)mω²A² (మాధ్యమిక స్థానం)
y = A అయినప్పుడు, (గతిజశక్తి)_{కనిష్ఠం} = 0 (అంత్యస్థానాల వద్ద)
∴ మాధ్యమిక స్థానం వద్ద గతిజశక్తి గరిష్ఠంగాను, అంత్యస్థానాల వద్ద గతిజశక్తి కనిష్టంగా ఉంటుంది.

స్థితిజశక్తి :
సరళ హరాత్మక చలనాలు చేయుచున్న కణం స్థానభ్రంశం పెరిగేకొద్ది పునః స్థాపక బలం కూడా పెరుగుతుంది. పునః స్థాపక బలం, స్థానభ్రంశానికి వ్యతిరేక దిశలో ఉంటుంది. పునఃస్థాపక బలానికి వ్యతిరేకంగా స్థానభ్రంశం చెందుటకు కొంత పని జరగాలి. y స్థానభ్రంశం వద్ద పునఃస్థాపకబలం F.
సగటు నిరోధకబలం = \(\frac{O+F}{2}\) = \(\frac{F}{2}\)
y స్థానభ్రంశాన్ని పొందేందుకు జరిగేపని = సగటుబలం × స్థానభ్రంశం
ω = \(\frac{F}{2}\) × y
ω = \(\frac{ma y}{2}\) …………… (3) (∵ F = ma)
స.హ.చ. లో కణం యొక్క త్వరణం, a = -ω²y …………. (4)
(3) మరియు (4) సమీకరణాలను ఉపయోగించి
మొత్తం పని (W) = \(\frac{1}{2}\)mω²y²
ఈ పని, దానిలో స్థితిజశక్తి రూపంలో ఉంటుంది.
∴ స్థితిజశక్తి = \(\frac{1}{2}\)mω²y² …………. (5)
∴ స్థితిజశక్తి = \(\frac{1}{2}\)mω²A² sin² ωt …………. (6) (∵ y = A sin ωt)
y = 0, అయితే (స్థితిజశక్తి)_{కనిష్టం} = 0 (మాధ్యమిక స్థానం వద్ద)
y = A, అయితే (స్థితిజశక్తి)_{గరిష్టం} = \(\frac{1}{2}\)mω²A² (అంత్యస్థానాల వద్ద)
∴ అంత్య స్థానాల వద్ద స్థితిజశక్తి గరిష్ఠంగాను, మాధ్యమిక స్థానం వద్ద స్థితిజశక్తి కనిష్టంగాను ఉంటుంది.

మొత్తం శక్తి (E) :
ఏ బిందువు వద్దనైనా స.హ.చ. లో వున్న కణం యొక్క మొత్తం శక్తి, స్థితిజ మరియు గతిజశక్తుల మొత్తానికి సమానం.

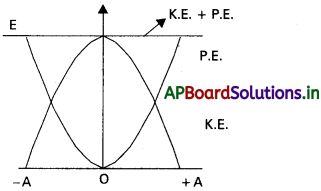
మొత్తం శక్తి (E) = గతిజశక్తి + స్థితిజశక్తి
గతిజశక్తి = \(\frac{1}{2}\)mω²(A² – y²)
స్థితిజశక్తి = \(\frac{1}{2}\)mω²y²
మొత్తం శక్తి = \(\frac{1}{2}\)mω²(A² – y²) + \(\frac{1}{2}\)mω²y² = \(\frac{1}{2}\)mω²A²
మాధ్యమిక స్థానంవద్ద y = 0, స్థితిజశక్తి = 0, (గతిజశక్తి)_{గరిష్టం} = \(\frac{1}{2}\)mω²A²
∴ మొత్తం శక్తి = గతిజశక్తి + స్థితిజ శక్తి
= \(\frac{1}{2}\)mω²A² + 0 = \(\frac{1}{2}\)mω²A²
అంత్యస్థానాల వద్ద y = A, గతిజశక్తి = 0 మరియు

(స్థితిజశక్తి)_{గరిష్టం} = \(\frac{1}{2}\)mω²A²
∴ మొత్తం శక్తి = గతిజశక్తి + స్థితిజ శక్తి
= 0 + \(\frac{1}{2}\)mω²A² = \(\frac{1}{2}\)mω²A²
మాధ్యమిక స్థానం నుండి అంత్యస్థానానికి పోయేసరికి గతిజశక్తి, స్థితిజశక్తిగా మారును.

లెక్కలు (Problems)

ప్రశ్న 1.
బోలుగా ఉండే ఇత్తడి గోళంతో ఒక లోలకం గుండును తయారు చేశారు. దాన్ని పూర్తిగా నీటితో నింపితే దాని డోలనావర్తన కాలం ఏమవుతుంది? ఎందువల్ల?
సాధన:
ఆవర్తన కాలం (T) = 2π\(\sqrt{\frac{l}{g}}\)
గోళం బోలుగా ఉన్నా (లేదా) పూర్తిగా నీటితో నింపి నప్పుడు, ఆవర్తన కాలం ఒకేవిధంగా ఉంటుంది. గోళం నుండి నీరు బయటకుపోతే, లోలకం పొడవు పెరిగి, ఆవర్తనకాలం కూడా పెరుగుతుంది. గోళం పూర్తిగా ఖాళీ అయిపోతే గరిమనాభిపైకి మారి, లోలకం పొడవు తగ్గుతుంది. అప్పుడు ఆవర్తనకాలం కూడా తగ్గుతుంది.

ప్రశ్న 2.
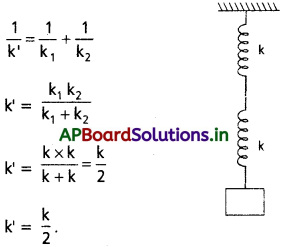
k బల స్థిరాంకం గల రెండు సర్వసమానమైన స్ప్రింగ్లను శ్రేణిలో (ఒకదాని కొనకు మరొకటి) కలిపితే సంయుక్త స్ప్రింగ్ ప్రభావత్మక బల స్థిరాంకం ఎంత ?
సాధన:
k₁ = k₂ = k
రెండు స్ప్రింగ్లను శ్రేణిలో కలిపితే

ప్రశ్న 3.
సరళ హరాత్మక చలనంలో మాధ్యమిక స్థానం వద్ద ఏయే భౌతికరాశులు గరిష్ఠ విలువను కలిగి ఉంటాయి?
సాధన:
i) వేగం V_{గరిష్టం} = Aω
ii) గతిజశక్తి (K.E)_{గరిష్టం} = \(\frac{1}{2}\)mω²A².

ప్రశ్న 4.
సరళ హరాత్మక చలనంలో ఉన్న కణం గరిష్ట వేగం, గరిష్ఠ త్వరణంలో సంఖ్యాత్మకంగా సగం ఉంది. దాని డోలనావర్తన కాలం ఎంత?
సాధన:
ఇచ్చినవి V_{గరిష్టం} = \(\frac{1}{2}\)a_{గరిష్టం}
Aω = \(\frac{1}{2}\)Aω²
ω = 2
T = \(\frac{2 \pi}{\omega}=\frac{2 \pi}{2}\) = πసెకన్

ప్రశ్న 5.
బల స్థిరాంకం 260 Nm^-1 గల స్ప్రింగ్కు 2 kg ద్రవ్యరాశిని వేలాడదీవారు. అది 100 డోలనాలు చేయడానికి పట్టే కాలం ఎంత ?
సాధన:
m = 2 kg, k = 260N/m

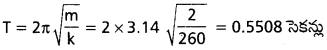
∴ 100 డోలనాలకు పట్టుకాలం = 100 × 0.5508 = 55.08 సెకన్లు

ప్రశ్న 6.
నిశ్చలంగా ఉన్న లిఫ్ట్ ని లఘులోలకం డోలనావర్తన కాలం T. లిఫ్ట్ (i) సమవేగంతో పైకి వెళుతున్నప్పుడు (ii) సమవేగంతో కిందికి వెళుతున్నప్పుడు (iii) సమత్వరణం a తో పైకి వెళుతున్నప్పుడు (iv) సమత్వరణం తో కిందికి వెళుతున్నప్పుడు (v) గురుత్వం వల్ల స్వేచ్ఛగా కిందికి పడుతున్నప్పుడు లోలకం డోలనావర్తన కాలం ఏవిధంగా మారుతుంది?
సాధన:
i) లిఫ్ట్ సమవేగంతో పైకిపోవుచున్నప్పుడు
T = 2π\(\sqrt{\frac{l}{g}}\)
ఆవర్తనకాలం మారదు.

ii) లిఫ్ట్ సమవేగంతో క్రిందకు దిగుతున్నప్పుడు, ఆవర్తనకాలం మారదు.
iii) లిఫ్ట్ త్వరణంతో పైకిపోవుచున్నప్పుడు
T = 2π\(\sqrt{\frac{l}{g+a}}\)
ఆవర్తనకాలం తగ్గుతుంది.

iv) లిఫ్ట్ త్వరణంతో క్రిందకు దిగుచున్నప్పుడు
T = 2π\(\sqrt{\frac{l}{g-a}}\)
ఆవర్తనకాలం పెరుగుతుంది.

v) లిఫ్ట్ స్వేచ్ఛగా దిగుతుంటే, a = g
T= 2π\(\sqrt{\frac{l}{g-g}}\) = 2π\(\sqrt{\frac{l}{O}}\) = ∝
ఆవర్తనకాలం అనంతం.

ప్రశ్న 7.
సరళ హరాత్మక చలనంలోఉండే కణం కంపన పరిమితి 4cm అది మాధ్యమిక స్థానం నుంచి 1 cm దూరంలో వున్నప్పుడు త్వరణం 3 cm s^-2 మాధ్యమిక స్థానం నుంచి 2 cm దూరంలో ఉన్నప్పుడు దాని వేగం ఎంత ?
సాధన:
A = 4 సెం.మీ, x₁ = 1 సెం.మీ, a = 30./s²
a = ω²x₁
3 = ω² × 1

ప్రశ్న 8.
సరళ హరాత్మక డోలకం డోలనావర్తన కాలం 25. డోలకం మాధ్యమికస్థానాన్ని దాటిన 0.25 s తరువాత దాని దశలో కలిగే మార్పు ఎంత?
సాధన:
T = 2 సెకన
t = 0.25 సెకను

ప్రశ్న 9.
సరళ హరాత్మక చలనం చేసే వస్తువు కంపన పరిమితి 5 cm డోలనావర్తన కాలం 0.2 s వస్తువు స్థానభ్రంశం (a) 5 cm. (b) 3 cm. (c) 0 cm వద్ద దాని త్వరణం, వేగాలను కనుక్కోండి.
సాధన:
A = 5 cm = 5 × 10^-2m
T = 0.2 సెకన

i) y = 5 cm = 5 × 10^-2m

ప్రశ్న 10.
ఒక గ్రహం ద్రవ్యరాశి, వాసార్థాలు భూమి ద్రవ్యరాశి, వ్యాసార్థాల కంటే రెట్టింపు, భూమిపై లఘులోలకం డోలనావర్తనకాలం T అయితే గ్రహంపై లోలకం డోలనావర్తన కాలం ఎంత?
సాధన:

ప్రశ్న 11.
1m ఉండే లఘులోలకం డోలనావర్తన కాలం 2 s నుంచి 1.5 s కు మారితే పొడవులో వచ్చే మార్పును లెక్కించండి.
సాధన:

ప్రశ్న 12.
ఒక గ్రహంపై 8 mఎత్తు నుంచి వస్తువు స్వేచ్ఛగా కిందికి పడేందుకు 2 s తీసుకొంటుంది. ఆ గ్రహంపై లోలకం డోలనావర్తన కాలం T S అయితే లోలకం పొడవును లెక్కించండి.
సాధన:
u = 0, t = 2 sec, s = h = 8m

ప్రశ్న 13.
ఒక లఘులోలకం పొడవును 0.6 m పెంచి నప్పుడు, డోలనావర్తన కాలం 50% పెరగడాన్ని గమనించడమైంది. g = 9.8 m s^-2 ఉన్న ప్రదేశంలో దాని తొలి పొడవు, తొలి డోలనా వర్తన కాలాలను లెక్కించండి.
సాధన:

ప్రశ్న 14.
సెకండ్ల లోలకంతో నియంత్రితమైన (regulated) ఒక గడియారం సరైన సమయాన్ని చూపిస్తూ ఉంది. వేసవి కాలంలో లోలకం పొడవు 1.02 m లకు పెరిగినట్లైతే గడియారం ఒక రోజులో ఎంత కాలాన్ని పొందుతుంది లేదా కోల్పోతుంది?
సాధన:

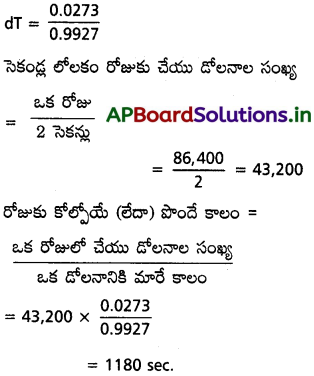
ప్రశ్న 15.
స్ప్రింగు వేలాడదీసిన వస్తువు ఆవర్తన కాలం T. ఆ స్ప్రింగ్ను రెండు సమానభాగాలుగా చేసి (i) వస్తువును ఒక భాగానికి వేలాడదీసినప్పుడు (ii) రెండు భాగాలకు (సమాంతరంగా) ఒకేసారి వస్తువును వేలాడదీసినప్పుడు డోలనావర్తన కాలాలను లెక్కించండి.
సాధన:

అదనపు లెక్కలు (Additional Problems)

ప్రశ్న 1.
కింది వాటిలో ఏవి ఆవర్తన చలనాలను సూచిస్తాయి?
a) చెరువు ఒక ఒడ్డు నుంచి అవతలి ఒడ్డుకు తిరిగి అవతలి ఒడ్డు నుంచి మొదటి ఒడ్డుకు ఒక ఈతగాడు పూర్తిచేసే ట్రిప్.
b) స్వేచ్ఛగా వేలాడదీసిన దండాయస్కాంతాన్ని N – S దిశ నుంచి కదిల్చి వదిలితే అది చేసే చలనం.
c) తన ద్రవ్యరాశి కేంద్రం చుట్టూ భ్రమణం చెందే హైడ్రోజన్ అణువు.
d) ధనుస్సు (విల్లు) నుంచి విడుదలైన బాణం.
సాధన:
a) ఇది ఆవర్తన చలనం కాదు. ఈతగాడి చలనం అటూ, ఇటూ ఉన్నప్పటికీ ఒక నిర్దిష్ట ఆవర్తనం లేదు.
b) ఇది ఆవర్తన చలనం, కారణం స్వేచ్ఛగా వ్రేలాడదీసిన అయస్కాంతంను కొద్దిగా N-S దిశ నుండి స్థాన భ్రంశం చెందిస్తే, అది డోలనాలు చేస్తుంది. ఇవి సరళహరాత్మక డోలనాలు కూడా.
c) ఇది కూడా ఆవర్తన చలనం.
d) ఇది ఆవర్తన చలనం కాదు.

ప్రశ్న 2.
కింది ఉదాహరణలలో ఏవి దాదాపు సరళ హరాత్మక చలనాలు, ఏవి సరళ హరాత్మకం కాని ఆవర్తన చలనాలను సూచిస్తాయి?
a) తన అక్షం పరంగా భూమి చేసే భ్రమణ చలనం.
b) U-గొట్టంలో డోలనం చేసే పాదరస స్థంభం చలనం.
c) నునుపైన వక్రత గల లోతు గిన్నెలో సమతాస్థితి స్థానం కంటే కొద్దిగా ఎగువన వదిలిన ఇనుప గుండు చలనం.
d) తన సమతా స్థితి స్థానం పరంగా బహు పరమాణుక అణువు చేసే సాధారణ కంపనాలు.
సాధన:
a) ఇది ఆవర్తన చలనమే కాని, సరళహరాత్మక చలనం కాదు. కారణం ఇది మాధ్యమిక స్థానానికి అటూ, ఇటూ తిరగదు.
b) ఇది సరళ హరాత్మక చలనం.
c) ఇది సరళ హరాత్మక చలనం.
d) ఇది ఆవర్తన చలనం, స.హ.చ. కాదు. బహు పరమాణుక వాయు అణువులలో అనేక సహజ పౌనః పున్యాలు ఉంటాయి. వాటి సాధారణ చలనం అనేక వేరు వేరు పౌనఃపున్యాల ఫలిత సరళ హరాత్మక చలనాలు. కాబట్టి ఫలిత చలనం ఆవర్తనమే కాని స.హ.చ. కాదు.

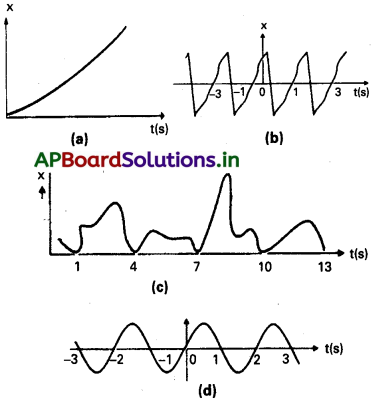
ప్రశ్న 3.
పటము కణం రేఖీయ చలనానికి x-t ల మధ్య గీచిన గ్రాఫ్లను సూచిస్తుంది. వాటిలో ఏవి ఆవర్తన చలనాన్ని సూచిస్తాయి? సూచిస్తే వాటి డోలనావర్తన కాలం ఎంత?

సాధన:

1. 1(a) పటంలో ఆవర్తన చలనంకాదు. చలనం పునరావృతం కావచ్చు (లేదా) మాధ్యమిక స్థితికి చేరవచ్చు.
2. 1(b) పటంలో ఆవర్తన కాలం 25 వద్ద ఆవర్తన చలనంను సూచిస్తుంది. ‘
3. 1(c) పటంలో ఆవర్తన చలనం కాదు. కారణం ఇది పునరావృతం కాదు.
4. 1(d) ఆవర్తన కాలం 25 వద్ద చలనం ఆవర్తన చలనంను సూచించును.

ప్రశ్న 4.
కింది వాటిలో ఏ కాల ప్రమేయాలు (a) సరళ హఠాత్మక, (b) ఆవర్తనమే కానీ సరళ హరాత్మకం కాని, (c) ఆవర్తనం కాని చలనాలను సూచి స్తాయి? ప్రతి ఆవర్తన చలన సందర్భంలో ఆవర్తన కాలాన్ని తెలియచేయండి (ఎ ఏదైనా ధన స్థిరాంకం)
a) sin ωt – cos ωt
b) sin³ ωt
c) 3 cos (π/4 – 2ωt)
d) cos ωt + cos 3ωt + cos 5 ωt
e) exp (-ω²t²)
f) 1 + ωt + ω²t².
సాధన:
ప్రమేయం ఆవర్తన చలనంను సూచిస్తుంది. సమాన కాల వ్యవధులలో చలనం పునరావృతం అవుతుంది. ఇది సరళ హరాత్మక చలనంను సూచించును. దీనిని ఈ క్రింది

ఇది సరళ హరాత్మక చలనం మరియు దాని ఆవర్తన చలనం 2π/ω.

b) sin³ ωt = \(\frac{1}{4}\)[3sin ωt – sin 3ωt]
విడివిడిగా 3 sin ot మరియు sin 3ut సరళ
హరాత్మక చలనాన్ని సూచించును. కాని (ii) కేవలం ఆవర్తన చలనమే కాని సరళహరాత్మక చలనం కాదు. దాని ఆవర్తన చలనం 2π/ω.

c) 3 cos(\(\frac{2 \pi}{4}\) – 2ωt) = 3 cos (2ωt – \(\frac{2 \pi}{4}\))
(∵ cos (-θ) = cos θ).
స్పష్టంగా ఇది సరళహరాత్మక చలనం మరియు దాని ఆవర్తన కాలం 2π/2ω.

d) cos ωt + cos 3wt + cos 5ut, ఇది ఆవర్తనమే కాని, సరళహరాత్మక చలనం కాదు. దాని ఆవర్తన కాలం 2π/ω.

e) e^-ω²t² ఇది ఘాతాంక ప్రమేయము. ఆవర్తనం కాదు. కాబట్టి ఇది ఆవర్తన చలనం కాదు.

f) 1 + ωt + ω²t² కూడా ఆవర్తన చలనం కాదు.

ప్రశ్న 5.
10 cm ఎడంతో ఉండే రెండు బిందువులు A, B ల మధ్య ఒక కణం రేఖీయ సరళ హరాత్మక చలనం చేస్తుంది. A నుంచి B కి దిశను ధన దిశగా తీసుకొని, కింద ఇచ్చిన స్థానాల వద్ద కణం ఉన్నప్పుడు వేగం, త్వరణం, బలం దిశలను తెలపండి.
a) A
b) B
c) A, B ల మధ్య బిందువు వద్ద A వైపు వెళ్ళేటప్పుడు
d) నుంచి 2 cm దూరంలో, A వైపు వెళ్ళేటప్పుడు
e) A నుంచి 3 cm దూరంలో, B వైపు వెళ్ళేటప్పుడు
f) B నుంచి 4 cm దూరంలో, A వైపు వెళ్ళేటప్పుడు
సాధన:

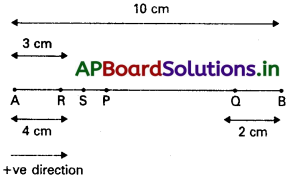
పటంలో A మరియు Bలు స.హ.చ. యొక్క రెండు అంత్యస్థానాలు. A నుండి B వైపు వేగంను ధనాత్మకంగా తీసుకోవాలి. త్వరణం మరియు బలం దిశను AP వైపు ధనాత్మకం మరియు BP దిశవైపు ఋణాత్మకం.

a) Aచివర వద్ద, కణం అంత్యస్థానం వద్ద విరామస్థితికి వస్తూ, కణం స.హ.చ.లో ఉంది. కాబట్టి వేగం సున్నా, త్వరణం AP వైపు ధనాత్మకం. బలం కూడా AP దిశలో ధనాత్మకం.

b) B చివర వద్ద, వేగం సున్నా. కావున త్వరణం మరియు బలం ఋణాత్మకం. ఇది BP దిశలో ఉంటుంది. అనగా ఋణదిశను సూచించును.

c) A వైపు పోవుచున్నప్పుడు, మధ్యబిందువు AB వద్ద, కణం మాధ్యమిక స్థానం P వద్ద PA దిశలో అనగా ఋణదిశలో ఉంటుంది. కాబట్టి వేగం ఋణాత్మకం. త్వరణం మరియు బలం రెండూ సున్నా.

d) B నుండి A వైపు 2 సెం. మీ. దూరంలో ఉన్నప్పుడు, కణం Q వద్ద ఉంది ఇది QP దిశలో చలిస్తూ అనగా ఋణదిశలో చలిస్తుంది. వేగం, త్వరణం మరియు బలం అన్నీ ఋణాత్మకం.

e) A నుండి 3 cm దూరంలో B వైపు, కణం R వద్ద ఉన్నప్పుడు RP ధన దిశలో సూచిస్తుంది. ఇక్కడ వేగం, త్వరణం మరియు బలం అన్నీ ధనాత్మకం.

f) A నుండి 4 cm దూరంలో A వైపుకు పోవుచున్న ప్పుడు, కణం S వద్ద SA దిశలో వేగం ఋణదిశను సూచిస్తుంది. వేగం ఋణాత్మకం కారణం త్వరణం మాధ్యమిక స్థానం SP దిశలో ధనాత్మకం, అదేవిధంగా బలం ధనాత్మకం.

ప్రశ్న 6.
కణం త్వరణం a స్థానభ్రంశం X ల మధ్య సంబంధాన్ని తెలిపే కింది సమీకరణాల్లో ఏవి సరళ హరాత్మక చలనాన్ని కలిగి ఉన్నాయి?
a) a = 0.7x
b) a = −200x²
c) a = -10x
d) a = 100x³
సాధన:
స.హ.చ.లో త్వరణం, స్థానభ్రంశం మధ్య సంబంధం a = -kx, ఇది (c) సంబంధాన్ని సూచిస్తుంది.

ప్రశ్న 7.
సరళ హరాత్మక చలనం చేస్తున్న కణం చలనాన్ని కింది స్థానభ్రంశ ప్రమేయం వర్ణిస్తుంది.
x(t) = A cos (ωt + Φ).
కణం తొలి (t = 0)స్థానం 1 cm తొలి వేగం ω cm/s అయితే కణం కంపన పరిమితి, తొలిదశా కోణం విలువలు ఎంత? కణం కోణీయ పౌనః పున్యం πs^-1. కణం సరళ హరాత్మక చలనాన్ని కొసైన్ ప్రమేయంతో కాకుండా సైన్ ప్రమేయం : x = B sin (ωt + α)తో వర్ణిస్తే పైన తెలిపిన తొలి పరిస్థితుల వద్ద కణం కంపన పరిమితి, తొలి దశలు ఎలా ఉంటాయి?
సాధన:
ఇక్కడ t = 0 వద్ద, x = 1 cm మరియు
v = ω cm s^-1, Φ = ? ; ω = πs^-1
x = A cos (ωt + Φ)
∴ 1 = A cos (π × 0 + Φ)
= A cos Φ ………… (i)
వేగం, v = \(\frac{dx}{dt}\) = – Aω sin (ωt + Φ)
∴ ω = -Aω sin (π × 0 + Φ) or 1 = – A sin Φ
(లేదా) A sin Φ = -1 ………….. (ii)
(i) మరియు (ii) వర్గం చేసి కూడగా
A²(cos² Φ + sin² Φ) = 1 + 1 = 2
(లేదా) A² = 2 (లేదా) A = √2cm
సమీకరణం (ii)ను (i) చే భాగించగా
tan Φ = −1 (లేదా) Φ = \(\frac{3 \pi}{4}\) (లేదా) \(\frac{7 \pi}{4}\)
x = B sin (ωt + α) …………… (iii)
t = 0, x = 1, వద్ద
1 = B sin (ω × 0 + α) = B sin α …………… (iv)
(iii)ను tతో అవకలనం చేయగా
వేగం v = \(\frac{dx}{dt}\) = Bω cos (ωt + α)
t = 0, v = ω తొలిషరతును అన్వర్తించగా
ω = Bω cos (π × 0 + α)
(లేదా) 1 = B cos α …………… (v)
(iv) మరియు (v)ను వర్గంచేసి, కూడగా
B² sin² α + B² cos²α = 1² + 1² = 2
(లేదా) B² = 2 (లేదా) B = √2 cm
(iv)ను (v) చే భాగించగా

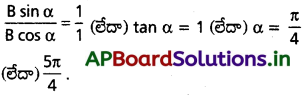
ప్రశ్న 8.
స్ప్రింగ్ త్రాసు స్కేలుపై 0 నుంచి 50 kg వరకు రీడింగ్ల లు కలవు. స్కేలు పొడవు 20 cm. ఈ త్రాసుకు వేలాడదీసిన వస్తువును లాగి వదిలితే అది 0.6 s డోలనావర్తన కాలంతో డోలనాలు చేస్తుంది. అయితే వేలాడదీసిన వస్తువు భారం ఎంత?
సాధన:
m = 50 kg, గరిష్ఠ సాగుదల,
y = 20 – 0 = 20 cm = 0.2 m; T = 0.6s
గరిష్ఠ బలం F = mg = 5 × 9.8 N


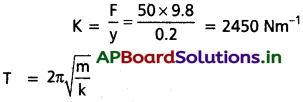
∴ వస్తువు భారం = mg = 22.36 × 9.8
= 219.1N
= 22.36 kgf

ప్రశ్న 9.
పటం లో చూపిన విధంగా 1200 Nm^-1 స్ప్రింగ్ స్థిరాంకం గల స్ప్రింగ్ను క్షితిజ సమాంతరంగా ఉండే బల్లపై అమర్చారు. స్ప్రింగ్ స్వేచ్ఛా చివరకు 3 kg ద్రవ్యరాశిని తగిలించారు. ద్రవ్యరాశి 2.0 cm దూరం పక్కకు లాగి వదిలారు.

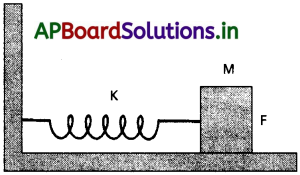
(i) డోలనాల పౌనఃపున్యం (ii) ద్రవ్యరాశి గరిష్ఠ త్వరణం (iii) ద్రవ్యరాశి
సాధన:
ఇక్కడ k = 1200 N/m, m =
a = 2.0 cm = 0.02 m
a) పౌనఃపున్యం,

c) ద్రవ్యరాశి మాధ్యమిక స్థానం గుండా పోవునపుడు వేగం గరిష్టం.

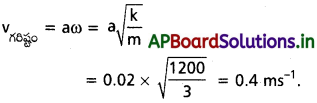
ప్రశ్న 10.
పై అభ్యాసం (9)లో స్ప్రింగ్ సాగదీయనప్పుడు ద్రవ్యరాశి స్థానం x = 0 అని, ఎడమ నుంచి కుడికి ధనాత్మక X- అక్షం అని తీసుకోండి. t = 0 వద్ద స్టాప్ వాచు మొదలు పెట్టినట్లెటే, డోలనాలు చేస్తున్న ద్రవ్యరాశి కింది స్థానాల వద్ద ఉన్నప్పుడు t ప్రమేయంగా x విలువను తెలపండి.
a) మాధ్యమిక స్థానం
b) గరిష్ఠంగా సాగిన స్థానం
c) గరిష్టంగా సంపీడం (నొక్కిన) చెందిన స్థానం పై సరళ హరాత్మక చలన ప్రమేయాలు పౌనః పున్యం, కంపన పరిమితి, తొలిదశల్లో ఒకదానితో ఒకటి ఏవిధంగా విభేదిస్తాయో తెలపండి ?
సాధన:
ఇక్కడ a = 2.0 cm; ω = \(\sqrt{\frac{k}{m}}=\sqrt{\frac{1200}{3}}\) = 20s^-1

a) మాధ్యమిక స్థానం నుండి కాలాన్ని గుర్తిస్తే
x = a sin ωt, x = 2 sin 20t.

b) గరిష్టంగా సాగదీసినపుడు, వస్తువు కుడి అంత్యస్థానం వద్ద, తొలిదశ \(\frac{\pi}{2}\).
అయితే x = a sin (ωt + \(\frac{\pi}{2}\))
= a cos ωt = 2 cos 20 t

c) గరిష్టంగా సంపీడించినపుడు, వస్తువు ఎడమ అంత్య స్థానం వద్ద తొలిదశ \(\frac{3 \pi}{2}\) అయితే
x = a sin (ωt + \(\frac{3 \pi}{2}\))
= -a cos ωt = -2 cos 20t
ఈ ప్రమేయాలు కంపన పరిమితి, పౌనఃపున్యం వేరువేరుగా ఉన్నాయి. వాటి తొలిదశ వేరువేరుగా ఉంది.

ప్రశ్న 11.
పటం రెండు వృత్తాకార చలనాలను సూచి స్తుంది. వృత్త వ్యాసార్ధం, భ్రమణ కాలం, తొలి స్థానం, తిరిగే దిశ (సవ్య లేదా అపసవ్య) మొదలైన అంశాలు పటంలో చూపించడమైంది.

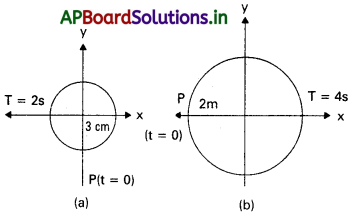
పై రెండు సందర్భాల్లో భ్రమణం చెందే కణం P యొక్క వ్యాసార్థ సదిశ X-అక్ష విక్షేపం యొక్క సహచలనాలను రాబట్టండి.
సాధన:
పటంలో (a) నుండి, T = 2s; a = 3 cm;
t = 0 వద్ద x అక్షంతో OP చేయు కోణం \(\frac{\pi}{2}\) అనగా
Φ = \(\frac{\pi}{2}\) రేడియన్ సవ్యదిశలో చలిస్తే Φ = + \(\frac{\pi}{2}\) అయిన
t కాలం వద్ద OP యొక్క స.హ.చ. సమీకరణం,

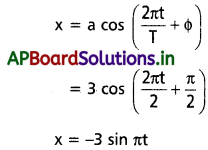
పటం (b) నుండి, T = 4s ; a = 2m
t = 0 వద్ద, ధన X-అక్షంతో OP చేయు కోణం π అనగా
Φ = π, అపసవ్యదిశలో Φ = + π.
t కాలం వద్ద OP యొక్క స.హ.చ. సమీకరణం

ప్రశ్న 12.
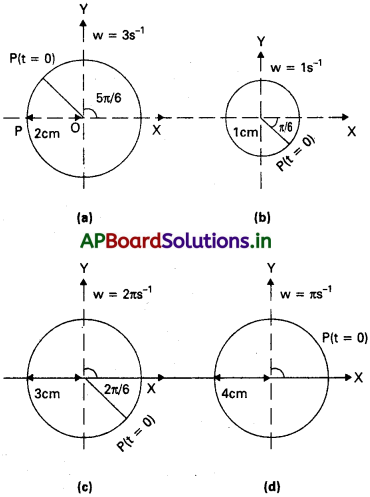
కింది ప్రతి సరళ హరాత్మక చలనానికి అనురూపంగా ఉండే నిర్దేశ వృత్తాలను గీయండి. కణం తొలిస్థానం (t = 0), వృత్త వ్యాసార్ధం, భ్రమణం చెందే కణం కోణీయ వేగాలను సూచించండి. సౌలభ్యం కోసం ప్రతి సందర్భంలో భ్రమణ దిశను అపసవ్య దిశగా తీసుకోండి. (xని cm లలో tని సెకండ్లలో తీసుకోండి).
a) x = -2 sin (3t + π/3)
b) x = cos (π/6 – t)
c) x = 3 sin (2πt + π/4)
d) x = 2 cos πt.
సాధన:
ప్రతిప్రమేయాన్ని ఈ రూపంలో తెలుపవచ్చు.
x = a cos (ωt + Φ) ………….. (i)
Φ అనునది తొలిదశ. అనగా Φ కణం యొక్క తొలి వ్యాసార్థం సదిశ, ధన X-అక్షంతో చేయు కోణం.

సమీకరణం (i)తో పోల్చితే, పటం (a)లో నిర్దేశిక వృత్తాన్ని చూడవచ్చు.

సమీకరణం (i)తో పోల్చితే, a = 3, ω = 2π
మరియు Φ = \(\frac{3 \pi}{2}+\frac{\pi}{4}=\frac{4 \pi}{4}\)
పటం (c)లో నిర్దేశిక వృత్తాన్ని చూడవచ్చు.

d) x = 2 cos πt
సమీకరణం (i)తో పోల్చితే, a = 2, ω = π మరియు Φ = 0.
పటం (d)లో నిర్దేశిక వృత్తాన్ని చూడవచ్చు.

ప్రశ్న 13.
పటం (a) లో చూపించిన విధంగా k బల స్థిరాంకం గల స్ప్రింగ్ ఒక చివరను ద్రుఢంగా బిగించి, రెండో స్వేచ్ఛా చివరకు ద్రవ్యరాశి mని బిగించారు. స్వేచ్ఛా చివర ప్రయోగించిన బలం F వల్ల స్ప్రింగ్ కొంత సాగుతుంది. పటం (b) లో చూపించిన విధంగా అదే స్ప్రింగ్ రెండు స్వేచ్ఛా చివరలను m ద్రవ్యరాశి గల రెండు దిమ్మెలకు అనుసంధానం చేసి, రెండు చివరలా అంతే బలం F ప్రయోగించి స్ప్రింగ్ను సాగదీశారు.

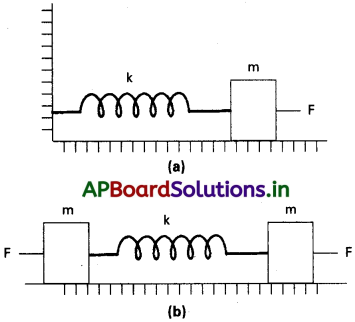
a) రెండు సందర్భాల్లో స్ప్రింగ్ పొందే గరిష్ఠ సాగుదల ఎంత?
b) పటం (a) లో ద్రవ్యరాశిని, పటం (b)లో రెండు ద్రవ్యరాశులను వదిలిపెడితే ప్రతి సందర్భంలో స్ప్రింగ్ చేసే డోలనా వర్తన కాలం ఎంత?
సాధన:

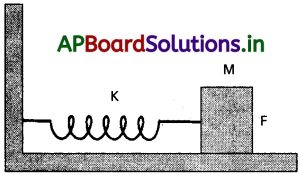
a) రెండు సందర్భాలలో స్ప్రింగ్ యొక్క గరిష్టసాగుదల = \(\frac{F}{K}\) ఇక్కడ K స్ప్రింగ్ స్థిరాంకం.
b) పటం (a)లో, × అనునది స్ప్రింగ్లో సాగుదల, m ద్రవ్యరాశి స్వేచ్ఛగా విడిచిన తర్వాత మాధ్యమిక స్థానం వైపుకు పనిచేసే పునఃస్థాపక బలం
F = -Kx i.e., F ∝ x,

F దిశ మాధ్యమిక స్థానం వైపు ఉంటుంది. కాబట్టి స్ప్రింగ్ స.హ.చ.లో ఉంటుంది.
స్ప్రింగ్ కారకం = స్ప్రింగ్ స్థిరాంకం = K
జఢత్వకారకం = వ్యవస్థ యొక్క ద్రవ్యరాశి = m

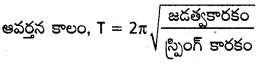
∴ T = 2π\(\sqrt{\frac{m}{K}}\)
పటం (b)లో రెండు వస్తువుల వ్యవస్థలో స్ప్రింగ్ స్థిరాంకం K మరియు క్షీణ ద్రవ్యరాశి,

ప్రశ్న 14.
ఒక వాహన ఇంజన్లో లోని సిలిండర్ లో గల ముషలకం 1.0 m. (కంపన పరిమితికి రెట్టింపు) ఘాతం (stroke) ను ఇస్తుంది. ఒక వేళ ముషలకం 200 rad/min పౌనఃపున్యంతో సరళ హరాత్మక చలనం చేస్తున్నట్లైతే, దాని గరిష్ఠ వడి ఎంత?
సాధన:
a = \(\frac{1}{2}\)m ; ω = 200 rev/min;
V_max = aω
= \(\frac{1}{2}\) × 200
= 100 m/min.

ప్రశ్న 15.
చంద్రుడిపై గురుత్వ త్వరణం విలువ 1.7 ms^-2 భూమిపై 3.5 s డోలనావర్తన కాలం గల లఘులోలకాన్ని చంద్రుడి పైకి తీసుకొని పోతే అక్కడ దాని డోలనావర్తన కాలం ఎంత? (భూమిపై g విలువ 9.8 ms^-2)
సాధన:
ఇక్కడ g_m = 1.7 ms^-2 ; g_e = 9.8 ms^-2;
T_m = ? ; T_e = 3.5 s^-1

ప్రశ్న 16.
కింది ప్రశ్నలకు సమాధానాలివ్వండి :
a) సహచ చేసే కణం డోలనావర్తన కాలం బల స్థిరాంకం k కణం ద్రవ్యరాశి m పై ఆధార పడి ఉంటుంది.
T = 2π\(\sqrt{\frac{m}{K}}\)
లములోలకం ఉజ్జాయింపుగా సరళ హరాత్మక చలనం చేస్తుంది. అయితే లోలకం డోలనావర్తన కాలం ఎందుకు గుండు ద్రవ్యరాశిపై ఆధారపడి ఉండదు?
b) తక్కువ కోణీయ స్థానభ్రంశాలకు లఘు లోలకం చలనం సరళ హరాత్మకం. అధిక కోణాలకు, మరింత విశ్లేషణతో తెలిపిన విషయం ఏమిటంటే T విలువ 2π\(\sqrt{\frac{l}{g}}\) కంటే ఎక్కువగా ఉంటుందని, ఈ ఫలితాన్ని గుణాత్మకంగా వివరించే ఆలోచన చేయండి.
c)చేతిగడియారం కలిగి ఉన్న వ్యక్తి శిఖరంపై నుంచి కిందికి పడుతున్నాడు. అతని స్వేచ్ఛా పతన సమయంలో గడియారం సరైన సమయాన్ని సూచిస్తుందా?
d) గురుత్వం వల్ల స్వేచ్ఛగా పడుతున్న గది (cabin) లో ఉంచిన లఘులోలకం డోలన పౌనఃపున్యం ఎంత?
సాధన:
a) లఘులోలకం యొక్క స్ప్రింగ్ కారకం (లేదా) బలస్థిరాంకం K ద్రవ్యరాశి mకు అనులోమాను పాతంలో ఉంటుంది. m హారం మరియు లవంలో కొట్టివేయబడుతుంది. అందుకని లఘులోలకం ఆవర్తన కాలం, గోళం ‘ద్రవ్యరాశిపై ఆధారపడదు.

b) లఘులోలకం యొక్క గోళంను స్థానభ్రంశం చెందిస్తే ప్రభావ బలస్థిరాంకం
F = -mg sin θ. ఇక్కడ 9 స్వల్పం. sin θ = θ.
లఘులోలకం ఆవర్తనకాలం T = 2π\(\sqrt{\frac{l}{g}}\)
θ ఎక్కువైతే sin θ < θ, పునఃస్థాపక బలం mg sin 6కు బదులు mge, అధిక కోణాలకు g విలువ క్షీణిస్తుంది. కాబట్టి ఆవర్తన కాలం T పెరుగుతుంది.

c) అవును, చేతి గడియారం పని తీరు స్ప్రింగ్ చర్యపై ఆధారపడును. ఇక్కడ గురుత్వ ప్రభావం ఉండదు.

d) స్వేచ్ఛగా క్రిందకు పడే వ్యక్తిపై గురుత్వం ప్రభావం కనిపించదు. కాబట్టి పౌనఃపున్యం శూన్యం.

ప్రశ్న 17.
M ద్రవ్యరాశి గల గుండును కలిగి వున్న పొడవు గల లఘులోలకాన్ని కారులో వేలాడ దీశారు. కారు R వాసార్థం గల వృత్తాకార మార్గంపై U సమవడితో చలిస్తోంది. లోలకం వ్యాసార్థ దిశలో సమతాస్థితి స్థానం పరంగా స్వల్ప డోలనాలను చేస్తే, దాని ఆవర్తన కాలం ఎంత?
సాధన:
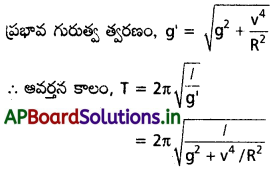
అభికేంద్ర త్వరణం a_c = \(\frac{v^2}{R}\), ఇది క్షితిజ సమాంతరంగా పని చేస్తుంది.

గురుత్వత్వరణం g నిట్టనిలువుగా క్రిందకు పని చేస్తుంది.

ప్రశ్న 18.
ρ సాంద్రత, A ఆధార వైశాల్యం, h ఎత్తుగల స్థూపాకార కార్క్ ముక్క ρ₁ సాంద్రత గల ద్రవంలో తేలుతోంది. కార్ను కొద్దిగా కిందకు నెట్టి వదిలితే అది ఆవర్తన కాలం T = 2π\(\sqrt{\frac{h \rho}{\rho_1 g}}\) తో సరళ హరాత్మక చలనం చేస్తుందని చూపండి. (ద్రవం స్నిగ్ధత వల్ల కలిగే అవరోధాన్ని ఉపేక్షించండి).
సాధన:
స్థూపం యొక్క ద్రవ్యరాశి (m) = ఘనపరిమాణం × సాంద్రత = Ahρ ……….. (1)
F₁ = l పొడవు గల స్థూపం వలన స్థానభ్రంశం చెందిన ద్రవం యొక్క భారం = (Al)ρ₁g ………… (2)
స్థూపం యొక్క భారం = mg ………… (3)
సమతాస్థితిలో, mg = alρ₁g
m = Αlρ₁ ………… (4)
F₂ = A(l + y)ρ₁g ………… (5)

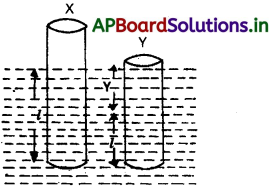
పునఃస్థాపక బలం (F) = -(F₂ – mg)
= -[A(l + y)ρ₁g – Alρ₁g]
F = -Ayρ₁g = -(Aρ₁g)y ………… (6)
సరళహరాత్మక చలనంలో, F = -Ky ………….. (7)
(6) మరియు (7) సమీకరణాల నుండి
స్ప్రింగ్-కారకం (K) = Aρ₁g ………… (8)
జడత్వ కారకం, m = Ahρ ……………… (9)

ప్రశ్న 19.
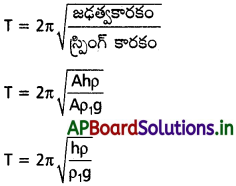
U-ఆకారపు గొట్టంలో పాదరసం ఉంది. గొట్టం ఒక చిరను పీల్చే పంపు (suction pump) కు, రెండో చివరను వాతావరణంతో అనుసంధానం చేసి, రెండు చివరల మధ్యకొంత పీడన వ్యత్యాసాన్ని ఏర్పరచారు. పీల్చే పంపును తొలగిస్తే, గొట్టంలోని పాదరస స్థంభం సరళ హరాత్మక చలనం చేస్తుందని చూపండి.
సాధన:
ద్రవం యొక్క సాంద్రత p అనుకొనుము.

ఈ ద్రవం A అడ్డుకోత వైశాల్యం గల U- గొట్టంలో ఉంది అనుకొనుము. P నుండి P₁ వరకు ద్రవస్తంభం మొత్తం పొడవు L.

ద్రవ్యరాశి (m) = LAρ
PQ = y, P₁Q₁ = y, QQ₁ = 2y
పునఃస్థాపక బలం (F) = -(A2y)ρg
=-(2Aρg)y ………… (1)
F ∝ -y
కాబట్టి U-గొట్టంలో డోలనాలు సరళహరాత్మక చలనంలో ఉంటాయి.

ప్రశ్న 20.
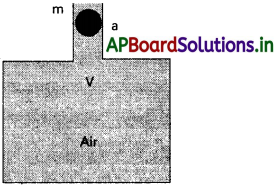
పటం లో చూపిన విధంగా V ఘనపరిమాణం గల గాలి గది మెడ (neck) మధ్యచ్ఛేద వైశాల్యం a. దీనిలో m ద్రవ్యరాశి గల బంతి సరిగ్గా సరిపోయి ఎలాంటి ఘర్షణ లేకుండా పైకి కిందికి కదలగలదు. బంతిని కొద్దిగా కిందికి నెట్టి వదిలితే అది సరళ హరాత్మక చలనం చేస్తుందని చూపండి. గది లోని గాలి పీడన – ఘనపరిమాణాల్లో కలిగే మార్పులు సమ ఉష్ణోగ్రతా మార్పులని భావించి, బంతి డోలనా వర్తన కాలానికి సమీకరణాన్ని రాబట్టండి.

సాధన:
ఏకరీతి అడ్డుకోత వైశాల్యం A గల పొడవైన మేడ‘గల గాలి ఛాంబర్ ఘనపరిమాణం V అనుకొనుము. Cస్థానం వద్ద m ద్రవ్యరాశి గల ఘర్షణలేని బంతిని ఉంచామని అనుకొనుము. ఛాంబర్ లోపల, బంతి అడుగున గాలిపీడనం, వాతావరణ పీడనానికి సమానం. బంతి మీద కొద్దిగా బలం P ని పెంచితే బంతి కొద్దిగా D స్థానం వద్దకు దిగుతుంది. CD = y ఛాంబర్ లోపల , ఘనపరిమాణం తగ్గి, పీడనం పెరుగుతుంది. ఛాంబర్ లోపల తగ్గిన గాలి ఘనపరిమాణం, ∆V = Ay

ఇక్కడ ఋణగుర్తు. పీడనం పెరిగి, గాలి ఘన పరిమాణం తగ్గుటను సూచిస్తుంది.

F ∝ y మరియు ఋణగుర్తు, బలం మాధ్యమిక స్థానం వైపు సూచిస్తుంది. బంతిపై పెంచిన పీడనాన్ని తొలగిస్తే, బంతి C వద్ద (మాధ్యమిక స్థానం) స.హ.చ.లో ఉంటుంది. పునఃస్థాపక బలం
F = -Ky

ప్రశ్న 21.
3000 kg ద్రవ్యరాశి గల వాహనంలో నీవు ప్రయాణిస్తూ దాని స్ప్రింగ్ వ్యవస్థ (suspen- sion system) డోలనాల లక్షణాలను పరీక్షిస్తు న్నారనుకోండి. వాహనం మొత్తం బరువు వల్ల స్ప్రింగ్ల వ్యవస్థ15 cm కిందికి కుంగినాయి. అంతేగాక, ఒక పూర్తి డోలనంలో డోలన కంపన పరిమితి కూడా 50% తగ్గింది. అయితే (a) స్ప్రింగ్ స్థిరాంకం k విలువను (b) ప్రతి చక్రం 750 kg. ద్రవ్యరాశిని మోయగలిగితే స్ప్రింగ్, షాక్ అబ్సార్బర్ల వ్యవస్థ యొక్క అవరోధ స్థిరాంకం b విలువను అంచనా వేయండి.
సాధన:
a) M = 3000.kg ; x = 0.15 cm ; K అనునది స్ప్రింగ్ స్థిరాంకం. సమాంతరంగా కలిపిన నాలుగు స్ప్రింగ్ల మొత్తం స్ప్రింగ్ స్థిరాంకం K = 4 K.
4 kx = Mg
k = \(\frac{Mg}{4x}\)

ప్రశ్న 22.
రేఖీయ సరళ హరాత్మక చలనం చేసే కణం విషయంలో ఒక డోలనావర్తన కాలానికి సగటు గతిజ శక్తి, అంతే కాలానికి ఉండే సగటు స్థితిజ శక్తికి సమానం అని చూపండి.
సాధన:
m ద్రవ్యరాశి గల కణం స.హ.చ. లో ఉంది. దాని ఆవర్తన కాలం T. t కాలం వద్ద కణం యొక్క స్థానభ్రంశం
Y = a sin wt

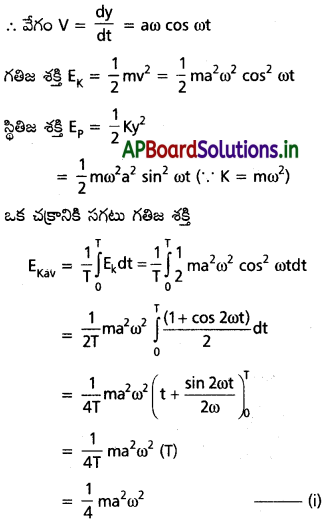
ప్రశ్న 23.
10 kg ద్రవ్యరాశి గల వృత్తాకార లోహపలక కేంద్రం వద్ద తీగతో కట్టి పలకను వేలాడదీశారు. తీగను మెలి తిప్పి వదిలితే పలక చేసే విమోటన బీగిలనాల ఆవర్తన కాలం 1.5s. పలక వ్యాసార్థం 15 cm అయితే తీగ విమోటన స్ప్రింగ్ స్థిరాంకం విలువను కనుక్కోండి. (విమోటన స్ప్రింగ్ స్థిరాంకం αను J = -α θ తో నిర్వచిస్తారు. ఇక్కడ పునఃస్థాపక టార్క్, θ పురి తిప్పిన కోణం)
సాధన:
m = 10 kg; R = 15 cm = 0.15 m;
T = 1.55, a = ?
పళ్లెం జడత్వ భ్రామకం

ప్రశ్న 24.
5 cm కంపన పరిమితి, 0.2 s. డోలనావర్తన కాలంతో ఒక వస్తువు సహచ చేస్తుంది. వస్తువు స్థానభ్రంశాలు (a) 5 cm (b) 3 cm (c) 0 cm అయినప్పుడు దాని త్వరణం, వేగాలను కనుక్కోండి.
సాధన:
ఇక్కడ r = 5 cm = 0.05 m; T = 0.25 సెకన్;
ω = \(\frac{2 \pi}{T}=\frac{2 \pi}{0.2}\)
= 10π rad/s
స్థానభ్రంశం y అయితే త్వరణం A = -ω²y
వేగం V = ω\(\sqrt{{r^2}-{y^2}}\)

సందర్భం (a) : y = 0.05 m = 0.05 m
A = -(10π)² × 0.05
= -5π² m/s²
V = 10π \(\sqrt{{(0.05)^2}-{(0.05)^2}}\) = 0

సందర్భం (b) : y = 3 cm = 0.03 m
A = -(10π)² × 0.03
= -3π² m/s²
V = 10π × \(\sqrt{{(0.05)^2}-{(0.03)^2}}\)
= 10π × 0.04
= 0.4π m/s

సందర్భం (c) : y = 0,
A = −(10π)² × 0 = 0
V = 10π \(\sqrt{{(0.05)^2}-{0^2}}\)
= 10π × 0.05
= 0.5π m/s.

ప్రశ్న 25.
క్షితిజ సమాంతరంగా ఉండే స్ప్రింగ్ స్వేచ్ఛా చివరన కట్టిన ద్రవ్యరాశి, తలంపై ఎలాంఇ ఘర్షణ లేదా అవరోధం లేనప్పుడు ఆకోణీయ వేగంతో స్వేచ్ఛా డోలనాలు చేస్తుంది. t = 0 కాలం వద్ద ద్రవ్యరాశిని ×, దూరం లాగి కేంద్రం వైపు v₀ వేగంతో నెట్టినప్పుడు కలిగే ఫలత డోలనాల కంపన పరిమితిని ω, x₀, y₀ పదాలలో కనుక్కోండి. (సూచన:x = a cos (ωt + θ) సమీకరణంతో ప్రారంభించండి. తొలివేగం రుణాత్మకం అని గమనించండి.
సాధన:
x = A cos (ωt + θ)

సాధించిన సమస్యలు (Solved Problems)

ప్రశ్న 1.
మానవ గుండె, సగటు స్పందనరేటు నిమిషానికి 75. గుండె పౌనఃపున్యం, ఆవర్తన కాలాలను లెక్కించండి.
సాధన:
గుండె స్పందన పౌనఃపున్యం = 75/(1 min)
= 75/(60 s)
= 1.25 s^-1
= 1.25 Hz

ఆవర్తన కాలం, T = 1/(1.25 s^-1)
= 0.8 s.

ప్రశ్న 2.
కింది ఏ కాల ప్రమేయాలు (a) ఆవర్తనం (b) ఆవర్తనం కాని చలనాలను సూచిస్తాయి. ఆవర్తన చలనం ప్రతి సందర్భానికి ఆవర్తన కాలాన్ని తెలపండి. [ω ఏదైనా ధన స్థిరాంకం]
(i) sin ωt + cos ωt (ii) sin ωt + cos 2 ωt + sin 4 ωt (iii) e^-ax (iv) log (ωt).
సాధన:
i) sin ωt + cos ωt ఆవర్తన ప్రమేయం. దీన్ని

ii) ఇది ఆవర్తన చలనానికి ఒక ఉదాహరణ. ఇందులోని ప్రతి పదం వేరువేరు కోణీయ పౌనఃపున్యాలతో ఉండే ఆవర్తన ప్రమేయాన్ని సూచిస్తుంది. ప్రమేయం పునరావృతం అయ్యే కనిష్ట కాలవ్యవధి ఆవర్తన కాలం కాబట్టి sin ωt ఆవర్తన కాలం T_o = \(\frac{2 \pi}{\omega}\), cos 2 ωt ఆవర్తన కాలం \(\frac{\pi}{\omega}=\frac{T_0}{2}\), sin 4 ωt ఆవర్తన కాలం \(\frac{2 \pi}{4 \omega}=\frac{T_0}{4}\).

మొదటి ఆవర్తన కాలం, చివరి రెండు పదాల ఆవర్తన కాలాల గుణిజం అవుతుంది. కాబట్టి మూడు పదాల మొత్తం పునరావృతం అయ్యే కనిష్ఠ కాలవ్యవధి T_o. అందువల్ల మూడు పదాల మొత్తం ఆవర్తన కాలం \(\frac{2 \pi}{4 \omega}\)తో ఒక ఆవర్తన ప్రమేయం.

iii) ప్రమేయం e^-ωt ఆవర్తన ప్రమేయం కాదు. కాలం t విలువ పెరిగేకొద్దీ ప్రమేయం విలువ ఏకదిష్టంగా (monotonically) తగ్గుతుంది. t → ∞ అయ్యేకొద్దీ ప్రమేయం శూన్యం అవుతుంది. కాబట్టి ప్రమేయం దాని విలువను ఎప్పటికీ పునరావృత్తం చేయదు.

iv) log (ωt) ప్రమేయం కాలం tతో ఏకదిష్టంగా పెరుగుతుంది. కాబట్టి ఇది ఎప్పటికీ తన విలువను పునరావృతం చేయదు. ఆవర్తనం కాని ప్రమేయం కాబట్టి t → ∞ అయ్యేకొద్దీ log (ωt) అనంతానికి అపసరణం (diverges) చెందుతుంది. ఇది ఏరకమైన భౌతిక స్థానభ్రంశాన్ని సూచించదు.

ప్రశ్న 3.
కింది కాల ప్రమేయాల్లో ఏది (a) సరళ హరాత్మక చలనం (b) ఆవర్తన చలనమే కాని సరళ హరాత్మక చలనం కాదు. రెండు సందర్భాల్లో ఆవర్తన కాలాలను తెలపండి.
(a) sin ωt – cos ωt (b) sin² ωt
సాధన:
a) sin ωt – cos ωt = sin ωt – sin (π/2 – ωt)
= 2 cos (π/4) sin (ωt – π/4)
= √2 sin (ωt – π/4)

పై సమీకరణం ఆవర్తన కాలం T = 2π/ω దశా కోణం (-π/4) లేదా (7π/4)తో ఉండే సరళ హరాత్మక చలనాన్ని సూచిస్తుంది.

b) sin² ωt = \(\frac{1}{2}-\frac{1}{2}\) cos 2 ωt
ఇది ఆవర్తన కాలం T = π/ω తో ఉండే ఆవర్తన చలనాన్ని సూచిస్తుంది. ఇది O వద్ద కాక \(\frac{1}{2}\) వద్ద సమతాస్థితి స్థానాన్ని కలిగి ఉండే హరాత్మక చలనాన్ని కూడా సూచిస్తుంది.

ప్రశ్న 4.
కింది పటాలు రెండు వృత్తాకార చలనాలను సూచిస్తున్నాయి. వృత్త వ్యాసార్థం, పరిభ్రమణ కాలం, తొలి స్థానం, చలన దిశలు పటంలో సూచించినట్లు ఉన్నాయి. వృత్తాకార చలనం చేసే కణం P వ్యాసార్ధ సదిశ x- విక్షేపం యొక్క సరళ హరాత్మక చలనాలను రెండు సందర్భాల్లో రాబట్టండి.

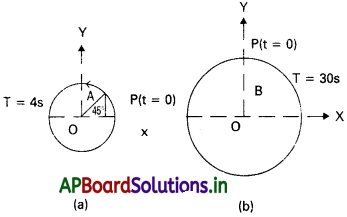
సాధన:
a) t = 0 వద్ద OP, ధన x-అక్షంతో 45° = \(\frac{2 \pi}{\lambda}\) రేడియన్ కోణం చేస్తుంది. t కాలం తరువాత అపసవ్యదిశలో OP పొందే కోణీయ స్థాన భ్రంశం \(\frac{2 \pi}{T}\) t.t తరువాత x-అక్షంతో చేసే కోణం \(\frac{2 \pi}{T}\)t + \(\frac{2 \pi}{4}\) t సమయం వద్ద x-అక్షం పై OP యొక్క విక్షేపం

ప్రశ్న 5.
కింది ఇచ్చిన సమీకరణాల (SI ప్రమాణాలలో) నికి అనుగుణంగా ఒక వస్తువు సరళ హరాత్మక చలనం చేస్తుంది. X = 5 cos [2πt + π/4]. t = 1.5 s వద్ద వస్తువు (a) స్థానభ్రంశం, (b) వడి, (c) త్వరణాలను లెక్కించండి.
సాధన:
వస్తువు కోణీయ పౌనఃపున్యం ) = 2πs^-1 ఆవర్తన కాలం T = 1s.
t = 1.5 s వద్ద

a) స్థానభ్రంశం
= (5.0 m) cos [(2πs^-1) × 1.5 s + π/4]
= (5.0 m) cos [(3π + π/4)]
=-5.0 × 0.707 m.
= -3.535 m

b) సమీకరణం (8.9) ని ఉపయోగించి, వస్తువు వడి
= -(5.0 m) (2πs^-1) sin [(2πs^-1) × 1.5 s + π/4]
= -(5.0 m) (2πs^-1) sin [(3π + π/4)]
= 10π × 0.707 ms^-1
= 22 ms^-1

c) సమీకరణం (8.10) ని ఉపయోగించి, వస్తువు
= – (2π s^-1)² × స్థానభ్రంశం
= -(2π s^-1)² × (-3.535 m)
= 140 ms^-2.

ప్రశ్న 6.
పటం 8.14 లో చూపిన విధంగా, K స్ప్రింగ్ స్థిరాంకం గల రెండు సర్వసమానమైన స్ప్రింగ్లను m ద్రవ్యరాశి గల దిమ్మెకు జోడించి, వాటి మిగతా రెండు చివరలను స్థిర ఆధారాలకు బిగించారు. దిమ్మెను సమతాస్థితి స్థానం నుంచి ఎటువైపు స్థానభ్రంశం చెందించినా అది సరళ హరాత్మక చలనం చేస్తుందని నిరూపించండి.

సాధన:
పటం 8.15 లో చూపినట్లు దిమ్మెను సమతాస్థితి స్థానం నుంచి కుడివైపుకు × దూరం స్థానభ్రంశం చెందిస్తే ఎడమవైపు స్ప్రింగ్ × దూరం సాగితే కుడివైపు స్ప్రింగ్ × దూరం సంపీడనం చెందుతుంది.

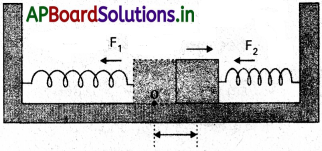
దిమ్మెపై పనిచేసే బలాలు

F₁ = -kx (దిమ్మెను మాధ్యమిక స్థానంలోకి తెచ్చేందుకు ఎడమవైపు స్ప్రింగ్ దిమ్మెను లాగే బలం)
F₂ = -kx (దిమ్మెను మాధ్యమిక స్థానంలోకి తెచ్చేందుకు కుడివైపు స్ప్రింగ్ దిమ్మెను నెట్టే బలం) దిమ్మెపై పనిచేసే నికర బలం
F = -2kx
దిమ్మెపై పనిచేసే బలం స్థానభ్రంశానికి అనులోమాను పాతంలో ఉండి మాధ్మమిక స్థానంపైపు పనిచేయడం వల్ల దిమ్మె చలనం సరళ హరాత్మక చలనం. దిమ్మె డోలనావర్తన కాలం
T = 2π\(\sqrt{\frac{m}{2k}}\)

ప్రశ్న 7.
8.750 Nm^-1 స్ప్రింగ్ స్థిరాంకం గల ఒక స్ప్రింగ్కు 1 kg ద్రవ్యరాశి దిమ్మెను బిగించారు. x = 0 వద్ద సమతాస్థితి స్థానం నుంచి t = 0 వద్ద విరామస్థితిలో గల దిమ్మెను x = 10 cm దూరం వరకు ఘర్షణ లేని తలంపై లాగితే మాధ్యమిక స్థానం నుంచి 5 cm దూరంలో దిమ్మె ఉన్నప్పుడు దాని గతిజ, స్థితిజ, మొత్తం శక్తులను లెక్కించండి.
సాధన:
సరళ హరాత్మక చలనం చేసే దిమ్మె కోణీయ పౌనః పున్యం సమీకరణం (8.14b) నుండి

ఏదైనా కాలం t వద్ద దిమ్మె స్థానభ్రంశం
x(t) 0.1 cos (7.07t)
కాబట్టి దిమ్మె మాధ్యమిక స్థానం నుంచి 5cm దూరంలో ఉన్నప్పుడు
0.05 = 0.1 cos (7.07t)
లేదా cos (7.07t) = 0.5
∴ sin (7.07t) = \(\frac{\sqrt{3}}{2}\) = 0.866
x = 5 cm వద్ద దిమ్మె వేగం
= 0.1 × 7.07 × 0.866 ms^-1
= 0.61 ms^-1

∴ దిమ్మె గతిజ శక్తి K.E = \(\frac{1}{2}\)mv²
= \(\frac{1}{2}\)[1kg × (0.6123 ms^-1)²]
= 0.19 J

దిమ్మె స్థితిజ శక్తి P.E.
= \(\frac{1}{2}\)kx²
= \(\frac{1}{2}\)(50 Nm^-1 × 0.05 m × 0.05 m)
= 0.0625 J

x = 5 cm వద్ద దిమ్మె కలిగి ఉండే మొత్తం శక్తి
= K.E. + P.E.
= 0.25 J

గరిష్ఠ స్థానభ్రంశం వద్ద గతిజశక్తి (K.E) శూన్యం కాబట్టి అక్కడ మొత్తం శక్తి స్థితిజ శక్తి (P.E)కి సమానం అని మనకు తెలుసు కాబట్టి వ్యవస్థ మొత్తం శక్తి
= \(\frac{1}{2}\)(50 Nm^-1 × 0.1 m × 0.1 m)
= 0.25 J

ఇది 5 cm స్థానభ్రంశం వద్ద ఉండే మొత్తం శక్తికి సమానం కాబట్టి శక్తి నిత్యత్వ నియమానికి అనుగుణ్యంగా ఉందని తెలుస్తోంది.

ప్రశ్న 8.
8.8 500 Nm^-1 బల స్థిరాంకం గల స్ప్రింగ్కు 5 kg ద్రవ్యరాశి గల లోహ కంకణాన్ని (ring) బిగించారు. క్షితిజ సమాంతరంగా ఉండే కడ్డీపై ఘర్షణ లేకుండా కంకణం జారుతుంది. మాధ్యమిక స్థానం నుంచి కంకణాన్ని 10.0cm లాగి వదిలారు. అయితే కంకణం
(a) డోలనావర్తన కాలం (b) గరిష్ట వడి (c) గరిష్ఠ త్వరణాలను లెక్కించండి.
సాధన:
a) సమీకరణం (8.21) నుంచి డోలనావర్తన కాలం

b) సరళ హరాత్మక చలనం చేసే కంకణం వేగం
v(t) = -Aω sin (ωt + Φ)
గరిష్ఠ వడి
v_m = Aω

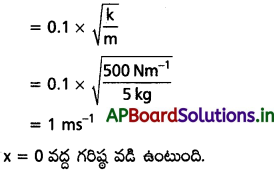
c) మాధ్యమిక స్థానం నుంచి x(t)స్థానభ్రంశం వద్ద కంకణం త్వరణం
a(t) = -ω²x(t)

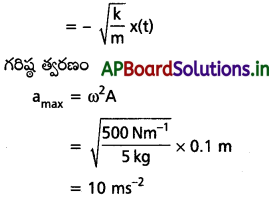
ఇది అంత్యస్థానాల వద్ద ఉంటుంది.

ప్రశ్న 9.
8.9 సెకండులను టికే చేసే లఘులోలకం పొడవు ఎంత?
సాధన:
లఘు లోలకం డోలనావర్తన కాలం
T = 2π \(\sqrt{\frac{L}{g}}\)
దీని నుంచి కింది విధంగా రాయవచ్చు.

ప్రశ్న 10.
8.10 పటం 8:19 లో చూపిన అవరుద్ధ డోలకంలో దిమ్మె ద్రవ్యరాశి (m) 200 g, k = 90 Nm^-1 అవరోధ స్థిరాంకం b విలువ 40 gs^-1 అయితే (a) డోలనావర్తన కాలం, (b) కంపన పరిమితి తొలి కంపన పరిమితిలో సగం అయ్యేందుకు పట్టేకాలం, (c) యాంత్రిక శక్తి తొలి విలువలో సగం అయ్యేందుకు పట్టే కాలాలను లెక్కించండి.
సాధన:
a) km = 90 × 0.2 = 18 kg Nm^-1 = kg² s^-2;
కాబట్టి √km = 4.243 kg s^-1, b = 0.04 kg s^-1
అంటే b విలువ √km కంటే చాలా తక్కువ. కాబట్టి సమీకరణం (8.34) నుంచి డోలనావర్తన కాలం.

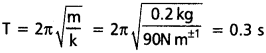
b) సమీకరణం (8.33) నుంచి కంపన పరిమితి తొలి విలువలో సగం అయ్యేందుకు పట్టే కాలం T_1/2 అయితే

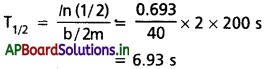
c) యాంత్రిక శక్తి తొలి విలువలో సగం అయ్యేందుకు పట్టే కాలం t_1/2 ని లెక్కించేందుకు సమీకరణం (8.35)ని ఉపయోగిస్తాం.
= E(t_1/2)/E(0) exp (-bt_1/2/m)
లేదా \(\frac{1}{2}\) = exp (-b_1/2/m)
ln (1/2) = −(bt12/m)
లేదా t_1/2 = \(\frac{0.693}{40 gs^{-1}}\) × 200g
= 3.46 s